In this section we present the main results starting with how firms use information in a given network. Then we study information sharing first in the case of homogeneous signals (with and without side payments and linking costs) and then we move to the case of heterogeneous signals that allow more complex equilibrium architectures.
3.1. Bayesian Cournot Equilibrium for a Given Network
By standard results on linear Cournot games with incomplete information (see Radner (1962)), equilibrium strategies are affine in signals, that is:
where
is the constant term of the equilibrium strategy of firm
i, and by
the coefficient applied by firm
i to each element
of the vector
.
Proposition 1. Equilibrium parameters are defined by the following set of equations: The proof this and all other results of the paper can be found in the
Appendix A. We first note that the
parameters are defined by an independent set of equations, and that they do not depend on the network
g. Since the expected values of all signals is zero, this implies that the expected aggregate quantity is the same in each network.
We then observe that the expression for the terms
has intuitive interpretations that highlight the role of the network in shaping equilibrium behaviour. The term
(measuring the reaction of firm
i to the observed signal
) is determined by the use that firm
i makes of signal
to estimate the intercept minus a term that measures the use that other firms make of signal
, that is, firm
i reacts less to signal
the more numerous are the firms that observe
and base their decisions on it. Intuitively, the information provided by signal
is more valuable the less it is observed by other firms—a clear congestion effect on which we will return in the next sections. From (
5) we note that for each
j, the equilibrium coefficients applied to signal
by the firms in
are determined by an independent set of identical equations, so that
for all
i and
h in
. From (
6)
for all
. These considerations are summarised in the following corollary.
Corollary 1. Equilibrium parameters are: We finally determine expected equilibrium profits in
. The following result relates the expected profits of a firm to its equilibrium quantity (see Proposition 1 in [
14]).
Lemma 1. Ex-ante expected profits of firm i in the game are given by: Since
is a square of a linear function in
(i.e., Equation (
4)), using the assumption of signals independence and Corollary 1, it follows that ex-ante profits are given by a constant term plus a term that is proportional to the variance of the equilibrium quantities.
Corollary 2. Ex-ante profits are of firm i in the game are given by: Note that the summatory represents the variance of the equilibrium quantities multiplied by parameter b. Therefore the ex-ante profits of firm i are increasing with the variability of its strategy. It directly follows that the difference in ex-ante profits in two different networks is measured by the difference in the variance of equilibrium quantities.
3.2. Information Sharing When Signals Are Homogeneous
Here we assume that signals have the same variance. For this case the next proposition states necessary and sufficient conditions for a network to be pairwise stable.
Proposition 2. A network g is pairwise stable if and only if both of the following conditions are verified.
The intuition behind conditions (
10)–(
13) can be explained as follows. Conditions (
10) and (
11) require that no link in a stable network is severed. On the LHS of (
10) is the loss to firm
i from severing the link
in terms of
i’s equilibrium quantity’s variance; this is measured by the variability of firms
i’s strategy with respect to signal
(see Lemma 1), normalised by the number of firms that see signal
(the larger this number, the less valuable is signal
). This loss in expected profits has to be larger than the gain from severing link
(RHS); this is measured as the increase in the “value” of signal
, which in case of severance of link
is observed by one less firm. Condition (
11) requires the same for
j. Conditions (
12) and (
13) requires that no link is added to a stable network. On the LHS of (
12) is the gain to firm
i from forming the new link in terms of the variability of firm
i’s strategy with respect to the newly acquired signal
; on the RHS is the net loss in variability due to the fact that one additional firm (firm
j) observes signal
. If the LHS exceeds the RHS for firm
i, then the reverse must hold for firm
j (condition (
13)).
Note that the incentives to form or sever link
only depend on the degrees of the nodes
i and
j, and on no other features of the network. In particular, the gain in profit due to a link with node
j decreases with the degree of
j. It is indeed possible to determine two thresholds in the degree of a node
j: the value
above which a node
i of degree
would not maintain the link
that is, if
condition (
10) is not satisfied; the value
above which a node
i of degree
would not form the new link
; that is, if
inequality (
12) is not satisfied. These thresholds are formally defined in Lemma A1 in the
Appendix A, where we show, together with other properties, that both
F and
f are increasing in
, meaning that the incentives of node
i to link with a given node
j increase with the degree of
i.
The next proposition fully characterises the set of pairwise stable networks for the case of i.i.d. signals.
Proposition 3. Let . The set of pairwise stable networks contains: the empty network, the complete network, and all networks made of isolated nodes and completely connected components of size such that for all .
The set of pairwise stable networks characterised in Proposition 3 is very large. However, Proposition 3 provides two precise qualitative predictions on how information is shared in equilibrium. First, information sharing is essentially organised in
groups (the completely connected components), within which the transmission of information is equivalent to one in which firms publicly disclose their signal to all other firms in the group. This type of public disclosure characterises all previous works on the subject, and is here obtained endogenously as a result of private and bilateral arrangements. Second, information sharing groups must be of different size, to make sure that firms in different groups do not form links (in fact, from point
3.d in Lemma A1 in the
Appendix A, firms with similar degree link together).
Now we study two extensions: in the first we allows for side-payments, in the second we impose an exogenous link cost.
3.2.1. Side-Payments
The above definition of pairwise stability implicitly rules out the possibility of side payments between firms which are contingent on the sharing of information. In the presence of such transfers, conditions (
2) and (
3) would be replaced by the following condition (see [
1]):
We obtain a more narrow prediction for the case in which firms can agree on side-payments which are contingent on information sharing. In this case, the formation of links that bridge two components is made easier by the sharing of individual gains, and at most one component of information sharing firms can be compatible with stability.
Proposition 4. When side payments are possible, the set of pairwise stable networks contains: the empty network, the complete network, all networks g made of one completely connected component h of size and isolated nodes.
So far, all stable structures that differ from the empty network only admitted fully connected components.
3.2.2. Costly Links
Now we study the case in which the formation of a link has a fixed and exogenous cost
c, representing all monetary expenditures that a firm bears in order to arrange and execute an information sharing arrangement. Interestingly, in this new setting both market conditions (the slope
b of the demand function) and the variance
of signals turn out to play a role in shaping the incentives of firms to form and sever links. The following new stability conditions are obtained by a minor modification of the proof of Proposition 2: for all
:
A more elastic demand (small
b) provides higher incentives to maintain (and to form) links (this is in line with the intuition that more competitive markets, and therefore a lower strategic interdependence of firms, facilitate information sharing—see [
15]). These incentives also increase with the variance
, which has the effect of scaling up the informational gain of new connections. It will be convenient to refer to the gross cost parameter
, and refer to the single elements of
C only when these provide interesting economic insights.
An interesting question is whether incomplete and stable components can emerge, and, in this case, of which size. For all
, let
be the value above which a node
i of degree
would not form the new link
; that is, if
condition (
18) is not satisfied; and let
(
be the first integer above (below) the smaller (larger) solution of
. With this notation we can state the following proposition.
Proposition 5. Let , then the set of pairwise stable networks contains the empty network and all networks made of isolated nodes and regular components h with . Components h with have the following characteristics: (i) if are fully connected, otherwise have degree equal to ; (ii) each pair of components h, with satisfies .
Proposition 5 basically sets the upper bound on the degree of a stable completely connected component. Although one may be tempted to understand this as a consequence of the large aggregate cost paid in completely connected components of large size, this is not the case. Indeed, here the decision to sever or maintain a given link only depends on the comparison between the change in payoffs and the marginal cost c. What drives the existence of the upper bound is, instead, the fact that the incentives to maintain a link are decreasing in the degree of the nodes, and larger components fail to be stable as a result. There is therefore an inverse relation between the density of a component (ratio between average degree and size) and its size.
3.3. Sharing Heterogeneous Signals in Core-Periphery Networks
In this section we relax the assumption that signals are identically distributed, and allow the variances of signals (i.e., the parameters ) to differ across firms. The stability conditions of Proposition 2 are modified to account for this new source of heterogeneity: the network g is pairwise stable if and only if:
We see that, given the degrees
and
, the incentive of
i to sever the link
increases with the ratio of variances
(conditions (
20) and (
21)) and the incentive of
i to form the link
decreases with
(condition (
22)). This effect can be understood in terms of the additional variability of
i’s equilibrium quantity coming from the link
. The higher the term
, the higher the additional variability of
i’s quantity due to the link
, and the higher the informational “ value” of
j’s signal for firm
i. Similarly, the higher the term
, the lower the incentive of firm
i to form the link
; this because it is more costly to share a signal with higher variance with one additional firm. Again, a high value of
reflects therefore a high informational value of
i’s signal.
Note that in this setting of heterogeneous variance, a firm with high variance may not wish to maintain a link (or to form a new one) with another firm with same degree but lower variance. As a consequence, while the empty network is always a pairwise stable information structure (as was proved for the case of i.i.d. signals), the complete network may fail to be stable when firms have significant heterogeneity in variances. However, as the next proposition shows, this can only happen when the number of firms is small.
Proposition 6. (1) The empty network is pairwise stable for all distributions of variances, even if side payments are possible; (2) There exist configurations of variances for which the complete network is not pairwise stable; (3) For every configuration of variances, there exists a finite number of firms such that for all the complete network is pairwise stable.
While we refer to the
Appendix A for details, the intuition of this result is clear: when the degree of two nodes increases, their difference in variances becomes less and less relevant in the stability conditions (
20) and (
21).
We next turn to the existence of pairwise stable networks with non completely connected components. Since signals with large variance possess higher informational value, the incentive to link to firms observing such signals may remain high even when these firms have a large degree. We can therefore envisage stable architectures in which firms with large variance have larger degree than firms with low variance. We show that a special class of incomplete architectures, usually referred to as “core-periphery networks”, can be pairwise stable for suitable distributions of variances. In more detail, core periphery networks present a dense set of interconnected nodes—the core—each linked with all nodes in the network, and sets of peripheral nodes which are internally connected and are linked with the core nodes. Formally, a core-periphery network g consists of a set of fully connected subnetworks, such that and implies that for all such that and , and such that and implies for all . We call the subnetwork core (with size ), and the subnetworks peripheries. We define a symmetric core-periphery network as one in which all peripheral firms have the same size . We also say that peripheries are consecutive in variances if they can be obtained as a consecutive partition of the set of peripheral nodes ordered with respect to variance.
Proposition 7 provides two qualitative features of pairwise stable symmetric core-periphery networks: peripheral firms are organised in groups that are consecutive in variance, and core firms have larger variance than peripheral firms.
Proposition 7. Every symmetric pairwise stable core periphery network is such that peripheries are consecutive in variances. Moreover, for each given size , there exists a finite such that if then every symmetric pairwise stable core periphery network is such that .
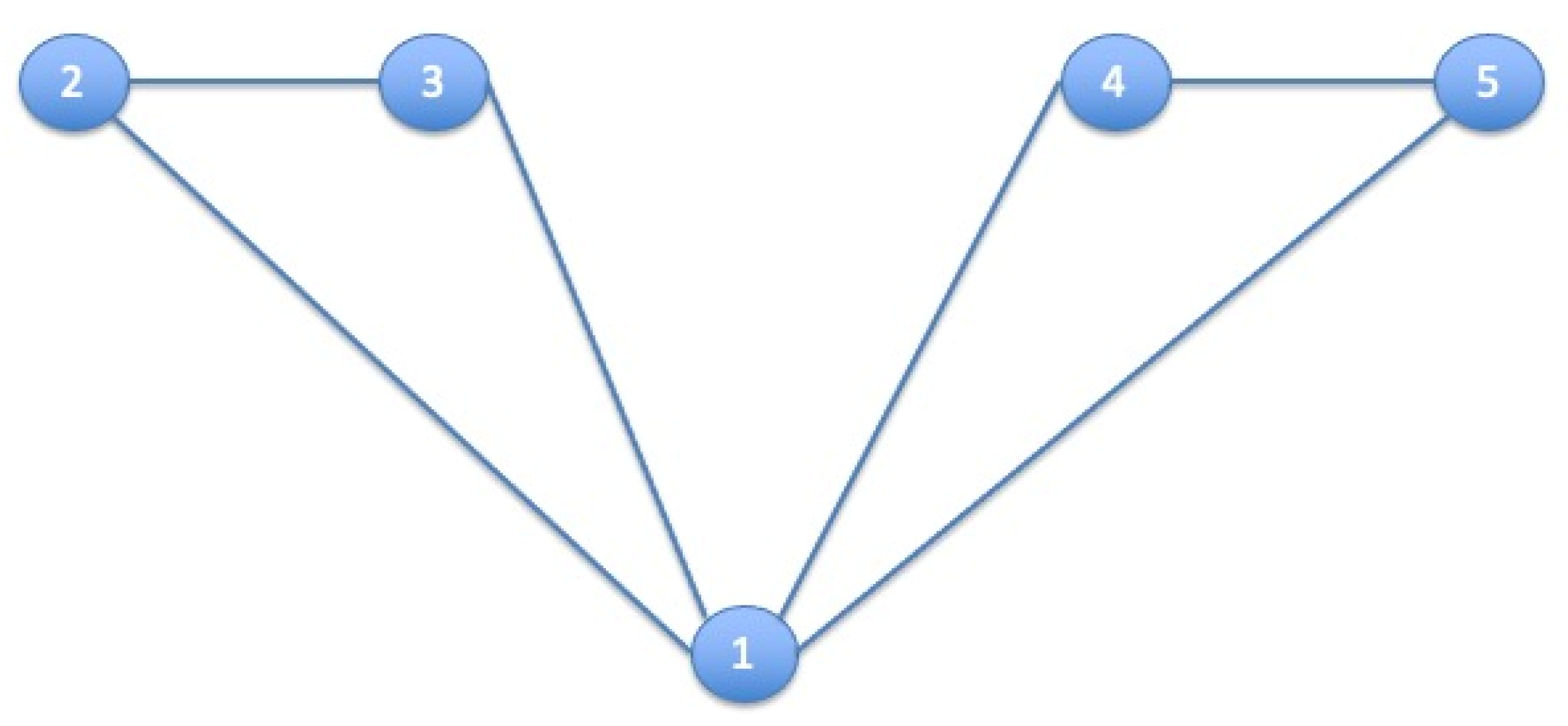
Intuitively, core firms observe signals that are publicly observed, and have therefore lower informational value. These signals are more“desirable” the larger their variance, from which the second result in Proposition 7. An example of pairwise stable core periphery network is the following (see
Figure 1).
Example 1. Consider a network with 5 nodes: node 1 is the “core” node, while the two peripheries are and . Variances are , , . Relevant stability conditions (20)–(23) (for links 12, 15 and 34, respectively) are satisfied: