Abstract
Hierarchical decision-making processes traditionally modeled as bilevel optimization problems are widespread in modern engineering and social systems. In this work, we deal with a leader with a population of followers in a hierarchical order of play. In general, this problem can be modeled as a leader–follower Stackelberg equilibrium problem using a mathematical program with equilibrium constraints. We propose two interconnected dynamical systems to dynamically solve a bilevel optimization problem between a leader and follower population in a single time scale by a predictive-sensitivity conditioning interconnection. For the leader’s optimization problem, we developed a gradient descent algorithm based on the total derivative, and for the followers’ optimization problem, we used the population dynamics framework to model a population of interacting strategic agents. We extended the concept of the Stackelberg population equilibrium to the differential Stackelberg population equilibrium for population dynamics. Theoretical guarantees for the stability of the proposed Stackelberg population learning dynamics are presented. Finally, a distributed energy resource coordination problem is solved via pricing dynamics based on the proposed approach. Some simulation experiments are presented to illustrate the effectiveness of the framework.
1. Introduction
Hierarchical decision-making processes, where a leader is making decisions affected by the response of the follower(s), are widespread in modern engineering and social systems. Hierarchical decision-making structures or leader–follower problems appear in diverse domains of applications such as terrorism analysis [1], communications and network security [2], traffic management [3], smart grids [4,5,6], machine learning [7], and market systems [8]. A particular promising application domain is the intersection between machine learning and game theory to model hierarchical interactions between learning agents. Classic simultaneous play games have been extended to problems in machine learning such as robust supervised learning [9] or generative adversarial network [10] and, most recently, in multiagent system (MAS) reinforcement learning [11]. For hierarchical machine-learning approaches based on game theory, just a few works have been proposed. A couple of relevant contributions can be found in [12], where a gradient descent with time scale separation was proposed, and in [7], where Stackelberg learning dynamics was developed; both works focused on a leader with a single follower.
Traditionally, hierarchical decision-making processes have been modeled as bilevel optimization problems, which can be classified into two main theoretical domains [13]. On the one hand are models based on game theory [14], which have used bilevel programming methods to develop the concept of Stackelberg equilibria. On the other hand is mathematical programming, which proposed a first attempt to solve bilevel optimization problems as an upper-level optimization problem with a lower-level optimization problem as a constraint [15]. Considering its nested nature, bilevel optimization problems have challenged the optimization and mathematical community ever since; they have been proven to be strongly NP-hard [16], and even the evaluation of the optimality of a solution is NP-hard [17,18]. Recent critical literature reviews recount the historical developments and current perspectives of the field [13,19,20].
In this work, we deal with a leader with a population of followers in a hierarchical order of play. In general, this problem can be modeled as a leader–follower Stackelberg equilibrium problem using a mathematical program with equilibrium constraints (MPEC) [21]. Some applications of this modeling have been recently proposed [22,23,24,25]. A preliminary MPEC model for a multiple leaders with multiple followers game was presented in [22]. A discrete-time iterative algorithm was proposed to compute a Stackelberg–Nash saddle-point in a leader with multiple followers problem. In [24], a Stackelberg differential game based on pricing for the bandwidth usage of the Internet was solved. Finally, a semi-decentralized algorithm was formulated to compute a local solution to the leader with multiple followers Stackelberg aggregate game in [25]. On the other hand, for power system applications, there is an emerging market-based control approach called transactive energy systems (TESs) [26,27,28]. This method is based on a privacy-preserving, market-based framework for the management of devices exchanging energy [6,29]. Hierarchical decision-making modeling has been studied as a cornerstone in this framework, where a coordinator agent is responsible for solving the market-clearing price of the distribution network. In several scenarios, the control signal of the leader agent or coordinator is not a price, but a pricing function depending on the preferences of the follower agents forming a reverse Stackelberg game [30,31]. Considering the multiple applications based on hierarchical decision-making structures, we propose a Stackelberg game learning framework to solve bilevel optimization problems as a dynamical system in a single time scale. In this paper, we focus on a single leader with a follower population of agents due to the motivation of the coordinator agent problem in TESs. For the upper-level optimization problem, we propose gradient descent dynamics in continuous-time [32,33], and for the lower-level optimization problem, we propose population games dynamics based on the replicator dynamics [34,35], in order to obtain two nested dynamical systems. This allows us to bring theoretical tools from the dynamical system theory for the design of algorithms to solve optimization problems. In contrast with traditional time scale separation methods for interconnected dynamical systems such as singular perturbation analysis [36], we used predictive-sensitivity conditioning [37,38] to integrate the two interconnected dynamical systems in a single time scale to guarantee the stability and convergence of the solution to a differential Stackelberg population equilibrium.
The main contribution of this paper is threefold. First, we propose two interconnected dynamical systems to dynamically solve a bilevel optimization problem between a leader and follower population in a single time scale by a predictive-sensitivity conditioning interconnection [37]. For the leader optimization problem, we developed a gradient descent algorithm based on the total derivative using the implicit function theorem [39]. For the follower MAS optimization problem, we used the population dynamics framework to model MAS interacting strategic agents, as shown in [34,35,40,41,42] and the reference therein. We extended the concept of the Stackelberg population equilibrium [43] to the differential Stackelberg population equilibrium for population dynamics. Second, theoretical guarantees for the stability of the proposed Stackelberg population learning dynamics are presented. Finally, a distributed energy resource (DER) coordination problem was solved via pricing dynamics based on the proposed approach. Some simulation experiments are presented to illustrate the effectiveness of the framework.
The rest of the paper is organized as follows. In Section 2, the formulation of the bilevel optimization problem and the main concepts of Stackelberg equilibria are introduced. Section 3 presents the population game’s essential concepts, and the Stackelberg population learning dynamics is developed based on the predictive-sensitivity conditioning interconnection. Stability results are established to guarantee the convergence of the proposed dynamics. In Section 4, an application of the proposed framework is developed for DER coordination. Finally, the main conclusions are drawn in Section 5.
2. Stackelberg Games and Bilevel Optimization Problems
In this section, we introduce a general formulation of a noncooperative game between an agent called a leader and a finite set of agents called followers. In this case, we have a Stackelberg game with multiple followers, where the leader plays first and then the followers make their decision. This Stackelberg game can be modeled by a bilevel optimization problem. Traditionally, the leader’s optimization problem is referred to as the upper-level problem, and the followers’ optimization problem is referred as the lower-level problem. Each level has its own set of variables, constraints, and objective functions, and the upper-level problem has as a constraint the lower-level problem:
where is the upper-level variable, are the lower-level variables, is the objective function of the leader agent, and is the objective function of the followers. It was assumed that each follower has an objective function with , and then, without loss of generality, we assumed that the global objective function is:
Let us recall the main equilibrium concept studied in hierarchical play games: consider one leader agent and one follower agent .
Definition 1
(Local Stackelberg equilibrium (SE)). Let Λ be the set of strategies for the leader agent and Xf be the set of strategies for the follower agent. Let BRf (λ) be the best response function for the follower defined as:
A leader strategy and a follower strategy are in Stackelberg equilibrium if the following conditions hold:
- (a)
- ;
- (b)
- .
The local notions of the equilibrium concepts are preferred since it is standard in population games where the concavity or convexity is not assumed in the objective functions.
Some assumptions have to be considered to assure the optimality and existence of the solutions to Problem (1) such as the connectivity of the communication graph and the regularity of objective functions.
Assumption 1.
The communication graph connecting each agent of the system such as the leader and follower population agents is connected.
Assumption 2.
Every objective function and is assumed to be differentiable everywhere and with Lipschitz continuous partial derivatives, and the Hessian matrices and are globally invertible.
Local solutions’ concepts and first- and second-order necessary and sufficient conditions for bilevel optimization problems [19] are needed to establish the Stackelberg population flow with predictive-sensitivity conditioning in the next section.
Definition 2.
A point is said to be a local solution to the bilevel optimization problem (1) if:
- (a)
- is a local minimum of ;
- (b)
- There exists a neighborhood of such that for all local solutions such that is a local minimum of .
Lemma 1
(First-order optimality conditions). If is a local solution of Problem (1), then it is a stationary point satisfying the first-order Karush–Kuhn–Tucker (KKT) conditions:
For a given , Assumption 2 guarantees that the lower-level problem in (1) has at most a single optimal solution satisfying the first-order optimality conditions in Lemma 1 of the lower-level . The implicit function theorem [39] guarantees the local existence of the optimal solution function , and its derivative is obtained as:
In addition, this optimal solution function can be used to give an expression for the directional derivative, also known as the total derivative in points and defined as:
Here, stands for the vector or matrix transpose.
Lemma 2
(Second-order optimality conditions). If a stationary point satisfies:
then is a local solution of the bilevel optimization Problem (1).
The second-order total derivative can be deduced similarly as the first-order (4) as follows,
The following definition introduces the differential versions of the Nash and Stackelberg equilibria [7].
Definition 3
(Differential Nash equilibrium (DNE)). The joint strategy is a differential Nash equilibrium if , , , and .
Definition 4
(Differential Stackelberg equilibrium (DSE)). The joint strategy is a differential Stackelberg equilibrium if the total derivative , , , and .
In the next section, we present the main contribution of this work using the concept introduced above.
3. Stackelberg Population Games with Predictive-Sensitivity Conditioning
In this section, we show how the bilevel optimization problem in two time scales can be solved in a single time scale using an interconnection based on a predictive-sensitivity matrix of two dynamical systems in continuous-time, namely a gradient descent and population dynamics. First, the basic concepts of population games are introduced. Thus, the definitions and results for Stackelberg population games are derived. Finally, the interconnection using the predictive-sensitivity matrix for Stackelberg population games is shown.
3.1. Population Games’ Essentials
Population games have been proposed as a multiagent model to find the Nash equilibrium for a large set of agents or a population. The main dynamical model in population games is the replicator dynamics. Replicator dynamics has been successfully implemented in various engineering applications where real-time adaptation and robustness to dynamic environmental uncertainties is of vital importance [35]. Replicator dynamics represents a mass M of players choosing strategies evolving in time. It is assumed that a finite set of pure strategies , and the analysis is based on a payoff function associated with the selected strategy. The population states are denoted by the vector , and the population states are constrained by all possible distributions of individuals among the strategies given by the simplex:
The agents playing strategy i obtain a reward depending on the population state. A fitness function representing the reward for agents playing strategy i is defined as for . The replicator dynamics is interpreted as an evolutionary game where the proportion of the population of agents playing the most successful strategy (higher payoff than the average) is increasing. Agents dynamically compare their fitness function with the other agents’ performance through the average fitness function of the whole population , also understood as the expected average payoff of the population. The replicator dynamics associated with each population of agents playing the i-th strategy is given by:
As mentioned, the solution concept of the replicator dynamics is an equilibrium, and the Nash equilibrium is the preferred solution concept in population games. Let F be a population game: the Nash equilibrium set is defined as:
All agents obtain the same profit in a Nash equilibrium. An important type of population games is potential games. Potential games can be defined as follows.
Definition 5.
Let be a vector of fitness functions with positive population game payoffs. Let be a continuously differentiable function and the following condition hold,
Then, F is a full potential game.
In potential games, a single scalar-valued function is associated with the game, called the potential function, which retains key information about the payoffs of the agents. If there exists a continuously differentiable potential function , then a potential game satisfies:
and (8) also implies that F must satisfy the external symmetry:
In potential games, the Nash equilibrium is related to local maximizers of potential functions [34]; this is stated in the following lemma.
Lemma 3.
In a full potential game, the Nash equilibrium is equal to the solution of the first-order KKT conditions of the maximizing subject to a feasible set Δ.
Finally, an important result on the stability of population games claims that a population game satisfying (8) is a stable game if the potential function V is concave [34].
3.2. Stackelberg Population Games
One of the main concepts in the design of population games is the selection of the fitness functions such that the replicator dynamics (7) can be used as a distributed optimization algorithm. In order to obtain fitness functions to accomplish a stable and convergent solution, we use the following Lemma 4, which characterizes an optimal solution for the lower-level optimization problem (1) satisfying Assumption 2 [44].
Lemma 4.
A solution of the bilevel optimization problem (1) , with and belonging to the feasible set Δ, is an optimal solution for the population game if and only if for all .
Definition 6.
Let Λ be the set of strategies for the leader agent and be the set of strategies for the follower population. Let the best response function for the follower population be defined as:
A leader strategy and a follower population strategy vector are in a Stackelberg population equilibrium if the following conditions hold:
- (a)
- ;
- (b)
- .
Definition 7
(Differential Stackelberg population equilibrium (DSPE)). The joint strategy is a differential Stackelberg population equilibrium if the following KKT conditions hold:
- (a)
- First-order: , ;
- (b)
- Second-order: , .
For the leader upper-level optimization problem (1), we propose a continuous-time gradient descent flow using the concept of the directional derivative, also known as total derivative obtained following the traditional ideas of gradient dynamics for convex optimization problems [45] as follows:
For the lower-level optimization problem, we propose the follower population game dynamics using the replicator dynamics (7). In order to guarantee the convergence properties of the population games, a full potential game introduced in Definition 5 is chosen using the objective function as the potential function, i.e., . Notice that the potential games are related to maximizing the potential function , and in this case, we seek to minimize, so we convert the problem. With this potential function, we can obtain the fitness function using (8), yielding for each agent i:
and since is separable, then the fitness function for each agent i is:
The average fitness function is then:
With fitness functions for each agent (11) and the average fitness function (12), the replicator dynamics is the lower-level flow as follows:
In compact form, we can define the vector of fitness functions . We obtain the replicator dynamics in compact form as:
We used the notation “·” to indicate an elementwise product between vectors. In this leader–follower population dynamics, we have a nested interaction model in two time scales, which could slow down the convergence of the dynamics. In order to solve these limitations in two time scales, we propose to use the prediction-sensitivity conditioning concept presented in the next section.
3.3. Predictive-Sensitivity for Stackelberg Population Games
In this section, we introduce the predictive-sensitivity conditioning approach to deal with the bilevel optimization problem (1). The regularity introduced in Assumption 2 guarantees that the bilevel problem has at most one solution, and this also ensures that the problem is well posed. Then, it is possible to define the sensitivity of . The main idea is represented in Figure 1, where it is shown that the sensitivity matrix is used to integrate in one single level the dynamics associated with the upper-level by the gradient dynamics (10) and the lower-level by the replicator dynamics (13), respectively.
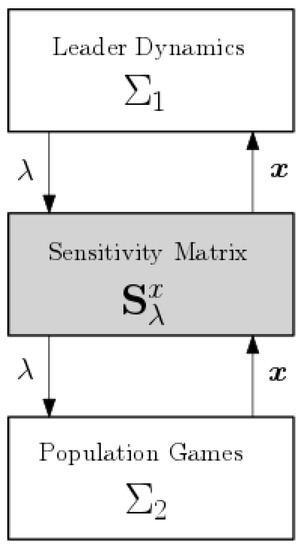
Figure 1.
Predictive-sensitivity conditioning interconnection.
Considering Assumption 2, the analytic expression of (4) is well defined at any point , so defining an extended sensitivity for any point is possible as:
while:
is satisfied. The total derivative using the sensitivity matrix can be extended to any point as:
The two-level interconnected dynamical system represented by and can be integrated into a single time scale using the sensitivity matrix (14) and the total derivative (15). A feed-forward term is added as the predictive-sensitivity conditioning based on the optimization sensitivity to the follower population dynamics (13) to predict the dynamics of the leader gradient descent dynamics (10).
Based on a recent work [37], we used a predictive-sensitivity conditioning interconnection between the two-time-scale systems without the need for the time scale separation. This interconnection preserves the optimal solution and its convergence properties. A sensitivity-based conditioning matrix is used as the interconnection between both subsystems as shown in Figure 1, and it is defined as follows.
Definition 8.
Consider the extended sensitivity defined in (14): the conditioning matrix is defined as:
where I is an identity matrix of the appropriate dimension.
Using Definition 8, we obtain the predictive-sensitivity Stackelberg learning dynamics:
It is observed that the extended sensitivity term modifies the dynamics of the follower population as:
where the first term drives the population state x to the optimal solution , while the predictive-sensitivity feed-forward term anticipates the variation of due to the dynamics . The complete predictive-sensitivity Stackelberg population flow is given by:
In the next result, the relation between the differential Stackelberg population equilibrium concepts defined in Definition 7 and the stability of the predictive-sensitivity Stackelberg population dynamics is established (18).
Theorem 1.
Proof.
Consider that (18) satisfies Assumptions 1 and 2. Since we are proving local stability, it is sufficient to prove that the eigenvalues of the Jacobian of the system at the joint strategy have a strictly negative real part [36]. For this, observe that by Definition 7, if the point is a DSPE, then the second-order conditions are satisfied at this point, and in addition, it has been proven that if the population dynamics are a full potential game, this implies that the Stackelberg follower population (see Definition 6) is asymptotically stable [35], then it is guaranteed that the Jacobian would have a strictly negative part at point . Conversely, if a point of the system (18) is locally exponentially stable, then the corresponding Jacobian must have eigenvalues with a negative real part; thus, it is a strictly local solution satisfying the conditions in Definition 7. □
In the next section, an interesting application to the coordination of distributed energy resources via pricing dynamics is presented to illustrate the theoretical results of the proposed framework.
4. DER Coordination via Pricing Dynamics
A distributed energy resource (DER) coordination problem via pricing dynamics [6] is presented to illustrate the applicability of the proposed predictive-sensitivity Stackelberg learning dynamics. A dynamic transactive control involving a feedback loop is implemented to solve a bilevel optimization problem via a pricing dynamics. The DERs consist of a set of distributed generators (follower population) interacting with a distribution system operator (DSO) (leader) to reach a Stackelberg equilibrium.
Consider a set of distributed generators : each distributed generator has a payoff function:
where is the amount of power produced by each generator i (this power is stacked in a vector as ), is the energy price defined by the DSO, and is the cost function for producing energy for each generator. The cost function is traditionally chosen as a convex quadratic function such as , where , are the cost coefficients. The power resource allocation is constrained by the power balance equation , where is the total power demand of the distribution network.
On the other hand, the main goal of the pricing problem is to determine the market clearing price (MCP) for the energy producer. The DSO solves an optimization problem that maximize the welfare of the population over a market cycle. It is observed that the coordination scheme is cast as a Stackelberg game, which is a challenging bilevel optimization problem. In the objective function, it is assumed that the DERs will have chosen the optimal generation profile for a particular price . The optimal market clearing price is then obtained by solving the following bilevel optimization problem:
Since we posed the proposed dynamics for minimization problems, we define the objective functions as . Following the population game’s description, the fitness function for each generator is given by:
In order to obtain the pricing dynamics, we need the sensitivity matrix (14):
With this sensitivity matrix, we can obtain the total derivative (15) for the gradient descent for the upper-level pricing variable . Now, we are ready to introduce the predictive-sensitivity Stackelberg learning dynamics (18) for the DER coordination problem:
where is the vector with elements .
The distributed generators’ (DGs) capacities and coefficients for the simulation experiments are presented in Table 1. The numerical experiments were simulated in a IEEE 9-bus test feeder adapted from [41], where each DG was modeled using a voltage–source inverter with local controllers. In Figure 2 is presented the distribution network with three distributed generators and three loads. The test case scenario is as follows. Initially, the system has to supply a total load of W, corresponding to three loads as W, W, and W in the distribution network. The distributed generators in the distribution network dynamically interact with each other and with the DSO to reach the optimal solution via a pricing dynamics that determines the optimal price and the optimal energy allocation for each based on the proposed predictive-sensitivity Stackelberg learning dynamics (18). Then, at s of simulation, an additional load is added to the grid, summing up the total to W.

Table 1.
System parameters’ simulation.
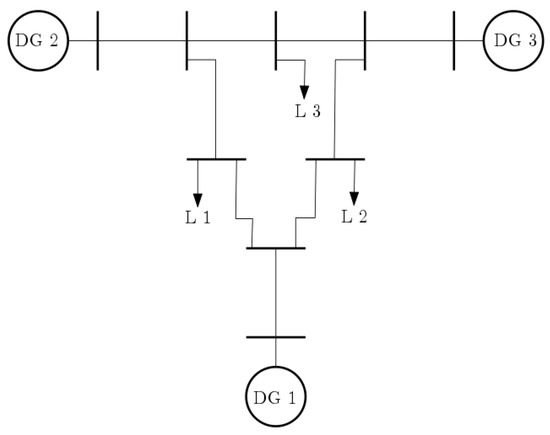
Figure 2.
Distribution network with DERs adapted from an IEEE 9-bus test feeder.
In Figure 3 is presented the frequency response. It is shown that the system maintains the frequency stable around the reference of 60 Hz. The variations of the load are observed as small overshoots, but the system returns to the equilibrium point with a rapid response.
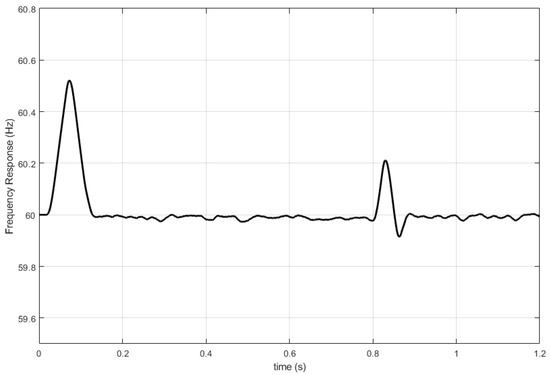
Figure 3.
Frequency response of the distribution network.
In Figure 4 is presented the power behavior of each DG. It is shown that the less expensive DG3 (with small ) dispatches more power to the system, while the more expensive DG2 (with the bigger ) dispatches less power. The response to variations of the load (see Figure 5) at s is observed, and the generators dynamically adapt to the new demand with a small overshoot.
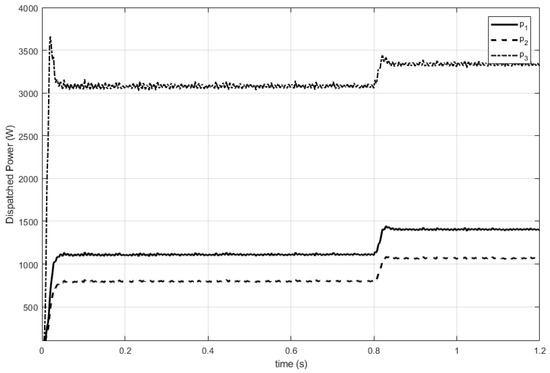
Figure 4.
Power response of each DG.
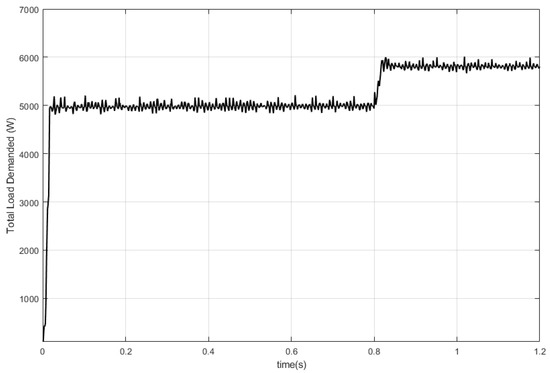
Figure 5.
Total load demanded response.
Finally, Figure 6 presents the price dynamics . Behavior towards the stable point is observed and, then, the dynamic response to the variation of the load at s, as expected.
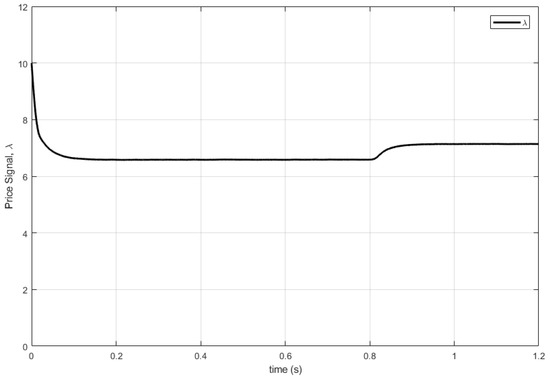
Figure 6.
Price dynamics response.
5. Conclusions
To solve bilevel optimization problems between a leader and a follower population, we proposed two dynamical systems interconnected by a predictive-sensitivity conditioning matrix in a single time scale. For the leader optimization problem, we developed a gradient descent algorithm based on the total derivative, and for the followers’ optimization problem, we used the population dynamics framework to model a population of interacting strategic agents. We extended the concept of the Stackelberg population equilibrium to the differential Stackelberg population equilibrium for population dynamics. Theoretical guarantees for the stability of the proposed Stackelberg population learning dynamics were presented. A distributed energy resource coordination problem was solved via a pricing dynamics based on the proposed approach. Some simulation experiments were presented to illustrate the effectiveness of the framework. As future work, several research avenues are available. For instance, extensions of this work to include uncertainty would be very useful for real-life problems.
Author Contributions
Conceptualization, E.M.-N. and F.R.; methodology, E.M.-N. and F.R.; software, E.M.-N.; validation, E.M.-N. and F.R.; formal analysis, E.M.-N. and F.R.; investigation, E.M.-N. and F.R.; writing—original draft preparation, E.M.-N.; writing—review and editing, E.M.-N. and F.R.; funding acquisition, F.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Politecnico di Milano grant number AU20INTZ01, project: ”Large-scale Optimization and Operator-theoretic Methods Applied to Smartgrids”.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data are available.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; nor in the decision to publish the results.
References
- Novak, A.; Feichtinger, G.; Leitmann, G. A differential game related to terrorism: Nash and Stackelberg strategies. J. Optim. Theory Appl. 2010, 144, 533–555. [Google Scholar] [CrossRef]
- Li, Y.; Shi, D.; Chen, T. False data injection attacks on networked control systems: A Stackelberg game analysis. IEEE Trans. Autom. Control 2018, 63, 3503–3509. [Google Scholar] [CrossRef]
- Groot, N.; Zaccour, G.; De Schutter, B. Hierarchical game theory for system-optimal control: Applications of reverse Stackelberg games in regulating marketing channels and traffic routing. IEEE Control Syst. Mag. 2017, 37, 129–152. [Google Scholar]
- Motalleb, M.; Siano, P.; Ghorbani, R. Networked Stackelberg competition in a demand response market. Appl. Energy 2019, 239, 680–691. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Q. A Stackelberg game approach for two-level distributed energy management in smart grids. IEEE Trans. Smart Grid 2017, 9, 6554–6565. [Google Scholar] [CrossRef]
- Baron-Prada, E.; Mojica-Nava, E. A population games transactive control for distributed energy resources. Int. J. Electr. Power Energy Syst. 2021, 130, 106874. [Google Scholar] [CrossRef]
- Fiez, T.; Chasnov, B.; Ratliff, L. Implicit learning dynamics in Stackelberg games: Equilibria characterization, convergence analysis, and empirical study. In Proceedings of the International Conference on Machine Learning, PMLR 2020, Online, 13–18 July 2020; pp. 3133–3144. [Google Scholar]
- Hirose, K.; Matsumura, T. Comparing welfare and profit in quantity and price competition within Stackelberg mixed duopolies. J. Econ. 2019, 126, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2021; Volume 325, pp. 321–384. [Google Scholar]
- Jin, C.; Netrapalli, P.; Jordan, M. What is local optimality in nonconvex-nonconcave minimax optimization? In Proceedings of the International Conference on Machine Learning. PMLR 2020, Online, 13–18 July 2020; pp. 4880–4889. [Google Scholar]
- Sinha, A.; Malo, P.; Deb, K. A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications. IEEE Trans. Evol. Comput. 2018, 22, 276–295. [Google Scholar] [CrossRef]
- Stackelberg, H.V. Theory of the Market Economy; Oxford University Press: Oxford, UK, 1952. [Google Scholar]
- Bracken, J.; McGill, J.T. Mathematical programs with optimization problems in the constraints. Oper. Res. 1973, 21, 37–44. [Google Scholar] [CrossRef]
- Hansen, P.; Jaumard, B.; Savard, G. New branch-and-bound rules for linear bilevel programming. SIAM J. Sci. Stat. Comput. 1992, 13, 1194–1217. [Google Scholar] [CrossRef]
- Vicente, L.; Savard, G.; Júdice, J. Descent approaches for quadratic bilevel programming. J. Optim. Theory Appl. 1994, 81, 379–399. [Google Scholar] [CrossRef]
- Deng, X. Complexity issues in bilevel linear Programming. In Multilevel Optimization: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 1998; pp. 149–164. [Google Scholar]
- Bard, J.F. Practical Bilevel Optimization: Algorithms and Applications; Springer Science & Business Media: Boston, MA, USA, 1998; Volume 30. [Google Scholar]
- Li, T.; Sethi, S.P. A review of dynamic Stackelberg game models. Discret. Contin. Dyn. Syst.-B 2017, 22, 125. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Pang, J.S.; Ralph, D. Mathematical Programs with Equilibrium Constraints; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kulkarni, A.A.; Shanbhag, U.V. An existence result for hierarchical Stackelberg v/s Stackelberg games. IEEE Trans. Autom. Control 2015, 60, 3379–3384. [Google Scholar] [CrossRef] [Green Version]
- Kebriaei, H.; Iannelli, L. Discrete-time robust hierarchical linear-quadratic dynamic games. IEEE Trans. Autom. Control 2017, 63, 902–909. [Google Scholar] [CrossRef]
- Başar, T.; Srikant, R. A Stackelberg network game with a large number of followers. J. Optim. Theory Appl. 2002, 115, 479–490. [Google Scholar] [CrossRef]
- Fabiani, F.; Tajeddini, M.A.; Kebriaei, H.; Grammatico, S. Local Stackelberg equilibrium seeking in generalized aggregative games. IEEE Trans. Autom. Control 2021, 1–6. [Google Scholar] [CrossRef]
- Kok, K.; Widergren, S. A Society of Devices: Integrating Intelligent Distributed Resources with Transactive Energy. IEEE Power Energy Mag. 2016, 14, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Bejestani, A.K.; Annaswamy, A.; Samad, T. A hierarchical transactive control architecture for renewables integration in smart grids: Analytical modeling and stability. IEEE Trans. Smart Grid 2014, 5, 2054–2065. [Google Scholar] [CrossRef]
- Hu, J.; Yang, G.; Kok, K.; Xue, Y.; Binder, H.W. Transactive control: A framework for operating power systems characterized by high penetration of distributed energy resources. J. Mod. Power Syst. Clean Energy 2017, 5, 451–464. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Lian, J.; Conejo, A.J.; Zhang, W. Transactive Energy Systems: The Market-Based Coordination of Distributed Energy Resources. IEEE Control. Syst. Mag. 2020, 40, 26–52. [Google Scholar] [CrossRef]
- Barreto, C.; Mojica-Nava, E.; Quijano, N. Incentive mechanisms to prevent efficiency loss of non-profit utilities. Int. J. Electr. Power Energy Syst. 2019, 110, 523–535. [Google Scholar] [CrossRef] [Green Version]
- Groot, N.; De Schutter, B.; Hellendoorn, H. On Systematic Computation of Optimal Nonlinear Solutions for the Reverse Stackelberg Game. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 1315–1327. [Google Scholar] [CrossRef]
- Arrow, K.J.; Azawa, H.; Hurwicz, L.; Uzawa, H. Studies in Linear and Non-Linear Programming; Stanford University Press: Palo Alto, CA, USA, 1958; Volume 2. [Google Scholar]
- Helmke, U.; Moore, J.B. Optimization and Dynamical Systems; Springer Science & Business Media: Boston, MA, USA, 2012. [Google Scholar]
- Sandholm, W.H. Population Games and Evolutionary Dynamics; MIT Press: Boston, MA, USA, 2010. [Google Scholar]
- Quijano, N.; Ocampo-Martinez, C.; Barreiro-Gomez, J.; Obando, G.; Pantoja, A.; Mojica-Nava, E. The Role of Population Games and Evolutionary Dynamics in Distributed Control Systems. IEEE Control Syst. 2017, 37, 70–97. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Patience Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Picallo, M.; Bolognani, S.; Dörfler, F. Predictive-sensitivity: Beyond Singular Perturbation for Control Design on Multiple Time Scales. arXiv 2021, arXiv:2101.04367. [Google Scholar]
- Dempe, S.; Mordukhovich, B.S.; Zemkoho, A.B. Sensitivity analysis for two-level value functions with applications to bilevel programming. SIAM J. Optim. 2012, 22, 1309–1343. [Google Scholar] [CrossRef]
- Krantz, S.G.; Parks, H.R. The Implicit Function Theorem: History, Theory, and Applications; Springer Science & Business Media: Boston, MA, USA, 2012. [Google Scholar]
- Mojica-Nava, E.; Macana, C.A.; Quijano, N. Dynamic Population Games for Optimal Dispatch on Hierarchical Microgrid Control. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 306–317. [Google Scholar] [CrossRef]
- Mojica-Nava, E.; Barreto, C.; Quijano, N. Population Games Methods for Distributed Control of Microgrids. IEEE Trans. Smart Grid 2015, 6, 2586–2595. [Google Scholar] [CrossRef]
- Mojica-Nava, E.; Rivera, S.; Quijano, N. Game-theoretic dispatch control in microgrids considering network losses and renewable distributed energy resources integration. IET Gener. Transm. Distrib. 2017, 11, 1583–1590. [Google Scholar] [CrossRef]
- Zhan, Y.T.; Li, X.S.; Huang, N.J. A Stackelberg population competition model via variational inequalities and fixed points. Carpathian J. Math. 2020, 36, 331–339. [Google Scholar] [CrossRef]
- Lakshmanan, H.; De Farias, D.P. Decentralized resource allocation in dynamic networks of agents. SIAM J. Optim. 2008, 19, 911–940. [Google Scholar] [CrossRef]
- Bertsekas, D.; Nedic, A.; Ozdaglar, A. Convex Analysis and Optimization; Athena Scientific Belmont: Nashua, NH, USA, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).