1. Introduction
Since the seminal contribution of Kandori et al. [
1], evolutionary game theorists have used stochastic stability analysis and 2 × 2 coordination games to study the formation of social conventions (Lewis [
2] and Bicchieri [
3] are classical references on social conventions from philosophy, while for economics, see Schelling [
4], Young [
5], and Young [
6]). Some of these works focus on coordination games such as the battle of sexes: a class that describes situations in which two groups of people prefer to coordinate on different actions. In this framework, the long-run convention may depend on how easily people can learn each other’s preferences.
Think about Bob and Andy, who want to hang out together: they can either go to a football match or to the cinema. Both Andy and Bob prefer football, but they do not know what the other prefers. In certain contexts, learning each other’s preferences may require too much effort. In these cases, if Bob and Andy know that everybody usually goes to the cinema, they go to the cinema without learning each other’s preferences. In other situations, learning each other’s preferences may require a small effort (for instance, watching each other’s Facebook walls). In this case, Bob and Andy learn that they both prefer football, so they go to a football match together.
In this work, we contribute to the literature on coordination games. We show which conventions become established between two groups of people different in preferences if people can learn each other’s preferences by exerting an effort. We do so, formalizing the previous example and studying the evolution of conventions in a dynamic setting. We model the coordination problem as a repeated language game (Neary [
7]): we use evolutionary game theory solution concepts and characterize the long-run equilibrium as the stochastically stable state (see Foster and Young [
8], Kandori et al. [
1] and Young [
9]).
We consider a population divided into two groups, which repeatedly play a 2 × 2 coordination game. We assume that one group is larger than the other and that the two groups differ in preferences towards the coordination outcomes. At each period, players can learn the group of their opponent if they pay a cost. Such a cost represents the effort to exert if they want to learn their opponent’s group. If they pay this cost, they can condition the action to the player they meet. If they do not pay it, they can only play the same action with every player. Given this change in the strategic set, we introduce a new possible perturbation. Players can make a mistake in the information choice and a mistake in the coordination choice. We model two situations: one where the cost is equal to zero, and players always learn their opponent’s group, and one where the cost is strictly positive and players can learn their opponent’s group only if they pay that cost. Players decide myopically their best reply based on the current state, which is always observable. We say that a group has a stronger preference for its favorite action than the other if it assigns higher payoffs to its favorite outcome or lower payoffs to the other outcome compared to the other group.
We find that cost level, strength in preferences, and group size are crucial drivers for the long-run stability of outcomes. Two different scenarios can happen, depending on the cost. Firstly, low cost levels favor coordination: players always coordinate on their favorite action with players of their group. If one group has a stronger preference for its favorite action or its size is sufficiently large compared to the other, every player plays the action preferred by that group in inter-group interactions. Interestingly, players from the group that is stronger in preferences never need to buy the information because they play their favorite action with everyone, while players from the other group always need to buy it.
Secondly, when the cost is high, players never learn the group of their opponents, and they play the same action with every player. Some players coordinate on one action that they do not like, even with players of their group. Indeed, we find that when one group is stronger in preferences than the other for its favorite action, or if its size is sufficiently large compared to the other, every player coordinates on that group’s favorite action. Even worse, the two groups may play their favorite action and miscoordinate in inter-group interactions. We find that this outcome occurs when both groups have strong enough preferences for their favorite action or if the two groups are sufficiently close in size.
Neary [
7] considers a similar model, where each player decides one single action valid for both groups. Hence, it is as if learning an opponent’s group requires too much effort, and no player ever learns it. Given this scenario, Neary’s results are the same as in our analysis when the cost is high.
It is helpful to highlight our analysis with respect to the one proposed by Neary, from which we started. We firstly enlarge Neary’s analysis to the case when players learn their opponent’s group at zero cost. In this case, only states where all the players in one group buy the information can be stochastically stable: this result was not possible in the analysis of Neary. Overall, controlling for the cost equal to zero may be seen as a robustness exercise; nevertheless, we find that the model is more tractable under this specification than under Neary’s one. Indeed, if the cost is equal to zero, we can consider inter-group dynamics separated from inside-group ones, and hence, we can consider two absorbing states at a time.
The behavioral interpretation is similar for high and low levels of the cost: either the minority adapts to the majority, or the weaker group in preferences adapt to the strongest. Indeed, when the cost is low, the weakest group always needs to buy the information, while the strongest group does not, since it plays its favorite action with everyone. Similarly, when the cost is high, everybody will play the action favored by the strongest group in preferences in the long run. However, comparing the high-cost case with the low-cost case enriches the previous analysis. From this comparison, we can say that reducing the cost of learning the opponent’s group increases the probability of inter-group coordination in the long run. Indeed, inter-group miscoordination does not occur without incomplete information and a high cost. Unlike in Neary, strength in preferences or group size alone does not cause inter-group miscoordination.
The paper is organized as follows: In
Section 2, we explain the model’s basic features. In
Section 3, we determine the results for the complete information case where the cost is 0. In
Section 4, we derive the results for the case with incomplete information and costly acquisition. We distinguish between two cases: low cost and high cost. In
Section 5, we discuss results, and in
Section 6, we conclude. We give all proofs in the
Appendix A and we give the intuition during the text.
2. The Model
We consider
N players divided into two groups
A and
B,
. We assume
and
. Each period, players are randomly matched in pairs to play the 2 × 2 coordination game represented in
Table 1,
Table 2 and
Table 3. Matching occurs with uniform probability, regardless of the group.
Table 1 and
Table 2 represent inside-group interactions, while
Table 3 represents inter-group interactions (group
A row player and group
B column player). We assume that
, and thus, we name
a the favorite action of group
A. Equally, we assume
, and hence,
b is the favorite action of group
B. We do not assume any particular order between
, and
. However, without loss of generality, we assume that
. Consider
, and
. We say that group
K is stronger in preferences for its favorite action than group
if
or equivalently
.
Each period, players choose whether to pay a cost to learn their opponent’s group or not before choosing between action a and b. If they do not pay it, they do not learn the group of their opponent, and they play one single action valid for both groups. If they pay it, they can condition the action on the two groups. We call information choice the first and coordination choice the second.
Consider player . is the information choice of player i: if , player i does not learn the group of her/his opponent. If , player i pays a cost c and learns the group. We assume that . is the coordination choice when . If , is the coordination choice when player i meets group K, while is the coordination choice when player i meets group .
A pure strategy of a player consists of her/his information choice,
, and of her/his coordination choices conditioned on the information choice, i.e.,
Each player has sixteen strategies. However, we can safely neglect some strategies because they are both payoff-equivalent (a player earns the same payoff disregarding which strategy s/he chooses) and behaviorally equivalent (a player earns the same payoff independently from which strategy the other players play against her/him).
We consider a model of noisy best-response learning in discrete time (see Kandori et al. [
1], Young [
9]).
Each period
, independently from previous events, there is a positive probability
that a player is given the opportunity to revise her/his strategy. When such an event occurs, each player who is given the revision opportunity chooses with positive probability a strategy that maximizes her/his payoff at period
t.
is the strategy played by player
i at period
t.
is the payoff of player
i that chooses strategy
against the strategy profile
played by all the other players except
i. Such a payoff depends on the random matching assumption and the payoffs of the underlying 2 × 2 game. At period
, player
i chooses
If there is more than one strategy that maximizes the payoff, player
i assigns the same probability to each of those strategies. The above dynamics delineates a Markov process that is ergodic thanks to the noisy best response property.
We group the sixteen strategies into six analogous classes that we call behaviors. We name behavior a as the set of strategies when player chooses , and . We name behavior as the set of strategies when player i chooses , , and , and so on. Z is the set of possible behaviors: . is the behavior played by player i at period t as implied from . is the behavior profile played by all the other players except i at period t as implied from . Note that behaviors catch all the relevant information as defined when players are myopic best repliers. is the payoff for player i that chooses behavior against the behavior profile . Such a payoff depends on the random matching assumption and the payoffs of the underlying 2 × 2 game. The dynamics of behaviors as implied by strategies coincide with the dynamics of behaviors, assuming that players myopically best reply to a behavior profile. We formalize the result in the following lemma.
Lemma 1. Given the dynamics of as implied by , it holds that
Consider a player such that the best thing to do for her/him is to play a with every player s/he meets regardless of the group. In this case, both and maximize her/his payoff. In contrast, does not maximize her/his payoff since in this case, s/he plays b with every player s/he meets. Moreover, the payoff of player i is equal whether or but different if . Therefore, all the strategies that belong to the same behavior are payoff equivalent and behaviorally equivalent.
A further reduction is possible because is behaviorally equivalent to a for each player. The last observation and the fact that we are interested in the number of players playing a with each group lead us to introduce the following state variable. We denote with the number of players of group A playing action a with group A, and the number of players of group A playing action a with group B. We define states as vectors of four components: , with being the state space and the state at period t. At each t, all the players know all the components of . Consider player i playing behavior at period t. is the payoff of i if s/he chooses behavior at period against the state . All that matters for a decision-maker is and . We formalize the result in the following lemma.
Lemma 2. Given the dynamics of generated by , it holds that . Moreover, , and .
If players are randomly matched, it is as if each player plays against the entire population. Therefore, each player of group K myopically best responds to the current period by looking at how many players of each group play action a with group K. Moreover, a player that is given the revision opportunity subtracts her/himself from the component of where s/he belongs. If is playing behavior a, or at period t, s/he knows that players of group K are playing action a with group K at period t.
Define with the set of players that are given the revision opportunity at period t. Given Lemma 2, it holds that depends on and on . That is, we can define a map such that . The set reveals whether the players who are given the revision opportunity are playing a behavior between a, , and , or a behavior between b, , and . In the first case we should look at , while in the second at .
From now on, we will refer to behaviors and states following the simplifications described above.
We illustrate here the general scheme of our presentation. We divide the analysis into two cases: complete information and incomplete information. For each case, we consider unperturbed dynamics (players choose the best reply behavior with probability 1) and perturbed dynamics (players choose a random behavior with a small probability). First, we help the reader understand how each player evaluates her/his best reply behavior and which states are absorbing. Second, we highlight the general structure of the dynamics with perturbation and then determine the stochastically stable states. In the next section, we analyze the case with complete information, hence, when the cost is zero.
3. Complete Information with Free Acquisition
In this section, we assume that each player can freely learn the group of her/his opponent when randomly matched with her/him. Without loss of generality, we assume that players always learn the group of their opponent in this case. We refer to this condition as free information acquisition. Each player has four possible behaviors as defined in the previous section. , with , and in this case.
Define and .
Equations (
1)–(
4) are the payoffs for a player
playing
or
at period
t.
3.1. Unperturbed Dynamics
We begin the analysis for complete information by studying the dynamics of the system when players play their best reply behavior with probability one.
We can separate the dynamics of the system into three different dynamics. The two regarding inside-group interactions, i.e., and , and the one regarding inter-group interaction, i.e., and . We call this subset of states . Both and are one-dimensional; instead is two-dimensional.
Lemma 3. Under free information acquisition, , and .
The intuition behind the result is as follows. If players always learn their opponent’s group, the inter-group dynamics does not interfere with the inside-group and vice-versa. If player is given the revision opportunity, s/he chooses only based on .
Consider a subset of eight states: , ,
, , , , and .
Lemma 4. Under free information acquisition, the states in are the unique absorbing states of the system.
We call and Monomorphic States ( from now on). Specifically, we refer to the first one as and to the second as . We label the remaining six as Polymorphic States ( from now on). We call and . In , every player plays the same action with any other player; in , at least one group is conditioning the action. In , every player plays ; in , every player plays . In , group A plays and group B plays . In , group A plays while group B plays . In both and , all players coordinate on their favorite action with their similar.
In the model of Neary, only three absorbing states were possible: the two and a Type Monomorphic State where group A plays and group B plays . The were not present in the previous analysis. We observe these absorbing states in our analysis, thanks to the possibility of conditioning the action on the group.
We can break the absorbing states in into the three dynamics in which we are interested. This simplification helps in understanding why only these states are absorbing. For instance, in inter-group interactions, there are just two possible absorbing states, namely and . For what concerns inside-group interactions, and 0 matter for , and and 0 for . For each dynamic, the states where every player plays a or where every player plays b with one group are absorbing. In this simplification, we can see the importance of Lemma 3. As a matter of fact, in all the dynamics we are studying, there are just two candidates to be stochastically stable. This result simplifies the stochastic stability analysis.
3.2. Perturbed Dynamics
We now introduce perturbations in the model presented in the previous section; that is, players can make mistakes while choosing their behaviors: there is a small probability that a player does not choose her/his best response behavior when s/he is given the revision opportunity. We use tools and concepts developed by Freidlin andWentzell [
10] and refined by Ellison [
11].
Given perturbations, depends on , and on which players make a mistake among those who are given the revision opportunity. We define with the set of players who do not choose their best reply behavior among those who are given the revision opportunity. Formally, .
We use uniform mistakes: the probability of making a mistake is equal for every player and every state. At each period, if a player is given the revision opportunity, s/he makes a mistake with probability . In this section, we assume that players make mistakes only in the coordination choice: assuming , adding mistakes also in the information choice would not influence the analysis. Note that Lemma 3 is still valid under this specification.
If we consider a sequence of transition matrices , with associated stationary distributions , by continuity, the accumulation point of that we call , is a stationary distribution of . Mistakes guarantee the ergodicity of the Markov process and the uniqueness of the invariant distribution. We are interested in states which have positive probability in .
Definition 1. A state is stochastically stable if and it is uniquely stochastically stable if .
We define some useful concepts from Ellison [
11]. Let
be an absorbing state of the unperturbed process.
is the basin of attraction of
: the set of initial states from which the unperturbed Markov process converges to
with probability one. The radius of
is the number of mistakes needed to leave
when the system starts in
. Define a path from state
to state
as a sequence of distinct states
, with
and
.
is the set of all paths from
to
. Define
as the resistance of the path
, namely the number of mistakes that occurs to pass from state
to state
. The radius of
is then
Now define the Coradius of
as
Thanks to Theorem 1 in Ellison [
11], we know that if
, then
is uniquely stochastically stable.
We are ready to calculate the stochastically stable states under complete information.
Theorem 1. Under free information acquisition, for N large enough, if , then is uniquely stochastically stable. If , then is uniquely stochastically stable.
When the cost is null, players can freely learn the group of their opponent. Therefore, in the long run, they succeed in coordinating on their favorite action with those who are similar in preference. Hence, always converges to , and always converges to 0. This result rules out Monomorphic States and the other four Polymorphic States: only and are left. Which of the two is selected depends on strength in preferences and group size. Two effects determine the results in the long run. Firstly, if , is uniquely stochastically stable. The majority prevails in inter-group interactions if the two groups are equally strong in preferences.
Secondly, if , there is a trade-off between strength in preferences and group size. If , either group A is stronger in preferences than group B, or group A is sufficiently larger than group B. In both of the two situations, the number of mistakes necessary to leave is bigger than the one to leave : in a sense, more mistakes are needed to make b best reply for A players than to make a best reply for B players. Therefore, every player will play action a in inter-group interactions. Similar reasoning applies if .
Interestingly, in both cases, only players of one group need to learn their opponent’s group: the players from the group that is weaker in preferences or sufficiently smaller than the other.
Unlike in the analysis of Neary, if learning the opponent’s group is costless, the Monomorphic States are never stochastically stable. This result is a consequence of the possibility to condition the action on the group. Indeed, if players can freely learn the opponent’s group, they will always play their favorite action inside the group.
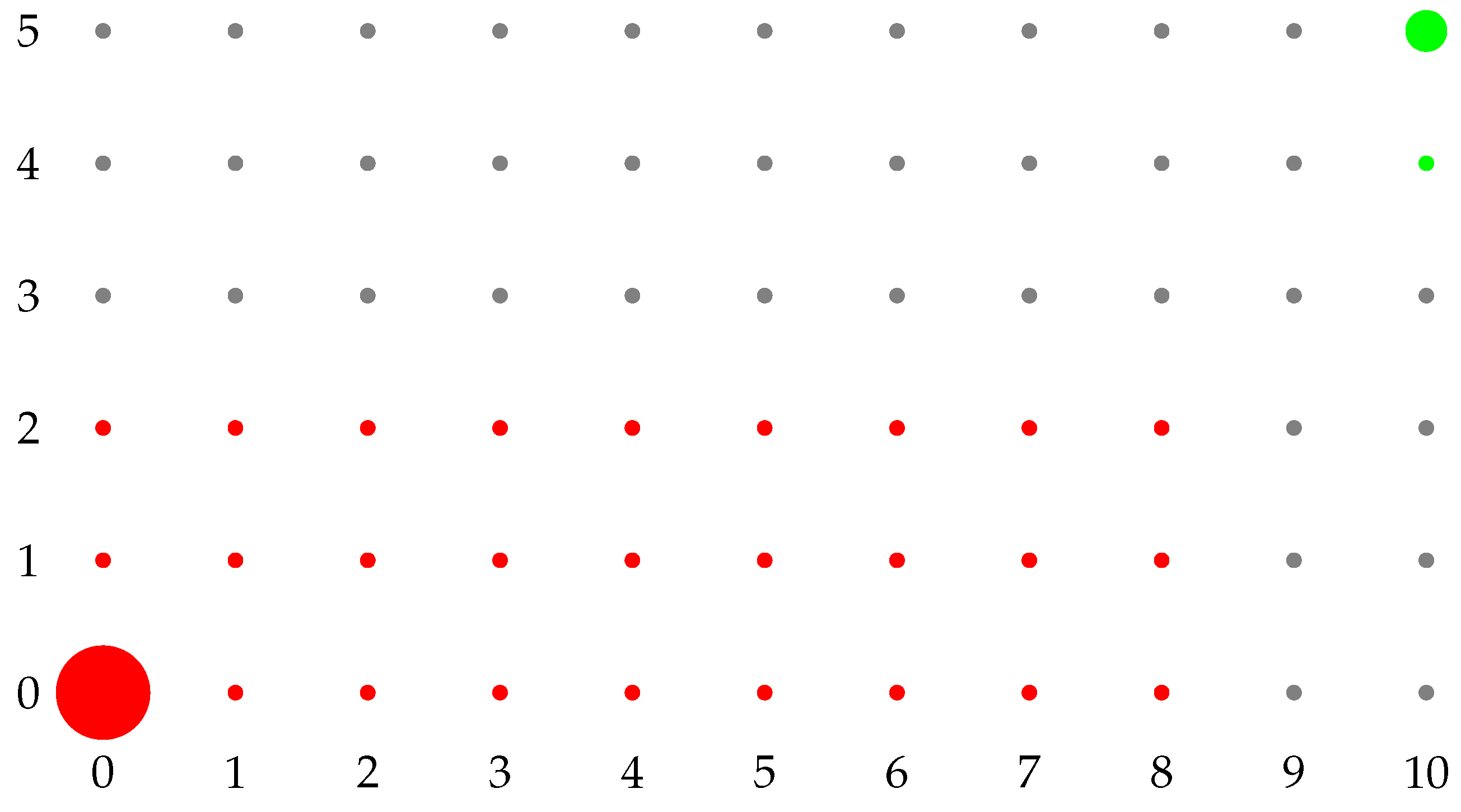
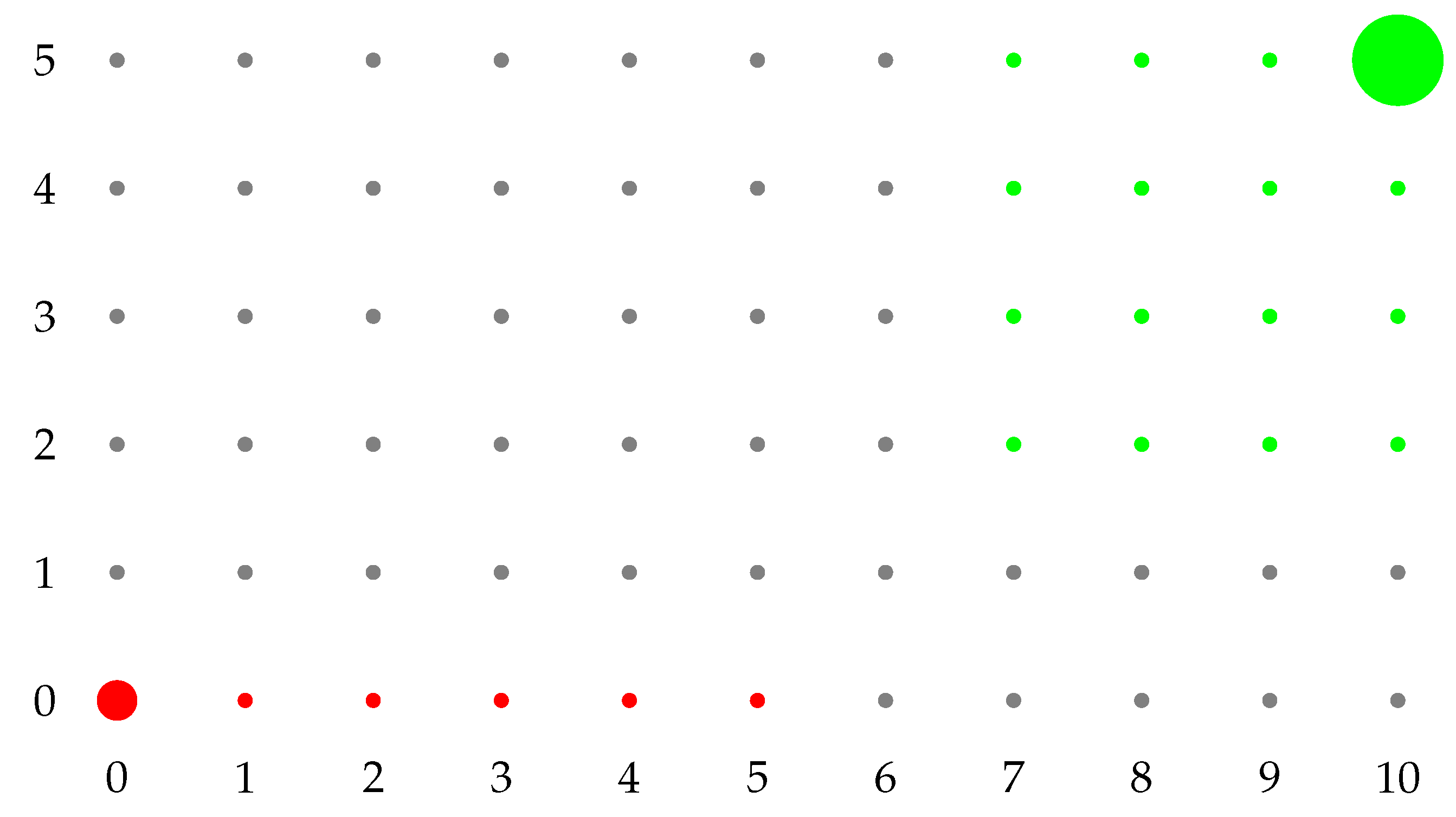
We provide two numerical examples to explain how the model works in
Figure 1 and
Figure 2. We represent just
, hence, a two-dimensional dynamics. Red states represent the basin of attraction of
, while green states the one of
. From gray states, there are paths of zero resistance both to
and to
. Any path that involves more players playing
a within red states has a positive resistance. Every path that involves fewer people playing
a within green states has a positive resistance. The radius of
is equal to the coradius of
, and it is the minimum resistance path from
to gray states. The coradius of
is equal to the radius of
, and it is the minimum resistance path from
to gray states.
Firstly, consider the example in
Figure 1.
,
,
,
,
,
. Clearly,
. In this case
, while
. Hence,
is the uniquely stochastically stable state. We give here a short intuitive explanation. Starting from
, the minimum-resistance path to gray states is the one that reaches
. The minimum resistance path from
to gray states is the one that reaches
. Hence, fewer mistakes are needed to exit from the green states than to exit from the red states, and
is uniquely stochastically stable.
Secondly, consider the example in
Figure 2.
,
,
,
,
,
. Note that
. In this case,
,
. Hence,
is uniquely stochastically stable. In this case, the minimum resistance path from
to gray states is the one that reaches
or
. The one from
to gray states is the one that reaches
.
4. Incomplete Information with Costly Acquisition
In this section, we assume that each player can not freely learn the group of her/his opponent. Each player can buy this information at cost . We refer to this condition as costly information acquisition. It is trivial to notice that Lemma 3 is not valid anymore. Indeed, since players learn the group of their opponent conditional on paying a cost, not every player pays it, and the dynamics are no longer separable.
This time, . It is trivial to show that there are four strictly dominant behaviors; indeed, and . Hence, and , and . We define strictly dominant behaviors as , with being a strictly dominant behavior of player i.
Equations (
5)–(
8) are the payoffs at period
t, for a player
currently playing
a or
.
Note that if
, then
and
. We begin the analysis with the unperturbed dynamics.
4.1. Unperturbed Dynamics
So far, there are no more random elements with respect to
Section 3. Therefore,
. Nine states can be absorbing under this specification.
Lemma 5. Under costly information acquisition, there are nine possible absorbing states: .
We summarize all the relevant information in
Table 4. The reader can note two differences with respect to
Section 3: firstly, some states are absorbing if and only if some conditions hold, and secondly, there is one more possible absorbing state, that is,
. Such an absorbing state was also possible in Neary under the same conditions on payoffs and group size.
Where we write “none”, we mean that a state is always absorbing for every value of group size, payoffs, and/or the cost. We name the Type Monomorphic State ( from now on): each group is playing its favorite action in this state, causing miscoordination in inter-group interactions. In both and , no player is buying the information, while in , at least one group is buying the information.
Monomorphic States are absorbing states for every value of group size, payoffs, and cost. Indeed, when each player is playing one action with any other player, players do not need to learn their opponent’s group (the information cost does not matter): they best reply to these states by playing the same action.
Polymorphic States are absorbing if and only if the cost is low enough: if the cost is too high, buying the information is too expensive, and players best reply to Polymorphic States by playing a or b. The Type Monomorphic State is absorbing if group B is either sufficiently close in size to group A or strong enough in preferences for its favorite action and if the cost is high enough. The intuition is the following. On the one hand, if the cost is high and if group B is weak in preferences or small enough, every player of group B best replies to by playing a. On the other hand, if the cost is low enough, every player best replies to this state by buying the information and conditioning the action.
4.2. Perturbed Dynamics
We now introduce perturbed dynamics. In this case, we assume that players can make two types of mistakes: they can make a mistake in the information choice and in the coordination choice. Choosing the wrong behavior, in this case, can mean both. We say that with probability , a player who is given the revision opportunity at period t chooses to buy the information when it is not optimal. With probability , s/he makes a mistake in the coordination choice. We could have chosen to set only one probability of making a mistake with a different behavior or strategy.
The logic behind our assumption is to capture behaviorally relevant mistakes. We assume a double punishment mechanism for players choosing by mistake the information level and the coordination action. Specifically, our mistake counting is not influenced by our definition of behaviors. We could have made the same assumption starting from the standard definition of strategies assuming that players can make different mistakes in choosing the two actions that constitute the strategy. Our assumption is in line with works such as Jackson and Watts [
12] and Bhaskar and Vega-Redondo [
13], which assume mistakes in the coordination choice and the link choice.
Formally, , where is the set of players who make a mistake at period t among those who are given the revision opportunity, is the set of players who make a mistake in the coordination choice, and the set of players that make a mistake in the information choice.
Since we assume two types of mistakes, the concept of resistance changes. We then need to consider three types of resistances. We call the path from state to state with mistakes (players make a mistake in the coordination choice). We call the path with mistakes (players make a mistake in the information choice). Finally, we call the path with mistakes both in the coordination choice and the information choice. Since we do not make further assumptions on and (probability of making mistakes uniformly distributed), we can assume .
We count each mistake in the path of both and mistakes as 1; however, is always double since it implies a double mistake. Indeed, we can see this kind of mistake as the sum of two components, one in and the other in , namely .
For example, think about , and that one player from B is given the revision opportunity at period t. Consider the case where s/he makes a mistake both in the information choice and in the coordination choice. For example, s/he learns the group and s/he plays a with A and b with B. This mistake delineates a path from to the state of resistance . Next, think about : the transition from to happens with one mistake. One player from A should make a mistake in the information choice and optimally choosing . In this case, . With a similar reasoning, : a player of group A makes a mistake in the coordination choice and chooses b.
Before providing the results, we explain why using behaviors instead of strategies does not influence the stochastic stability analysis. Let us consider all the sixteen strategies as presented in
Section 2, and just one kind of mistake in the choice of the strategy. Let us take two strategies
and a third strategy
. Now consider the state
, where
, and the state
, where
,
and
,
. Since
and
are both payoff-equivalent and behaviorally equivalent,
and
are the best reply strategies
in both states
and
. Therefore at each period, every player who is given the revision opportunity in state
or
chooses
and
with equal probability. Now let us consider the state
where
. When considering the transition between
and
, the number of mistakes necessary for this transition is the same whether the path passes through
or not because the best reply strategy is the same in both
and
. Therefore, when computing the stochastically stable state, we can neglect
and
.
We divide this part of the analysis into two cases, the first one where the cost is low and the second one when the cost is high.
4.2.1. Low Cost
This section discusses the case when c is as low as possible but greater than 0.
Corollary 1. Under costly information acquisition, if , and are absorbing states, while is not an absorbing state.
The proof is straightforward from
Table 4. In this case, there are eight candidates to be stochastically stable equilibria.
Theorem 2. Under costly information acquisition, for large enough N, take . If , then is uniquely stochastically stable. If , then is uniquely stochastically stable.
The conditions are the same as in Theorem 1. When the cost is low enough, whenever a player can buy the information, s/he does it. Consequently, the basins of attraction of both Monomorphic States and Polymorphic States have the dimension they had under free information acquisition. Due to these two effects, the results are the same as under free information acquisition. This result is not surprising per se but serves as a robustness check of the results of
Section 3.2.
4.2.2. High Cost
In this part of the analysis, we focus on a case when only and are absorbing states.
Define the following set of values:
Corollary 2. Under costly information acquisition, if and , then only and are absorbing states. If , then only are absorbing states.
The proof is straightforward from
Table 4, and therefore, we omit it. We previously gave the intuition behind this result. Let us firstly consider the case in which
is not an absorbing state, hence, the case when
.
Theorem 3. Under costly information acquisition, for large enough N, take and . If , then is uniquely stochastically stable. If , then is uniquely stochastically stable.
If group A is sufficiently large or strong enough in preferences, the minimum number of mistakes to exit from the basin of attraction of is higher than the minimum number of mistakes to exit from the one of . Therefore, is uniquely stochastically stable: every player plays behavior a in the long run.
Now we analyze the case when also is a strict equilibrium.
Theorem 4. Under costly information acquisition, for large enough N, take and .
If , then is uniquely stochastically stable.
If , then is uniquely stochastically stable.
If , then is uniquely stochastically stable.
Moreover, when all the above conditions simultaneously do not hold:
If , then is uniquely stochastically stable.
If , then is uniquely stochastically stable.
If , then both and are stochastically stable.
We divide the statement of the theorem into two parts for technical reasons. However, the reader can understand the results from the first three conditions. The first condition expresses a situation where group A is stronger in preferences than group B or group A is sufficiently larger than group B. In this case, there is an asymmetry in the two costs for exiting the two basins of attraction of and . Exit from the first requires more mistakes than exit from the second. Moreover, reaching from requires fewer mistakes than reaching from . For this reason, and is uniquely stochastically stable in this case. A similar reasoning applies to the second condition.
The third condition expresses a case where both groups are strong enough in preferences or have sufficiently similar sizes. Many mistakes are required to exit from , compared to how many mistakes are required to reach from the two . Indeed, is the state where both groups are playing their favorite action. Since they are both strong in preferences or large enough, in this case, all the players play their favorite action in the long run, but they miscoordinate in inter-group interactions.
The results of Theorems 3 and 4 reach the same conclusions as Neary. However, our analysis allows us to affirm that only with a high cost, the or the is stochastically stable. This result enriches the previous analysis.
As a further contribution, comparing these results with those in
Section 4.2.1, we can give the two conditions for inter-group miscoordination to happen in the long run. First, the cost to pay to learn the opponent’s group should be so high that players never learn their opponent’s group. Second, both groups should be strong enough in preferences or sufficiently close in size. The following lemma states what happens when the cost takes medium values.
Lemma 6. If , then the stochastically stable states must be in the set .
When the cost lowers a tiny quantity from the level of
Section 4.2.2,
is not absorbing anymore. Therefore, only
and
can be stochastically stable when the cost is in the interval above. However, not all the
can be stochastically stable, only the two where all the players play their favorite action in inside-group interactions. The intuition of this result is simple: if players condition their action on the groups in the long run, they play their favorite action with those with similar preferences.
We do not study when
are stochastically stable or when
are: we leave this question for future analysis. Nevertheless, given the results of
Section 4.2.1 and
Section 4.2.2, we expect that for higher levels of cost,
is stochastically stable, and for lower levels,
is stochastically stable.
5. Discussion
The results of our model involve three fields of the literature. Firstly, we contribute to the literature on social conventions. Secondly, we contribute to the literature on stochastic stability analysis, and lastly, we contribute to the literature on costly information acquisition.
For what concerns social conventions, many works in this field study the existence in the long run of heterogeneous strategy profiles. We started from the original model of Neary [
7], which considers players heterogeneous in preferences, but with a smaller strategic set than ours (Heterogeneity has been discussed in previous works such as Smith and Price [
14], Friedman [
15], Cressman et al. [
16], Cressman et al. [
17] or Quilter [
18]). Neary’s model gives conditions for the stochastic stability of a heterogeneous strategy profile that causes miscoordination in inter-group interactions in a random matching case. Neary and Newton [
19] expands the previous idea to investigate the role of different classes of graphs on the long-run result. It finds conditions on graphs such that a heterogeneous strategy profile is stochastically stable. It also considers the choice of a social planner that wants to induce heterogeneous or homogeneous behavior in a population.
Carvalho [
20] considers a similar model, where players choose their actions from a set of culturally constrained possibilities and the heterogeneous strategy profile is labeled as miscoordination. It finds that cultural constraints drive miscoordination in the long run. Michaeli and Spiro [
21] studies a game between players with heterogeneous preferences and who feel pressure from behaving differently. Such a study characterizes the circumstances under which a biased norm can prevail on a non-biased norm. Tanaka et al. [
22] studies how local dialects survive in a society with an official language. Naidu et al. [
23] studies the evolution of egalitarian and inegalitarian conventions in a framework with asymmetry similar to the language game. Likewise, Belloc and Bowles [
24] examines the evolution and the persistence of inferior cultural conventions.
We introduce the assumption that players can condition the action on the group if they pay a cost. This assumption helps to understand the conditions for the stability of the Type Monomorphic State, where players miscoordinate in inter-group interactions. We show that a low cost favors inter-group coordination: incomplete information, high cost, strength in preferences, and group size are key drivers for inter-group miscoordination. Like many works in this literature, we show the importance of strength in preferences and group size in the equilibrium selection.
Concerning network formation literature, Goyal et al. [
25] conducts an experiment on the language game, testing whether players segregate or conform to the majority. van Gerwen and Buskens [
26] suggests a variant of the language game similar to our version but in a model with networks to study the influence of partner-specific behavior on coordination. Concerning auctions theory, He [
27] studies a framework where each individual of a population divided into two types has to choose between two skills: a “majority” and a “minority” one. It finds that minorities are advantaged in competition contexts rather than in coordination ones. He and Wu [
28] tests the role of compromise in the battle of sexes with an experiment.
Like these works, we show that group size and strength in preferences matter for the long-run equilibrium selection. The states where the action preferred by the minority is played in most of the interactions ( or ) are stochastically stable provided that the minority is strong enough in preferences or sufficiently large.
A parallel field is the one of bilingual games such as the one proposed by Goyal and Janssen [
29] or Galesloot and Goyal [
30]: these models consider situations in which players are homogeneous in preferences towards two coordination outcomes, but they can coordinate on a third action at a given cost.
Concerning the technical literature on stochastic stability, we contribute by applying standard stochastic stability techniques to an atypical context, such as costly information acquisition. Specifically, we show that with low cost levels, Polymorphic States where all players in one group condition their action on the group are stochastically stable. Interestingly, only one group of players needs to learn their opponent’s group. With high cost levels, Monomorphic States where no player conditions her/his action on the group are stochastically stable. Since the seminal works by Bergin and Lipman [
31] and Blume [
32], many studies have focused on testing the role of different mistake models in the equilibrium selection. We use uniform mistakes, and introducing different models could be an interesting exercise for future studies.
Among the many models that can be used, there are three relevant variants: payoff/cost-dependent mistakes (Sandholm [
33], Dokumacı and Sandholm [
34], Klaus and Newton [
35], Blume [
36] and Myatt and Wallace [
37]), intentional mistakes (Naidu et al. [
38] and Hwang et al. [
39]), and condition-dependent mistakes (Bilancini and Boncinelli [
40]). Important experimental works in this literature have been done by Lim and Neary [
41], Hwang et al. [
42], Mäs and Nax [
43], and Bilancini et al. [
44].
Other works contribute to the literature on stochastic stability from the theoretical perspective (see Newton [
45] for an exhaustive review of the field). Recently, Newton [
46] has expanded the domain of behavioral rules regarding the results of stochastic stability. Sawa and Wu [
47] shows that with loss aversion individuals, the stochastic stability of Risk-Dominant equilibria is no longer guaranteed. Sawa and Wu [
48] introduces reference-dependent preferences and analyzes the stochastic stability of best response dynamics. Staudigl [
49] examines stochastic stability in an asymmetric binary choice coordination game.
For what concerns the literature on costly information acquisition, many works interpret the information’s cost as costly effort (see the seminal contributions by Simon [
50] or Grossman and Stiglitz [
51]). Our paper is one of those. Many studies place this framework in a sender-receiver game. This is the case of Dewatripont and Tirole [
52], which builds a model of costly communication in a sender-receiver setup.
More recent contributions in this literature are Dewatripont [
53], Caillaud and Tirole [
54], Tirole [
55], and Butler et al. [
56]. Bilancini and Boncinelli [
57] applies this model to persuasion games with labeling. Both Bilancini and Boncinelli [
58] and Bilancini and Boncinelli [
59] consider coarse thinker receivers, combining costly information acquisition with the theory of Jehiel [
60]. Rational inattention is a recent field where the information cost is endogenous (see Mackowiak et al. [
61] for an exhaustive review). We assume that the cost is exogenous and homogeneous for each player.
Güth and Kliemt [
62] firstly uses costly information acquisition in evolutionary game theory in a game of trust. It finds conditions such that developing a conscience can be evolutionarily stable. More recently, Berger and De Silva [
63] uses a similar concept in a deterrence game where agents can buy costly information on past behaviors of their opponents.
Many works use similar concepts of cost in the evolutionary game theory literature on coordination games. For example, Staudigl and Weidenholzer [
64] considers a model where players can pay a cost to form links. The main finding is that when agents are constraint in the possible number of interactions, the payoff-dominant convention emerges in the long run.
The work by Bilancini and Boncinelli [
65] extends Staudigl and Weidenholzer [
64]. The model introduces the fact that interacting with a different group might be costly for a player. It finds that when this cost is low, the Payoff-Dominant strategy is the stochastically stable one. When the cost is high, the two groups in the population coordinate on two different strategies: one on the risk-dominant and the other on the payoff-dominant. Similarly, Bilancini et al. [
66] studies the role of cultural intolerance and assortativity in a coordination context. In that model, there is a population divided into two cultural groups, and each group sustains a cost from interacting with the other group. It finds interesting conditions under which cooperation can emerge even with cultural intolerance.
6. Conclusions
We can summarize our results as follows. When players learn the group of their opponent at a low cost, they always coordinate: they play their favorite action with their similar, while in inter-group interactions, they play the favorite action of the group that is stronger in preferences or with large enough size. If the cost is high, players never learn the group of their opponent. All the players play the same action with every player, or they play their favorite action.
By comparing
Section 4.2.1 and
Section 4.2.2, we can see the impact of varying the cost levels on the long-run results. Surely a low cost favors inter-group coordination. However, a change in the cost level produces two effects that perhaps need further investigation. The first effect concerns the change in the payoff from the interactions between players. The second concerns the change in the purchase of the information.
Consider a starting situation where the cost is low. Players always coordinate on their favorite action in inside-group interactions. If the cost increases, players stop learning their opponent’s group (hence, they stop paying the cost), and they begin to play the same action as any other player. If this happens, either Monomorphic States are established in the long run, or the Type Monomorphic State emerges. In the first case, a group of players coordinates on its second best option, even in inside-group interactions. For this group, there could be a certain loss in terms of welfare. In the second case, players miscoordinate in inter-group interactions, and hence, all of them could have a certain loss in welfare.
Nevertheless, when the cost is low, there is a “free-riding” behavior that vanishes if the cost increases. In fact, with low cost levels, only one group needs to pay the cost, and the other never needs to pay it. In one case, players of group A play their favorite action both in inside-group and inter-group interactions; hence, they never need to pay the cost, while group B always needs to afford it. In the other case, the opposite happens. Therefore, when the cost increases, one of the two groups will benefit from not paying for the information anymore. Future studies could address the implications of this trade-off between successful coordination and the possibility of not paying the cost.
We conclude with a short comparison of our result with the one of Neary [
7]. Indeed, it is worthwhile to mention a contrast that is a consequence of the possibility of conditioning the action on the group of the player. In the model of Neary, a change in the strength of preferences or the group size of one group does not affect the behavior of the other group. We can find this effect even in our model when the cost is high. For example, when
is stochastically stable and group
B becomes strong enough in preferences or sufficiently large, the new stochastically stable state becomes
. Therefore, group
A does not change its behavior. However, when the cost is sufficiently low, the change in payoffs or group size of one group influences the other group’s behavior in inter-group interactions. For instance, when
is stochastically stable, if group
B becomes strong enough in preferences or sufficiently large,
becomes stochastically stable. Hence, both groups change the way they behave in inter-group interactions.
Nevertheless, we can interpret similarly the passing from to and the one from to . In both cases, both groups keep playing their favorite action in inside-group interactions, and what happens in inter-group interactions depends on strength in preferences and group size. Therefore, in this respect, the behavioral interpretation of our results is similar to Neary’s.