Brexit and Power in the Council of the European Union
Abstract
:1. Introduction
2. Materials and Methods
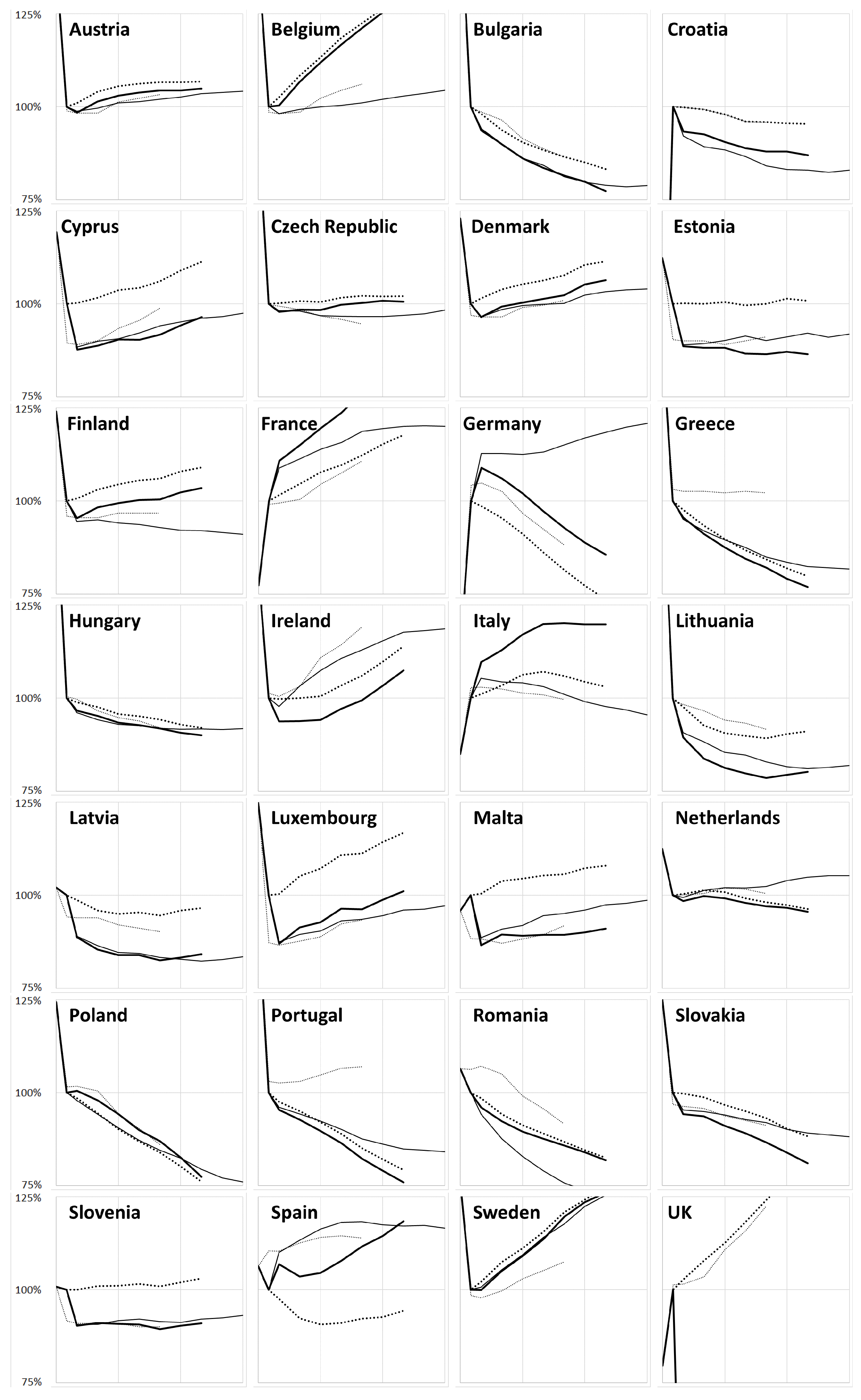
3. Results
3.1. Who Wins?
3.2. Do They Really Benefit?
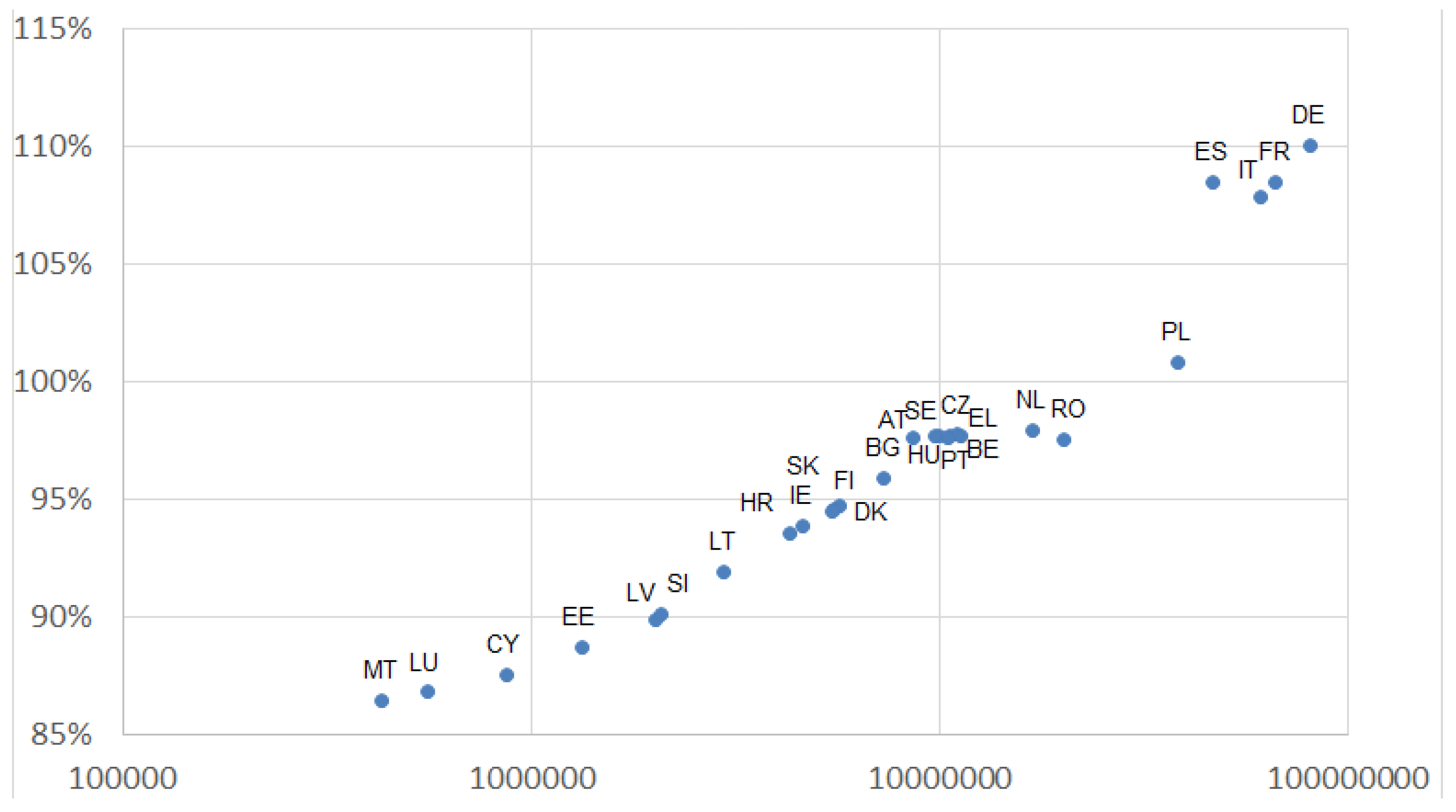
3.3. Small vs. Large
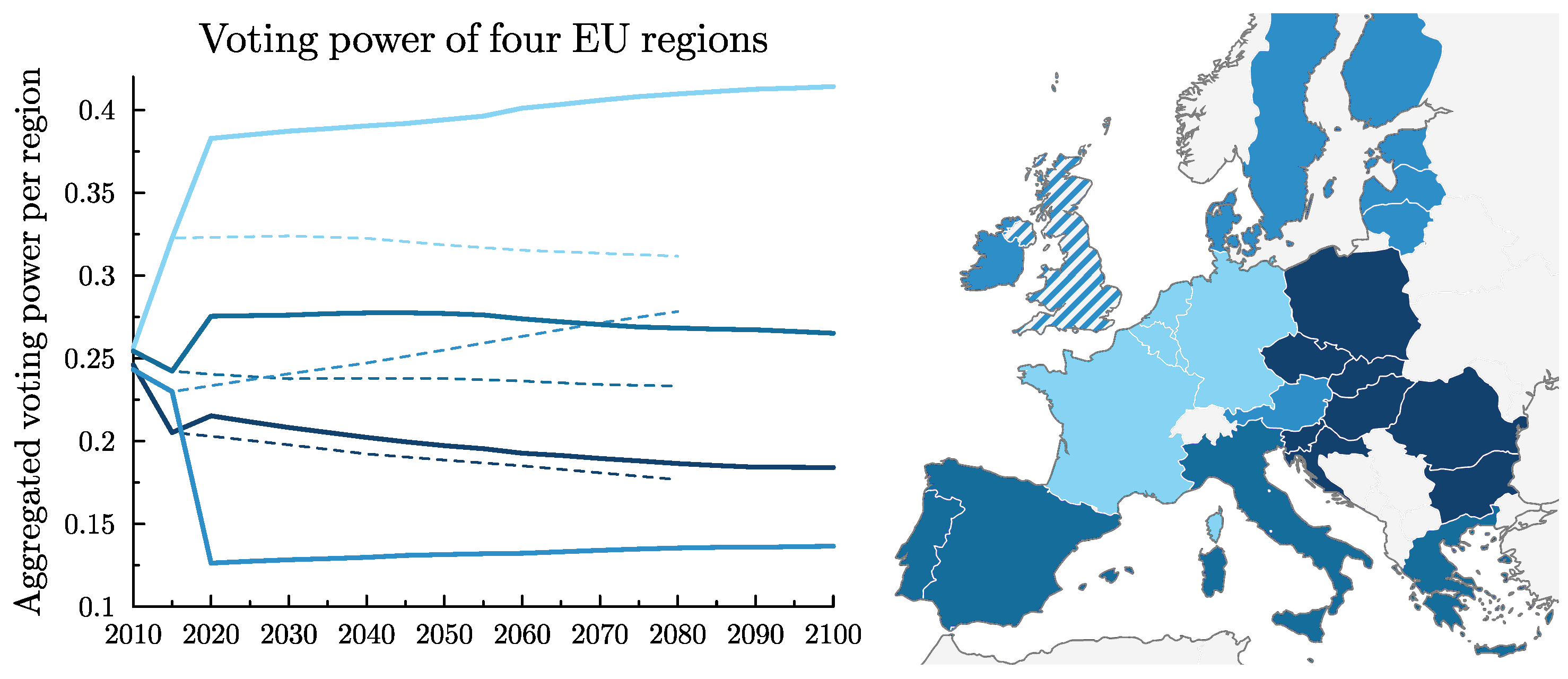
3.4. Power Balance
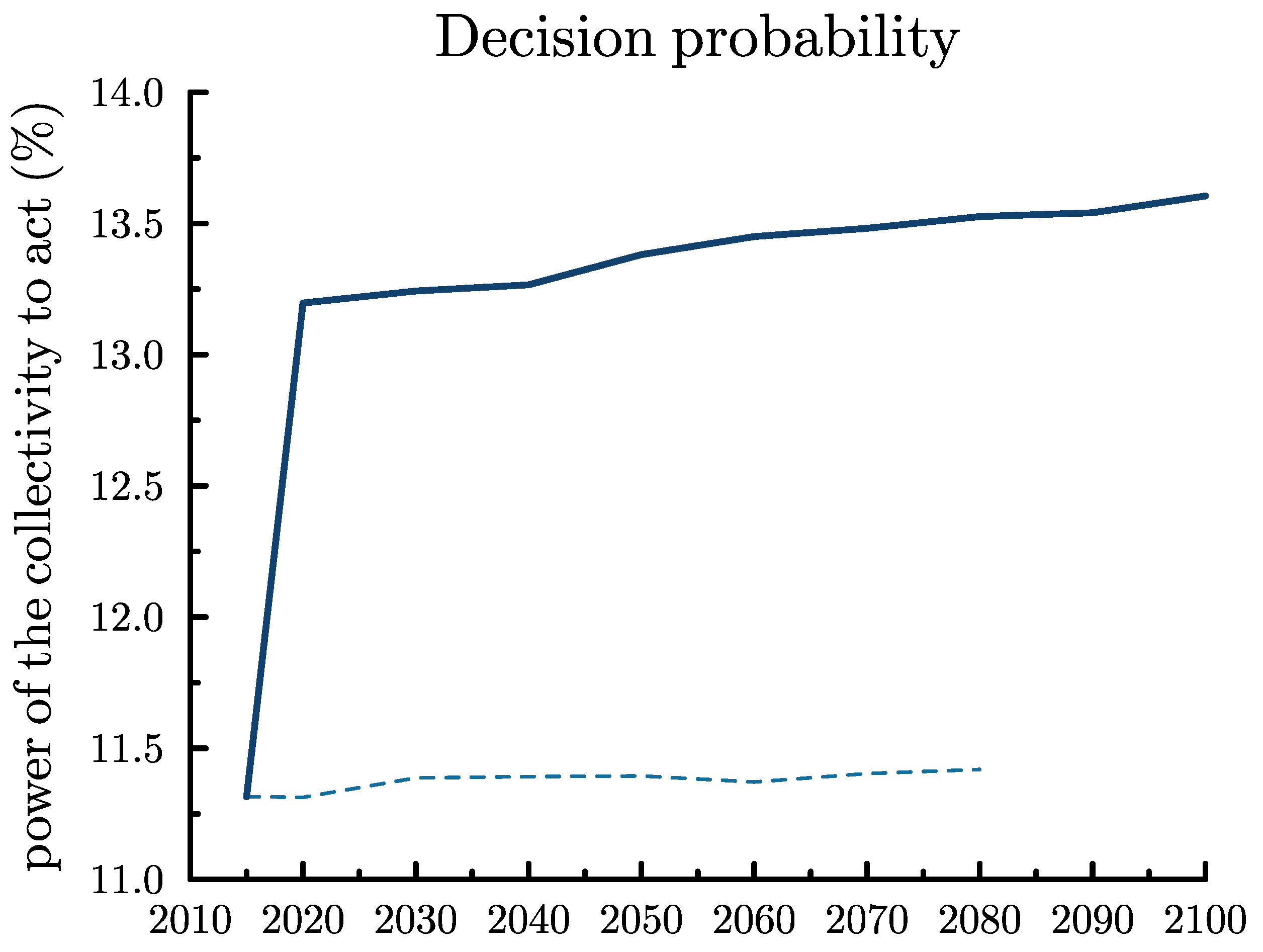
3.5. Inertia
3.6. Brexit as a Threat
3.7. Extensions and Generalizations
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CEEC | Central and Eastern European Country |
| EEC | European Economic Community |
| EU | European Union |
| UK | United Kingdom |
Appendix A. Tables
| 2015 | 2020 | 2030 | 2040 | 2050 | 2060 | 2070 | 2080 | |
|---|---|---|---|---|---|---|---|---|
| Austria | 2.02 | 2.04 | 2.10 | 2.13 | 2.14 | 2.15 | 2.15 | 2.15 |
| Belgium | 2.42 | 2.48 | 2.62 | 2.73 | 2.86 | 2.96 | 3.05 | 3.13 |
| Bulgaria | 1.82 | 1.78 | 1.70 | 1.64 | 1.60 | 1.57 | 1.54 | 1.51 |
| Croatia | 1.39 | 1.38 | 1.38 | 1.36 | 1.33 | 1.33 | 1.32 | 1.32 |
| Cyprus | 0.92 | 0.92 | 0.94 | 0.95 | 0.96 | 0.98 | 1.00 | 1.02 |
| Czech Republic | 2.30 | 2.30 | 2.31 | 2.31 | 2.33 | 2.35 | 2.34 | 2.34 |
| Denmark | 1.59 | 1.61 | 1.65 | 1.67 | 1.68 | 1.71 | 1.75 | 1.77 |
| Estonia | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.98 | 0.99 | 0.99 |
| Finland | 1.57 | 1.58 | 1.62 | 1.64 | 1.66 | 1.67 | 1.70 | 1.71 |
| France | 11.27 | 11.45 | 11.78 | 12.13 | 12.35 | 12.65 | 12.98 | 13.26 |
| Germany | 14.43 | 14.23 | 13.76 | 13.15 | 12.43 | 11.74 | 11.14 | 10.61 |
| Greece | 2.37 | 2.31 | 2.21 | 2.13 | 2.06 | 2.00 | 1.94 | 1.89 |
| Hungary | 2.21 | 2.18 | 2.15 | 2.11 | 2.10 | 2.08 | 2.05 | 2.03 |
| Ireland | 1.44 | 1.44 | 1.44 | 1.45 | 1.49 | 1.53 | 1.58 | 1.65 |
| Italy | 10.24 | 10.35 | 10.59 | 10.88 | 10.97 | 10.85 | 10.69 | 10.55 |
| Latvia | 1.08 | 1.06 | 1.03 | 1.02 | 1.03 | 1.02 | 1.03 | 1.04 |
| Lithuania | 1.20 | 1.17 | 1.11 | 1.09 | 1.08 | 1.07 | 1.08 | 1.09 |
| Luxembourg | 0.88 | 0.88 | 0.92 | 0.94 | 0.97 | 0.98 | 1.00 | 1.02 |
| Malta | 0.85 | 0.85 | 0.88 | 0.89 | 0.90 | 0.90 | 0.91 | 0.92 |
| Netherlands | 3.27 | 3.28 | 3.31 | 3.29 | 3.24 | 3.20 | 3.18 | 3.14 |
| Poland | 6.43 | 6.33 | 6.07 | 5.79 | 5.58 | 5.39 | 5.15 | 4.89 |
| Portugal | 2.28 | 2.22 | 2.17 | 2.10 | 2.03 | 1.94 | 1.87 | 1.81 |
| Romania | 3.74 | 3.69 | 3.53 | 3.42 | 3.33 | 3.25 | 3.16 | 3.09 |
| Slovakia | 1.56 | 1.55 | 1.54 | 1.51 | 1.48 | 1.45 | 1.41 | 1.37 |
| Slovenia | 1.09 | 1.09 | 1.10 | 1.10 | 1.11 | 1.10 | 1.11 | 1.12 |
| Spain | 7.56 | 7.37 | 6.98 | 6.85 | 6.88 | 6.97 | 7.00 | 7.13 |
| Sweden | 2.18 | 2.22 | 2.34 | 2.42 | 2.51 | 2.63 | 2.70 | 2.78 |
| United Kingdom | 10.95 | 11.25 | 11.80 | 12.33 | 12.94 | 13.59 | 14.15 | 14.66 |
| 2015 | 2020 | 2030 | 2040 | 2050 | 2060 | 2070 | 2080 | |
|---|---|---|---|---|---|---|---|---|
| Austria | 2.16 | 2.18 | 2.24 | 2.27 | 2.29 | 2.31 | 2.31 | 2.32 |
| Belgium | 2.59 | 2.66 | 2.82 | 2.96 | 3.09 | 3.21 | 3.32 | 3.41 |
| Bulgaria | 1.91 | 1.87 | 1.79 | 1.71 | 1.66 | 1.62 | 1.59 | 1.54 |
| Croatia | 1.42 | 1.42 | 1.41 | 1.38 | 1.35 | 1.34 | 1.34 | 1.32 |
| Cyprus | 0.88 | 0.89 | 0.90 | 0.91 | 0.91 | 0.93 | 0.95 | 0.97 |
| Czech Republic | 2.46 | 2.46 | 2.48 | 2.48 | 2.51 | 2.52 | 2.54 | 2.53 |
| Denmark | 1.65 | 1.68 | 1.73 | 1.74 | 1.76 | 1.78 | 1.83 | 1.85 |
| Estonia | 0.95 | 0.95 | 0.94 | 0.94 | 0.93 | 0.93 | 0.93 | 0.93 |
| Finland | 1.63 | 1.64 | 1.69 | 1.71 | 1.73 | 1.73 | 1.76 | 1.78 |
| France | 13.41 | 13.68 | 14.21 | 14.77 | 15.28 | 15.94 | 16.58 | 17.19 |
| Germany | 17.42 | 17.23 | 16.77 | 16.14 | 15.38 | 14.67 | 14.05 | 13.53 |
| Greece | 2.54 | 2.48 | 2.37 | 2.27 | 2.20 | 2.13 | 2.06 | 2.00 |
| Hungary | 2.36 | 2.34 | 2.30 | 2.26 | 2.24 | 2.22 | 2.19 | 2.18 |
| Ireland | 1.49 | 1.48 | 1.49 | 1.49 | 1.54 | 1.57 | 1.64 | 1.70 |
| Italy | 12.12 | 12.31 | 12.68 | 13.15 | 13.47 | 13.50 | 13.46 | 13.46 |
| Latvia | 1.06 | 1.05 | 1.01 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 |
| Lithuania | 1.21 | 1.18 | 1.10 | 1.07 | 1.05 | 1.03 | 1.04 | 1.06 |
| Luxembourg | 0.84 | 0.84 | 0.88 | 0.89 | 0.93 | 0.93 | 0.95 | 0.97 |
| Malta | 0.81 | 0.81 | 0.83 | 0.83 | 0.83 | 0.83 | 0.84 | 0.85 |
| Netherlands | 3.51 | 3.53 | 3.57 | 3.55 | 3.51 | 3.48 | 3.46 | 3.42 |
| Poland | 7.11 | 7.08 | 6.90 | 6.64 | 6.34 | 6.13 | 5.82 | 5.45 |
| Portugal | 2.44 | 2.39 | 2.32 | 2.24 | 2.16 | 2.06 | 1.98 | 1.90 |
| Romania | 4.01 | 3.94 | 3.79 | 3.68 | 3.60 | 3.52 | 3.45 | 3.36 |
| Slovakia | 1.61 | 1.61 | 1.60 | 1.56 | 1.52 | 1.48 | 1.43 | 1.38 |
| Slovenia | 1.08 | 1.08 | 1.09 | 1.09 | 1.08 | 1.07 | 1.08 | 1.09 |
| Spain | 9.00 | 8.86 | 8.58 | 8.67 | 8.94 | 9.26 | 9.49 | 9.81 |
| Sweden | 2.33 | 2.39 | 2.51 | 2.60 | 2.71 | 2.85 | 2.95 | 3.01 |
| 2015 | 2020 | 2030 | 2040 | 2050 | 2060 | 2070 | 2080 | |
|---|---|---|---|---|---|---|---|---|
| Austria | 1.97 | 1.98 | 2.04 | 2.07 | 2.09 | 2.10 | 2.10 | 2.11 |
| Belgium | 2.36 | 2.42 | 2.57 | 2.70 | 2.82 | 2.92 | 3.03 | 3.11 |
| Bulgaria | 1.74 | 1.70 | 1.63 | 1.56 | 1.52 | 1.48 | 1.45 | 1.40 |
| Croatia | 1.30 | 1.29 | 1.28 | 1.25 | 1.23 | 1.22 | 1.22 | 1.20 |
| Cyprus | 0.81 | 0.81 | 0.82 | 0.83 | 0.83 | 0.84 | 0.87 | 0.89 |
| Czech Republic | 2.24 | 2.25 | 2.26 | 2.26 | 2.29 | 2.30 | 2.31 | 2.31 |
| Denmark | 1.50 | 1.53 | 1.57 | 1.59 | 1.61 | 1.62 | 1.67 | 1.69 |
| Estonia | 0.87 | 0.87 | 0.86 | 0.86 | 0.85 | 0.84 | 0.85 | 0.84 |
| Finland | 1.49 | 1.50 | 1.54 | 1.56 | 1.58 | 1.58 | 1.61 | 1.63 |
| France | 12.22 | 12.48 | 12.95 | 13.46 | 13.93 | 14.54 | 15.11 | 15.67 |
| Germany | 15.88 | 15.71 | 15.29 | 14.71 | 14.03 | 13.37 | 12.81 | 12.34 |
| Greece | 2.32 | 2.26 | 2.16 | 2.07 | 2.00 | 1.94 | 1.87 | 1.82 |
| Hungary | 2.16 | 2.13 | 2.10 | 2.06 | 2.05 | 2.03 | 2.00 | 1.99 |
| Ireland | 1.36 | 1.35 | 1.35 | 1.36 | 1.40 | 1.44 | 1.49 | 1.55 |
| Italy | 11.05 | 11.23 | 11.56 | 11.99 | 12.28 | 12.31 | 12.27 | 12.27 |
| Latvia | 0.97 | 0.95 | 0.92 | 0.90 | 0.90 | 0.89 | 0.90 | 0.90 |
| Lithuania | 1.10 | 1.07 | 1.01 | 0.98 | 0.96 | 0.94 | 0.95 | 0.96 |
| Luxembourg | 0.76 | 0.76 | 0.80 | 0.81 | 0.85 | 0.84 | 0.87 | 0.89 |
| Malta | 0.73 | 0.74 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 | 0.77 |
| Netherlands | 3.20 | 3.21 | 3.26 | 3.24 | 3.20 | 3.17 | 3.16 | 3.12 |
| Poland | 6.48 | 6.45 | 6.29 | 6.05 | 5.78 | 5.59 | 5.31 | 4.97 |
| Portugal | 2.23 | 2.18 | 2.12 | 2.05 | 1.97 | 1.88 | 1.80 | 1.73 |
| Romania | 3.65 | 3.59 | 3.45 | 3.35 | 3.28 | 3.21 | 3.14 | 3.06 |
| Slovakia | 1.47 | 1.47 | 1.46 | 1.42 | 1.39 | 1.35 | 1.31 | 1.26 |
| Slovenia | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 |
| Spain | 8.20 | 8.08 | 7.83 | 7.90 | 8.15 | 8.44 | 8.65 | 8.95 |
| Sweden | 2.13 | 2.18 | 2.29 | 2.37 | 2.47 | 2.60 | 2.69 | 2.74 |
| 2020 | 2030 | 2040 | 2050 | 2060 | 2070 | 2080 | 2090 | 2100 | |
|---|---|---|---|---|---|---|---|---|---|
| Austria | 1.99 | 2.01 | 2.04 | 2.04 | 2.06 | 2.07 | 2.08 | 2.09 | 2.10 |
| Belgium | 2.37 | 2.40 | 2.41 | 2.42 | 2.44 | 2.46 | 2.48 | 2.50 | 2.52 |
| Bulgaria | 1.70 | 1.63 | 1.56 | 1.53 | 1.47 | 1.45 | 1.43 | 1.42 | 1.43 |
| Croatia | 1.28 | 1.24 | 1.23 | 1.20 | 1.17 | 1.15 | 1.15 | 1.14 | 1.15 |
| Cyprus | 0.81 | 0.83 | 0.83 | 0.85 | 0.87 | 0.88 | 0.89 | 0.89 | 0.90 |
| Czech Republic | 2.25 | 2.25 | 2.22 | 2.22 | 2.22 | 2.22 | 2.22 | 2.23 | 2.26 |
| Denmark | 1.53 | 1.56 | 1.58 | 1.58 | 1.59 | 1.62 | 1.64 | 1.64 | 1.65 |
| Estonia | 0.87 | 0.87 | 0.88 | 0.89 | 0.88 | 0.89 | 0.90 | 0.89 | 0.90 |
| Finland | 1.48 | 1.49 | 1.48 | 1.47 | 1.46 | 1.45 | 1.45 | 1.44 | 1.43 |
| France | 12.26 | 12.54 | 12.83 | 13.03 | 13.36 | 13.45 | 13.52 | 13.54 | 13.52 |
| Germany | 16.27 | 16.27 | 16.23 | 16.33 | 16.61 | 16.87 | 17.09 | 17.30 | 17.43 |
| Greece | 2.25 | 2.18 | 2.12 | 2.07 | 2.01 | 1.98 | 1.95 | 1.94 | 1.93 |
| Hungary | 2.12 | 2.08 | 2.05 | 2.04 | 2.03 | 2.02 | 2.02 | 2.02 | 2.03 |
| Ireland | 1.41 | 1.49 | 1.55 | 1.60 | 1.63 | 1.67 | 1.70 | 1.71 | 1.71 |
| Italy | 10.79 | 10.68 | 10.66 | 10.56 | 10.35 | 10.14 | 10.01 | 9.91 | 9.78 |
| Latvia | 0.96 | 0.93 | 0.91 | 0.91 | 0.90 | 0.89 | 0.89 | 0.89 | 0.90 |
| Lithuania | 1.09 | 1.06 | 1.03 | 1.02 | 1.00 | 0.98 | 0.97 | 0.98 | 0.98 |
| Luxembourg | 0.77 | 0.79 | 0.79 | 0.82 | 0.82 | 0.83 | 0.84 | 0.84 | 0.85 |
| Malta | 0.75 | 0.77 | 0.78 | 0.80 | 0.81 | 0.82 | 0.83 | 0.83 | 0.84 |
| Netherlands | 3.25 | 3.31 | 3.33 | 3.33 | 3.34 | 3.39 | 3.42 | 3.44 | 3.44 |
| Poland | 6.29 | 6.05 | 5.82 | 5.60 | 5.43 | 5.29 | 5.10 | 4.95 | 4.88 |
| Portugal | 2.19 | 2.15 | 2.11 | 2.06 | 2.00 | 1.96 | 1.94 | 1.93 | 1.92 |
| Romania | 3.53 | 3.28 | 3.10 | 2.96 | 2.84 | 2.76 | 2.69 | 2.65 | 2.65 |
| Slovakia | 1.48 | 1.48 | 1.46 | 1.44 | 1.43 | 1.40 | 1.39 | 1.38 | 1.37 |
| Slovenia | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.01 | 1.01 |
| Spain | 8.32 | 8.57 | 8.79 | 8.93 | 8.94 | 8.88 | 8.85 | 8.87 | 8.81 |
| Sweden | 2.19 | 2.29 | 2.38 | 2.48 | 2.56 | 2.66 | 2.73 | 2.75 | 2.78 |
References
- Goodwin, M.; Hix, S.; Pickup, M. For and against Brexit: A survey experiment of the impact of campaign effects on public attitudes toward EU membership. Br. J. Political Sci. 2020, 50, 481–495. [Google Scholar] [CrossRef] [Green Version]
- Buckle, R.; Hewish, T.; Hulsman, J.C.; Mansfield, I.; Oulds, R. Directions for Britain Outside the EU; Institute or Economic Affairs: London, UK, 2015. [Google Scholar]
- Celebi, K. Quo Vadis, Britain?—Implications of the Brexit process on the UK’s real economy. Int. Econ. Econ. Policy 2021, 18, 267–307. [Google Scholar] [CrossRef]
- Dagnis Jensen, M.; Snaith, H. When politics prevails: The political economy of a Brexit. J. Eur. Public Policy 2016, 1763, 1–9. [Google Scholar]
- Oliver, T. European and international views of Brexit. J. Eur. Public Policy 2016, 1763, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kóczy, L.Á. Beyond Lisbon: Demographic trends and voting power in the European Union Council of Ministers. Math. Soc. Sci. 2012, 63, 152–158. [Google Scholar] [CrossRef] [Green Version]
- Felsenthal, D.S.; Machover, M. A priori voting power: What is it all about? Political Stud. Rev. 2004, 2, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Kauppi, H.; Widgrén, M. What determines EU decision making? Needs, power or both? Econ. Policy 2004, 39, 221–266. [Google Scholar] [CrossRef]
- Shapley, L.S.; Shubik, M. A method for evaluating the distribution of power in a committee system. Am. Political Sci. Rev. 1954, 48, 787–792. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games II, Vol. II of Annals of Mathematics Studies; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar]
- Zaporozhets, V.; García-Valiñas, M.; Kurz, S. Key drivers of EU budget allocation: Does power matter? Eur. J. Political Econ. 2016, 43, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Montero, M. On the nucleolus as a power index. Homo Oeconomicus 2013, 22, 551–567. [Google Scholar]
- Schmeidler, D. The nucleolus of a characteristic function game, SIAM. J. Appl. Math. 1969, 17, 1163–1170. [Google Scholar]
- Eurostat, 2014, EUROPOP2013—Convergence Scenario, National Level, Population Predictions—[tps00002]. Available online: https://ec.europa.eu/eurostat/databrowser/view/tps00002/default/table?lang=en (accessed on 16 April 2016).
- Eurostat, 2020, EUROPOP2019—Convergence Scenario, National Level, Population Predictions—[tps00002]. Available online: https://ec.europa.eu/eurostat/databrowser/view/PROJ_19NP/default/table?lang=en (accessed on 29 May 2020).
- Bräuninger, T.; König, T. Indices of Power IOP 2.0. 2005. Available online: http://www.tbraeuninger.de/IOP.html (accessed on 10 November 2018).
- Brams, S.J.; Affuso, P.J. Power and size: A new paradox. Theory Decis. 1976, 7, 29–56. [Google Scholar] [CrossRef]
- Kóczy, L.Á. Measuring voting power: The paradox of new members vs. the null player axiom. In Towards Intelligent Engineering and Information Technology; Rudas, I.J., Fodor, J., Kacprzyk, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 67–78. [Google Scholar]
- van Deemen, A.; Rusinowska, A. Paradoxes of voting power in Dutch politics. Public Choice 2003, 115, 109–137. [Google Scholar] [CrossRef]
- Rusinowska, A.; van Deemen, A. The Redistribution Paradox and the Paradox of New Members in the German Parliament. In Game Theory and Applications; Petrosyan, L.A., Mazalov, V.V., Eds.; Nova: New York, NY, USA, 2005; pp. 153–174. [Google Scholar]
- European Parliament. EU Budget Explained: Expenditure and Contribution by Member State. United Kingdom. 2015. Available online: http://www.europarl.europa.eu/news/en/news-room/20141202IFG82334/EU-budget-explained-expenditure-and-contribution-by-member-state (accessed on 16 April 2016).
- Petróczy, D.G.; Rogers, M.F.; Kóczy, L.Á. Brexit: The belated threat. arXiv 2018, arXiv:1808.05142v1. [Google Scholar]
- Göllner, R.T. The Visegrád Group—A rising star post-Brexit? Changing distribution of power in the European Council. Open Political Sci. 2008, 1, 1–6. [Google Scholar] [CrossRef]
- Coleman, J.S. Control of collectives and the power of a collectivity to act. In Social Choice; Lieberman, B., Ed.; Gordon and Breach: New York, NY, USA, 1971; pp. 192–225. [Google Scholar]
- Kroll, D.A.; Leuffen, D. Ties that bind, can also strangle: The Brexit threat and the hardships of reforming the EU. J. Eur. Public Policy 2016, 23, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Hix, S.; Hagemann, S.; Frantescu, D. Would Brexit Matter? The UK’s Voting Record in the Council and the European Parliament, Tech. Rep. April, VoteWatch Europe, Brussels. 2016. Available online: http://www.votewatch.eu/blog/special-report-would-brexit-matter-the-uks-voting-record-in-the-council-and-the-european-parliament/ (accessed on 16 May 2018).
- Gładysz, B.; Mercik, J.; Ramsey, D.M. The Effect of Brexit on the Balance of Power in the European Union Council Revisited: A Fuzzy Multicriteria Attempt. In Transactions on Computational Collective Intelligence XXXI. Lecture Notes in Computer Science; Nguyen, N., Kowalczyk, R., Mercik, J., Motylska-Kuźma, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 11290, pp. 87–107. [Google Scholar]
- Mercik, J.; Ramsey, D.M. The effect of Brexit on the balance of power in the European Union Council: An approach based on pre-coalitions. In Transactions on Computational Collective Intelligence XXVII. Lecture Notes in Computer Science; Nguyen, N., Kowalczyk, R., Mercik, J., Eds.; Springer: Cham, Switzerland, 2017; Volume 10480, pp. 87–107. [Google Scholar]
- Mayer, A. Luxembourg in the Early Days of the EEC: Null Player or Not? Games 2018, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Fertő, I.; Kóczy, L.Á.; Kovács, A.; Sziklai, B.R. The power ranking of the member s of the Agricultural Committee of the European Parliament. Eur. J. Agric. Econ. 2020, 47, 1897–1919. [Google Scholar] [CrossRef]
- Kóczy, L.Á.; Sziklai, B. Electing the Pope. Homo Oeconomicus 2015, 32, 101–116. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kóczy, L.Á. Brexit and Power in the Council of the European Union. Games 2021, 12, 51. https://doi.org/10.3390/g12020051
Kóczy LÁ. Brexit and Power in the Council of the European Union. Games. 2021; 12(2):51. https://doi.org/10.3390/g12020051
Chicago/Turabian StyleKóczy, László Á. 2021. "Brexit and Power in the Council of the European Union" Games 12, no. 2: 51. https://doi.org/10.3390/g12020051
APA StyleKóczy, L. Á. (2021). Brexit and Power in the Council of the European Union. Games, 12(2), 51. https://doi.org/10.3390/g12020051






