Abstract
We show that even if information transmission through an honest outside agency is not possible due to the possibility of collusion between the firms and the outside agency, information transmission is still possible through technology licensing. However, unlike the case of a cost-free honest outside agency, where information transmission always occurs under a quantity setting oligopoly, information transmission through licensing does not always occur.
1. Introduction
It is argued that firms prefer to share private information about their costs of production in a quantity setting oligopoly ([1,2,3,4])1. However, this conclusion is based on the important assumption that a cost-free “honest outside agency” verifies reports about firms’ costs (or technologies) and transmits this information. We will use the term technology and cost interchangeably, and a lower cost of production implies better technology.
The simplest way to solve the asymmetric information problem of a firm’s technology is to allow the competitors to see its technology. However, information disclosure through direct inspection of the technology by the competitors is not a feasible option if the competitors can imitate or invent around the technology without having to compensate the technology owner sufficiently for doing so.
If direct inspection is not a feasible option, information disclosure is possible if a cost-free honest outside agency verifies the technology and reports its findings. However, the assumption of an honest outside agency is debatable. First, there may not be any outside agency that can verify the costs. Second, even if the outside agency can verify the reports, appealing to [5], there may be the possibility of collusion between the firms and the outside agency which makes verification by an outside agency ineffective. For example, the firm with private information may collude with the outside agency for a favourable report that gives it a strategic advantage in the product market. Or the outside agency may pass technical information about the technology to the firm with the lack of information, and if imitation is easy, as is assumed in this paper2, the firm with the lack of information can use that information to ”invent around” the technology to enjoy the benefits in the product market. Hence, the possibility of collusion between the firm(s) and the outside agency reduces the effectiveness of information transmission through an outside agency.
Considering one sided private information, we show in this paper that even if information transmission either through direct inspection or through an outside agency is not possible, technology licensing helps information sharing and may make the firms better off. However, unlike the papers on information sharing through an outside agency, information sharing through technology licensing does not always occur in a quantity setting oligopoly. This difference occurs because the technological information is verifiable but inimitable when information disclosure occurs through an outside agency, but it is imitable when information disclosure occurs through licensing. Hence, information disclosure through an outside agency does not allow the uninformed firm to be more competitive in the product market but information disclosure through licensing makes the uninformed firm more competitive in the product market. Although licensing allows the informed firm to receive compensation for disclosing information about its technology, increased competitiveness of the uninformed firm reduces the incentive for information disclosure through licensing compared to an outside agency.
In what follows, we considered a Cournot duopoly with asymmetric costs of production. We assumed that the firm with the lower cost of production has private information about its cost, while the other firm’s cost is common knowledge. New technological development maybe the reason for asymmetric information about the quality of the technology. For simplicity, we assumed that the cost of the low-cost firm may be either or , where and both and are lower than the cost of production of the other firm.
We argue in Section 2 that information disclosure always occurs in the presence of an honest outside agency. In Section 3, we considered the possibility of collusion between the firms and the outside agency and the resulting problem of imitation by the high-cost firm that makes information transmission through an outside agency or direct inspection ineffective. We show that information transmission in this situation may occur through technology licensing with a fixed fee3. Since technology licensing allows the high-cost firm to use the technology of the low-cost firm, the low-cost firm faces higher competition from the high-cost firm. This effect tends to reduce the incentive for licensing. On the other hand, technology licensing helps to reveal information and allows the low-cost firm to increase its profit due to the licensing fee. These effects tend to create the incentive for information revelation. We show the condition under which the former competition enhancing effect is not strong, and makes technology licensing profitable.
Thus, our paper also contributes to the vast literature on technology licensing by considering asymmetric information. It is well-known that if there is complete information and imitation is easy, licensing occurs with an up-front fixed-fee, and it occurs if the technological difference between the licenser and the licensee is not large ([6,7,8,9]). We derived a condition for technology licensing with an up-front fixed fee in the presence of asymmetric information.
There are some other papers where licensing occurs under asymmetric information. In [10], a situation in which the licensee’s benefit from the licensed technology is private information is considered, while [11] assumes that the initial cost of the licensee is private information. In contrast, the quality of the licenser’s technology is private information in our analysis. In [12,13,14,15,16,17], licensing under asymmetric information is also considered. However, unlike our paper, those papers do not consider the competition between the licenser and licensee in the product market.
The remainder of the paper is organized as follows. We describe the model in Section 2 and show the preference for information sharing if there is a cost-free honest outside agency, which acts as the benchmark for our analysis in Section 3 where the possibility of collusion between the firms and the outside agency make the use of an outside agency ineffective. Section 4 concludes.
2. The Model and the Benchmark Case of an Honest outside Agency
Assume that there are two firms, called firm 1 and firm 2, producing homogeneous goods. Firm 1 has constant average cost of production and this is known to both firms. However, the production technology of firm 2 is private information. For simplicity, assume that the production technology of firm 2 can be one of the two types—generating the constant average cost or , where . While firm 2 knows its cost of production perfectly, firm 1 knows that the cost of production of firm 2 will be either with probability or with probability . We assumed that both firms know the probability distribution. Innovation by firm 2 may be the reason for generating a new technology, whose quality is not perfectly known to firm 1. Hence, similar to [6,7,8,9,14,18,19], we considered a situation where firms differ in production technologies and product substitutability is not dependent on the technology of production.
We considered in this section that firm 2 can take the help of a cost-free honest outside agency to disclose the true information about its cost. Hence, firm 1 can know the true cost of firm 2 but cannot obtain the knowledge about firm 2’s technology. Hence, this section will act as the benchmark for our main analysis with no honest outside agency that we considered in Section 3.
We considered the following game in this section. In stage 1, firm 2 decides whether to disclose information through an honest outside agency. In stage 2, the firms choose their outputs like Cournot duopolists. We solved the game through backward induction.
Assume that the inverse market demand function is
where P is price and q is the total output. Throughout the analysis, we assumed that . This restriction guarantees that both firms always produce positive outputs irrespective of the cost of production of firm 2. Hence, the market structure is a duopoly always. We assumed that the firms maximize expected profits.
Proposition 1.
If there is Cournot competition between the firms and there is a cost-free honest outside agency, firm 2’s true cost will be disclosed in equilibrium.
Proof.
Firms compete like Cournot duopolists. If there is no information disclosure, firm 1 considers firm 2 having the cost with probability or with probability . Hence, the equilibrium profits of firm 2 having the actual cost and are, respectively, and .
If the information is disclosed, the equilibrium profits of firm 2 having the actual cost and are, respectively, and .
Since and 4, firm 2 having the actual cost will prefer to disclose information, but firm 2 having the actual cost will not prefer to disclose the information. Hence, if firm 2 does not disclose the information, firm 1 will correctly infer that firm 2’s actual cost is .
Therefore, firm 2 having the actual cost will disclose information, and firm 2 having the actual cost will either disclose information or its cost will be inferred correctly by firm 1, implying that correct information will be disclosed. □
Since the profit of a firm increases as its marginal cost reduces, we obtained the above result.
3. Technology Licensing in the Absence of an Honest outside Agency
Now, consider the situation where an honest outside agency is not available. As discussed in the introduction, the possibility of collusion between the firms and the outside agency makes the use of an outside agency ineffective. Since firm 1 can imitate the technology of firm 2 easily after obtaining the technology, one way firm 2 can disclose information is through technology licensing.
We consider the following game in this section. In stage 1, firm 2 decides whether to license its technology to firm 1. Following [6,7,8,9] and many others, we assumed that, in the case of licensing, firm 2 licenses its technology against an up-front fixed fee. The reasons for the licensing contract are either costless imitation (that is, ”inventing around”5 the licensed technology by firm 1 after obtaining it) or the lack of information about firm 1’s output. In the case of licensing, firm 2 makes a take-it-or-leave-it offer to firm 1, who either accepts or rejects it. Firm 1 accepts an offer if the offer does not make it worse off compared to no licensing. Conditional on the decision on technology licensing, the firms choose their outputs in stage 2 like Cournot duopolists.
We considered a Perfect Bayesian Equilibrium. The following strategy and firm 1’s belief about firm 2’s cost, after observing firm 1’s decision on technology licensing (i.e., whether or not to license the technology), constitute a Perfect Bayesian Equilibrium: Firm 2’s strategy is to license its technology irrespective of its cost if , where is shown below in (2). Firm 1’s strategy is to accept the licensing contract if it is not worse off under licensing compared to no licensing. If licensing does not occur, firm 1 correctly believes that the cost of firm 2 is with probability and with probability
If licensing occurs, which is on the equilibrium path, the net profits of firm 1 are either , if firm 2 has the cost , or , if firm 2 has the cost , where the term is the fixed fee under licensing charged by firm 2.
Under licensing, the net profits of firm 2 are , if firm 2 has the cost (which occurs with probability p), or , if firm 2 has the cost (which occurs with probability (1 − p)).
If licensing does not occur, firm 1’s expected profit is , since the off equilibrium belief by firm 1 is that firm 2’s cost is with probability z and its cost is with probability (1 − z).
Under no licensing, the profits of firm 2 are either if its cost is or if its cost is .
Since the up-front fixed-fee, F, is paid at the time of licensing, the maximum amount firm 1 is willing to pay is ,6 where is firm 1’s expected profit under licensing, and is firm 1’s expected profit under no licensing. Firm 1’s net expected profit under licensing is . Hence, both the fixed-fee and firm 1’s net expected profit depend on the off-equilibrium outcome.
Now, let us check if licensing makes firm 2 better off. If firm 2 has the cost , it will find licensing profitable if . Similarly, if firm 2 has the cost , it will find licensing profitable if . Since it implies that firm 2 will license the technology irrespective of its cost if , which happens for , where
The above discussion is summarized in the following proposition.
Proposition 2.
If the firms compete like Cournot duopolists and no licensing induces firm 1 to believe that firm 2’s cost iswith probability z andwith probability (1 − z), firm 2 discloses information about its technology through licensing in equilibrium irrespective of its cost ifwhereis shown in (2).
The above result suggests that even if information disclosure via an outside agency is not a feasible option, information disclosure may occur through technology licensing. However, unlike the literature where information disclosure through an outside agency occurs for any cost difference, here, information disclosure occurs provided is sufficiently high.
As an example, we plotted in Figure 1 for the following two cases: (i) , , , , and , and (ii) , , , , and . If increases, it reduces the licensing fee and the low-cost firm 2’s expected profit under no licensing. However, the loss under no licensing due to asymmetric information is more than the loss from the licensing fee, since asymmetric information reduces the low-cost firm 2’s market share significantly under no licensing. As a result, a higher makes the curves in Figure 1 upward sloping. In Figure 1, is given by the point where the curves intersect the horizontal axis, i.e., for case (i) and for case (ii). Hence, as z falls, the possibility of information disclosure reduces. If z falls, on one hand, it reduces firm 2’s profit under no licensing, which tends to increase the incentive for licensing, but, on the other hand, it reduces the fixed-fee, which tends to reduce the incentive for licensing. Since licensing makes firm 1 more competitive in the product market, the effect due to a lower fixed fee dominates the effect created by firm 2’s lower profit under no licensing, thus reducing the possibility of information disclosure through licensing.
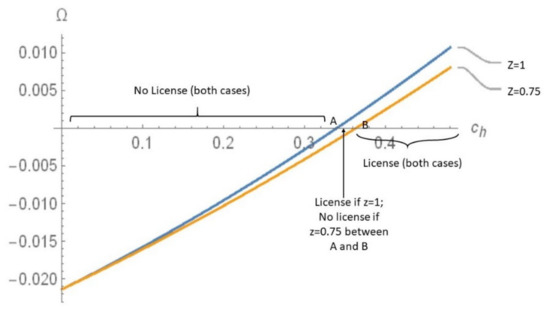
Figure 1.
Licensing vs. No Licensing for Cases (i) and (ii).
The purpose of this paper is to show that even if direct inspection or using an honest outside agency is not effective to disclose information, information disclosure may occur through licensing. Proposition 2 shows an equilibrium where information disclosure occurs through licensing. The next question examines whether there is any other equilibrium that is preferable by firm 2 compared to the equilibrium considered in Proposition 2, and if firm 2 can have both the options—information disclosure through an outside agency and through licensing—which one will be its preferable option? We leave this question for future research, yet it will be still useful to discuss whether firms will prefer an outside agency or licensing to disclose information for the equilibria shown in Propositions 1 and 2.
If there is an honest outside agency, the profit of firm 2 will be either or depending on its cost as either or respectively. However, if information disclosure occurs through licensing, the profits of firm 2 are either or , depending on its cost as either or , respectively, where . Hence, firm 2 prefers (does not prefer) licensing compared to an outside agency if or , depending on its cost as either or , respectively. We used the following two diagrams to show that firm 2 may or may not prefer an honest outside agency compared to information disclosure through licensing.
Figure 2 plots for the values of (iii) , , and and (iv) , , and . The curves in Figure 2 are downward sloping with respect to , since a higher reduces the licensing fee. Figure 3 plots for the values of (v) , , and and (vi) , , and . A higher reduces firm 2’s profits under both licensing and information disclosure through an outside agency. However, firm 2’s higher market share under an outside agency compared to licensing helps to create its loss from a higher more under the former than the latter. As a result, a higher makes the curves in Figure 3 upward sloping. In both Figures, firm 2 prefers licensing compared to an outside agency if the curves are in the positive quadrant.
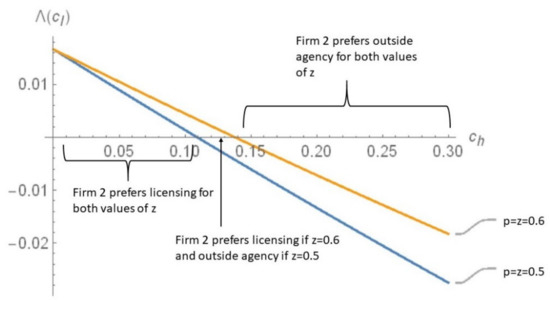
Figure 2.
Outside agency vs. licensing for Cases (iii) and (iv).
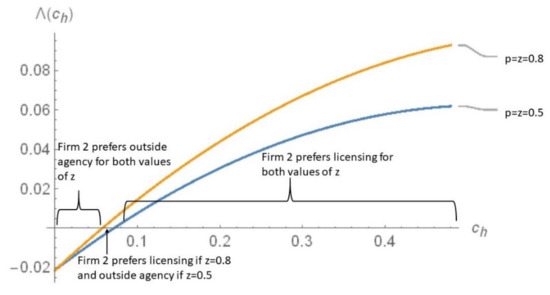
Figure 3.
Outside agency vs. licensing for Cases (v) and (vi).
It follows from Figure 2 and Figure 3 that whether firm 2 prefers licensing compared to an outside agency for low (high) values of depends on whether firm 1’s cost is (). This happens since firm 2 benefits (loses) from asymmetric information if its cost is ().
Now consider firm 1’s preference for an outside agency compared to licensing. If information disclosure occurs through an outside agency, firm 1’s expected profit is . However, firm 1’s expected profit under licensing is . If , we obtain . Since the difference increases with z, it is immediate that for . Now consider the case where p > z and the difference between (p − z) is maximum, i.e., p = 1 and z = 0. If p = 1 and z = 0, we obtain . Hence, firm 1 prefers an outside agency compared to licensing if either or but the difference between p and z is small; otherwise, it prefers licensing. We considered that firm 2 offers a take-it-or-leave-it licensing contract. If firm 1 could bargain for the licensing fee, it would increase its preference for licensing compared to outside agency.
4. Conclusions
It has been argued that firms in a quantity setting oligopoly have the incentive to disclose information through a cost-free honest outside agency. However, the possibility of collusion between the firms and the outside agency may make the use of an outside agency ineffective. We show that even if the use of an outside agency is ineffective, information disclosure may still occur through technology licensing for certain cost difference between the firms, which is different from the case of using an outside agency where information disclosure always occurs. Our paper also contributes to the literature on technology licensing by considering licensing under asymmetric information.
Author Contributions
Conceptualization, A.M. and A.B.; methodology, A.M. and A.B.; formal analysis, A.M. and A.B.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank two anonymous referees of this journal, Roger Hartley, Tarun Kabiraj, and Uday Bhanu Sinha for helpful comments and suggestions on a different version of this paper. We also benefited from discussion with Martin Sefton. This paper is a significantly improved version of a paper that was circulated as a working paper entitled “Licensing under asymmetric information”. The usual disclaimer applies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fried, D. Incentives for information production and disclosure in a duopolistic environment. Q. J. Econ. 1984, 99, 367–381. [Google Scholar] [CrossRef]
- Li, L. Cournot oligopoly with information sharing. RAND J. Econ. 1985, 16, 521–536. [Google Scholar] [CrossRef]
- Gal-Or, E. Information transmission—Cournot and Bertrand equilibria. Rev. Econ. Stud. 1986, 53, 85–92. [Google Scholar] [CrossRef]
- Shapiro, C. Exchange of cost information in oligopoly. Rev. Econ. Stud. 1986, 53, 433–446. [Google Scholar] [CrossRef]
- Tirole, J. Hierarchies and bureaucracies: On the role of collusion in organizations. J. Law Econ. Organ. 1986, 2, 181–214. [Google Scholar]
- Rockett, K. The quality of licensed technology. Int. J. Ind. Organ. 1990, 8, 559–574. [Google Scholar] [CrossRef]
- Katz, L.M.; Shapiro, C. On the licensing of innovations. RAND J. Econ. 1985, 16, 504–520. [Google Scholar] [CrossRef]
- Marjit, S. On a non-cooperative theory of technology transfer. Econ. Lett. 1990, 33, 293–298. [Google Scholar] [CrossRef]
- Mukherjee, A. Technology transfer with commitment. Econ. Theory 2001, 17, 345–369. [Google Scholar] [CrossRef]
- Heywood, J.S.; Le, J.; Ye, G. Per unit vs. ad valorem royalties under asymmetric royalties. Int. J. Ind. Organ. 2014, 37, 38–46. [Google Scholar] [CrossRef]
- Sen, N.; Bhattacharya, S. Technology licensing between rival firms in presence of asymmetric information. B.E. J. Theor. Econ. 2017, 17, 20150097. [Google Scholar] [CrossRef]
- Gallini, T.N.; Wright, B.D. Technology transfer under asymmetric information. RAND J. Econ. 1990, 21, 147–160. [Google Scholar] [CrossRef]
- Beggs, A.W. The licensing of patents under asymmetric information. Int. J. Ind. Organ. 1992, 10, 171–191. [Google Scholar] [CrossRef]
- Sen, D.; Tauman, Y. General licensing schemes for a cost-reducing innovation. Games Econ. Behav. 2007, 59, 163–186. [Google Scholar] [CrossRef]
- Singh, N. Multinationals. technology and government policy. In Development Policy and Economic Theory; Basu, K., Nayak, P., Eds.; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Poddar, S.; Sinha, U.B. The Role of Fixed Fee and Royalty in Patent Licensing; Department of Economics, National University of Singapore: Singapore; Mimeo: New York, NY, USA, 2002. [Google Scholar]
- Schmitz, P.W. On monopolistic licensing strategies under asymmetric information. J. Econ. Theory 2002, 106, 177–189. [Google Scholar] [CrossRef][Green Version]
- Stamatopoulos, G.; Tauman, T. On the superiority of fixed fee over auction in asymmetric markets. Games Econ. Behav. 2009, 67, 331–333. [Google Scholar] [CrossRef]
- Wang, X.H. Fee versus royalty licensing in a Cournot duopoly model. Econ. Lett. 1998, 60, 55–62. [Google Scholar] [CrossRef]
| 1 | In [3], it is shown that information sharing does not occur under price competition. |
| 2 | Since direct observation of the technologies is not an option in [1,2,3,4]; the threat of imitation under direct observation is implicit in those papers. |
| 3 | The possibility of imitation by the high-cost firm may eliminate the possibility of royalty in the licensing contract (see, e.g., [6]). The lack of information about firm 1’s output is also a reason for a fixed-fee licensing contract. |
| 4 | We obtained these inequalities because as firm 1’s perception about firm 2’s low cost increases, it encourages firm 1 to reduce its equilibrium output and firm 2 to increase its equilibrium output. |
| 5 | We assumed that noninfringing imitation or “inventing around” is permissible. |
| 6 | It can be checked that F > 0. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).