1. Introduction
Last decade has witnessed rampant development of ecommerce. One of its salient features is drastic reduction in consumers’ search costs, which further facilitates implementation of different selling mechanisms, e.g., posted prices, auctions, auctions with a buy-it-now price and best offers (first-price sealed-bid auctions). Most online trading platforms allow sellers to list their items using several mechanisms, but the two most prevalent of them are auctions and posted prices.
Online platforms also differ in the structure of supply. Some online markets (primarily in business-to-consumer and business-to-business segments) are characterized by effectively infinite supply, when businesses are able to provide any quantity demanded. Other online markets (primarily in the consumer-to-consumer segment) are depicted by finite supply. On such markets, the supply side is predominantly represented by either very small businesses or ordinary people who are simply reselling previously bought items. eBay is likely the most popular consumer-to-consumer platform, but there are many other platforms, which commonly occupy a particular niche in online retail, e.g., Listia, Catawiki or Shopgoodwill.
When there is an effectively infinite number of homogeneous objects listed by posted prices and auctions, buyers have to choose whether they want to bid in the auction or purchase the same good from the posted price. The major parameters of decision are their valuation for the object and time of arrival. If a buyer places a high value on the object or arrives to the market when the auction has just commenced, he is more likely to buy the good at the posted price rather than bid in the auction. This result is due to [
1,
2,
3] who model a decision of a buyer arriving to a market between buying the good at a posted price and participating in a second-price sealed auction. These papers establish a threshold-type buyer based on arrival time and show that buyers with higher valuations buy the good at the posted price while those with lower valuations—participate in the auction.
When a seller offers unlimited objects at posted prices and open-bid auctions, and bidders are locked into the auction, but are able to observe their bids and even revise them as the auction continues, the equilibrium is still defined in threshold strategies [
4]. Finally, another paper considers a model when an infinite number of objects is sold simultaneously by auctions and posted prices and also shows that in the equilibrium there exists a threshold-type buyer separating buyers who choose to buy the good at the posted price and buyers who choose to participate in the auction [
5].
As mentioned earlier, consumer-to-consumer markets are different from those analyzed by the literature in that the supply on them is limited. In this note I consider such a market with buyers who can bid dynamically switching between the mechanisms. In contrast to the situation with unlimited supply and “locked-in” buyers, some of them may not be able to purchase the good at all. It creates an incentive for buyers who can afford the object outside to exit the auction before its price matches the price of the good outside. These incentives are intuitive and resonate with the behavior observed in auctions with a buy-it-now (BIN) price. However, I show below that the conditions for them to exist are different.
When implementing a BIN option a seller adds a posted price to an auction-style listing allowing buyers to either buy the item right away or place a bid in the auction. On eBay, it is possible to buy the good at the BIN price before the auction starts or until the auction price reaches a “secret” reserve price set by the seller. Yahoo! design allows to buy the good at the BIN price during the auction
1.
In auctions with a Yahoo!-type BIN price, bidders with high valuations have an incentive to end the auction early by buying the good at the BIN price [
6]. This mechanism has received much scrutiny, e.g., [
6,
7,
8,
9,
10]. The focus of the literature is on sellers’ profits and rationale for using the BIN price. It shows that the implementation of the BIN option is viable due to sellers’ or buyers’ risk aversion. Here, I do not attempt to characterize sellers’ equilibrium strategies on markets with auctions and posted prices where the supply is limited.
2 The focus of this note is to analyze the differences between auctions with a BIN price and auctions with an outside option from the buyers’ perspective. I show that when the buyout price is posted outside the auction, buyers follow cutoff strategies only when they are able to observe the number of active bidders. As shown by [
6], in auctions with a BIN price, this information is not required for buyers to follow cutoff strategies. In other words, in an environment with both an auction and a posted price the necessary condition is that buyers need to not only know the total number of buyers, but also the number of active bidders in the auction for the equilibrium in cutoff strategies to exist.
2. The Model
Consider a market where two homogeneous goods are put up for sale. One of them is offered by an ascending clock auction, the other one is offered at a posted price
p. To keep things simple I assume that there are three risk neutral buyers with valuations
who have unitary demands and independent private values distributed according to a cumulative distribution function
with support
, where
is continuous and positive with
and
. Reservation price is normalized to zero
3.
In the beginning, all buyers decide whether they want to buy the good at the posted price or start bidding in the auction, but have a choice to exit it later at any time and buy the good at the posted price. The auction ends when only one buyer remains. This buyer receives the object and pays the price at the clock. A buyer who decides to exit the auction and buy the good at the posted price gets the good and pays its price
p. If several bidders attempt to exit the auction and buy the good at the posted price at the same time, the good is awarded randomly to one of the buyers, and the rest return to the auction
4.
Clearly, buyers with valuations less than the posted price outside cannot afford it and thus bid their valuations [
12]. They drop out from the auction when the clock moves past their valuations. Buyers with valuations higher than the posted price never have an incentive to drop out from the auction. On the other hand, bidding their valuations cannot be best response as well. To see this, consider three buyers with
bidding in the auction. When the clock reaches
p each of them would want to exit and buy the good at
p, but only one is randomly permitted to do so. The remaining buyers continue bidding in the auction and eventually receive a lower payoff from either having to pay more (since
) or losing the auction. Any buyer can do better by exiting the auction right before the clock matches the price outside. However, other buyers forseeing this may exit even earlier. Hence, there is such a price
at which a buyer exits the auction, and there is no loss of generality in looking for an equilibrium in cutoff strategies when valuations are higher than the posted price outside.
A strategy for a buyer with a valuation higher than the posted price (at the start of the auction) is a function , which gives each a cutoff bid price at which the bidder leaves the auction and buys the good at p. The strategy is defined similarly to auctions with a BIN price. However, if a buyer is allowed to observe the number of buyers, then at price c he is able to update the information on the number of active buyers in the auction and revise his strategy.
3. Comparing Cutoff Strategies
It was previously proved that the equilibrium in cutoff strategies exists in auctions with a BIN price when
, where
x is the first order statistic of all buyers except the buyer with valuation
v, and
B is the buyout price [
6]. In auctions with a BIN price, the expected payoff of a buyer depends only on the realization of the first order statistic among his opponents, because the former buyer’s beliefs about the latter valuation are updated directly via the clock
5. In other words, in a BIN setting, if the auction is active, it means that the clock has not yet passed the first order statistic, and a buyer does not need to know the exact number of active bidders. In contrast, when there is an additional object outside the auction (instead of the BIN price), the expected payoff of a buyer also depends on the realization of the second order statistic among his opponents. Whether the auction is active or not does not provide any information on the second order statistic. To see this, consider a buyer who follows a cutoff strategy. In a BIN setting, if the auction ended before the clock reached the price at which this buyer was supposed to use the BIN option, it means that the first order statistic was below this price. In a setting with an outside price, when the clock reaches the exit price of the buyer, if the second order statistic has dropped out, it is no longer profitable to follow a cutoff strategy, because there are only two buyers left in the market, and each of them may get the good at most at
p. However, this information may only be received from observing the second order statistic.
First, I allow buyers to observe the number of active bidders in the auction. Consider a buyer with a value
v (wlog). Let his opponents have valuations
x and
y with
. In other words,
x is the first (highest) order statistic and
y is the second order statistic. Then, their joint density is equal to
. To calculate the expected payoff of the buyer with valuation
v we need to consider all possible realizations of his opponents’ values. There are several cases to consider (
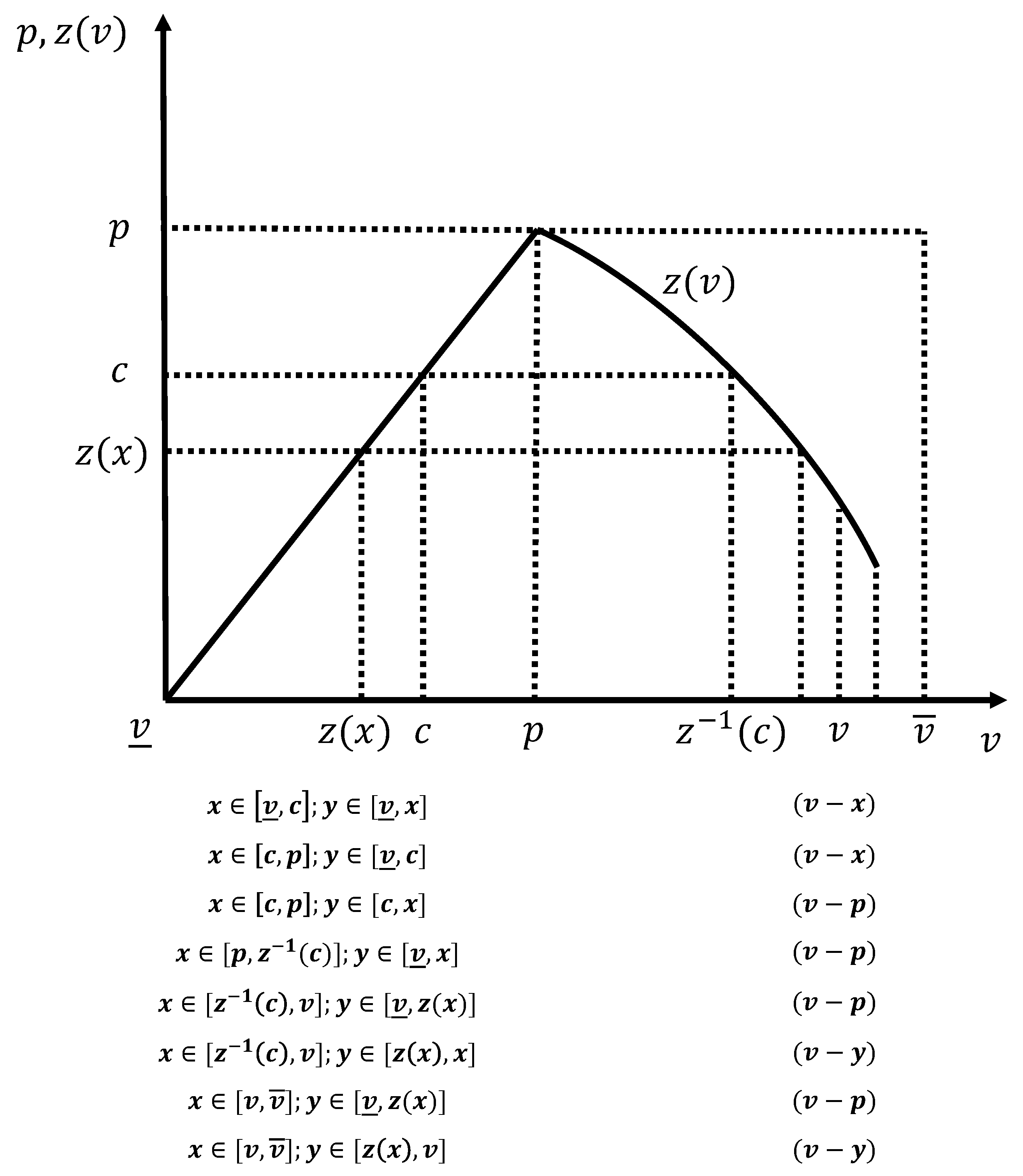
Figure 1 is helpful in this analysis):
(a) . In this situation, x and y cannot do better but to bid their valuations. Both of the opponents drop out when the auction price reaches their valuations, and the buyer in question wins the auction paying the second highest bid: .
(b) (i) and . In this scenario, when the auction price reaches y, this buyer drops out. At c, the buyer with valuation v observes that one of his opponents has dropped out from the auction and that the good outside is still available, so he no longer exits the auction. It is easy to check that his best response is to bid instead. Because , the first order statistic stays in the auction until its price reaches its value. Hence, the buyer in question pays the second highest bid: .
(ii) and . In this case, when the auction price reaches the exit price of the buyer in question, he leaves the auction and buys the good at the posted price: .
(c) (i) and . This situation is similar to the one described in b(i): the auction continues until the auction price reaches y: second order statistic drops out from the auction, and the remaining bidders play according to . Bidding continues until the auction price matches the outside posted price. At p one bidder leaves the auction and buys the good at the posted price, while the other buyer wins the auction and pays the same amount: .
(ii) and . In this case, when the auction price reaches c, the buyer in question leaves the auction and buys the good at the posted price: .
(iii)
and
. Nothing changes from c(ii) — the buyer in question is still the first to leave the auction and buy the good at the posted price:
.
6(d) (i) and . In this case, y drops out before the exit price of the first order statistic, and the remaining buyers (v and x) bid according to . The auction continues until its price matches the outside posted price. At p one bidder leaves the auction and buys the good at the posted price, while the other buyer wins the auction and pays the same amount: .
(ii) and . In this scenario, the first order statistic leaves the auction and buys the good at the posted price. The remaining buyers bid according to . When the auction price reaches y, the buyer in question wins the auction and receives a payoff of . Since the good outside of the auction is no longer available it is readily seen that the same outcome will also be observed when : .
(e) (i) and . In this case, the second order statistic drops out from the auction before the exit price of the first order statistic, and the remaining buyers bid according to , resulting in both buyers getting the objects at p: .
(ii) and . In this scenario, the first order statistic leaves the auction and buys the good at the posted price. The remaining buyers bid according to . When the auction price reaches y, the buyer in question wins the auction and receives a payoff of . Since the good outside of the auction is no longer available, it is readily seen that the same outcome will also be observed when : .
(iii) When the buyer in question gets a payoff of 0.
Summing up all the examined cases produces the following maximization problem:
where
.
When a buyer with valuation v is able to observe the number of active bidders, at c, he will continue following his strategy if the number of buyers remains the same. As stated above, if one buyer dropped out from the auction before c, then it is the best response of the buyer with valuation v to bid . If one of his opponents left the auction before c and bought the good outside, then the buyer with valuation v simply bids his valuation. Notice that the revision of the strategy is conditional on the observance of the buyer with valuation y (second order statistic among his opponents) when the clock reaches c.
Taking the first-order condition for (
1) produces the following differential equation (technical details are delegated to the
Appendix A):
For the equilibrium in cutoff strategies to exist two conditions must be met. First, the underlying function
must exist, which happens only when
. If
then the denominator is either 0 or undefined. Second, the derivative of the cutoff function needs to be negative. Observe that the denominator of (
2) is positive, because
. Hence, for the whole fraction to be negative the numerator should also be negative which happens only when
or
, where the latter term is the expected value of the buyer with valuation
y on the interval
. In other words, a buyer with valuation
v follows a cutoff strategy only if the valuation of the second order statistic among his opponents is higher than the posted price outside, i.e.,
8.
The result above is intuitive. If all buyers are bidding in the auction, and at price c the number of active bidders did not change, a buyer with valuation v expects the second order statistic among his opponents to be higher than p and follows a cutoff strategy. If the lowest-valuation buyer has dropped out before c, the former buyer is able to observe it and no longer follows a cutoff strategy, but instead bids .
Now, consider the objective function of a buyer with valuation
v who can no longer observe the number of active bidders. There are two main alterations. When
and
(case b(i)), the buyer with valuation
v does not observe that
y has dropped out and follows cutoff strategy
earning
instead of
. Additionally, when
and
(cases d(i) and e(i)), the buyer with valuation
x does not observe that
y has dropped out before his cutoff price and follows the cutoff strategy. The buyer with valuation
v now wins the auction and pays
instead of
:
where
.
Taking the first-order condition by an analogy with (
1) produces:
Contrary to the previous example, function now exists for any , which contradicts the definition of , i.e., . Hence, the equilibrium in cutoff strategies does not exist when buyers are not able to observe the number of active bidders in the auction.