Measuring and Comparing Two Kinds of Rationalizable Opportunity Cost in Mixture Models
Abstract
:1. Introduction
2. Measuring Departures in Utility from a Baseline Model
- They use different objective functionals to make their decisions: e.g., some decisions may be made using Expected Utility theory, and others using Prospect Theory. This is the “mixture” part of the mixture model: the econometrician assumes that there is more than one process generating their data, and sets out to estimate the fraction of the data that are generated by each process.
- Their decisions are noisy: even if two people have the same preferences and use the same objective function, they choose the action that maximizes their objective function with probability less than one. This part of the econometric specification has (at least) two interpretations. It can be motivated through a belief that subjects make mistakes. It can also be interpreted as a component of utility that is random.2
- They have different preferences, conditional on having the same objective functional: e.g., one individual may be more risk-averse than another.
2.1. A Classification of Behavior
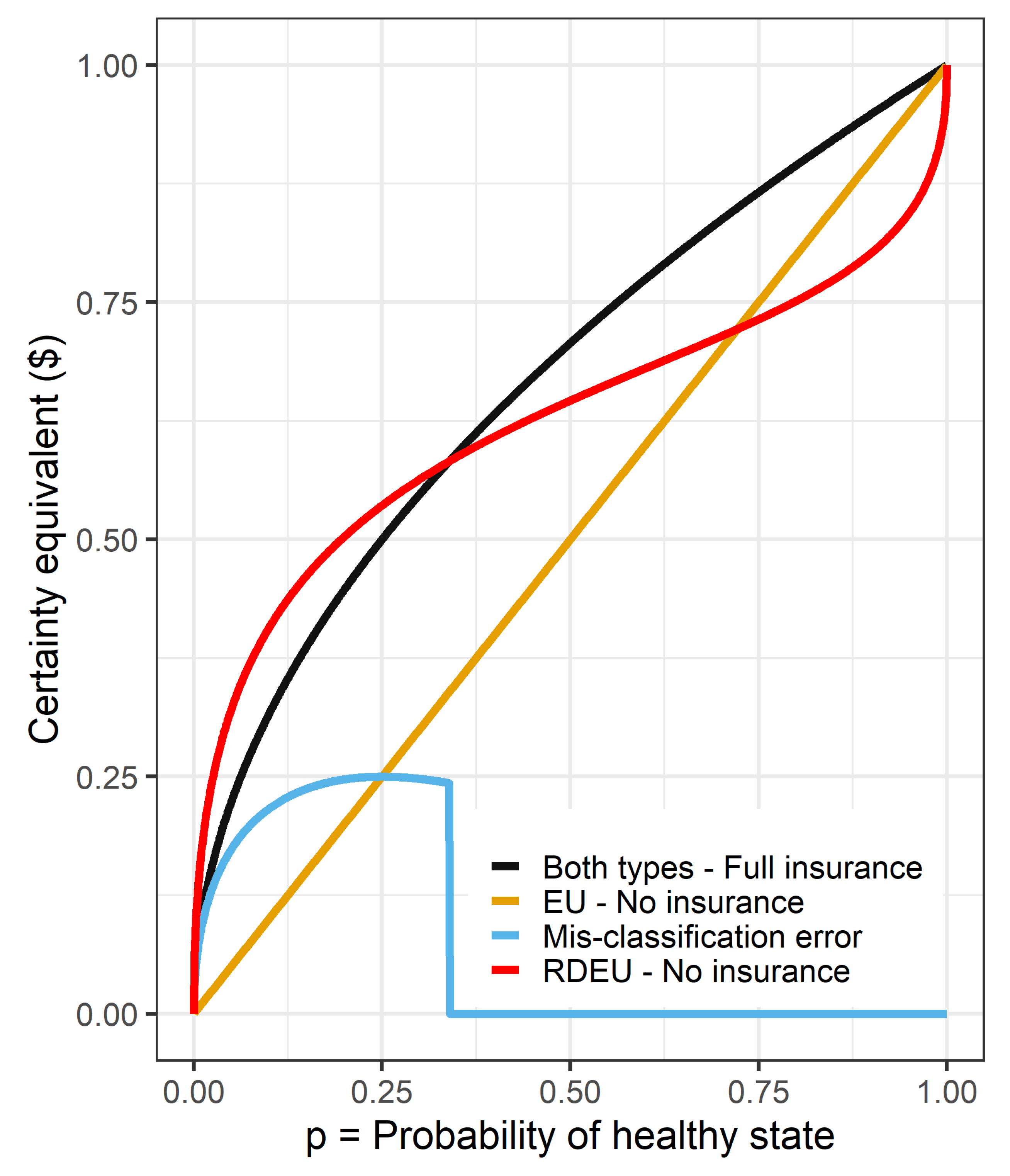
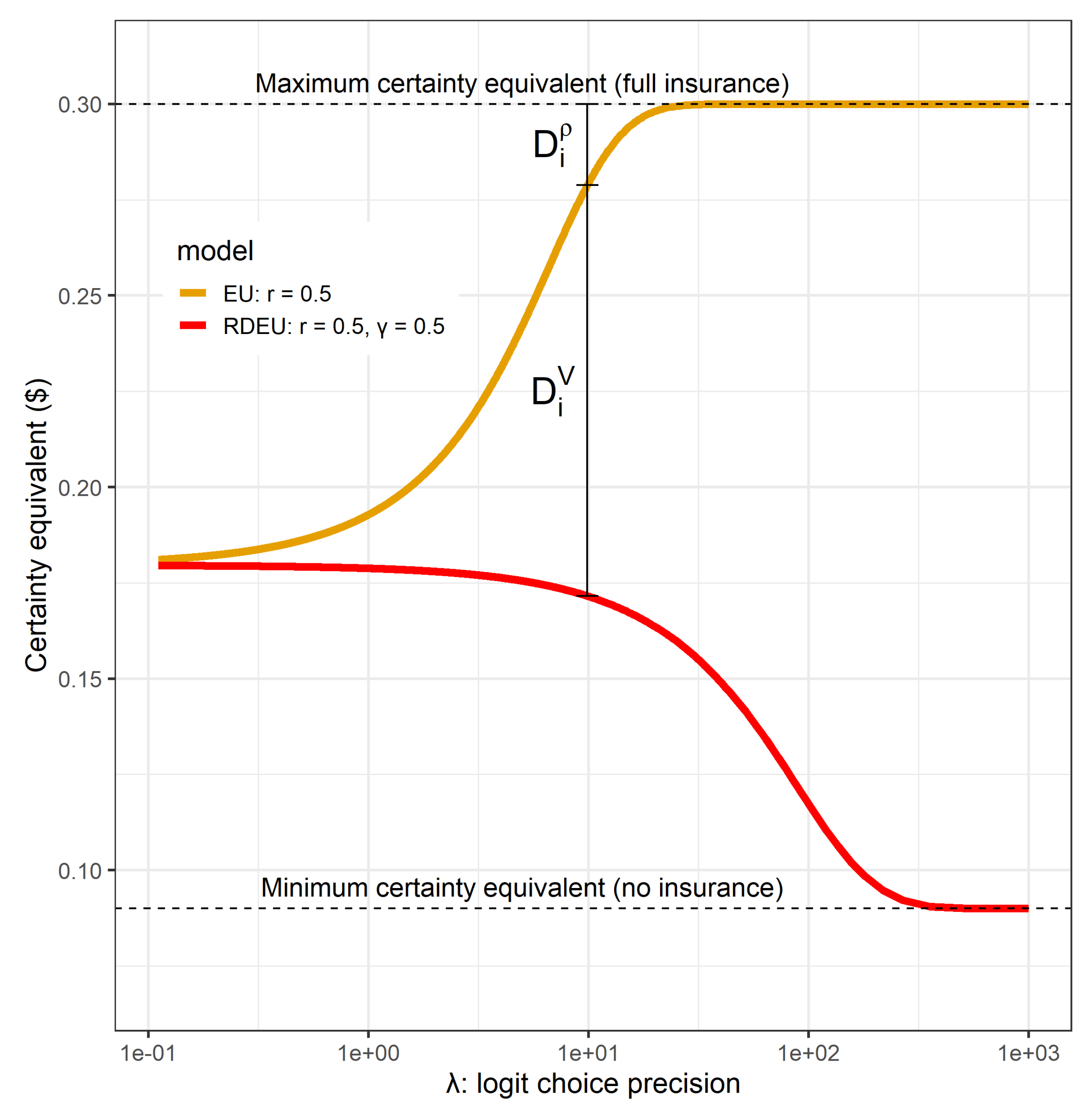
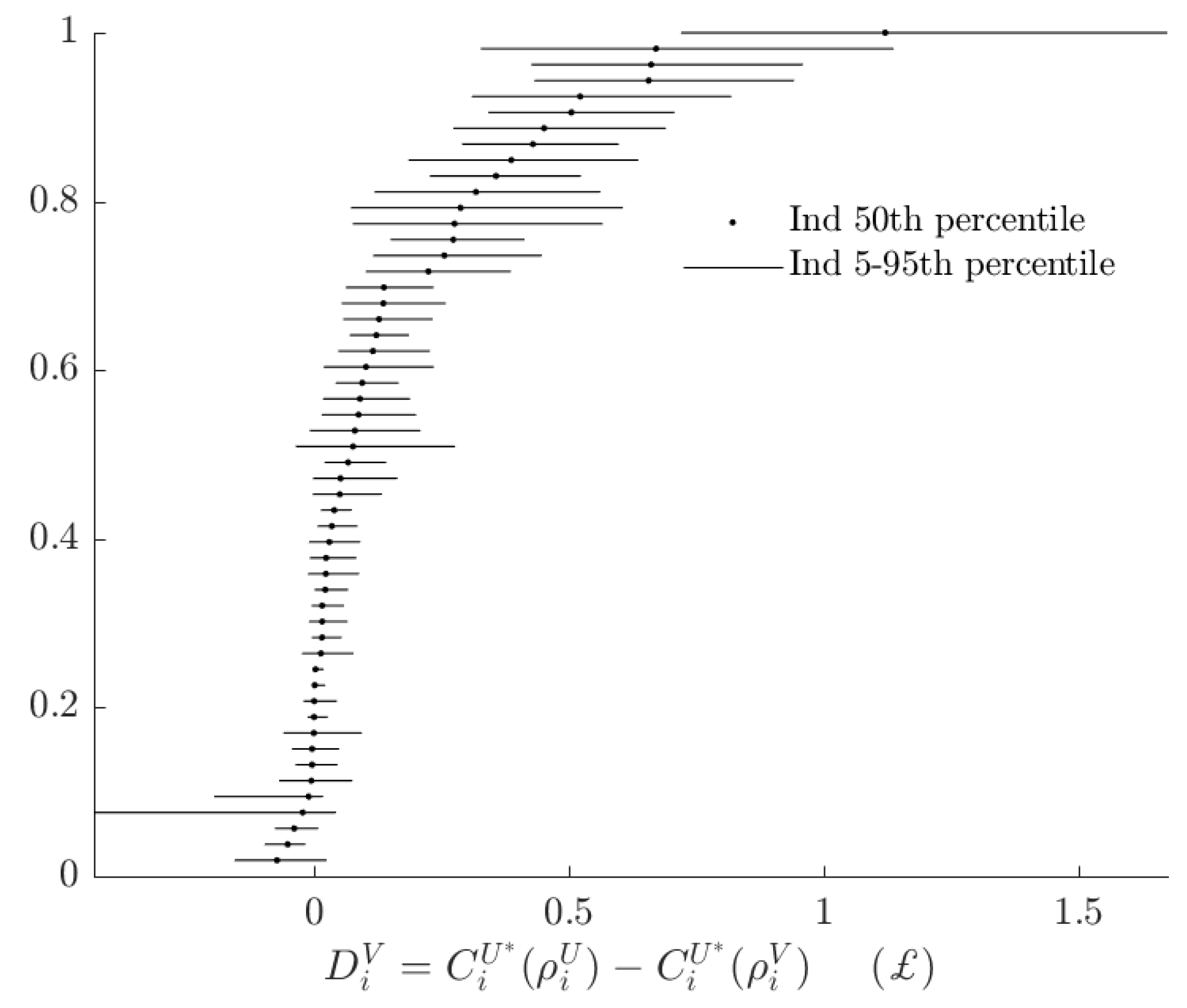
2.2. Rationalizable Opportunity Cost of Using the Alternative Model
2.3. Absolute Welfare Cost of Probabilistic Choice
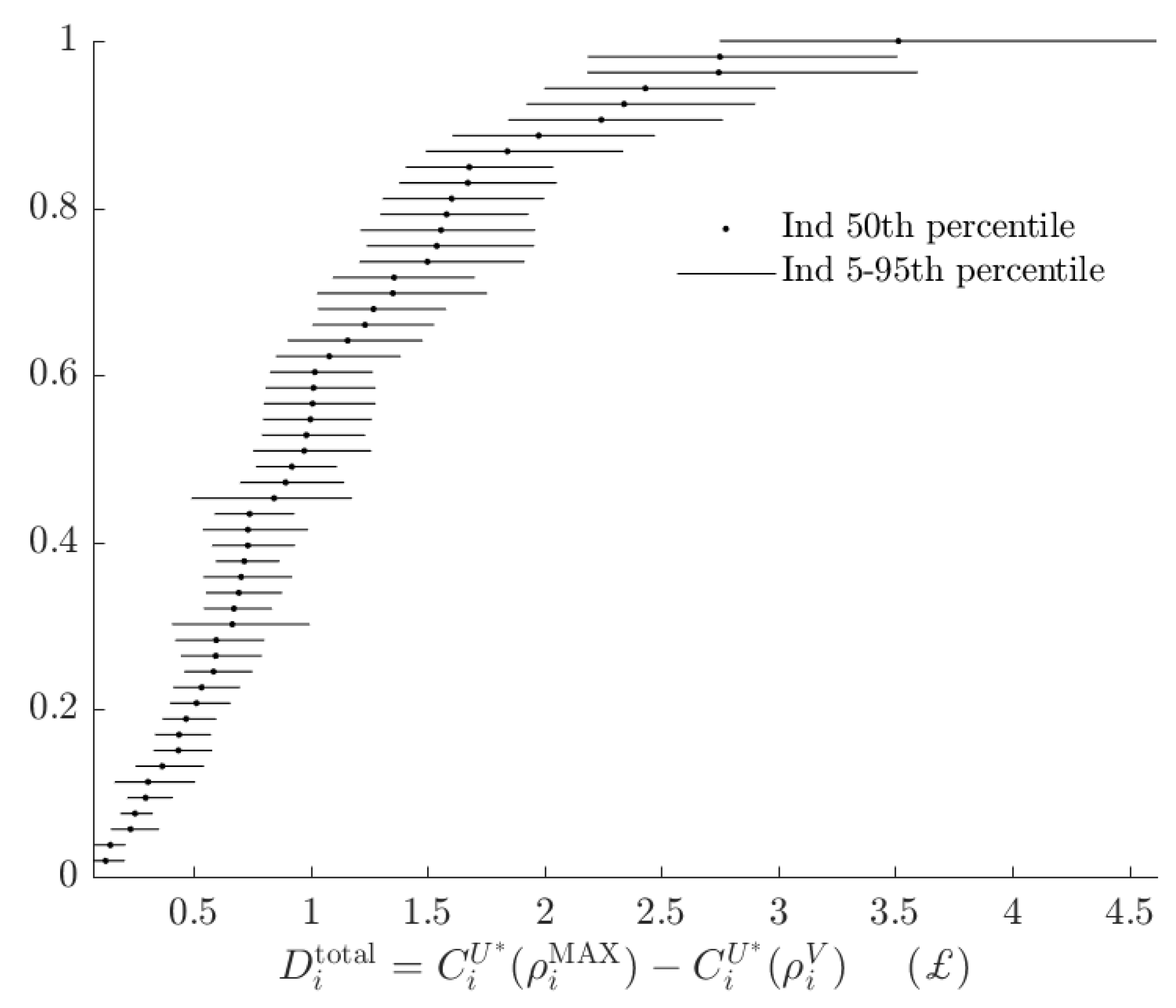
2.4. Total Rationalizable Opportunity Cost
2.5. Additional Considerations
3. Application
3.1. Data and Econometric Models
- The above specification does not assume subjects have the same decision error variance (i.e., ), while Conte et al. [2] assume that is type-specific, instead of decision-specific. I relax their assumption here as I am directly interested in the economic significance of this variable at the subject level.
- Conte et al. [2] includes decision trembles (not model trembles) in addition to probit errors. I exclude these trembles for simplicity of exposition, but in principle they could be included in the probabilistic choice model.
- Conte et al. [2] allow the distribution of subjects’ parameters to depend on their type. For simplicity, I assume that they are all drawn from the same multivariate normal distribution, with simply not being used if they are the EU type.
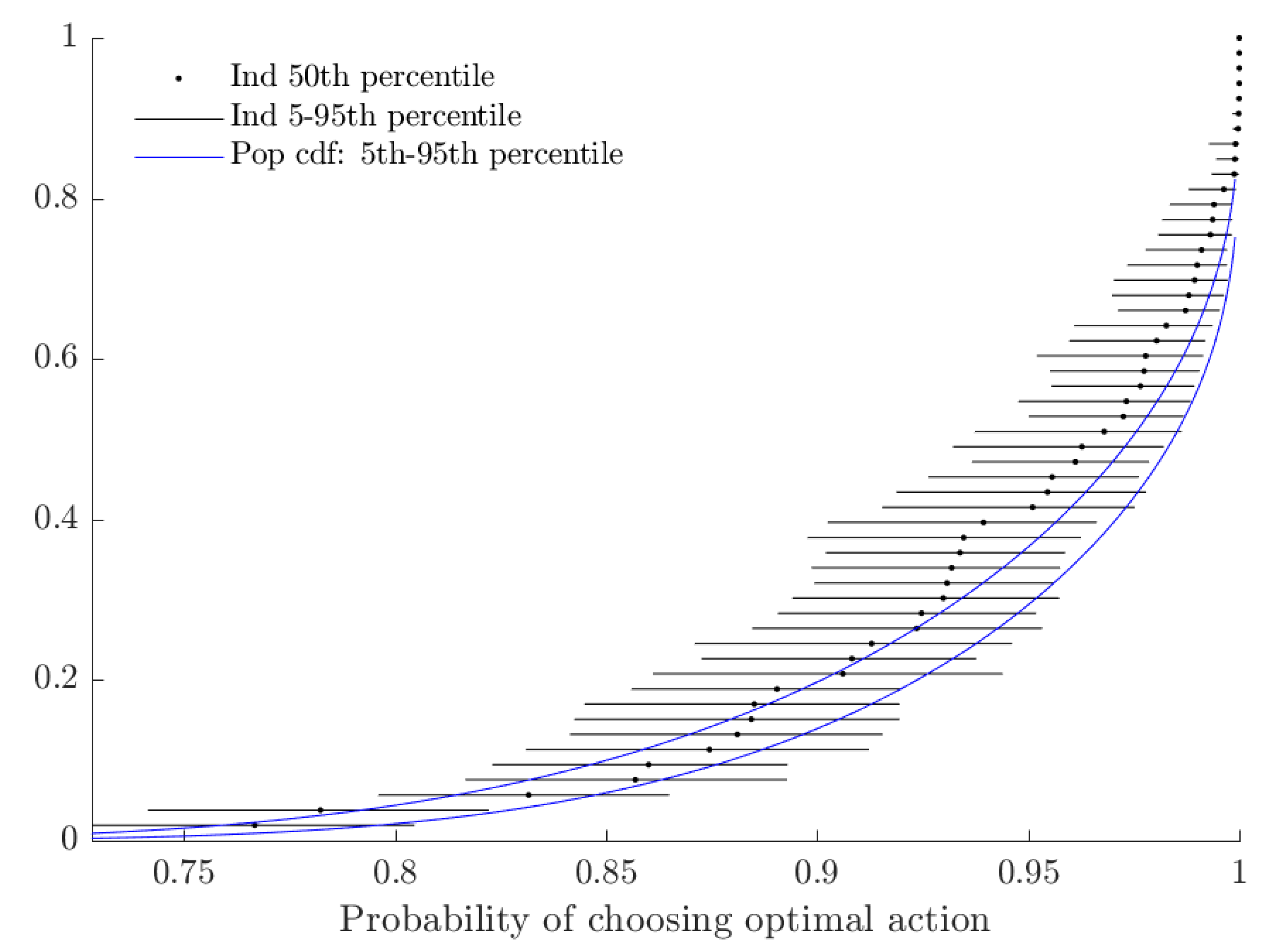
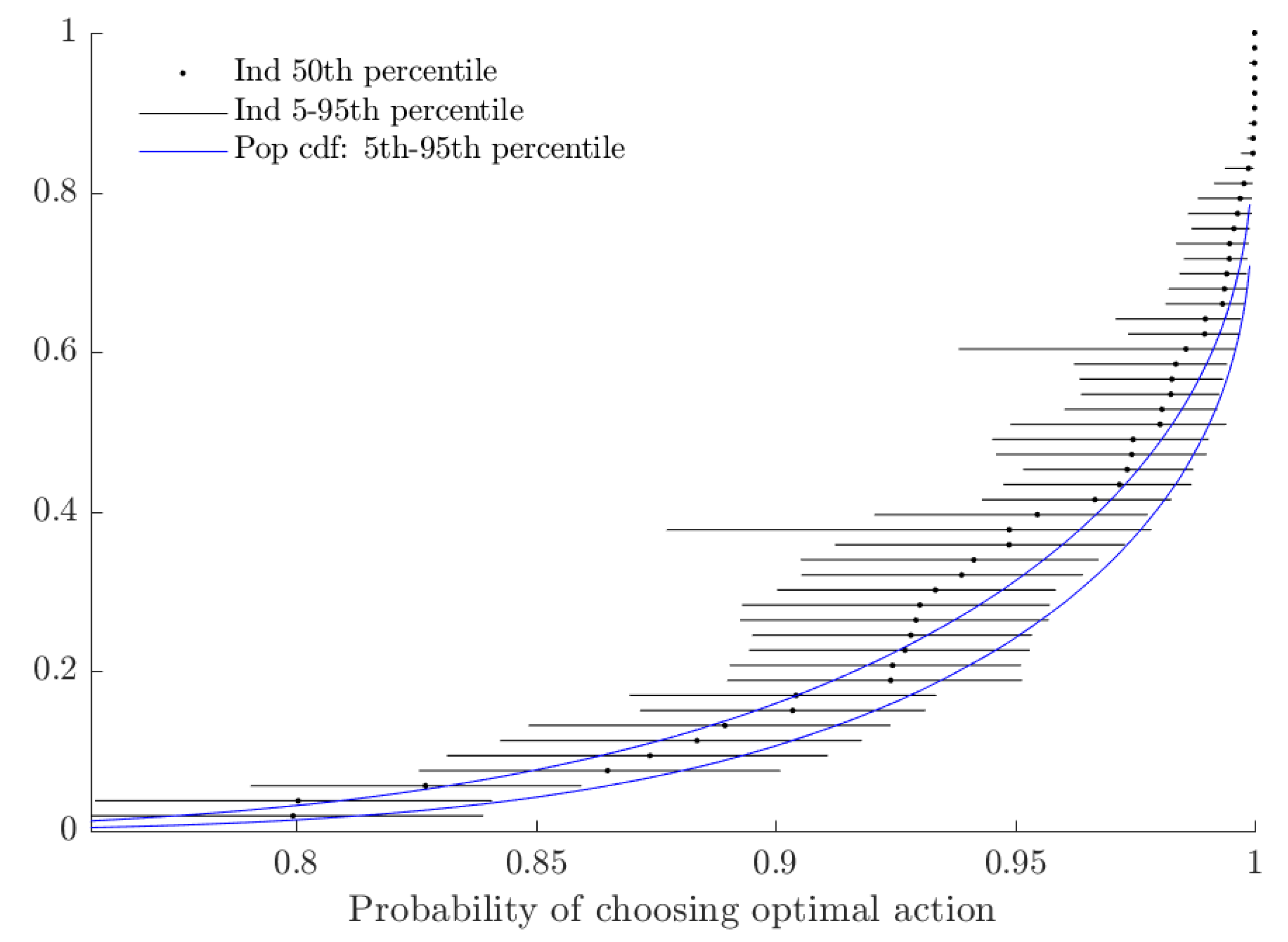
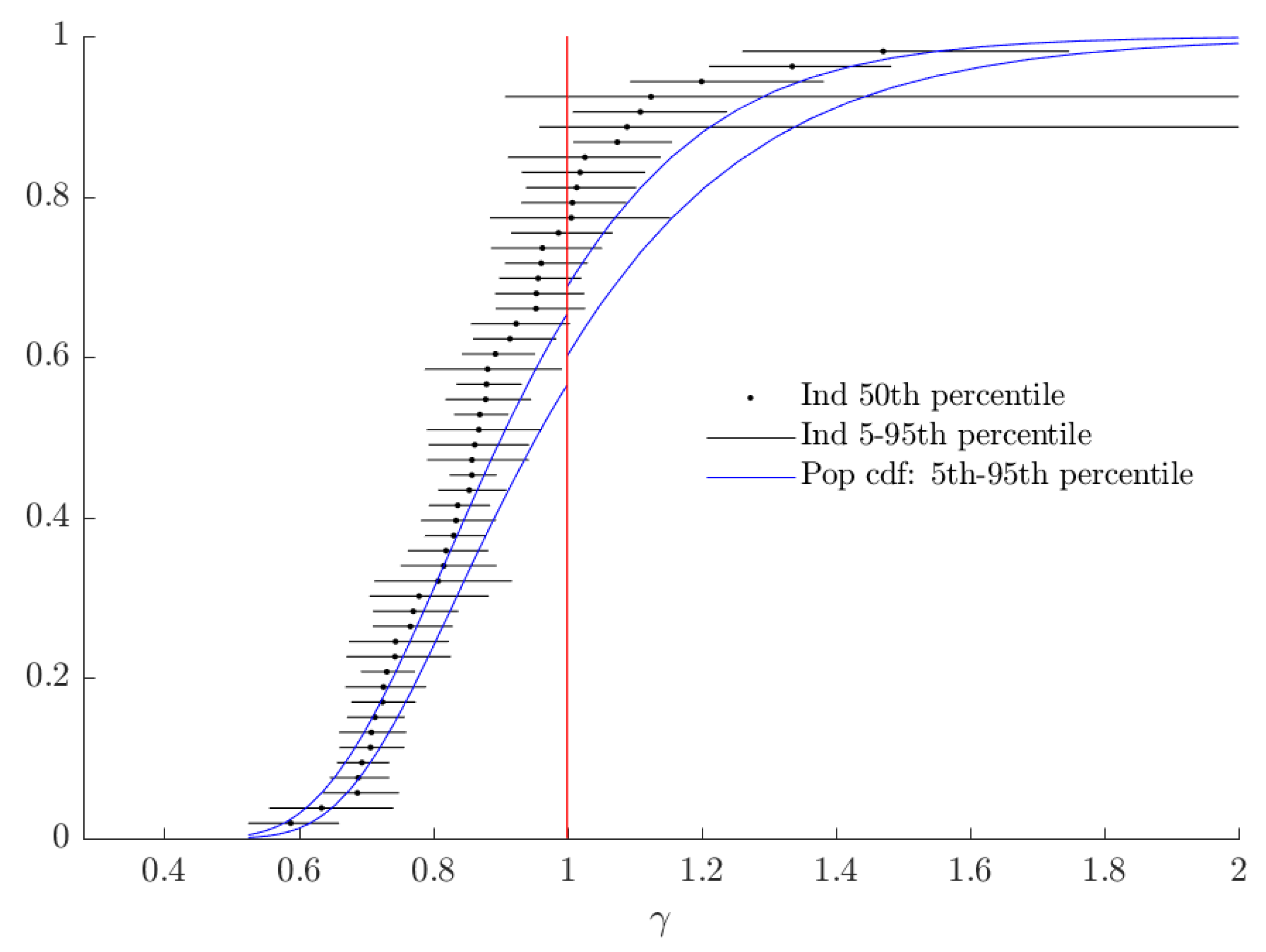
3.2. Results
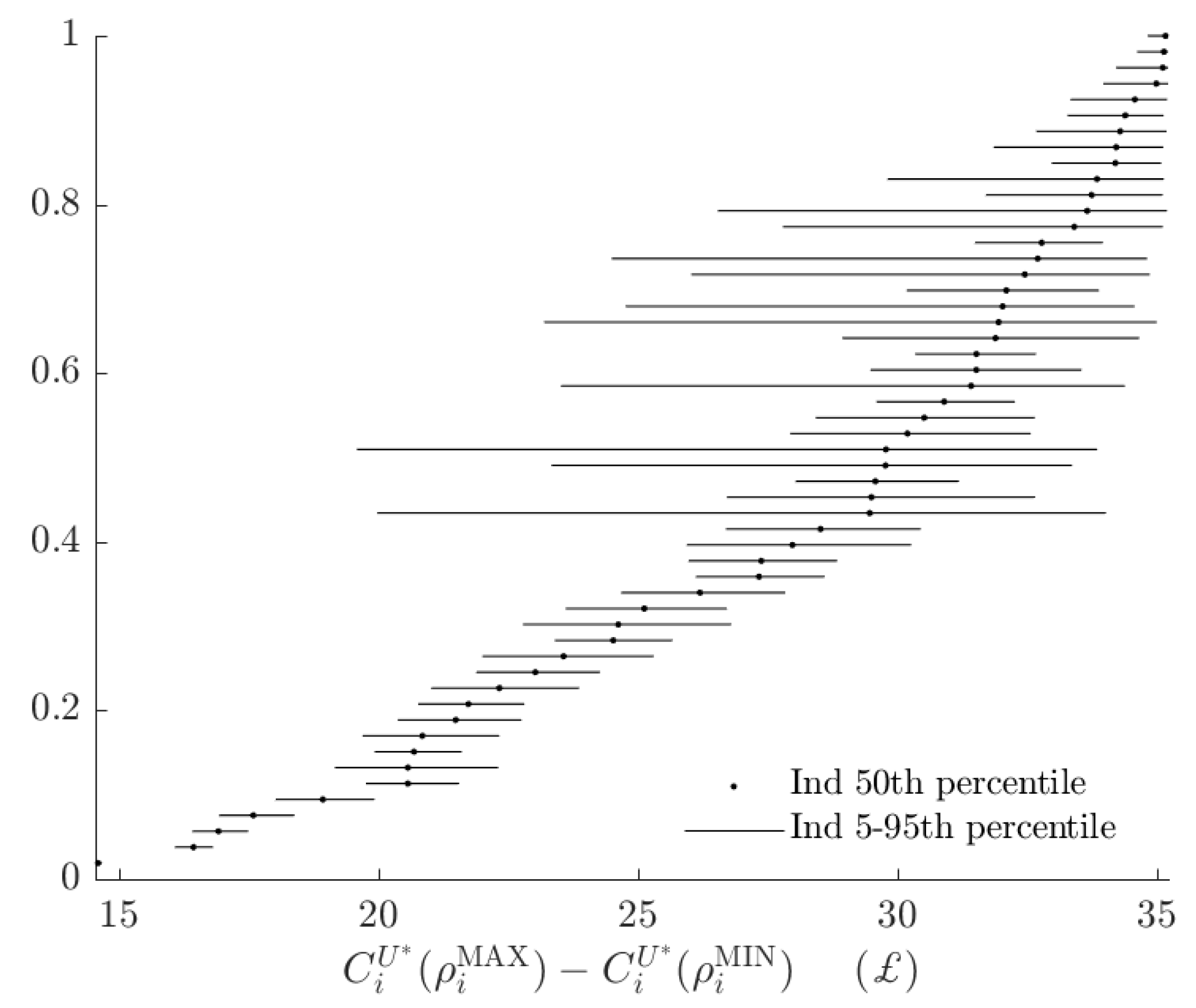
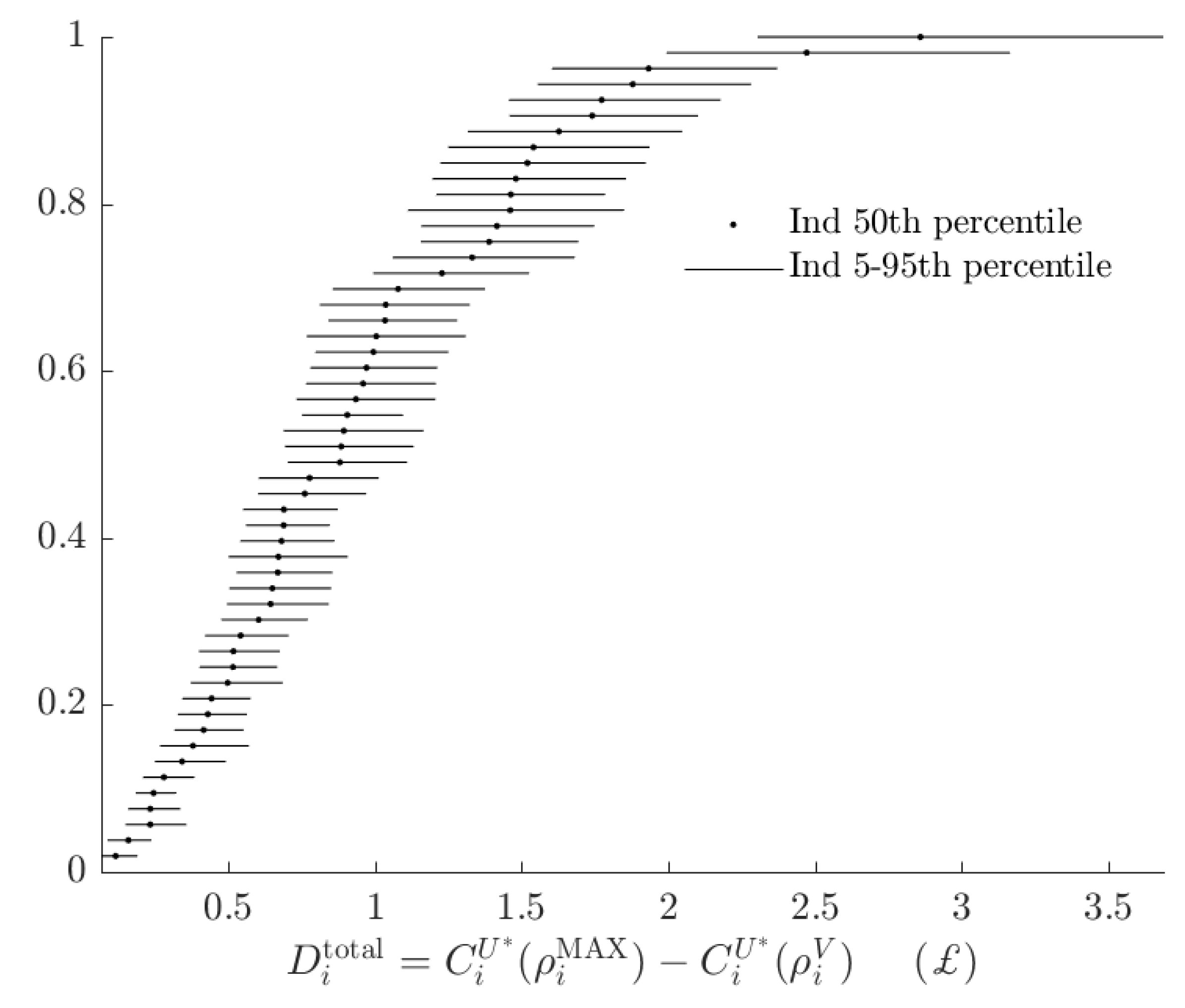
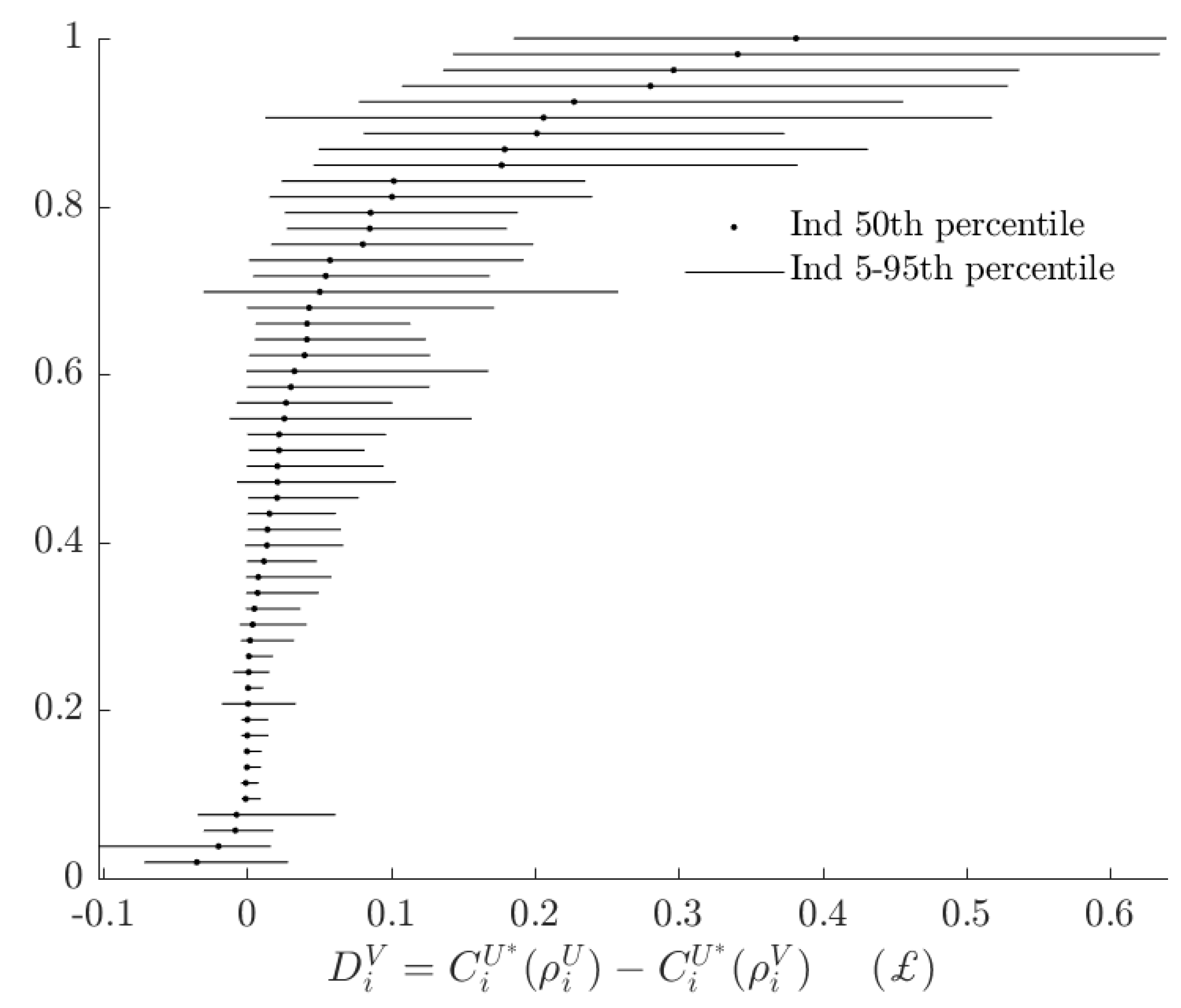
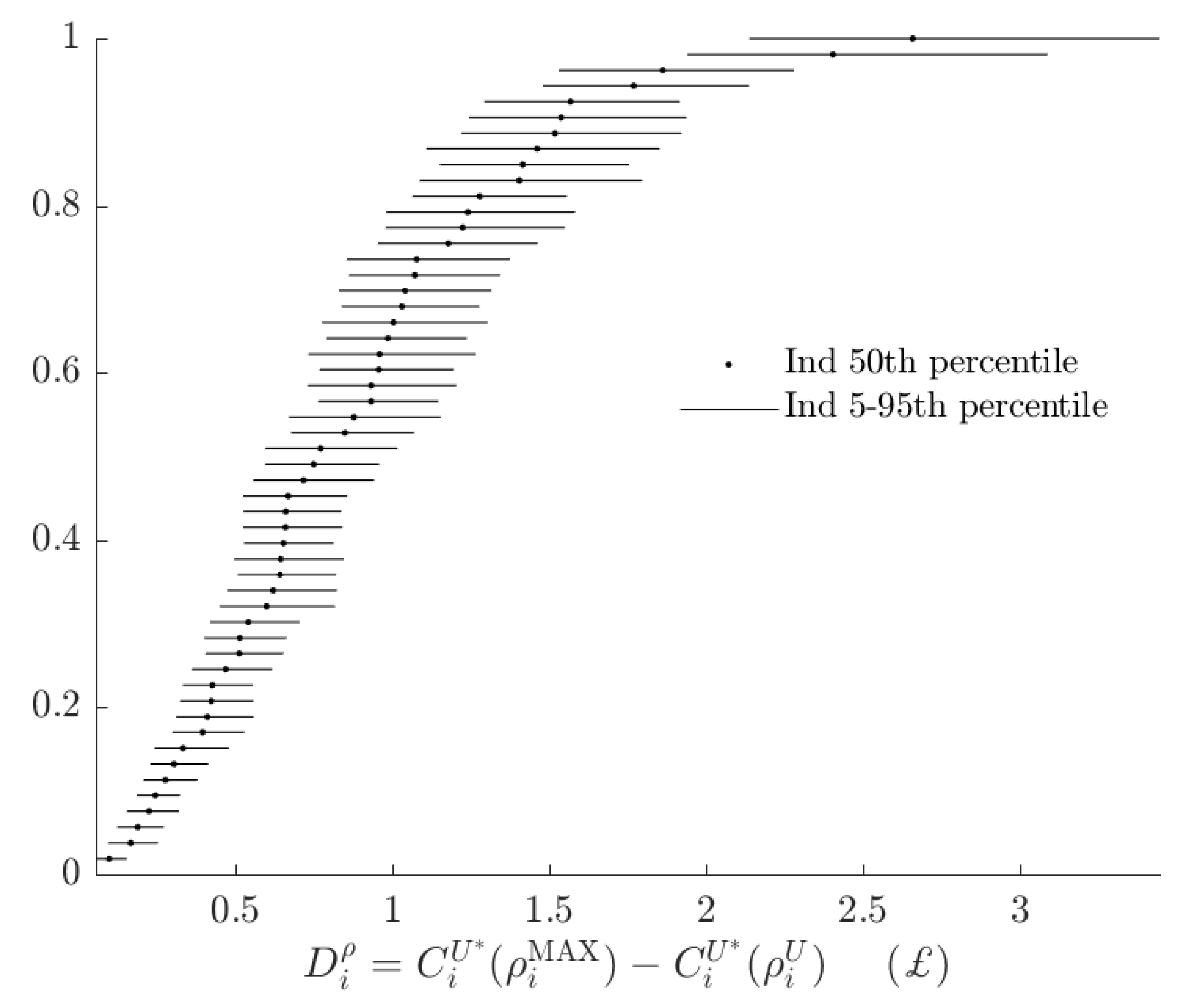
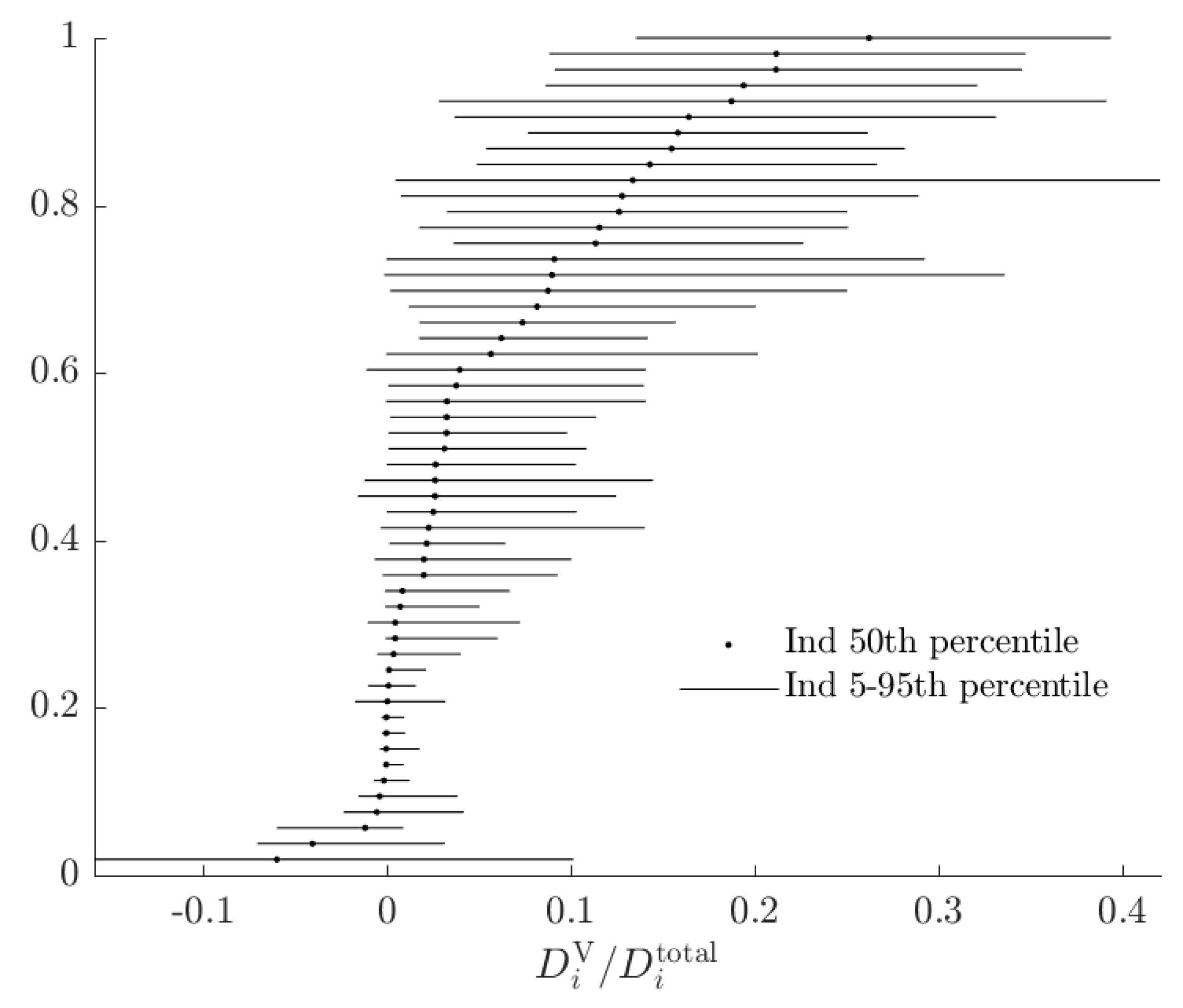
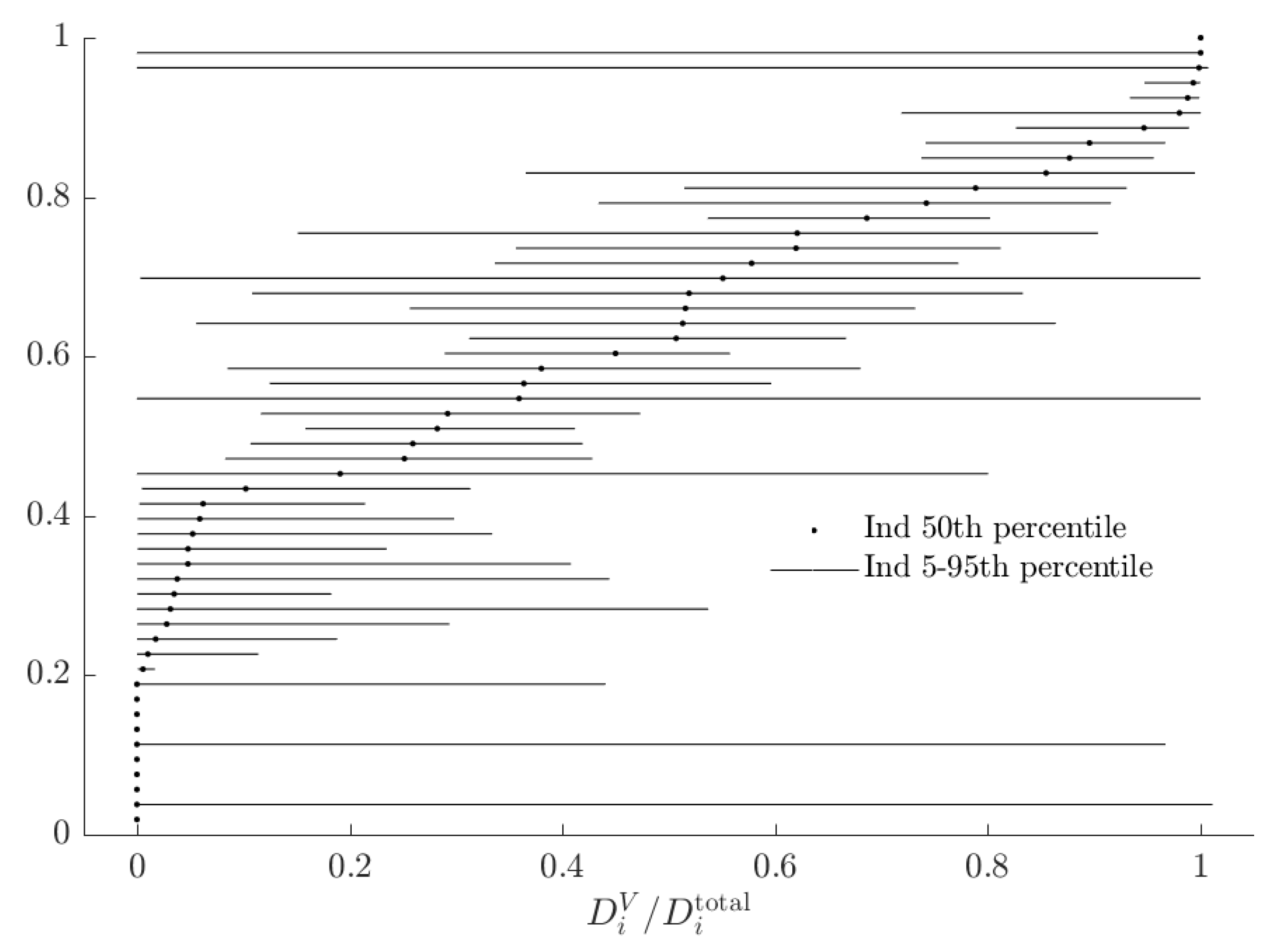
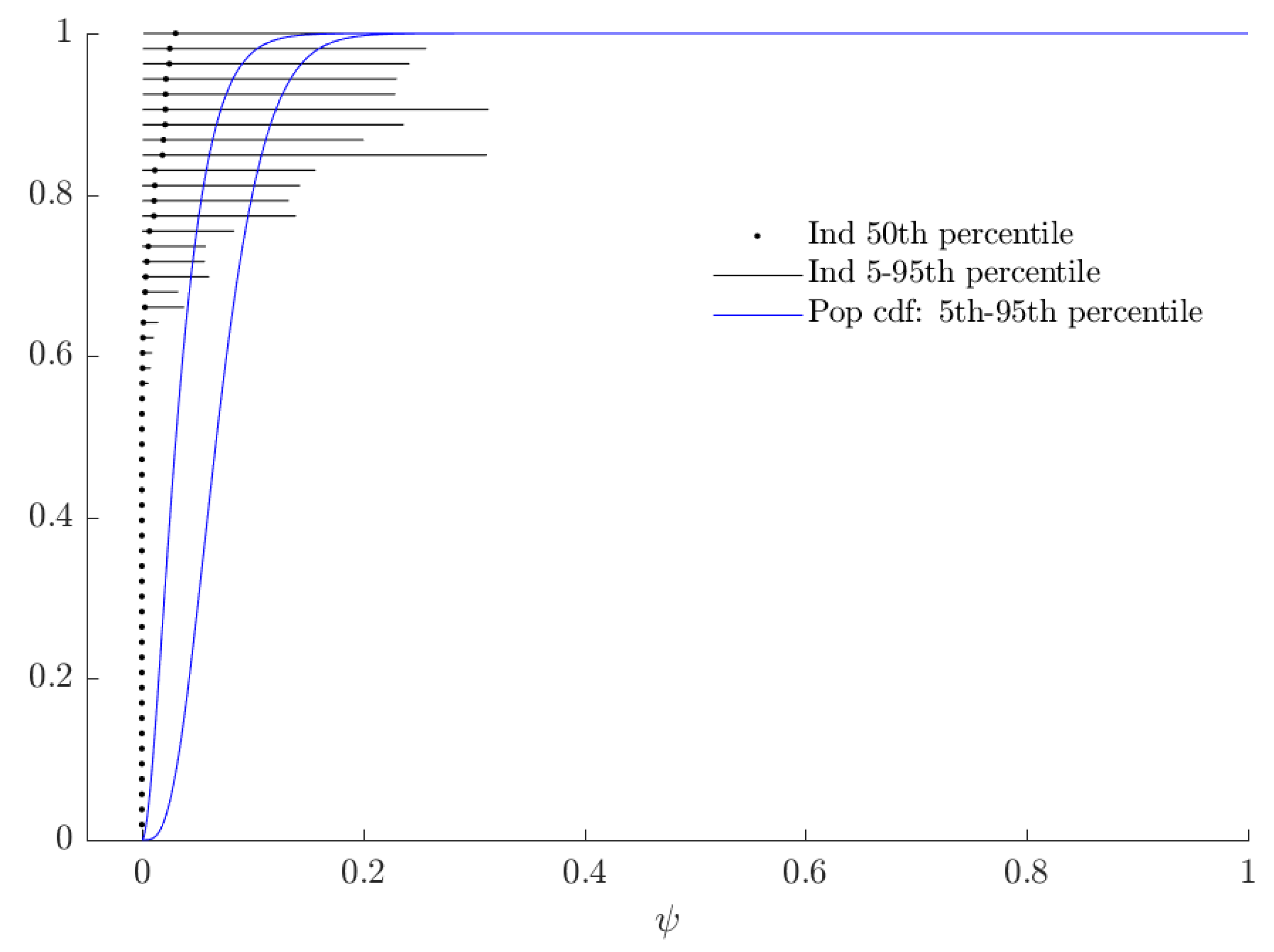
3.3. Rationalizable Opportunity Cost
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alternative-Deterministic |
| AWC | Absolute Welfare Cost |
| BD | Baseline-Deterministic |
| AP | Alternative-Probabilistic |
| BP | Baseline-Probabilistic |
| CRRA | Constant relative Risk Aversion |
| EU | Expected Utility |
| RDEU | Rank Dependent Expected Utility |
| ROC | Rationalizable Opportunity Cost |
Appendix A. Additional Tables and Figures
| r | |||
|---|---|---|---|
| Mean–Transformed | 0.404 | 21.973 | 0.927 |
| (0.03) | (1.59) | (0.03) | |
| Mean–Raw | −1.093 | 2.962 | −0.478 |
| (0.08) * | (0.07) * | (0.04) * | |
| Variance | |||
| r | 0.366 | - | - |
| (0.07) | |||
| −0.096 | 0.251 | - | |
| (0.05) * | (0.05) | ||
| 0.035 | 0.028 | 0.087 | |
| (0.03) | (0.02) | (0.02) | |
| Mean tremble probability | 0.3229 | (0.0307) |

| r | ||
|---|---|---|
| Mean–Transformed | 0.421 | 1.069 |
| (0.03) | (0.18) | |
| Mean–Raw | −1.043 | −0.317 |
| (0.08) * | (0.20) * | |
| Variance | ||
| r | 0.349 | - |
| (0.07) | ||
| 0.010 | 0.116 | |
| (0.09) | (0.05) | |
| 0.5224 | (0.0684) | |
| 0.0376 | (0.0013) | |
| 0.0481 | (0.0017) | |
| (decision tremble) | 0.0069 | (0.0009) |
Appendix B. Notes on Bayesian Estimator
- At the individual level, subjects’ behavior is described by one of two models, indexed . Each model specifies a likelihood function mapping individual parameters into a probability distribution over actions . These models are:where () if and only if subject i chose ( ) in lottery pair t.
- Subjects’ behavior is independent:
- Individual-level parameters are iid multivariate normal draws:
- Subjects are type 1 () with probability , and type 2 otherwise.
- 0.
- Initialization: Choose initial values
- 1.
- Draw from . Inspection of (A9) yields that:Using a Normal-Inverse-Wishart prior , with independent of in the prior distribution, then:where . See (Ex. 12.1, Koop et al. [19]) for a more general derivation of this result. We can therefore draw from as follows:
- l.1
- Draw
- l.2
- Draw
I choose the following parameters for this part of the prior distribution: - 2.
- Draw for each model . The relevant component of (A9) is:As is non-standard, I use the Metropolis-Hastings algorithm to complete this step.
- 3.
- Draw , and update to be the one from above specific to this draw. The relevant component of (A9) is:Note that the simulated values of (A18) can be used to assign posterior probabilities to individual subjects being each type.
- 4.
- Draw . From (A9):If we assume a Dirichlet prior:then:Here I choose prior parameters , which corresponds to a uniform prior over the fraction of subjects who are the EU type.
- 5.
- Go back to step 1.
References
- Harrison, G.W.; Rutström, E.E. Expected utility theory and prospect theory: One wedding and a decent funeral. Exp. Econ. 2009, 12, 133–158. [Google Scholar] [CrossRef]
- Conte, A.; Hey, J.D.; Moffatt, P.G. Mixture models of choice under risk. J. Econ. 2011, 162, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Harrison, G.W.; Lau, M.I.; Rutström, E.E. Individual discount rates and smoking: Evidence from a field experiment in Denmark. J. Health Econ. 2010, 29, 708–717. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.R. How many games are we playing? An experimental analysis of choice bracketing in games. J. Behav. Exp. Econ. 2019, 80, 80–91. [Google Scholar] [CrossRef]
- Quiggin, J. A theory of anticipated utility. J. Econ. Behav. Org. 1982, 3, 323–343. [Google Scholar] [CrossRef]
- Harrison, G.W. Theory and Misbehavior of First-Price Auctions. Am. Econ. Rev. 1989, 79, 749–762. [Google Scholar]
- Alekseev, A.; Harrison, G.W.; Lau, M.; Ross, D. Deciphering the Noise: The Welfare Costs of Noisy Behavior. Available online: https://research.cbs.dk/en/publications/deciphering-the-noise-the-welfare-costs-of-noisy-behavior (accessed on 17 April 2018).
- Hey, J.D. Does repetition improve consistency? Exp. Econ. 2001, 4, 5–54. [Google Scholar] [CrossRef]
- Hey, J.D.; Orme, C. Investigating generalizations of expected utility theory using experimental data. Econ. J. Econ. Soc. 1994, 62, 1291–1326. [Google Scholar] [CrossRef]
- Rabin, M.; Weizsäcker, G. Narrow bracketing and dominated choices. Am. Econ. Rev. 2009, 99, 1508–1543. [Google Scholar] [CrossRef] [Green Version]
- Harrison, G.W.; Martínez-Correa, J.; Swarthout, J.T. Reduction of compound lotteries with objective probabilities: Theory and evidence. J. Econ. Behav. Org. 2015, 119, 32–55. [Google Scholar] [CrossRef] [Green Version]
- Bland, J.R.; Rosokha, Y. Learning Under Uncertainty with Multiple Priors: Experimental Investigation. 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3419020 (accessed on 12 July 2019).
- Machina, M.J. Stochastic Choice Functions Generated From Deterministic Preferences Over Lotteries. Econ. J. 1985, 95, 575–594. [Google Scholar] [CrossRef]
- Elabed, G.; Carter, M.R. Compound-risk aversion, ambiguity and the willingness to pay for microinsurance. J. Econ. Behav. Org. 2015, 118, 150–166. [Google Scholar] [CrossRef]
- Andreoni, J.; Sprenger, C. Uncertainty Equivalents: Testing the Limits of the Independence Axiom; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2011. [Google Scholar]
- Agranov, M.; Ortoleva, P. Stochastic choice and preferences for randomization. J. Political Econ. 2017, 125, 40–68. [Google Scholar] [CrossRef] [Green Version]
- Moffatt, P.G. Stochastic Choice and the Allocation of Cognitive Effort. Exp. Econ. 2005, 8, 369–388. [Google Scholar] [CrossRef]
- Thaler, R.H. Misbehaving: The Making of Behavioral Economics; WW Norton & Company: New York, NY, USA, 2015. [Google Scholar]
- Koop, G.; Poirier, D.J.; Tobias, J.L. Bayesian Econometric Methods; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
| 1. | |
| 2. | Stochastic choice rules are also an econometric necessity when using likelihood-based techniques: if a subject makes just one decision that does not maximize her objective function, then without a probabilistic choice rule, the likelihood function (before taking logs) is zero everywhere, and hence cannot be maximized. |
| 3. | Such a mis-classification could be reasonably likely if the alternative model generalizes the baseline. For example, consider a simple mixture model that assumes subjects either maximize expected value (the baseline type), or maximize a constant relative risk aversion utility function (the alternative type). It is likely in this situation that some expected value-maximizers will be classified as expected utility-maximizers. |
| 4. | Note that while it may at first seem reasonable that could only be positive, this is not necessarily the case. This is because, for the choice set under consideration, it is possible that the alternative objective function exaggerates the utility differences. For example, a risk-neutral subject faced with choosing between a 25% chance of winning $2, or zero otherwise, and $1 for sure, would evaluate this utility difference as . Alternatively, if a subject weighs probability with weighting function , but was otherwise risk-neutral, then they will perceive this difference as . Holding the level of noise constant in the probabilistic choice rule, the subject who weighs probability is more likely to choose the lottery that maximizes U, even though they are not seeking to maximize it. |
| 5. | Alekseev et al. [7] define this quantity more generally as “the monetary welfare that the agent would be allowed to give up for exactly of her choices to be rationalized by the model, given noise ” ( in the insurance example). Within this framework, I set , and hence compute the monetary welfare that the agent would be allowed to give up for all of her choices to be rationalized by the baseline model. |
| 6. | e.g., for an expected utility model, simply normalizing utility over money to be between 0 and 1 means that the expected utility is the uncertainty equivalent. |
| 7. | In the experiment, subjects were presented these prizes as -£25, £25, £75, and £125, plus a £25 show-up fee. I maintain the assumption of Conte et al. [2] that subjects integrate the show-up fee with the lottery prize, so I will proceed in terms of the integrated payoffs only. |
| 8. | Here I assume for simplicity that if i is indifferent, she will choose . |
| 9. | As this is a CRRA utility function, this normalization is equivalent to multiplying the utility function by (a constant at the subject level), and hence dos not affect estimates of . It will affect estimate of the variance of decision errors (i.e., they will be inflated by ). |
| 10. | The lower bound of ensures that the probability weighting function is always increasing in p. |
| 11. | See Bland and Rosokha [12] for an exception. |
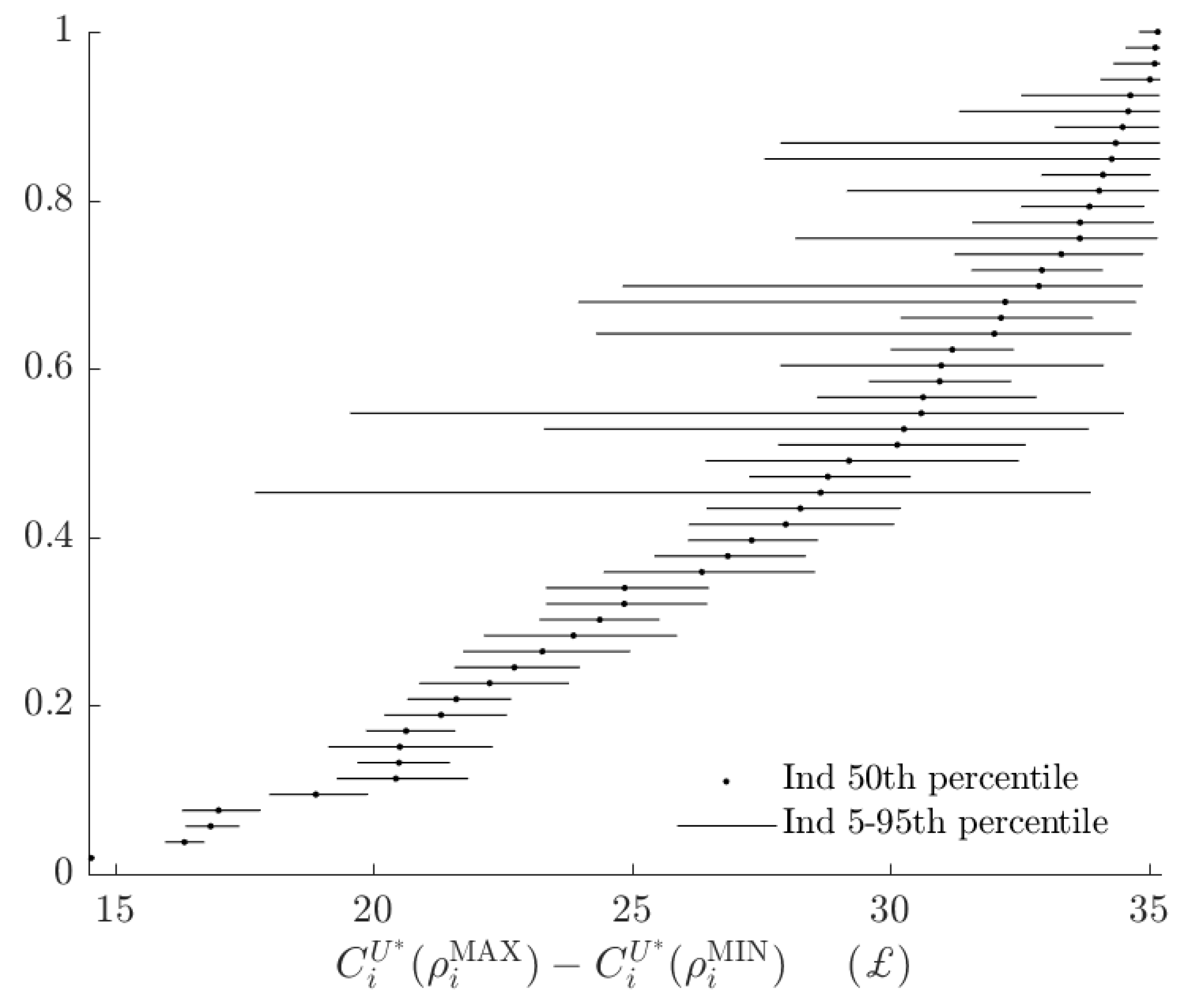
| 12. | In Appendix A I show the results of a model that assumes subjects tremble between the two preference functionals, rather than using one for the entire experiment. This specification is similar to the specification for mixing in Harrison and Rutström [1]. While the mixing probability is substantially larger in this model, the other results for this model are quantitatively similar to the results discussed in the main part of this paper. |
| 13. | Conte et al. [2] estimate this number to be 20%. I suspect this difference is due to several differences in the econometric specification outlined above. |
| 14. | For reference, the average difference in expected values for this experiment was £15.19. As I divide prizes by the maximum payout, this corresponds to a difference of units of normalized utility difference for a risk-neutral subject. |
| 15. | Alternatively, from a maximum likelihood perspective, suppose that I estimated a subjects’ parameters on the individual level to be , and then estimated a restricted model that only permitted EU types, producing estimates . I need to use when determining what a subject would do conditional on being the alternative type, but I need to use when evaluating the certainty equivalent associated with doing this, because I need the best possible estimate of their parameters conditional on being the baseline type. |
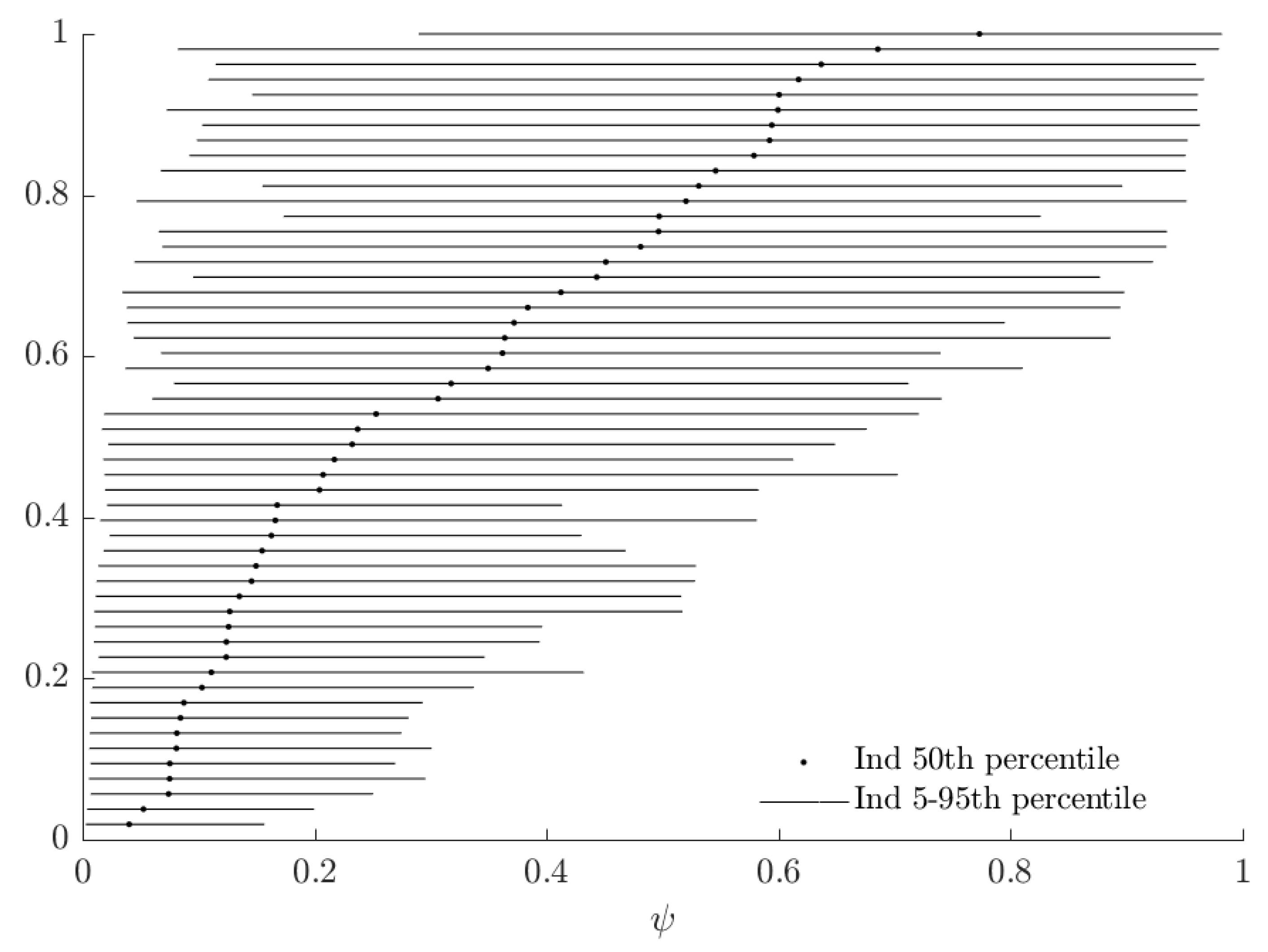
| 16. | See Figure A1 in Appendix A for these estimates. |
| 17. | Because I use a constant relative risk aversion specification, the stakes do not change these estimates. |
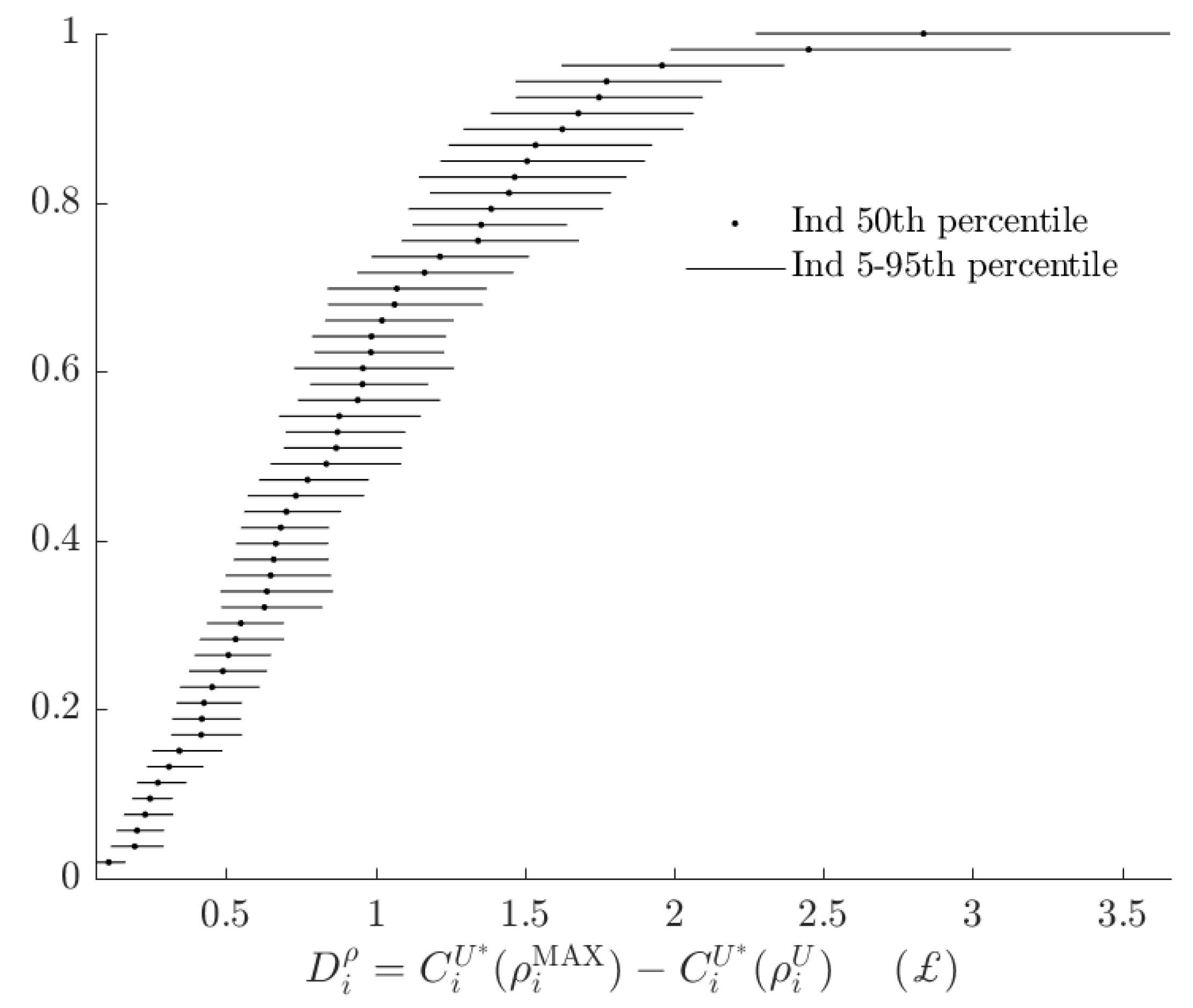
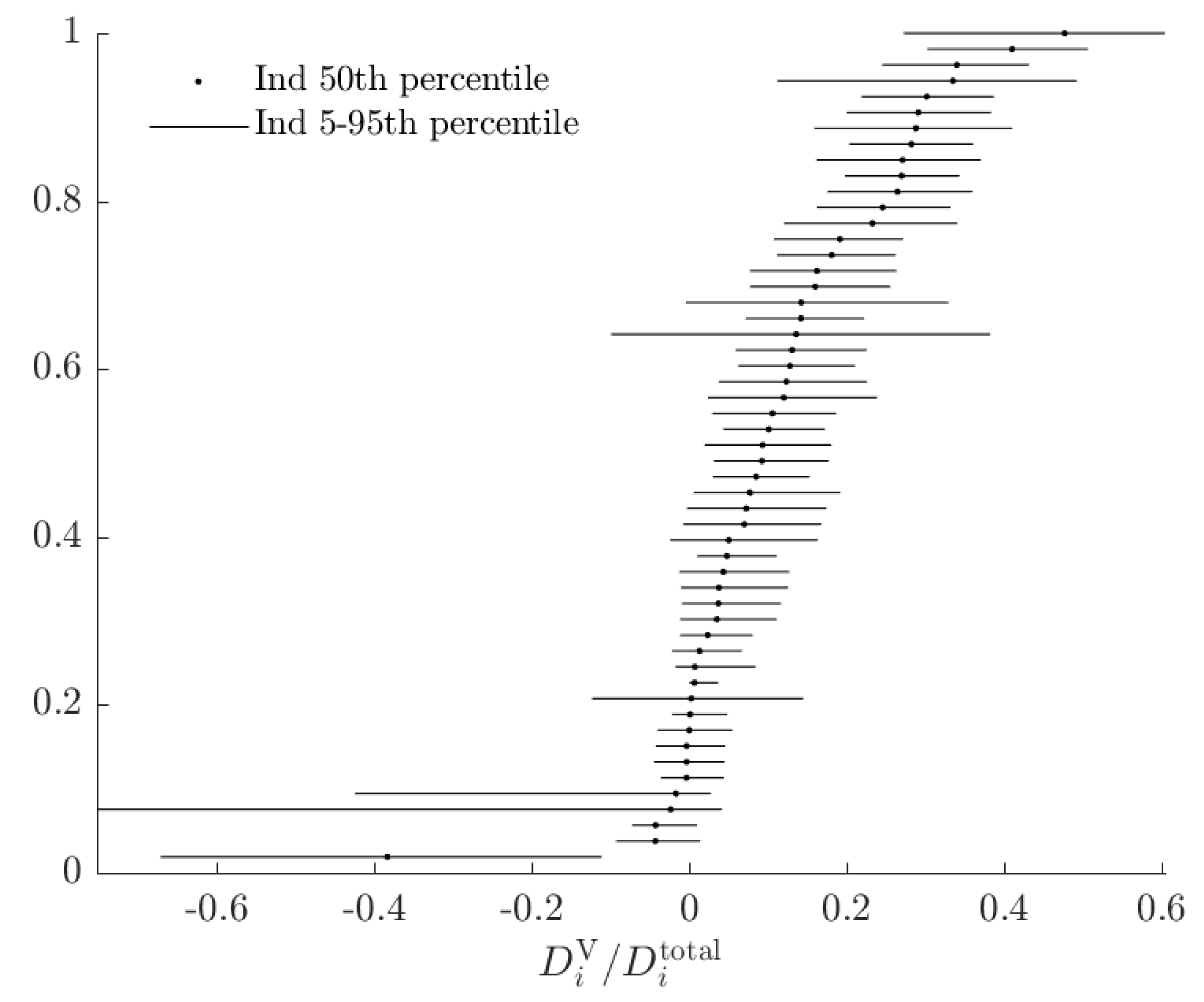
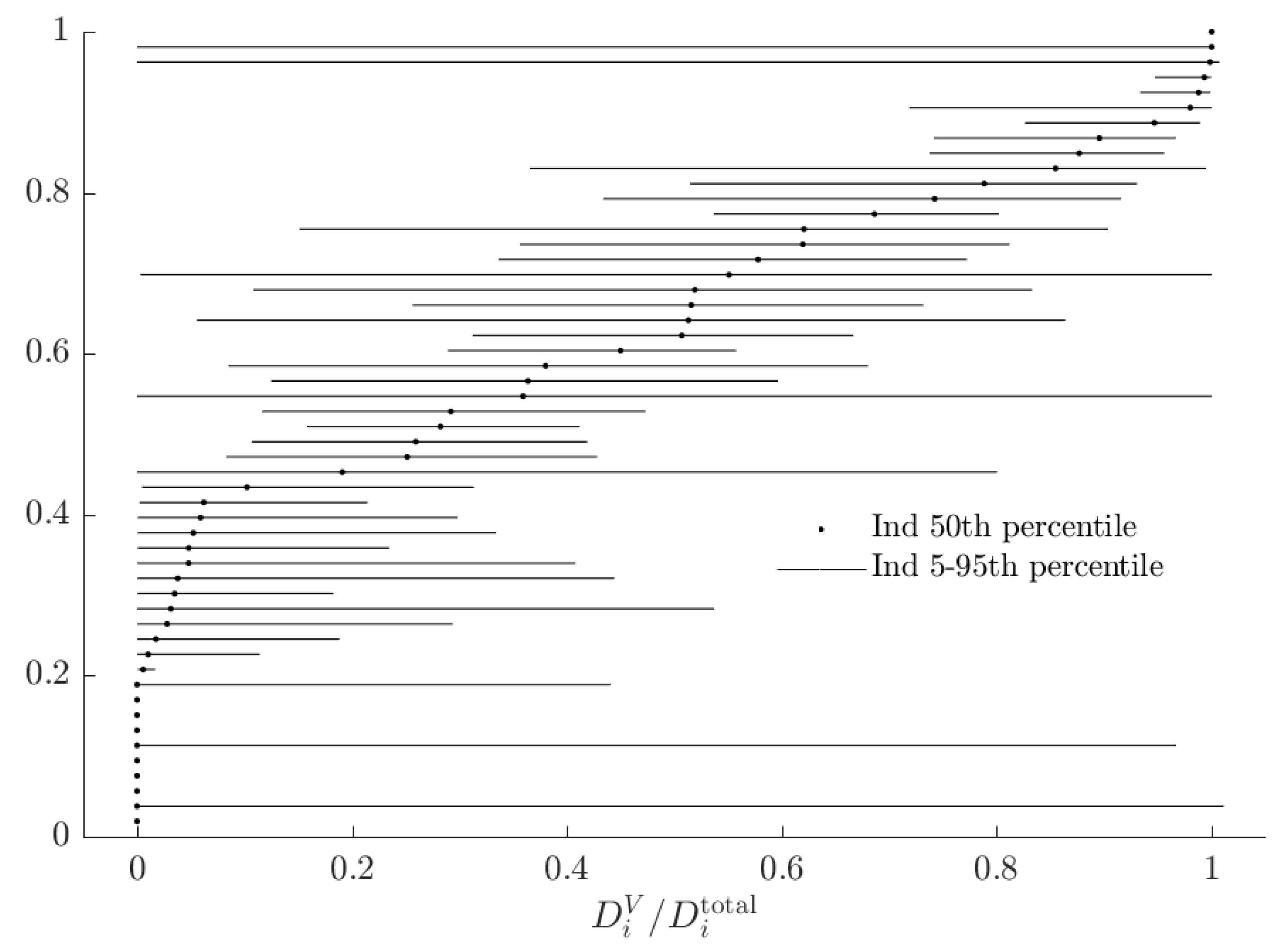
| Paper | Baseline Type | Alternative Type | Errors |
|---|---|---|---|
| Harrison [6] | Risk neutrality | Risk aversion | - |
| Hey and Orme [9] | Expected utility | Any or all of the remaining 10 models considered | power |
| Harrison and Rutström [1] | Expected utility | Prospect Theory | Logistic |
| Rabin and Weizsäcker [10] | Broad bracketing | Narrow bracketing | Logistic |
| Harrison et al. [3] | Exponential discounting | Hyperbolic discounting | Logistic |
| Conte et al. [2] | Expected utility | Rank dependent expected utility | Probit + trembles |
| Harrison et al. [11] | Reduces compound lotteries | Treats simple and compound lotteries differently | Logistic |
| Bland [4] | Broad bracketing | Narrow bracketing | Logistic |
| Bland and Rosokha [12] | Bayesian updating | Ambiguity aversion | Logistic |
| Probabilistic | Deterministic | |
|---|---|---|
| Baseline | ||
| Alternative |
| r | |||
|---|---|---|---|
| Mean–Transformed | 0.426 | 23.572 | 0.931 |
| (0.03) | (1.73) | (0.03) | |
| Mean–Raw | −1.009 | 3.032 | −0.493 |
| (0.07) * | (0.07) * | (0.05) * | |
| Variance | |||
| r | 0.306 | - | - |
| (0.06) | |||
| −0.094 | 0.250 | - | |
| (0.04) * | (0.05) | ||
| 0.046 | −0.001 | 0.127 | |
| (0.03) | (0.03) | (0.03) | |
| 0.0329 | (0.0309) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bland, J.R. Measuring and Comparing Two Kinds of Rationalizable Opportunity Cost in Mixture Models. Games 2020, 11, 1. https://doi.org/10.3390/g11010001
Bland JR. Measuring and Comparing Two Kinds of Rationalizable Opportunity Cost in Mixture Models. Games. 2020; 11(1):1. https://doi.org/10.3390/g11010001
Chicago/Turabian StyleBland, James R. 2020. "Measuring and Comparing Two Kinds of Rationalizable Opportunity Cost in Mixture Models" Games 11, no. 1: 1. https://doi.org/10.3390/g11010001





