Response Times and Tax Compliance
Abstract
1. Introduction
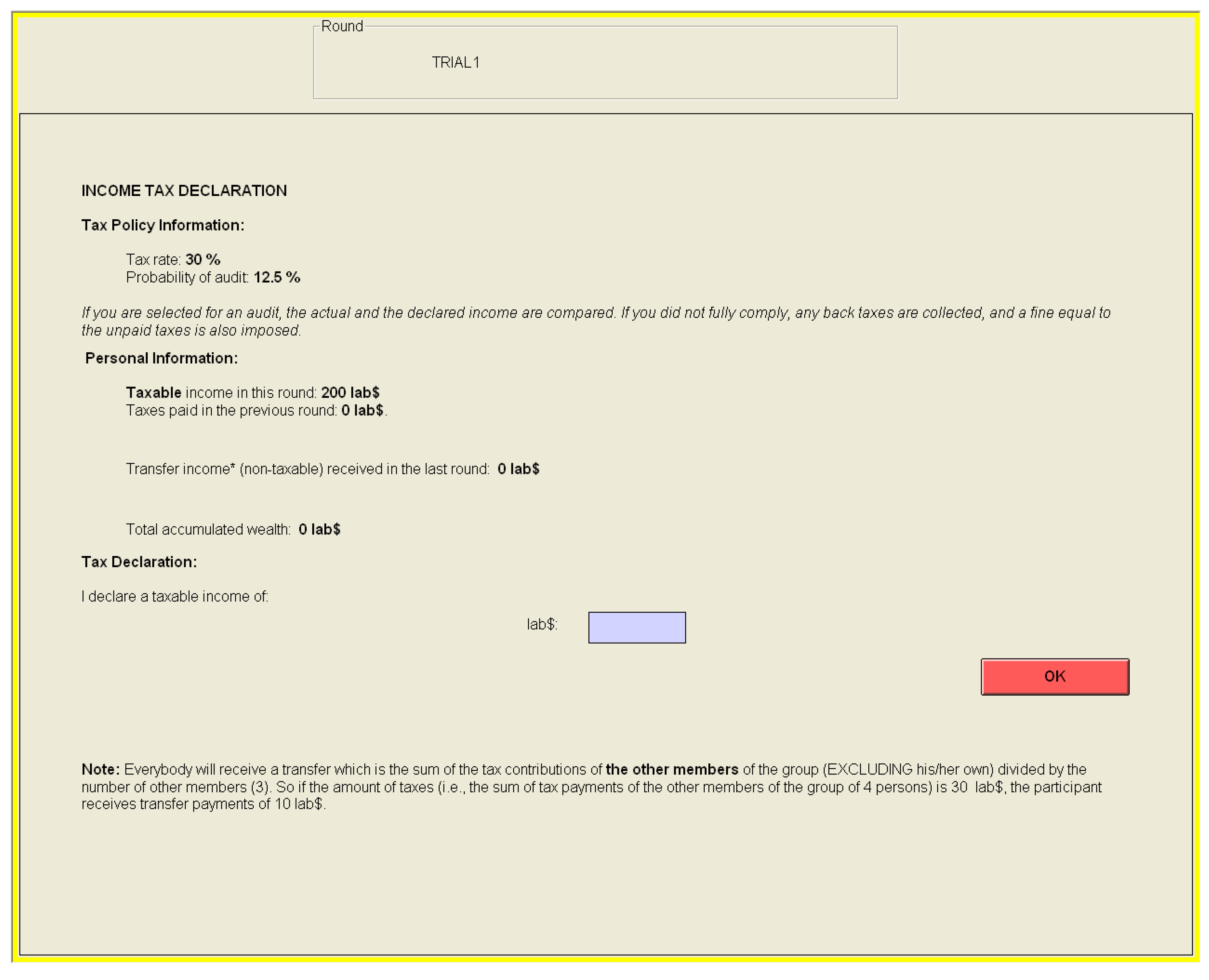
2. Decision Process
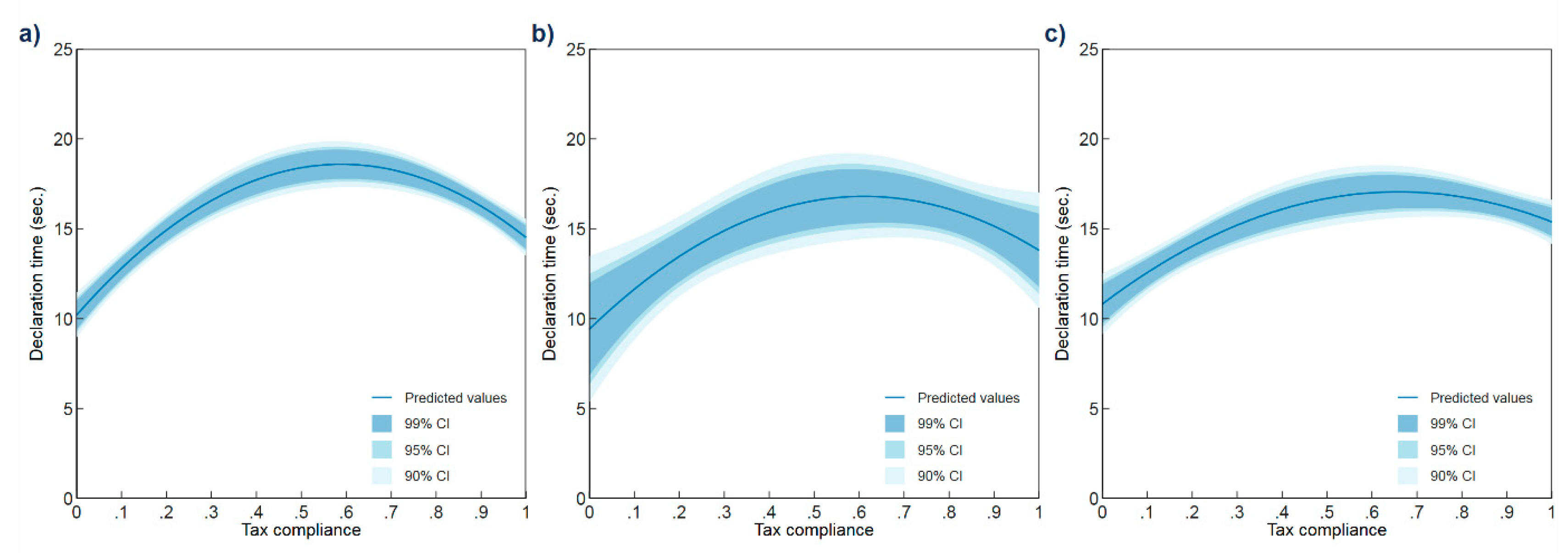
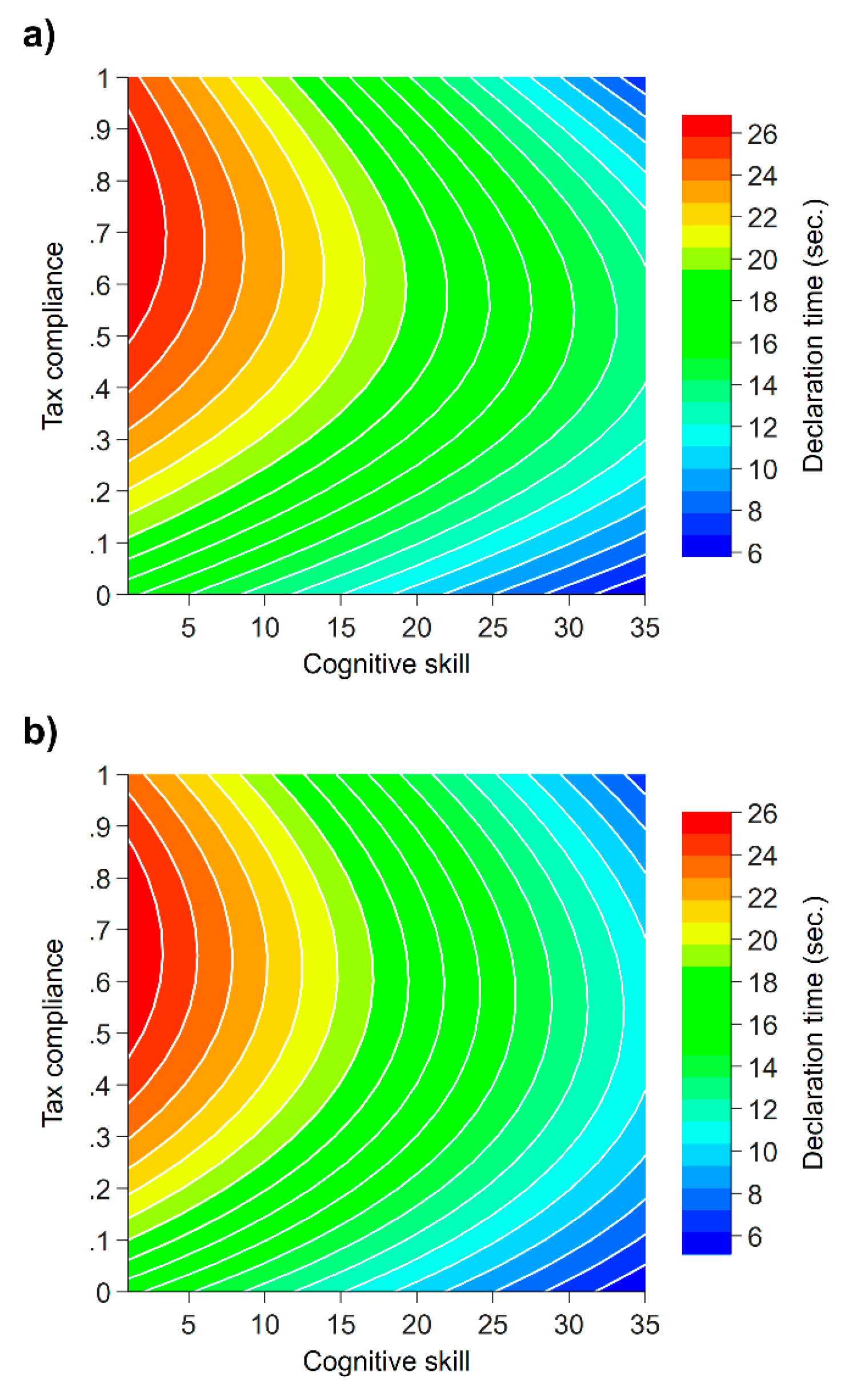
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Numerical Reasoning | Look at the Row of Numbers. What Number Should Come Next? 27 9 3 1 1/3 1/9 1/? |
|---|---|
| Verbal reasoning | IMPRISON is the opposite of 1. capture, 2. endanger, 3. free, 4. discover, 5. heal |
| Spatial reasoning | Which figure can be made from the two figures in the brackets? |
References
- Benjamin, L.T., Jr. A Brief History of Modern Psychology; John Wiley & Sons: New York, NY, USA, 2018. [Google Scholar]
- Sokal, M.M. An Education in Psychology: James McKeen Cattell’s Journal and Letters from Germany and England, 1880–1888; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Meyer, D.E.; Osman, A.M.; Irwin, D.E.; Yantis, S. Modern mental chronometry. Biol. Psychol. 1988, 26, 3–67. [Google Scholar] [CrossRef]
- Posner, M.I. Chronometric Explorations of Mind; Erlbaum: Hillsdale, NJ, USA, 1978. [Google Scholar]
- Rubinstein, A. A typology of players: Between instinctive and contemplative. Q. J. Econ. 2016, 131, 859–890. [Google Scholar] [CrossRef]
- Rubinstein, A. Instinctive and cognitive reasoning: A study of response times. Econ. J. 2007, 117, 1243–1259. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Gladwin, T.E.; Figner, B. “Hot” cognition and dual systems: Introduction, criticisms, and ways forward. In Frontiers of Cognitive Psychology Series: Neuroeconomics, Judgment, and Decision Making; Psychology Press: New York, NY, USA, 2014; pp. 157–180. [Google Scholar]
- Freud, S. An Outline of Psychoanalysis; W. W. Norton: New York, NY, USA, 1949. [Google Scholar]
- Dulleck, U.; Schaffner, M.; Torgler, B. Heartbeat and economic decisions: Observing mental stress among proposers and responders in the ultimatum bargaining game. PLoS ONE 2014, 9, e108218. [Google Scholar] [CrossRef]
- Rubinstein, A. Response time and decision making: An experimental study. Judgm. Decis. Mak. 2013, 8, 485–494. [Google Scholar]
- Spiliopoulos, L.; Ortmann, A. The BCD of response time analysis in experimental economics. Exp. Econ. 2018, 21, 383–433. [Google Scholar] [CrossRef]
- Dulleck, U.; Fooken, J.; Newton, C.; Ristl, A.; Schaffner, M.; Torgler, B. Tax compliance and psychic costs: Behavioral experimental evidence using a physiological marker. J. Public. Econ. 2016, 134, 9–18. [Google Scholar] [CrossRef]
- Jiang, T. Cheating in mind games: The subtlety of rules matters. J. Econ. Behav. Organ. 2013, 93, 328–336. [Google Scholar] [CrossRef]
- Coricelli, G.; Joffily, M.; Montmarquette, C.; Villeval, M.C. Cheating, emotions, and rationality: An experiment on tax evasion. Exp. Econ. 2010, 13, 226–247. [Google Scholar] [CrossRef]
- Carroll, J.S. A Cognitive-Process Analysis of Taxpayer Compliance. Available online: https://www.semanticscholar.org/paper/A-cognitive-process-analysis-of-taxpayer-compliance-Carroll/bcea7f83435ff11dade5919138e7cba1dece3779 (accessed on 15 January 1986).
- Krajbich, I.; Bartling, B.; Hare, T.; Fehr, E. Rethinking fast and slow based on a critique of reaction-time reverse inference. Nat. Commun. 2015, 6, 7455. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, G.; Fugelsang, J.A.; Koehler, D.J.; Thompson, V.A. Commentary: Rethinking fast and slow based on a critique of reaction-time reverse inference. Front. Psychol. 2016, 7, 1174. [Google Scholar] [CrossRef] [PubMed]
- Piovesan, M.; Wengström, E. Fast or fair? A study of response times. Econ. Lett. 2009, 105, 193–196. [Google Scholar] [CrossRef]
- Recalde, M.P.; Riedl, A.; Vesterlund, L. Error-prone inference from response time: The case of intuitive generosity in public-good games. J. Public. Econ. 2018, 160, 132–147. [Google Scholar] [CrossRef]
- Evans, A.M.; Rand, D.G. Cooperation and decision time. Curr. Opin. Psychol. 2019, 26, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Vogel, J. Taxation and public opinion in Sweden: An interpretation of recent survey data. Natl. Tax. J. 1974, 499–513. [Google Scholar]
- Torgler, B. Tax morale, rule-governed behaviour and trust. Const. Polit. Econ. 2003, 14, 119–140. [Google Scholar] [CrossRef]
- Alm, J.; Jackson, B.; McKee, M. Institutional uncertainty and taxpayer compliance. Am. Econ. Rev. 1992, 82, 1018–1026. [Google Scholar]
- Alm, J.; Jackson, B.R.; McKee, M. Fiscal exchange, collective decision institutions, and tax compliance. J. Econ. Behav. Organ. 1993, 22, 285–303. [Google Scholar] [CrossRef]
- Alm, J.; McClelland, G.H.; Schulze, W.D. Changing the social norm of tax compliance by voting. Kyklos 1999, 52, 141–171. [Google Scholar] [CrossRef]
- Torgler, B. Speaking to theorists and searching for facts: Tax morale and tax compliance in experiments. J. Econ. Surv. 2002, 16, 657–683. [Google Scholar] [CrossRef]
| 1 | Cattell is an important figure in the history of psychology, who not only founded leading journals such as Psychological Review of Psychological Bulletin, but was also editor of Science. |
| 2 | The ultimatum game consists of a two-stage game between two players where the second player (responder) decides whether to accept or reject the offer (split of a total sum amount) proposed by the first player. If accepted, each player gets money based on the offer. If the responder rejects, each player receives nothing. |
| 3 | See also Dulleck et al. [10] for an exploration of the ultimatum game applying a physiological marker on both, the proposer and the responder. |
| 4 | For a detailed discussion on the benefits, challenges, and possibilities of exploring response time in cognitive psychology and experimental or behavioural economics see Spiliopoulos and Ortmann [12]. |
| 5 | The public goods game models a collective contribution problem in which individuals can decide how much to contribute towards the group. The collective contribution is multiplied by a certain factor and then equally shared among the individuals of the group. In the experiment all the taxes paid by individuals in a group were multiplied with three different factors (0 = no public good, 1, and 2) being equally redistributed to the group members. |
| 6 | Nevertheless, we examined the effect of being audited or fined in the previous round and find that it does reduce respond time (on average by ~2 s), after controlling for subject fixed effects). |
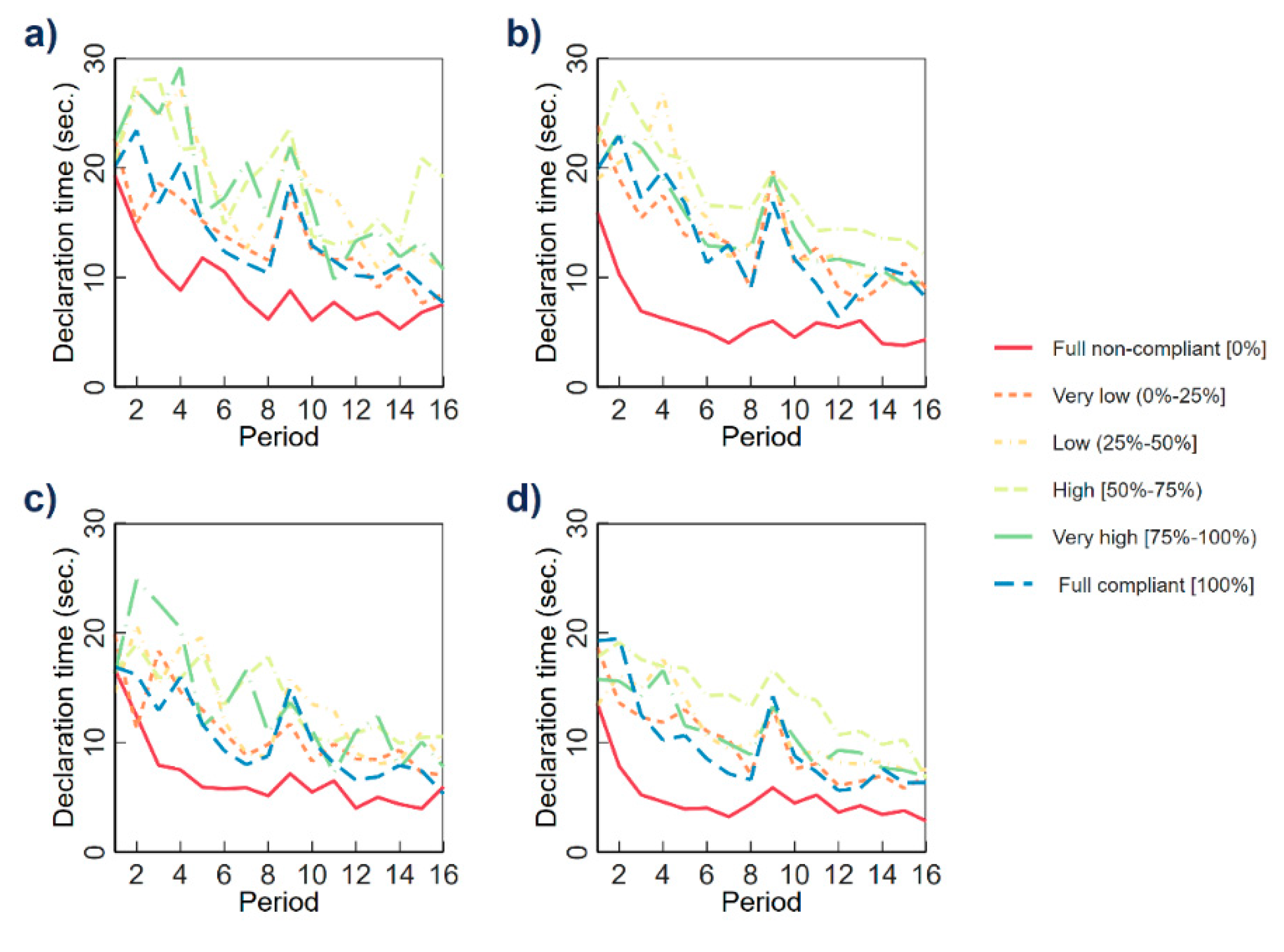
| 7 | In the first eight rounds, the redistributed amount for each participant in the public good component of the experiment is based on the total contribution all four members to the group. In the remaining rounds, the calculation of redistribution amount only considered the total contribution of the other three members of the group. We also noted a larger impact on decision time for groups all groups except when full non-compliance was observed (see red line Figure 2). |
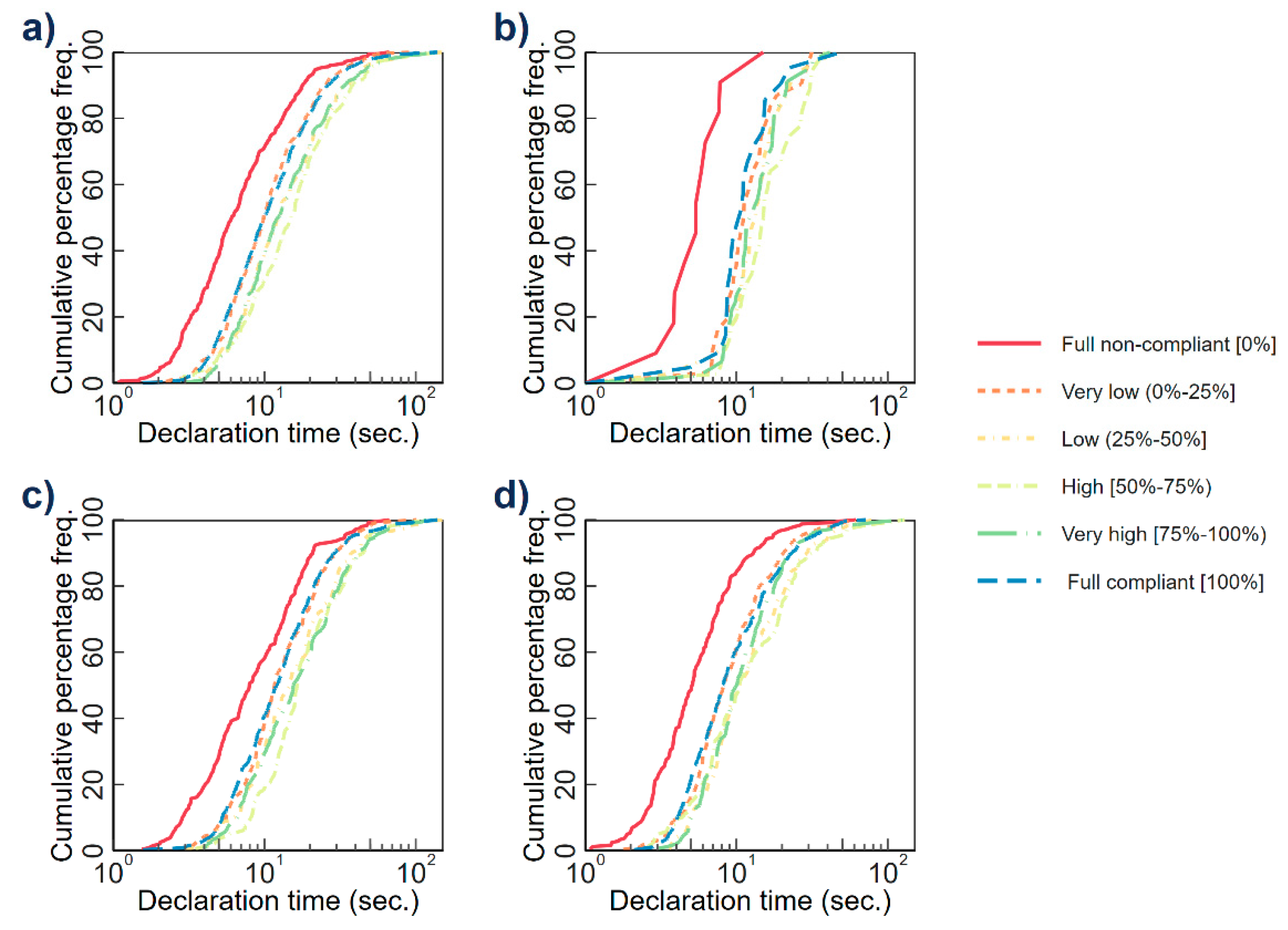
| Tax Compliance Level | Individual-Decisions | Individual-Average | ||||||
|---|---|---|---|---|---|---|---|---|
| N | Percent | Median (s) | 1st half | 2nd half | N | Percent | Median (s) | |
| Full non-compliant (0%) | 478 | 16.6 | 6.09 | 7.97 | 5.13 | 11 | 6.11 | 5.4 |
| Very low (0–25%) | 516 | 17.92 | 9.88 | 11.68 | 8.25 | 31 | 17.22 | 11.18 |
| Low (25–50%) | 348 | 12.08 | 12.48 | 14.68 | 10.56 | 36 | 20 | 13.37 |
| High (50–75%) | 312 | 10.83 | 14.88 | 16.46 | 10.45 | 36 | 20 | 15.12 |
| Very high (75–100%) | 296 | 10.28 | 12.38 | 15.62 | 10.10 | 45 | 25 | 12.75 |
| Full compliant (100%) | 930 | 32.29 | 9.95 | 12.16 | 8.16 | 21 | 11.67 | 10.72 |
| Total | 2880 | 100 | 180 | 100 | ||||
| Group 1 | Group 2 | (a) Average | (b) Average | (c) Median | (d) Median | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| diff. | t | punadj | pBon | sig. | diff. | t | punadj | pBon | sig. | diff. | t | punadj | pBon | sig. | diff. | t | punadj | pBon | sig. | ||
| Full non-compliant | Very low | −4.45 | −6.76 | <0.001 | <0.001 | *** | −7.27 | −9.69 | <0.001 | <0.001 | *** | −4.20 | −6.44 | <0.001 | <0.001 | *** | −4.91 | −8.56 | <0.001 | <0.001 | *** |
| Full non-compliant | Low | −8.65 | −7.55 | <0.001 | <0.001 | *** | −8.72 | −7.68 | <0.001 | <0.001 | *** | −5.95 | −6.31 | <0.001 | <0.001 | *** | −6.02 | −7.69 | <0.001 | <0.001 | *** |
| Full non-compliant | High | −10.08 | −9.2 | <0.001 | <0.001 | *** | −11.57 | −13.35 | <0.001 | <0.001 | *** | −6.86 | −8.69 | <0.001 | <0.001 | *** | −8.95 | −12.48 | <0.001 | <0.001 | *** |
| Full non-compliant | Very high | −8.69 | −7.05 | <0.001 | <0.001 | *** | −8.51 | −9.92 | <0.001 | <0.001 | *** | −6.72 | −6.22 | <0.001 | <0.001 | *** | −5.93 | −9.38 | <0.001 | <0.001 | *** |
| Full non-compliant | Full compliant | −4.75 | −5.87 | <0.001 | <0.001 | *** | −7.06 | −7.42 | <0.001 | <0.001 | *** | −3.57 | −5.87 | <0.001 | <0.001 | *** | −4.76 | −7.00 | <0.001 | <0.001 | *** |
| Very low | Full compliant | −0.30 | −0.46 | 0.6514 | 1 | 0.21 | 0.35 | 0.7299 | 1 | 0.63 | 1.01 | 0.3271 | 1 | 0.15 | 0.30 | 0.7719 | 1 | ||||
| Low | Full compliant | 3.89 | 7.22 | <0.001 | <0.001 | *** | 1.66 | 2.43 | 0.0282 | 0.4233 | 2.38 | 4.07 | 0.001 | 0.015 | * | 1.27 | 1.72 | 0.1057 | 1 | ||
| High | Full compliant | 5.32 | 5.3 | <0.001 | 0.0013 | ** | 4.51 | 9.52 | <0.001 | <0.001 | *** | 3.29 | 4.38 | <0.001 | 0.0081 | ** | 4.19 | 6.13 | <0.001 | <0.001 | *** |
| Very high | Full compliant | 3.93 | 5.38 | <0.001 | 0.0011 | ** | 1.45 | 2.96 | 0.0098 | 0.1468 | 3.14 | 3.51 | 0.0032 | 0.0478 | * | 1.18 | 1.85 | 0.0837 | 1 | ||
| Very low | Low | −4.20 | −4.8 | <0.001 | 0.0035 | ** | −1.45 | −1.73 | 0.1036 | 1 | −1.75 | −1.87 | 0.0806 | 1 | −1.12 | −1.96 | 0.0692 | 1 | |||
| Very low | High | −5.63 | −4.93 | <0.001 | 0.0027 | ** | −4.30 | −5.6 | <0.001 | <0.001 | *** | −2.66 | −3.29 | 0.005 | 0.0746 | † | −4.04 | −7.76 | <0.001 | <0.001 | *** |
| Very low | Very high | −4.24 | −4.3 | <0.001 | 0.0095 | ** | −1.24 | −1.85 | 0.0841 | 1 | −2.51 | −2.38 | 0.0312 | 0.4679 | −1.03 | −2.13 | 0.05 | 0.7506 | |||
| Low | High | −1.43 | −1.32 | 0.2062 | 1 | −2.84 | −4.08 | <0.001 | 0.0147 | * | −0.91 | −1.04 | 0.3166 | 1 | −2.92 | −6.66 | <0.001 | <0.001 | *** | ||
| Low | Very high | −0.04 | −0.05 | 0.9641 | 1 | 0.22 | 0.36 | 0.7219 | 1 | −0.76 | −0.73 | 0.4778 | 1 | 0.09 | 0.29 | 0.7787 | 1 | ||||
| High | Very high | 1.39 | 1.32 | 0.2059 | 1 | 3.06 | 10.94 | <0.001 | <0.001 | *** | 0.15 | 0.16 | 0.8779 | 1 | 3.01 | 7.16 | <0.001 | <0.001 | *** | ||
| Group 1 | Group 2 | (a) Individual-Decisions | (b) Individuals | (c) Decisions, First Half | (d) Decisions, Second Half | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | punadj | pBon | sig. | D | punadj | pBon | sig. | D | punadj | pBon | sig. | D | punadj | pBon | sig. | ||
| Full non-compliant | Very low | 0.3068 | <0.001 | <0.001 | *** | 0.2724 | <0.001 | <0.001 | *** | 0.3639 | <0.001 | <0.001 | *** | 0.7478 | <0.001 | 0.0034 | ** |
| Full non-compliant | Low | 0.3969 | <0.001 | <0.001 | *** | 0.3236 | <0.001 | <0.001 | *** | 0.4749 | <0.001 | <0.001 | *** | 0.8258 | <0.001 | <0.001 | *** |
| Full non-compliant | High | 0.4254 | <0.001 | <0.001 | *** | 0.417 | <0.001 | <0.001 | *** | 0.418 | <0.001 | <0.001 | *** | 0.8813 | <0.001 | <0.001 | *** |
| Full non-compliant | Very high | 0.3802 | <0.001 | <0.001 | *** | 0.3235 | <0.001 | <0.001 | *** | 0.4462 | <0.001 | <0.001 | *** | 0.8646 | <0.001 | <0.001 | *** |
| Full non-compliant | Full compliant | 0.2666 | <0.001 | <0.001 | *** | 0.2382 | <0.001 | <0.001 | *** | 0.2969 | <0.001 | <0.001 | *** | 0.8139 | <0.001 | 0.0021 | ** |
| Very low | Full compliant | 0.0521 | 0.3291 | 1 | 0.0597 | 0.6365 | 1 | 0.0774 | 0.2449 | 1 | 0.1705 | 0.8599 | 1 | ||||
| Low | Full compliant | 0.1455 | <0.001 | <0.001 | *** | 0.1508 | 0.0063 | 0.0951 | † | 0.1852 | <0.001 | 0.0051 | ** | 0.3135 | 0.1475 | 1 | |
| High | Full compliant | 0.211 | <0.001 | <0.001 | *** | 0.261 | <0.001 | <0.001 | *** | 0.1778 | 0.0026 | 0.0389 | * | 0.381 | 0.0426 | 0.6386 | |
| Very high | Full compliant | 0.1367 | <0.001 | 0.0068 | ** | 0.1886 | <0.001 | 0.0089 | ** | 0.1797 | 0.0016 | 0.0242 | * | 0.2635 | 0.2732 | 1 | |
| Very low | Low | 0.151 | <0.001 | 0.0023 | ** | 0.1326 | 0.0628 | 0.9419 | 0.1866 | 0.001 | 0.0152 | * | 0.2195 | 0.3983 | 1 | ||
| Very low | High | 0.247 | <0.001 | <0.001 | *** | 0.2776 | <0.001 | <0.001 | *** | 0.1997 | 0.0012 | 0.0185 | * | 0.3118 | 0.0784 | 1 | |
| Very low | Very high | 0.1562 | <0.001 | 0.0031 | ** | 0.1797 | 0.0057 | 0.0852 | † | 0.1683 | 0.0084 | 0.1255 | 0.1728 | 0.6438 | 1 | ||
| Low | High | 0.1162 | 0.0236 | 0.3541 | 0.1784 | 0.008 | 0.12 | 0.0955 | 0.4832 | 1 | 0.1944 | 0.5041 | 1 | ||||
| Low | Very high | 0.0281 | 0.9998 | 1 | 0.0836 | 0.6293 | 1 | 0.096 | 0.4543 | 1 | 0.1278 | 0.8997 | 1 | ||||
| High | Very high | 0.1209 | 0.0235 | 0.353 | 0.1505 | 0.0516 | 0.7737 | 0.1508 | 0.0802 | 1 | 0.2056 | 0.3667 | 1 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, H.F.; Dulleck, U.; Torgler, B. Response Times and Tax Compliance. Games 2019, 10, 45. https://doi.org/10.3390/g10040045
Chan HF, Dulleck U, Torgler B. Response Times and Tax Compliance. Games. 2019; 10(4):45. https://doi.org/10.3390/g10040045
Chicago/Turabian StyleChan, Ho Fai, Uwe Dulleck, and Benno Torgler. 2019. "Response Times and Tax Compliance" Games 10, no. 4: 45. https://doi.org/10.3390/g10040045
APA StyleChan, H. F., Dulleck, U., & Torgler, B. (2019). Response Times and Tax Compliance. Games, 10(4), 45. https://doi.org/10.3390/g10040045





