An Experimental Study of Self-Enforcing Coalitions
Abstract
1. Introduction
1.1. Experimental Testing of the Theory
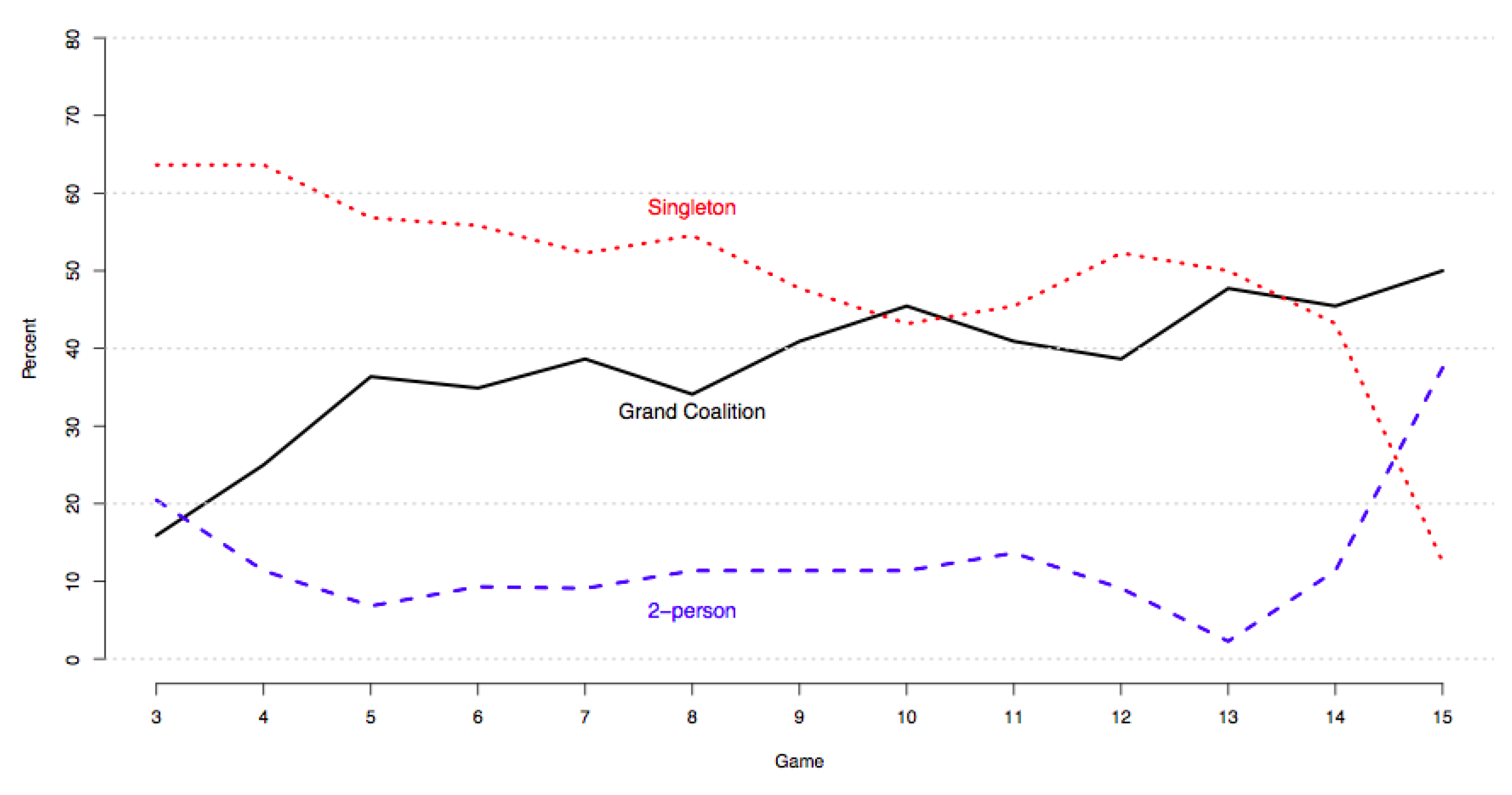
1.2. Overview of the Results
2. Literature
2.1. Experiments on Coalition Formation
2.2. Learning and Experience
2.3. Stake Size
3. Theoretical Considerations
- Nature picks a proposer agent for .
- Agent proposes a winning coalition , such that .
- Agents vote yes or no regarding forming coalition . The vote of the proposing agent is recorded as yes. The votes of the agents in , who are not part of the proposed coalition, are recorded as no. The agents in vote sequentially following a random ordering thereof. If the agents who voted yes form a winning coalition in , then proceed to Step 4; otherwise, proceed to Step 5.
- If , proceed to Step 6. If not, players from are eliminated and the game reverts back to Step 1 with (and j increases by 1).
- If , the next agenda setter is picked randomly from among those in who have not yet proposed at this stage, and the game proceeds to Step 2 with q increased by 1. If , the game proceeds to step 6.
- becomes the ruling coalition, where each agent receives pay-off .
4. Experimental Design
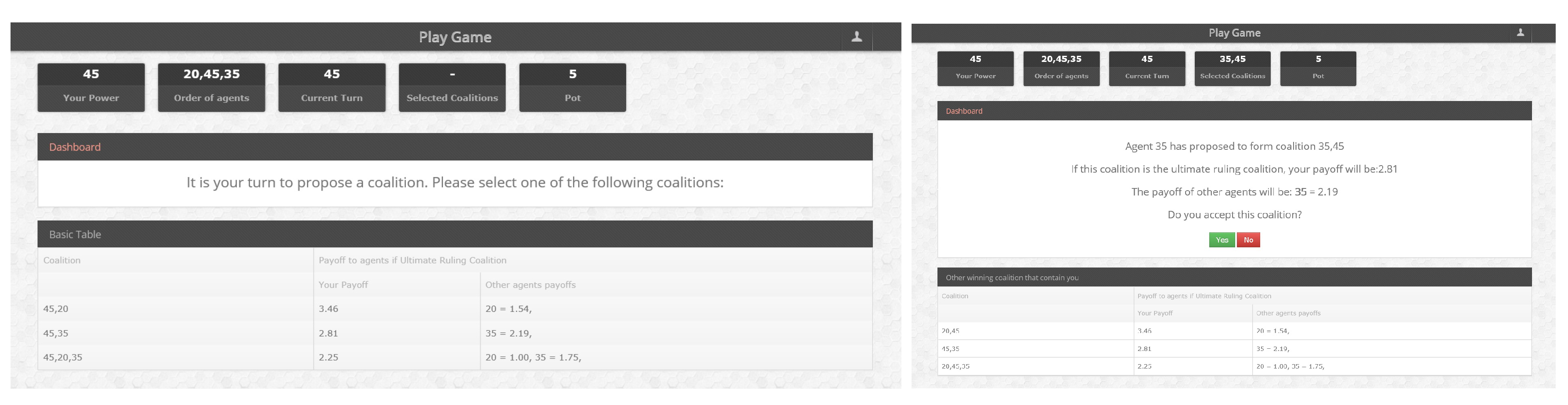
- An agent is chosen randomly to be the proposer, and he proposes to form a winning coalition.
- Agents sequentially vote yes or no on whether to join the proposed coalition. We assume that the proposer votes yes and the agents outside the proposed coalition vote no.
- A coalition passes if the players who voted yes have over 50% of the power of the current coalition.
- If a coalition passes, the game is repeated but only with the agents inside this passed coalition.
- If the coalition fails, a new proposer is chosen randomly, and the game begins again.
- The game ends if one of the following three cases happens:
- -
- if no coalition is passed after everyone in the remaining coalition has been given a chance to propose. In this case, the remaining coalition is implemented, and the pot is divided in proportion to their power.
- -
- if a dictator (unique agent) is left in the game. In this case, the dictator earns the full pot of money.
- -
- if the two-person coalition is proposed and accepted by the two agents inside it. In this case, the two-person coalition is implemented and the pot is divided in proportion to their power.
- -
- if the current grand coalition is proposed and unanimously accepted. In this case, the current grand coalition is implemented, and the pot is divided in proportion to their power.
5. Results
5.1. Analysis of Strategies
5.2. Typology of Agents
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Experiment Instruction and Quiz
Appendix A.1. Oral Instructions Given to Students
- Good afternoon, everyone, in a few minutes we will be starting our experiment. Please sign the consent form that basically tells us that you agree to participate in this experiment. If at any time you feel uncomfortable with the experiment, please inform us and you will have the option to leave it.
- A few house rules: Always remember that you cannot talk with anyone while doing the experiment. Please refrain from texting, browsing, or any other activity not related to the experiment. If you have any questions, please raise your hand and ask the experimenters and they will address your concerns.
- We will be watching a video that gives instructions to the experiment. Be sure you use your headphones so that you do not bother anyone. Again, if there are any questions regarding the video instructions, please raise your hand. (The video was played for every student in a computer and headset available in the lab. Students had the option to rewind, pause/play the video at any time. See link to video and screenshots below).
- Please go to Google Chrome and open the following link (given to students after everyone finished watching the video). The link contains a quiz to test whether you have understood the instructions in the video. Again, if there are any questions, please raise your hand (see quiz below).
- We are handing out the earnings sheet. We have two (2) practice games that are designed to familiarize you with the game. You will not be paid in these practice games. After the practice games, we will play up to twelve (12) games, where you will be paid based on your performance. The pot for each game is $5. You must write your SEC number, your power, and your final pay-off for each game. Your final pay-off that will appear in your screen is in dollar amounts.
- Now, we will be handing out strips of paper that contain a website’s details. Please copy the address as it appears on the strip of paper. Remember that the address is case-sensitive.Step 7 was repeated for up to 13 times, for every game after the initial and final game.
- Please close all windows now. We will be handing out new strips of paper with the website that you should go to.The next step notifies the student that this is the final game. It also tells them the pot amount of the final game (keep at $5 or increase to $20–$50). Please note that students were never notified about the availability of the $20/$50 pots until the start of the final game.
- The next is the final game. We will increase the pot from $5 to $20/$50 (keep the pot at $5 dollars).
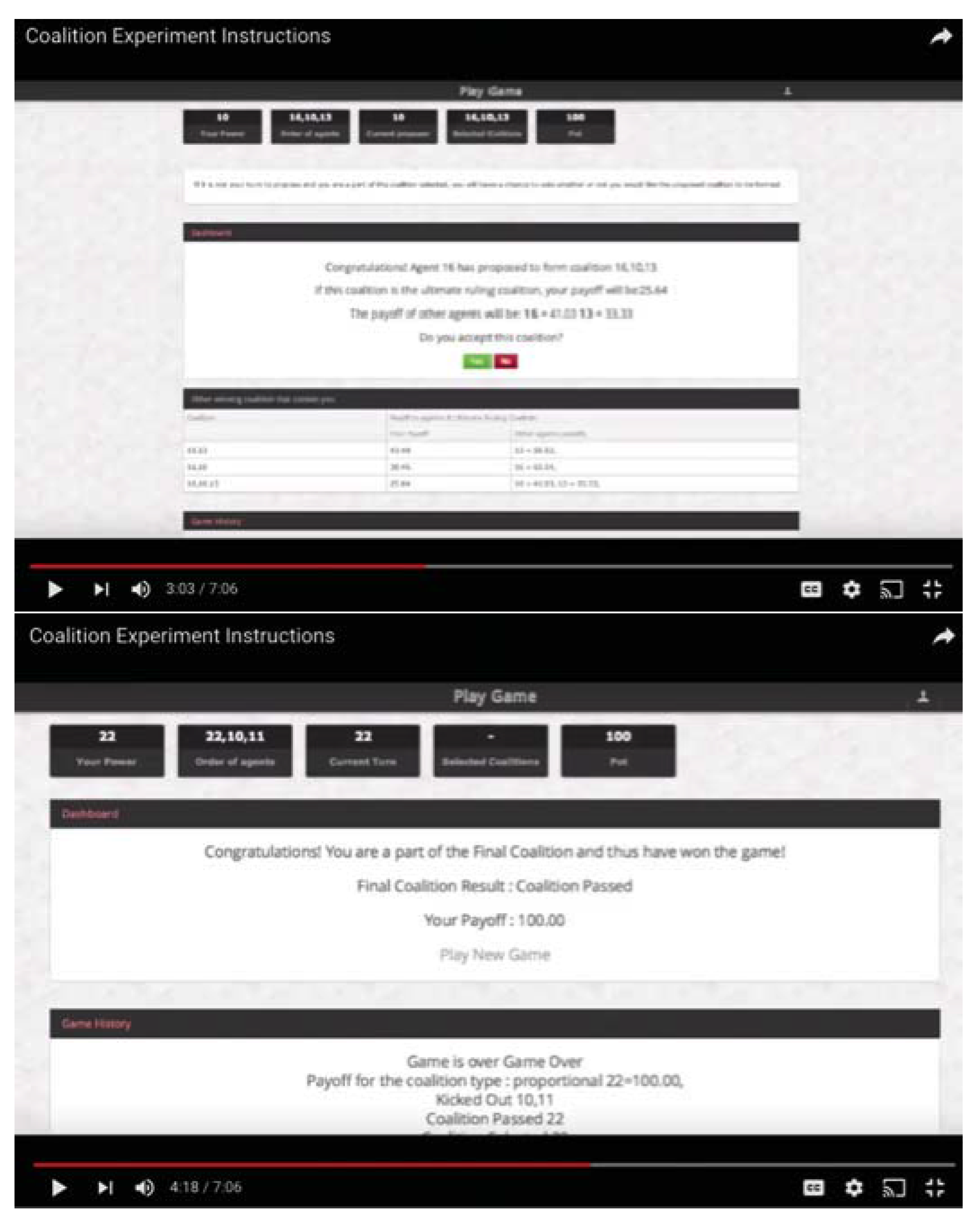
Appendix A.2. Screenshots of Video and Instructions

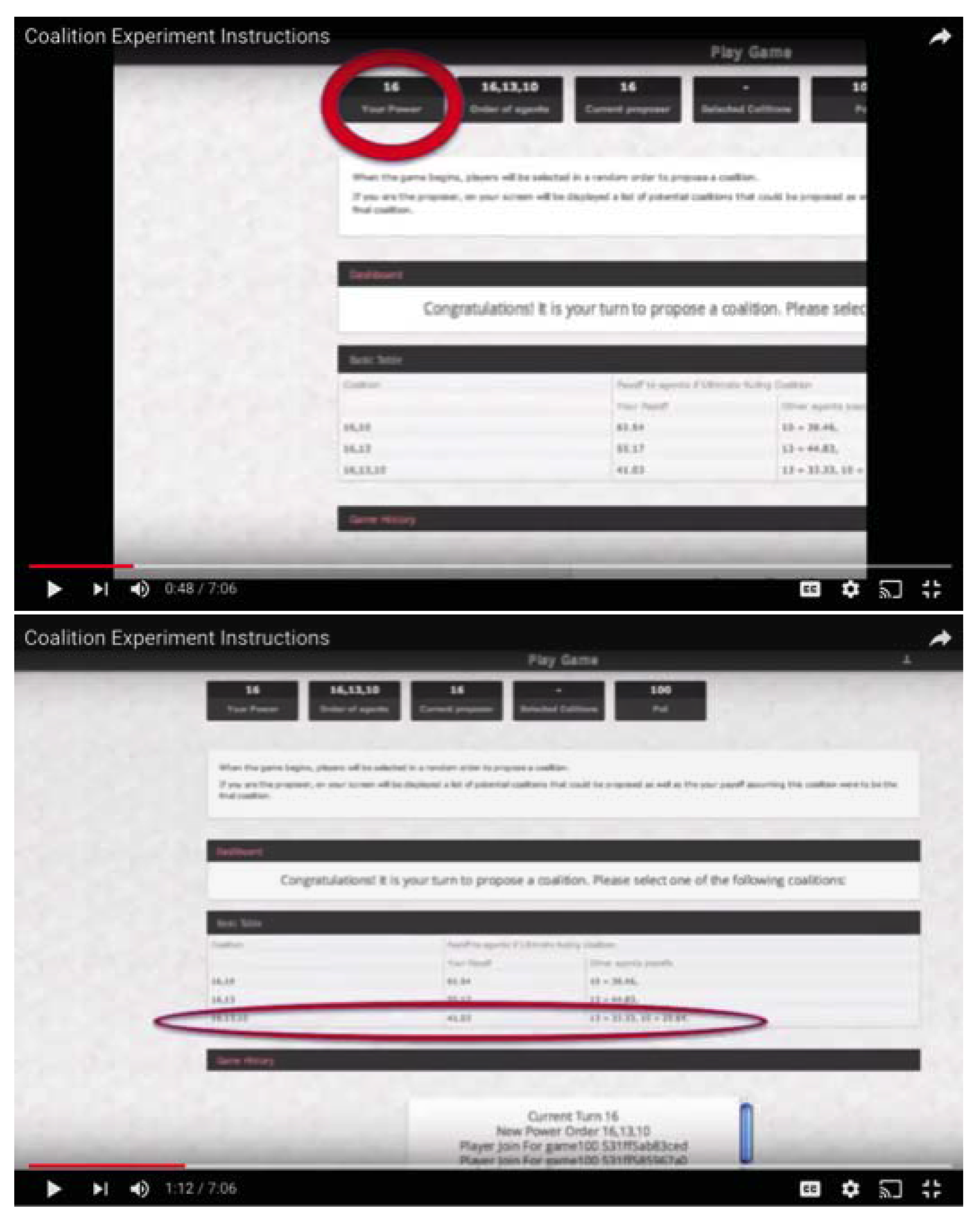
- Question 1: What is your power?
- Question 2: What is your pay-off if the proposed coalition is accepted?
- Question 3: What are the powers of your opponents?
- Question 4: If the coalition proposed by player with power 13 were to be rejected, what is the power of the player who would propose a coalition next?
- Question 5: If the player with powers 20 and 25 voted in favor of a coalition, and players with powers 5, 10, and 15 voted against, would the coalition be accepted or rejected?
Appendix B. Proposal Strategies and Expected Payoffs
| Proposer = 20 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 60 | 34 | 6 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 92 | 8 | 100 | 0 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | C | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 57 | 4 | 0 | 1 | 25 | 13 | 21 | 79 | 40 | 20 | 0 | 20 | 0 | 20 | 8 | 92 | 0 | 0 | 0 | 0 | 0 | 0 |
| (7) Final pay-off ($) | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.82 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.54 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 |
| (8) Expected pay-off ($) | 0.64 | 0.42 | 0.12 | |||||||||||||||||||
| Proposer = 35 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 20 | 73 | 7 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 39 | 61 | 92 | 8 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 55 | 0 | 3 | 0 | 17 | 25 | 30 | 70 | 70 | 4 | 0 | 3 | 8 | 15 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 100 |
| (7) Final pay-off ($) | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 3.18 | 5 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 2.19 | 0 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 |
| (8) Expected pay-off ($) | 1.80 | 2.84 | 0 | |||||||||||||||||||
| Proposer = 45 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 33 | 40 | 27 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 39 | 61 | 35 | 65 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | C | F | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 47 | 0 | 0 | 0 | 46 | 7 | 25 | 75 | 45 | 14 | 0 | 0 | 34 | 7 | 12 | 88 | 0 | 0 | 0 | 0 | 0 | 0 |
| (7) Final pay-off ($) | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 3.46 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 2.81 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 |
| (8) Expected pay-off ($) | 1.40 | 2.62 | 2.49 | |||||||||||||||||||
| Proposer = 20 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 41 | 48 | 11 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 95 | 5 | 100 | 0 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | C | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 54 | 3 | 0 | 0 | 17 | 26 | 23 | 77 | 50 | 50 | 0 | 0 | 0 | 0 | 11 | 89 | 0 | 0 | 0 | 0 | 0 | 0 |
| (7) Final pay-off ($) | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.82 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.54 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 |
| (8) Expected pay-off ($) | 0.59 | 0.46 | 0.17 | |||||||||||||||||||
| Proposer = 35 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 17 | 73 | 10 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 47 | 53 | 100 | 0 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 58 | 0 | 3 | 0 | 21 | 21 | 22 | 78 | 67 | 10 | 0 | 0 | 6 | 17 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| (7) Final pay-off ($) | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 3.18 | 5 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 2.19 | 0 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 |
| (8) Expected pay-off ($) | 2.07 | 3.11 | 0 | |||||||||||||||||||
| Proposer = 45 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 24 | 48 | 28 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 38 | 62 | 41 | 59 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | C | F | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 38 | 0 | 0 | 0 | 58 | 4 | 6 | 94 | 52 | 17 | 0 | 0 | 24 | 7 | 18 | 82 | 50 | 6 | 0 | 0 | 44 | 0 |
| (7) Final pay-off ($) | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 3.46 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 2.81 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 |
| (8) Expected pay-off ($) | 1.05 | 2.81 | 2.54 | |||||||||||||||||||
| Proposer = 20 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 76 | 21 | 3 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 85 | 15 | 100 | 0 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | C | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 59 | 4 | 0 | 1 | 29 | 7 | 18 | 82 | 33 | 0 | 0 | 33 | 0 | 34 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| (7) Final pay-off ($) | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.82 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 | 1.54 | 0 | 1 | 1.82 | 1.54 | 0 | 0 | 0 |
| (8) Expected pay-off ($) | 0.66 | 0.32 | 0 | |||||||||||||||||||
| Proposer = 35 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 23 | 73 | 4 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 33 | 67 | 75 | 25 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | B | E | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 55 | 0 | 5 | 0 | 13 | 27 | 39 | 61 | 72 | 0 | 0 | 4 | 9 | 15 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 100 |
| (7) Final pay-off ($) | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 3.18 | 5 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 | 2.19 | 0 | 1.75 | 3.18 | 0 | 2.19 | 5 | 0 |
| (8) Expected pay-off ($) | 1.63 | 2.61 | 0 | |||||||||||||||||||
| Proposer = 45 | ||||||||||||||||||||||
| (1) Proposed Coalition | ||||||||||||||||||||||
| (2) Percentage of Total Proposals | 43 | 31 | 26 | |||||||||||||||||||
| (3) Outcome of Response | Pass | Pass | Fail | Pass | Fail | |||||||||||||||||
| (4) Outcome by Percentage | 100 | 40 | 60 | 29 | 71 | |||||||||||||||||
| (5) Final Coalition (see Note) | A | B | C | D | E | F | C | F | A | B | C | D | E | F | D | F | A | B | C | D | E | F |
| (6) Frequency (Percentage) | 54 | 0 | 0 | 0 | 37 | 9 | 60 | 40 | 33 | 7 | 0 | 0 | 53 | 7 | 0 | 100 | 34 | 13 | 0 | 0 | 40 | 13 |
| (7) Final pay-off ($) | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 3.46 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 | 2.81 | 5 | 2.25 | 0 | 3.46 | 2.81 | 0 | 5 |
| (8) Expected pay-off ($) | 1.65 | 2.28 | 2.44 | |||||||||||||||||||
Appendix C. Probability of Proposal and Response Strategies
| Dependent Variable: | |||||
|---|---|---|---|---|---|
| Grand Coalition Proposed = 1 | |||||
| (1) | (2) | (3) | (4) | (5) | |
| Power = 35 | −1.743 *** | −1.194 *** | −1.961 *** | −1.259 *** | |
| (0.249) | (0.200) | (0.239) | (0.194) | ||
| Power = 45 | −1.102 *** | −0.769 *** | −1.272 *** | −0.800 *** | |
| (0.281) | (0.236) | (0.256) | (0.219) | ||
| Late games | 1.512 *** | 1.973 *** | |||
| (0.377) | (0.431) | ||||
| Power = 35 × Late games | −1.160 *** | −1.482 *** | |||
| (0.438) | (0.567) | ||||
| Power = 45 × Late games | −0.659 | −0.943 ** | |||
| (0.487) | (0.382) | ||||
| Proposed two-person, in final | 0.236 | 0.362 | 0.120 | ||
| (0.308) | (0.344) | (0.417) | |||
| Proposed two-person, out of final | 0.277 | 0.271 | 0.268 | ||
| (0.256) | (0.309) | (0.513) | |||
| Proposed grand, in final | 1.517 *** | 1.865 *** | 1.667 *** | ||
| (0.184) | (0.196) | (0.494) | |||
| Proposed grand, out of final | 1.327 *** | 1.483 *** | 0.830 | ||
| (0.297) | (0.346) | (0.514) | |||
| $5 stake | 0.044 | ||||
| (0.427) | |||||
| $20 stake | 0.744 | ||||
| (0.475) | |||||
| $50 stake | 1.215 ** | ||||
| (0.489) | |||||
| Constant | 0.392 ** | −0.357 * | −1.019 *** | −0.134 | −0.606 ** |
| (0.179) | (0.198) | (0.222) | (0.277) | (0.290) | |
| Experience/Late Game Interaction | No | No | No | No | Yes |
| Observations | 535 | 535 | 535 | 535 | 535 |
| Log Likelihood | −324.462 | −308.903 | −334.516 | −299.883 | −287.569 |
| Akaike Inf. Crit. | 654.923 | 629.806 | 679.032 | 613.766 | 609.137 |
| Dep. Variable: Accepting the Grand Coalition = 1 | |||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| Power = 35 | −1.686 ** | −1.896 * | −1.609 ** | −2.459 ** | |
| (0.745) | (0.998) | (0.801) | (1.124) | ||
| Power = 45 | −0.715 | 0.260 | −0.585 | 0.179 | |
| (0.768) | (0.161) | (0.863) | (0.280) | ||
| Late games | −0.297 | 15.787 *** | |||
| (0.784) | (1.386) | ||||
| Power = 35 × Late games | 0.331 | 1.164 | |||
| (0.838) | (1.073) | ||||
| Power = 45 × Late games | −1.188 | −0.653 | |||
| (0.896) | (0.899) | ||||
| Accept two-person, in final | −1.386 | −1.259 | −1.559 | ||
| (0.959) | (1.036) | (1.233) | |||
| Accept two-person, out of final | −2.079 ** | −1.906 ** | −0.831 | ||
| (0.821) | (0.931) | (1.217) | |||
| Reject two-person, in final | −1.144 | −1.107 | −1.827 | ||
| (0.912) | (0.934) | (1.221) | |||
| Reject two-person, out of final | −1.553 | −1.653 | 16.662 *** | ||
| (1.048) | (1.025) | (0.712) | |||
| Accept grand, in final | 1.602 | 1.684 | 16.603 *** | ||
| (1.250) | (1.321) | (0.871) | |||
| Accept grand, out of final | −0.907 | −0.763 | 16.574 *** | ||
| (0.658) | (0.705) | (1.134) | |||
| Reject grand, in final | −3.104 *** | −3.080 *** | −2.953 | ||
| (0.938) | (0.964) | (2.775) | |||
| Reject grand, out of final | −1.649 | −1.480 | 17.440 *** | ||
| (1.377) | (1.323) | (2.022) | |||
| $5 stake | 17.569 *** | ||||
| (1.150) | |||||
| $20 stake | 18.185 *** | ||||
| (1.222) | |||||
| $50 stake | 0.804 | ||||
| (1.351) | |||||
| Constant | 3.423 *** | 3.611 *** | 3.258 *** | 4.220 *** | 4.584 *** |
| (0.675) | (0.945) | (0.666) | (0.846) | (1.179) | |
| Experience/Late Game Interaction | No | No | No | No | Yes |
| Observations | 406 | 406 | 406 | 406 | 406 |
| Log Likelihood | −117.490 | −116.122 | −103.694 | −98.239 | −87.699 |
| Akaike Inf. Crit. | 240.979 | 244.243 | 225.387 | 218.477 | 225.398 |
| Dep. Variable: Accepting Two-Person Coalition = 1 | |||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| Power = 35, {20,35} | 2.876 *** | 3.297 *** | 2.963 *** | 3.341 *** | |
| (0.727) | (0.860) | (0.794) | (0.934) | ||
| Power = 35, {35,45} | −0.141 | −0.048 | −0.178 | −0.041 | |
| (0.290) | (0.505) | (0.282) | (0.576) | ||
| Power = 45 | 18.026 *** | 17.893 *** | 18.044 *** | 18.004 *** | |
| (0.463) | (0.479) | (0.473) | (0.467) | ||
| Late games | −0.288 | 0.451 | |||
| (0.360) | (1.255) | ||||
| Power = 35, {20,35} × Late games | −0.948 | −0.596 | |||
| (0.982) | (1.159) | ||||
| Power = 35, {35,45} × Late games | −0.254 | −0.470 | |||
| (0.928) | (0.956) | ||||
| Power = 45 × Late games | 0.288 | −0.261 | |||
| (0.773) | (0.663) | ||||
| Accept two-person, in final | −0.285 | −0.311 | −0.319 | ||
| (0.311) | (0.328) | (0.467) | |||
| Accept two-person, out of final | −0.144 | 0.165 | −0.057 | ||
| (0.271) | (0.334) | (0.401) | |||
| Reject two-person, in final | −1.534 *** | −1.724 *** | −1.185 | ||
| (0.379) | (0.455) | (0.745) | |||
| Reject two-person, out of final | −0.818 * | −0.755 * | −0.838 | ||
| (0.457) | (0.446) | (1.018) | |||
| Accept grand, in final | −0.814 *** | −0.660 *** | −0.558 | ||
| (0.258) | (0.200) | (0.403) | |||
| Accept grand, out of final | −0.859 ** | −0.534 ** | −0.376 | ||
| (0.338) | (0.239) | (0.574) | |||
| Reject grand, in final | −0.076 | −0.056 | 0.141 | ||
| (0.715) | (0.773) | (1.410) | |||
| Reject grand, out of final | 13.930 *** | 17.575 *** | 17.173 *** | ||
| (0.688) | (0.718) | (1.337) | |||
| $5 stake | −1.488 *** | ||||
| (0.529) | |||||
| $20 stake | −0.781 | ||||
| (1.680) | |||||
| $50 stake | 0.691 | ||||
| (0.643) | |||||
| Constant | −0.460 ** | −0.327 * | 0.636 *** | −0.009 | −0.058 |
| (0.203) | (0.184) | (0.195) | (0.190) | (0.196) | |
| Experience/Late Game Interaction | No | No | No | No | Yes |
| Observations | 332 | 332 | 332 | 332 | 332 |
| Log Likelihood | −181.300 | −179.578 | −218.975 | −171.540 | −170.199 |
| Akaike Inf. Crit. | 370.600 | 375.157 | 455.949 | 367.080 | 384.398 |
References
- Ray, D. A Game-Theoretic Perspective on Coalition Formation; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Bueno de Mesquita, B.; Smith, A.; Siverson, R.; Morrow, J. The Logic of Political Surival; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Tullock, G. Autocracy; Kluwer Academic Publishers: Dorderecht, The Netherlands, 1987. [Google Scholar]
- Acemoglu, D.; Egorov, G.; Sonin, K. Coalition Formation in Non-Democracies. Rev. Econ. Stud. 2008, 75, 987–1009. [Google Scholar] [CrossRef]
- Ward, A.; Bishop, K.; Sonnenfeld, J. Pyrrhic Victories: The Cost to the Board of Ousting the CEO. J. Organ. Behav. 1999, 20, 767–781. [Google Scholar] [CrossRef]
- Bogomolnaia, A.; Jackson, M. The Stability of Hedonic Coalition Structures. Games Econ. Behav. 2002, 38, 201–230. [Google Scholar] [CrossRef]
- Ehlers, L. Coalitional Strategy-proof House Allocation. J. Econ. Theory 2002, 105, 298–317. [Google Scholar] [CrossRef]
- Juarez, R. Group Strategyproof Cost Sharing: The Role of Indifferences. Games Econ. Behav. 2013, 82, 218–239. [Google Scholar] [CrossRef]
- Jandoc, K.; Juarez, R. Self-enforcing Coalitions with Power Accumulation. Int. J. Game Theory 2017, 42, 327–355. [Google Scholar] [CrossRef]
- Frederick, S.; Loewenstein, G.; O’Donoghue, T. Time Discounting and Time Preference: A Critical Review. J. Econ. Lit. 2002, 40, 351–401. [Google Scholar] [CrossRef]
- Gabaix, X.; Laibson, D. Myopia and Discounting; NBER Working Paper No. DP11914; National Bureau of Economic Research: Cambridge, MA, USA, 2017. [Google Scholar]
- LePine, J.; Erez, A.; Johnson, D. The Nature and Dimensionality of Organizational Citizenship Behavior: A Critical Review and Meta-Analysis. J. Appl. Psychol. 2002, 87, 52–65. [Google Scholar] [CrossRef]
- Charness, G.; Rabin, M. Understanding Social Preferences with Simple Tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Gruning, C.; Peters, W. Can Justice and Fairness and Enlarge International Environmental Agreements? Games 2010, 1, 137–158. [Google Scholar] [CrossRef]
- Horowitz, A. A Test of the Core, Bargaining Set, Kernel, and Shapley Models in n-person Quota Games with One Weak Player. Theory Decis. 1977, 8, 49–65. [Google Scholar] [CrossRef]
- Rapoport, A.; Kahan, J. When Three is Not Always Two Against One: Coalitions in Experimental Three-person Cooperative Games. J. Exp. Soc. Psychol. 1976, 12, 253–273. [Google Scholar] [CrossRef]
- Fiorina, M.; Plott, C. Committee Decisions under Majority Rule: An Experimental Study. Am. Political Sci. Rev. 1978, 72, 575–598. [Google Scholar] [CrossRef]
- Baron, D.; Ferejohn, J. Bargaining in Legislatures. Am. Political Sci. Rev. 1989, 83, 1181–1206. [Google Scholar] [CrossRef]
- McKelvey, R. An Experimental Test of a Stochastic Game Model of Committee Bargaining. In Laboratory Research in Political Economy; Palfrey, T., Ed.; University of Michigan Press: Ann Arbor, MI, USA, 1991. [Google Scholar]
- Frechette, G.; Kagel, J.; Morelli, M. Nominal Bargaining Power, Selection Protocol, and Dicounting in Legislative Bargaining. J. Public Econ. 2005, 89, 1497–1517. [Google Scholar] [CrossRef]
- Battaglini, M.; Palfrey, T. The Dynamics of Distributive Politics. Econ. Theory 2012, 49, 739–777. [Google Scholar] [CrossRef]
- Nash, J.; Nagel, R.; Ockenfels, A.; Selten, R. The Agencies Method for Coalition Formation in Experimental Games. Proc. Natl. Acad. Sci. USA 2012, 109, 20358–20363. [Google Scholar] [CrossRef]
- Sanchez-Pages, S. Endogenous Coalition Formation in Contests. Rev. Econ. Des. 2007, 11, 139–163. [Google Scholar] [CrossRef]
- Herbst, L.; Konrad, K.; Morath, F. Endogenous Group Formation in Experimental Contests. Eur. Econ. Rev. 2015, 74, 163–189. [Google Scholar] [CrossRef]
- Dechenaux, E.; Kovenock, D.; Sheremeta, R. A Survey of Experimental Research on Contests, All-pay Auctions and Tournaments. Exp. Econ. 2015, 18, 609–669. [Google Scholar] [CrossRef]
- Tremewan, J.; Vanberg, C. The Dynamics of Coalition Formation: A Multilateral Bargaining Experiment with Free Timing of Moves. J. Econ. Behav. Organ. 2016, 130, 33–46. [Google Scholar] [CrossRef]
- Merida-Campos, C.; Willmott, S. The Effect of Heterogeneity on Coalition Formation in Iterated Request for Proposal Scenarios. In Proceedings of the Fourth European Workshop on Multi-Agent Systems (EUMAS 06), Lisbon, Portugal, 14–15 December 2006. [Google Scholar]
- Chalkiadakis, G.; Boutilier, C. Sequentially Optimal Repeated Coalition Formation Under Uncertainty. Auton. Agents Multi-Agent Syst. 2012, 24, 441–484. [Google Scholar] [CrossRef]
- Hyndman, K.; Ozbay, E.; Schotter, A.; Ehrblatt, W. Convergence: An Experimental Study of Teaching and Learning in Repeated Games. J. Eur. Econ. Assoc. 2012, 10, 573–604. [Google Scholar] [CrossRef]
- Mengel, F. Learning by (Limited) Forward Looking Players. J. Econ. Behav. Organ. 2014, 108, 59–77. [Google Scholar] [CrossRef]
- Harrison, G.; List, J. Field Experiments. J. Econ. Lit. 2004, 42, 1009–1055. [Google Scholar] [CrossRef]
- Slonim, R.; Roth, A. Learning in High Stakes Ultimatum Games: An Experiment in the Slovak Republic. Econometrica 1998, 66, 569–596. [Google Scholar] [CrossRef]
- Kachelmeier, S.; Shehata, M. Examining Risk Preferences Under High Monetary Incentives: Experimental Evidence from the Peoples Republic of China. Am. Econ. Rev. 1992, 82, 1120–1141. [Google Scholar]
- Cameron, L. Raising the Stakes in the Ultimatum Game: Experimental Evidence from Indonesia. Econ. Inq. 1999, 37, 47–59. [Google Scholar] [CrossRef]
- Greiner, B. Subject Pool Recruitment Procedures: Organizing Experiments with ORSEE. J. Econ. Sci. Assoc. 2015, 1, 114–125. [Google Scholar] [CrossRef]
- Bolton, G.; Ockenfels, A. ERC: A Theory of Equity, Reciprocity and Competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Nagel, R.; Fang, T. Experimental Results on the Centipede Game in Normal Form: An Investigation on Learning. J. Math. Psychol. 1998, 42, 356–384. [Google Scholar] [CrossRef]
- Selten, R. Axiomatic Characterization of the Quadratic Scoring Rule. Exp. Econ. 1998, 1, 43–62. [Google Scholar] [CrossRef]
- Jandoc, K.; Juarez, R. Forming Coalitions Under Sharing Disagreements; University of Hawaii: Honolulu, HI, USA, 2019. [Google Scholar]
| 1. | Power is the ability to influence the behavior of other agents and could emanate from different sources, for instance political, military, or monetary. |
| 2. | AES’s main stability concept, self-enforcement, requires that there will be no subcoalition of the winning coalition that will be powerful enough to encourage further deviations. Self-enforcement is a robustness property that ensures that the coalition that forms will never disintegrate thereafter. Another appealing axiom they use is rationality, which requires agents to pick the coalition that gives them their highest pay-off among self-enforcing coalitions. Rationality is related to immunity to group manipulations in models discussed by Bogomolnaia and Jackson [6], Ehlers [7], and Juarez [8]. |
| 3. | |
| 4. | Here and in succeeding sections, we use the term dictator if an agent is able to deviate and form a singleton coalition. |
| 5. | We use myopia as the tendency of agents to choose earlier rewards over future ones. There are proposed explanations for why people choose short-term rewards. First, agents’ time preference may exhibit hyperbolic discounting where future rewards are more heavily discounted the longer is the horizon (Frederick et al. [10]). Second, agents may exhibit imperfect forecasting where agents fail to judge or forecast the value of rewards that occurs further in time (Gabaix and Laibson [11]). This might happen, for instance, when agents lack the ability to properly backward induct. In this paper, we use the terms “myopic” and “shortsighted” interchangeably, and is meant to describe agents that prefer to form coalitions that may potentially reduce their future payoffs compared to playing the AES equilibrium strategies. |
| 6. | In the AES model, agents outside the winning coalition are killed and the surviving agents can therefore learn from observing past actions of agents that were killed. Indeed, with a large population, such inter-game learning can affect subsequent stages of the coalition formation game. In our experimental bargaining setup with three agents, however, there will be no scope for inter-game learning since the only feasible deviation is into a two-person coalition which will end in the subsequent round either as a dictator or a two-person coalition. Since we play the experiment repeatedly, we will mainly capture the effect of intra-game learning, or learning by playing many subsequent games. |
| 7. | Tremewan and Vanberg [26] point out that if the outcome from these experiments deviates from theoretical predictions, failure will emanate from behavioral rather than from procedural assumptions. |
| 8. | It is common to assume to restrict the game such that the power profile has no ties in the power of any two coalitions; that is, for any . Please note that the games that do not satisfy this condition has a Lebesgue measure equal to zero, so this is a weak condition (See Jandoc and Juarez [9], Acemoglu et al. [4]). |
| 9. | The pay-off in AES assumes an arbitrarily small cost that is interpreted as the cost of eliminating some of the players from the coalition or as a cost in organizing new coalitions. |
| 10. | While our paper focuses on testing the game proposed by AES, where the determination of the ruling coalition is done sequentially, we note that this assumption is strong and comes with limitations, such as the larger information-exchange needed for the determination of a ruling coalition and applicability to real-world events (e.g., elections or battles in business), where the selection of the ruling coalition is often done simultaneously. A natural extension not studied in our paper is the determination of the equilibrium and its testing for simultaneous versions of the AES’s game. |
| 11. | We note that the determination of the self-enforcing coalition is very robust to the selection of power. In particular, for a three-agent society, unless one agent is a dictator, or two agents have each exactly 50% power, the only possible self-enforcing coalition is the grand coalition. |
| 12. | Please note that this screen is only viewed by those agents included in the proposed coalition. If they are not part of the proposed coalition, their vote is an automatic “No” and they must wait to see whether the proposed coalition passes or fails. If the proposed coalition passes, then they must wait until the game ends. |
| 13. | The instructions can be viewed here: https://www.youtube.com/watch?v=ECl6kXPYyh8. Appendix A provides screenshots of the instructions and the quiz. |
| 14. | The players’ payoffs are in real money (US dollars) to make the amount more salient as has been done in the literature on high-stake games, e.g., Cameron [34]. |
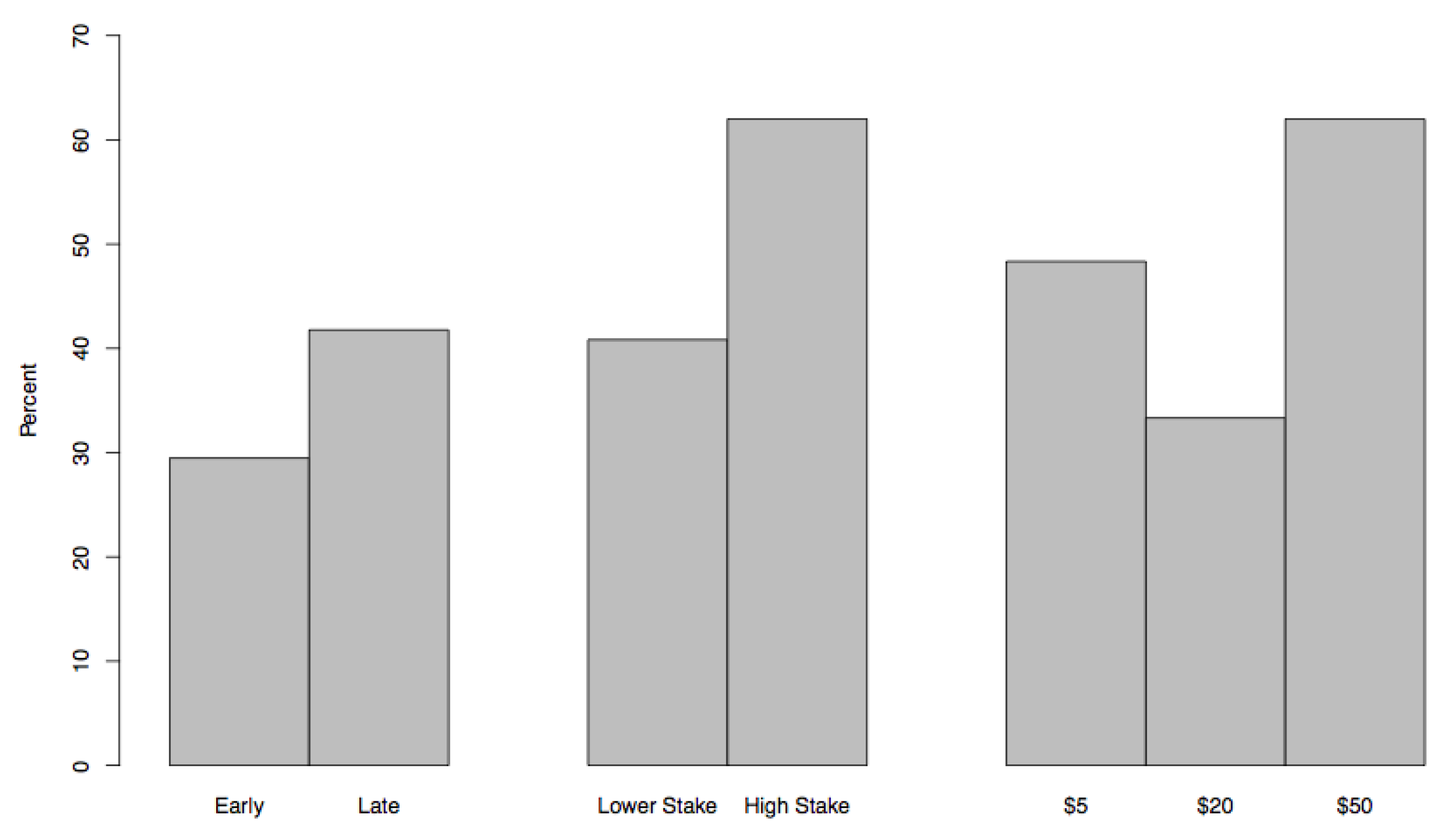
| 15. | We announced the stake prior to the start for each of these final games regardless whether it was a high stake (i.e., $20 or $50) or a low stake (i.e., $5). We implemented the change in stakes in the last round to ensure that agents have learned the game sufficiently and any change in behavior would be purely attributed to the stake. |
| 16. | There are only 3 out of a possible 624 group games in which the grand coalition forms because all agents rejected every proposal made. |
| 17. | We also include a specification where we define the late games to exclude the last game of each session. |
| 18. | However, it is also instructive to examine proposals after a deviation to a two-person coalition if it is part of a person’s empirical best response strategy. This we do in Section 5.2. |
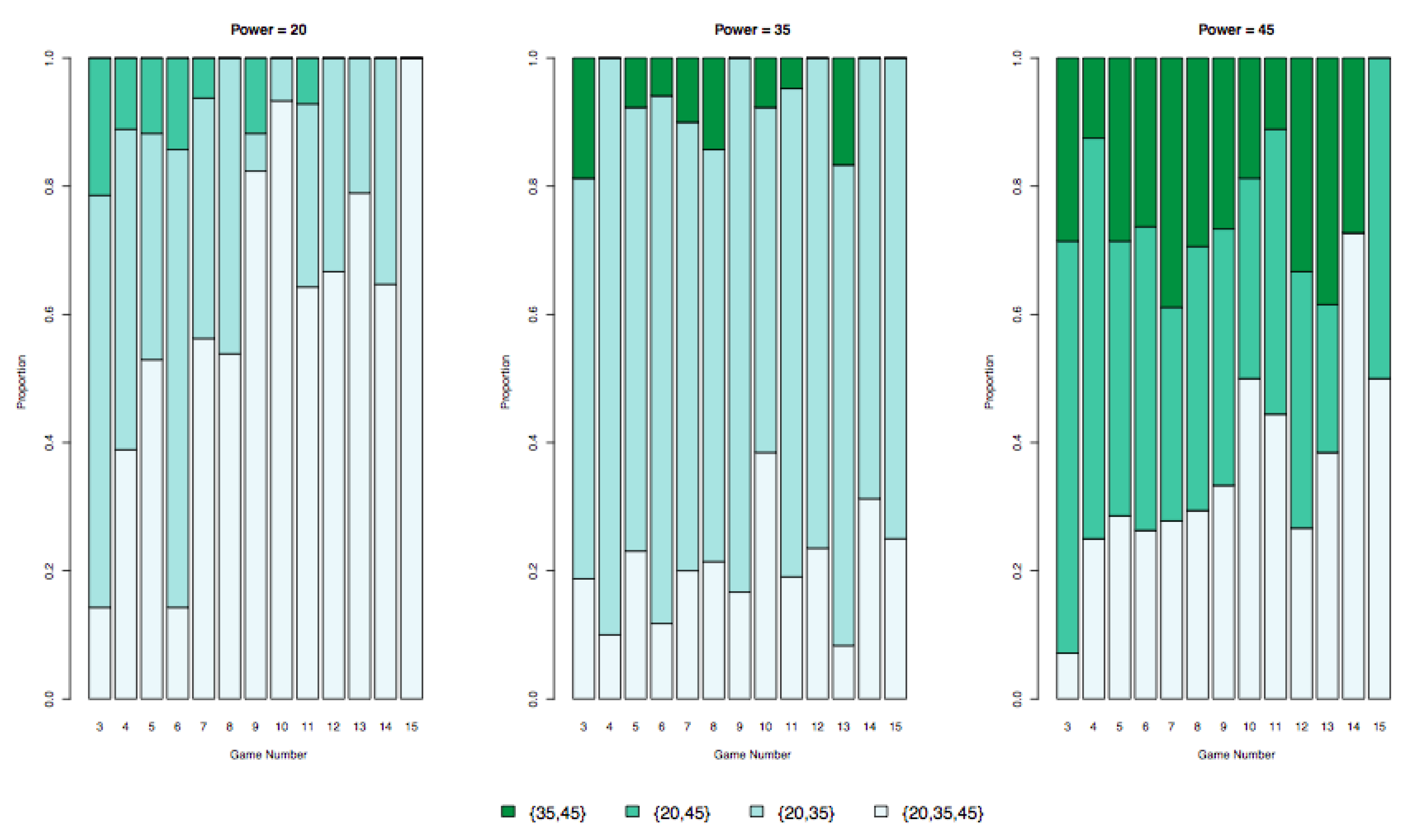
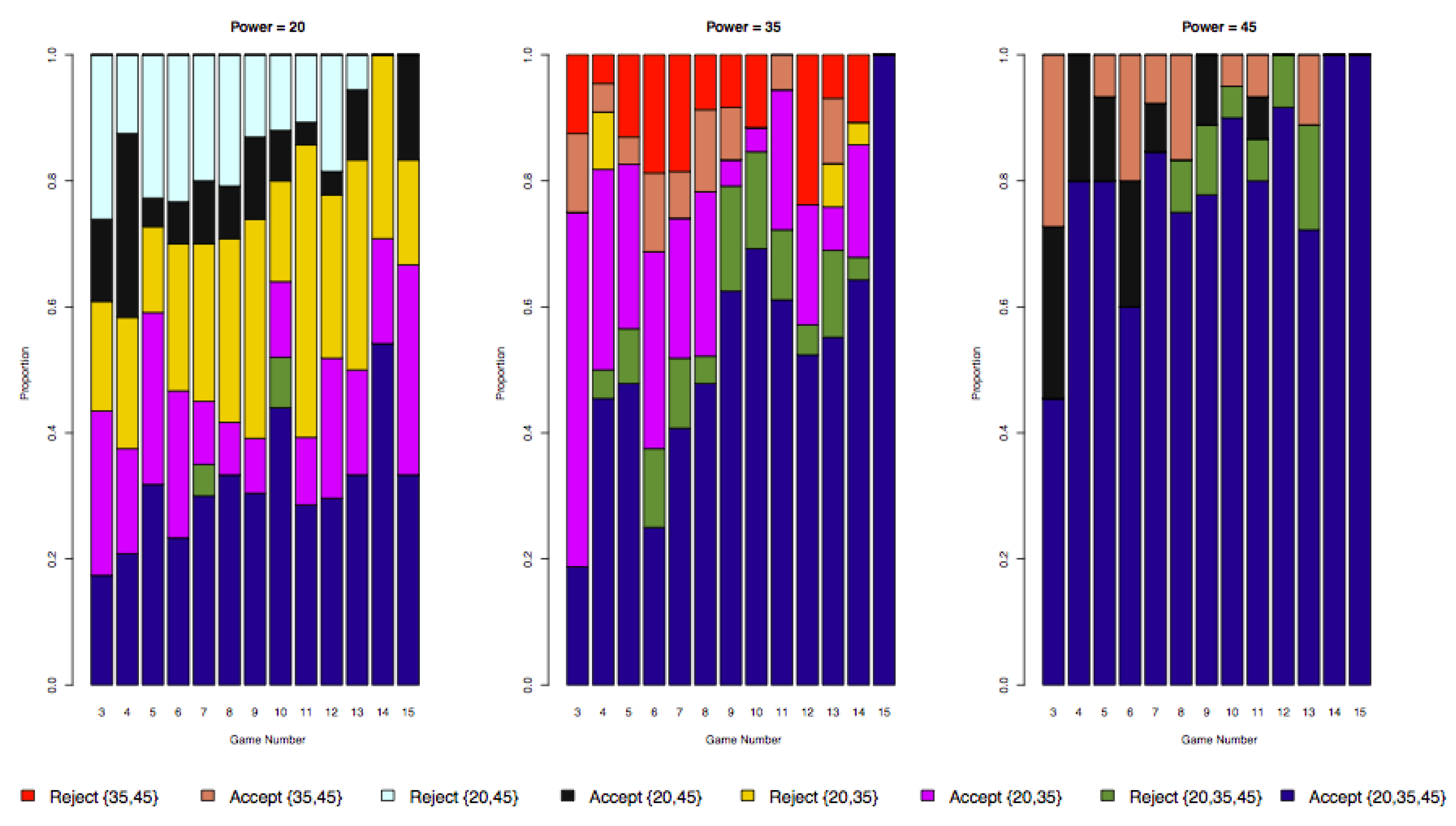
| 19. | Please note that there are no singleton coalitions in Table 3 because agents do not have sufficient power to propose themselves at the start of every game. |
| 20. | The complete details on how to obtain the expected payoffs in these tables are shown in Appendix B. |
| 21. | There may be other explanations as to why subjects propose or accept two-person coalitions, such as errors (or anticipation of errors) and reciprocity. If there is a small chance of the weaker player accepting a two-person coalition by mistake, then there it is in the best interest of the stronger player to propose such a coalition. On the other hand, a weaker player proposing a two-person coalition can be viewed as a trust game. The weaker player takes the risk in increasing the other player’s share in the hope that the stronger player reciprocates by not eliminating him. These issues are beyond the scope of this paper, and so we leave these for further studies. |
| 22. | This is also consistent with the results in Table 3 where the grand coalition constitutes 60% of Agent 20’s proposals while coalition only constitutes 6% of his proposals. Agent 35, on the other hand, proposes the grand coalition 20% of the time while proposing only 7% of the time. |
| 23. | In Appendix C, we further analyze the proposal and response strategies using a logit model that further corroborates the main findings of this section. |
| 24. | |
| 25. | Here we note that Agent 20’s empirical best response coincides with his subgame perfect equilibrium strategies. |
| 26. | The only case where it does not happen is in the late games, when Agent 45 proposes and, if passed, about 60% of the time this two-person coalition still forms. |
| 27. | Equal sharing or proportional sharing satisfy a property whereby agents have the same ordinal ranking over coalitions in which they belong. See Jandoc and Juarez [39] for a more detailed discussion of this property they call “consistent ranking”. |
| 28. | Please note that if the grand coalition is proposed, the coalition always passes, since it is the default starting coalition when a majority of responders votes “no” for it. |
| Session Date | Number of Games per Session | Number of Subjects | Last Game Stake |
|---|---|---|---|
| Low-stake sessions | |||
| 6 May 2014 | 14 | 15 | $5 |
| 4 February 2015 | 14 | 15 | $5 |
| 5 February 2015 | 14 | 12 | $5 |
| Medium-stake sessions | |||
| 6 May 2014 | 14 | 12 | $20 |
| 7 May 2014 | 14 | 12 | $20 |
| 6 June 2014 | 14 | 12 | $20 |
| High-stake sessions | |||
| 5 June 2014 | 15 | 9 | $50 |
| 23 June 2014 | 15 | 9 | $50 |
| 24 June 2014 | 15 | 6 | $50 |
| 4 February 2015 | 14 | 15 | $50 |
| 5 February 2015 | 14 | 15 | $50 |
| Dependent Variable: | ||||||
|---|---|---|---|---|---|---|
| Grand Coalition Formed = 1 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Late Games | 0.832 *** | 0.909 *** | 0.762 *** | 0.840 *** | 0.840 *** | |
| (0.159) | (0.160) | (0.160) | (0.161) | (0.161) | ||
| Last game, $5 stake | 0.774 | 0.336 | 0.199 | 1.039 ** | ||
| (0.558) | (0.547) | (0.466) | (0.523) | |||
| Last game, $20 stake | 0.081 | −0.357 | −0.494 | 0.346 | ||
| (0.320) | (0.387) | (0.384) | (0.274) | |||
| Last game, $50 stake | 1.468 *** | 1.030 * | 1.467 *** | 2.307 *** | ||
| (0.564) | (0.536) | (0.465) | (0.500) | |||
| Constant | −1.099 *** | −0.774 *** | −0.814 *** | −1.099 *** | −0.797 *** | −0.797 *** |
| (0.144) | (0.154) | (0.075) | (0.144) | (0.089) | (0.089) | |
| Observations | 624 | 624 | 624 | 624 | 624 | 624 |
| Log Likelihood | −384.089 | −390.397 | −360.528 | −381.598 | −357.020 | −357.020 |
| Akaike Inf. Crit. | 772.177 | 788.794 | 745.057 | 773.195 | 744.041 | 744.041 |
| $5 vs. $20 Stake Wald test p-value | 0.39 | 0.39 | 0.42 | 0.41 | ||
| $20 vs. $50 Stake Wald test p-value | 0.08 | 0.08 | 0.03 | 0.03 | ||
| Session FE | No | No | Yes | No | Yes | Yes |
| {20,35,45} | {20,35} | {20,45} | {35,45} | |
|---|---|---|---|---|
| Power = 20 | 60 | 34 | 6 | - |
| Power = 35 | 20 | 73 | - | 7 |
| Power = 45 | 33 | - | 40 | 27 |
| (A) | (B) | |||||
|---|---|---|---|---|---|---|
| Agent with Power 35 | Agent with Power 45 | |||||
| All games | ||||||
| Proposed Coalition | ||||||
| Expected pay-off ($) | 0 | |||||
| Early games | ||||||
| Proposed Coalition | ||||||
| Expected pay-off ($) | 0 | |||||
| Late games | ||||||
| Proposed Coalition | ||||||
| Expected pay-off ($) | 0 | |||||
| {20,35,45} | {20,35} | {20,45} | {35,45} | |||||
|---|---|---|---|---|---|---|---|---|
| Accept | Reject | Accept | Reject | Accept | Reject | Accept | Reject | |
| Power = 20 | 31 | 1 | 17 | 26 | 10 | 15 | - | - |
| Power = 35 | 51 | 10 | 20 | 2 | - | - | 6 | 11 |
| Power = 45 | 81 | 5 | - | - | 7 | 0 | 7 | 0 |
| Sessions | Number of Subjects | All Games | Early Games | Late Games | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Equilibrium | Myopic | Empirical Best Response | Equilibrium | Myopic | Empirical Best Response | Equilibrium | Myopic | Empirical Best Response | ||
| 6 May 2014, AM | 12 | 5 | 2 | 5 | 6 | 2 | 4 | 7 | 2 | 3 |
| 6 May 2014, PM | 15 | 9 | 2 | 4 | 8 | 2 | 5 | 7 | 4 | 4 |
| 7 May 2014 | 12 | 7 | 3 | 2 | 5 | 4 | 3 | 8 | 2 | 2 |
| 5 June 2014 | 9 | 1 | 4 | 4 | 3 | 4 | 2 | 4 | 3 | 2 |
| 6 June 2014 | 12 | 3 | 4 | 5 | 1 | 4 | 5 | 5 | 2 | 5 |
| 23 June 2014 | 9 | 0 | 7 | 2 | 3 | 5 | 1 | 0 | 6 | 3 |
| 24 June 2014 | 6 | 2 | 1 | 3 | 1 | 2 | 3 | 4 | 1 | 1 |
| 4 February 2015, AM | 15 | 10 | 1 | 4 | 8 | 5 | 2 | 11 | 1 | 3 |
| 4 February 2015, PM | 15 | 9 | 1 | 5 | 8 | 4 | 3 | 11 | 1 | 3 |
| 5 February 2015, AM | 12 | 5 | 4 | 3 | 4 | 4 | 4 | 6 | 2 | 4 |
| 5 February2015, PM | 15 | 7 | 2 | 6 | 8 | 2 | 5 | 10 | 1 | 4 |
| Overall (Number) | 132 | 58 | 31 | 43 | 55 | 38 | 39 | 73 | 25 | 34 |
| Overall (Percentage) | 100 | 44 | 23 | 33 | 41 | 29 | 30 | 55 | 19 | 26 |
| Min QDM | 0 | 0.12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Max QDM | 7.31 | 11.6 | 7.68 | 3.26 | 10.56 | 3.27 | 4.76 | 10.56 | 5.33 | |
| Mean QDM | 1.39 | 3.17 | 1.40 | 0.83 | 1.51 | 0.65 | 0.74 | 1.88 | 0.89 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jandoc, K.; Juarez, R. An Experimental Study of Self-Enforcing Coalitions. Games 2019, 10, 31. https://doi.org/10.3390/g10030031
Jandoc K, Juarez R. An Experimental Study of Self-Enforcing Coalitions. Games. 2019; 10(3):31. https://doi.org/10.3390/g10030031
Chicago/Turabian StyleJandoc, Karl, and Ruben Juarez. 2019. "An Experimental Study of Self-Enforcing Coalitions" Games 10, no. 3: 31. https://doi.org/10.3390/g10030031
APA StyleJandoc, K., & Juarez, R. (2019). An Experimental Study of Self-Enforcing Coalitions. Games, 10(3), 31. https://doi.org/10.3390/g10030031





