Explaining Cooperative Behavior in Public Goods Games: How Preferences and Beliefs Affect Contribution Levels
Abstract
1. Introduction
2. Cooperation in Social Dilemmas
2.1. On the Importance of Considering Endogenous Factors
2.2. How Social Preferences and Beliefs Affect Cooperation Behavior in PGGs
2.2.1. Distributive Other-Regarding Preferences
2.2.2. Beliefs and Conditional Cooperation
2.3. Connecting the Streams of Research
A form of cooperation that is consistent with all of our findings can be found in the classical psychological literature on differences in individual ‘value orientation’ …
2.4. Research Questions
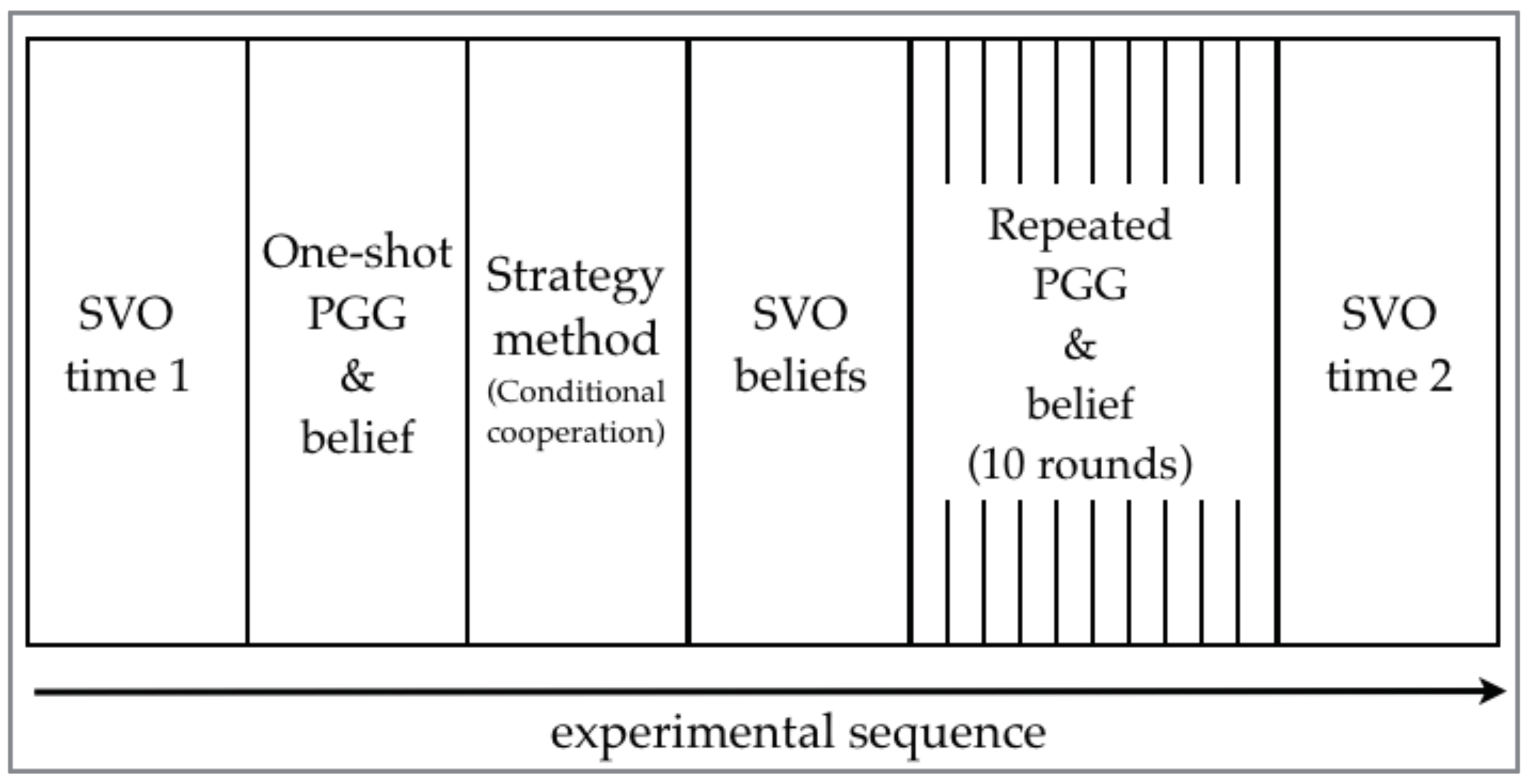
3. Method
3.1. Measures
3.1.1. SVO
3.1.2. SVO Beliefs
3.1.3. PGG Contributions and Beliefs
One-Shot PGG and Strategy Method
Repeated PGG
3.1.4. Questionnaires
4. Results
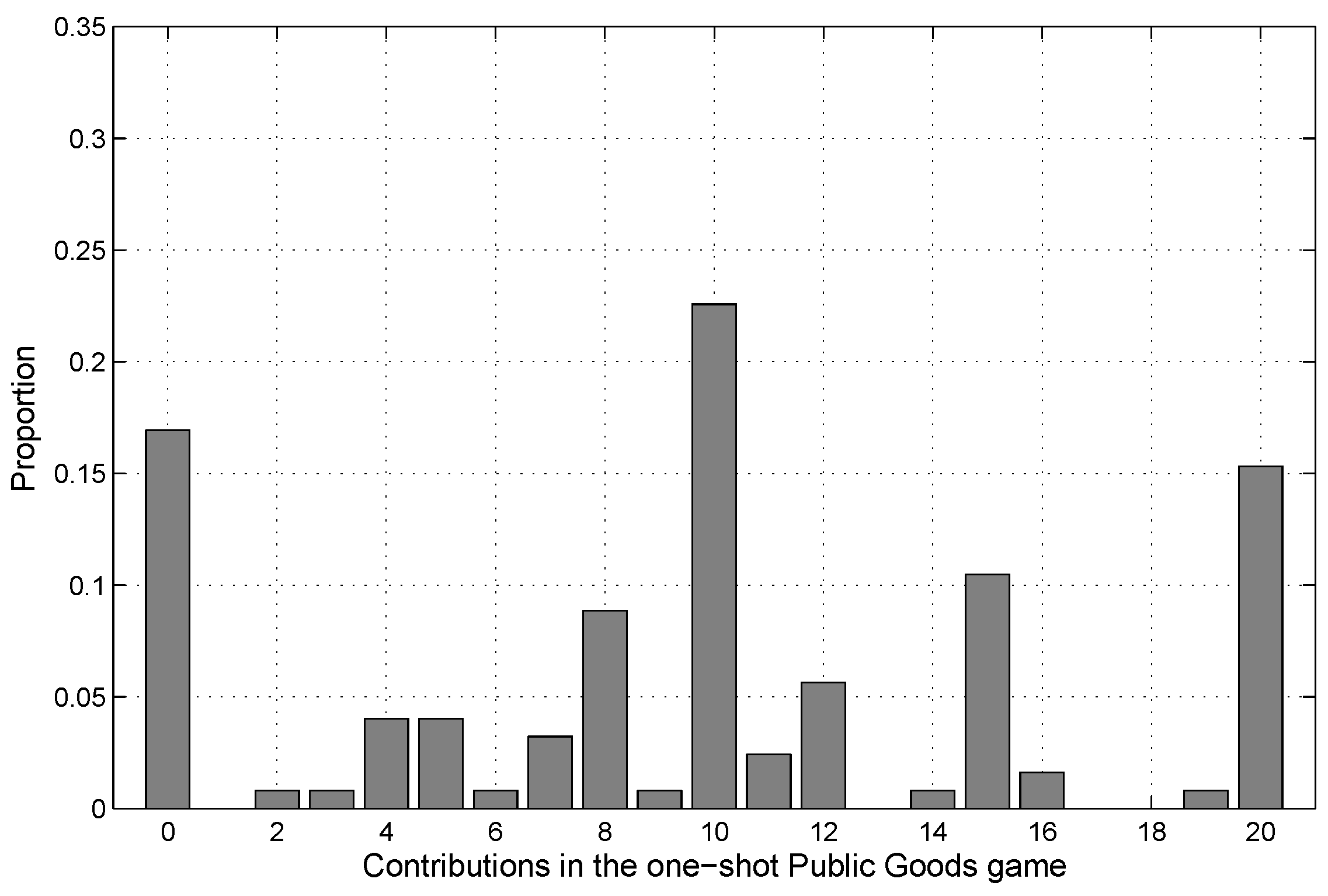
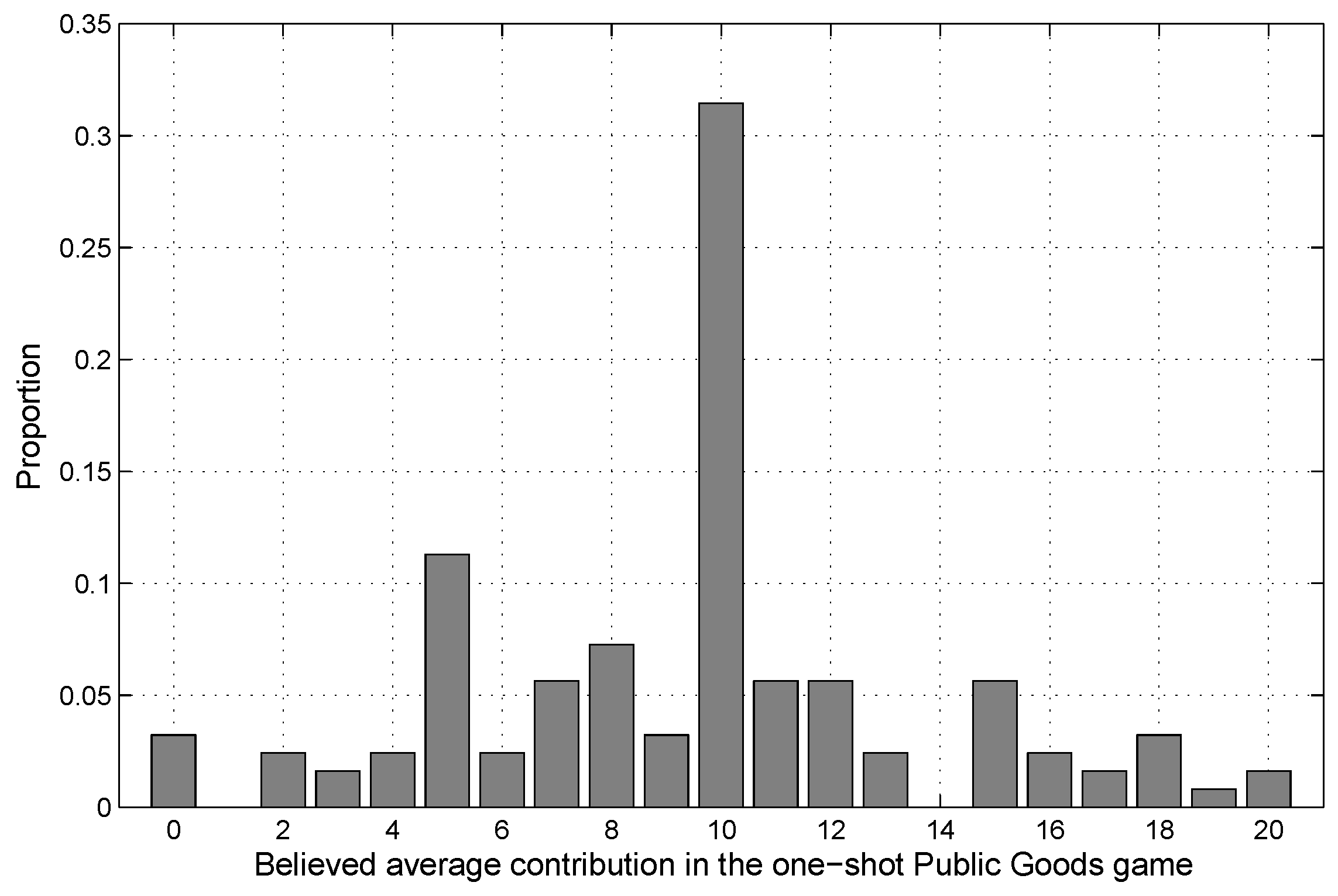
4.1. Explaining Behavior in the One-Shot PGG
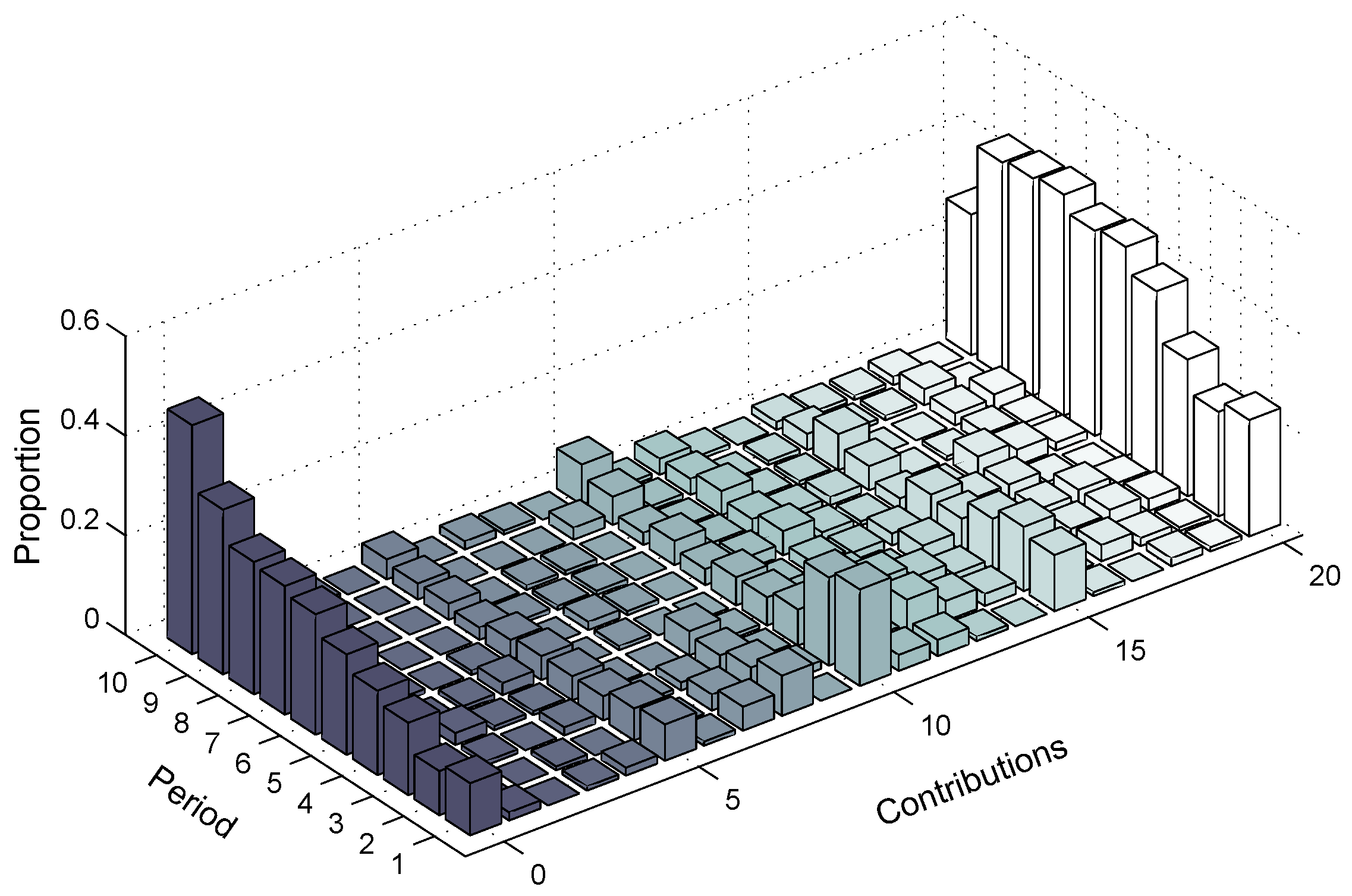
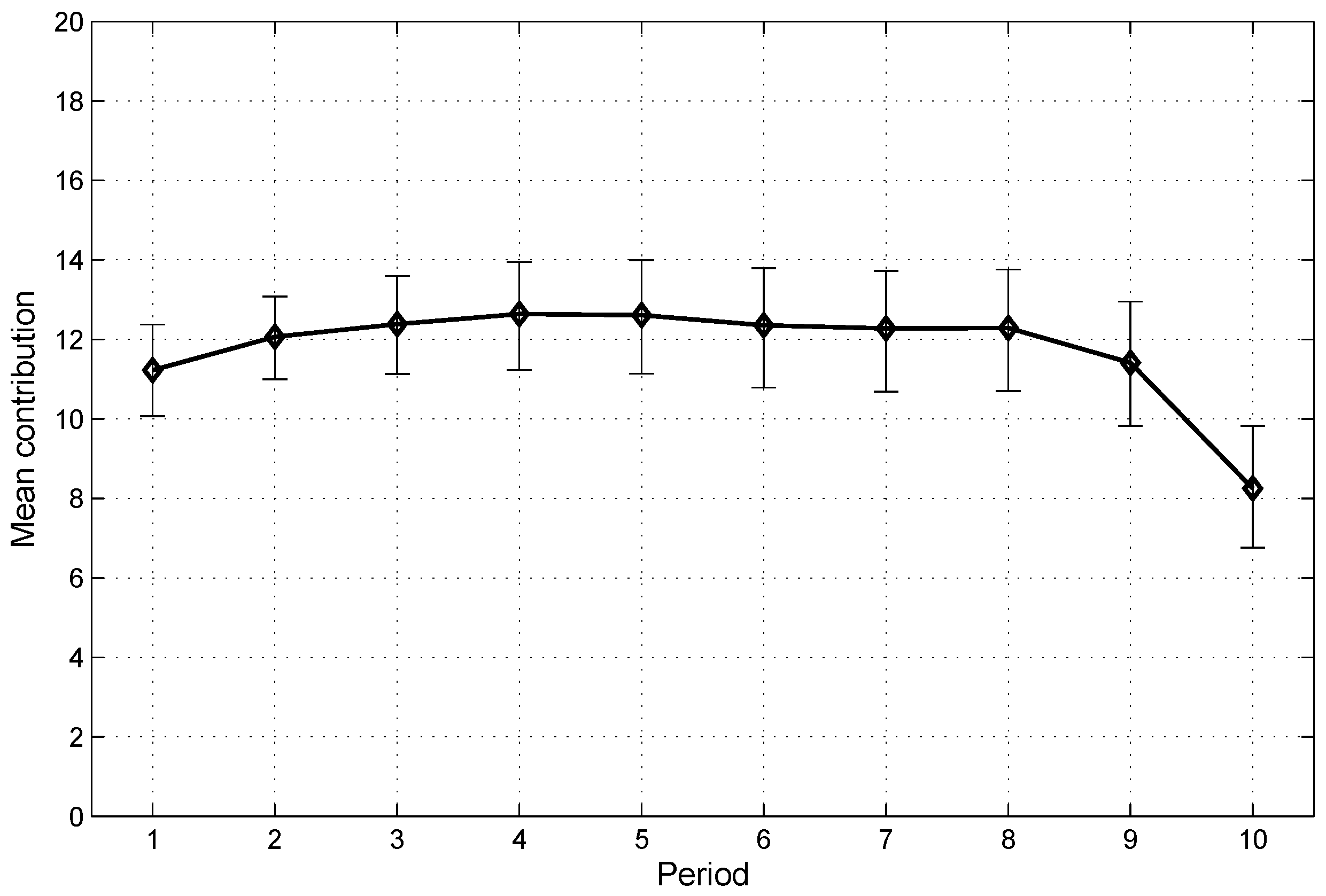
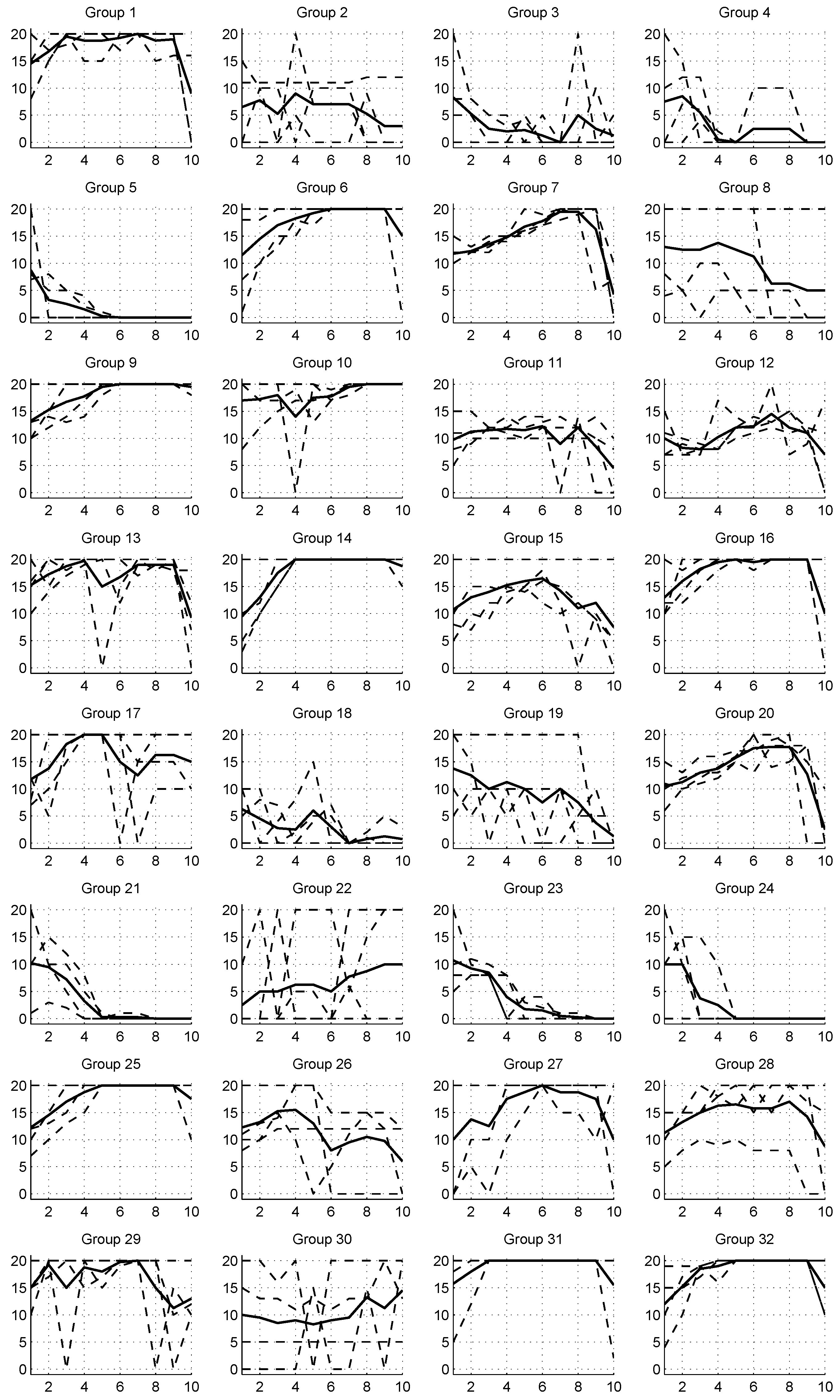
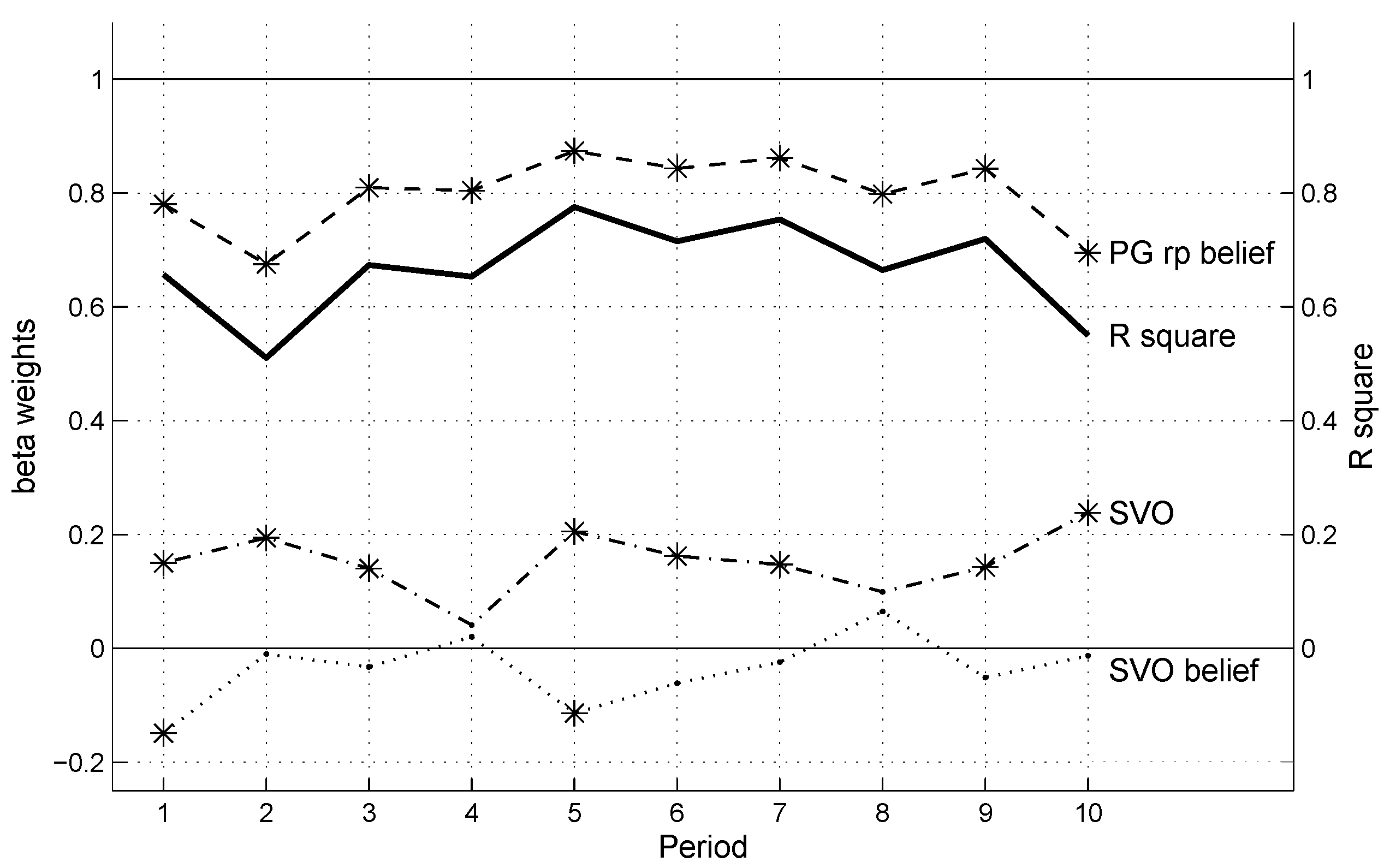
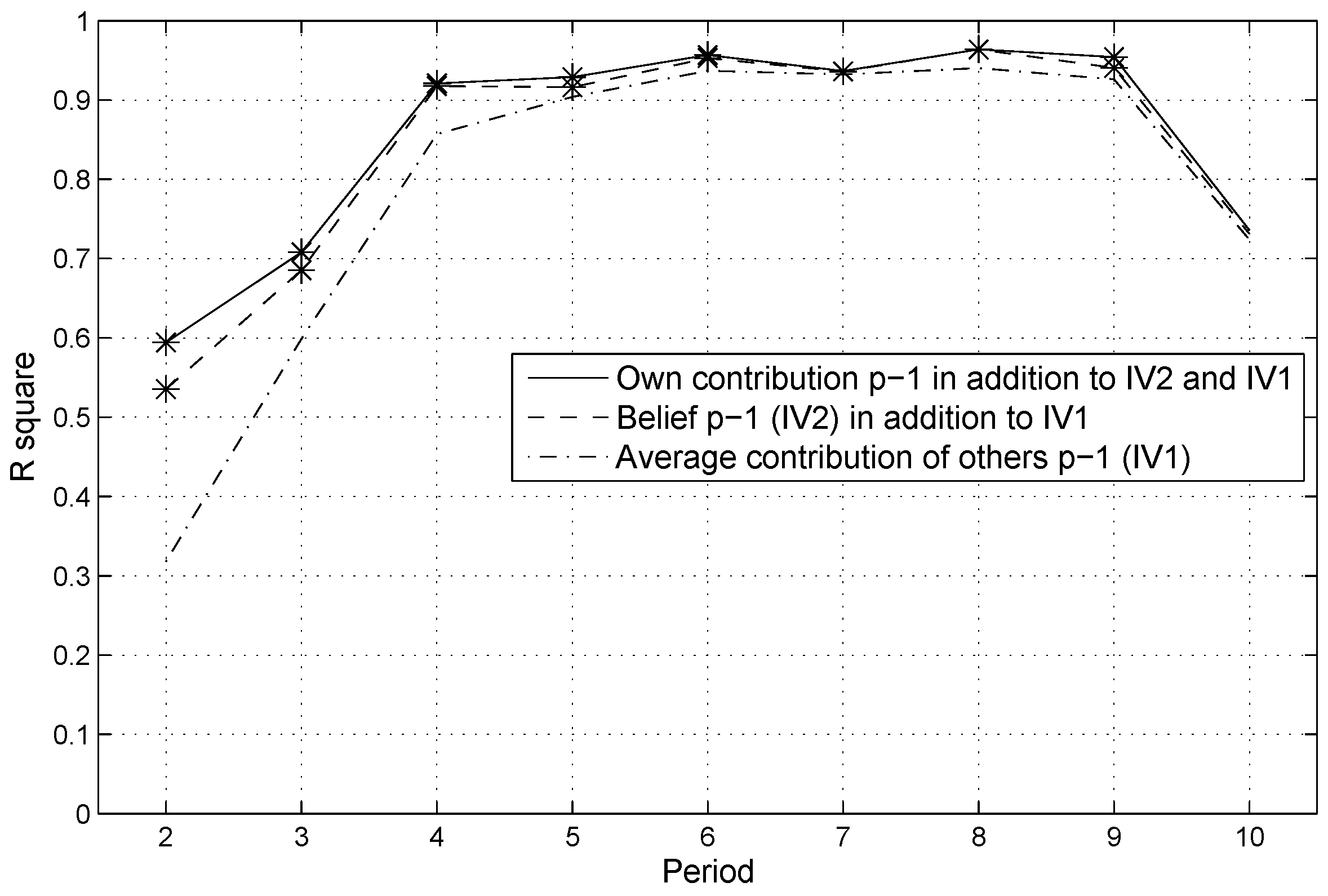
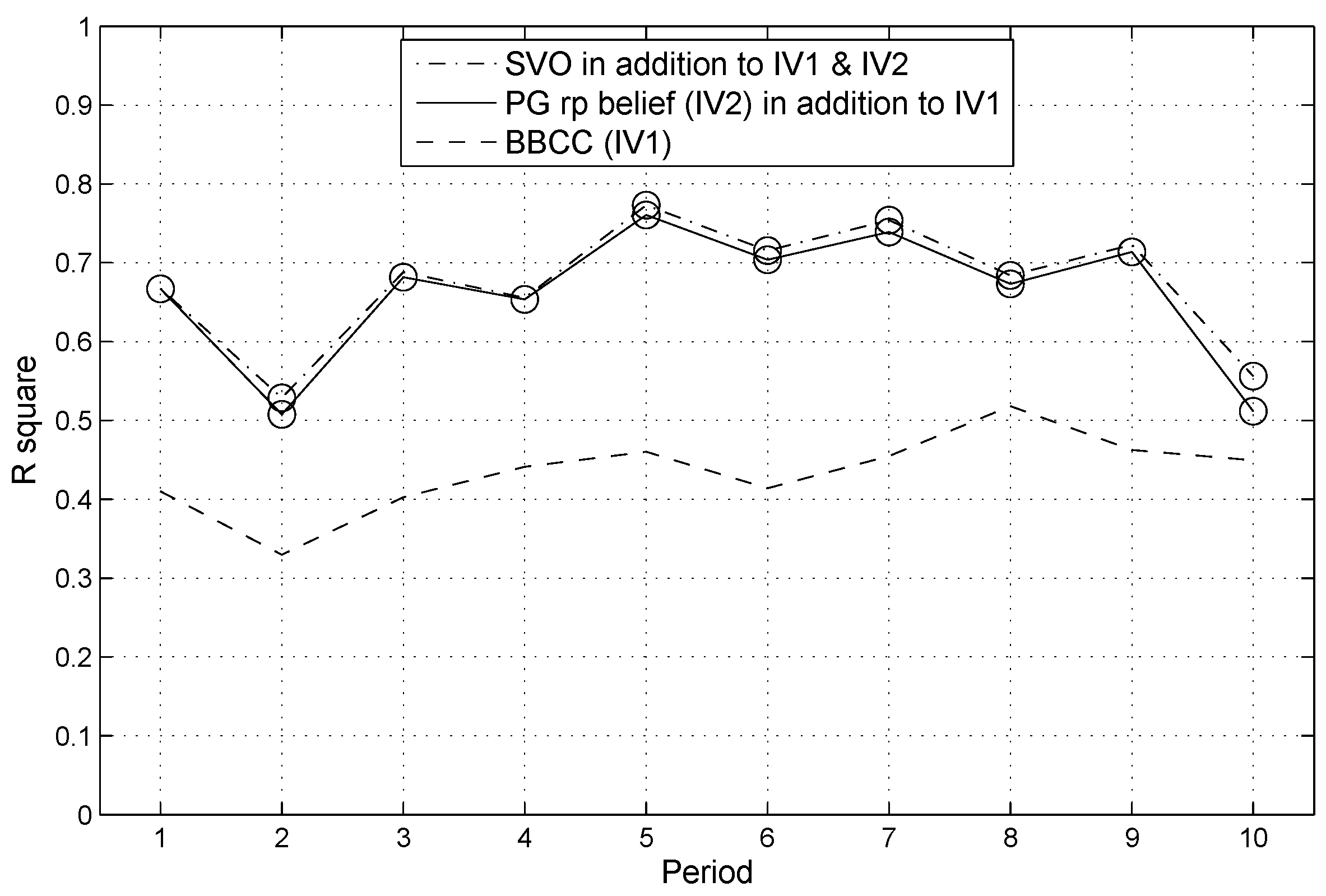
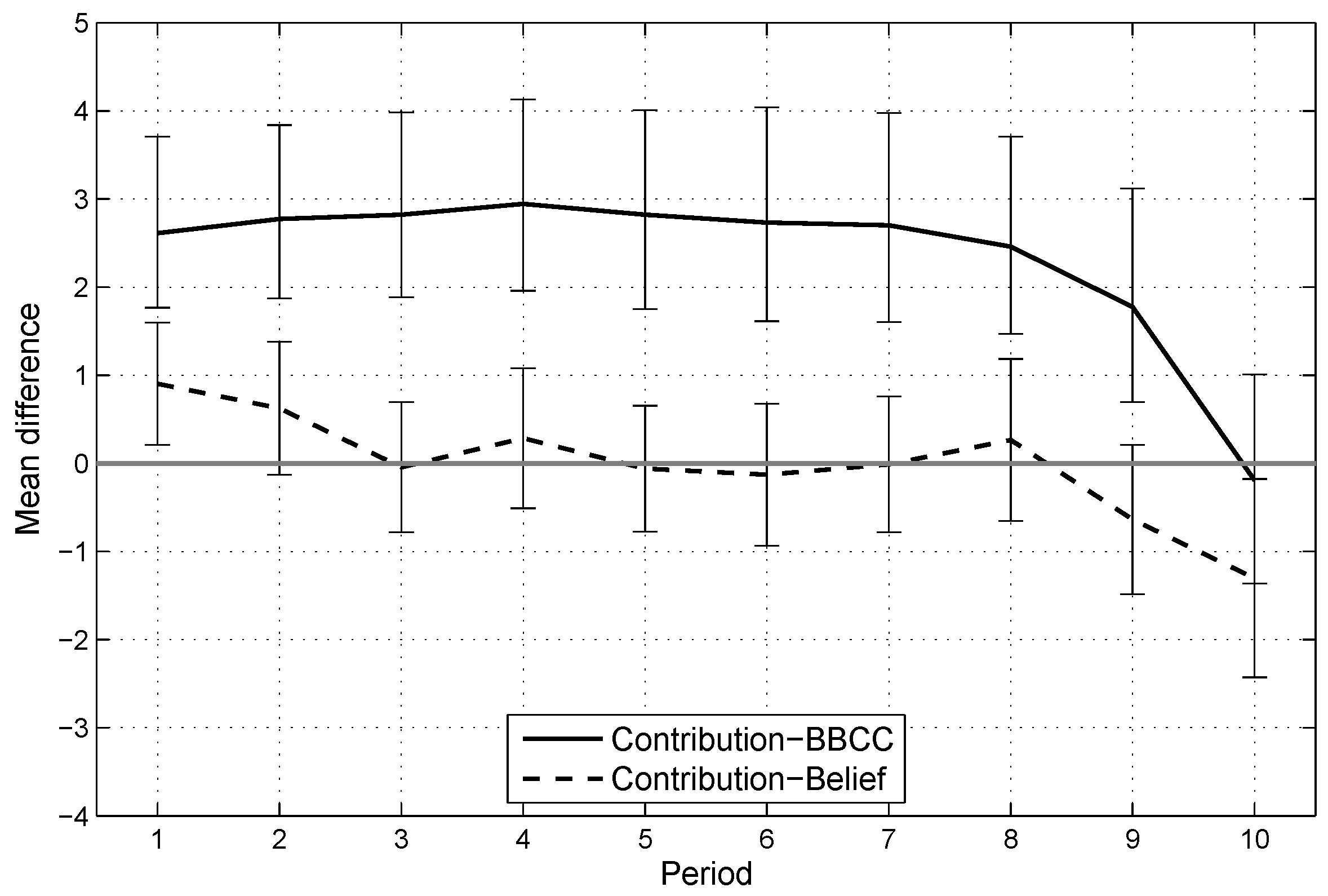
4.2. Explaining Behavior in the Repeated PGG
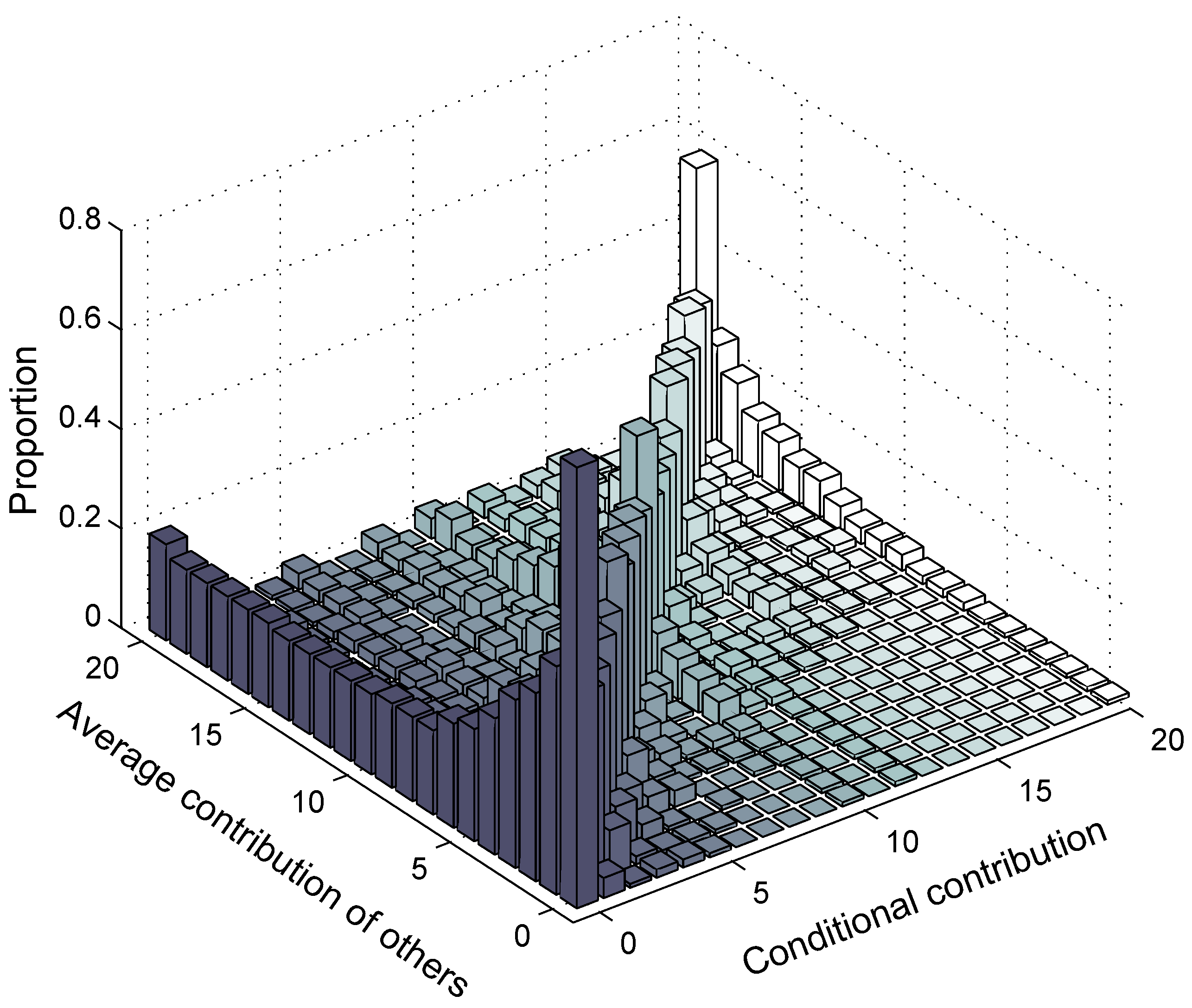
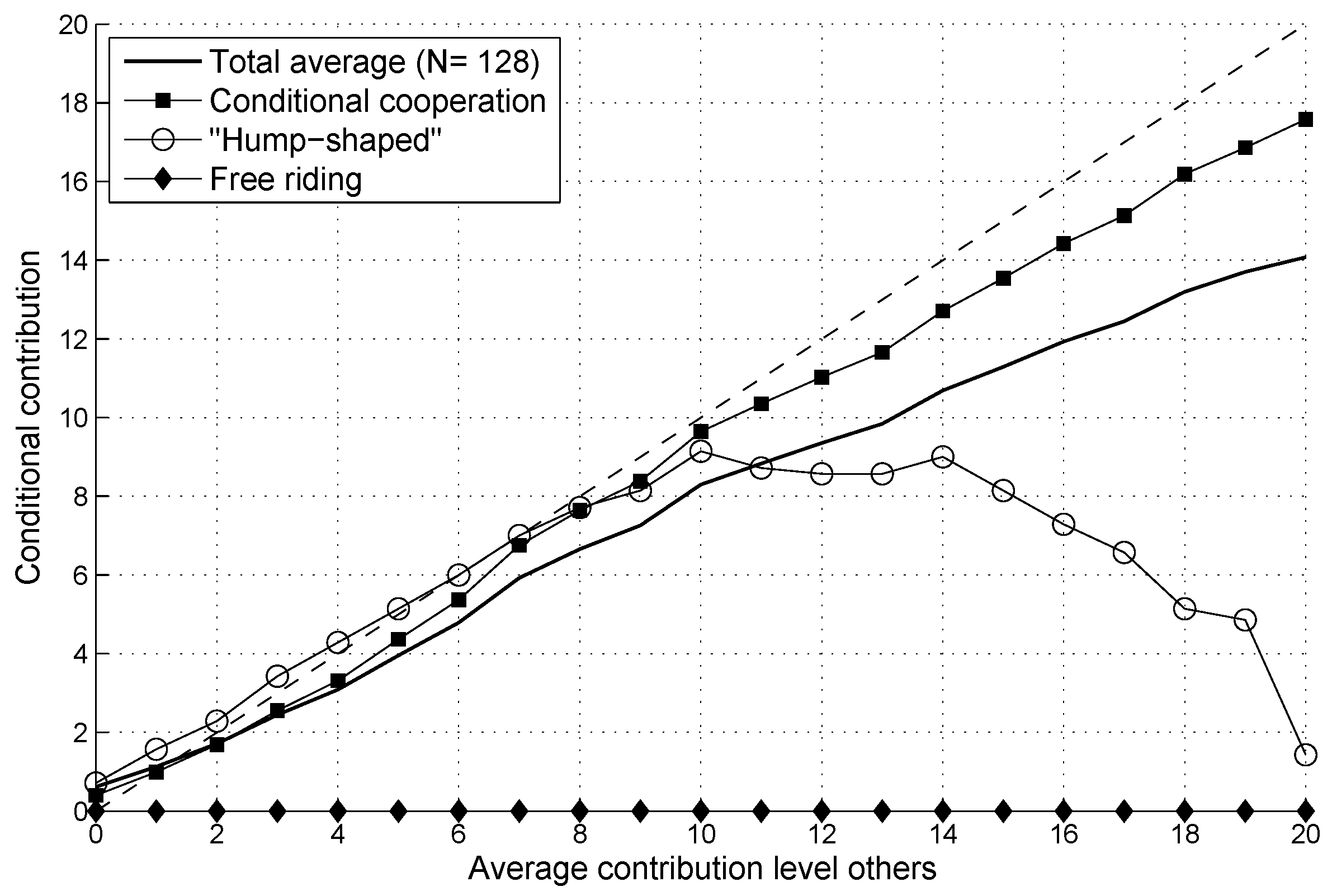
4.3. Conditional Cooperation
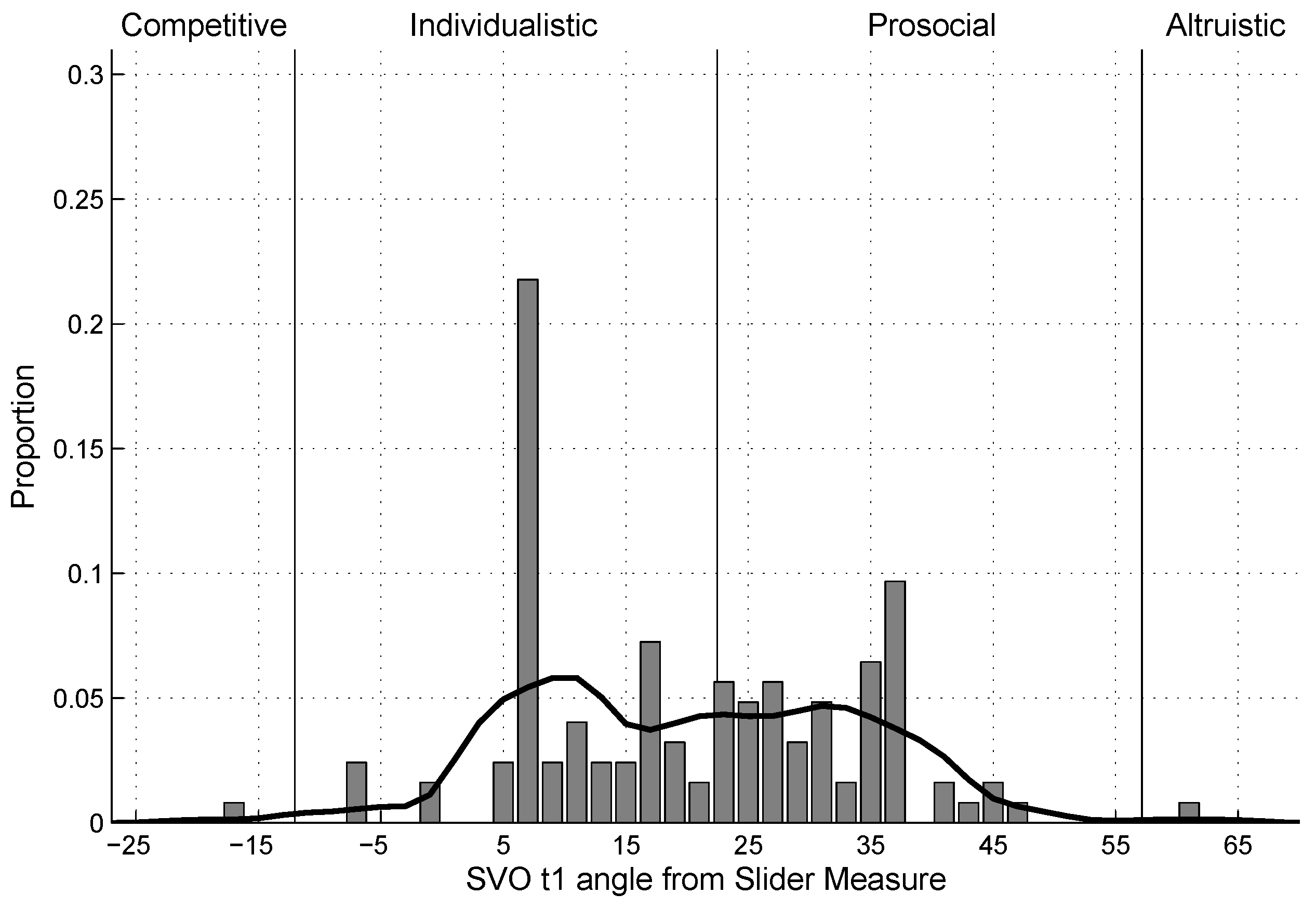
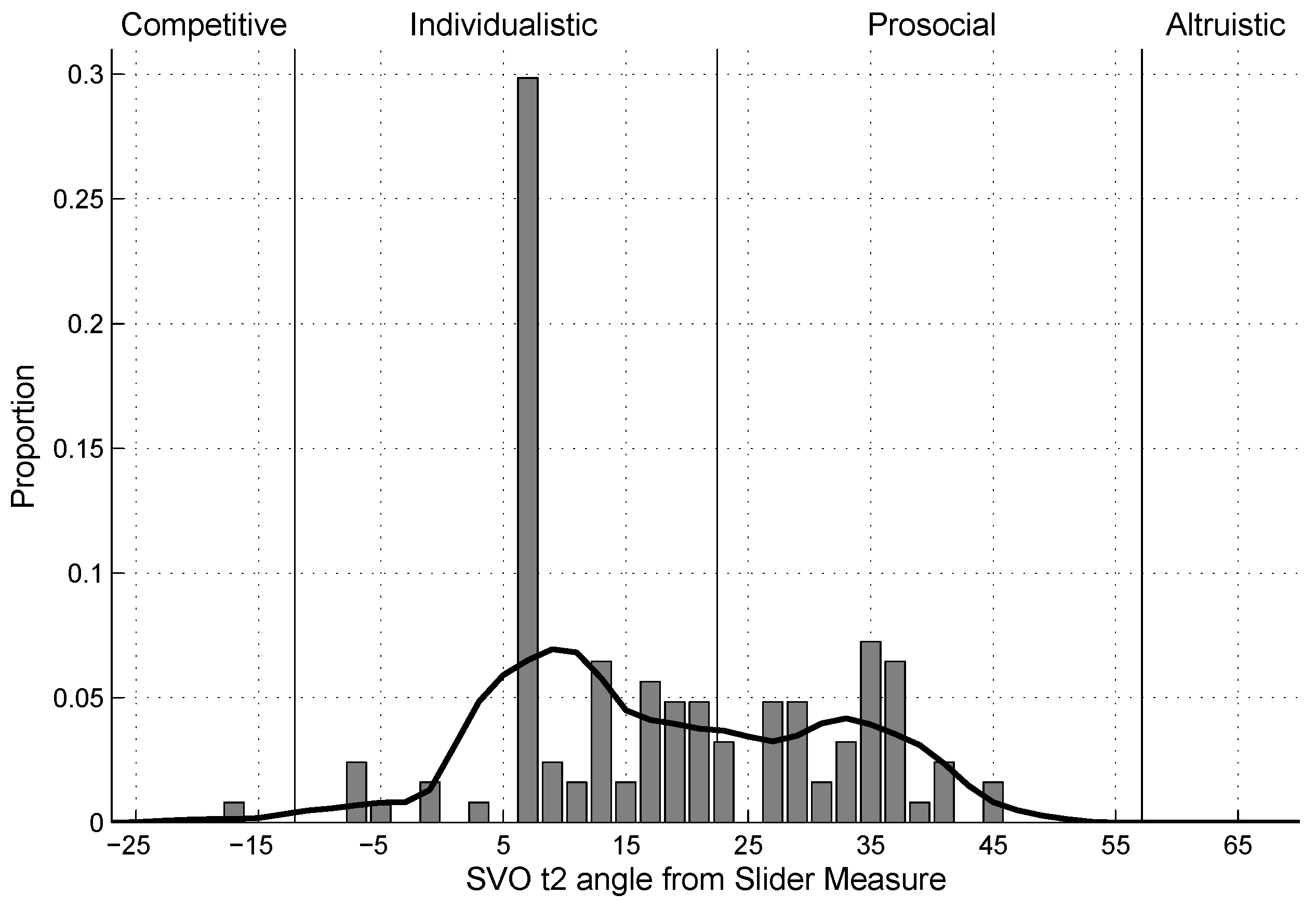
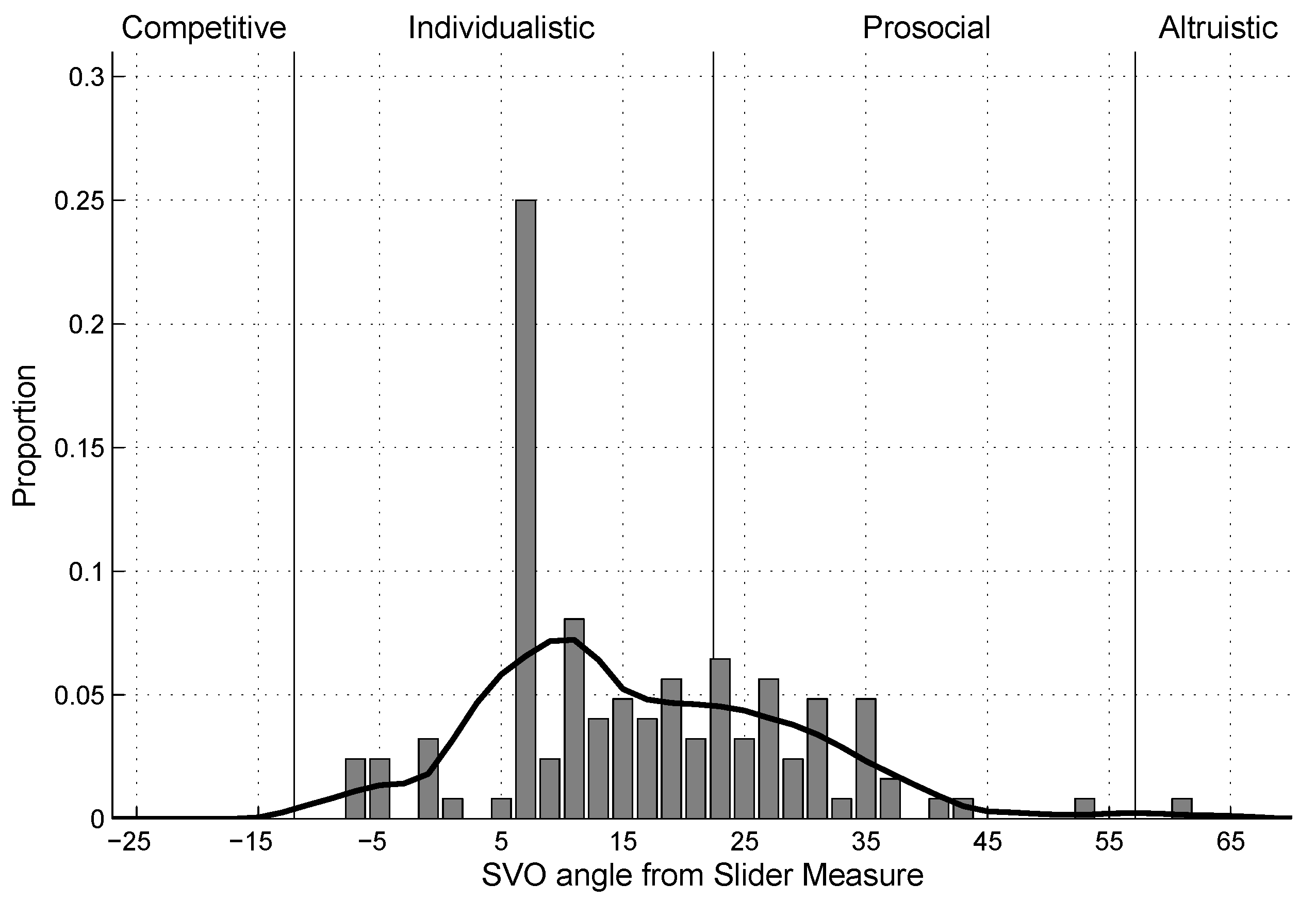
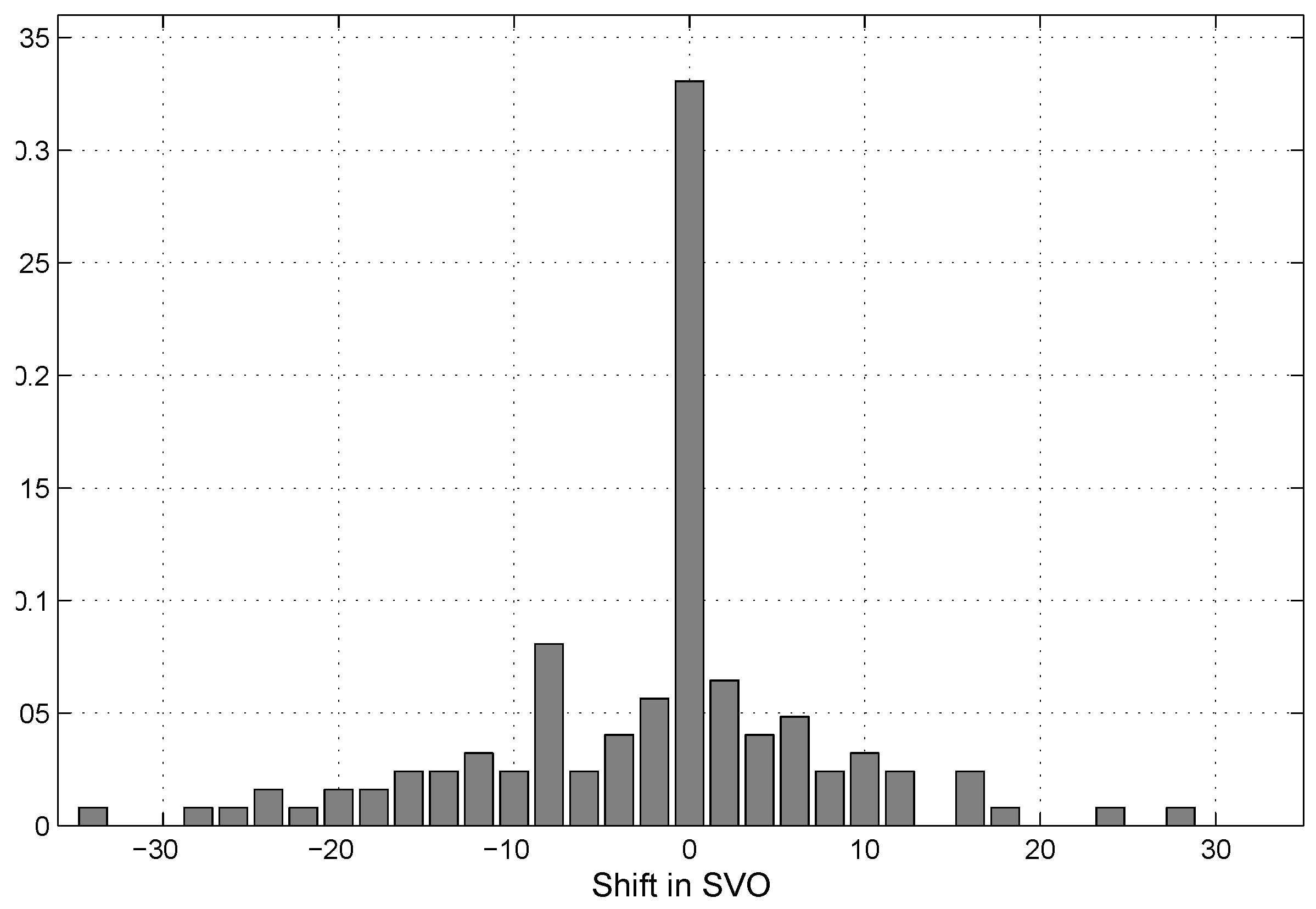
4.4. SVO
4.5. Questionnaire Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| PG1 | PG2 | PG3 | PG4 | PG5 | PG6 | PG7 | PG8 | PG9 | PG10 | BBCC1 | BBCC2 | BBCC3 | BBCC4 | BBCC5 | BBCC6 | BBCC7 | BBCC8 | BBCC9 | BBCC10 | PGb1 | PGb2 | PGb3 | PGb4 | PGb5 | PGb6 | PGb7 | PGb8 | PGb9 | PGb10 | CCA | SVOt1 | SVOt2 | SVOb | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PG1 | - | |||||||||||||||||||||||||||||||||
| PG2 | 0.74 | - | ||||||||||||||||||||||||||||||||
| PG3 | 0.52 | 0.74 | - | |||||||||||||||||||||||||||||||
| PG4 | 0.41 | 0.72 | 0.77 | - | ||||||||||||||||||||||||||||||
| PG5 | 0.34 | 0.59 | 0.72 | 0.83 | - | |||||||||||||||||||||||||||||
| PG6 | 0.35 | 0.68 | 0.73 | 0.83 | 0.85 | - | ||||||||||||||||||||||||||||
| PG7 | 0.33 | 0.56 | 0.75 | 0.78 | 0.76 | 0.86 | - | |||||||||||||||||||||||||||
| PG8 | 0.29 | 0.52 | 0.70 | 0.74 | 0.78 | 0.81 | 0.88 | - | ||||||||||||||||||||||||||
| PG9 | 0.32 | 0.54 | 0.71 | 0.74 | 0.74 | 0.80 | 0.86 | 0.84 | - | |||||||||||||||||||||||||
| PG10 | 0.15 | 0.31 | 0.44 | 0.52 | 0.58 | 0.56 | 0.60 | 0.63 | 0.67 | - | ||||||||||||||||||||||||
| BBCC1 | 0.64 | 0.50 | 0.39 | 0.31 | 0.30 | 0.30 | 0.28 | 0.28 | 0.32 | 0.32 | - | |||||||||||||||||||||||
| BBCC2 | 0.43 | 0.57 | 0.57 | 0.47 | 0.49 | 0.46 | 0.45 | 0.49 | 0.46 | 0.45 | 0.76 | - | ||||||||||||||||||||||
| BBCC3 | 0.33 | 0.50 | 0.63 | 0.55 | 0.56 | 0.53 | 0.52 | 0.56 | 0.51 | 0.46 | 0.64 | 0.88 | - | |||||||||||||||||||||
| BBCC4 | 0.32 | 0.49 | 0.60 | 0.66 | 0.67 | 0.62 | 0.62 | 0.65 | 0.62 | 0.53 | 0.57 | 0.78 | 0.90 | - | ||||||||||||||||||||
| BBCC5 | 0.31 | 0.45 | 0.59 | 0.64 | 0.68 | 0.61 | 0.62 | 0.65 | 0.60 | 0.52 | 0.54 | 0.76 | 0.89 | 0.96 | - | |||||||||||||||||||
| BBCC6 | 0.29 | 0.46 | 0.59 | 0.64 | 0.66 | 0.64 | 0.64 | 0.66 | 0.61 | 0.52 | 0.53 | 0.75 | 0.87 | 0.95 | 0.97 | - | ||||||||||||||||||
| BBCC7 | 0.27 | 0.42 | 0.56 | 0.59 | 0.64 | 0.62 | 0.67 | 0.69 | 0.61 | 0.52 | 0.50 | 0.74 | 0.85 | 0.92 | 0.95 | 0.96 | - | |||||||||||||||||
| BBCC8 | 0.30 | 0.48 | 0.59 | 0.65 | 0.69 | 0.66 | 0.69 | 0.72 | 0.66 | 0.58 | 0.55 | 0.76 | 0.82 | 0.91 | 0.92 | 0.94 | 0.95 | - | ||||||||||||||||
| BBCC9 | 0.31 | 0.48 | 0.59 | 0.65 | 0.68 | 0.64 | 0.67 | 0.70 | 0.68 | 0.58 | 0.57 | 0.76 | 0.81 | 0.91 | 0.92 | 0.93 | 0.93 | 0.98 | - | |||||||||||||||
| BBCC10 | 0.24 | 0.43 | 0.55 | 0.59 | 0.63 | 0.61 | 0.62 | 0.64 | 0.64 | 0.67 | 0.54 | 0.69 | 0.74 | 0.82 | 0.81 | 0.83 | 0.82 | 0.88 | 0.89 | - | ||||||||||||||
| PGb1 | 0.80 | 0.51 | 0.30 | 0.21 | 0.18 | 0.21 | 0.22 | 0.23 | 0.19 | 0.11 | 0.65 | 0.31 | 0.19 | 0.20 | 0.19 | 0.19 | 0.18 | 0.23 | 0.24 | 0.19 | - | |||||||||||||
| PGb2 | 0.46 | 0.69 | 0.60 | 0.54 | 0.49 | 0.51 | 0.50 | 0.47 | 0.43 | 0.29 | 0.36 | 0.63 | 0.53 | 0.51 | 0.51 | 0.49 | 0.51 | 0.53 | 0.52 | 0.46 | 0.40 | - | ||||||||||||
| PGb3 | 0.32 | 0.57 | 0.81 | 0.66 | 0.65 | 0.66 | 0.71 | 0.67 | 0.63 | 0.47 | 0.24 | 0.51 | 0.64 | 0.61 | 0.60 | 0.60 | 0.62 | 0.62 | 0.59 | 0.57 | 0.16 | 0.69 | - | |||||||||||
| PGb4 | 0.29 | 0.56 | 0.75 | 0.81 | 0.80 | 0.78 | 0.79 | 0.77 | 0.74 | 0.56 | 0.30 | 0.54 | 0.65 | 0.78 | 0.75 | 0.74 | 0.73 | 0.75 | 0.74 | 0.69 | 0.18 | 0.64 | 0.85 | - | ||||||||||
| PGb5 | 0.27 | 0.53 | 0.71 | 0.80 | 0.87 | 0.81 | 0.78 | 0.78 | 0.74 | 0.52 | 0.21 | 0.46 | 0.56 | 0.68 | 0.70 | 0.68 | 0.68 | 0.68 | 0.67 | 0.62 | 0.15 | 0.56 | 0.73 | 0.90 | - | |||||||||
| PGb6 | 0.23 | 0.49 | 0.70 | 0.77 | 0.84 | 0.84 | 0.82 | 0.80 | 0.76 | 0.56 | 0.20 | 0.42 | 0.53 | 0.65 | 0.66 | 0.71 | 0.68 | 0.68 | 0.67 | 0.63 | 0.13 | 0.48 | 0.71 | 0.87 | 0.94 | - | ||||||||
| PGb7 | 0.23 | 0.45 | 0.65 | 0.71 | 0.79 | 0.79 | 0.86 | 0.80 | 0.75 | 0.53 | 0.20 | 0.44 | 0.54 | 0.65 | 0.67 | 0.68 | 0.74 | 0.72 | 0.68 | 0.65 | 0.10 | 0.49 | 0.72 | 0.83 | 0.90 | 0.92 | - | |||||||
| PGb8 | 0.24 | 0.48 | 0.65 | 0.75 | 0.83 | 0.80 | 0.83 | 0.80 | 0.78 | 0.55 | 0.26 | 0.47 | 0.56 | 0.66 | 0.67 | 0.69 | 0.72 | 0.76 | 0.72 | 0.67 | 0.12 | 0.48 | 0.68 | 0.83 | 0.90 | 0.91 | 0.96 | - | ||||||
| PGb9 | 0.24 | 0.49 | 0.67 | 0.75 | 0.80 | 0.80 | 0.85 | 0.83 | 0.84 | 0.59 | 0.24 | 0.45 | 0.52 | 0.65 | 0.65 | 0.67 | 0.69 | 0.72 | 0.74 | 0.68 | 0.13 | 0.47 | 0.67 | 0.83 | 0.89 | 0.91 | 0.93 | 0.95 | - | |||||
| PGb10 | 0.15 | 0.38 | 0.53 | 0.61 | 0.69 | 0.66 | 0.68 | 0.68 | 0.70 | 0.70 | 0.36 | 0.52 | 0.58 | 0.68 | 0.68 | 0.70 | 0.71 | 0.76 | 0.76 | 0.86 | 0.08 | 0.39 | 0.58 | 0.72 | 0.75 | 0.77 | 0.79 | 0.83 | 0.83 | - | ||||
| CCA | 0.32 | 0.35 | 0.33 | 0.32 | 0.33 | 0.30 | 0.25 | 0.30 | 0.28 | 0.31 | 0.77 | 0.79 | 0.79 | 0.71 | 0.69 | 0.67 | 0.63 | 0.62 | 0.63 | 0.61 | 0.21 | 0.24 | 0.23 | 0.31 | 0.22 | 0.21 | 0.21 | 0.25 | 0.21 | 0.37 | - | |||
| SVOt1 | 0.30 | 0.24 | 0.14 | 0.08 | 0.12 | 0.09 | 0.11 | 0.14 | 0.11 | 0.26 | 0.34 | 0.25 | 0.22 | 0.16 | 0.16 | 0.13 | 0.14 | 0.15 | 0.14 | 0.13 | 0.32 | 0.07 | 0.02 | 0.03 | −0.02 | −0.04 | −0.02 | 0.00 | −0.00 | 0.04 | 0.30 | - | ||
| SVOt2 | 0.26 | 0.32 | 0.31 | 0.35 | 0.32 | 0.31 | 0.33 | 0.32 | 0.35 | 0.40 | 0.36 | 0.38 | 0.40 | 0.38 | 0.34 | 0.33 | 0.33 | 0.33 | 0.32 | 0.29 | 0.19 | 0.18 | 0.22 | 0.27 | 0.22 | 0.22 | 0.24 | 0.28 | 0.25 | 0.26 | 0.36 | 0.72 | - | |
| SVOb | 0.09 | 0.15 | 0.09 | 0.08 | 0.05 | 0.05 | 0.09 | 0.17 | 0.08 | 0.17 | 0.18 | 0.18 | 0.16 | 0.09 | 0.08 | 0.07 | 0.09 | 0.08 | 0.08 | 0.06 | 0.19 | 0.05 | 0.04 | 0.04 | 0.04 | 0.01 | 0.02 | 0.05 | 0.05 | 0.05 | 0.15 | 0.63 | 0.55 | - |
References
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Camerer, C.F.; Fehr, E. When does “economic man” dominate social behavior? Science 2006, 311, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Camerer, C.F.; Thaler, R.H. Anomalies: Ultimatums, dictators and manners. J. Econ. Perspect. 1995, 9, 209–219. [Google Scholar] [CrossRef]
- Andreoni, J.; Miller, J.H. Giving according to GARP: An experimental test of the consistency of preferences for altruism. Econometrica 2002, 70, 737–753. [Google Scholar] [CrossRef]
- Fisman, R.; Kariv, S.; Markovits, D. Individual preferences for giving. Am. Econ. Rev. 2007, 97, 1858–1877. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S. Social preferences, beliefs, and the dynamics of Free Riding in Public Goods experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Dawes, R.M. Social dilemmas. Annu. Rev. Psychol. 1980, 31, 169–193. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U. The nature of human altruism. Nature 2003, 425, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.D. The genetical evolution of social behavior. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Kollock, P. Social dilemmas: The anatomy of cooperation. Annu. Rev. Sociol. 1998, 24, 183–214. [Google Scholar] [CrossRef]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Ostrom, E. Collective action and the evolution of social norms. J. Econ. Perspect. 2000, 14, 137–158. [Google Scholar] [CrossRef]
- Sell, A.; Tooby, J.; Cosmides, L.; Orians, G.H. Formidability and the logic of human anger. Proc. Natl. Acad. Sci. USA 2009, 106, 15073–15078. [Google Scholar] [CrossRef] [PubMed]
- Tricomi, E.; Rangel, A.; Camerer, C.F.; O’Doherty, J.P. Neural evidence for inequality-averse social preferences. Nature 2010, 463, 1089–1091. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Gächter, S. Cooperation and punishment in public goods experiments. Am. Econ. Rev. 2000, 90, 980–994. [Google Scholar] [CrossRef]
- Frey, B.; Meier, S. Social comparisons and pro-social behavior: Testing “conditional cooperation” in a field experiment. Am. Econ. Rev. 2004, 94, 1717–1722. [Google Scholar] [CrossRef]
- Gächter, S.; Herrmann, B. Reciprocity, culture and human cooperation: Previous insights and a new cross-cultural experiment. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 791–806. [Google Scholar] [CrossRef] [PubMed]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Charness, G.; Rabin, M. Understanding Social Preferences with Simple Tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Games Econ. Behav. 2006, 54, 293–315. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Geanakoplos, J.; Pearce, D.; Stacchetti, E. Psychological games and sequential rationality. Games Econ. Behav. 1989, 1, 60–79. [Google Scholar] [CrossRef]
- Levine, D.K. Modeling altruism and spitefulness in experiments. Rev. Econ. Dyn. 1998, 1, 593–622. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game-theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Cox, J.; Friedman, D.; Gjerstad, S. A tractable model of reciprocity and fairness. Games Econ. Behav. 2007, 59, 17–45. [Google Scholar] [CrossRef]
- Luce, R.D.; Raiffa, H. Games and Decisions. Introduction and Critical Survey; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Andreoni, J.; Miller, J.H. Rational cooperation in the finitely repeated Prisoner’s Dilemma: Experimental evidence. Econ. J. 1993, 103, 570–585. [Google Scholar] [CrossRef]
- Cooper, R.; De Jong, D.V.; Forsythe, R.; Ross, T.W. Cooperation without reputation: Experimental evidence from prisoner’s dilemma games. Games Econ. Behav. 1996, 12, 187–218. [Google Scholar] [CrossRef]
- Rapoport, A.; Dale, P.S. The “end” and “start” effects in iterated Prisoner’s Dilemma. J. Confl. Resolut. 1966, 10, 363–366. [Google Scholar] [CrossRef]
- Ledyard, J. Public goods: A survey of experimental research. In Handbook of Experimental Economics; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Rapoport, A. A note on index of cooperation for prisoners dilemma. J. Confl. Resolut. 1967, 11, 100–103. [Google Scholar] [CrossRef]
- Stivers, A.W.; Murphy, R.O.; Kuhlman, D.M. A Taxonomy of Prisoner’s Dilemma Indexes. In Working Paper; College of Arts & Sciences, Gonzaga University: Spokane, WA, USA, 2019. [Google Scholar]
- Isaac, R.M.; Walker, J.; Thomas, S. Divergent evidence on free riding: An experimental examination of possible explanations. Public Choice 1984, 43, 113–149. [Google Scholar] [CrossRef]
- Murphy, R.O.; Ackermann, K.A. Social preferences, positive expectations, and trust based cooperation. J. Math. Psychol. 2015, 67, 45–50. [Google Scholar] [CrossRef]
- Moisan, F.; ten Brincke, R.; Murphy, R.O.; Gonzalez, C. Not All Prisoner’s Dilemma Games Are Equal: Incentives, Social Preferences, and Cooperation. Decision 2018, 5, 306–322. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.C.; Santos, M.D.; Pacheco, J.M. Social diversity promotes the emergence of cooperation in public goods games. Nature 2008, 454, 213. [Google Scholar] [CrossRef] [PubMed]
- Javarone, M.A.; Atzeni, A.E. The role of competitiveness in the Prisoner’s Dilemma. Comput. Soc. Netw. 2015, 2, 15. [Google Scholar] [CrossRef]
- Javarone, M.A.; Antonioni, A.; Caravelli, F. Conformity-driven agents support ordered phases in the spatial public goods game. EPL (Europhys. Lett.) 2016, 114, 38001. [Google Scholar] [CrossRef]
- Murphy, R.O.; Ackermann, K.A. Social value orientation: Theoretical and measurement issues in the study of social preferences. Pers. Soc. Psychol. Rev. 2014, 18, 13–41. [Google Scholar] [CrossRef] [PubMed]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. Games Econ. Behav. 2011, 72, 321–338. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Inequality aversion, efficiency, and maximin preferences in simple distribution experiments. Am. Econ. Rev. 2004, 94, 857–869. [Google Scholar] [CrossRef]
- Erlei, M. Heterogeneous social preferences. J. Econ. Behav. Organ. 2008, 65, 436–457. [Google Scholar] [CrossRef]
- Kohler, S. Altruism and fairness in experimental decisions. J. Econ. Behav. Organ. 2011, 80, 101–109. [Google Scholar] [CrossRef]
- Ones, U.; Putterman, L. The ecology of collective action: A public goods and sanctions experiment with controlled group formation. J. Econ. Behav. Organ. 2007, 62, 495–521. [Google Scholar] [CrossRef]
- Burlando, R.M.; Guala, F. Heterogeneous agents in public goods experiments. Exp. Econ. 2005, 8, 35–54. [Google Scholar] [CrossRef]
- Offerman, T.; Sonnemans, J.; Schram, A. Value orientations, expectations, and voluntary contributions in public goods. Econ. J. 1996, 106, 817–845. [Google Scholar] [CrossRef]
- Van Winden, F.; Van Dijk, F.; Sonnemans, J. Intrinsic motivation in a public good environment. In Handbook of Experimental Economics Results; Plott, C., Smith, V., Eds.; North-Holland: Amsterdam, The Netherlands, 2008; Volume 1. [Google Scholar]
- Fehr, E.; Williams, T. Social norms, endogenous sorting and the culture of cooperation. In Working Paper; Department of Economics, University of Zurich: Zurich, Switzerland, 2018. [Google Scholar]
- Murphy, R.O.; Ackermann, K.A.; Handgraaf, M.J.J. Measuring social value orientation. Judg. Decis. Mak. 2011, 6, 771–781. [Google Scholar] [CrossRef]
- Balliet, D.; Parks, C.; Joireman, J. Social Value Orientation and Cooperation in Social Dilemmas: A Meta-Analysis. Group Process. Intergroup Relat. 2009, 12, 533–547. [Google Scholar] [CrossRef]
- Croson, R. Theories of commitment, altruism, and reciprocity: Evidence from linear public goods games. Econ. Inq. 2007, 45, 199–216. [Google Scholar] [CrossRef]
- Neugebauer, T.; Perote, J.; Schmidt, U.; Loos, M. Selfish-biased conditional cooperation: On the decline of contributions in repeated public goods experiments. J. Econ. Psychol. 2009, 30, 52–60. [Google Scholar] [CrossRef]
- Andreoni, J. Why free ride? J. Public Econ. 1988, 37, 291–304. [Google Scholar] [CrossRef]
- Andreoni, J. Cooperation in Public-Goods experiments: Kindness or confusion? Am. Econ. Rev. 1995, 85, 891–904. [Google Scholar]
- Burlando, R.M.; Hey, J.D. Do Anglo-Saxons free ride more? J. Public Econ. 1997, 64, 41–60. [Google Scholar] [CrossRef]
- Brandts, J.; Schram, A. Cooperation and noise in public goods experiments: Applying the contribution function approach. J. Public Econ. 2001, 79, 399–427. [Google Scholar] [CrossRef]
- Croson, R. Partners and strangers revisited. Econ. Lett. 1996, 53, 25–32. [Google Scholar] [CrossRef]
- Carpenter, J. Punishing free-riders: How group size affects mutual monitoring and the provision of public goods. Games Econ. Behav. 2007, 60, 31–51. [Google Scholar] [CrossRef]
- Isaac, R.M.; McCue, K.F.; Plott, C.R. Public goods provision in an experimental environment. J. Public Econ. 1985, 26, 51–74. [Google Scholar] [CrossRef]
- Isaac, R.M.; Walker, J.M. Group size effects in public goods provision: The voluntary contributions mechanism. Q. J. Econ. 1988, 103, 179–199. [Google Scholar] [CrossRef]
- Keser, C.; Van Winden, F. Conditional cooperation and voluntary contributions to public goods. Scand. J. Econ. 2000, 102, 23–39. [Google Scholar] [CrossRef]
- Kim, O.; Walker, M. The free rider problem: Experimental evidence. Public Choice 1984, 43, 3–24. [Google Scholar] [CrossRef]
- Laury, S.K.; Walker, J.M.; Williams, A.W. Anonymity and the voluntary provision of public goods. J. Econ. Behav. Organ. 1995, 27, 365–380. [Google Scholar] [CrossRef]
- Weimann, J. Individual behavior in a free riding experiment. J. Public Econ. 1994, 54, 185–200. [Google Scholar] [CrossRef]
- Selten, R. Die Strategiemethode zur Erforschung des eingeschränkten rationalen Verhaltens im Rahmen eines Oligopolexperimentes. In Beiträge zur Experimentellen Wirtschaftsforschung; Sauermann, H., Ed.; J.C.B. Mohr: Tübingen, Germany, 1967; pp. 136–168. [Google Scholar]
- Kachelmeier, S.T.; Shehata, M. Internal auditing and voluntary cooperation in firms: A cross-cultural experiment. Account. Rev. 1997, 72, 407–431. [Google Scholar]
- Andreoni, J. Impure altruism and donations to public goods: A theory of warm-glow giving. Econ. J. 1990, 100, 464–477. [Google Scholar] [CrossRef]
- Ashley, R.; Ball, S.; Eckel, C. Motives for giving: A reanalysis of two classic public goods experiments. South. Econ. J. 2010, 77, 15–26. [Google Scholar] [CrossRef]
- Palfrey, T.R.; Prisbrey, J.E. Anomalous behavior in Public Goods experiments: How much and why? Am. Econ. Rev. 1997, 87, 829–846. [Google Scholar]
- Bardsley, N.; Moffatt, P.G. The experimetrics of public goods: Inferring motivations from contributions. Theory Decis. 2007, 62, 161–193. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Laury, S.K. Private costs and public benefits: Unraveling the effects of altruism and noisy behavior. J. Public Econ. 2002, 83, 255–276. [Google Scholar] [CrossRef]
- Stevens, S.S. On the theory of scales of measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef] [PubMed]
- Gächter, S. Conditional cooperation. Behavioral regularities from the lab and the field and their policy implications. In Economics and Psychology. A Promising New Cross-Disciplinary Field; Frey, B., Stutzer, A., Eds.; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Kurzban, R.; Houser, D. Experiments investigating cooperative types in humans: A complement to evolutionary theory and simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 1803–1807. [Google Scholar] [CrossRef] [PubMed]
- Hermann, B.; Thöni, C. Measuring conditional cooperation: A replication study in Russia. Exp. Econ. 2009, 12, 87–92. [Google Scholar] [CrossRef]
- Kocher, M.G.; Cherry, T.; Kroll, S.; Netzer, R.J.; Sutter, M. Conditional cooperation on three continents. Econ. Lett. 2008, 101, 175–178. [Google Scholar] [CrossRef]
- Falk, A.; Fehr, E.; Fischbacher, U. Testing theories of fairness—Intentions matter. Games Econ. Behav. 2008, 62, 287–303. [Google Scholar] [CrossRef]
- Stanca, L.; Bruni, L.; Corazzini, L. Testing theories of reciprocity: Do motivations matter? J. Econ. Behav. Organ. 2009, 71, 233–245. [Google Scholar] [CrossRef]
- Ackermann, K.A.; Fleiß, J.; Murphy, R.O. Reciprocity as an individual difference. J. Confl. Resolut. 2016, 60, 340–367. [Google Scholar] [CrossRef]
- Nax, H.H.; Murphy, R.O.; Ackermann, K.A. Interactive preferences. Econ. Lett. 2015, 135, 133–136. [Google Scholar] [CrossRef]
- Nyarko, Y.; Schotter, A. An experimental study of belief learning using elicited beliefs. Econometrica 2002, 70, 971–1005. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Crosetto, P.; Weisel, O.; Winter, F. A flexible z-Tree implementation of the Social Value Orientation Slider Measure (Murphy et al. 2011)—Manual. In Jena Economic Research Paper; Friedrich Schiller University and Max Planck Institute of Economics: Jena, Germany, 2012; Volume 62. [Google Scholar]
- Greiff, M.; Ackermann, K.; Murphy, R.O. Playing a Game or Making a Decision? Methodological Issues in the Measurement of Distributional Preferences. Games 2018, 9, 80. [Google Scholar] [CrossRef]
- Gunnthorsdottir, A.; McCabe, K.; Smith, V. Using the Machiavellianism instrument to predict trustworthiness in a bargaining game. J. Econ. Psychol. 2002, 23, 49–66. [Google Scholar] [CrossRef]
- Christie, R.; Geis, F.L. Studies in Machiavellianism; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Dalbert, C.; Montada, L.; Schmitt, M. Belief in a just world: Validity correlates of two scales. Psychol. Beiträge 1987, 29, 596–615. [Google Scholar]
- Perugini, M.; Gallucci, M.; Presaghi, F.; Ercolani, A.P. The personal norm of reciprocity. Eur. J. Pers. 2003, 17, 251–283. [Google Scholar] [CrossRef]
- Ross, L.; Greene, D.; House, P. The false consensus effect: An egocentric bias in social perception and attribution processes. J. Exp. Soc. Psychol. 1977, 13, 279–301. [Google Scholar] [CrossRef]
- Ebbinghaus, H. On Memory: A Contribution to Experimental Psychology; Teachers College: New York, NY, USA, 1913. [Google Scholar]
- Atkinson, R.C.; Shiffrin, R.M. Human memory: A proposed system and its control processes. In The Psychology of Learning and Motivation: Advances in Research And Theory; Spence, K., Spence, J., Eds.; Academic Press: New York, NY, USA, 1968; Volume 2, pp. 89–195. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Sonnemans, J.; van Dijk, F.; van Winden, F. On the dynamics of social ties structures in groups. J. Econ. Psychol. 2006, 27, 187–204. [Google Scholar] [CrossRef]
- Fleeson, W. Toward a structure-and process-integrated view of personality: Traits as density distributions of states. J. Pers. Soc. Psychol. 2001, 80, 1011. [Google Scholar] [CrossRef] [PubMed]
- Fleeson, W. Moving personality beyond the person-situation debate: The challenge and the opportunity of within-person variability. Curr. Direct. Psychol. Sci. 2004, 13, 83–87. [Google Scholar] [CrossRef]
- Nax, H.H.; Perc, M. Directional learning and the provisioning of public goods. Sci. Rep. 2015, 5, 8010. [Google Scholar] [CrossRef] [PubMed]
- Burton-Chellew, M.N.; Nax, H.H.; West, S.A. Payoff-based learning explains the decline in cooperation in public goods games. Proc. R. Soc. B Biol. Sci. 2015, 282, 20142678. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.H.; Burton-Chellew, M.N.; West, S.A.; Young, H.P. Learning in a black box. J. Econ. Behav. Organ. 2016, 127, 1–15. [Google Scholar] [CrossRef]
| 1. | P, R, S, and T stand for Punishment payoff (resulting from mutual defection), Reward payoff (resulting from mutual cooperation), Sucker payoff (resulting from unilateral cooperation), and Temptation payoff (resulting from unilateral defection), respectively. |
| 2. | Offerman et al. ([49] , p. 818). explicitly point out the importance of an independent measure of social preferences for precisely the reasons brought out above. |
| 3. | Please note that this also means that free riders do not cause the decline of cooperation per se, but their presence does accelerate it. |
| 4. | For example, referring to phenomena observed in PGGs, Palfrey and Prisbrey [72], p. 843, wrote:
|
| 5. | SVO data collected in previous experiments served as the reference data for evaluating accuracy. |
| 6. | We did not mention the term “public goods game” in the instructions, but rather used the neutral term “task”. Also, we did not use the term “contribute”, but rather “transfer to the group account” to minimize potential demand effects. |
| 7. | When a participant answered a question incorrectly, a pop-up window appeared on that participant’s computer screen explaining the task once more and then giving the participant another opportunity to answer the question. An experimental session continued only if all participants had answered the questions correctly. |
| 8. | However, representing a contribution profile with a single number discards information, i.e., a subject’s CCA () is ambiguous. A CCA of 1, for instance, can result from perfect conditional cooperation, but may also be a result of a radically different contribution profile, such as contributing zero for average contributions of others between 0 and 9, matching an average contribution of 10 exactly, and contributing 20 for any average contribution of others strictly above 10. Hence, the CCA should be interpreted with some caution, but it is still a useful approximate representation of the subjects’ general tendencies to condition their own contributions on the average contribution of others. |
| 9. | If we add BCC in addition to CCA in model 2 of the regression, then BBCC takes over all of the variance explained by CCA, thereby rendering the relative effect of CCA non-significant. This is not surprising, since both variables are computed on the basis of the same data, namely subjects’ indications of contribution decisions in the strategy method, while BBCC—as it is informed by the subject’s elicited beliefs in the one-shot PGG—is by far a more specific indicator of behavior compared to the general CCA index. |
| 10. | An non-significant Kolmogorov-Smirnov test corroborates this null result. |
| 11. | Again, a non-significant Kolmogorov-Smirnov test also supports this conclusion. |
| 12. | The pattern of results does not change when the groups with subjects who showed intransitive choice patterns in the Slider Measure are excluded from the analyses. |
| 13. | The mean CCA per group is also quite predictive of a group’s average contribution in the final period, but the minimum CCA turns out to show more predictive power than the mean. |
| 14. | If the average contribution in period 9 is used as dependent variable, the two variables together explain almost half () of the variance. |
| 15. | Since average contributions in period 1 are used as predictor, we only use the average contributions across periods 2 to 10 as dependent variable in order to avoid artificial inflation of . |
| 16. | For this analysis, we included all the subjects. |
| 17. | For example, one subject indicated to unconditionally contribute the full endowment, and another subject to unconditionally contribute 10. |
| 18. | This conclusion is also supported by the fact that in our sample, the subjects’ average contribution in the one-shot PGG was 9.80 tokens (i.e., almost 50% of the endowment), compared to 6.7 tokens (33.5% of the endowment) reported by Fischbacher et al. [7]. |
| 19. | PR shows a significantly positive relation with contribution levels in the final period of the repeated PGG (), though, but since this is the only instance where PR shows a significant correlation with any of the variables we have assessed or computed (except Machiavellianism)—including several measures of reciprocity, such as CCA, mean difference between own contribution and believed average contribution of others, and further variables of this kind—we do not pay serious attention to this one single correlation which may have reached significance just by chance alone. |

| PG os | SVO | PG os | SVO | CCA | PG rp | PG rp | PG rp | PG rp | SVO | |
|---|---|---|---|---|---|---|---|---|---|---|
| t1 | Belief | Belief | p1 | Belief p1 | p10 | Belief p10 | t2 | |||
| PG os | - | |||||||||
| SVO t | 0.32 *** | - | ||||||||
| PG os belief | 0.75 *** | 0.26 ** | - | |||||||
| SVO belief | 0.09 | 0.63 *** | 0.16 | - | ||||||
| CCA | 0.47 *** | 0.30 *** | 0.39 *** | 0.15 | - | |||||
| PG rp p | 0.70 *** | 0.30 *** | 0.59 *** | 0.09 | 0.32 *** | - | ||||
| PG rp belief p | 0.58 *** | 0.32 *** | 0.69 *** | 0.19 * | 0.21 * | 0.80 *** | - | |||
| PG rp p | 0.27 ** | 0.26 ** | 0.20 * | 0.17 | 0.31 *** | 0.15 | 0.11 | - | ||
| PG rp belief p | 0.27 ** | 0.04 | 0.21 * | 0.05 | 0.37 *** | 0.15 | 0.08 | 0.70 *** | - | |
| SVO t | 0.32 *** | 0.72 *** | 0.25 ** | 0.55 *** | 0.36 *** | 0.26 ** | 0.19 * | 0.40 *** | 0.26 ** | - |
| Dependent Variable: Contributions in the One-Shot PGG | |||
|---|---|---|---|
| Model | (1) | (2) | (3) |
| SVO | 0.26 *** | 0.22 ** | 0.23 ** |
| PG belief | 0.71 *** | 0.66 *** | 0.54 *** |
| SVO belief | −0.19 * | −0.18 * | −0.19 ** |
| CCA | 0.17 ** | ||
| BBCC | 0.25 ** | ||
| 0.60 | 0.63 | 0.63 | |
| 0.59 | 0.61 | 0.62 | |
| Dependent Variable: Contributions across the Repeated PGG | ||||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | ||||
| SVO | 0.09 | (0.04) * | 0.09 | (0.04) * | 0.07 | (0.04) |
| PG belief | 0.84 | (0.04) *** | 0.84 | (0.04) *** | 0.70 | (0.07) *** |
| SVO belief | −0.03 | (0.02) | −0.03 | (0.02) | −0.02 | (0.02) |
| Period | −0.17 | (0.05) ** | −0.17 | (0.05) *** | ||
| BBCC | 0.20 | (0.06) ** | ||||
| Constant | 0.57 | (0.55) | 1.52 | (0.57) ** | 1.53 | (0.59) * |
| 0.66 | 0.66 | 0.67 | ||||
| Low SVO | Medium SVO | High SVO | |
|---|---|---|---|
| Free Rider | 7 (19.4 ∣ 38.9) | 7 (14.3 ∣ 38.9) | 4 (10.3 ∣ 22.2) |
| Perfect CC | 7 (19.4 ∣ 23.3) | 13 (26.5 ∣ 43.3) | 10 (25.6 ∣ 33.3) |
| Excessive CC | 1 (2.8 ∣ 7.7) | 4 (8.2 ∣ 30.8) | 8 (20.5 ∣ 61.5) |
| Imperfect CC | 15 (41.7 ∣ 45.5) | 11 (22.4 ∣ 33.3) | 7 (17.9 ∣ 21.2) |
| Mixed CC | 4 (11.1 ∣ 20.0) | 7 (14.3 ∣ 35.0) | 9 (23.1 ∣ 45.0) |
| Hump Shaped | 1 (2.8 ∣ 14.3) | 6 (12.2 ∣ 85.7) | 0 (0.0 ∣ 0.0) |
| Other | 1 (2.8 ∣ 33.3) | 1 (2.0 ∣ 33.3) | 1 (2.6 ∣ 33.3) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ackermann, K.A.; Murphy, R.O. Explaining Cooperative Behavior in Public Goods Games: How Preferences and Beliefs Affect Contribution Levels. Games 2019, 10, 15. https://doi.org/10.3390/g10010015
Ackermann KA, Murphy RO. Explaining Cooperative Behavior in Public Goods Games: How Preferences and Beliefs Affect Contribution Levels. Games. 2019; 10(1):15. https://doi.org/10.3390/g10010015
Chicago/Turabian StyleAckermann, Kurt A., and Ryan O. Murphy. 2019. "Explaining Cooperative Behavior in Public Goods Games: How Preferences and Beliefs Affect Contribution Levels" Games 10, no. 1: 15. https://doi.org/10.3390/g10010015
APA StyleAckermann, K. A., & Murphy, R. O. (2019). Explaining Cooperative Behavior in Public Goods Games: How Preferences and Beliefs Affect Contribution Levels. Games, 10(1), 15. https://doi.org/10.3390/g10010015




