Evolution of Cooperation with Peer Punishment under Prospect Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Game and Strategies
2.2. Payoff and Strategy Switching
2.2.1. Linear Expected Utility Theory
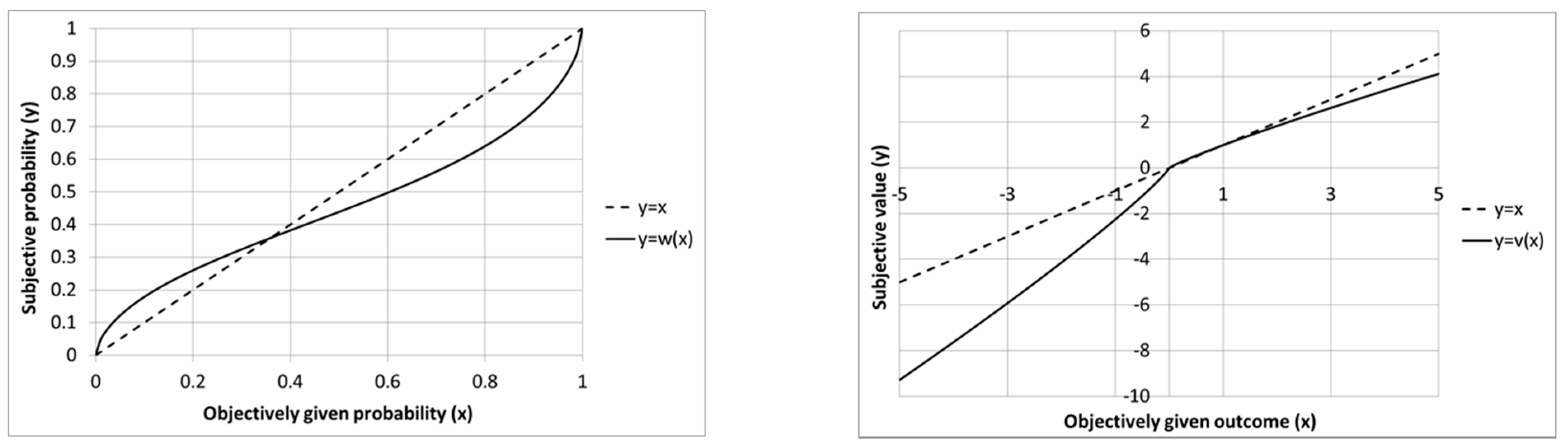
2.2.2. Prospect Theory
3. Results
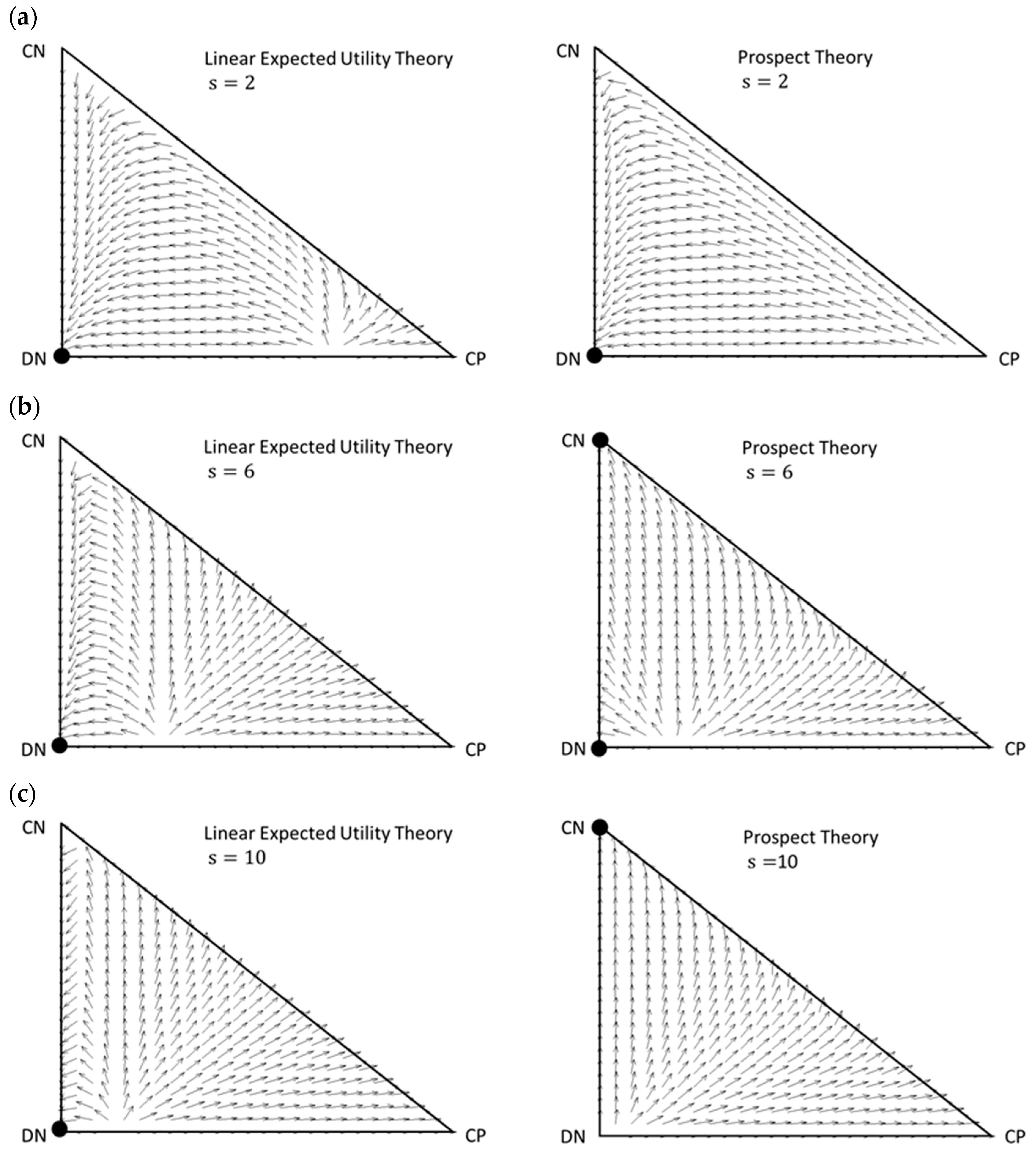
3.1. Vector Fields
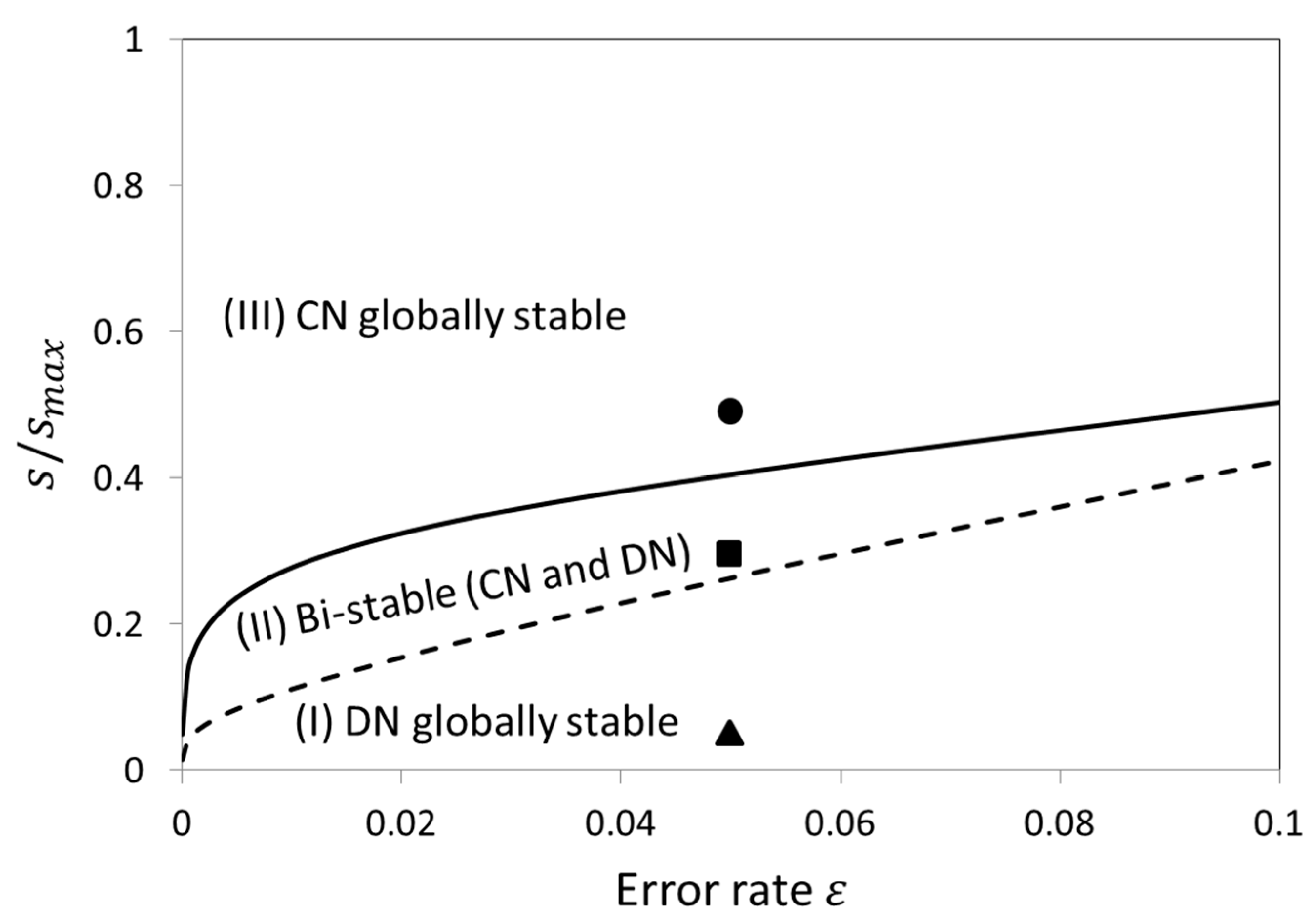
3.2. Stability Analysis of DN and CN
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Nowak, M.A.; Highfield, R. Super Cooperators; Free Press: New York, NY, USA, 2011. [Google Scholar]
- Ostrom, E. Governing the Commons: The Evolution of Institutions for Collective Action; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Bowls, S.; Gintis, H. A Cooperative Species; Princeton University Press: Princeton, UK; Oxford, UK, 2011. [Google Scholar]
- Yamagishi, T. Trust: The Evolutionary Game of Mind and Society; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, UK; Oxford, UK, 2010. [Google Scholar]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 68, 1–51. [Google Scholar] [CrossRef]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Balliet, D.; Mulder, L.B.; Van Lange, P.A. Reward, punishment, and cooperation: A meta-analysis. Psychol. Bull. 2011, 137, 594–615. [Google Scholar] [CrossRef] [PubMed]
- Guala, F. Reciprocity: Weak or strong? What punishment experiments do (and do not) demonstrate. Behav. Brain Sci. 2012, 35, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R. An evolutionary approach to norms. Am. Political Sci. Rev. 1986, 80, 1095–1111. [Google Scholar] [CrossRef]
- Henrich, J.; McElreath, R.; Barr, A.; Ensminger, J.; Barrett, C.; Bolyanatz, A.; Cardenas, J.C.; Gurven, M.; Gwako, E.; Henrich, N.; et al. Costly punishment across human societies. Science 2006, 312, 1767–1770. [Google Scholar] [CrossRef] [PubMed]
- Mathew, S.; Boyd, R. Punishment sustains large-scale cooperation in prestate warfare. Proc. Natl. Acad. Sci. USA 2011, 108, 11375–11380. [Google Scholar] [CrossRef] [PubMed]
- Casari, M.; Luini, L. Cooperation under alternative punishment institutions: An experiment. J. Econ. Behav. Organ. 2009, 71, 273–282. [Google Scholar] [CrossRef]
- Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R.; Gintis, H.; Bowles, S.; Richerson, P.J. The evolution of altruistic punishment. Proc. Natl. Acad. Sci. USA 2003, 100, 3531–3535. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K.; Hauert, C.; Nowak, M.A. Reward and punishment. Proc. Natl. Acad. Sci. USA 2001, 98, 10757–10762. [Google Scholar] [CrossRef] [PubMed]
- Milinski, M.; Rockenbach, B. Human behaviour: Punisher pays. Nature 2008, 452, 297–298. [Google Scholar] [CrossRef] [PubMed]
- Kosfeld, M.; Okada, A.; Riedl, A. Institution formation in public goods games. Am. Econ. Rev. 2009, 99, 1335–1355. [Google Scholar] [CrossRef]
- Boyd, R.; Richerson, P.J. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethol. Sociobiol. 1992, 13, 171–195. [Google Scholar] [CrossRef]
- Sigmund, K.; de Silva, H.; Traulsen, A.; Hauert, C. Social learning promotes institutions for governing the commons. Nature 2010, 466, 861–863. [Google Scholar] [CrossRef] [PubMed]
- Yamagishi, T. The provision of a sanctioning system as a public good. J. Personal. Soc. Psychol. 1986, 51, 110–116. [Google Scholar] [CrossRef]
- Traulsen, A.; Röhl, T.; Milinski, M. An economic experiment reveals that humans prefer pool punishment to maintain the commons. Proc. Biol. Sci. 2012, 279, 3716–3721. [Google Scholar] [CrossRef] [PubMed]
- Andreoni, J.; Gee, L.K. Gun for hire: Delegated enforcement and peer punishment in public goods provision. J. Public Econ. 2012, 96, 1036–1046. [Google Scholar] [CrossRef]
- Zhang, B.; Li, C.; De Silva, H.; Bednarik, P.; Sigmund, K. The evolution of sanctioning institutions: An experimental approach to the social contract. Exp. Econ. 2014, 17, 285–303. [Google Scholar] [CrossRef]
- Schoenmakers, S.; Hilbe, C.; Blasius, B.; Traulsen, A. Sanctions as honest signals—The evolution of pool punishment by public sanctioning institutions. J. Theor. Biol. 2014, 356, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Okada, I.; Yamamoto, H.; Toriumi, F.; Sasaki, T. The effect of incentives and meta-incentives on the evolution of cooperation. PLoS Comput. Biol. 2015, 11, e1004232. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Uchida, S.; Chen, X. Voluntary rewards mediate the evolution of pool punishment for maintaining public goods in large populations. Sci. Rep. 2015, 5, 8917. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, C.; Traulsen, A.; Röhl, T.; Milinski, M. Democratic decisions establish stable authorities that overcome the paradox of second-order punishment. Proc. Natl. Acad. Sci. USA 2014, 111, 752–756. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Brännström, Å.; Dieckmann, U.; Sigmund, K. The take-it-or-leave-it option allows small penalties to overcome social dilemmas. Proc. Natl. Acad. Sci. USA 2012, 109, 1165–1169. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Okada, I.; Uchida, S.; Chen, X. Commitment to cooperation and peer punishment: Its evolution. Games 2015, 6, 574. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Judgement under uncertainty: Heuristics and biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A.; Kahneman, D. Extensional vs. intuitive reasoning: The conjunction fallacy in probability judging. Psychol. Rev. 1983, 90, 293–315. [Google Scholar] [CrossRef]
- Schmeidler, D. Subjective probability and expected utility without additivity. Econometrica 1989, 57, 571–587. [Google Scholar] [CrossRef]
- Gilboa, I.; Schmeidler, D. Maxmin expected utility with a non-unique prior. J. Math. Econ. 1989, 18, 141–153. [Google Scholar] [CrossRef]
- Starmer, C. Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. J. Econ. Lit. 2000, 38, 332–382. [Google Scholar] [CrossRef]
- Machina, M.J. Expected utility analysis without the independence axiom. Econometrica 1982, 50, 277–323. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: Analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Loss aversion in riskless choice: A reference-dependent model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]
- Wakker, P.P. Prospect Theory: For Risk and Ambiguity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Boyd, R.; Gintis, H.; Bowles, S. Coordinated punishment of defectors sustains cooperation and can proliferate when rare. Science 2010, 328, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Raihani, N.J.; Bshary, R. The evolution of punishment in n-player public goods games: A volunteer’s dilemma. Evolution 2011, 65, 2725–2728. [Google Scholar] [CrossRef] [PubMed]
- Brandt, H.; Hauert, C.; Sigmund, K. Punishing and abstaining for public goods. Proc. Natl Acad. Sci. USA 2006, 103, 495–497. [Google Scholar] [CrossRef] [PubMed]
- Dercole, F.; De Carli, M.; Della Rossa, F.; Papadopoulos, A.V. Overpunishing is not necessary to fix cooperation in voluntary public goods games. J. Theor. Biol. 2013, 326, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Traulsen, A.; Brandt, H.; Nowak, M.A.; Sigmund, K. Via freedom to coercion: The emergence of costly punishment. Science 2007, 316, 1905–1907. [Google Scholar] [CrossRef] [PubMed]
- Nikiforakis, N. Punishment and counter-punishment in public good games: Can we really govern ourselves? J. Public Econ. 2008, 92, 91–112. [Google Scholar] [CrossRef]
- Rand, D.G.; Nowak, M.A. The evolution of antisocial punishment in optional public goods games. Nat. Commun. 2011, 2, 434. [Google Scholar] [CrossRef] [PubMed]
- García, J.; Traulsen, A. Leaving the loners alone: Evolution of cooperation in the presence of antisocial punishment. J. Theor. Biol. 2012, 307, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Iwasa, Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006, 239, 435–444. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1292–1298. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Okada, I.; Nakai, Y. The evolution of conditional moral assessment in indirect reciprocity. Sci. Rep. 2017, 7, 41870. [Google Scholar] [CrossRef] [PubMed]
- Uchida, S.; Sigmund, K. The competition of assessment rules for indirect reciprocity. J. Theor. Biol. 2010, 263, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Chalub, F.; Santos, F.C.; Pacheco, J.M. The evolution of norms. J. Theor. Biol. 2006, 241, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. A Theoretical Approach to Norm Ecosystems: Two Adaptive Architectures of Indirect Reciprocity Show Different Paths to the Evolution of Cooperation. Front. Phys. 2018, 6, 14. [Google Scholar] [CrossRef]
- Yamamoto, H.; Okada, I.; Uchida, S.; Sasaki, T. A norm knockout method on indirect reciprocity to reveal indispensable norms. Sci. Rep. 2017, 7, 44146. [Google Scholar] [CrossRef] [PubMed]
- Schlaepfer, A. The emergence and selection of reputation systems that drive cooperative behaviour. Proc. R. Soc. B Biol. Sci. 2018, 285, 20181508. [Google Scholar] [CrossRef] [PubMed]
| Player B’s Options Player A’s Options | Cooperate (C) | Defect (D) |
|---|---|---|
| Cooperate (C) | b − c | −c |
| Defect (D) | b | 0 |
| Player B’s Options Player A’s Options | Cooperate Punish (CP) | Cooperate Not-Punish (CN) | Defect Punish (DP) | Defect Not-Punish (DN) |
|---|---|---|---|---|
| Cooperate Punish (CP) | b − c | b − c | −c − r | −c − r |
| Cooperate Not-punish (CN) | b − c | b − c | −c | −c |
| Defect Punish (DP) | b − s | b | −s − r | −r |
| Defect Not-punish (DN) | b − s | b | −s | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. Evolution of Cooperation with Peer Punishment under Prospect Theory. Games 2019, 10, 11. https://doi.org/10.3390/g10010011
Uchida S, Yamamoto H, Okada I, Sasaki T. Evolution of Cooperation with Peer Punishment under Prospect Theory. Games. 2019; 10(1):11. https://doi.org/10.3390/g10010011
Chicago/Turabian StyleUchida, Satoshi, Hitoshi Yamamoto, Isamu Okada, and Tatsuya Sasaki. 2019. "Evolution of Cooperation with Peer Punishment under Prospect Theory" Games 10, no. 1: 11. https://doi.org/10.3390/g10010011
APA StyleUchida, S., Yamamoto, H., Okada, I., & Sasaki, T. (2019). Evolution of Cooperation with Peer Punishment under Prospect Theory. Games, 10(1), 11. https://doi.org/10.3390/g10010011







