Evolution of Cooperation with Peer Punishment under Prospect Theory

Abstract

Social dilemmas are among the most puzzling issues in the biological and social sciences. Extensive theoretical efforts have been made in various realms such as economics, biology, mathematics, and even physics to figure out solution mechanisms to the dilemma in recent decades. Although punishment is thought to be a key mechanism, evolutionary game theory has revealed that the simplest form of punishment called peer punishment is useless to solve the dilemma, since peer punishment itself is costly. In the literature, more complex types of punishment, such as pool punishment or institutional punishment, have been exploited as effective mechanisms. So far, mechanisms that enable peer punishment to function as a solution to the social dilemma remain unclear. In this paper, we propose a theoretical way for peer punishment to work as a solution mechanism for the dilemma by incorporating prospect theory into evolutionary game theory. Prospect theory models human beings as agents that estimate small probabilities and loss of profit as greater than they actually are; thus, those agents feel that punishments are more frequent and harsher than they really are. We show that this kind of cognitive distortion makes players decide to cooperate to avoid being punished and that the cooperative state achieved by this mechanism is globally stable as well as evolutionarily stable in a wide range of parameter values.

1. Introduction

Although cooperative relationships can be found in diverse systems ranging from microbiological communities to global economic spheres, cooperation frequently poses a scientific puzzle. Cooperation is clearly important to make biological and human societies effective and smooth, and evolutionary biologists and social scientists have long puzzled over the origin of cooperation. In recent decades, extensive theoretical efforts from various disciplines, such as economics, biology, mathematics, or even physics, have been made to figure out solution mechanisms to the cooperation dilemma [1,2,3,4,5,6,7].

In the literature, the cooperation puzzle is often called the social dilemma or the free rider problem. This can be described as follows: (1) individuals in a society have binary choices: cooperation (contributing to the community) or defection (refusing to contribute, i.e., free-riding), (2) a society consisting of cooperators is more profitable than that with only defectors, (3) but within a society, individual defectors do better than individual cooperators, since cooperators must incur a cost for contribution, while defectors do not.

Thus, the defective strategy dominates the cooperative strategy and is the Nash equilibrium in the framework of game theory. In other words, it is more advantageous for individuals to choose defection regardless of what other individuals choose, which, by natural selection or social learning, leads to a society with only defectors. The theoretical issue therefore is to explain why cooperation is so ubiquitous in the real world.

In the literature on the evolution of cooperation, various mechanisms have been proposed and investigated. Representative examples include kin selection, direct reciprocity, indirect reciprocity, group selection, and spatial and network reciprocity [8]. Besides these well-studied mechanisms, punishment is thought to be one of the effective mechanisms and is extensively investigated in the literature [9,10,11,12,13,14]. If individuals have a possibility of being punished when they do not pay costs for cooperation and if the strength of the punishment is so harsh that it cancels the profit obtained by free-riding, the players are expected to choose cooperation.

The most elementary type of punishment is informal or peer punishment, typified by the “As you wronged me, I will punish you” attitude. However, the evolution of this type of punishment remains a theoretical challenging puzzle [15,16,17]: a simple theory on the evolution of peer punishment predicts that no one chooses to punish to avoid bearing the implementation cost of the punishment. This new type of dilemma caused by the introduction of punishment is called the second-order dilemma. In fact, punishment itself incurs a cost on punishers; consequently, those who perform the punishment earn less payoff than those who do not punish. Punishment would be effective if there were those who choose to punish in the population. In this sense, punishers can be interpreted as a different type of contributor than cooperators. However, rational individuals will never choose to punish others. Thus, the second-order dilemma occurs.

Peer punishment itself is interpreted as a cooperative act; thus, it could be used for the avoidance of the second-order dilemma. One way is to introduce the possibility of punishing those who do not punish defectors—the second-order punishment. However, this again raises the third-order dilemma that no one chooses to implement the second-order punishment since it is costly. In general, an introduction of the $n$-th order punishment raises the $\left(n+1\right)$-th order dilemma, which results in an infinite regress of peer punishment [18,19,20]. The theoretical task is therefore to search for ways or mechanisms to cut the infinite chain.

In order to prevent the emergence of higher order dilemmas (which mean the $n$-th order dilemmas for $n>1$), additional and mostly complex mechanisms have been proposed in the literature on evolutionary game theory [21,22,23,24,25,26,27,28,29,30,31]. For instance, if players are asked whether to contribute to public goods that will be used for punishment in the future, the second-order dilemma can be avoided; thus, cooperation evolves. This type of punishment is called formal or pool punishment.

In this present paper, we show a way for peer punishment to work without additional mechanisms. To do this, we take cognitive distortions of human beings into account. Most game-theory studies on the evolution of cooperation are based on the linear expected utility theory, which asserts that individuals’ decisions rely on accurate calculations of expected payoffs. On the other hand, experimental researches in behavioral economics and experimental economics have revealed that real human beings are not so rational that they can objectively estimate probabilities and values without biases, both of which are elements of expected payoffs [32,33,34,35,36,37]. Thus, payoffs attributed to real human beings are subjective, and this fact plays an essential role in actual decision-making processes.

One of the most successful theories describing irrationality is prospect theory [38,39,40]. In this theory, distortions of probabilities and values are modeled as a weighted function and a value function, respectively. The nonlinearities and asymmetric properties of these functions represent the irrationality of human beings in prospect theory. What happens if we analyze peer punishment, not assuming the linear expected utility theory but based on prospect theory to estimate expected payoffs? This is the main issue considered in this paper.

Thus, this paper gives the first opportunity to study the coevolution of cooperation and peer punishment in the framework of evolutionary game theory combined with prospect theory. Our main finding is that enlarging the effect of small probabilities makes it possible to avoid the second-order dilemma, which enables cooperation to evolve and to be sustained.

In the next section, we describe the game, strategies, and the model setting of this paper. Then, we derive the results and discuss them.

2. Materials and Methods

2.1. Game and Strategies

An infinitely large, well-mixed population of individuals (or players) is considered. From time to time, two players are selected at random from the population and made to engage in a “donation game” [5]: each player decides whether to support the opponent at a personal cost, $\mathrm{c}$. If a player chooses to support the other, the opponent receives a benefit $\mathrm{b}>\mathrm{c}$; otherwise, the player obtains nothing. Each individual in the population will experience such decision-making many times. From here on, we denote the action “support” by “C” and “refuse” by “D”.

Table 1. Payoffs player A obtains in donation game.

Player B’s Options Player A’s Options	Cooperate (C)	Defect (D)
Cooperate (C)	b − c	−c
Defect (D)	b	0

shows the payoffs player A obtains when playing the donation game with player B.

After they have played the donation game, both players consider whether to punish their opponents or not if the other player chose D in the donation game. If a player chooses to punish its opponent, the other player’s payoff is reduced by $s$. The punishment is not free but costly and therefore incurs a cost $r$ on the punisher. We assume the strength of punishment $s$ is greater than the punishment cost $r$. We denote the decisions “punish” and “not punish” by “P” and “N”, respectively.

Thus, the game considered in this paper consists of two phases, which we call “donation phase” and “punishment phase”. We call the combined game “donation–punishment game”. In the donation phase, individuals consider whether to cooperate (support the other) or not, and in the punishment phase, they consider whether to punish their opponents when they choose D in the donation phase.

As a result, individuals have 4 options in total, i.e., there are 4 types of strategies: cooperate punish (CP), cooperate not-punish (CN), defect punish (DP), and defect not-punish (DN). Each individual follows one of these strategies and makes decisions according to the strategy. We denote the payoff matrix of the donation–punishment game described in

Table 2. Payoffs player A obtains in donation-punishment game.

Player B’s Options Player A’s Options	Cooperate Punish (CP)	Cooperate Not-Punish (CN)	Defect Punish (DP)	Defect Not-Punish (DN)
Cooperate Punish (CP)	b − c	b − c	−c − r	−c − r
Cooperate Not-punish (CN)	b − c	b − c	−c	−c
Defect Punish (DP)	b − s	b	−s − r	−r
Defect Not-punish (DN)	b − s	b	−s	0

by $M$.

We assume that individuals sometimes deviate from their strategies due to error. By a small probability, those individuals who intend to cooperate do not cooperate and vice versa. In the same way, individuals who intend to punish may not punish and vice versa. Note that we assume symmetric deviations in double meanings to reduce parameters. Firstly, probabilities of deviations from C (P) to D (N) and from D (N) to C (P) are the same. Secondly, probabilities of deviations from C to D and from P to N are the same, which implies that error between C and D and error between P and N are independent. All probabilities of deviations are denoted by one parameter, $\mathsf{\epsilon }$.

2.2. Payoff and Strategy Switching

2.2.1. Linear Expected Utility Theory

The long-term payoff of an individual depends on its strategy and other individuals’ strategies. For the sake of convenience, we denote the strategies by numbers: we call CP strategy 1, CN strategy 2, DP strategy 3, and DN strategy 4. Then $x_i$ denotes the frequency of the $i$-th strategy in the population. These frequencies affect the expected payoffs that individuals obtain.

As mentioned above, we assume that individuals sometimes commit errors. This means that the strategy of an individual and its decisions may be different since actual actions can deviate from its strategies due to errors. We denote a strategy and an action actually chosen in a game by the same label. For instance, $i=1$ either means strategy CP or action CP, depending on the context.

Clearly, errors also affect the expected payoffs. Since an error occurs in decisions both for the donation and for the punishment, an individual with strategy $i$ may actually choose any other action. In order to calculate the expected payoffs, considering these, we introduce error vectors. A player with strategy 1 actually chooses its actions according to the following error vector: ($\overline{\epsilon }=1-\epsilon$ is the probability that an error does not occur.)

$${\overrightarrow{E}}_1={\left({\overline{\epsilon }}^2,\overline{\epsilon }\epsilon ,\epsilon \overline{\epsilon },{\epsilon }^2\right)}^T.$$

(1)

Here, the first element of the vector (the square of $\overline{\epsilon }$) gives the probability that the individual chooses action 1 (CP), because a player with strategy 1 actually chooses action C (cooperation) with probability $\overline{\epsilon }$ and P (punishment) with the same probability $\overline{\epsilon }$. The second, the third, and the fourth elements are defined in the same way. Thus, ${\overrightarrow{E}}_1$ provides the probability distribution of actions chosen in a game of individuals with strategy 1.

Similarly, the vectors ${\overrightarrow{E}}_2={\left(\overline{\epsilon }\epsilon ,{\overline{\epsilon }}^2,{\epsilon }^2,\epsilon \overline{\epsilon }\right)}^T,{\overrightarrow{E}}_3={\left(\epsilon \overline{\epsilon },{\epsilon }^2,{\overline{\epsilon }}^2,\overline{\epsilon }\epsilon \right)}^T,{\overrightarrow{E}}_4={\left({\epsilon }^2,\epsilon \overline{\epsilon },\overline{\epsilon }\epsilon ,{\overline{\epsilon }}^2\right)}^T$ characterize the probability distributions on the action space of individuals with their corresponding strategies.

With these error vectors, the expected payoff of an individual with strategy $i$ when playing a game with an individual with strategy $j$ is given by

$$P_{ij}={\overrightarrow{E}}_i^{T}M{\overrightarrow{E}}_j.$$

(2)

Since the probability that an individual with strategy $i$ encounters an individual with strategy $j$ is $x_j$ by the definition, the expected payoff of an individual with strategy $i$ is given by

$$P_i={\displaystyle \sum }_{j=1}^4{P}_{ij}{x}_j.$$

(3)

We obtain the same expected payoff with a different approach. This approach will be used to derive distorted expected payoffs in the framework of prospect theory. The vector

$$\overrightarrow{A}={\displaystyle \sum }_{j=1}^4{\overrightarrow{E}}_j{x}_j,$$

(4)

represents the probability distribution of actions chosen by an arbitrary player selected at random from the population. Now we define matrix $B_i$ by

$$B_i={\overrightarrow{E}}_i{\overrightarrow{A}}^T.$$

(5)

The element ${(B_i)}_{mn}$ of the matrix is interpreted as the probability that a player with strategy $i$ obtains a payoff of ${\left(M\right)}_{mn}$ of the payoff matrix of the donation–punishment game. Thus, matrix $B_i$ is a probability distribution over payoff matrix $M$ in the eyes of individuals with strategy $i$. The expected payoff is then expressed as a sum of values (payoffs) multiplied by probabilities.

$$P_i={\displaystyle \sum }_{m=1}^4{\displaystyle \sum }_{n=1}^4{\left(M\right)}_{mn}{\left(B_i\right)}_{mn}.$$

(6)

Players adaptively switch their strategies, aiming at more expected payoffs, which results in gradual changes of strategy frequencies. We assume that the time evolution of the frequency of strategy $i$ is governed by the replicator equation [41]:

$${\dot{x}}_i=x_i\left(P_i-{\displaystyle \sum }_{j=1}^4{P}_j{x}_j\right).$$

(7)

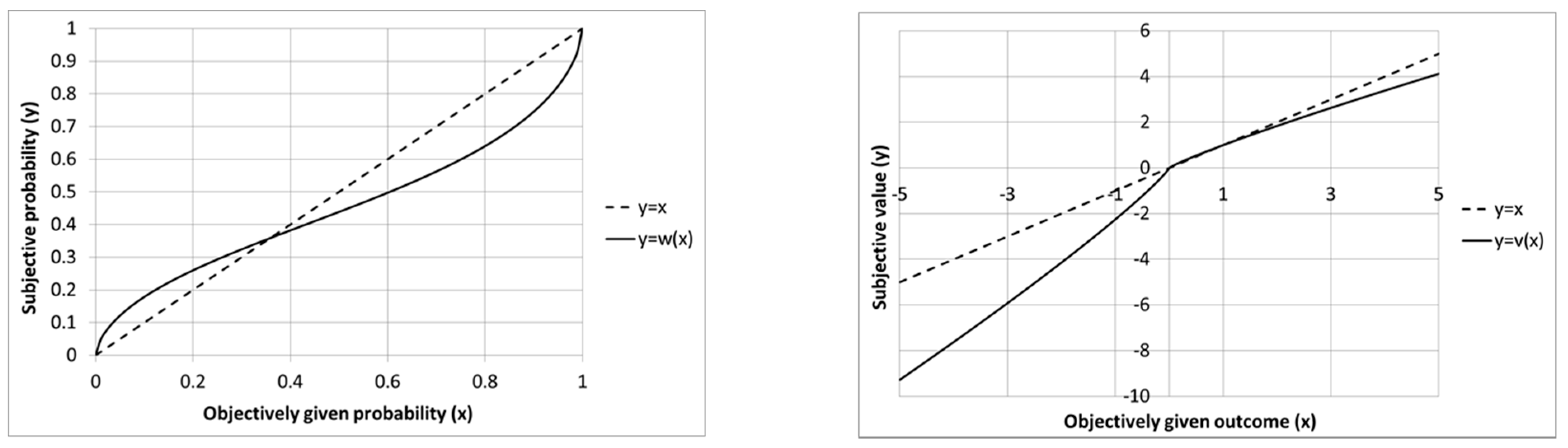
2.2.2. Prospect Theory

The element ${(B_i)}_{mn}$ of the matrix $B_i$ represents the probability that the outcome $\left(m,n\right)$ of the game is realized. Following prospect theory, we assume that this probability is subjectively calculated in a distorted way. The subjective probability is given by applying a nonlinear function called weighted function to the objective probability ${(B_i)}_{mn}:$

$${\left(W_i\right)}_{mn}=w\left({\left(B_i\right)}_{mn}\right),$$

(8)

with

$$w\left(x\right)=\frac{x^{\gamma }}{{\left[x^{\gamma }+{\left(1-x\right)}^{\gamma }\right]}^{\frac{1}{\gamma }}},$$

(9)

where $x$ is an objectively given probability.

The function contains a parameter $\mathsf{\gamma }$. If $\mathsf{\gamma }=1$, the function is linear, and this case corresponds to linear expected utility theory. The smaller $\mathsf{\gamma }$ is, the more distorted the subjective probability is. If $\mathsf{\gamma }$ is too small ($\mathsf{\gamma }<0.28),$ the function is not monotonically increasing anymore. Therefore $\mathsf{\gamma }$ must be equal to or greater than 0.28 theoretically. In the literature of prospect theory, it is reported that values of $\mathsf{\gamma }$ around 0.65 best fit experimental results [38,39,40]. We set $\mathsf{\gamma }$ to 0.65 in the following analysis. The shape of the function with this parameter value is shown in the left panel of Figure 1. According to this function, small objective probabilities are estimated to be greater than they are because of $w\left(x\right)>x$ for small $x$. Analyses with other values of $\mathsf{\gamma }$ can be found in the supporting material.

Thus, the matrix $W_i$ is interpreted as a subjective probability distribution on $M$ in the eyes of individuals with strategy $i$. Note that the probability distribution is not normalized; thus, the sum of subjective probabilities is not one in general because there is no experimental evidence that people are so rational that they normalize probabilities. In fact, the weighted function given by Equation (9) is asymmetric with respect to $x=1/2$, which implies that $w\left(x\right)+w\left(1-x\right)$ is not equal to one (see the left panel of Figure 1).

In the same way as in the case of probabilities, the payoff matrix $M$ is also distorted by a nonlinear function

$${\left(V\right)}_{mn}=v\left({\left(M\right)}_{mn}\right).$$

(10)

The function is called the value function, which is given by

$$v\left(x\right)=\{\begin{array}{c}{x}^{\alpha } \left(x\ge 0\right)\\ -\lambda {\left(-x\right)}^{\alpha } \left(x\le 0\right)\end{array},$$

(11)

where $x$ represents an objectively given outcome. The value function depends on two parameters $\mathsf{\alpha }$ and $\mathsf{\lambda }$. If both parameters are one, the function is linear, which corresponds with the linear expected utility theory. In the original literature on the prospect theory [38], $\mathsf{\alpha }=0.88$ and $\mathsf{\lambda }=2.25$ are typical values that best fit experimental data. We adopt these parameter values in the following analysis. The right panel in Figure 1 shows the value function with these parameter values. Parameter $\mathsf{\alpha }<1$ implies that the value function is concave and that a person obeying this function is risk-averse. Parameter $\mathsf{\lambda }>1$ means that a person following this function is more sensitive to a loss than a gain (“loss-averse” so to say).

The subjectively distorted payoff matrix $V$ does not depend on strategies. Note that since the function is nonlinear, the baseline of the payoff matrix or the reference point influences the results, which is different from the linear expected utility theory. We assume that the payoff obtained from the outcome $\left(4,4\right)$ in $M$, which is zero, is the reference point.

With these subjective probabilities and payoffs, the expected payoff is calculated by

$$P_i={\displaystyle \sum }_{m=1}^4{\displaystyle \sum }_{n=1}^4{\left(V\right)}_{mn}{\left(W_i\right)}_{mn}.$$

(12)

The strategy change is described by the ordinary replicator dynamics mentioned in the last subsection (Equation (7)).

3. Results

By calculating $P_{ij}$ for all $i$ and $j$, we find some basic characteristics of the model. Firstly, the contradictory strategy DP (strategy three) is dominated by DN. Since it never becomes evolutionarily stable, we eliminate the strategy from the analysis. We are interested in the time evolution of the vector $\left(x_1,x_2,x_4\right)$, which we call the state of the population.

Secondly, if the strength of punishment $\mathrm{s}$ is so large that it exceeds $\mathrm{c}/\mathsf{\epsilon }$, $P_2>P_4$ holds for the linear expected utility theory. This means that strategy two (CN) dominates strategy four (DN). In other words, the second-order dilemma does not occur even with the linear expected utility theory. We exclude these trivial situations and focus on the parameter region $\mathrm{s}<\frac{\mathrm{c}}{\mathsf{\epsilon }}\stackrel{\mathrm{def}}{=}{s}_{max}$, in which the second-order dilemma (thus the first-order dilemma) occurs in the framework of the linear expected utility theory. The addressed question is whether the second-order dilemma will be solved in this parameter region under the prospect theory.

In the following analysis, we set $c=r=1$ and $b=4$ to reduce the dimension of the parameter space. Therefore, the variable parameters are the strength of punishment $s$ and error rate $\mathsf{\epsilon }$.

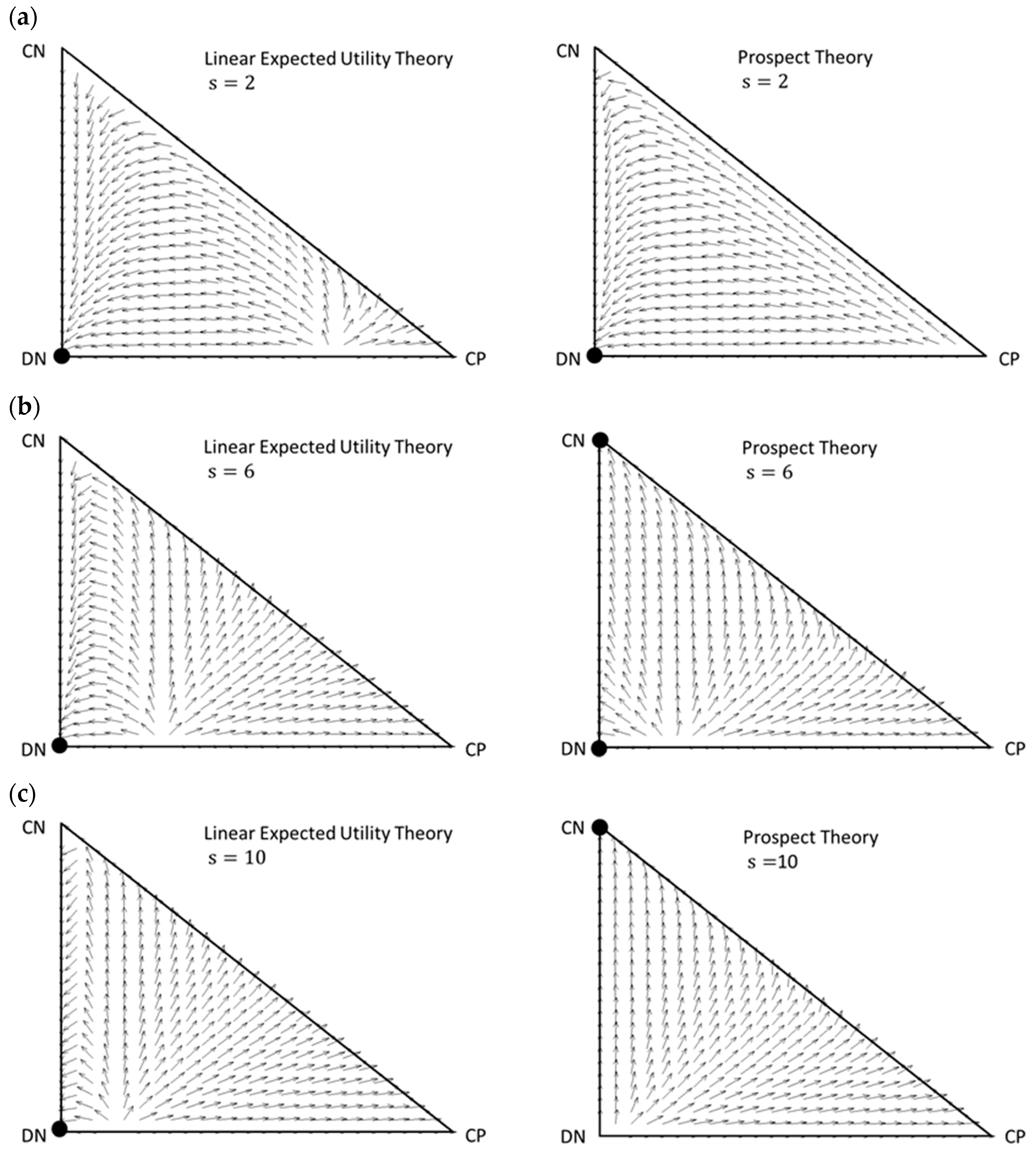
3.1. Vector Fields

We show vector fields generated by the respective replicator dynamics derived from the linear expected utility theory and prospect theory, and we compare them in Figure 2. The state space is the simplex $\left\{\left(x_1,x_2,x_4\right)\right|0\le x_1\le 1,0\le x_2\le 1,0\le x_4\le 1,x_1+x_2+x_4=1\}$, which will be represented as a rectangular triangle in Figure 2. The vertex CP corresponds to $\left(x_1,x_2,x_4\right)=\left(1,0,0\right)$, CN to $\left(0,1,0\right)$, and DN to $\left(0,0,1\right)$. The state of the population $\left(x_1,x_2,x_4\right)$ evolves along the vector fields in the state space. In the figure, stable fixed points are illustrated as solid circles. Note that the vector fields are normalized so that all vectors’ lengths are one. The strength of punishment is varied from $s=2$, $s=6$, to $s=10$ and we set the error rate at 0.05 as an example here. As we will see, we find qualitatively different outcomes (vector fields) with these three parameter sets. The same changes in outcomes occur if we set the error rate at other values (see Figure 3 in the next subsection in which both parameters $s$ and $\mathsf{\epsilon }$ are varied).

If the strength of the punishment is low (panel (a)), the defective state DN is the only stable fixed point in both cases. On the edge CP–CN, CN dominates, and on the edge CN–DN, DN dominates. The difference of the two theories is found in the edge DN–CP. In the case of the linear expected utility theory, there is an unstable fixed point in the edge, and the system is bistable. On the other hand, strategy DN dominates strategy CP in the edge in case of prospect theory.

This tendency does not change if the strength of punishment is increased in the framework of the linear expected utility theory (the left picture of panel (b)). However, in the case of the prospect theory (the right picture of panel (b)), two unstable fixed points emerge in the edge CN–DN and in the edge DN–CP. As a result, the system becomes bistable. Thus, depending on initial conditions, trajectories approach either the cooperative state CN or defective state DN.

When the strength of punishment is increased further, there is no qualitative change for the linear expected utility theory (the left picture of panel (c)). Still, DN is the unique stable fixed point. In the case of prospect theory, however, DN becomes unstable and CN is the only stable fixed point in the state space; all trajectories (except for trajectories starting in the edge DN–CP) approach the cooperative state CN.

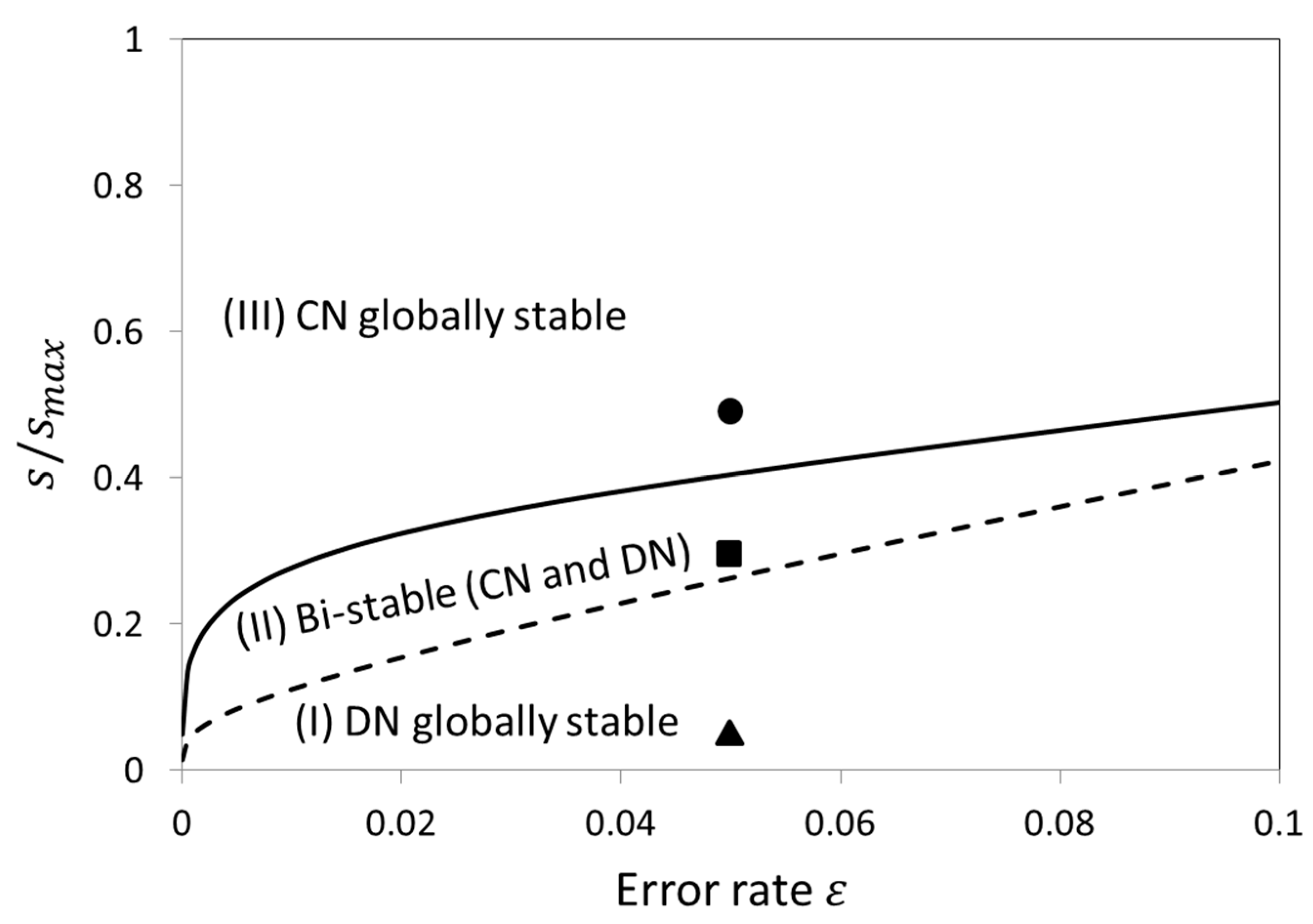
3.2. Stability Analysis of DN and CN

The above analysis clarified that the strength of punishment largely affects the system in the prospect theory. In fact, CN becomes “more” stable as the strength of punishment becomes large. Moreover, CP is always unstable regardless of the parameters. Taking these into account, we focus on the relation between CN and DN in the framework of prospect theory in this subsection. In order to investigate the effect of both parameters $s$ and $\mathsf{\epsilon }$, we look for conditions for the parameters with which CN can invade DN and/or vice versa.

To do this, we define $H_{ij} \left(i\in \left\{2,4\right\}, j\in \left\{2,4\right\}\right)$ as the expected payoff of individuals with strategy $i$ in the situation where they only encounter individuals with strategy $j$. This expected payoff is given by

$$H_{ij}={\displaystyle \sum }_{m=1}^4{\displaystyle \sum }_{n=1}^{4}v\left({\left(M\right)}_{mn}\right)w\left(E_{im}{E}_{jn}\right),$$

(13)

where $v$ and $w$ are the value function and the weighted function, respectively, ${\left(M\right)}_{mn}$ is the $\left(m,n\right)$-element of payoff matrix $M$, and $E_{im} \left(E_{jn}\right)$ is the m-th (n-th) element of the error vector ${\overrightarrow{E}}_i ({\overrightarrow{E}}_j)$. Or, we can obtain $H_{ij}$ by substituting $x_j=1$ into $P_i$ defined by Equation (12): $H_{ij}=P_i$ with $x_j=1$.

For instance, $H_{42}$ represents the expected payoff in the situation where individuals with the DN strategy only encounter those with the CN strategy, and $H_{24}$ is the expected payoff in the situation where individuals with the CN strategy only encounter those with the DN strategy.

Then, the inequality $H_{22}<H_{42}$ implies that a DN individual can invade into the population consisting of CN individuals. The inequality $H_{44}>H_{24}$ means that the population consisting of DN individuals cannot be invaded into by a CN individual. If both inequalities hold, which corresponds to the right panel of Figure 2a), we see that DN is globally stable. Likewise, if both inequalities $H_{22}>H_{42}$ and $H_{44}<H_{24}$ are true, CN is globally stable, which corresponds to the right panel of Figure 2c. If both $H_{22}>H_{42}$ and $H_{44}>H_{24}$ hold, DN cannot invade into CN and vice versa. Therefore, the system is bistable (The right panel of Figure 2b). We look for regions in the parameter space $\left(\mathsf{\epsilon },\mathrm{s}\right)$ in which the above inequalities hold.

The result is shown in Figure 3. Note that the strength of punishment $s$ is normalized; thus, the vertical axis represents the value of $s/s_{max}$. If this parameter value exceeds 1, the second-order dilemma is resolved even in the case of the linear expected utility theory, and CN is globally stable. This means that in the parameter space given in the figure, the second-order dilemma occurs in the case of the linear expected utility theory; thus, DN is globally stable. The question is where the prospect theory can resolve the dilemma in this parameter region.

In the framework of the prospect theory, regardless of parameter $\mathsf{\epsilon }$, DN is globally stable with small $\mathrm{s}$ (region (I)). In this region there is no qualitative difference from the linear expected utility theory. The solid triangle illustrated in this region in the figure corresponds to the parameter set $\left(\mathsf{\epsilon }=0.05,s=1\right)$ used to generate Figure 2a. However, increasing the strength of punishment gradually destabilizes DN and alternatively stabilizes CN in the case of the prospect theory. As a result, the system becomes bistable (region (II)) with moderate $\mathsf{\epsilon }$. The solid square in this region corresponds to $\left(\mathsf{\epsilon }=0.05,s=6\right)$, which was used to generate Figure 2b. With high $\mathsf{\epsilon }$, CN becomes able to invade DN populations, and CN becomes globally stable. We also see that the values of $\frac{s}{s_{max}}$ that represent boundaries between the regions (illustrated by solid and dashed curves in the figure) become large as functions of error rate $\mathsf{\epsilon }$. The solid circle put above the boundary in this region corresponds to $\left(\mathsf{\epsilon }=0.05,s=10\right)$ used for Figure 2c.

The boundary drawn by the dashed curve in Figure 3 was found by numerically solving the equation $H_{22}=H_{42}$ with respect to $s$ for $\mathsf{\epsilon }={\epsilon }_{min},{\epsilon }_{min}+\delta ,{\epsilon }_{min}+2\delta ,\cdots ,{\epsilon }_{max}$, where ${\epsilon }_{min}={10}^{-5}$, ${\epsilon }_{min}=0.1$, and $\delta =\left({\epsilon }_{max}-{\epsilon }_{min}\right)/200$. Note that we excluded $\mathsf{\epsilon }=0$, since cooperation cannot evolve even under the prospect theory in this case. The inequality $H_{22}<H_{42}$ ($H_{22}>H_{42})$ holds under (above) this boundary. In order to find the boundary illustrated by the solid curve in Figure 3, the equation $H_{24}=H_{44}$ with respect to $s$ was solved. The inequality $H_{24}<H_{44}$ ($H_{24}>H_{44})$ holds under (above) this boundary.

As mentioned above, we used a specific set of values for parameters $\mathsf{\gamma },\mathsf{\alpha }$, and $\mathsf{\lambda }$ to produce Figure 3. We also generated figures with different parameter values, which are presented in the supporting material. No qualitative differences are found when the values of these parameters are varied. Nevertheless, we see that stable regions become larger as values of parameters $\mathsf{\gamma }$ and $\mathsf{\alpha }$ are smaller and that the parameter $\mathsf{\lambda }$ does not affect the results very much. This indicates that the system becomes more easily stable as the weighted function, and the value function gains “more nonlinearity”.

4. Discussion

We explored the effects of cognitive distortions described by the prospect theory in the context of the evolution of cooperation by peer punishment. Our main finding is that cognitive distortions make it possible for cooperation to evolve even in the parameter region in which cooperation cannot be achieved in the framework of the linear expected utility theory. We also found that the cooperative punitive strategy (CP) is dominated by cooperative nonpunitive strategy (CN). Thus, not CP but CN plays an essential role to sustain cooperation.

The CN players basically do not punish others, but they actually punish with a small probability due to error. This erroneous punishment effectively drives cooperation as far as the prospect theory is utilized. The same erroneous punishment cannot promote cooperation when the linear expected utility theory is adopted.

A key reason for why the error has a large impact on the population in the case of the prospect theory is found in the weighted function $w$ and the value function $v$. According to the weighted function, individuals estimate small probabilities greater than they really are, and according to the value function, they assess the loss of benefit more than it actually is. Therefore, agents described by the prospect theory feel that punishment is more frequent and harsher than they really are.

In other words, individuals described by prospect theory are more sensitive to peer punishment than those described by the linear expected theory. Alternatively, we could say that individuals described by the prospect theory have the ability to imagine punishment, and this kind of imagination induces the fear to be punished. Such individuals who are afraid of punishment, even if it seldom occurs due to error, choose to cooperate to avoid being punished.

In spite of the findings mentioned so far, we have to remark that there remain several issues relevant for the coevolution of cooperation and peer punishment. The model studied in this present research especially has many limitations, which offers some tasks for future research.

Here, we mention the following two issues: the emergence problem and antisocial punishment. The emergence problem relates to the question about who starts giving punishment for the first time in the population [28]. Even in pool punishment, it is not easy to start costly punishment successfully, since punishing right and left in a sea of defectors imposes too much effort and cost on punishers. Several studies have proposed additional mechanisms or assumptions to overcome this emergence problem [42,43,44,45,46]. A similar problem holds for the peer punishment studied in this paper. We assumed that individuals punish others due to an error with a small probability. That is, individuals have an idea that they have the option to punish others from the beginning, even though the punishing activities are performed unintentionally. Under this assumption, we analyzed differences between the linear expected utility theory and the prospect theory.

Moreover, we assumed that only defectors are punished, and there is no chance for cooperators to be punished. Allowing punishment against prosocial behavior, such as cooperative actions, can offset the payoff advantage of the cooperators over free-riding. If antisocial punishment is included into our model, individuals afraid of counterpunishment might stop choosing cooperation. This problem caused by antisocial punishment occurs not only in our model, but is widely recognized as a serious issue in the literature of evolution of cooperation with punishment [47,48,49].

On the other hand, if we turn our attention to indirect reciprocity, which is known to be a powerful mechanism for the evolution of cooperation, the evolution of social norms is extensively investigated [50,51,52,53,54,55]. Social norms are defined as views on what is “good” or “bad”, and indirect reciprocity works in the way that bad individuals are discriminated in the population (bad individuals are not supported). However, there are many possibilities for the definitions of what is good or bad (thus social norms), and one of the main tasks in indirect reciprocity is to search for evolutionarily stable social norms that can maintain cooperation.

From the viewpoint of indirect reciprocity, the assumption that only defectors are punished is equivalent to assuming that the population has the unique social norm that prescribes to assessments of defectors as bad (and bad individuals are punished). This type of social norm is named “Scoring” in the literature. Then, punishing cooperators (antisocial punishment) is equivalent to the social norm that regards cooperators as bad (“Antiscoring”). However, these are just a few examples of social norms. It is possible to consider other types of social norms, for instance, a norm that regards those as bad who cooperate with bad individuals.

A recent study using agent-based simulations revealed that prosocial norms such as “Scoring” can evolve, and antisocial norms such as “Antiscoring” become extinct in the melting pot of social norms if not a few but diverse norms coexist in the population [56]. In the model of this study, bad individuals are not punished, but they are not given help in the population. We can modify the model so that bad individuals are punished. Whether prosocial norms can also evolve in this modified model and thus whether the problem of antisocial punishment is solved is interesting and necessary research yet to be done. Recently, a paper was published which studies the coevolution of indirect reciprocity and punishment [57].

In extending our model with many social norms, agent-based simulations could be useful rather than an analytical approach taken in this paper. In this paper, we have discussed the evolution of cooperation in an analytical way under the assumption that there is a unique social norm in the population, and we have provided the first step to study the effects of cognitive distortions on the evolution of cooperation via peer punishment.