Local Interaction on Random Graphs ^†

Abstract

We analyze dynamic local interaction in population games where the local interaction structure (modeled as a graph) can change over time: A stochastic process generates a random sequence of graphs. This contrasts with models where the initial interaction structure (represented by a deterministic graph or the realization of a random graph) cannot change over time.

1. Introduction

Interaction in an economic, social, political or computational context is often local in the sense that it consists of pairwise interactions between neighbors. Since the early 90s, a sizeable literature on pairwise interactions between neighbors on a graph has emerged. For pioneering contributions to this literature, see Anderlini and Ianni [1], Berninghaus and Schwalbe [2,3], Blume [4,5], Ellison [6], Goyal and Janssen [7], among others. The main feature of the models is that direct interaction of an agent is confined to his neighbors, frequently but not necessarily a small group, while indirect interaction via a chain of neighbors may occur between any pair of agents. As a rule, it has been assumed that the underlying interaction structure (network, graph) does not change over time. This assumption captures the case of rather rigid social ties.

However, social ties are not always rigid. First, they may change because of stochastic shocks. Examples of the latter are random encounters or noisy communication. Second, social ties may be formed or severed as the consequence of deliberate actions taken by individuals. See the literature on strategic network formation in the tradition of Jackson and Wolinsky [8] and Bala and Goyal [9], which is surveyed in Jackson [10,11] and Goyal [12], respectively. Third, network design and network utilization may go hand in hand. See the specific contributions by Droste, Gilles and Johnson [13], Jackson and Watts [14], Goyal and Vega-Redondo [15], Hojman and Szeidl [16], and Ehrhardt, Marsili and Vega-Redondo [17].

Here we explore the first possibility. The interaction structure is exogenous and random. It changes over time, following an i.i.d. process. This assumption is motivated by the aim to analyze the effects of extremely volatile social ties which may be disrupted or formed at any time in an unpredictable way. The assumption allows us to directly compare the effects of two polar cases—fixed versus random interaction structure, rigid versus loose social ties—without altering the local interaction model in other respects. The assumption of an exogenous, randomly changing interaction structure also offers an interesting contrast to models where both network formation and network utilization are endogenous. The game evolves in discrete time and has the following particular features:

■ Base or constituent game. In every period, the players play a local interaction or spatial game. Every time, each player has to make a binary choice between two actions, X and Y, and receives the sum of his payoffs from interacting once with each of his neighbors. Payoffs from each pairwise interaction are based on the same symmetric $2\times 2$ coordination game, called base or constituent game in the literature. Consequently, players are conformists: If all his neighbors play X, a player prefers to play X; if all the neighbors play Y, he prefers Y.

■ Interaction structure. An interaction structure describes who interacts with whom. It specifies for each agent a set of neighbors, the set of agents with whom the agent interacts. In the sequel, an “interaction structure” is modeled as an undirected finite graph whose vertices or nodes are the members of the player population. Two players are neighbors, if they form an edge of the graph. Global interaction prevails if any two players are neighbors. Otherwise, interaction is local. In principle, one can generalize and replace the graph by a weighted graph. But we refrain from doing so in the present paper and rather generalize in a different direction, allowing for random graphs.

■ Dynamics. The model has two dynamic elements. On the one hand, the interaction structure (modeled as a graph) can change over time: A stochastic process generates a random sequence of graphs. This contrasts with models where the initial interaction structure (represented by a deterministic graph or the realization of a random graph) cannot change over time. In the setting of Blume [5] and Berninghaus and Schwalbe [2,3], the same exogenously given interaction structure (graph) is present in all periods. In the model of López-Pintado [18], an interaction structure (network, graph) is chosen at random prior to the game and does not change throughout a particular play of the game.

On the other hand, we consider myopic best response dynamics where at each time, one or every player chooses a (static) best response against the empirical distribution of the last strategies played by his neighbors. This constitutes rational behavior impaired by myopia. Myopia in the temporal sense means that the player is not forward looking, does not take into account that other players might be changing their strategies. Hence, unlike the standard treatment of repeated games, our analysis is not concerned with perfectly rational outcomes such as the perfect equilibria of the repeated game. Myopia in the spatial sense means that the player is influenced only by his local environment, the previous choices of his neighbors. Deterministic best response dynamics of local interaction games has been pioneered by Blume [5] and Berninghaus and Schwalbe [2,3].

Unless specified otherwise, we shall proceed under the assumption of simultaneous updating. An important exception is asynchronous updating in subsection 3.4.

■ Contagion. Contagion is said to occur if one action can spread by a contact effect from a particular group of agents, typically a small group, to the entire population. Our definition of contagion, which requires that an action, trait, defect, virus, etc. spreads to the entire population, has been used in computer science [Flocchini et al. [19,20], Peleg [21,22]], economics [Morris [23], Lee and Valentinyi [24]], and game theory [Berninghaus et al. [25], Durieu et al. [26]]. Different definitions of contagion have been proposed and are appealing in certain contexts. In a social context, our definition rules out the long-run coexistence of conventions. A less demanding definition of contagion would require that an action spreads to a significant proportion of the player population and remains there forever. This definition—which allows for the long-run coexistence of conventions—is akin to that adopted by López-Pintado [18] in a social interaction setting and by Pastor-Satorrás and Vespignani [27] in an epidemiological model.

■ Digression on pairwise matching. For the widely used pairwise matching model, where each player has exactly one neighbor, the analysis is straightforward and brief. With fixed pairwise matchings, two players in a dyad (matched pair of players) keep playing with each other forever, which as a rule, prohibits contagion. With simultaneous updating and fixed pairwise matching, if the two players in a dyad start out with different actions, then each will alternate his action over time. If they start out with the same action, then both will repeat that action forever. Thus, the myopic best response dynamics finds itself either in a 2-cycle or in a steady state from the very beginning. In the latter case, players in a dyad play the same action, but actions may differ across dyads. With asynchronous updating (by a randomly selected player) and fixed pairwise matchings, convergence to a steady state occurs with probability one. In a steady state, players in a dyad play the same action while actions may differ across dyads. It follows that fixed pairwise matchings are unsuitable for the study of contagion. To enable contagion, one needs a (randomly) changing interaction structure or a connected graph (interaction structure) or both.

Next, let us briefly consider random matching.1 With random pairwise matching and simultaneous updating, the number of players who choose X remains constant over time, whereas the set of players who choose X changes randomly. Hence random matching does not further contagion. With random pairwise matching and asynchronous updating, with probability one, contagion (with respect to X or with respect to Y) occurs.2 Hence random matching does further contagion in this case. However, this special case does not allow to draw general conclusions. With a different random graph model and asynchronous updating, random reformation of the interaction structure can make contagion less likely; see subsection 3.4. Furthermore, it turns out that risk dominance proves irrelevant in this special case whereas it does affect contagion in general.

■ Main results. Our subsequent analysis is focused on models with two kinds of random graphs. In the first type of models, the support of the random graph consists of regular graphs, where all players have the same number of neighbors. In the second type of models, the underlying random graph is binomial. Our general observations GO1–GO4 below and the further insights gained in Section 3 and Section 4 suggest that the study of dynamic local interaction on a random sequence of graphs different from pairwise matchings does not only offer a descriptive extension, but also contributes to a better understanding of contagion. Before we report more detailed results, let us make the general observations which are more or less obvious yet instructive:

GO1 

Large neighborhoods can impede contagion with respect to an action that is initially played by few players. This is a consequence of conditions (3) and (4) given below.

GO2 

(More) risk dominance of an action works in favor of contagion with respect to that action. This is also a consequence of conditions (3) and (4) given below.

GO3 

Random reformation of the interaction structure can disrupt cycles and facilitate clusters, which may induces contagion with respect to the risk dominant action.

GO4 

Random reformation of the interaction structure can also break up clusters, which makes contagion less likely.

GO3 and GO4 describe opposite effects. Our analysis will reveal that either one can dominate under particular model specifications.

Among regular graphs, circular graphs are of special interest. Presumably, circular graphs are the local interaction structures most frequently studied in game theory and economics. In such a graph, the players can be arranged in a circle so that each player has one neighbor to the left and one neighbor to the right. We find that if the support of the underlying random graph consists of all circular graphs, at least one player chose the risk dominant action initially, and updating is simultaneous, then contagion with respect to the risk dominant action occurs. In contrast, with simultaneous updating, an even number of players, and a fixed circular graph, convergence to a two-cycle can occur. We extend the analysis to so-called OR networks à la Goles and Hernández [30] and to arbitrary regular graphs where each player has more than two neighbors. We obtain less conclusive results in the latter case.

In a binomial random graph, also known as an Erdős-Rényi random graph, each possible edge is included independently of others with a given probability, which is the same for all edges. This is the random graph model most commonly studied in mathematics and statistics, sometimes even referred to as “the random graph.” In a dynamic context it reflects best the idea of loose social ties. We find that when the evolution of the interaction structure is based on a binomial random graph, then with probability one, contagion (either with respect to action X or with respect to action Y) occurs. We further show that if at least one player chooses the risk dominant action initially, then with positive probability, all players choose the risk dominant action in period 2. However, given a limited number of players choosing an action initially, the probability that eventually all players choose the alternative action approaches one as the population size goes to infinity. Thus, if just a few players choose the risk dominant action initially, then with positive probability, contagion with respect to the risk dominant action occurs very rapidly; but in a large population, it is much more likely that contagion with respect to the alternative action occurs.

In the next section, we present the general model. In Section 3, we consider interaction on regular graphs, with a special emphasis on circular graphs and OR networks. In Section 4, we study interaction on binomial graphs. In Section 5, we offer concluding remarks.

2. Preliminaries

We consider a dynamic game that evolves in discrete time, with periods $t=0,1,2,\dots$. The game is played by a finite population of $N\ge 3$ players $i\in I=\{1,\dots ,N\}$. In each period t each player i is matched with every player in his neighborhood $V_i\left(t\right)$ to play a 2-person coordination game.

The primitive data of the model are the player set I, a binary individual action set $\{X,Y\}$, payoffs for the 2-player coordination game, a stochastic process $\tilde{V}\left(0\right),\tilde{V}\left(1\right),\dots$, generating sequences of interaction structures (graphs, networks) $V\left(0\right),V\left(1\right),\dots$, and an updating rule.

2.1. Base or Constituent Game

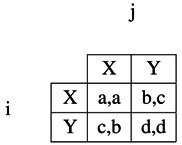
In each period, each player i chooses an action $s_i\in S_i=\{X,Y\}$. The binary action set is the same for all players at all times. $S={\{X,Y\}}^N$ is the set of all action profiles. If players i and j interact once, i chooses action $s_i$ and j chooses action $s_j$, then player i receives payoff $\pi (s_i,s_j)$ and player j receives payoff $\pi (s_j,s_i)$ from their pairwise interaction. The pairwise interaction payoff function $\pi :{\{X,Y\}}^2\to \mathbb{R}$ applies to all players at all times, where the first argument is always the action taken by the player, say i, whose payoff is to be determined while the second argument is the action of the particular player j with whom i interacts. If i and j, $i\ne j$, is an arbitrary pair of players, then their one time pairwise interaction is described by a symmetric $2\times 2$ game, the base or constituent game. In case i is treated as row player and j as column player, the base game assumes the matrix form

where $a=\pi (X,X),b=\pi (X,Y),c=\pi (Y,X),d=\pi (Y,Y)$. We assume that the base game is a coordination game, that is $a>c$ and $d>b$. In that case, the Nash equilibrium $(X,X)$ is payoff dominant if $a>d$ whereas $(Y,Y)$ is payoff dominant if $a<d$. The Nash equilibrium $(X,X)$ or the action X is risk dominant if $a-c>d-b$. $(Y,Y)$ or Y is risk dominant if $a-c<d-b$.

2.2. Interaction Structures

An interaction structure describes who interacts with whom. This can simply be achieved by listing, for each player $i\in I$, the group $V_i\subseteq I\backslash \left\{i\right\}$ of players with whom i interacts. Now a binary relation $V\subseteq I\times I$ can be equivalently represented by its sections $V_i\equiv \{j\in I|(i,j)\in V\},i\in I$. The pair $(I,V)$ is also called a graph or network with I as its set of nodes and V as the set of edges. Thus listing who interacts with whom amounts to fixing a graph. It often proves convenient to refer to V rather than $(I,V)$ as the graph.

We only consider graphs which have no loops [V is irreflexive: $(i,i)\notin V$ for $i\in I$] and are undirected [V is symmetric: $(i,j)\in V\Rightarrow (j,i)\in V$ or, equivalently, $j\in V_i\iff i\in V_j$]. Let $\mathbb{V}$ denote the set of all such “graphs" V. The elements $V\in \mathbb{V}$ are interpreted as interaction structures, describing who interacts with whom: If V is the prevailing interaction structure and $i,j\in I$, then i can interact with j and vice versa if and only if $j\in V_i$ and $i\in V_j$. In particular, $V\left(t\right)$ denotes the interaction structure existing at time t and the section $V_i\left(t\right)$ is the set of neighbors or partners with whom player i is matched and interacts in period t.

Instead of representing an undirected graph as a symmetric binary relation, it is often advantageous to resort to an alternative representation: Edges are unordered pairs $\{i,j\}$. Hence, $j\in V_i$ and $i\in V_j$ iff $\{i,j\}\in V$. We shall resort to the latter representation from now on.

2.3. Special Classes of Graphs

Our analysis in Section 3 is focused on circular graphs or interaction structures. Here we introduce circular graphs and related graph-theoretic concepts.

For a player or node $i\in I$ and a graph $V\in \mathbb{V}$, the degree of i in V, $d_i\left(V\right)$, is defined as the number of i’s neighbors in V: $d_i\left(V\right)\equiv \left|V_i\right|$. Let n be a nonnegative integer. The graph V is n-regular, if each player has n neighbors in V: $d_i\left(V\right)=n$ for all $i\in I$. Let $\mathcal{R}\left(n\right)$ denote the class of all n-regular graphs in $\mathbb{V}$.

We further need the concept of a connected graph. For $V\in \mathbb{V}$, $\ell \in \mathbb{N}$, and $i,j\in I$ with $i\ne j$, a path of length ℓ in V from player i to j is a finite sequence $i_0,i_1,\dots ,i_{\ell }$ such that $i_0=i$, $i_{\ell }=j$, and $\{i_k,i_{k+1}\}\in V$ for $k=0,\dots ,\ell -1$. V is connected if for any two different elements i and j of I, there exists a path in V from i to j. A subset C of I is called a connected component of V, if for any two different elements i and j of C, there exists a path in V from i to j and there is no strict superset of C for which this holds true. I is the only connected component of V if and only if $V$is connected. Let ${\mathcal{R}}^c\left(n\right)$ denote the class of all connected n-regular graphs in $\mathbb{V}$.

Circular graphs and especially 2-circular graphs conceivably are the local interaction structures most frequently studied in game theory and economics. In such a graph, the players can be arranged in a circle so that each player has an equal number of neighbors to the left and to the right. Let us first consider 2-circular graphs where the players can be arranged in a circle so that each player has one neighbor to the left and one neighbor to the right. In applications, the term “circular city model” is sometimes used for a 2-circular graph. Formally, such a graph assumes the form $V^{\beta }$ with sections $V_i^{\beta }=\{j\in I|\beta \left(j\right)=\beta \left(i\right)\pm 1\mathrm{modulo}N\}$ where β is a permutation of I. In $V^{\beta }$, we say that j is the left neighbor of i with respect to β if $\beta \left(j\right)=\beta \left(i\right)-1modN$ and j is the right neighbor of i with respect to β if $\beta \left(j\right)=\beta \left(i\right)+1modN$. Notice that there exist permutations $\alpha \ne \beta$ such that $V^{\alpha }=V^{\beta }$, but j is a left neighbor of i with respect to α and a right neighbor of i with respect to β. Let $\mathcal{C}\left(2\right)$ denote the class of 2-circular graphs on I. It is easy to see that ${\mathcal{R}}^c\left(2\right)=\mathcal{C}\left(2\right)$.

For a permutation β of I, ${\beta }^{-1}$ denotes the inverse of β. Observe that for $i,j\in I$, $i\ne j$, by definition ${\beta }^{-1}\left(\beta \left(i\right)\right)=i$ and ${\beta }^{-1}\left(\beta \left(j\right)\right)=j$; hence, $\beta \left(j\right)\in V_{\beta \left(i\right)}^{{\beta }^{-1}}$ if and only if $j=i\pm 1modN$. For instance, $\beta \left(1\right)$ and $\beta \left(2\right)$ are neighbors in $V^{{\beta }^{-1}}$.

In analogy to $\mathcal{C}\left(2\right)$, we can define the set $\mathcal{C}\left(n\right)$ of n-circular graphs for any even number n with $2\le n\le N-1$. In an n-circular graph, the players can be arranged in a circle so that each player has $n/2$ left neighbors and $n/2$ right neighbors (with respect to a permutation β of I that defines the graph). Let $\mathcal{C}\left(n\right)$ denote the class of n-circular graphs on I. Then $\mathcal{C}\left(n\right)\subseteq {\mathcal{R}}^c\left(n\right)$.

2.4. Dynamics

Let $s_i\left(t\right)\in S_i$ denote the action chosen by player i in period t. Further let $x\left(t\right)=\left|\right\{i\in I:s_i\left(t\right)=X\left\}\right|$ denote the number of players choosing action X and $s\left(t\right)=(s_1\left(t\right),\dots ,s_N\left(t\right))$ denote the action profile in period t.

We are interested in properties of the sequences $s\left(t\right),t=0,1,\dots$, and $x\left(t\right),t=0,1,\dots$, which of course depend on how the sequences are generated. In contrast to most models of biological evolution, models of economic and social evolution have explored the assumption that a player can only interact with a subset of the population, his neighborhood or reference group. See Berninghaus and Schwalbe [2,3], Blume [4,5], and references therein and thereafter. Moreover, it has been typically assumed that the exogenously given interaction structure is totally rigid over time: $V_i\left(t\right)=V_i\left(0\right)$ for all i and t. While many socio-economic relations are fairly stable, others are not or emerge only over time, and few are totally stable. Here we keep the concept of an interaction structure, but allow for the possibility that the structure changes over time. In principle, there could be inertia in the system so that only a few edges are added or deleted from one period to the next. The interaction structure of the next period could depend on the current interaction structure as well as the current action profile. Here we ignore these possibilities and focus on the direct opposite of a totally rigid interaction structure. We assume a stochastic process of i.i.d. random variables $\tilde{V}\left(t\right):\Omega \to \mathcal{V},t=0,1,\dots$, defined on an underlying probability space $(\Omega ,\mathcal{F},\mathcal{P})$ and assuming values in a subset $\mathcal{V}$ of $\mathbb{V}$. In $(\Omega ,\mathcal{F},\mathcal{P})$, Ω is a set of states of nature, $\mathcal{F}$ is a σ-field or σ-algebra of subsets of Ω and $\mathcal{P}$ is a σ-additive probability measure on $\mathcal{F}$. The realizations of the process $\tilde{V}\left(0\right),\tilde{V}\left(1\right),\dots$ constitute sequences of interaction structures (graphs, networks) $V\left(0\right),V\left(1\right),\dots$. The independence assumption means that past connections do not influence current or future connections and, thus, captures the idea that social connections may not be rigid at all.

Given an action profile $s=(s_1,\dots ,s_N)\in S$ and an interaction structure V in a particular period, player i receives an aggregate payoff

$$u_i[s;V]=\sum _{j\in V_i}\pi (s_i,s_j)$$

(1)

from pairwise interactions in that period. The dynamic game starts with an initial state $s\left(0\right)\in S$ and an initial interaction structure, $V\left(0\right)$. In every period $t\ge 1$, given the realization $V\left(t\right)$ of $\tilde{V}\left(t\right)$, players update their strategies, following a “myopic best response rule": Player i chooses a best response against the previous play of his current neighbors,

$$s_i\left(t\right)\in arg\underset{s_i\in S_i}{max}{u}_i[(s_i,s_{-i}(t-1));V\left(t\right)]$$

(2)

Ties are broken in favor of X unless a player has no neighbors. In some realizations of some random graph, a player may end up neighborless, $V_i\left(t\right)=\varnothing$, in which case we assume that the player exhibits inertia: $s_i\left(t\right)=s_i(t-1)$. Simultaneous updating means that all players follow the myopic best response rule at all times.

Next we translate the myopic best response rule (2) into the more manageable threshold criterion (3). To this end, let $n_i\left(t\right)=\left|V_i\left(t\right)\right|$ be the number of i’s neighbors and $x_i(t-1)=\left|\{j\in V_i\left(t\right):s_j(t-1)=X\}\right|$ be the number of i’s neighbors who chose X last period. Moreover, set $\vartheta =(d-b)/(a-c+d-b)$. Then i with $V_i\left(t\right)\ne \varnothing$ will choose X this period if

$$x_i(t-1)\ge \vartheta ·n_i\left(t\right)$$

(3)

Accordingly, player i with $V_i\left(t\right)\ne \varnothing$ will choose Y in period t if

$$x_i(t-1)<\vartheta ·n_i\left(t\right)$$

(4)

López-Pintado [18] calls the parameter ϑ the “degree of risk dominance” of action X. X is risk dominant if $\vartheta <1/2$. X becomes more risk dominant when ϑ becomes smaller. That means, ceteris paribus, the more risk dominant is action X, the more likely occurs contagion with respect to action X.

On purely descriptive grounds, one can envisage that an updating player maximizes against previous play of previous neighbors, that is $s_i\left(t\right)$ maximizes $u_i[(s_i,s_{-i}(t-1));V(t-1)]$. Yet given the i.i.d. assumption on the process $\tilde{V}\left(0\right),\tilde{V}\left(1\right),\dots$, this descriptive difference merely translates into a notational difference and not a material one. Namely, let $\widehat{s}\left(0\right),\widehat{s}\left(1\right),\dots$ and $\widehat{x}\left(0\right),\widehat{x}\left(1\right),\dots$ denote the sequences generated with the differently timed updating. Since $\mathsf{Prob}\left(V\right(t)=V)=\mathsf{Prob}\left(V\right(t-1)=V)$ for any $V\in \mathcal{V}$ and $t=1,2,\dots$, the sequences $s\left(0\right),s\left(1\right),\dots$ and $\widehat{s}\left(0\right)=s\left(0\right),\widehat{s}\left(1\right),\dots$ are realizations of two dynamic processes with identical distributions.

2.5. Long-Run Behavior and Contagion

We examine the long-run behavior of the path $s\left(0\right),s\left(1\right),\dots$. Contagion (with respect to action X) occurs from an initial subset $I_0$ of I, if $s_i\left(0\right)=X$ for $i\in I_0$, $s_i\left(0\right)=Y$ for $i\notin I_0$, and there exists $T\in \mathbb{N}$ such that $s_i\left(t\right)=X$ for all $i\in I$ and $t\ge T$ or, equivalently, $x\left(t\right)=N$ for all $t\ge T$. Contagion with respect to action Y is defined in an analogous way. Contagion is especially forceful, if an action spreads to the entire population starting from a small group of players.

In the case of a fixed deterministic interaction structure, that is $V\in \mathbb{V}$ such that $V\left(t\right)=V$ for $t=1,2,\dots$, one obtains that $s\left(t\right)$ converges either to a fixed point (steady state) or to a two-cycle; see Berninghaus and Schwalbe [3, Theorem 2], Goles [31], Goles and Olivos [32], Goles and Martinez [33]. Notice that convergence to a steady state does not necessarily imply occurrence of contagion. Berninghaus and Schwalbe [3] give an example of a discrete $6\times 6$ torus (lattice with von Neumann neighborhoods) and a steady state where both conventions or actions, X and Y, coexist.

In general, the path $s\left(0\right),s\left(1\right),\dots$ generated by simultaneous myopic best response updating is random when the sequence of interaction structures is random. There can be other sources of randomness in models of adaptive play: With asynchronous updating, there may be a random selection of the player who updates. Players may play stochastically perturbed best responses caused by errors, trembles, or mutations. A player may respond to a random sample of his neighbors.

3. Interaction on Regular Graphs

The fact that the interaction structure is newly formed each period can drastically affect contagion, even if the same network architecture is realized every period. The difference in outcomes between a fixed deterministic interaction structure and a random sequence of interaction structures becomes evident in the case of 2-circular graphs (2-regular connected graphs) studied in the next subsection.

3.1. Interaction on 2-Circular Graphs

For the sake of comparison, let us briefly reconsider the adjustment dynamics in the case of a fixed deterministic interaction structure of the form $V^{\beta }$, with β a permutation of I. Let $k\in I$, $s_k\left(0\right)=X$ and $s_i\left(0\right)=Y$ for all $i\ne k$. If action Y is risk dominant then in one step contagion with respect to action Y occurs. If action X is risk dominant and N is even, then convergence to a two-cycle occurs. If action X is risk dominant and N is odd, then contagion with respect to action X occurs.

Let us next consider i.i.d. random variables $\tilde{V}\left(t\right):\Omega \to \mathcal{C}\left(2\right),t=0,1,\dots$, so that $\mathcal{V}=\mathcal{C}\left(2\right)=\left\{V^{\beta }\right|\beta a\mathrm{permutation} \mathrm{of}I\}$ and each $\tilde{V}\left(t\right)$ is uniformly distributed on $\mathcal{C}\left(2\right)$. Now again, if $k\in I$, $s_k\left(0\right)=X$, $s_i\left(0\right)=Y$ for all $i\ne k$, and action Y is risk dominant, then in one step contagion with respect to action Y occurs. However, if action X is risk dominant, contagion with respect to action X occurs regardless of $N\ge 3$:

Proposition 1 

Suppose each $\tilde{V}\left(t\right)$ is uniformly distributed on the set of 2-circular graphs. If X is risk dominant and $x\left(0\right)>0$, then with probability one, the entire population will end up choosing X in finite time.

proof. Let X be risk dominant. Notice that then on a 2-circular graph, a player chooses X if at least one of his neighbors has chosen X. First we show

Claim 1: 

$x\left(t\right)$ is nondecreasing in t.

Namely, let $V\left(t\right)=V^{\beta }$ for some permutation β. If $s_i(t-1)=X$ and $s_i\left(t\right)=Y$, then $s_j(t-1)=Y$ and $s_j\left(t\right)=X$ where j is i’s right-hand neighbor with respect to β. Hence there are at least as many switches from Y to X as there are from X to Y, which shows the claim. Next we show

Claim 2: 

If $0<x(t-1)<N$ then $x\left(t\right)>x(t-1)$with probability $\ge 1/\left|\mathcal{C}\right(2\left)\right|$.

For if $x(t-1)=1$, $s_i(t-1)=X$, and $V\left(t\right)=V^{\beta }$, then i’s left and right neighbors with respect to β choose X in period t. If $1<x(t-1)<N$ then with probability at least $1/\left|\mathcal{C}\right(2\left)\right|$, $V\left(t\right)$ assumes the form $V^{{\beta }^{-1}}$ such that

$$\begin{array}{l}{s}_{\beta \left(1\right)}(t-1),s_{\beta \left(2\right)}(t-1),\dots ,s_{\beta \left(N\right)}(t-1)\mathrm{equals}\\ XX\dots XY\mathrm{or}YX\dots XY\mathrm{or}YX\dots XYY\mathrm{or}\\ Y\underset{x(t-1)\mathrm{times}}{\underbrace{X\dots X}}YY\dots Y,\mathrm{respectively},\end{array}$$

and, therefore,

$$\begin{array}{l}{s}_{\beta \left(1\right)}\left(t\right),s_{\beta \left(2\right)}\left(t\right),\dots ,s_{\beta \left(N\right)}\left(t\right)\mathrm{equals}\\ XX\dots XX\mathrm{or}XX\dots XX\mathrm{or}XX\dots XXY\mathrm{or}\\ \underset{x(t-1)+2\mathrm{times}}{\underbrace{XX\dots XX}}Y\dots Y,\mathrm{respectively}.\end{array}$$

This shows the claim. The assertion of the proposition follows from the two claims.     Q.E.D.

In the deterministic case (with a fixed interaction structure of the form $V^{{\beta }^{-1}}$, say) when action X is risk dominant and N is even, convergence to a two-cycle occurs. Given the prevailing interaction structure $V^{{\beta }^{-1}}$, the two elements $s^{\prime },s^{\prime \prime }$ of the two-cycle exhibit an alternating pattern of X’s and Y’s, say $s_{\beta \left(1\right)}^{\prime },\dots ,s_{\beta \left(N\right)}^{\prime }=XYXY\dots XY$ and $s_{\beta \left(1\right)}^{\prime \prime },\dots ,s_{\beta \left(N\right)}^{\prime \prime }=YXYX\dots YX$. In the stochastic case, even if at some time t, $s\left(t\right)$ exhibits an alternating pattern with respect to $V\left(t\right)$, this does not lead to a permanent two-cycle. For the probability that $s\left(\tau \right)$ constitutes an alternating pattern with respect to $V\left(\tau \right)$ for all $\tau >t$ is zero. With probability one, the cycle will be interrupted and contagion occurs. That means that with random reformation of the interaction structure, the effect observed in item GO3 of the introduction dominates the effect observed in item GO4.

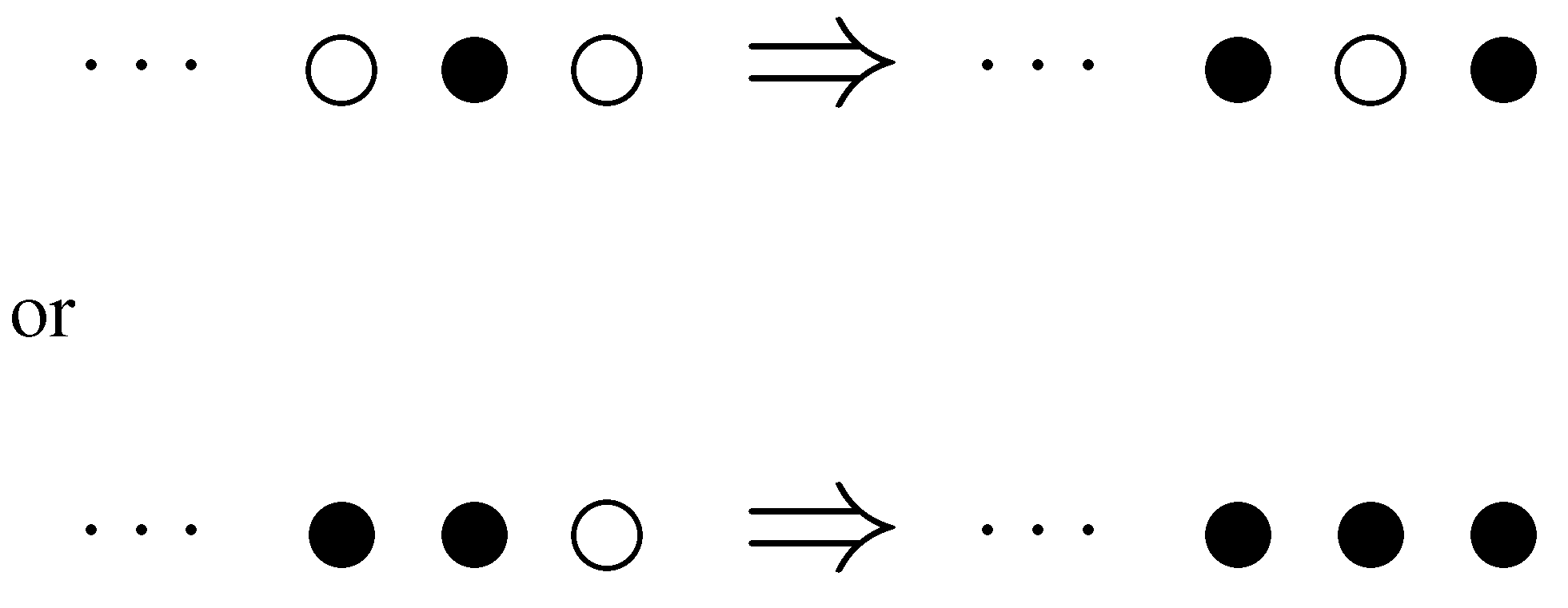
Simultaneous myopic best-response updating on a 2-circular graph can be visualized as follows, where • stands for a node (player) choosing the risk dominant action X and ∘ stands for a node (player) choosing Y:

Figure 1. Local updating.

Figure 1. Local updating.

In the first row, an isolated X-player (•-player) switches to Y (∘). But the player’s right-hand neighbor, a Y-player (∘-player) has at least one neighbor who chose X before, hence switches to X (•). This illustrates Claim 1 in the proof, that $x\left(t\right)$ is nondecreasing in t. Furthermore, the original X-player’s left-hand neighbor switches from Y (∘) to X (•), which demonstrates Claim 2 of the proof for $x(t-1)=1$: $x\left(t\right)=2$ with probability 1. In the second row, a cluster of X-players (•-players) is expanding to the neighbor(s) playing Y (∘) before. This illustrates Claim 2 of the proof that if $1<x(t-1)<N$, then $x\left(t\right)>x(t-1)$ with probability $\ge 1/\left|\mathcal{C}\right(2\left)\right|$. For if $x(t-1)>1$, then with probability at least $\ge 1/\left|\mathcal{C}\right(2\left)\right|$, the previous X-players (•-players) form a cluster in $V\left(t\right)$.

Incidentally, Figure 1 also explains the adjustment dynamics in the case of a fixed deterministic interaction structure of the form $V^{\beta }$.

The key arguments of the proof of Proposition 1 are not confined to that particular model. The proposition can be generalized in several ways.

First, it suffices to assume that each of the i.i.d. random variables $\tilde{V}\left(t\right)$ has as support the set $\mathcal{C}\left(2\right)$ of 2-circular graphs. In the proof, the probability $1/\left|\mathcal{C}\right(2\left)\right|$ has to be replaced by $min\left\{\mathsf{Prob}\right(V\left(1\right)=V):V\in \mathcal{C}(2\left)\right\}>0$.

Second, the set $\mathcal{C}\left(2\right)$ of all 2-circular graphs can be replaced by the set $\mathcal{R}\left(2\right)$ of all 2-regular graphs, that is graphs where each player has exactly two neighbors. The reason is that each 2-regular graph $V\in \mathcal{R}\left(2\right)$ is composed of 2-circular graphs on the connected components of V.

Third, updating can occur at a lower speed than neighborhood evolution. For instance, updating may occur only every hundredth period, say in periods $t=100,200,\dots$, or only in periods $t=2^k,k=1,2,\dots$. Updating may occur at random times. For instance, there can be a sequence of i.i.d. $\{0,1\}$-valued random variables $a_t$ with $\mathsf{Prob}(a_1=1)\in (0,1)$ so that updating occurs in period t if and only if $a_t=1$.

Forth, as suggested by Lars Koch-Metzger, we can dispense with the i.i.d. assumption and consider the endogenous co-evolution of actions and interaction structure (graph) instead. The crucial assumption is that there exists $\epsilon >0$ such that in any period $t>0$, if $x(t-1)>1$ then with probability at least ε, $V\left(t\right)$ has a cluster and, consequently, $x\left(t\right)>x(t-1)$. Specifically, let $\Delta \left(\mathcal{C}\right(2\left)\right)$ be the set of probability distributions on $\mathcal{C}\left(2\right)$ and ${\Delta }_{\epsilon }\left(\mathcal{C}\left(2\right)\right)=\{\mu \in \Delta \left(\mathcal{C}\left(2\right)\right)|\mu \left(V\right)\ge \epsilon \mathrm{for} \mathrm{all}V\in \mathcal{C}\left(2\right)\}$ where $\epsilon >0$ is small enough so that ${\Delta }_{\epsilon }\left(\mathcal{C}\left(2\right)\right)\ne \varnothing$. Let us assume that for $t=1,2,\dots$, there exist transition probabilities given by

$$K\left(t\right)[·,·]:\mathcal{C}\left(2\right)\times S⟶{\Delta }_{\epsilon }\left(\mathcal{C}\left(2\right)\right)$$

(5)

That is, given an interaction structure $V(t-1)\in \mathcal{C}\left(2\right)$ and an action profile $s(t-1)\in S$ in period $t-1$, the probability that interaction structure $V\in \mathcal{C}\left(2\right)$ is realized in period t is

$$\mathsf{Prob}\left(V\right(t)=V|V(t-1),s(t-1))=K(t\left)\right[V(t-1),s(t-1)\left]\right(V)$$

(6)

$K\left(t\right)[V(t-1),s(t-1)]\in {\Delta }_{\epsilon }(\mathcal{C}\left(2\right)$ implies $\mathsf{Prob}\left(V\right(t)=V|V(t-1),s(t-1))\ge \epsilon$ for all $V(t-1),s(t-1)$, and $V\in \mathcal{C}\left(2\right)$. Therefore, if $N>x(t-1)>1$, then with probability at least ε, $V\left(t\right)$ has a cluster and, consequently, $x\left(t\right)>x(t-1)$. It follows that $\mathsf{Prob}(x\left(T\right)=x(t-1))\le {(1-\epsilon )}^{T+1-t}$ for $T\ge t$, by the (possibly non-stationary) Markov property of the process. Hence $\mathsf{Prob}\left(x\right(T)>x(t-1\left)\right)\to 1$ as $T\to \infty$. Reiterating the argument at most $N-x(t-1)$ times yields $\mathsf{Prob}\left(x\right(T)\to N)\to 1$ as $T\to \infty$. We obtain:

Corollary 1 

Suppose simultaneous updating, (2), (5), and (6). If X is risk dominant and $x\left(0\right)>0$, then with probability one, the entire population will end up choosing X in finite time.

3.2. Interaction with More than Two Neighbors

Proposition 1, Corollary 1 and variations thereof show the relevance of risk dominance for contagion in societies with small neighborhood groups. The following two examples and Proposition 2 demonstrate that only weaker conclusions can be drawn when neighborhood size increases. From here on, we return to the assumption of i.i.d. random variables $\tilde{V}\left(t\right),t=0,1,\dots$.

Suppose $n\in \mathbb{N},2\le n<N$ and that the support of each $\tilde{V}\left(t\right)$ is contained in the set of $n-regular$ graphs on I, the graphs where each player has exactly n neighbors. If $x\left(0\right)/n<\vartheta$, then Equation (4) holds for $t=1$ and all i and, therefore, contagion with respect to action Y occurs in one step. Example 1 illustrates the observation in item GO1 of the introduction—as does Example 2.

Example 1. 

While risk dominance of an action favors contagion with respect to that action, nevertheless the risk dominant action gets extinct when only a relatively small fraction of players has chosen it and the random graph generates rather large neighborhoods. For example, let $a=3,d=2,b=c=0$. Then action X is both payoff dominant and risk dominant. Further let $N\ge 4$ be even — to guarantee the existence of 3-regular graphs — and $x\left(0\right)=1$. If $n=2$ and the support of each $\tilde{V}\left(t\right)$ is $\mathcal{C}\left(2\right)$ or $\mathcal{R}\left(2\right)$, then a variant of Proposition 1 applies: With probability one, contagion with respect to action X occurs. If $n=3$ and $V\left(1\right)\in \mathcal{R}\left(3\right)$, then $x\left(0\right)/3=1/3<2/5=\vartheta$ and contagion with respect to Y occurs in a single step.

Now let $n\ge 2$ be even and consider the set $\mathcal{C}\left(n\right)$ of n-circular graphs where each player has $n/2$ left neighbors and $n/2$ right neighbors (with respect to a permutation β of N that defines the graph).

Proposition 2 

Suppose each $\tilde{V}\left(t\right)$ has support $\mathcal{C}\left(n\right)$. If X is risk dominant and $N>x\left(0\right)>n/2$ then with positive probability, the entire population will end up choosing X in finite time.

proof. Let $p=min\left\{\mathsf{Prob}\right(V\left(1\right)=V):V\in \mathcal{C}(n\left)\right\}>0$. If $t\ge 1$ and $N>x(t-1)>n/2$, then with probability at least p, there exists a permutation β of I such that $V\left(t\right)$ is defined by ${\beta }^{-1}$,

• $s_{\beta \left(1\right)}(t-1)=\dots =s_{\beta \left(x\right(t-1\left)\right)}(t-1)=X$,
• $s_{\beta \left(1\right)}\left(t\right)=\dots \dots =s_{\beta \left(x\right(t-1)+1)}\left(t\right)=X$, and thus, $x\left(t\right)>x(t-1)$.

Hence for some $k\in \{1,\dots ,N-x(0\left)\right\}$:

• $x\left(0\right)<x\left(1\right)<\dots <x\left(k\right)=N$ with probability at least $p^k$,

since the random variables $\tilde{V}\left(1\right),\tilde{V}\left(2\right),\dots$ are i.i.d.        Q.E.D.

Proposition 2 draws a weaker conclusion than Proposition 1. Indeed, in Proposition 2, “positive probability” cannot be replaced by “probability one”. To see this, consider:

Example 2. 

Suppose each $\tilde{V}\left(t\right)$ has support $\mathcal{C}\left(n\right)$. Let $a=3,d=2,b=c=0$. Then $\vartheta =2/5$ and action X is both payoff dominant and risk dominant. Further let $N=18$ and $n=4$ so that $n/2=2$. Suppose that $s_i\left(0\right)=X$ for $i\in \{1,7,13\}$ and $s_i\left(0\right)=Y$ for $i\notin \{1,7,13\}$. Then $x\left(0\right)=3>n/2$. Now let $V^{\prime }\in \mathcal{C}\left(4\right)$ be defined by the permutation $\beta ={id}_N$, that is $\{i,j\}\in V^{\prime }$ iff $j=i\pm 1\mathrm{or}i\pm 2modN$. If $V\left(1\right)=V^{\prime }$, then $x_i\left(0\right)\in \{0,1\}$ and $\vartheta ·n_i\left(t\right)=\vartheta ·n=8/5$ for all $i\in I$; hence (4) holds for $t=1$ and all i and contagion with respect to action Y occurs in one step. With positive probability, $V\left(1\right)=V^{\prime }$. Thus, the hypothesis of Proposition 2 is satisfied whereas the event “the entire population will end up choosing X in finite time” has probability less than one.

3.3. OR Networks

A successful approach to the contagion question in the computer science literature is known under the rubric of AND and OR networks; see Goles and Hernández [30]. We are interested in OR networks. OR networks are often used to study the dynamics of boolean nets where each member of the network has a binary choice like in our model, say a choice between X and Y. The OR property refers to a particular decision rule or “law of motion”, not merely the graph. A network has the OR property (with respect to action X), if a network member i will choose X when at least one neighbor chose X in the previous period. In case i has neighborhood $V_i\left(t\right)=\{j_1,j_2,\dots ,j_k\}$ of size $n_i\left(t\right)=k>0$, i will choose $s_i\left(t\right)=X$ if and only if $s_{j_1}(t-1)=X$ or $s_{j_2}(t-1)=X$ or … or $s_{j_k}(t-1)=X$. This explains the terminology OR network. Our interest in OR networks stems from several facts:

• By imposing suitable restrictions on our base game, we can often treat our network dynamics as OR network dynamics. In short, OR network dynamics are governed by the following law of motion:

  $$s_i\left(t\right)=X⟺x_i(t-1)\ge 1$$

  (7)

  By (3) and (4), condition (7) is equivalent to $\vartheta ·n_i\left(t\right)\le 1$ in our context. In case $V\left(t\right)$ is n-regular with $n\ge 2$, the latter is equivalent to $\vartheta \le 1/n$ or $a-c\ge (n-1)(d-b)$. This condition obviously requires that X be sufficiently risk dominant in order to obtain an OR network. In case $n=2$, the risk dominance condition $a-c>d-b$ suffices. In case $n=4$, the stronger condition $a-c\ge 3(d-b)$ is required.
• OR network dynamics with a fixed interaction structure have been studied by Goles and Hernández [30]. This allows us to compare directly our findings for random interaction structures with those for fixed interaction structures.
• We gain insight into the sensitivity of the dynamics with respect to the risk dominance parameter ϑ.

Concerning contagion it is easy to see that arguments similar to those in the proof of Proposition 1 yield the following result:

Proposition 3 

Let $n\ge 2$ be even and $a-c\ge (n-1)(d-b)$. Suppose each $\tilde{V}\left(t\right)$ has support $\mathcal{C}\left(n\right)$—so that each realization $V\left(t\right)$ constitutes an OR network. If $x\left(0\right)>0$, then with probability one, the entire population will end up choosing X in finite time.

Proposition 3 can be extended to random graph processes where the support of each $\tilde{V}\left(t\right)$ contains $\mathcal{C}\left(n\right)$ and possibly includes other members of $\mathcal{R}\left(n\right)$ with the property that each node can be assigned a “select right-hand neighbor”. In the proof of Proposition 1, the argument for Claim 1 relies on the fact that for $V\in \mathcal{C}\left(2\right)$, $V=V^{\beta }$ and $i\in I$, we can assign to i its right-hand neighbor j with respect to β, given by $\beta \left(j\right)=\beta \left(i\right)+1modN$. Similarly, for any even $n>2$, $V\in \mathcal{C}\left(n\right)$ defined by a permutation β of N and $i\in I$, i’s neighborhood is $V_i=\{j\in I:\beta \left(j\right)=\beta \left(i\right)\pm 1\mathrm{or}\dots \mathrm{or}\beta \left(i\right)\pm n/2modN\}$ and i can be assigned a “select right neighbor j with respect to β”, again given by $\beta \left(j\right)=\beta \left(i\right)+1modN$. Therefore, the argument for Claim 1 can be made again. It can be generalized to graphs $V\in \mathcal{R}\left(n\right)\backslash \mathcal{C}\left(n\right)$ in which every node i can be assigned a “select right neighbor”, like the graphs in Example 3.

Example 3. 

For instance, let $N=60$ and $n=4$. Then each $i\in I$ has a unique representation $i=20i_1+i_2$ with $i_1\in \{0,1,2\}$ and $i_2\in \{1,\dots ,20\}$. Define a von Neumann neighborhood for i via $V_i\equiv$

$$\left\{j\in I\left|\begin{array}{c}j=20j_1+j_2\mathrm{with}{j}_1\in \{0,1,2\},j_1\ne i_1,j_2=i_2\mathrm{or}\hfill \\ j=20j_1+j_2\mathrm{with}{j}_1=i_1,j_2\in \{1,\dots ,20\},j_2=i_2\pm 1mod20\hfill \end{array}\right.\right\}$$

Then the $3\times 20$ lattice or torus V given by the neighborhoods $V_i,i\in I$, belongs to $\mathcal{R}\left(4\right)\backslash \mathcal{C}\left(4\right)$. To $i=20i_1+i_2$, one can assign the right-hand neighbor $j=20j_1+i_2$ with $j_1\in \{0,1,2\},j_1=i_1+1mod3$. This is not the only possibility: The assignment $j=20i_1+j_2$ with $j_2\in \{1,\dots ,20\},j_1=i_1+1mod20$ will also do. The construction can be applied to any $V\in \mathcal{R}\left(n\right)\backslash \mathcal{C}\left(n\right)$ which is representable as a finite lattice without boundary (discrete torus). Still for $N=60,n=4$, one can also consider a $5\times 2$ lattice or torus or a 3-dimensional $2\times 2\times 15$ lattice or cube, etc.

■ Fixed versus random interaction structure. In the case of a fixed interaction structure, Goles and Hernández [30] observe that OR networks form a class of neural networks and, hence, possess well known properties of neural networks. In particular, OR network dynamics with simultaneous updating exhibits contagion (with respect to action X or with respect action Y) or converges to a unique 2-cycle. In contrast to $n=2$, deterministic OR network dynamics based on a fixed network $V\in \mathcal{C}\left(n\right)$ with n even, $n>2$, and $x\left(0\right)>0$ always exhibits contagion with respect to action X. Thus, in the long-run, interaction based on a fixed interact structure and interaction on a sequence of random interaction structures results in the same outcome.

However, as elaborated in the paragraph after Proposition 3, the assumed support $\mathcal{C}\left(n\right)$ in Proposition 3 can be replaced by a superset of $\mathcal{C}\left(n\right)$ which contains other elements $V^{\prime }$ of $\mathcal{R}\left(n\right)$ where each node can be assigned a “select right neighbor”. For example, in case $N=16$, $n=4$, a $4\times 4$ torus (lattice without boundary) $V^{\prime }$ will qualify. OR network dynamics based on $V^{\prime }$ with $x\left(0\right)=1$ converges to a 2-cycle. In that case, interaction on a sequence of random interaction structures makes a difference: Replace the support $\mathcal{C}\left(4\right)$ in Proposition 3 by $\mathcal{C}\left(4\right)\cup \left\{V^{\prime }\right\}$ and set $ϵ\equiv \mathsf{Prob}(V\left(1\right)\ne V^{\prime })>0$. For arbitrarily small ϵ, contagion with respect to action X occurs although $V^{\prime }$ has a much greater chance to be realized than not.

■ Sensitivity analysis. The OR network property, that is sufficiently strong risk dominance of action X, proves very conducive to contagion with respect to action X. If, on the other hand, the OR network property fails to hold, then it is not surprising that contagion with respect to action X may fail in some instances as well. However, ceteris paribus, the impact of the lack of the OR network property turns out to be quite drastic: Suppose $a-c<(n-1)(d-b)$ while the other assumptions of Proposition 3 remain unchanged. Then in large populations, with positive probability contagion with respect to action Y occurs even when a vast majority of the players initially chooses action X—and even when X is risk dominant.

Proposition 4 

Let $n\ge 2$ be even and $a-c<(n-1)(d-b)$. Suppose each $\tilde{V}\left(t\right)$ has support $\mathcal{C}\left(n\right)$—so that none of the realizations $V\left(t\right)$ constitutes an OR network. If $N-x\left(0\right)\ge 5n^2$ then with positive probability, the entire population will end up choosing Y in finite time.

Returning to our earlier assertion, let us assume that $N=K{n}^2$ and $N-x\left(0\right)=5n^2$. Then $x\left(0\right)/N=1-5/K\to 1$ as $K\to \infty$. Thus for sufficiently large population size and $a-c<(n-1)(d-b)$ (i.e., $\vartheta >1/n$), with positive probability contagion with respect to action Y occurs even when a vast majority of the players initially chooses action X—and even when X is risk dominant. In contrast, Proposition 3 states that for $a-c=(n-1)(d-b)$ (i.e., $\vartheta =1/n$), with probability one contagion with respect to action X occurs as long as at least one player initially chooses action X. Hence the dynamics prove very sensitive to the risk dominance parameter ϑ.

proof. Let again $p=min\left\{\mathsf{Prob}\right(V\left(1\right)=V):V\in \mathcal{C}(n\left)\right\}>0$. By assumption, there are at least $5n^2$ players who initially choose action Y. In case $x\left(0\right)\ge 2n+1$ there exists a permutation β of I such that

$$s_{\beta \left(i\right)}\left(0\right)=\left\{\begin{array}{ccc}Y\hfill & \mathrm{for}& i=1,\dots ,2n\hfill \\ X\hfill & \mathrm{for}& i=(1+k)2n+1,k=0,1,\dots ,2n\hfill \\ Y\hfill & \mathrm{for}& i=(1+k)2n+\ell ,k=0,1,\dots ,2n,\ell =0,2,\dots ,2n\hfill \\ Y\hfill & \mathrm{for}& i=(2n+3)2n,\dots ,(2n+3)2n\hfill \\ & & +N-x\left(0\right)-(4n^2-1+2n)=4n+1+N-x\left(0\right)\hfill \\ X\hfill & \mathrm{for}& i=4n+1+N-x\left(0\right),\dots ,N\hfill \end{array}\right.$$

If $V\left(1\right)$ is the element of $\mathcal{C}\left(n\right)$ defined by ${\beta }^{-1}$, then the $2n+1$ players $\beta \left(i\right)$ with $i=(1+k)2n+1,$$k=0,1,\dots ,2n$ have at most one neighbor in $V\left(1\right)$ who previously played X. Because of $a-c<(n-1)(d-b)$, they switch from X in period 0 to Y in period 1. Each player $\beta \left(i\right)$ with $i\in \{n+1,\dots ,4n+1+N-x(0)-n\}$ and $s_{\beta \left(i\right)}\left(0\right)=Y$ has at most one neighbor in $V\left(1\right)$ who previously played X and, therefore, $\beta \left(i\right)$ keeps playing Y in period 1. Therefore, at most $2n$ players switch from Y in period 0 to X in period 1. Hence the number of players switching from Y to X (at most $2n$) is less than the number of players switching form X to Y (at least $2n+1$). With probability at least p, this realization of $V\left(1\right)$ occurs and $x\left(1\right)<x\left(0\right)$.

In case $x\left(0\right)<2n+1$, there exists a permutation β of I such that

$$s_{\beta \left(i\right)}\left(0\right)=\left\{\begin{array}{ccc}X\hfill & \mathrm{for}& i=2kn+1,k=0,1,\dots ,2n-1\hfill \\ Y\hfill & \mathrm{for}& i=2kn+\ell ,k=0,1,\dots ,2n,\ell =0,2,\dots ,2n\hfill \\ Y\hfill & \mathrm{for}& i=4n^2+2n,\dots ,N\hfill \end{array}\right.$$

If $V\left(1\right)$ is the element of $\mathcal{C}\left(n\right)$ defined by ${\beta }^{-1}$, then each player has at most one neighbor in $V\left(1\right)$ who previously played X. Because of $a-c<(n-1)(d-b)$, every player chooses action Y in period 1. With probability at least p, this realization of $V\left(1\right)$ occurs and $x\left(1\right)=0$.

We conclude that with probability at least p, $x\left(1\right)\le max\{0,x(0)-1\}$ and $N-x\left(1\right)\ge N-x\left(0\right)\ge 5n^2$. Since the random variables $\tilde{V}\left(1\right),\tilde{V}\left(2\right),\dots$ are i.i.d., induction with respect to t yields existence of $k\in \{1,\dots ,x(0\left)\right\}$ such that $x\left(k\right)=0$ with probability at least $p^k$.       Q.E.D.

About the proof. In the first part of the proof, the case $x\left(0\right)\ge 2n+1$, consider the players arranged on a circle, each with $n/2$ neighbors on either side. The circle is partitioned into four segments A, B, C, and D which are arranged clockwise, say. Segment A consists of $2n$ players choosing action Y initially. Segment B consists of $2n+1$ initial X-players plus $2n(2n-1)$ initial Y-players where any two X-players are separated by $2n-1$ initial Y-players. Segment C consists of the remaining at least $2n$ players choosing action Y initially. Segment D consists of the rest of the initial X-players. The initial X-players in segment B will switch from X to Y. All initial Y-players in segment B keep playing Y. At most n players (close enough to segment D) in segment A and at most n players (close enough to segment D) in segment C will switch from Y to X.

3.4. Asynchronous Updating on 2-Circular Graphs

Following in the footsteps of Berninghaus and Schwalbe [2,3], we have assumed simultaneous or synchronous updating so far. The main alternative, asynchronous updating means that only one player is updating his action at any time. Formally, this is modeled by means of a sequence $k\left(t\right),t=0,1,2,\dots$, of I-valued random variables. $k\left(t\right)$ determines which of the players will have a chance to alter his action at time t. The selected player $i=k\left(t\right)$ will update his action according to the rule Equation (2), amended by the tie breaking and inertia conventions. Players $j\ne k\left(t\right)$ repeat their previous action, $s_j\left(t\right)=s_j(t-1)$. Similar to Blume [5], we assume for the current purposes that the stochastic process $k\left(t\right),t=0,1,\dots$ is independent of the process $\tilde{V}\left(t\right),t=0,1,\dots$ and consists of a sequence of i.i.d. random variables with full support I. The assumption is frequently made in models with logit perturbed best responses. See Blume [34], Young [35], Baron et al. [36,37].

Huberman and Glance [38] suggest that the order of updating, synchronous versus asynchronous, can matter. This can be easily demonstrated in the context of 2-circular interaction structures. First, with a fixed deterministic interaction structure of the form $V^{\beta }$, each $k\left(t\right)$ uniformly distributed on I, risk dominance of action X, and $x\left(0\right)=1$, contagion with respect to action X occurs with probability 2/3 and contagion with respect to action Y occurs with probability 1/3. This is significantly different from the corresponding case with simultaneous updating, where either contagion with respect to action X (for N odd) or convergence to a 2-cycle (for N even) occurs. Second, we have seen that with simultaneous updating, a random change of the interaction structure can interrupt cycles and, therefore, is conducive for contagion with respect to the risk dominant action. In stark contrast, with asynchronous updating, a random change of the interaction structure can reverse the contagion process and prove detrimental to contagion with respect to the risk dominant action. This constitutes an instance where with random reformation of the interaction structure, the effect observed in item GO4 of the introduction dominates the effect observed in item GO3.

To see this, assume $N\ge 4$, that each $\tilde{V}\left(t\right)$ is uniformly distributed on the set of 2-circular graphs, and as before, each $k\left(t\right)$ is uniformly distributed on I, action X is risk dominant, and $x\left(0\right)=1$. Let P be the probability that contagion with respect to action X occurs. Further let $P^{\prime }\equiv \mathsf{Prob}\left(\mathrm{contagion} \mathrm{occurs}\right|x\left(1\right)=2)$. Recall that in the deterministic case, $P=2/3$. Also notice that in the deterministic case, $P^{\prime }=1$, since the two players choosing X at time $t=1$ will be neighbors forever.

We find that randomness of the interaction structure proves detrimental to contagion with respect to the risk dominant action, indeed:

Claim: 

With the random interaction structure, $P^{\prime }<1$ and $P<2/3$.

Namely, without loss of generality, suppose that $s_1\left(1\right)=s_2\left(1\right)=X$ and $s_j\left(1\right)=Y$ for $j\ne 1,2$. Since $N\ge 4$, there exists $V^{\beta }\in \mathcal{C}\left(2\right)$ such that 1 and 2 are not neighbors in $V^{\beta }$. Now if $V\left(2\right)$ is such that 1 and 2 are not neighbors and $K\left(2\right)\in \{1,2\}$, then the selected player $i\in \{1,2\}$ will change his action from $s_i\left(1\right)=X$ to $s_i\left(2\right)=Y$. The specific realizations will occur with probability $\frac{1}{\left|\mathcal{C}\right(2\left)\right|}·\frac{2}{N}$. Hence $\mathsf{Prob}(x\left(2\right)=1|x\left(1\right)=2)\ge \frac{1}{\left|\mathcal{C}\right(2\left)\right|}·\frac{2}{N}$. Further $\mathsf{Prob}\left(x\right(3)=0|x\left(2\right)=1)=1/N$. Therefore, $\mathsf{Prob}\left(x\right(3)=0|x\left(1\right)=2)>0$ and $P^{\prime }<1$. Finally,

$$\begin{array}{ccc}\hfill P& =& \mathsf{Prob}\left(\mathrm{contagion} \mathrm{occurs}\right|x\left(0\right)=1)\hfill \\ & =& \mathsf{Prob}(x\left(1\right)=1|x\left(0\right)=1)P+\mathsf{Prob}(x\left(1\right)=2|x\left(0\right)=1)P^{\prime }\hfill \\ & =& \frac{N-3}{N}P+\frac{2}{N}{P}^{\prime }\mathrm{or}\hfill \\ \hfill P& =& (2/3)·P^{\prime }<2/3\hfill \end{array}$$

which proves the claim.

Best response dynamics with asynchronous updating and a fixed interaction structure V are fairly well understood and in general different from the best response dynamics with simultaneous updating and interaction structure V:

The static game G with player set I, strategy spaces $\{X,Y\}$ and payoff functions (1) is a potential game, as shown by Baron et al. [36]. As a consequence, the sequence $s\left(t\right)$ converges with probability 1 to a local maximum of any potential of G, that is, a Nash equilibrium of G. $(X,\dots ,X)$ and $(Y,\dots ,Y)$ are always Nash equilibria of G. As a rule, if X is risk dominant, $0<x\left(0\right)<1$, and V is a 2-circular graph, then both equilibria are reached with positive probability. The exception is when X is risk dominant and two adjacent players choose X originally, in which case convergence to $(X,\dots ,X)$ occurs with probability one.

4. Interaction on Binomial Random Graphs

In the random graph model most commonly studied in mathematics and statistics, each possible edge $\{i,j\}$ is included independently of others with probability $p\in (0,1)$. The model is denoted by $G(N,p)$ and known as the Erdős-Rényi random graph or the binomial random graph. Sometimes, the term “random graph” is used for this particular random graph model.

Throughout this section, we assume an i.i.d. process $\tilde{V}\left(t\right):\Omega \to \mathbb{V},t=0,1,\dots$, where each $\tilde{V}\left(t\right)$ is distributed according to a binomial random graph $G(N,p)$. Hence $\mathsf{Prob}(V\left(1\right)=V)=p^{\left|V\right|}{(1-p)}^{N(N-1)/2-\left|V\right|}$ for $V\in \mathbb{V}$. In the literature, frequently $p=p\left(N\right)$ is assumed and asymptotic properties of the random graph $G(N,p(N\left)\right)$ as $N\to \infty$ are investigated. We are going to examine two special cases: (a) fixed p and $N$; (b) fixed p while $N\to \infty$.

Proposition 5 

Let $N>2$ and $p\in (0,1)$ be given. If $x\left(0\right)>0$ and X is risk dominant, then with positive probability, the entire population will choose the risk dominant action X in period 2.

proof. Suppose $s_i\left(0\right)=X$. With probability $p^{N-1}·{(1-p)}^{(N-1)(N-2)/2}$ the star with center i is formed in period 1, in which case $s_j\left(1\right)=X$ for all $j\ne i$. With probability $p^{N(N-1)/2}$, the complete network is formed in period 2. In that case $s_j\left(1\right)=X$ for $j\ne i$ implies $s_j\left(2\right)=X$ for all j. Hence with probability at least $p^{(N+2)(N-1)/2}·{(1-p)}^{(N-1)(N-2)/2}$, the population will choose X in period 2. Q.E.D.

In general, the probability $p^{(N+2)(N-1)/2}·{(1-p)}^{(N-1)(N-2)/2}$ given in the proof is merely a lower bound, since other sequences of networks can also have the entire population choose X in period 2, for instance the star with center i followed by a 2-circular graph. Nonetheless, the probability that the entire population chooses X in finite time may be very small, as the following result shows. Indeed, the probability that the population ends up choosing Y in period 1 (and in all subsequent periods) can become extremely high.

Proposition 6 

Let $p\in (0,1)$ be fixed. Suppose that exactly one player chooses the risk dominant strategy X in period 0. Then as $N$ tends to infinity, the probability that the population chooses Y in period 1 goes to one.

Notice that Y is player i’s best reply if (4) holds. In case exactly one player has chosen X, $x_i\left(0\right)$ equals 0 or 1 for every player. Then

$$1<\vartheta ·n_i\left(1\right)$$

(8)

for all i is a sufficient condition for the population choosing Y. We are going to show that with high probability, all neighborhoods are “too large” in the sense of inequality (8) as N becomes large. To be precise, let us define the event $E\equiv \langle \left(8\right)\mathrm{holds}\mathrm{for}\mathrm{all}i\rangle$. We shall show $\mathsf{Prob}\left(E\right)\to 1$ as $N\to \infty$.

proof. We want to show $\mathsf{Prob}\left(E\right)\to 1$ as $N\to \infty$. Let m denote the smallest integer greater than or equal to $1/\vartheta$. Then $n_i\left(1\right)>m$ is sufficient for (8).

Now consider $N>4m$. Define $N^{\prime }=(N-2)/2$ for N even and $N^{\prime }=(N-1)/2$ for N odd. For $i\in I$, consider the set of pairs (links, edges) $L_i=\{\{i,j\}:j=i+\ell \mathrm{mod}N\mathrm{for} \mathrm{some}\ell \in \{1,\dots ,N^{\prime }\}\}$. Then $|L_i|>m$ for all i and $L_i\cap L_{i^{\prime }}=\varnothing$ for $i\ne i^{\prime }$. Further consider, for $i\in I$, the events $E_i^{\prime }\equiv \langle \mathrm{More}\mathrm{than}m\mathrm{of}\mathrm{the}\mathrm{links}\mathrm{in}{L}_i\mathrm{exist}\rangle$ and $F_i^{\prime }\equiv \langle \mathrm{At}\mathrm{most}m\mathrm{of}\mathrm{the}\mathrm{links}\mathrm{in}{L}_i\mathrm{exist}\rangle$. Now

$$\begin{array}{ccc}\hfill \mathsf{Prob}\left(F_i^{\prime }\right)& =& \sum _{k=0}^m\left(\begin{array}{c}{N}^{\prime }\\ k\end{array}\right)p^k{(1-p)}^{N^{\prime }-k}\hfill \\ & \le & (m+1){\left(N^{\prime }\right)}^m/(m!)q·{(1-p)}^{N^{\prime }}=c·{\left(N^{\prime }\right)}^m·{(1-p)}^{N^{\prime }}\hfill \end{array}$$

where $q={max}_{k=0}^m{(p/(1-p))}^k$ and $c=q(m+1)/(m!)$. Since $N^{\prime }\to \infty$ for $N\to \infty$, it follows $c·{\left(N^{\prime }\right)}^m·{(1-p)}^{N^{\prime }}\to 0$ for $N\to \infty$.

Next observe that $E_1^{\prime },E_2^{\prime },\dots ,E_N^{\prime }$ are independent events. Hence for sufficiently large N, $c·{\left(N^{\prime }\right)}^m·{(1-p)}^{N^{\prime }}<1$ and

$$\begin{array}{ccc}& & \mathsf{Prob}\left(\bigcap _{i\in I}{E}_i^{\prime }\right)=\prod _{i\in I}\mathsf{Prob}\left(E_i^{\prime }\right)=\prod _{i\in I}\left[1-\mathsf{Prob}\left(F_i^{\prime }\right)\right]\hfill \\ & \ge & {\left[1-c·{\left(N^{\prime }\right)}^m·{(1-p)}^{N^{\prime }}\right]}^N\ge 1-Nc·{\left(N^{\prime }\right)}^m·{(1-p)}^{N^{\prime }}\hfill \\ \\ & \ge & 1-4c·{\left(N^{\prime }\right)}^{m+1}·{(1-p)}^{N^{\prime }}\hfill \end{array}$$

Finally, consider the events $E_i^{*}\equiv \langle n_i\left(1\right)>m\rangle$ and $E_i\equiv \langle \left(8\right)\rangle$ for $i\in I$. Then ${\bigcap }_i{E}_i^{\prime }\subseteq {\bigcap }_i{E}_i^{*}\subseteq {\bigcap }_i{E}_i=E$ and, consequently, $\mathsf{Prob}\left(E\right)\ge \mathsf{Prob}\left({\bigcap }_i{E}_i^{\prime }\right)\ge 1-4c·{\left(N^{\prime }\right)}^{m+1}·{(1-p)}^{N^{\prime }}$. Hence $\mathsf{Prob}\left(E\right)\to 1$ for $N\to \infty$ as asserted. Q.E.D.

The basic insight behind Proposition 6 is that large neighborhoods are very likely in a large population. In the event that all neighborhoods are sufficiently large, a single X cannot survive. The observation of item GO1 in the introduction applies. Obviously, the result can be generalized to the case where $s_i\left(0\right)=X$ for at most h players, for a fixed positive integer h. In that case replace the left-hand side of (8) by h and define m as the smallest integer greater than or equal to $h/\vartheta$.

We obtain almost analogous results after switching the roles of X and Y in Propositions 5 and 6. Namely, the analog of Proposition 5 holds under the assumption $1/(N-1)<\vartheta$. The analog of Proposition 6 holds without further stipulations.

One may wonder, as does one of the referees, whether the conclusion of Proposition 6 persists if $p=p\left(N\right)$. In case $p\left(N\right)N=const=\lambda$,

$$\mathsf{Prob}(n_i\left(1\right)=k)=\left(\begin{array}{c}N-1\\ k\end{array}\right)p^k{(1-p)}^{N-k}\stackrel{N\to \infty }{\stackrel{}{\to }}{\displaystyle \frac{{\lambda }^k{e}^{-\lambda }}{k!}}$$

for all $i\in I$ and $k=0,1,2,\dots$. Hence the probability of the occurrence of small neighborhoods does not asymptotically go to zero. Therefore, the method of proof for Proposition 6 does not work anymore. We do not know whether the conclusion of Proposition 6 still holds in this case. However, if $p\left(N\right)$ goes to zero very fast, then the conclusion of Proposition 6 also holds, albeit for a different reason: As the population becomes large, the probability that the initial X-player becomes isolated in period 1 approaches 1. For example, suppose $p\left(N\right)·N^2=1$. Then for each $i\in I$,

$$\mathsf{Prob}(n_i\left(1\right)=0)={(1-1/N^2)}^{N-1}\stackrel{N\to \infty }{\stackrel{}{\to }}1$$

There remains the question whether contagion (with respect to X or with respect to Y) always obtains. The answer in Corollary 2 is in the affirmative. We are going to show a more general result. To this end, we consider a symmetry condition.

• A stochastic process of random variables $\tilde{V}\left(t\right):\Omega \to \mathbb{V},t=0,1,\dots$, is symmetric in case it satisfies the following condition:
• If $V,V^{\prime }\in \mathbb{V}$ and β is a permutation of I such that $\{i,j\}\in V⟺\{\beta \left(i\right),\beta \left(j\right)\}\in V^{\prime }$, then $\mathsf{Prob}(V\left(t\right)=V)=\mathsf{Prob}(V\left(t\right)=V^{\prime })$ for each t.

To study the evolution of the variable $x\left(t\right)=\left|\right\{i\in I:s_i\left(t\right)=X\left\}\right|$, let $\mathfrak{X}=\{0,1,\dots ,N\}$ for given N.

Lemma 1 

If the stochastic process of random variables $\tilde{V}\left(t\right)$ is i.i.d. and symmetric, then the dynamic process $x\left(t\right),t=0,1,2,\dots$ is a stationary Markov process with state space $\mathfrak{X}$.

proof. First observe that the random graph evolves independently of players’ choices. Second, the random graph process $\tilde{V}\left(t\right):\Omega \to \mathcal{V},t=0,1,\dots$, is i.i.d. and symmetric. Hence for $x,x^{\prime }\in \mathfrak{X}$ and $t\ge 1$, $q\left(x^{\prime }\right|x)=\mathsf{Prob}\left(x\left(t\right)=x^{\prime }ifx(t-1)=x\right)$ is well defined (and independent of t) and $x\left(t\right)$ follows a stationary Markov process with state space $\mathfrak{X}$ and transition probabilities $q\left(x^{\prime }\right|x)$.   Q.E.D.

Proposition 7 

Suppose the stochastic process of i.i.d. random variables $\tilde{V}\left(t\right)$ is symmetric and each $\tilde{V}\left(t\right)$ has full support. Then with probability one, the population will be coordinated in finite time (on action X or on action Y).

proof. By Lemma 1, $x\left(t\right),t=0,1,2,\dots$ is a stationary Markov process with state space $\mathfrak{X}$. Full support of the random variables $\tilde{V}\left(t\right)$ implies for the transition probabilities

$q\left(x^{\prime }\right|x)=\mathsf{Prob}\left(x\left(t\right)=x^{\prime }ifx(t-1)=x\right)$:

• Under the assumption $1<(N-1)\vartheta$, the transition probabilities satisfy
  $q\left(0\right|0)=q(N\left|N\right)=1$
  $q(x-1|x)>0$ for $x\ne 0,N$
• Under the assumption $N-2\ge (N-1)\vartheta$, the transition probabilities satisfy
  $q\left(0\right|0)=q(N\left|N\right)=1$
  $q(x+1|x)>0$ for $x\ne 0,N$

But either $1<(N-1)\vartheta$ or $(N-1)\vartheta \le 1\le N-2$. Therefore, $\left\{0\right\}$ and $\left\{N\right\}$ are the only ergodic sets of the process. Consequently, ${lim}_{t\to \infty }\mathsf{Prob}(x\left(t\right)\in \{0,N\})=1$.      Q.E.D.

Corollary 2 

Consider the binomial random graph process. Then with probability one, the population will be coordinated in finite time (on action X or on action Y).

proof. The random variables $\tilde{V}\left(t\right)$ based on the binomial random graph $G(N,p)$ satisfy the symmetry condition and have full support. Hence the assertion, by Proposition 7.    Q.E.D.

Symmetry and full support are satisfied by the binomial random graph, the uniform distribution on $\mathcal{V}$, and many others. Under the assumption of Proposition 7, not everything goes: Only contagion, with respect to X or Y, is possible. The dynamics cannot reach a multi-member ergodic set and stay there. Whether the latter is possible under the hypothesis of Proposition 4 is an open question.

5. Conclusions

We saw that the random reformation of 2-circular graphs affects occurrence of contagion. The effect depends on the updating regime. With simultaneous updating, contagion with respect to the risk dominant action obtains, if at least one player chose it initially. With asynchronous updating, the probability of contagion with respect to the risk dominant action is reduced. We further saw that a binomial random graph affects occurrence of contagion in different ways. With simultaneous updating, always contagion (with respect to X or Y) occurs. Starting with few players choosing the risk dominant action initially, with positive probability, contagion with respect to the risk dominant occurs; but this probability goes to zero when ceteris paribus the number of players goes to infinity.

We observe a crucial role of risk dominance for contagion. We also observe that large initial neighborhoods can lead to the extinction of an action. Hence high connectivity in the sense of large neighborhoods is not necessarily conducive to contagion.

We find that in our context it matters both qualitatively and quantitatively whether the random graph is generated every period or only once before play begins. First, with a fixed 2-circular graph, an even number of players, and one player playing the risk dominant action initially, simultaneous updating converges to a 2-cycle. This also happens if the graph is drawn at random once before play. In contrast, with repeated random draws during play, contagion with respect to the risk dominant action occurs almost certainly. Second, with one player choosing the risk dominant action initially and asynchronous updating, the probability of contagion with respect to the risk dominant action is higher when a 2-circular graph is drawn once and for all before play then when repeated random draws are performed during play. Therefore, it makes a difference, in terms of the probability of contagion with respect to the risk dominant action, whether a new graph is drawn at random every period or only once before the play begins. In contrast, López-Pintado ([18]; p. 374) states “… the model that we analyze with the mean-field equations is analogous to one where the random network is generated every period, although the connectivity of each individual remains constant. We believe that the qualitative results of this alternative model coincide with the results of the original model where the network is fixed throughout the dynamics but has been generated by a random process.”

The literature has investigated many other features of local interaction. We mention three of the most interesting model variations: mutations (stochastic stability), imitation, and distinction between interacting neighbors and observed neighbors.

■ Mutations. One particular way of making the dynamic system random is to add noise in the form of random mutations, trembles or mistakes so that with some small probability, a player makes sub-optimal choices. If the noise renders the system an irreducible Markov process, then the randomly perturbed system has a unique invariant distribution. Long-run equilibria or stochastically stable states are the states with positive weight in the limit distribution as the noise tends to zero. See for instance, Blume [34], Ellison [6], Young [35]. The question is whether random perturbations have the same effect as a randomly changing interaction structure. To be precise: Does contagion with respect to X (Y) occur if and only if $(X,\dots ,X)$ ($(Y,\dots ,Y)$) is a stochastically stable state? While the answer is often in the affirmative, it is not in general. First of all, a limit distribution of the stochastically perturbed system need not exist. Further, the limit distribution and the set of stochastically stable states are sensitive to the nature of the noise, as Bergin and Lipman [39] have shown. Baron et al. ([36]; pp. 556–557) provide an example where uniform or Bernoulli trembles and logit trembles give rise to different sets of stochastically stable states. Finally, even if the answer to the above question is affirmative—like convergence in Proposition 1 to the unique stochastically stable state obtained in Ellison [6]—the randomly perturbed system is not converging to a steady state stricto sensu. For suppose there is very little but non-zero noise. Because of irreducibility, the randomly perturbed system tends to visit every state from time to time. However, the stochastically stable states are visited much more frequently than others.

■ Imitation. Instead of choosing a myopic best response, a player may choose the “best“ strategy or the most frequent strategy played by his current neighbors. Best performance imitation, akin to fitness criteria in biology, has been studied by, among others, Nowak and May [40] who find through simulation of Prisoner’s Dilemma games that local interactions are dramatically different from global ones. Subsequent theoretical analysis has been performed by Eshel, Samuelson and Shaked [41], Kirchkamp [42], and Outkin [43]. Alós-Ferrer and Weidenholzer [44] study best performance imitation dynamics of coordination games on circular graphs.

■ Distinction between interaction neighborhoods and information neighborhoods. Durieu and Solal [45] distinguish between an agent’s interaction neighborhood and a smaller information neighborhoods in a model similar to Ellison’s [6]. They confirm Ellison’s findings, but obtain faster convergence. Alós-Ferrer and Weidenholzer [46] study best performance imitation dynamics when an agent’s interaction neighborhood is contained in the agent’s information neighborhood.