Fusion Convolutional Neural Network for Cross-Subject EEG Motor Imagery Classification

Abstract

Brain–computer interfaces (BCIs) can help people with limited motor abilities to interact with their environment without external assistance. A major challenge in electroencephalogram (EEG)-based BCI development and research is the cross-subject classification of motor imagery data. Due to the highly individualized nature of EEG signals, it has been difficult to develop a cross-subject classification method that achieves sufficiently high accuracy when predicting the subject’s intention. In this study, we propose a multi-branch 2D convolutional neural network (CNN) that utilizes different hyperparameter values for each branch and is more flexible to data from different subjects. Our model, EEGNet Fusion, achieves 84.1% and 83.8% accuracy when tested on the 103-subject eegmmidb dataset for executed and imagined motor actions, respectively. The model achieved statistically significantly higher results compared with three state-of-the-art CNN classifiers: EEGNet, ShallowConvNet, and DeepConvNet. However, the computational cost of the proposed model is up to four times higher than the model with the lowest computational cost used for comparison.

1. Introduction

A brain–computer interface (BCI) is a system that implements human–computer communication by interpreting brain signals. As the user’s intention is strictly interpreted through brain signals, BCIs can enable users with limited motor abilities to communicate with devices like computers and prosthetics without physically executed movements.

One of the most common ways of collecting input from the brain is achieved through a process called electroencephalography (EEG), which is reading the brain waves of subjects using a device capable of electrophysiological measuring of the electrical activity of the brain [1]. Typically, this is achieved by placing fixed electrodes on the scalp in the international 10–20 standard system for electrode placement. EEG provides measurements of electrical potential in the form of a time signal for each electrode placed on the subject’s scalp. Although these measurements only partially reflect the brain’s underlying electrophysiological phenomena, they also contain a significant amount of information, which can be used in clinical diagnoses and cognitive sciences, as well as for the development of BCIs [2].

Due to its relatively low cost, ease of use, and sufficiently high temporal resolution, EEG-based BCI development has seen a wide range of use in medical applications [3,4], including neurorehabilitation [5], disorder diagnosis [6], and entertainment applications such as smart environments [7] and biofeedback-based games [8].

However, there are many challenges faced when building a BCI capable of classifying the subject’s intention, such as the highly individualized nature of brain waves, which makes the development of a cross-subject classifier difficult [9].

Recently, some studies have explored the possibility of automatic feature extraction using deep neural networks, such as a convolutional neural network (CNN). In a pioneering study [10], deep and shallow CNN architectures with various design decisions were explored. A neural network architecture suited for cross-paradigm BCI problems, dubbed EEGNet, was introduced in [11]. EEGNet is designed to be capable of accurately classifying EEG signals from various BCI paradigms like P300 visual-evoked potentials, error-related negativity responses (ERN), movement-related cortical potentials (MRCP), and sensory-motor rhythms (SMR).

In EEG-based classification, fusion networks have shown promise in overcoming the problem of poor generalization of cross-subject data. Fusion networks have been found to increase overall network classification accuracies by enabling the network to extract features from multiple branches with differing architectures or hyperparameters and fusing the features in a fusion layer. The intuition behind this approach is that each subject’s brain signal patterns are individual and for different subjects, the best performing architectures and hyperparameters can vary.

A multi-branch 3D convolutional network was evaluated with a shared base layer and three branches with varying kernel sizes and strides in the convolutional layers in work presented in [12]. The feature fusion was performed on the final fully connected layer before the softmax classification layer. The network achieved a mean accuracy of 75% for within-subject classification on the BCI Competition IV dataset 2a.

Instead of the usual feature fusion at the final fully connected or softmax layer, multilevel feature fusion was performed by extracting features after each pooling layer in [13]. These features were extracted from four branches and concatenated together in a fully connected layer before the final softmax classification layer. This approach achieved 74.5% accuracy on the BCI Competition IV 2a dataset.

Other recent methods of EEG classification include unsupervised learning with restricted boltzmann machines (RBMs) [14], multi-view common component discriminant analysis (MvCCDA) for cross-view classification, which is used to find a common subspace for multi-view data [15], and combining deep neural network columns in multi-column deep neural networks (McDNN) [16].

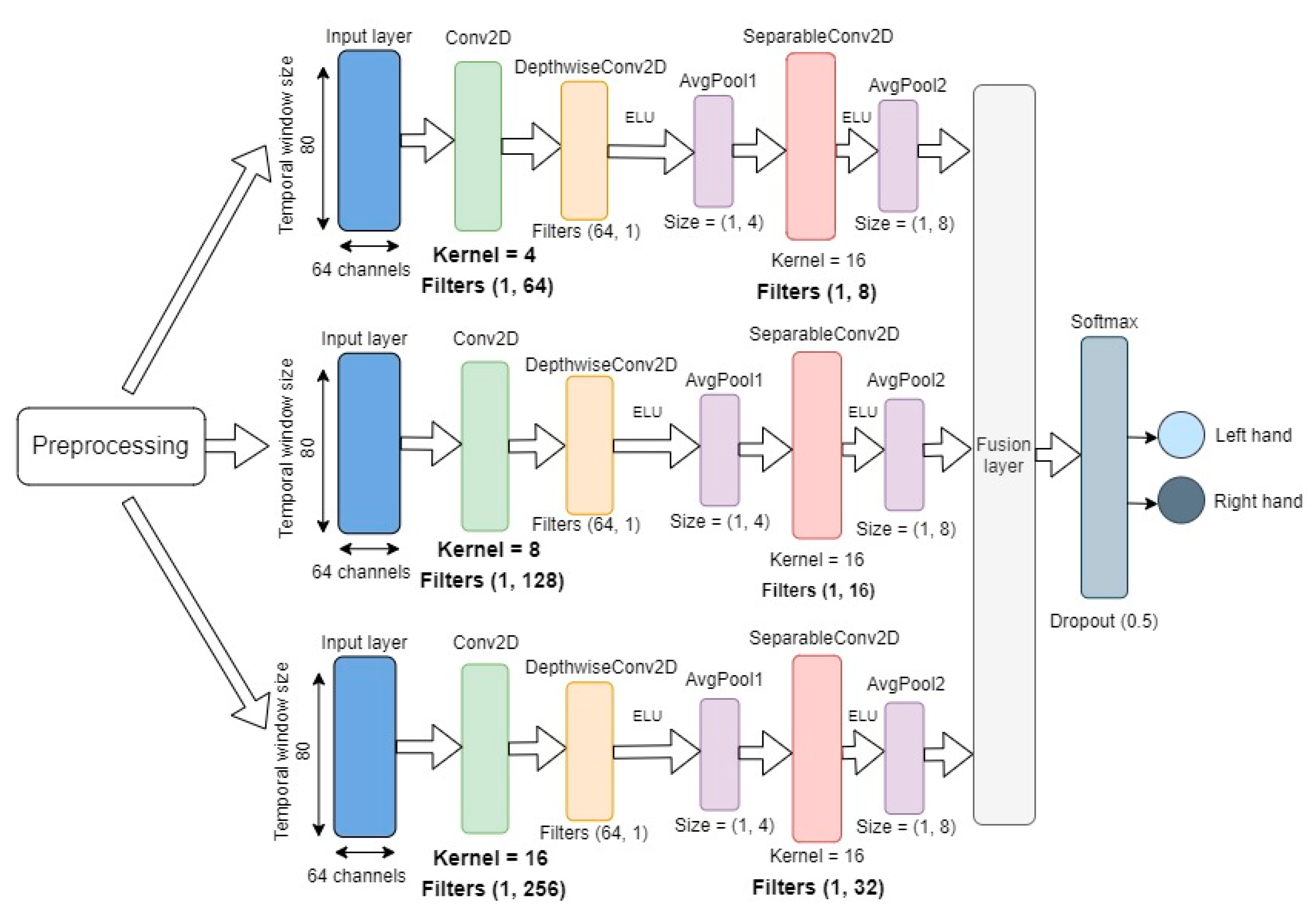
In this study, we propose a novel method of classifying motor imagery tasks using a multi-branch feature fusion convolutional neural network model, termed EEGNet Fusion (Implementation code of the models presented in this study and training and testing strategies are available at https://github.com/rootskar/EEGMotorImagery) (Figure 1), that is well suited for cross-subject classification. Comparative analysis is done, based on our EEGNet Fusion model, with three state-of-the-art models: EEGNet, ShallowConvNet, and DeepConvNet. Our experimental validation of the EEGNet Fusion model on the eegmmidb (The dataset used for model evaluation is publically available at https://physionet.org/content/eegmmidb/1.0.0/) dataset resulted in 84.1% accuracy for executed movement tasks, compared with the second-best result of 77% accuracy on the ShallowConvNet model. In addition, EEGNet Fusion achieved 83.8% accuracy on the imagined movement tasks, compared with the second-best result of 77.8% accuracy on the ShallowConvNet model. However, the downside of the increased accuracy for the proposed EEGNet Fusion model is an up to four times higher computational cost, compared with the lowest computational cost of the ShallowConvNet model.

2. Materials and Methods

In the following section, we describe the dataset and preprocessing methods used in this study, the proposed convolutional fusion network model architecture, the training and testing strategy, and the statistical significance methodology used for model evaluation.

2.1. Dataset

The PhysioNet [17] EEG Motor Movement/Imagery dataset was used for experimental validation of the proposed model. The dataset consists of over 1500 one- and two-minute EEG recordings, obtained from 109 volunteer subjects. The dataset is available at [18]. The subjects in the experiment performed different motor imagery tasks while EEG data was recorded using the BCI2000 [19] system. Each subject performed 14 experimental runs, including two baseline runs with eyes open and eyes closed and three two-minute runs of each of the following tasks: executing or imagining the opening and closing of the left or right hand and executing or imagining the opening and closing of both fists or both feet.

In this study, two subsets of the dataset were used. The first subset consists of only executed left- or right-hand movement tasks. The second subset consists of only imagined left- or right-hand movement tasks. In both subsets, 103 subjects out of the 109 were used, with subjects 38, 88, 89, 92, 100, and 104 being omitted due to incorrectly annotated data [20].

2.2. Preprocessing

The input data for each trial were sliced into dimensions (64, W), where W denotes the temporal dimension and 64 is the number of channels. As each trial for executed and imagined tasks contained 4 to 4.1 s of continuous, sustained executed or imagined movement, all of the trials were clipped to contain exactly 4 s of data, sampled at 160 Hz for a total of 640 samples to maintain a consistent dataset.

Using the sliding window approach, the 640 samples in each trial were sliced into 8 non-overlapping windows with 80 samples each. Each window was given the same target label as the original trial. This effectively increased the dataset size by 8 times the original size, giving us much more data to work with.

Next, the EEG signals were processed using the signal processing module in the Gumpy BCI library [21]. A notch filter was applied to the data to remove the alternating current (AC) noise in the 60 Hz frequency. The data was further band-pass filtered in the range of 2 Hz to 60 Hz with an order value of 5.

2.3. Model Architecture

The proposed model architecture was based on the EEG-based cross-paradigm CNN model, EEGNet [11]. According to the authors, the original architecture of EEGNet is well suited for any type of EEG-based classification problem.

The proposed model, termed EEGNet Fusion (see Figure 1), consisted of three different branches, with each branch given the same input. The overall structure of each branch was the same as the structure of the EEGNet architecture (see Figure 2), but the kernel size and the number of convolutional filters in the depth-wise and separable convolutional layers were different for each branch. The basic structure of the branches can be described as follows.

The input layer takes in two-dimensional input with spatial (number of channels) and temporal (datapoints per sample) dimensions for each sample. In each branch, the model first learns frequency filters with temporal convolutions by utilizing two-dimensional convolutional layers with kernel sizes 4, 8, and 16, and filters with sizes (1, 64), (1, 128), and (1, 256) for the three branches, respectively. The initial temporal convolutional layer is followed by a depth-wise convolutional layer with (64, 1) filters for all branches. The main benefit of the depth-wise convolutions is to reduce the number of trainable parameters, while providing a way to extract frequency-specific spatial filters for each temporal filter.

Finally, a separable convolutional layer with kernel size 16 for all branches and (1, 8), (1, 16), and (1, 32) filters was used for the three branches, respectively. The separable convolution combined depth-wise convolutions with pointwise convolutions to learn temporal summaries of each feature map individually and optimally mix the feature maps together [11]. Each convolutional layer was also followed by batch normalization, which is an effective method for reducing overfitting and improving the training speed of the network.

Furthermore, each depth-wise and separable convolutional layer was followed by an exponential linear unit (ELU) activation function, which is a popular alternative to the rectified linear unit (ReLU) activation function and is more computationally efficient in CNN-based classification [22].

Average pooling layers were used after the depth-wise and separable convolutional layers. The objective of the pooling function was to down-sample an input representation by reducing its dimensions. This in effect reduced the computational cost by having fewer parameters to learn. In addition, to reduce overfitting, each pooling layer was followed by a dropout function with the value 0.5.

After the final pooling layer, a feature fusion layer was used to merge the weights of the three CNN branches, and its output was given as input to the softmax classification layer, producing the probabilities for each of the two classes (left- or right-hand executed movement in one experiment and left- or right-hand imagined movement in the second experiment).

2.4. Implementation of the Models

The neural networks were implemented using the Python TensorFlow framework. Training and testing were performed on a single NVIDIA Tesla P100 GPU. For optimization, the Adam algorithm was used, along with a binary cross-entropy loss function and a learning rate of 0.1 × 10⁻⁴. The dropout probability value was 0.5 for all dropout layers.

2.5. Training and Testing Strategy

The dataset consisted of 45 trials per subject and, after preprocessing, the number of labeled samples was 360 for each subject. The total number of labeled samples for all 103 subjects in both executed and imagined task subsets was 37,080. 70% of the total samples were randomly selected for training, 10% for validation, and 20% for testing. The same data split was used for each experiment, as the random selection was implemented using a fixed seed value.

During the training phase, the validation loss was evaluated and the model weights with the best validation accuracies were saved. Before the testing phase, the model weights with the best validation accuracies were loaded, and the model was evaluated on the testing dataset by predicting target labels and calculating the accuracy as the ratio of correct predictions out of the total number of targets, as well as the precision, recall, and computational time per sample for the model.

2.6. Precision, Recall and F1-Score

In this study, precision, recall, and the F-score were calculated in the following manner. In the used dataset, there were no negative trials observed, as both left- and right-hand movement were considered positive trials. However, the calculations for each hand were performed separately. This means that in one set of evaluations, we considered the left-hand target label as the positive value, while the right-hand label was used as the negative value. This, however, does not mean that the right-hand label was considered a negative trial, but it was used as such to evaluate the model’s ability to distinguish left-hand movement from right-hand movement. In another set of evaluations, we considered the right-hand target label as the positive trial. As such, the values used for the evaluation of the metrics were as follows:

• True positive (TP), where the prediction was left-hand (or right-hand), and the correct label was also left-hand (or right-hand);
• False positive (FP), where the prediction was left-hand (or right-hand), but the correct label was right-hand (or left-hand);
• True negative (TN), where the prediction was right-hand (or left-hand), and the correct label was also right-hand (or left-hand);
• False negative (FN), where the prediction was right-hand (or left-hand), but the correct label was left-hand (or right-hand).

Using the total number of these values, we calculated the value of precision as given by the formula in Equation (1), recall as given by the formula in Equation (2), and the F-score as given by the formula in Equation (3).

Equation (1) Formula for the calculation of the precision metric.

$$Precision=\frac{tp}{tp+fp}$$

(1)

Equation (2) Formula for calculation of the recall metric.

$$Recall=\frac{tp}{tp+fn}$$

(2)

Equation (3) Formula for the calculation of the F-score metric.

$$F_1=2\times \frac{precision\times recall}{precision+recall}$$

(3)

2.7. Statistical Significance

It is common practice to evaluate the classification methods using 10-fold cross-validation and use the paired Student’s t-test to check if the difference in the mean accuracy between the two models is statistically significant. However, in the k-fold cross-validation procedure, a given observation was used in the training dataset k − 1 times. As such, the estimated skill scores were not independent, and it has been shown that this approach has an elevated probability of type I error [23].

The statistical significance of the experimental results in this study was evaluated using McNemar’s statistical test [24]. McNemar’s test is a paired nonparametric or distribution-free statistical hypothesis test. The test evaluated if the disagreements between the two evaluated classifiers matched.

Under the null hypothesis, the two classifier models compared should have had the same error rate. We could reject the null hypothesis if the two models made different errors and had a different relative proportion of errors on the test set. This type of test is shown to have a low type I error and can be used to show statistical significance when not using cross-validation [23].

3. Results

In the following section, the experimental setup and results of the experiments with the proposed model and three state-of-the-art models used for comparison are outlined.

3.1. Experimental Setup

The performance of the proposed classifier for both executed and imagined tasks was evaluated in the following manner. The 103-subject dataset was tested on EEGNet [11], ShallowConvNet, and DeepConvNet [10] architectures, and the results were recorded for comparison with the results of our proposed EEGNet Fusion model. For all experiments, if not specified otherwise, 70% of the samples were randomly chosen for training, 10% for validation, and 20% for testing.

3.2. Experimental Results

The testing accuracy, precision, recall, computational time per sample, and the calculated p-value relative to the proposed EEGNet Fusion model for executed movement tasks on all evaluated models can be seen in

Table 1. Executed motor task results.

Model	Accuracy	Precision		Recall		F-Score		Comp. Time (per Sample)	p-Value
		Left	Right	Left	Right	Left	Right
EEGNet	65.8%	63.3%	66.1%	54.6%	64.5%	58.6%	65.3%	39 ms	<0.001
ShallowConvNet	77%	77.2%	77.5%	76.4%	76.7%	76.8%	76.6%	23 ms	<0.001
DeepConvNet	76%	75.2%	76.9%	75.7%	73.8%	76%	75.3%	38 ms	<0.001
EEGNet Fusion	84.1%	84.2%	84.5%	83.8%	83.9%	84%	84.2%	107 ms	1

. For executed movement tasks, the proposed EEGNet Fusion model performed better than the benchmark classifiers, with a statistically significant result (p < 0.001) of 84.1% accuracy, an 84% left-hand F-score, and an 84.2% right-hand F-score, compared with the second-best accuracy of 77%, a left-hand F-score of 76.8% and a right-hand F-score of 76.6% for the ShallowConvNet model. The ShallowConvNet model achieved the fastest computational time per sample at 23 ms, while EEGNet Fusion was the slowest with an average computational time of 107 ms per sample.

For imagined movement tasks, EEGNet Fusion outperformed the benchmark models with a statistically significant result of 83.8% accuracy, an 83.9% left-hand F-score, and an 84% right-hand F-score against the second-best accuracy of 77.8%, a left-hand F-score of 78.4% and a right-hand F-score of 76.6% for the ShallowConvNet model. Furthermore, the ShallowConvNet model achieved the lowest computational time per sample at 24 ms, while EEGNet Fusion had the highest average computational time at 110 ms. The results for imagined tasks can be seen in

Table 2. Imagined motor task results.

Model	Accuracy	Precision		Recall		F-Score		Comp. Time (per Sample)	p-Value
		Left	Right	Left	Right	Left	Right
EEGNet	68.2%	68.9%	68.1%	66.9%	67.8%	68.5%	67.3%	39 ms	<0.001
ShallowConvNet	77.8%	79.4%	77.5%	75.4%	77.9%	78.4%	76.6%	24 ms	<0.001
DeepConvNet	75.8%	75.8%	74.3%	72.7%	76%	74.2%	75.1%	38 ms	<0.001
EEGNet Fusion	83.8%	85%	83.3%	82.9%	84.8%	83.9%	84%	110 ms	1

.

These results suggest that the EEGNet Fusion model is well suited for cross-subject EEG motor imagery classification when used in combination with the proposed preprocessing methodology.

4. Discussion

This study aimed to improve the accuracy of motor imagery classification to help people with limited motor abilities interact with their environment using brain–computer communication. In this work, we proposed a novel feature fusion-based multi-branch 2D convolutional neural network, termed EEGNet Fusion, for cross-subject EEG motor imagery classification. The model was evaluated on the PhysioNet Motor Movement/Imagery dataset to classify left- and right-hand executed and imagined movement. The 103-subject data were preprocessed using a moving window approach and band-pass signal filtering. The experimental results showed 84.1% and 83.8% classification accuracies for executed and imagined movements, respectively.

Our model, EEGNet Fusion, was computationally the slowest among the tested neural networks, with an average computational time per sample at 107 ms and 110 ms for executed and imagined movements, respectively. This was over four times as high as ShallowConvNet at 23 ms and 24 ms for the same tasks, but we believe the significantly higher accuracies of EEGNet Fusion mitigate the computational cost of the proposed network.

The results show that for cross-subject classification, this type of architecture outperforms other evaluated state-of-the-art models—EEGNet, ShallowConvNet, and DeepConvNet—with statistically significant results and, as such, could be an appropriate basis for further research. We consider our main contribution to be the evaluation of multi-branch feature fusion networks for EEG motor imagery data, which so far has not been widely researched. The statistically significant increase in accuracy for both executed and imagined movements, compared with the other evaluated models, can be explained by the flexibility of the multiple branches of the network. Each branch can be tuned to have the most optimal hyperparameters, and the fusion layer merges the features together to form a more complex feature map than is possible for only a single branch. We show that this type of network has the potential to alleviate the difficulty of cross-subject EEG classification by giving the neural network more flexibility in the choice of hyperparameters and, as a result, increase the accuracy of cross-subject classification.

Although the model was tested only on motor movement and imagery data, the underlying architecture is known to be well suited for different EEG-based tasks. In the future, more testing of the model should be done to validate its performance on a wider range of EEG-related areas, such as sleep stage and disorder detection or driver fatigue evaluation. Furthermore, the multi-branch architecture is not limited to three branches, and architectures with a higher number of branches could be explored.