Formation of Unique Characteristics of Hiding and Encoding of Data Blocks Based on the Fragmented Identifier of Information Processed by Cellular Automata ^†

Abstract

Currently, the following applications of the theory of cellular automata are known: symmetric encryption, data compression, digital image processing and some others. There are also studies suggesting the possibility of building a public key system based on cellular automata, but this problem has not been solved. The purpose of the study is to develop an algorithm for hiding and encoding data blocks based on a fragmented identifier of information processed on the basis of cellular automata in the scale of binary data streams using an original method containing an public parameter in the conversion key. A mathematical model of the formation of unique data characteristics is considered, based on the use of patterns that determine the individual neighborhood of elements in cell encryption. A multi-threaded computing scheme has been developed for processing confidential data using the single-key method with a public parameter based on cellular automata and using data segmentation. To study individual chains in data blocks, a software module has been developed that allows one to evaluate the uniformity of information distribution during encryption. A variant of estimating the distribution of bits is proposed that indirectly reflects the cryptographic strength of the method. Based on the developed theoretical principles, a software module is synthesized that implements a transformation rule that takes into account the individual neighborhood of the processed element on the basis of a cellular automata. Experimental studies have shown that this modification made it possible to increase the speed of the method by up to 13 percent due to segmentation and the possibility of parallel processing of the original matrix, as well as to increase cryptographic strength due to the use of a unique chain of pseudo-random neighborhood (hereinafter referred to as PRN) defined by the transformation key. At the same time, it was possible to maintain uniformity of distribution of the output chain at the bit level and to ensure that the number of inversions was included in the confidence interval.

1. Introduction

The rapid development of information technology involves the continuous improvement of tools that ensure information security when working with confidential data or ensure the completeness and integrity of information resources [1,2]. Special attention is paid to protecting information from unauthorized access using modern cryptographic methods and system analysis in distributed systems operating in real time [3,4]. As a rule, software and hardware solutions for providing integrated crypto protection are distinguished by the complexity of integration into the local computer network, and also require support with the involvement of experts in the field of information security [5,6]. The development of information technology involves the continuous improvement of tools that provide data processing and data accounting [7,8]. The solution of such problems in real time involves the improvement of streaming data processing methods [9,10].

In this paper, we propose a modification of the multithreaded data processing method based on a cellular automata, which we considered earlier in the work “Multi-Threaded Data Processing System Based on Cellular Automata”. In the previously proposed encryption method, data processing consisted of sequential processing of all blocks, starting from the first (the position of the first block is determined by the processing mode) with a fixed neighborhood that determines the bits involved in data processing.

The difference of the proposed method of data conversion based on a cellular automaton is the introduction of a local block processing rule based on a finite set of patterns. Moreover, the update function works with a cell if and only if there is a correspondence between the states of its neighbors and a given pattern. Another important feature of the proposed scheme is the use of an initialization and control unit for multithreaded data processing.

In order to increase cryptographic strength and maintain a high processing speed of data streams, it is proposed to use an extended key that determines the PRN (pseudo-random neighborhood) taking into account the position of the processed bit in the source data matrix. The public parameter in this case will be the number of columns of the information matrix, and the private key will consist of an encryption matrix and a rule to bypass the data matrix.

For experimental studies, a software module for the analysis and comparison of data blocks in the form of binary matrices was developed, with the help of which an analysis of individual chains in data blocks was carried out. The analysis confirmed the expected uniformity of the distribution of changed bits and a high conversion rate due to segmentation of data blocks based on a fragmented matrix identifier.

The practical significance of the method lies in the fact that the results can be used for research purposes when studying the methods of organizing multi-threaded calculations and ensuring information security when working with large data arrays. This method has the prospects of improving performance by integrating computing servers on a computer system scale.

The “Related Studies” section provides an overview of the main research in the field of cellular automata, as well as approaches to key formation during data transmission. The description of the proposed organization scheme for multi-threaded data processing based on cellular automata is presented.

The “Materials and Methods” section presents a conversion scheme based on sequentially changing the bits of the source file according to the instructions in the key. This section also describes the mathematical model and the encryption process. An encryption algorithm of the developed system is presented on the example of the first-order Moore neighborhood.

In the section “Results and discussion” presents the results of experiments and their analysis. In the course of research, the original and modified method of processing a data stream based on cellular automata was compared in terms of the processing speed of one stream, the uniform distribution of bits and the maximum delta between inverted matrix elements.

The section “Conclusion” presents the main conclusions and directions of development in the future.

2. Related Studies

The idea of cellular automata was proposed by J. von Neumann and K. Zuse in the late 40 s. Initially, cellular automata were considered as a universal computing environment for constructing algorithms and modeling physical processes, equivalent in its own capabilities to a Turing machine [11]. Since the beginning of the 1970s, international conferences on the parallel processing of information on cellular automata began to be regularly held in Berlin. At the same time, the game “Life”, based on two-dimensional cellular automata, gained fame. In 1983, the British mathematician S. Wolfram began work on a model of cellular automata, which he subsequently used in cryptography and hydrodynamics. In the field of symmetric encryption, it is worth highlighting the works [12,13], as well as the papers [14,15], in which the problem of the reversibility of cellular automata is considered. It is also worth noting the key generation approach for the secure transmission of information based on the Catalan key, proposed in the work [16]. This study was developed in the paper [17], in which a new method of data hiding was proposed, based on the generation of the key, and not on the replacement of bits.

A description of a cellular automata with an objective function was presented in [18], this idea was developed in [19], in which a definition of an improved cellular automata on a partition was proposed and a model of a cellular automata with a floating window was described. When using a cellular automata with a floating window, processing (encryption) starts from the first block (depends on the input parameters and processing mode), then the iterative process is repeated in order until all blocks are processed. Based on the studies conducted in this work, it was decided to introduce a local block processing rule based on a finite set of templates, which implies a reduction in encryption time without loss of cipher strength. Each pattern defines an individual neighborhood of information bits. The update function works with a cell if and only if there is a correspondence between the states of its neighbors and the given pattern. Let us consider in more detail this modification of the multithreaded data processing method.

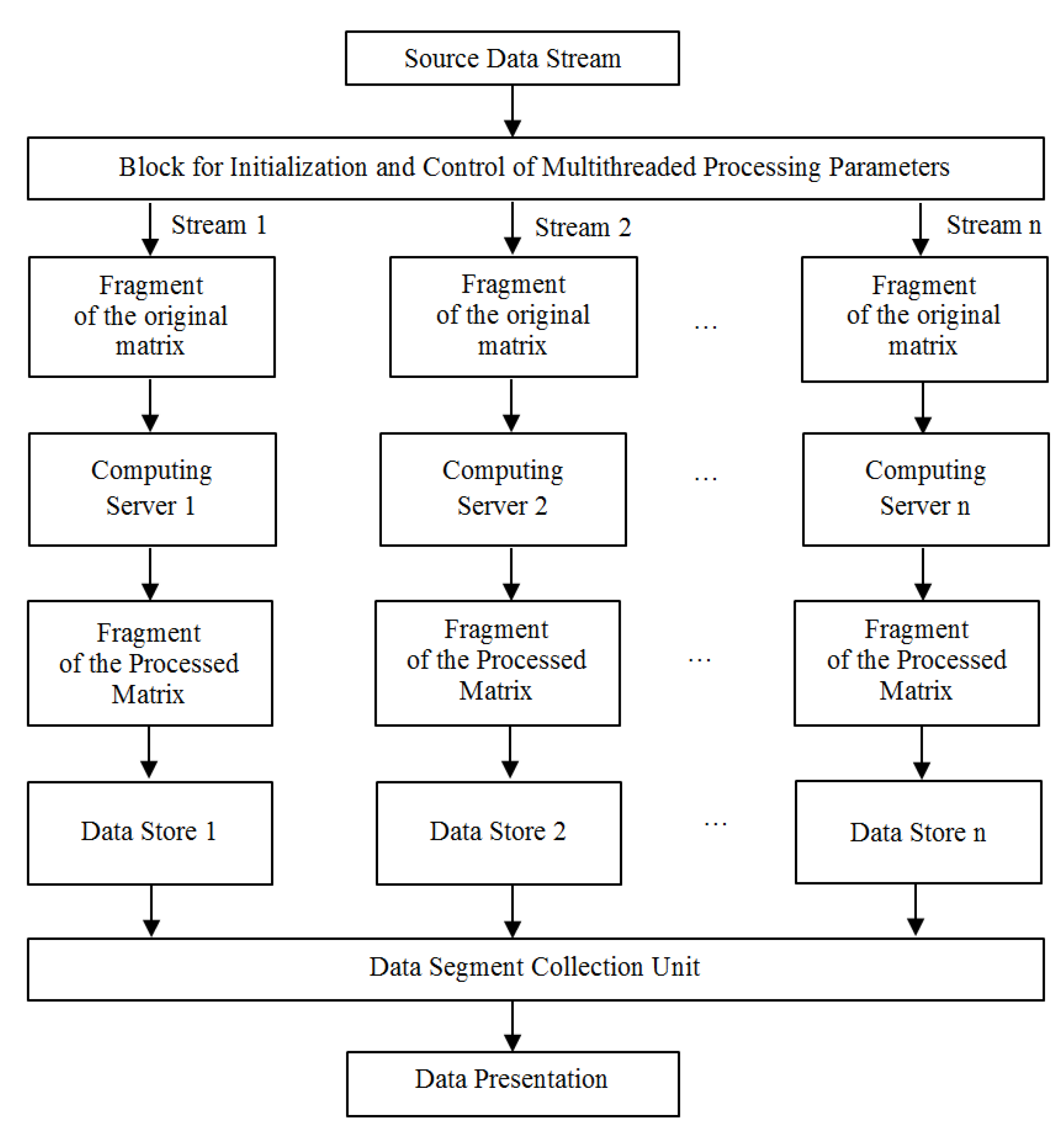
A feature of the proposed multi-threaded processing option is the use of an initialization and control block for multi-threaded processing parameters, with the help of which tasks are distributed between servers or CPU resources during processing on one computer. The proposed scheme of single-key encryption of data streams with a public parameter and the possibility of parallel computing based on cellular automata is shown in Figure 1. This scheme allows the rational use of computing resources [20].

The initial matrix is divided into segments defined by the initialization and control unit. Then the fragments of the original matrix are distributed between the calculators on which the data is processed. Thus, the encrypted matrix is formed in parallel on several computing resources and is represented by a set of segments at the output. Segments in accordance with the collection rule form an encrypted file. The use of multiple data stores is advisable since while recording by several streams simultaneously, the information storage device becomes a weak link in the performance chain [21]. The proposed organization makes it possible to implement a processing system on a scale of the Internet, and a separate server is an asynchronous link in the computing chain, the state of which is controlled by the segment collector at the level of a single database.

3. Materials and Methods

3.1. Data Conversion Scheme

The proposed conversion scheme is based on sequentially changing the bits of the source file according to the instructions in the key. A public parameter is the number of columns of the information matrix—this information is transmitted over a public communication channel. The private key consists of an encryption matrix and a data matrix bypass rule. The operation scheme of the binary data stream processing system is shown in Figure 2.

As the basis of the algorithm, we take a model of a cellular automata in which the elements of the system are determined according to a given neighborhood. An element n of the information matrix will be considered as a block. A rule is introduced for local processing of matrix elements based on a finite set of patterns P. Each pattern defines an individual neighborhood for information bits. The update function works with a cell if and only if there is a correspondence between the states of its neighbors and pattern P. Based on the studies presented in [22], we introduce two serious restrictions: all patterns in the composition have the same neighborhood as the final result their compositions, and all templates have the same shape. These simple restrictions provide a transparent and efficient implementation of computing resources.

3.2. Mathematical Model

To describe the operation of the method consider working with a binary matrix. Based on the studies, it is advisable to use the first-order Moore neighborhood, since when using larger-order neighborhoods, the encryption time increases, and the algorithm’s stability does not practically increase. Nevertheless, it is possible to use neighborhoods of arbitrary dimensions corresponding to the private key. The so-called square encryption matrix, which is set by a binary file, acts as a private key. It is a pattern that defines the PRN bits of the data matrix. The dimension X of the encryption matrix is defined as the integer part of the root of the number of bits in the matrix file (formula (1)):

$$X=[\sqrt{s\left(x\right)8}],$$

(1)

where $s\left(x\right)$ is a size of source file in bytes. Next, we determine the dimension of the data matrix segment. The number of columns of the information matrix $N_1$ is a public encryption parameter. The number of matrix rows is determined by the size of the initial data, and in the case of a network stream, it depends on the interaction session of the subscribers of the computer network and is calculated by the formula (2):

$$N_2=X8k,$$

(2)

where k is determined based on the size of the data buffer, $k={\displaystyle \frac{\left(Capacity{2}^{10}\right)}{\left(NX\right)}}$, where N is a dimension of the cipher matrix (defined as the integer part of the root of the number of bits in the matrix file). In this case, the last incomplete line is padded with zeros. The Capacity parameter determines the size of the nearest data segment in kilobytes; it is set depending on the performance of hardware resources and the size of the data stream. It should not be taken less than 256 KB and more than 100 MB because this can lead to a decrease in performance in multi-threaded processing [23].

It is recommended to accept $N_1>X$, since the open parameter sets the width of the working part of the matrix. Compliance with this recommendation maximizes the number of PRNs (since the cipher matrix works over the entire width) and increases the cryptographic stability of the conversion.

The method for generating the PRN consists in the fact that for each information bit (where n is the column number, m is the row number) a symmetric neighborhood of arbitrary order with a central element and not exceeding the dimension of the encryption matrix is superimposed. Thus, for a PRN of dimension w, the coordinates of the central element are determined by formula (3):

$$x=mmod(X-w)+[{\displaystyle \frac{w}{2}}]+1;y=nmod(X-w)+[{\displaystyle \frac{w}{2}}]+1.$$

(3)

Further, in accordance with the matrix bypass rule (a separate Slide directory), we perform encryption at the cellular level, taking into account the PRN. The basic level of data protection involves a single pass of matrix elements along the selected route, an advanced level of protection—two bypass options. Thus, a cellular automata with PRN and segmentation of fragments is called the totality:

$$C{A}_{OP}=<Z^n,(N_1,\dots ,N_n),A,P,(p_1,\dots ,p_n),X,Slide>,$$

(4)

where: $Z^n$ is a dimension of a cellular automata ($n=2$); $(N_1,\dots ,N_n)$ is a segment size of the data matrix, while $N_1$ is a public encryption parameter; $A=\{0,1\}$ is a value of data bits (alphabet); $(p_1,\dots ,p_n)$ is an encryption matrix; X is an encryption matrix dimension; $Slide$ is a rule for bypassing elements of the information matrix during processing.

The encryption process is as follows:

• In accordance with the $Slide$ matrix bypass rule, the current bit of the processed data matrix segment is taken. In the simplest case of traversal (line by line from left to right) the first is the upper left bit.
• According to the formula (3), the coordinate of the center of the PRN is determined, the unit values of the bits of which determine the neighbors involved in the conversion of the current data bit. Thus, when moving along a segment, movement along the cipher matrix occurs.
• Due to the fact that matrix expansion along the perimeter is not required, a logical operation $xor$ of the current matrix bit and single bits from the existing ones (taking into account the boundaries of the processed segment) and marked with the PRN rule is performed.
• If the result obtained in the previous step differs from the value of the current bit, it is inverted.
• If not the entire segment is processed, then the transition to the next bit is performed in accordance with the bypass rule.
• The processed chain of bits in the form of a matrix-result is unloaded into the output buffer, this completes the processing.
• The sign of processing the entire data stream is set to true when all segments created at the task scheduler level are processed.

The advantage of the method is the flexibility of processing and the possibility of positioning the processing stage on the scale of the computer network with the allocation of the target protected node that takes on the tasks of the initialization and assembly of the final fragments.

3.3. Conversion Algorithm

For clarity, consider the encryption algorithm of the developed system using the example of the first-order Moore neighborhood as it allows one to use a larger number of matrix elements than the von Neumann neighborhood.

At the first step of the algorithm, we determine the dimension of the encryption matrix in accordance with formula (1). The encryption matrix is a pattern in accordance with which an individual neighborhood of the information bit is specified (formula (5)):

$$P=\left[\begin{array}{ccc}{p}_{11}& p_{12}& p_{13}\\ p_{21}& ?& p_{23}\\ p_{31}& p_{32}& p_{33}\end{array}\right]$$

(5)

The recipient’s private key is recorded in the key matrix P. The principle of recording is shown in

Table 1. The principle of recording the key in the matrix P.

Matrix Element	${\mathit{p}}_{11}$	${\mathit{p}}_{12}$	${\mathit{p}}_{13}$	${\mathit{p}}_{21}$	${\mathit{p}}_{22}$	${\mathit{p}}_{23}$	${\mathit{p}}_{31}$	${\mathit{p}}_{32}$	${\mathit{p}}_{33}$
Bit Serial Number	1	2	3	4		5	6	7	8

.

It is important to note that the interval of values 1–3 for element indices reflects the local coordinates of the window whose center is positioned in accordance with formula (3). The serial number for element $p_{22}$ is skipped since it is not of interest and during processing is replaced by the value of the processed information bit from the data matrix.

Next, we determine the dimension of the data matrix segment in accordance with formula (2). Construct a matrix N of size $n\times m$. The number of columns of the matrix $N_1$ is in this case a public parameter ($N_1>X$ is recommended), where X is the dimension of the encryption matrix) (formula (6)):

$$N=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& \dots & a_{1m}\\ a_{21}& a_{22}& a_{23}& \dots & a_{2m}\\ a_{31}& a_{32}& a_{33}& \dots & a_{3m}\\ \dots & \dots & \dots & \dots & \dots \\ a_{n1}& a_{n2}& a_{n3}& \dots & a_{nm}\end{array}\right]$$

(6)

Moreover, $a_{11},a_{12},\dots ,a_{nm}$ correspond to the bits of the file $s_1,s_2,\dots ,s_i$. If the file size is $i<nm$, then fill the empty matrix elements with zeros, the number of such elements is calculated by formula (7):

$$z=nm-i.$$

(7)

In other words, the last segment of the matrix can be supplemented with zero bits (“tail”) to complete the rectangular segment [24]. The remaining segments do not need to be added because the dimension of the matrix in accordance with the proposed method is a multiple of eight. For reversibility of encryption and exclusion of the “tail”, it is possible to use cryptographic hash functions of the number of added elements, in which case it is advisable to use an arbitrary chain of bits [25]. During decryption, this will determine the number of bits that will not be taken into account during the operation of the software module [26].

The second step involves the formation of the matrix $N^{*}$. Direct and inverse transformations involve opposite rounds of elements; this is a necessary condition for convergence [27]. If the elements of the neighborhood of the central element of the key $L_{p_{22}}$ do not coincide with the similar elements of the neighborhood $L_{a_{ij}}$ of the element of the matrix $N^{*}$, then the value of the element remains the same, otherwise, a modulo-two addition operation with unit bits is applied to the element. The rule for processing an element of the matrix $a_{ij}$ within the considered neighborhood is presented in formula (8):

$$a_{ij}=[\sum _{k=i-1}^{i+1}\sum _{l=j-1}^{j+1}(p_{(k-i+2,l-j+2)}\&a_{kl})]mod2,$$

(8)

in this case $p_{22}=1$ o take into account the processed matrix element, and in case the indices go beyond the boundaries of the matrix, we take $a_{kl}=0$. Thus, the value of the element being processed is set to unity if and only if there is an odd number of unit bits among the neighbors defined by the PRN and the bit being processed.

At the final stage, the elements of the obtained matrix are recorded segmentally on the specified information storage devices and, if necessary, are assembled into a single object in accordance with the rule for collecting data segments determined at the stage of operation of the processing initialization block. An alternative option is to work in a distributed service mode, then the result is output at the level of data presentation, when the necessary part of the data is automatically downloaded from the drive only at the moment of direct access.

4. Results and Discussion

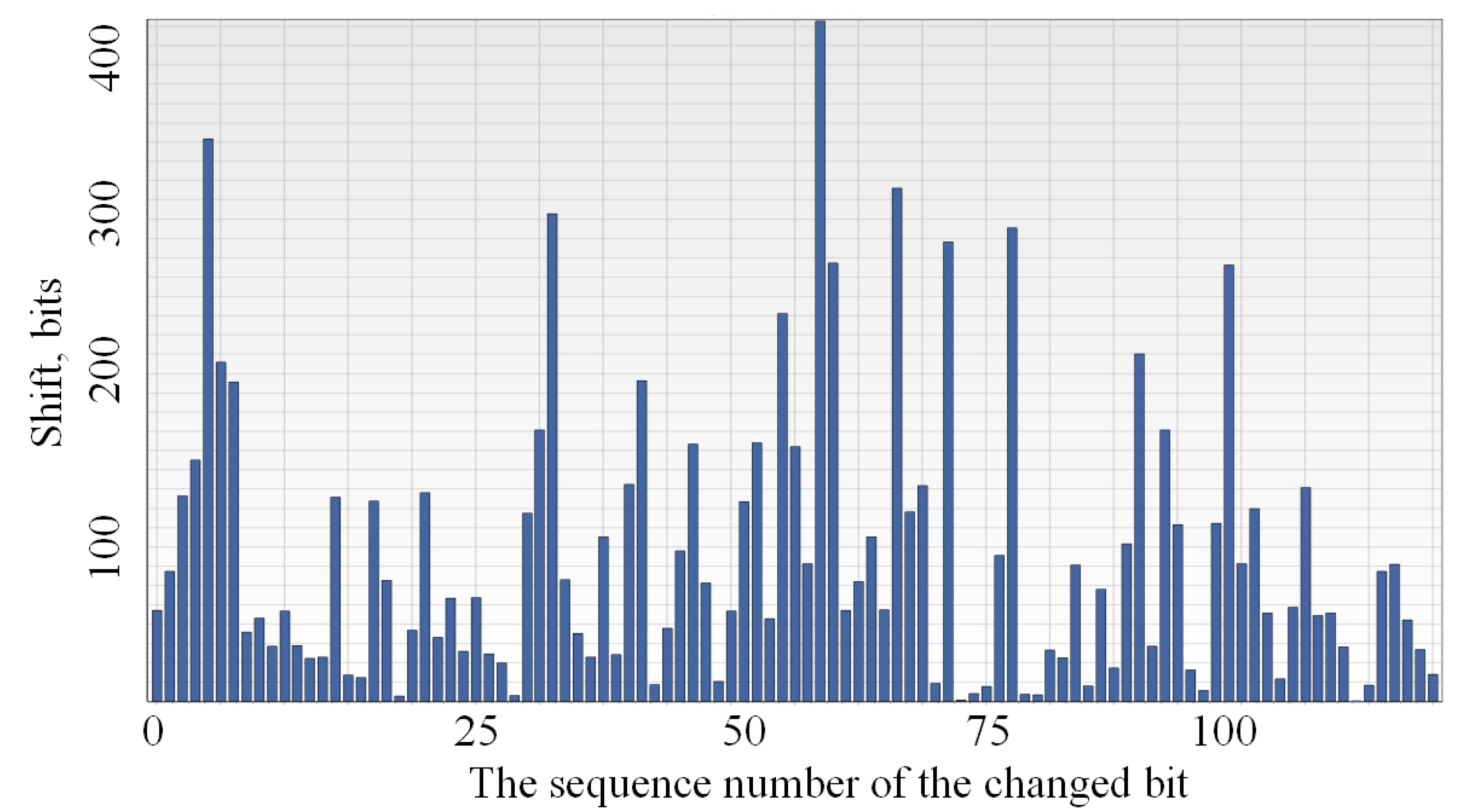
To conduct a detailed analysis of the proposed method, a software module has been developed to allow comparison of data blocks in the form of binary matrices. In the course of experimental studies, an analysis of individual chains was carried out taking into account the shift relative to the beginning of the file and the dimensions of the binary fragments. Figure 3 presents a typical graph of the distribution of the bit sequence generated on the basis of the original and processed matrices. As processing parameters, a composite key was used, consisting of a public parameter with values from the range 4200–9000, an encryption matrix in the form of a compressed raster image of 20 KB in size. As a data file, images were taken from a surveillance camera.

A small spread of heights in this graph shows a uniform distribution of bits during processing. The delta (the value of the column height corresponding to the distance between the changed data bits) determines the length of the binary chain matching in the original and processed matrix. A maximum value of eight is valid because involves a change at the byte level. The average is in the range of two to three bits, which indicates a significant difference in data streams on short bit fragments. In order to be able to identify and analyze potential deviations on the scale of the data fragment under consideration, in addition to the graph presented, the point of completion of the delta of maximum length in matrix coordinates is displayed. When analyzing network flows, the peak values were hundreds, and sometimes thousands, of bits, allowing identification of the entry point into the data segments separated by service headers. A similar situation was observed when bit shifts and noise in the communication lines occurred (Figure 4).

For a qualitative analysis of the distribution of changes during processing, we form a graphical representation of the superposition, which reflects the difference between matrices with reference to the coordinates. Figure 5a shows the state of the matrix using a pattern defining the PRN of the processed bit and based on a static sample for capturing elements ($3\times 3$ matrix size, Figure 5b). The value of the matrix element will be the values $\{-1,0,1\}$. White cells correspond to 0 (the value has not changed), horizontal hatching corresponds to a value of 1, vertical hatching corresponds to a value of −1. We see that both options allow us to achieve a fairly uniform distribution of changes at the bit level. The advantage of using a PRN (when the dimension of the encryption matrix is more than $3\times 3$) is the use of individual sets of boundary bits when processing at the cell level, which allows more efficient processing of matrix elements taking into account the rules at the secret key scale.

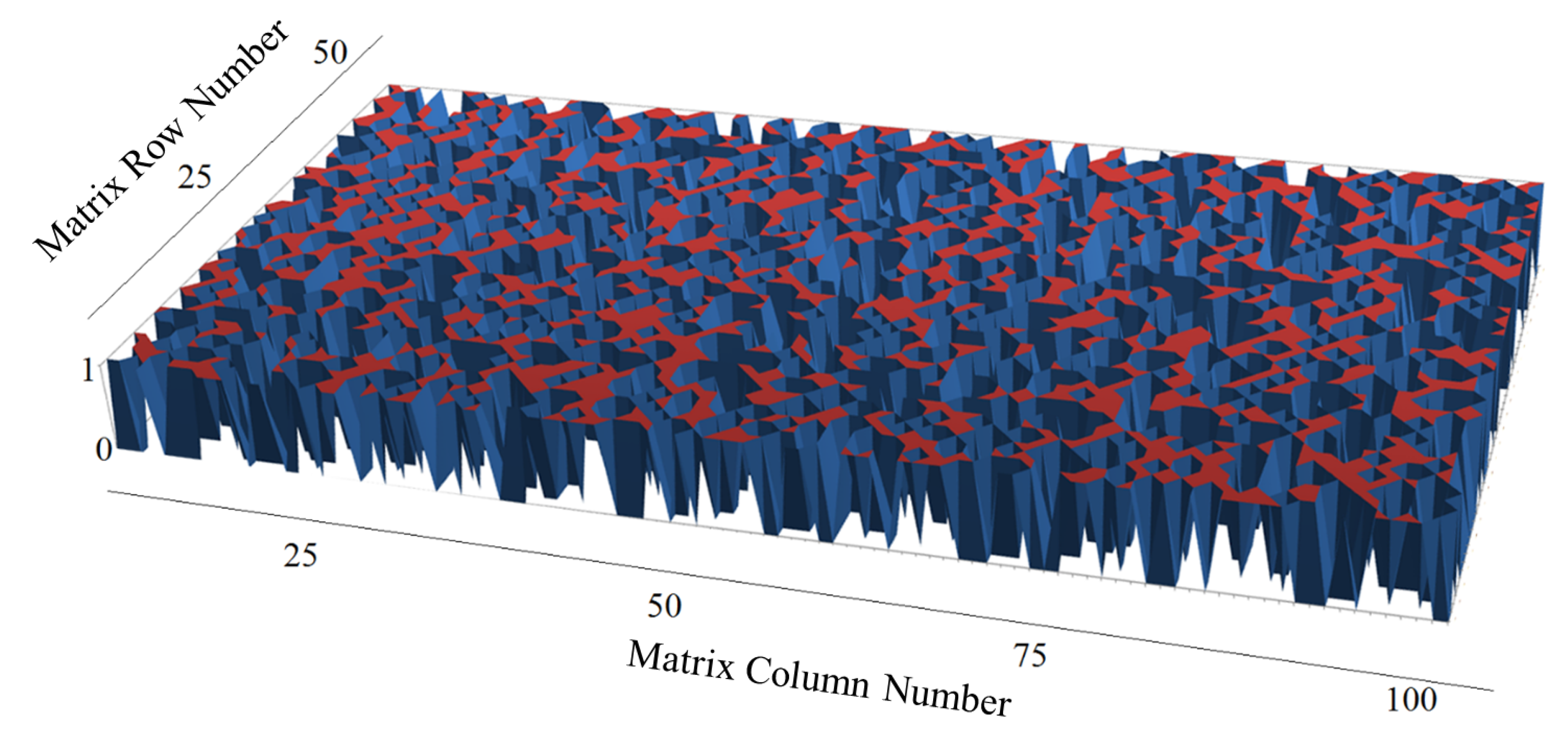
Data processing involves the use of the same displacements when forming matrices both when working with open data and with the results of transformations. This allows for the evaluation of cryptographic strength to take into account the mutual arrangement of bits located at the corresponding positions. Due to the fact that in the general case, it is not the specific value of the bit that is important, but the fact of its change from the initial state—we will produce a surface for the data obtained on the basis of the proposed method using the PRN. The result obtained is shown in Figure 6. Here, the points of difference rise from the main level and demonstrate the distribution of the changes made at the quantitative level. For clarity, a $50\times 100$ matrix fragment with a zero shift relative to the beginning of the file was selected. Inclined faces show a uniform transition between states, and “peaks” correspond to the centers of rectangular cells.

The view of the fragment of the graph “from below” (horizontal projection) coincides with Figure 5a. From the results it follows that the processed matrix contains at least 45 percent of the changes at the bit level and 100 percent of the changes at the byte level. Under the conditions of matching the bit position before and after processing, this excludes access to protected data from the side of the attacker without the inverse transformation involving knowledge or selection of key parameters. The number of options for generating a PRN depends on the key parameters, namely, on the size of the encryption matrix and grows exponentially. Considering the fact that an attacker who has an open part of the key, in addition to selecting a matrix-cipher, needs to search for options to bypass information bits, which can be combined. Based on this, we conclude that a high level of cryptographic strength is obtained.

In the original method, processing starts from the first block (depends on the input parameters and processing mode), then the iterative process is repeated in order until all blocks are processed. The modified method implies the use of a pattern, while the update function works with the cell if and only if there is a correspondence between the states of its neighbors and a given pattern. As the studies showed, the use of the template will significantly increase the cryptographic strength of the method, and when using the advanced processing mode (two or more workarounds), it will significantly increase the cryptographic strength of the proposed method and maintain an acceptable level of performance due to the distribution of computing load if it is necessary to work in real time.

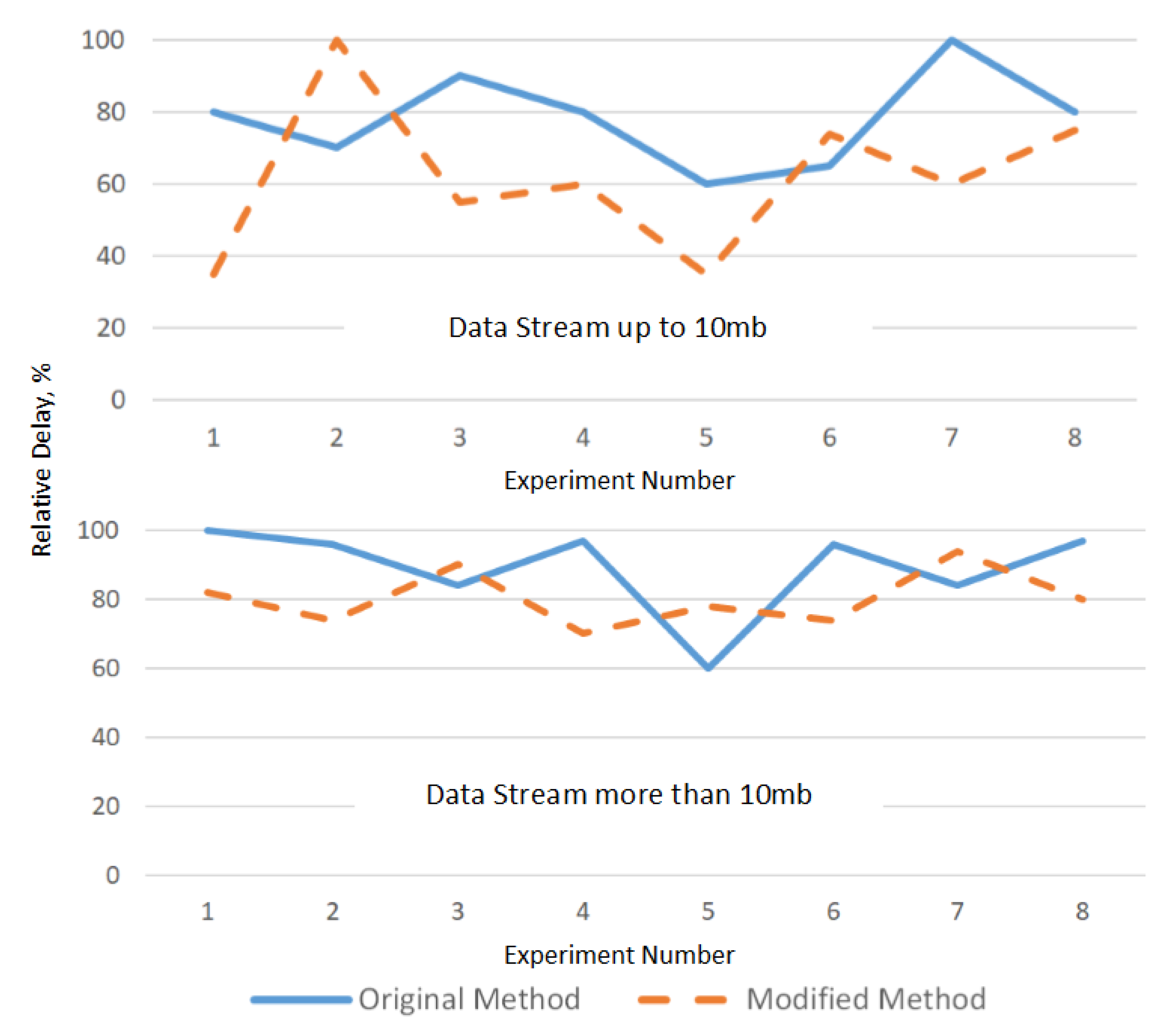
In the course of research, an original and modified method of processing a data stream based on cellular automata was compared in terms of the processing speed of one stream, the uniform distribution of bits, and the maximum delta value between inverted matrix elements. For the objectivity of the results, taking into account the length of the data stream, the group of experiments is divided into two stages of processing sequences of less than 10 MB (graphics, documents, audio files), and exceeding this value (video content, archives, etc.). All experiments were carried out on the same equipment (Figure 7, Figure 8, Figure 9 and Figure 10).

Figure 7 shows that the performance of the modified method remains at the original level, and when processing large data streams, it has smaller deviations from the average value. This makes it possible to predict the processing time and take into account when selecting the hardware.

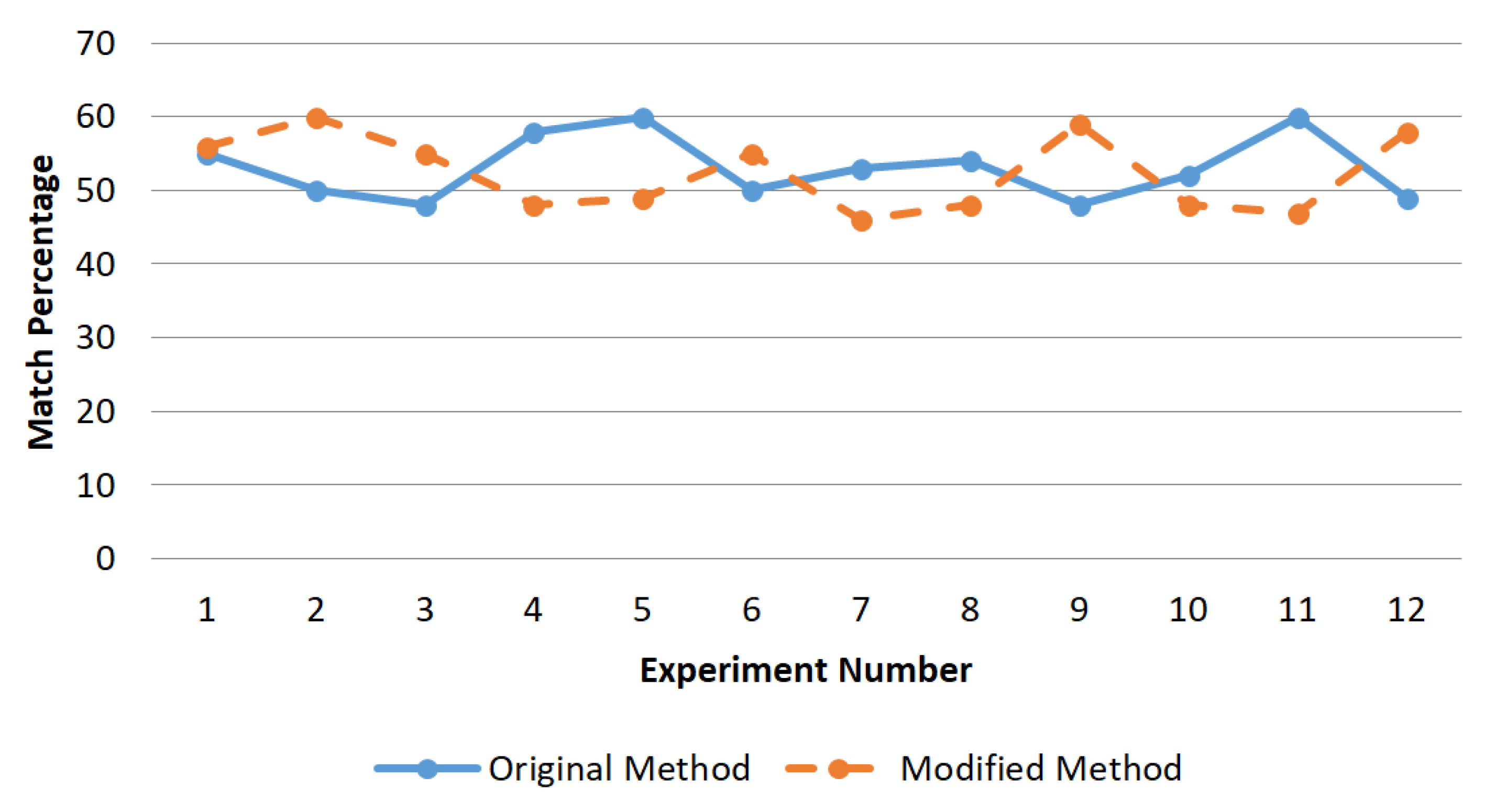
From Figure 8 it follows that matrices processed by both methods by the number of inversions enter the confidence interval of 40–60 percent, but the modified method increases cryptographic strength due to the need to use individual neighborhoods for each bit of the data matrix, which greatly complicates the task of the inverse transformation without knowledge of the key. Given that the key file determines a large number of PRNs that are used in strict sequence—the brute force method, which is suitable for opening the cipher of the original method, becomes inapplicable in the proposed modification.

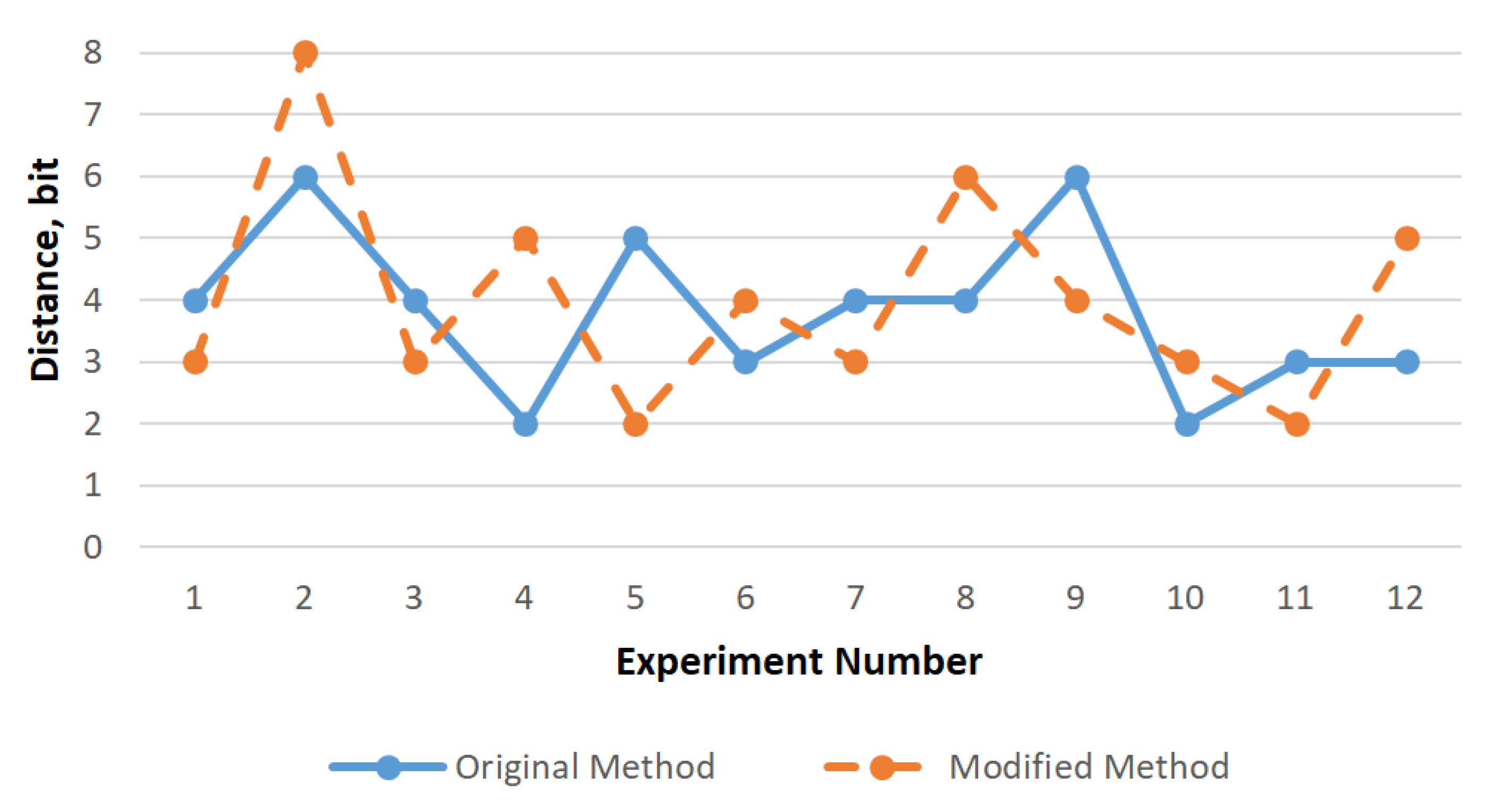
In addition to the number of inversions, it is important to evaluate the uniformity of the distribution (Figure 9). The value of this statistical parameter showed a change in the data stream at the byte level, the maximum delta value does not exceed 8 bits, while the average value is 3–4 bits, i.e., both methods make it impossible to recognize the source content without the inverse transformation.

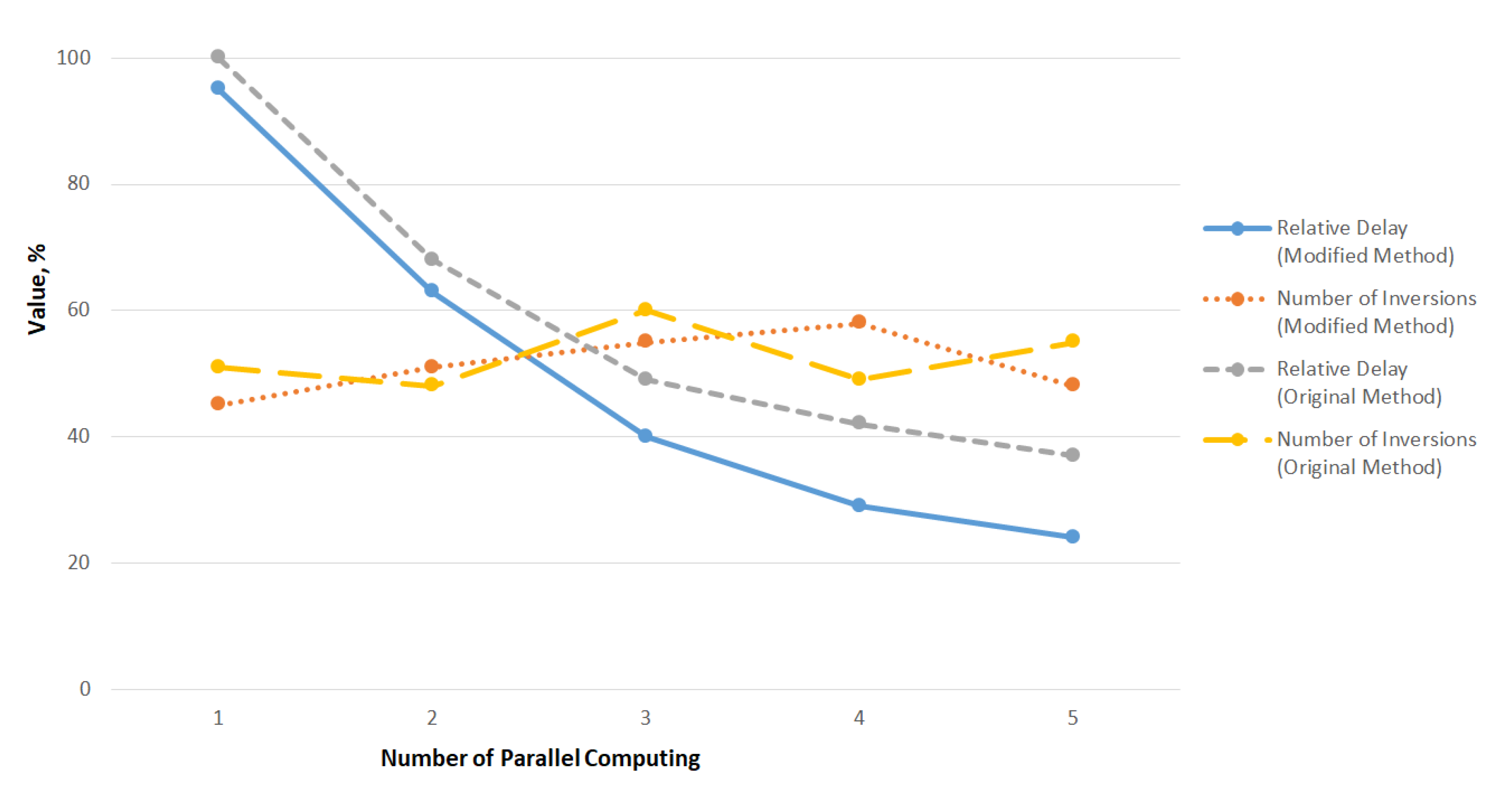
The advantage of the modified method is the ability to organize parallel computing at the segment level, which was not available in the original method. The results of the final experiment (Figure 10) showed that when processing by several calculators, the conversion time decreases in proportion to the number of threads, while the number of inversions and uniformity of distribution remain at an acceptable level since conversion is independent of the number of threads.

An analysis of the results showed that in the proposed embodiment, the speed of transformations was increased due to the preliminary stage of assessing the conformity of the current block to a user pattern. If the pattern is applicable to the block, then the cellular function is activated. This modification made it possible to increase the speed of the method to 13 percent on large data sets, while the bit distribution remained close to random and is uniform, and a decrease in the percentage of inversions did not lead to the exit from the confidence interval.

Thus, the proposed method is applicable for operation on a computational cluster scale and can process both confidential information in the form of separate files and data streams transmitted between subscribers of the computer network, and computing threads can “pick up” unprocessed segments, this significantly increases processing speed and enables efficient use of computer resources.

5. Conclusions

The main difference of the proposed data conversion scheme based on a cellular automata is the use of a public parameter, which is transmitted through a public communication channel. The public parameter is the number of columns of the information matrix. It is also worth noting that the private key in this case is composite and includes not only the encryption matrix, but also the rules for bypassing the data matrix, which in turn imply two levels of protection (basic and advanced). An advantage of the proposed scheme is that a separate data segment can be processed by a separate thread, which allows to implement the proposed processing method in the form of a network service. However, it is advisable to use multiple data stores, as while recording with multiple streams simultaneously, the information storage device becomes a weak link in the performance chain.

In the course of experimental studies, it was found that the speed of the method (with a sufficient number of computers) corresponds to the processing time of one segment, which is important for network interaction of subscribers or working with data transmitted in real time. Maintaining a local rule based on a user pattern allowed to increase the speed of the method up to 13 percent when working with large data sets, while the processed matrix contains at least 45 percent of changes at the bit level and 100 percent of changes at the byte level, which excludes access to protected data from an attacker without a reverse transformation that involves knowledge or selection of key parameters and makes the brute force method ineffective due to the unique sequence of PRNs defined by the private part of the key.

In further studies, it is planned to expand the neighborhood of the matrix and introduce the function of complementing the last segment of the matrix (“tail”) to complete the rectangular segment. It is also advisable to use a hash function that determines the sequence of processing blocks.