Indiscernibility Mask Key for Image Steganography †
Abstract
1. Introduction
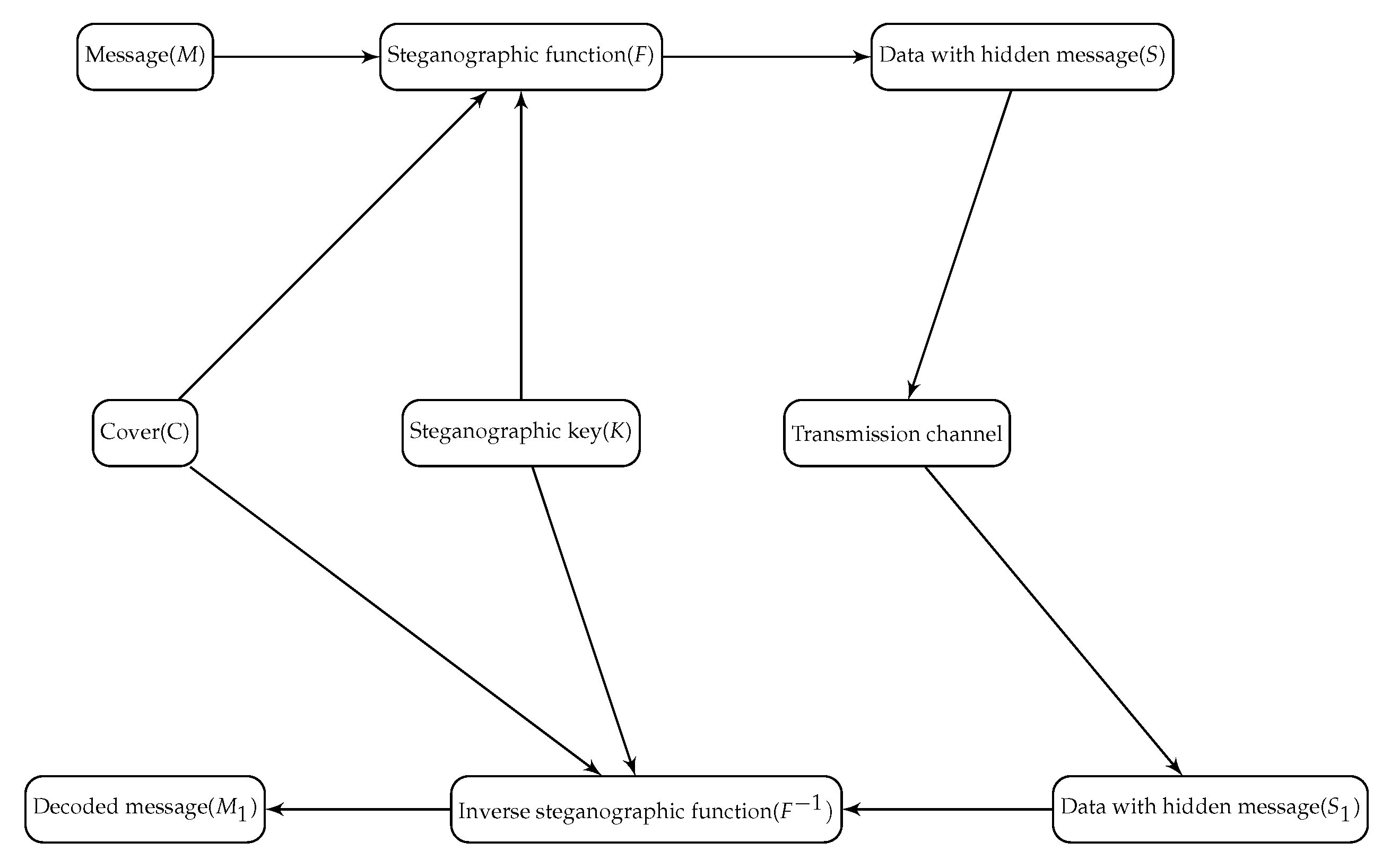
2. Image Steganography

2.1. Digital Representation of the Image
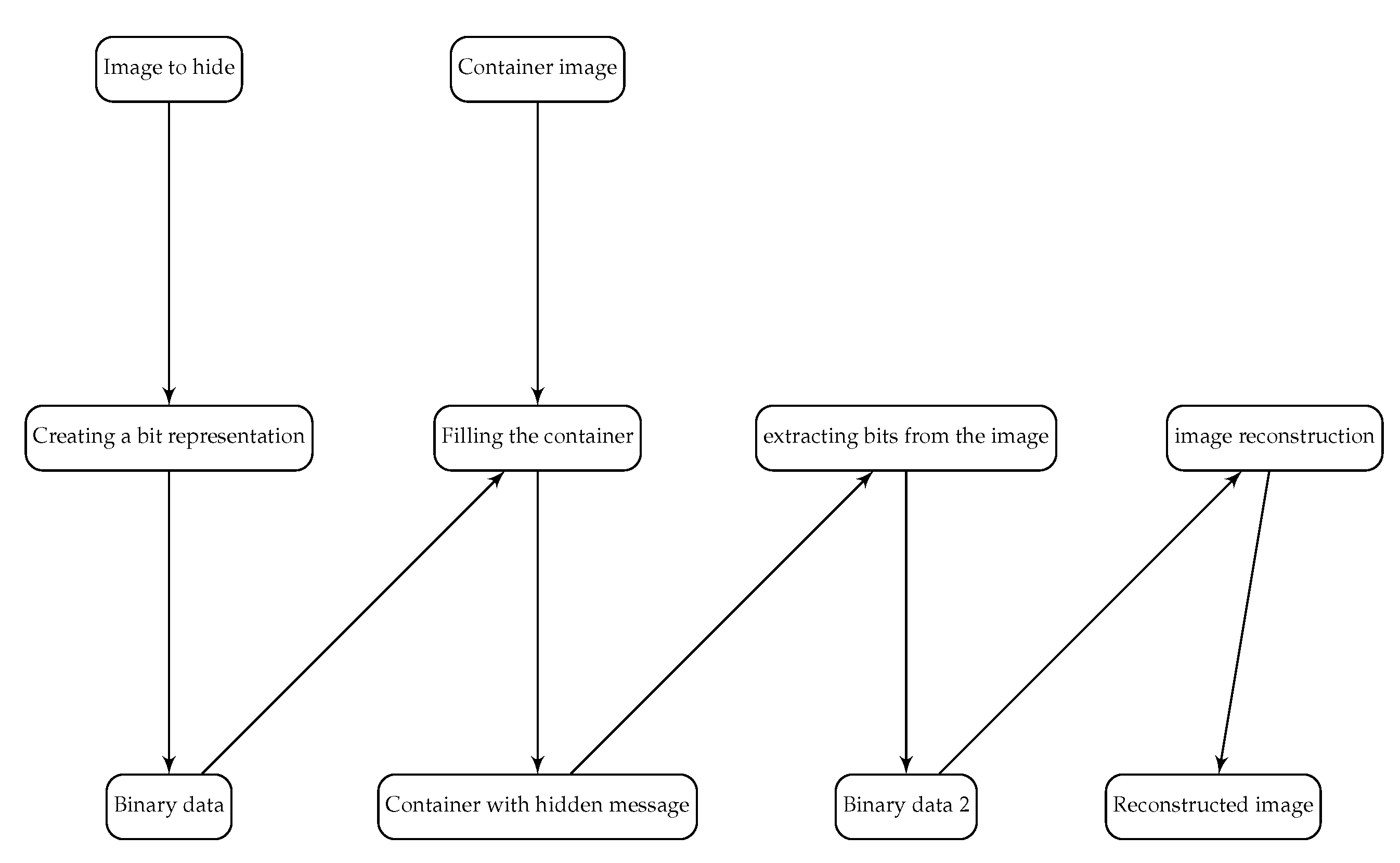
2.2. Basic LSB Technique
2.3. Limitations on the Use of Image Steganography
3. Stegoanalysis
3.1. Stegoanalisys-LSB Enhancement Attack
3.2. Stegoanalisys-Chi Square Attack
- (1)
- independent observations,
- (2)
- distribution,
4. Protection against Stegoanalisys
5. Theoretical Background for Indiscernibility in Degree
6. Usage of Our Steganographic Key-the Use of Rough Inclusion to Cover Up Information
7. Research Experiments
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zakaria, A.A.; Hussain, M.; Wahab, A.W.A.; Idris, M.Y.I.; Abdullah, N.A.; Jung, K.-H. High-Capacity Image Steganography with Minimum Modified Bits Based on Data Mapping and LSB Substitution. Appl. Sci. 2018, 8, 2199. [Google Scholar] [CrossRef]
- Yesilyurt, M.; Yalman, Y. New approach for cloud computing security: Using data hiding methods. Sadhana 2016, 41, 1289–1298. [Google Scholar] [CrossRef]
- Liu, Y.N.; Zhong, Q.; Xie, M.; Chen, Z.B. A novel multiple-level secret image sharing scheme. Multimed. Tools Appl. 2018, 77, 6017–6031. [Google Scholar] [CrossRef]
- Xiang, T.; Hu, J.; Sun, J. Outsourcing chaotic selective image encryption to the cloud with steganography. Digit. Signal Process. 2015, 43, 28–37. [Google Scholar] [CrossRef]
- Tondwalkar, A.; Jani, P.V. Secure localisation of wireless devices with application to sensor networks using steganography. Proc. Comput. Sci. 2016, 78, 610–616. [Google Scholar] [CrossRef]
- Yang, H.; Sun, X.; Sun, G. A high-capacity image data hiding scheme using adaptive LSB substitution. Radio Eng. 2009, 18, 509–516. [Google Scholar]
- Jung, K.H.; Yoo, K.Y. Steganographic method based on interpolation and LSB substitution of digital images. Multimed. Tools Appl. 2015, 74, 2143–2155. [Google Scholar] [CrossRef]
- Liao, X.; Wen, Q.Y.; Zhang, J. A steganographic method for digital images with four-pixel differencing and modified LSB substitution. J. Vis. Commun. Image Represent. 2011, 22, 1–8. [Google Scholar] [CrossRef]
- Khodaei, M.; Bigham, B.S.; Faez, K. Adaptive data hiding, using pixel-value-differencing and LSB substitution. Cybern. Syst. 2016, 47, 617–628. [Google Scholar] [CrossRef]
- Akhtar, N. An LSB substitution with bit inversion steganography method. In Proceedings of the 3rd International Conference on Advanced Computing, Networking and Informatics, New Delhi, India, 25–27 February 2016; pp. 515–521. [Google Scholar]
- Sethi, P.; Kapoor, V. A proposed novel architecture for information hiding in image steganography by using genetic algorithm and cryptography. Proc. Comput. Sci. 2016, 87, 61–66. [Google Scholar] [CrossRef]
- Al-Husainy, M.A.F. Message Segmentation to Enhance the Security of LSB Image Steganography. Int. J. Adv. Comput. Sci. Appl. 2012. [Google Scholar] [CrossRef][Green Version]
- Westfeld, A.; Pfitzmann, A. Attacks on Steganographic Systems. In Breaking the Steganographic Utilities EzStego, Jsteg, Steganos, and S-Tools and Some Lessons Learned; Springer: Berlin, Germany, 2000. [Google Scholar]
- Afrakhteh, M.; Ibrahim, S. Enhanced Least Significant Bit Scheme Robust against Chi-Squared Attack. In Proceedings of the 2010 Fourth Asia International Conference on Mathematical/Analytical Modelling and Computer Simulation, Bornea, Malaysia, 26–28 May 2010; pp. 286–290. [Google Scholar]
- Setiadi, D.R.I.M.; Jumanto, J. An enhanced LSB-image steganography using the hybrid Canny-Sobel edge detection. Cybern. Inf. Technol. 2018, 18, 74–88. [Google Scholar] [CrossRef]
- Fridrich, J. Steganography in Digital Media: Principles, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Shehzad, D.; Dag, T. LSB Image Steganography Based on Blocks Matrix Determinant Method, KSII Transactions on Internet and Information Systems; KSII Publisher: Gangnam-gu, South Korea, 2019; Volume 13, pp. 3778–3793. [Google Scholar]
- Sun, H.M.; Wang, K.H.; Liang, C.C.; Kao, Y.S. A LSB Substitution Compatible Steganography. In Proceedings of the IEEE Region 10 Conference, Taipei, Taiwan, 30 October–2 November 2007. [Google Scholar]
- Zadeh, L.A. Fuzzy sets and information granularity. In Advances in Fuzzy Set Theory and Applications; Gupta, M., Ragade, R., Yager, R.R., Eds.; North-Holland: Amsterdam, The Netherlands, 1979; pp. 3–18. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Polkowski, L. Rough Sets. In Mathematical Foundations; Physica Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Polkowski, L. Formal granular calculi based on rough inclusions. In Proceedings of the IEEE 2005 Conference on Granular Computing GrC05, Beijing, China, 25–27 July 2005; IEEE Press: Piscataway, NJ, USA, 2005; pp. 57–62. [Google Scholar]
- Morkel, T.; Eloff, J.H.; Olivier, M.S. An Overview of Image Steganography; ISSA: Phoenix, AZ, USA, 2005; pp. 1–11. [Google Scholar]
- Neeta, D.; Snehal, K.; Jacobs, D. Implementation of LSB steganography and its evaluation for various bits. In Proceedings of the 1st International Conference on Digital Information Management, Porto, Portugal, 19–21 September 2006; pp. 173–178. [Google Scholar]
- Juneja, M.; Sandhu, P.S. Improved LSB based Steganography Techniques for Color Images in Spatial Domain. Int. J. Netw. Secur. 2014, 16, 452–462. [Google Scholar]
- Robinson, S.J.; Schmidt, J.T. Fluorescent Penetrant Sensitivity and Removability-What the Eye Can See, a Fluorometer Can Measure. Mater. Eval. 1984, 42, 1029–1034. [Google Scholar]
- Krenn, R. Steganography and Steganalysis. Available online: http://www.krenn.nl/univ/cry/steg/article.pdf (accessed on 5 May 2020).
- Silman, J. Steganography and Steganalysis: An overview. Sans Institute. Available online: https://www.researchgate.net/publication/242743284_Steganography_and_Steganalysis_An_Overview (accessed on 5 May 2020).
- Wang, H.; Wang, S. Cyber warfare: Steganography vs. steganalysis. Commun. ACM 2004, 47, 76–82. [Google Scholar] [CrossRef]
- Westfeld, A.; Pfitzmann, A. Attack on Steganographic Systems, Lectures Notes in Computer Science; Springer: Berlin, Germany, 2000; Volume 1768, pp. 61–75. [Google Scholar]
- Chefranov, A.G.; Mazurova, T.A. Pseudo-Random Number Generator RC4 Period Improvement. In Proceedings of the 2006 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 25–28 May 2006; pp. 38–41. [Google Scholar]
- Radhakrishnan, R.; Kharrazi, M.; Memon, N. Data Masking: A New Approach for Steganography? J. VLSI Signal Process Syst. Signal Image Video Technol. 2005, 41, 293–303. [Google Scholar] [CrossRef]
- Sultana, S.; Khanam, A.; Islam, M.R.; Nitu, A.M.; Uddin, M.P.; Afjal, M.I.; Rabbi, M.F. A Modified Filtering Approach of LSB Image Steganography Using Stream Builder along with AES Encryption. Recent Trends Inf. Technol. Appl. 2018, 1, 1–10. [Google Scholar]
- Sun, H.M.; Chen, Y.H.; Wang, K.H. An Image Data Hiding Scheme being Perfectly Imperceptible to Histogram Attacks. Image Vis. Comput. N. Z. IVCNZ 2006, 16, 27–29. [Google Scholar]
- Franz, E. Steganography preserving statistical properties. In Proceedings of the 5th International Workshop on Information Hiding, Noordwijkerhout, The Netherlands, 7–9 October 2002; Volume 2578, pp. 278–294. [Google Scholar]
- Pawlak, Z.; Grzymala-Busse, J.; Slowinski, R.; Ziarko, W. Rough sets. Commun. ACM 1995, 38, 88–95. [Google Scholar] [CrossRef]
- Polkowski, L. Granulation of knowledge in decision systems: The approach based on rough inclusions. The method and its applications. In Proceedings of the RSEISP 07, Warsaw, Poland, 28–30 June 2007; Springer: Berlin, Germany, 2007; Volume 4585, pp. 271–279. [Google Scholar]
- Polkowski, L. A unified approach to granulation of knowledge and granular computing based on rough mereology: A survey. In Handbook of Granular Computing; Pedrycz, W., Skowron, A., Kreinovich, V., Eds.; John Wiley and Sons Ltd.: Chichester, UK, 2008; pp. 375–400. [Google Scholar]
- Polkowski, L. Approximate Reasoning by Parts. An Introduction to Rough Mereology; Springer: Berlin, Germany, 2011. [Google Scholar]
- Partow, A. C++ Bitmap Library. Available online: http://partow.net/programming/bitmap/index.html (accessed on 5 May 2020).
- Artiemjew, L. Collection of Artistic Works. Available online: http://el-art.com.pl (accessed on 5 May 2020).
- Artiemjew, L. The Image of Lech Artiemjew-Polish Mathematician, Sculptor, Painter and Musician. Available online: http://el-art.com.pl (accessed on 5 May 2020).
- Artiemjew, P. Macro Photography Collection. Available online: http://el-art.com.pl (accessed on 5 May 2020).














© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artiemjew, P.; Kislak-Malinowska, A. Indiscernibility Mask Key for Image Steganography. Computers 2020, 9, 38. https://doi.org/10.3390/computers9020038
Artiemjew P, Kislak-Malinowska A. Indiscernibility Mask Key for Image Steganography. Computers. 2020; 9(2):38. https://doi.org/10.3390/computers9020038
Chicago/Turabian StyleArtiemjew, Piotr, and Aleksandra Kislak-Malinowska. 2020. "Indiscernibility Mask Key for Image Steganography" Computers 9, no. 2: 38. https://doi.org/10.3390/computers9020038
APA StyleArtiemjew, P., & Kislak-Malinowska, A. (2020). Indiscernibility Mask Key for Image Steganography. Computers, 9(2), 38. https://doi.org/10.3390/computers9020038





