Cognification of Program Synthesis—A Systematic Feature-Oriented Analysis and Future Direction
Abstract
1. Introduction
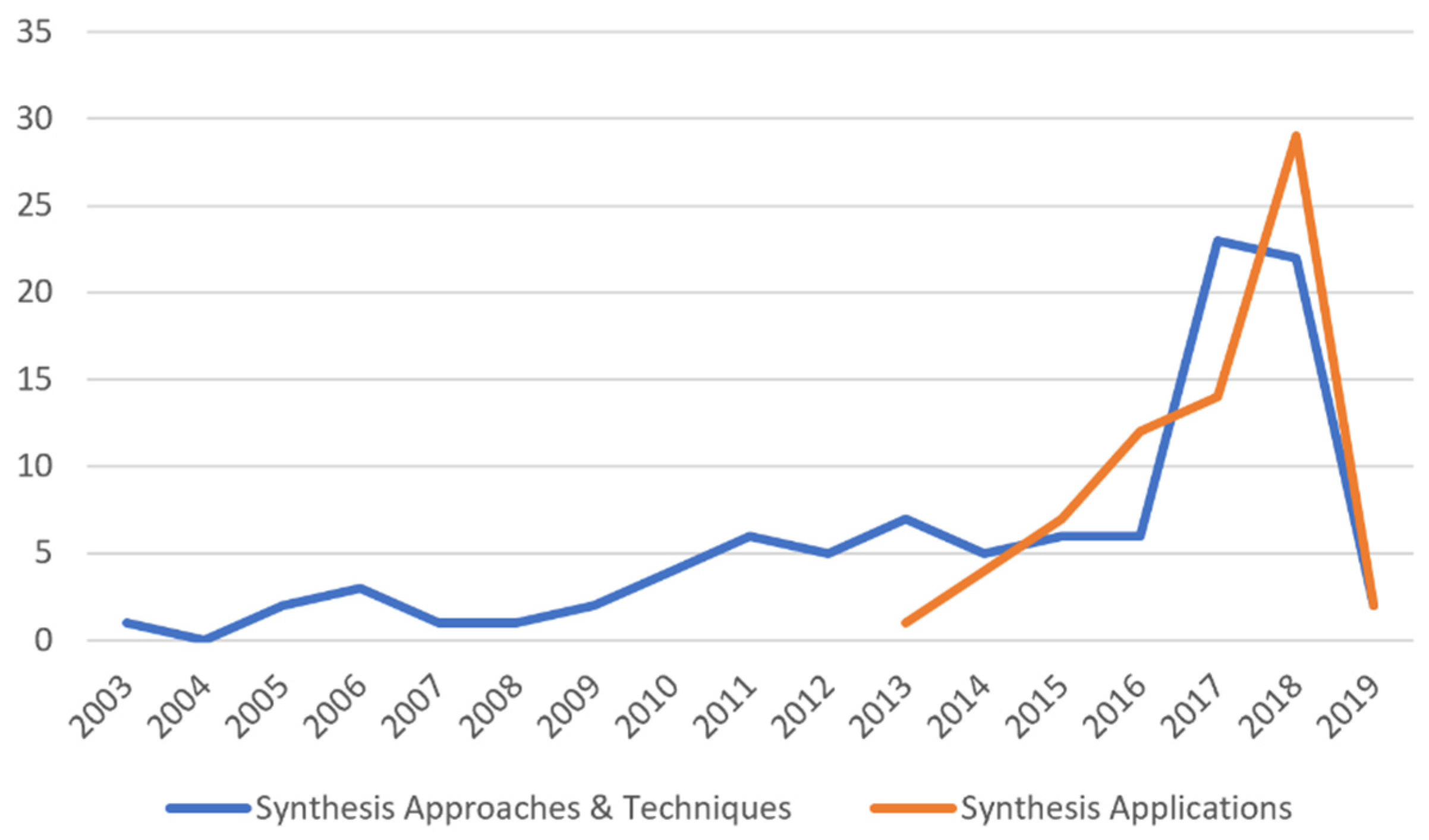
2. Brief History
3. Transformational Systems and Program Synthesis
4. Methodology
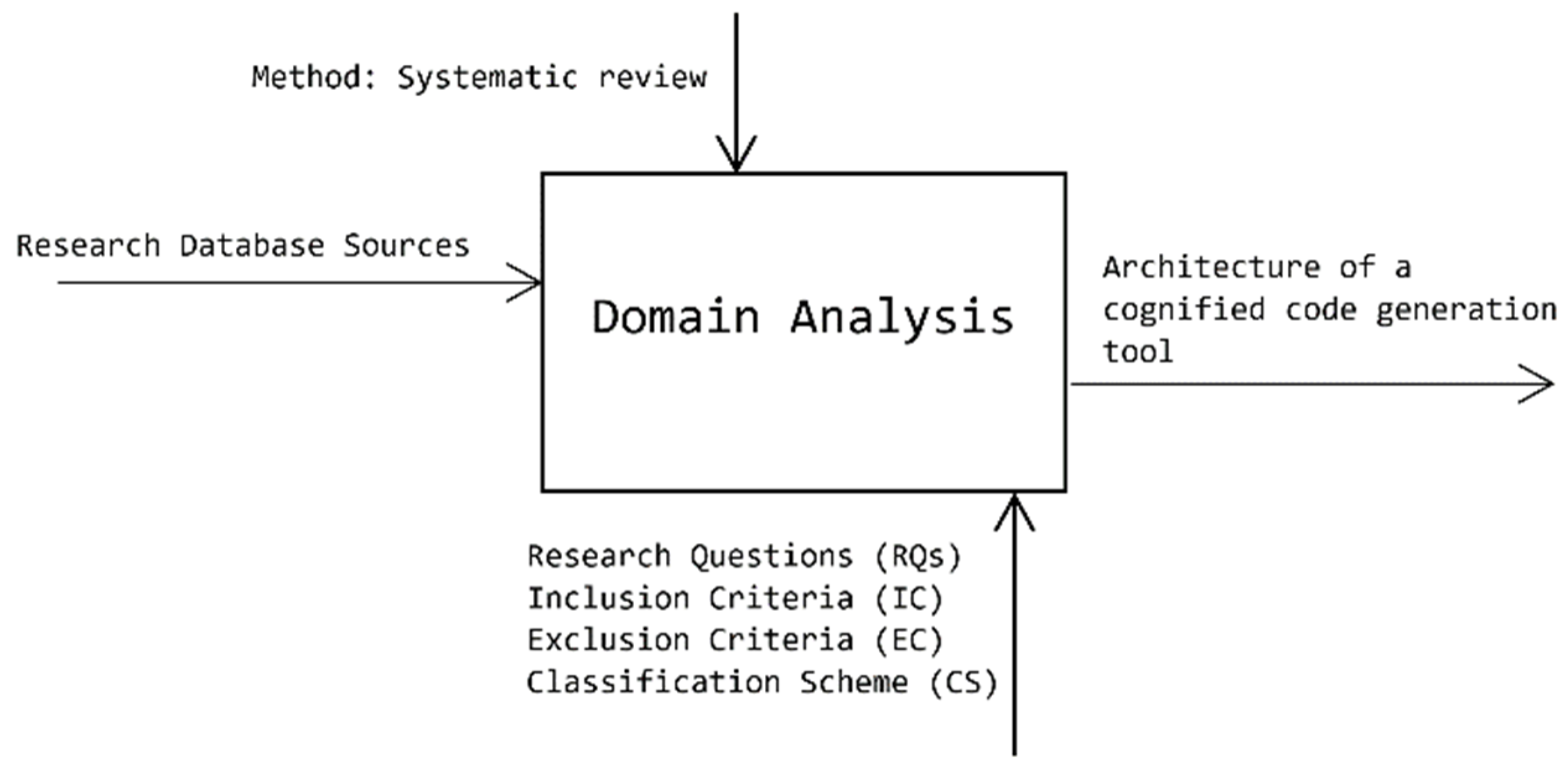
4.1. Strategy of Domain Analysis
- The first level of analysis identifies the differences between paradigms of program synthesis in terms of the synthesizing approach adopted in each paradigm. This level does not compare the detailed features of the program synthesis approach and its applications.
- The second level compares different program synthesis approaches in terms of the main three dimensions, namely, user intent, search space and search techniques.
- The third level identifies the applications of program synthesis from a software engineering perspective.
4.2. Definition of Research Questions
- RQ1:
- What was reported in peer-reviewed literature about paradigms and approaches to program synthesis with respect to the Software Engineering domain between 2003 and 2019?
- RQ2:
- What are the main characteristics (features) of each program synthesis approach reported in peer-reviewed research literature?
- RQ3:
- What are the common alternatives and trends in describing the user intent?
- RQ4:
- What are the common alternatives for describing the program space?
- RQ5:
- What are the common alternative approaches and trends used to deal with the synthesis problem?
- RQ6:
- What are common trending techniques that are applied over the program space for solving synthesis problem?
- RQ7:
- What are the spectra and trends of the program synthesis applications?
- RQ8:
- What kinds of search strategy were used for each application of program synthesis between 2009 and 2019?
4.3. Conduction of the Domain Analysis
4.4. Inclusion and Exclusion Criteria
4.5. Classification Scheme
4.6. Data Extraction Strategy
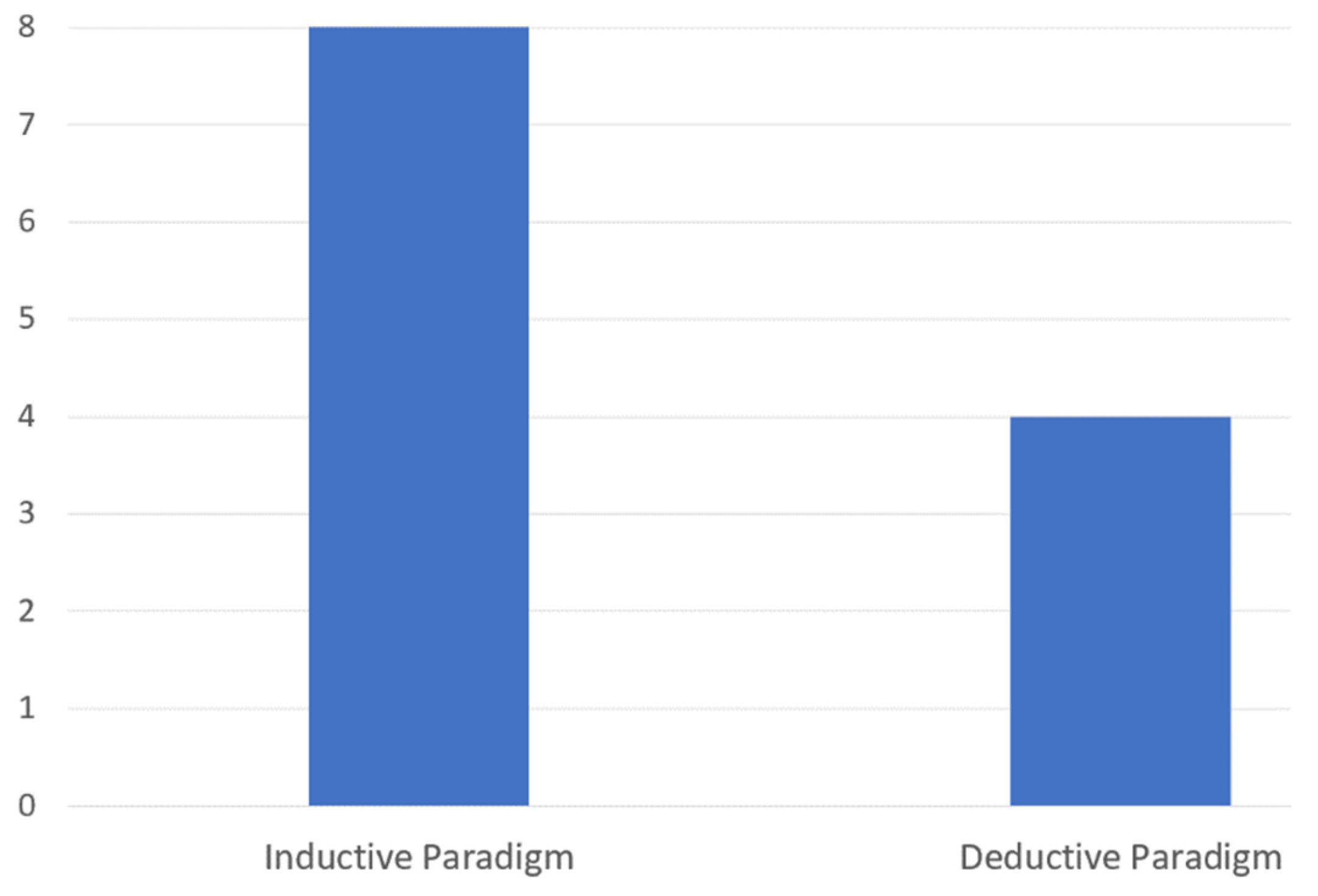
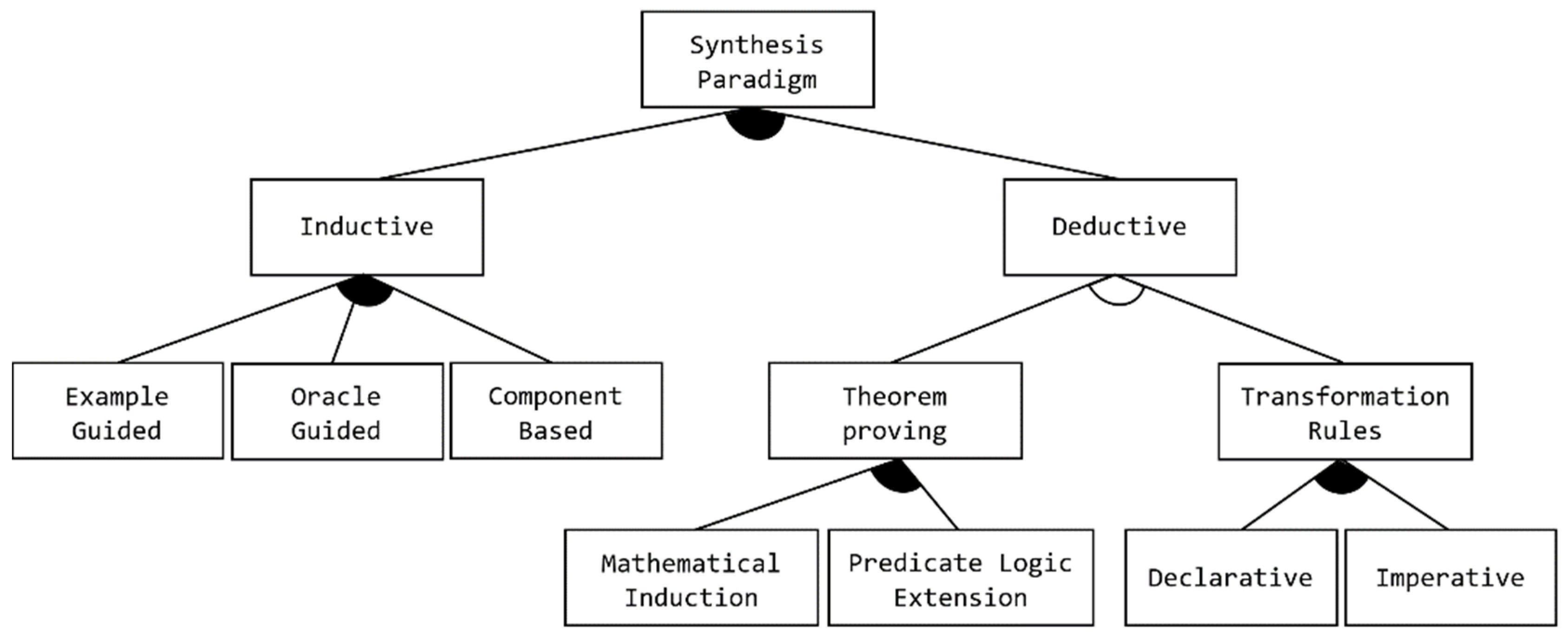
5. Paradigms of Program Synthesis
5.1. Inductive Program Synthesis Paradigm
- Example-Guided: Unlike synthesis approaches that completely rely on deductive techniques to assemble user-intended programs, here, learning synthesizers from a small number of examples are required.
- Oracle-Guided: Frameworks under this subcategory use a querying system (Oracle) as part of the synthesizer design. They focus on the Oracle to answer (interactively) queries produced by a learner, such as the counterexample-guided approaches discussed in [95].
- Component-based: The process of assembling programs (loop-free) avoids the use of formal specifications and replaces them with a collection of existing functions/methods, composed to provide building blocks that are required for obtaining implementation detail. The component functions are interchangeable with a set of library functions provided by an application program interface (API) [92,93]. User intent can be described via a set of input/output examples, for example in [94], or even as a set of test cases, for example, in the work presented in [92]. In addition, the FrAngel approach [178] is able to synthesize loops and other control structures using a desired signature.
5.2. Deductive Program Synthesis Paradigm
- Theorem-proving: This subfeature groups the deductive approaches that consider the derivation process of the final programs from specification as a problem of proving a mathematical or logical theorem. The given specification normally describes the relation between input and output without explaining the recommended way of implementing and computing it. It is worth mentioning that when trying to construct a program with recursive or iterative loops, the process of applying theorem-proving becomes more complex [172]. In this technique, for any input object of the program, the existence of an output that meets conditions is proved formally by one or more theories, such as:
- ○
- Mathematical Induction: A proof method that is based on the principle of mathematical induction.
- ○
- Predicate Logic Extension: A formal proof method based on logical theories.
- Transformation Rules: This subfeature groups the deductive approaches that rely on the direct application of transformations or program rewriting rules to a specification of a desired program [172]. The program derivation process, in this instance, is not regarded as a process of proving a theorem but as a process of transformational steps [171]. There are three mechanisms for expressing rules of transformation [30,135], as follows:
- ○
- Declarative Rules: Each transformation rule is designed as a relation between the source and target without going into operational detail of how the relation can be achieved. The rules can be implemented using transformation languages such as Query/View/Transformation (QVT) Relations.
- ○
- Imperative Rules: Each transformation rule is specified and designed as a number of operational mapping steps, which are required to obtain the target from the source, showing how the transformation itself is performed. The rules can be implemented using any Object-Oriented Programming (OOP) language, such as Java or C++.
- ○
- Hybrid Rules: A combination of both declarative and imperative rules, which is represented in Figure 5. It is mandatory that (at least one) notation follows the features of transformation rules.
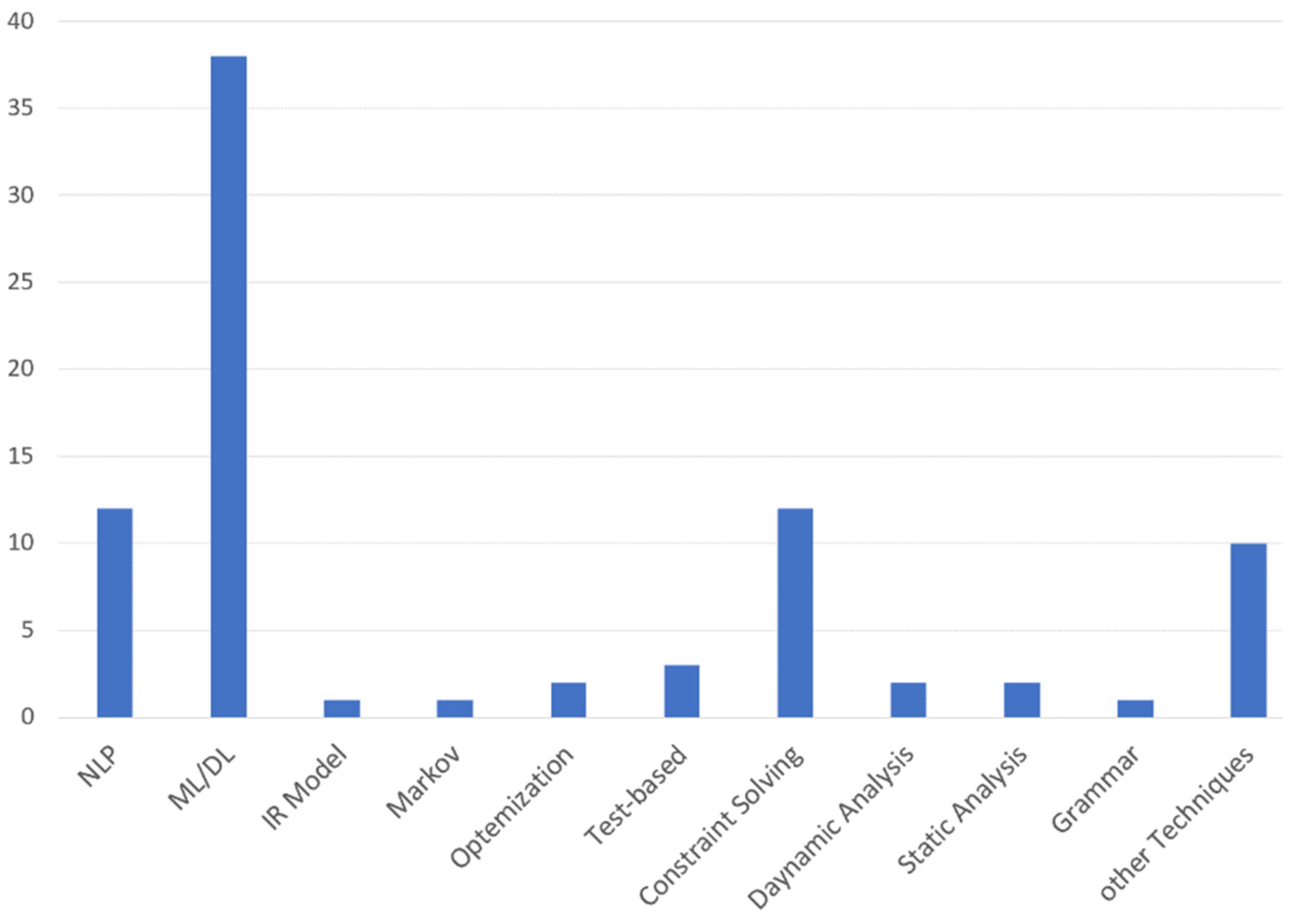
6. Features of Program Synthesis
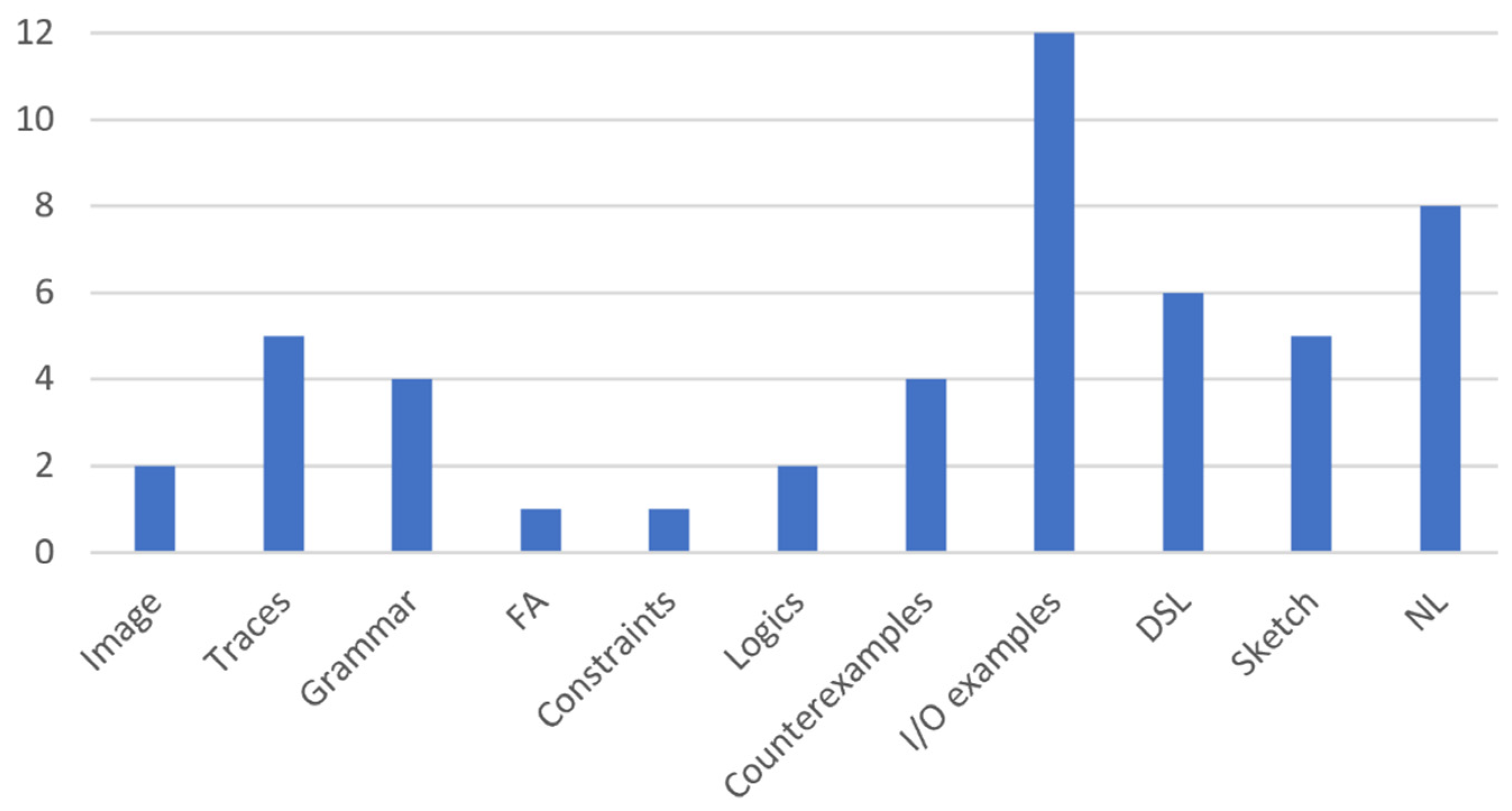
6.1. Developer & User Intent Specifications
- Natural Languages: Synthesis frameworks that fall under this subcategory use natural languages to describe the user intent program. Synthesizers then work to produce a program code from the NL description using a learning algorithm such as reinforcement or maximum marginal likelihood. The approaches presented in [116,139], and [19] are examples of synthesis frameworks that use an NL description for expressing user intent. Additionally, other frameworks, such as Tellina, adopt Recurrent Neural Networks to translate a program described using a natural language into an executable program [15].
- Program Sketches: According to frameworks presented in [25], synthesis frameworks allow a user to write an incomplete program (a program with holes or missing details) and a synthesizer and then derive the low-level implementation detail from the sketches by filling all given holes based on previously specified assertions.
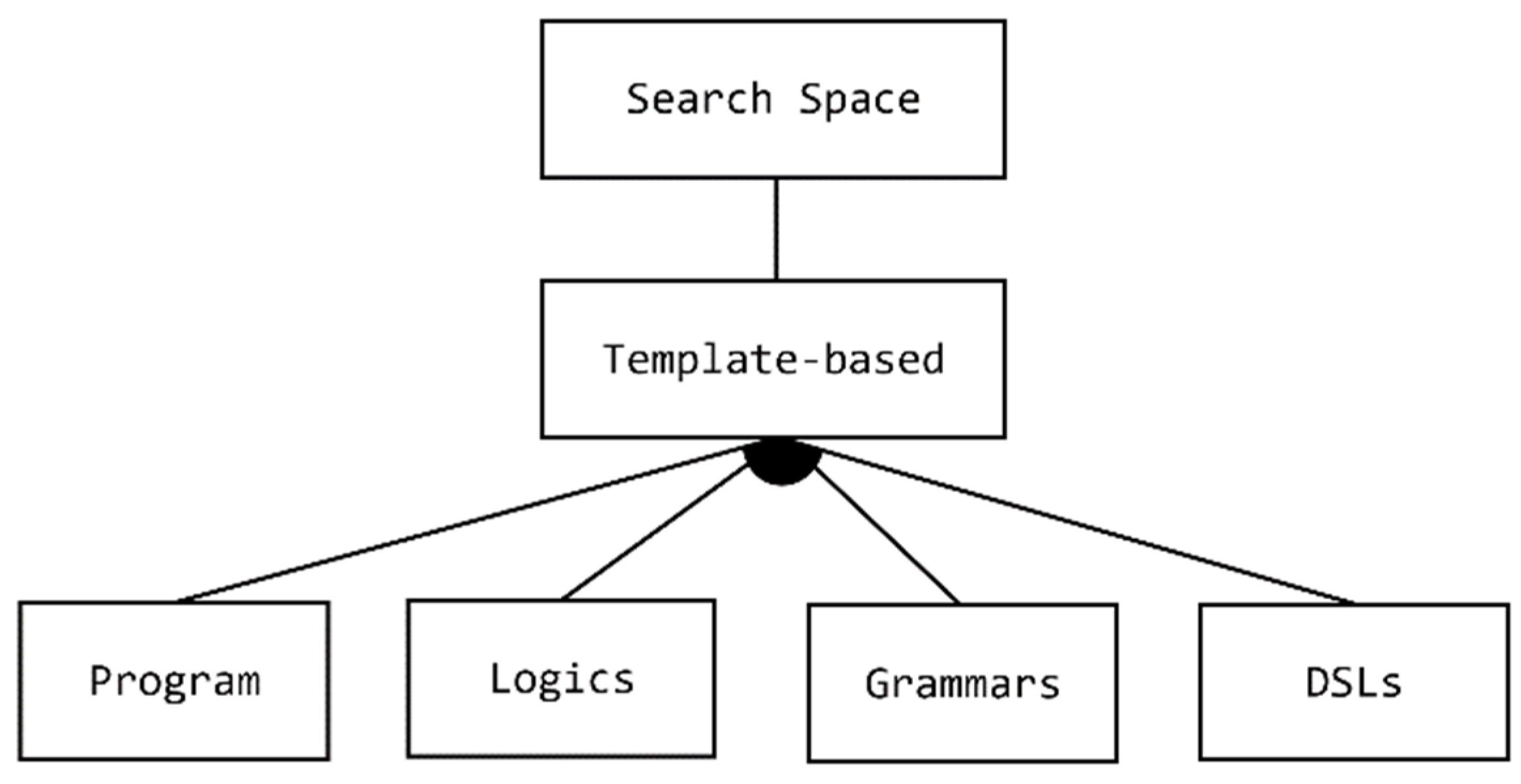
- Domain-Specific Languages: A Domain-Specific Language (DSL) is a restricted set of a programming language that is designed to be understood and adopted for a particular domain. Similar to the structure of general-purpose programming languages (like C++ and Java), a DSL is a set of typed and annotated symbol definitions that form the DSL terminology [97]. These symbols can be either terminals or non-terminals that are defined using some high-level specification rules (e.g., context-free grammar). Each rule describes the transformation of every non-terminal into another non-terminal or terminal token of the language. All possible transformation operators and source symbols (tokens) are typed and located on the right-hand-side of the rules. Every symbol in the grammar is annotated with a corresponding output. The PROgram Synthesis using examples (PROSE) approach [31] is an example of a program that falls under the deductive synthesis paradigm (explained previously in Section 5) where the synthesis problem is solved using transformation rules and version space algebra such as FlashExtract [44] and FlashMeta [32] Additionally, the solver-aided DSL (Rosette) that is based on theorem proving technique is designed in another DSL based approach for solving synthesis problem [33].
- Input/Output (I/O) Example: Frameworks under this subcategory adopt the use of I/O examples as an alternative strategy of expressing the user intent for a desired program. This kind of synthesis approach provides an interactive interface between the user and the synthesizer that allows the user to provide input/output example pairs until the desired program is reached, such as the approaches provided in [41,44,47].
- Counterexample: Synthesizers in frameworks under this subfeature adopt the so-called “Counterexample-guided” inductive synthesis strategy to produce possible candidate implementations from concrete examples of program behavior, whether this behavior is correct or not [27]. The synthesizer, in this instance, acts as a verifier or an Oracle in some approaches like [94,95] that performs a validation process on the candidate implementation code and produces (generates) counterexamples from its context to be used in the following iteration as input fed to the synthesizer. The counterexamples in this mechanism are used, iteratively, instead of new knowledge-free I/O examples generated for each solving iteration [27].
- Logic Formulas: The use of logical formulas is considered to be one of the classic methods for expressing high-level specifications of programs. There are two kinds of specifications considered for describing programs: semantics specifications and syntactic specifications. Frameworks that follow these subcategories use logic to describe semantic specifications, whereas they use grammar (e.g., context-free grammar) to describe constraints of syntactic specifications. Together, grammar and syntactic constraints provide a comprehensive template for the desired program. Using a template benefits the synthesizer by reducing the program search space [50,85].
- Constraints: Approaches that fall under this subfeature use formal language such as context-free grammar (attribute grammar) as a language for describing rich, structured constraints over desired programs. This kind of synthesis approach tries to tackle the problem of learning synthesizers, a rich set of constraints that must be satisfied from provided data, which is considered a difficult mission. The work presented in [54] is an example of this kind of synthesis framework.
- Finite Automata (FA): Frameworks under this subcategory allow a user to describe the desired program partially using finite state machines (FSMs) or, in some approaches, Extended FSMs with execution specifications and invariants to construct an FSM skeleton of the program. The synthesizer then completes the FSM skeleton from the desired specifications and invariants (supplied with the skeleton) using an inference technique [55]. In a TRANSIT tool [55], for instance, a computational-guided synthesis approach is adopted for a reactive system, where each process is expressed as an Extended FSM. The description of processes consists of a collection of internal state variables and control states and the transitions between them. The synthesis approach works by specifying these transitions through a set of guard conditions and an update code by inferring expressions using symbolic forms of functions, variables, and examples (Concolic snippets) to achieve a consistent system behavior.
- Grammar: In addition, there are other frameworks that may involve program synthesis activities, such as program analysis and debugging. They use semantics information about a program, such as a bug report or memory address, instead of using actual program syntax or formal representations of it (e.g., grammar). These frameworks are categorized as under the semantics-based subcategory, demonstrated in Figure 9. It is commonly known that execution traces of programs consist of rich semantics information about the code. Thus, the use of execution traces has become widely accepted in the domains of program analysis and synthesis, which has brought remarkable results [57]. According to [57], many learning processes of (learning-based) synthesizers [58,59,152], are improved when using execution traces generated from I/O graphical image examples. Based on this idea, the approach presented in [57] uses execution traces that contain no control flow constructs as the specifications of a desired program along with I/O examples to train the proposed (neural) program synthesis model. As a result, the accuracy is improved to 81.3% from the 77.12% of their prior work. Frameworks that fall under the semantics-based subfeature, shown in Figure 8 above, use execution traces that contain semantics information about I/O values rather than using the I/O values themselves.
- Traces: Frameworks with this subfeature provide a set of execution traces for learning synthesizers instead of a collection of I/O examples or logic rules [62]. This is because execution traces have been widely used for program analysis [63,64], where the traces are given as input to identify detailed (technical) characteristics about a program. Trace information may contain significant detail about the program, including dependencies, control flows (paths), values, memory addresses, and the inter-relationship between them. Reverse engineering techniques and tools are used to analyze traces and understand all possible scenarios and dynamic behaviors related to the code [64].
6.2. Search Space of the Program
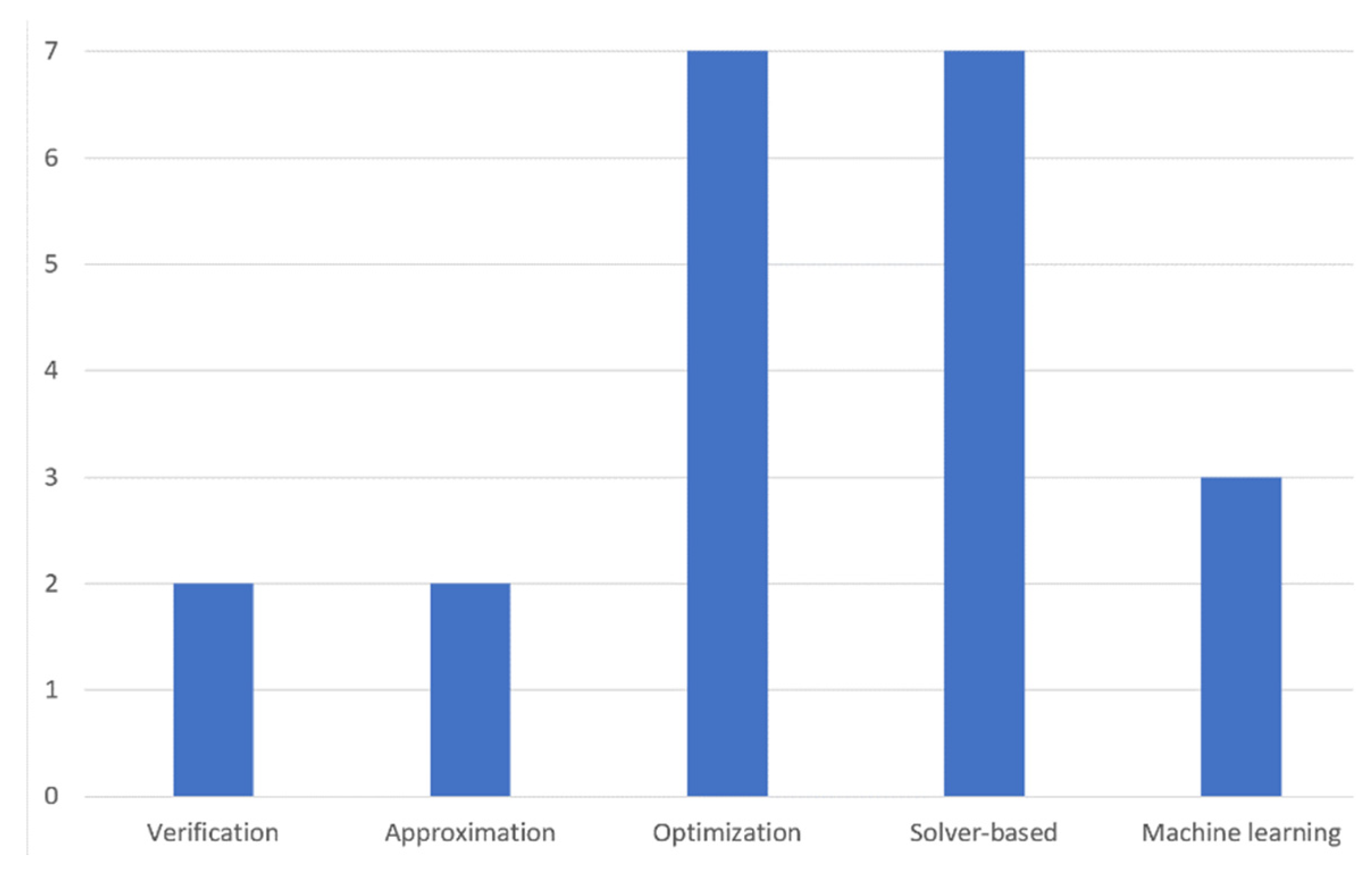
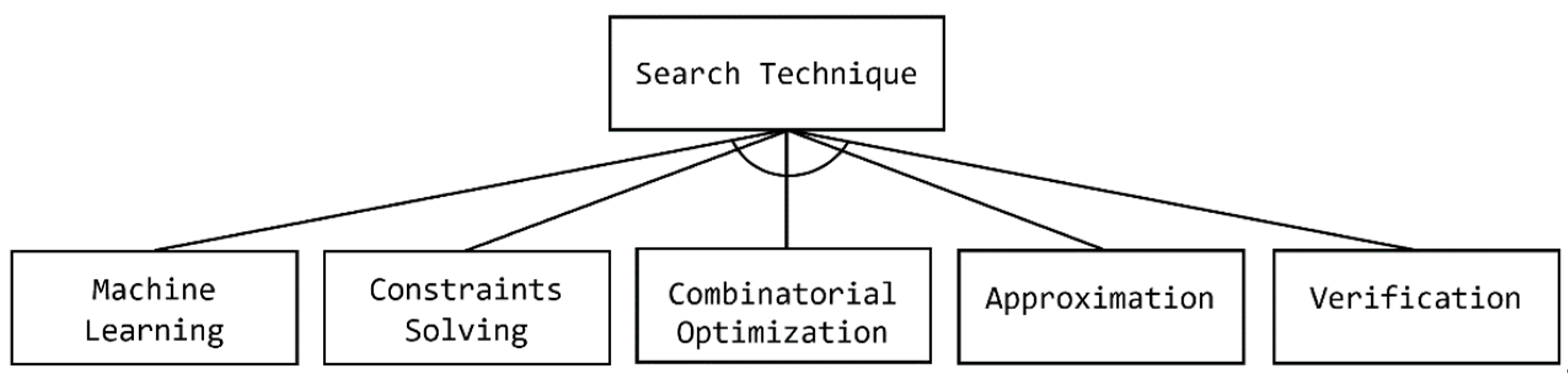
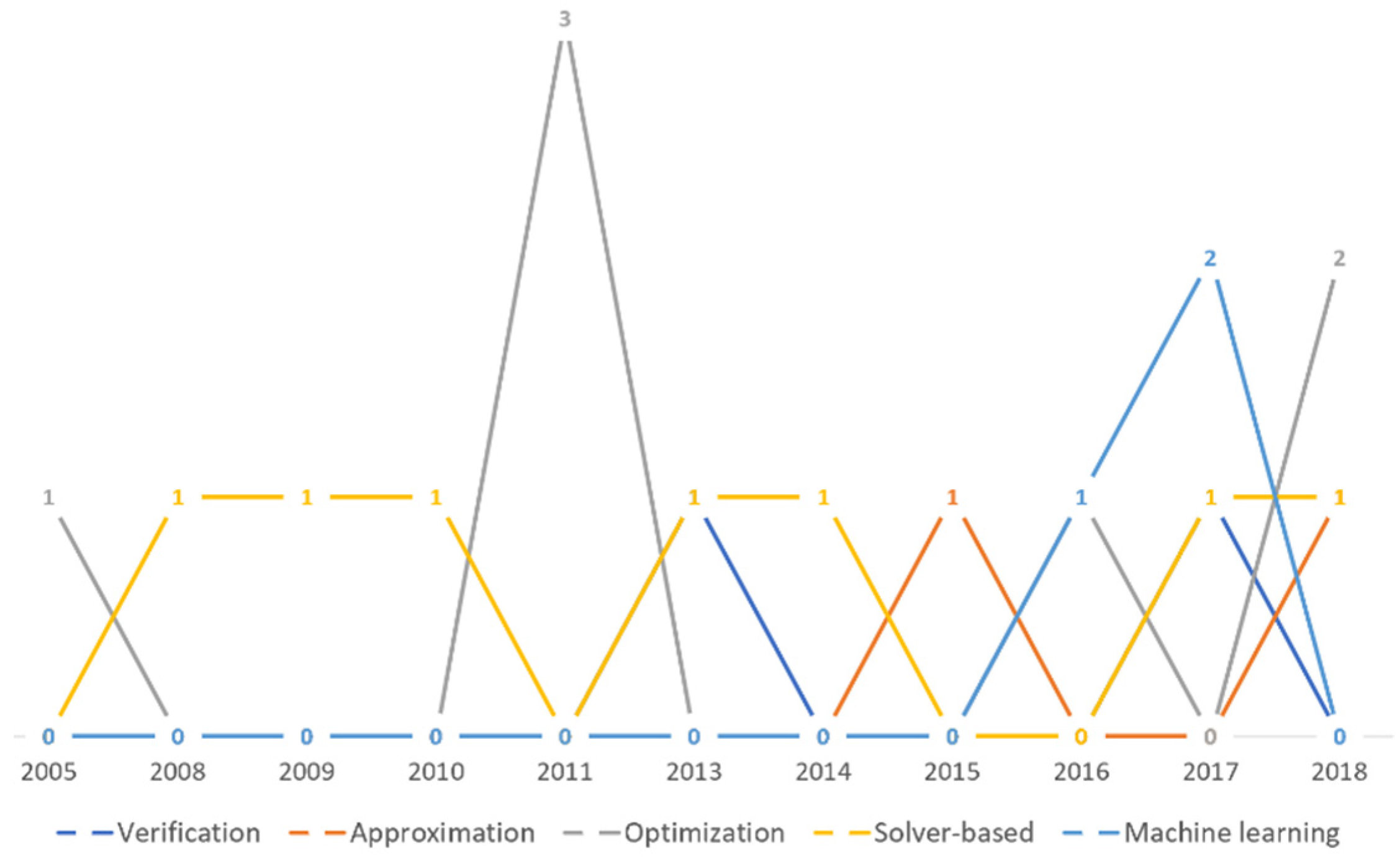
6.3. Search Strategy
- Verification: Verification can be defined as a process of solving a problem by checking that a program satisfies a high-level specification on all inputs brought from a very large or infinite set. Program synthesis frameworks that fall under the verification subcategory encode the synthesis problem as a verification problem to be solved using certain verification tools. This kind of program synthesis follows the correct-by-construction philosophy from the old school program design approach that appeared in the 1970s and 1980s. In the program verification approach, as discussed in [60], code statements are encoded as logical facts with some guards to be examined.The tool then infers some invariants and program statements until the program is synthesized automatically. The proof of correctness for these generated conditions is then produced theoretically using reasoning techniques. According to [65], the second phase of the common counterexample-guided inductive program synthesis approach is based on iterative verification processes. A verification step is performed on the candidate program in order to discover a counterexample input that violates the specification. This process continues until the candidate program checking is accomplished by either passing the verification check or failing a synthesis check [65].
- Approximation: Traditional program synthesis frameworks generally produce programs that only meet specifications without the guarantee that they will be the optimal solution. Some synthesis approaches treat the program synthesis problem as an approximation problem. The approximation problem usually results in the discovery of approximate solutions (the nearest solution) to the optimal one.Synthesis approaches in this category aim to automatically produce optimal programs that approximately meet a desired correctness specification with certain attributes, for example, the fastest program [66,67]. According to [67], a collection of large problems, where candidate programs have a search space that is too large and hard to explore, is introduced as a PARROT benchmark suite. The sketch-based program synthesis approach is used to solve PARROT problems, resulting in more efficient program solutions with a reasonable level of accuracy for all seven problems. It is worth mentioning that the syntax-based synthesis framework (SyGuS) fails to solve any PARROT collection problem [67].
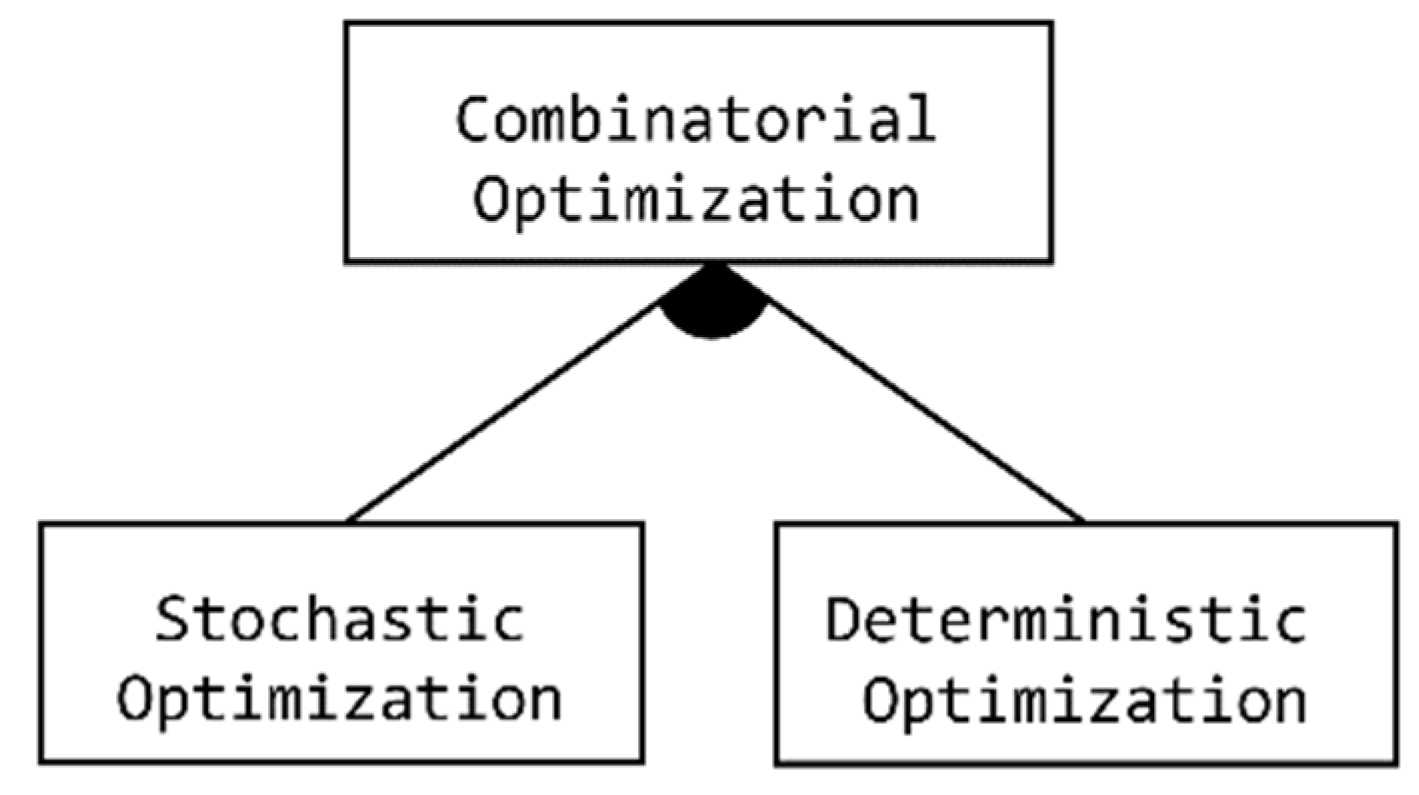
- Combinatorial Optimization: Combinatorial optimization is a type of mathematical optimization that reflects, in general terms, the process of selecting the best value that satisfies some given criterion from some available alternatives [74]. Combinatorial optimization is considered to be a field of theoretical computer science that solves discrete optimization problems through finding an optimal solution from a finite set of possibilities [74]. In the optimization process, an original program 𝓟 is given, and a search technique is applied over the program space to find another functionally equivalent program 𝓠 that satisfies some constraints for performance enhancement [69]. It improves the search performance by reducing the size of the search space. Although various real-world problems, such as finding variable assignments that satisfy constraints, partitioning graphs, coloring graphs, and more can be solved numerically by combinatorial optimization, most of these problems are often subject to uncertainty [74].
- Stochastic Optimization: The Stochastic Optimization method involves solving combinatorial optimization problems that involve uncertainties, whereas the deterministic one focuses on finding solutions for combinatorial optimization problems by evaluating a finite set of discrete variables. For each method, several efficient algorithms have been designed and successful search techniques have been adopted for solving many real-world problems, including program synthesis (demonstrated in the detailed feature diagram in Figure 16). According to the domain analysis, the Evolutionary Algorithm (Genetic programming), Dynamic Programming Algorithm (e.g., Viterbi algorithm), and Simulated Annealing are stochastic algorithms that are used in several program synthesis frameworks as techniques for seeking the target code constructs from the high-level specifications [68,155].
- ○
- Dynamic Programming: Dynamic Programming is an optimization technique that simplifies complex problems by boiling them down into many overlapping subproblems. Solutions of these simpler subproblems are combined to provide an optimal solution to the complicated problem. In a nested problem structure, a relation between the value of the larger problem and the values of the subproblems is specified, and each computed value of a subproblem’s solution is used recursively to find the overall optimal solution to the problem [70].It is worth mentioning that the synthesis problem must be described in a way in which its solution is constructed from some solutions to overlap subproblems [71]. Many implementation algorithms that improve the overall performance of the optimization process are based on dynamic programing, such as the divide-and conquer [70] and linear-time dynamic programming algorithms presented in [71].
- ○
- Simulated Annealing: The principles of simulated annealing were inspired and inherited from physical properties in annealing solid mechanics. In physics, defects of solids are removed first by heating the solids up to a high temperature and then transforming them into crystal materials by a slow cooling process. At the highest temperature, the material is considered to be at the highest (max) energy state, whereas the minimum energy state is the frozen state [72].Simulated annealing was introduced into the domain of computer science as a probabilistic strategy for solving combinatorial optimization problems with a large search space. For example, simulated annealing is used, via the Real-Time Software System Generator (RT-Syn) framework [72], to minimize the related resource costs of software applications, including design and maintenance, by synthesizing the implementation detail of the design. When considering program synthesis as an optimization problem, some crucial implementation decisions must be involved during problem resolution, such as data structures, control flows, and algorithms. In simulated annealing, the program space is treated as a configuration space that encompasses all legal decisions.Iteratively, a random current feasible design with some perturbations (move set) is proposed. At the end, this move set must achieve all feasible designs in the design space. In each iteration, a cost function is used to measure the goodness of the current design in order to find the best design that can be reached. The last characteristic of the simulation is the cooling schedule, which mimics the cooling process of materials in physics. Moves in the high-energy state that decrease gradually in the cost function are accepted to produce a suboptimal solution, whereas a quick decrease results in a near-optimal solution to the problem [72].
- ○
- Evolutionary Algorithm: An evolutionary algorithm is a kind of generic population-based optimization that is inspired by biological evolution mechanisms, such as reproduction, mutation, recombination, and selection. In biology, biological changes in characteristics, or evolution, occur when evolutionary mechanisms and genetic recombination react to these changes, resulting in different characteristics becoming more common or hidden in the population in the following generations [96,169]. In the domain of computer science, In the domain of computer science, algorithms for solving optimization problem is applied to a population of individuals, where fitness functions are used iteratively over the population to evolve the quality of the final solution [73].
- ○
- Genetic Programming (GP): is a kind of evolutionary algorithm that uses genetic operations, namely, mutation, crossover, and selection to evolve its populations iteratively, until the best solutions to a given optimization problem are achieved [154]. It performs better than the exhaustive search when searching a problem (program) space that is too broad, because the search over the space is guided by the measures produced by the fitness function [96,169]. GP is considered one of the common techniques that is applied in the domain of program synthesis and automatic program repairs [73,96,154,155,169].
- Deterministic Optimization: On the other hand, the simpler alternative to the Stochastic method is the Deterministic Optimization method, which is used in some synthesis frameworks as an implemented search technique (Figure 16). Exhaustive Enumeration is considered to be a very general search-based problem-solving technique that involves all possible alternatives to be examined during the problem resolution process in order to find the optimal solution to the problem [68]. The brute-force algorithm is considered to be a common technique of exhaustive enumeration optimization, as noted during the conducted domain analysis. In this optimization, three kinds of collection optimization input are given: formal representation of candidate expressions E, logical specification and constraints S, and a finite set of examples X. The targeted problem to be solved must satisfy the following (First-Order Predicate Logic with equality) formal rule:
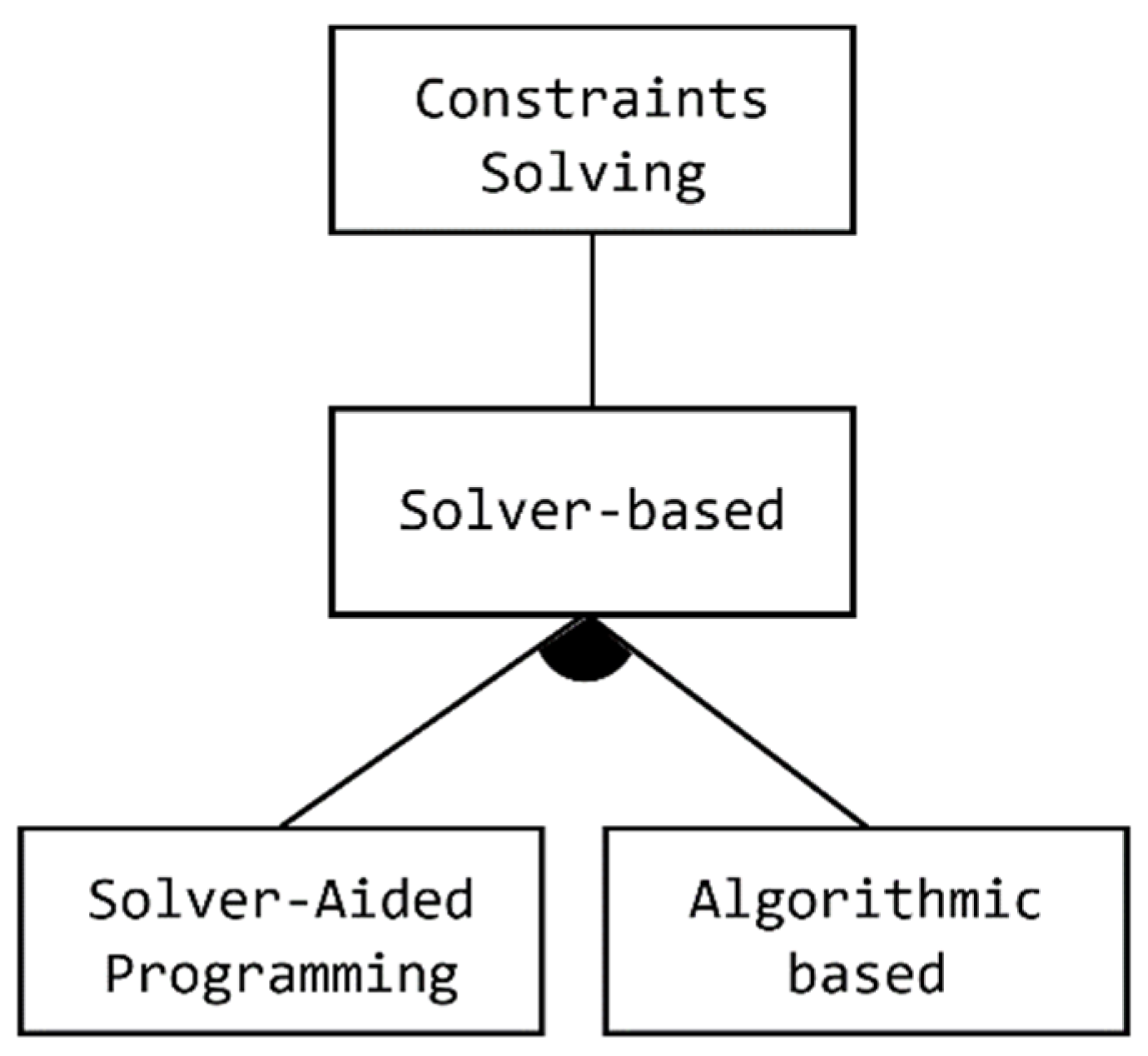
- Constraint Solving: The theory behind constraint solving program synthesis begins by expressing the semantics of a given program in some logic formulas. Instead of compiling the program into such a low-level executable machine code, it is compiled into logical constraints (formulas) as an intermediate representation of the given program. A solver-based strategy is then applied via solver-aided verification or synthesis tools to solve the condition satisfaction problem through proofing the correctness of the given program. It tries to find an input that makes the program fail (if it exists) when such a constraint is unsatisfied in an automatically generated test. Here, the program synthesis problem is treated as the Constraints’ Satisfaction Problem (CSP). The CSP can be defined as a collection of mathematical questions that are considered to be objects that must satisfy some constraints. Some intensive research has been conducted in the artificial intelligence (AI) and operational research domains when solving the CSP.
- ○
- Boolean Satisfiability Problem (SAT solver): The Boolean Satisfiability Problem (SAT) can be defined as a problem for checking whether or not a formula that is expressed using Boolean logic is satisfiable. SAT solving is considered the cornerstone of several software engineering applications, such as system design, model checking and hardware, debugging, pattern generation, and software verification [33]. The SAT problem is denoted as the first proven nondeterministic polynomial time (NP-complete problem) in which algorithms in their worst-case complexity that involve thousands of variables and millions of constraints are used for solving [33,75]. There are several program synthesis frameworks that use the SAT solver to resolve the synthesis problem, which is implemented based on an algorithmic approach using C++ or Python. For instance, the SKETCH framework utilizes the SAT solving technique in a counterexample-guided iteration that interacts with a verifier to check the candidate program against the specification and generates counterexamples until the final program that meets the complete specifications is found [27,94]. Additionally, SAT solving and the so-called gradient-based numerical optimization technique are combined and used for solving program synthesis problems in the Real Synthesis (REAS) framework [76]. The search space in REAS is explored using the SAT Solver for solving constraints on discrete variables to fix the set of Boolean expressions that appear in the program structure. This allows better tolerance with approximation errors, which leads to efficient approximation results. The REAS technique is implemented within the SKETCH framework. The end user, a programmer, writes their program with a set of unknowns using the high-level SKETCH language to express the intent. These unknowns are Boolean expressions (constraints) that need to be solved [76].
- ○
- Satisfiability Modulo Theories (SMT solver): The Satisfiability Modulo Theories (SMT) is a technique that is used to find satisfying solutions for the First-Order Logic (FOL) with an equality formula. The FOL formulas include the Boolean operations, belonging to Boolean Logic, which have more complicated expressions than variables including functions, predicates, and constants, as sometimes, the adoption of SAT solvers for a program synthesis problem requires richer logic formulas. Thus, in SMT formulas, some propositional variables in the SAT formula are replaced with some First-Order predicates. These predicates are Boolean functions that return the Boolean values of some variables [77]. The use of the Satisfiability Modulo Theory (SMT) solvers has emerged as a useful tool for verification, symbolic execution, theorem proving, and program synthesis approaches. There are many available SMT solvers, such as Z3 and the Cooperating Validity Checker (CVC4), that are used for solving the program synthesis problem. These frameworks are implemented based on an algorithmic approach using general-purposes programming languages [77].
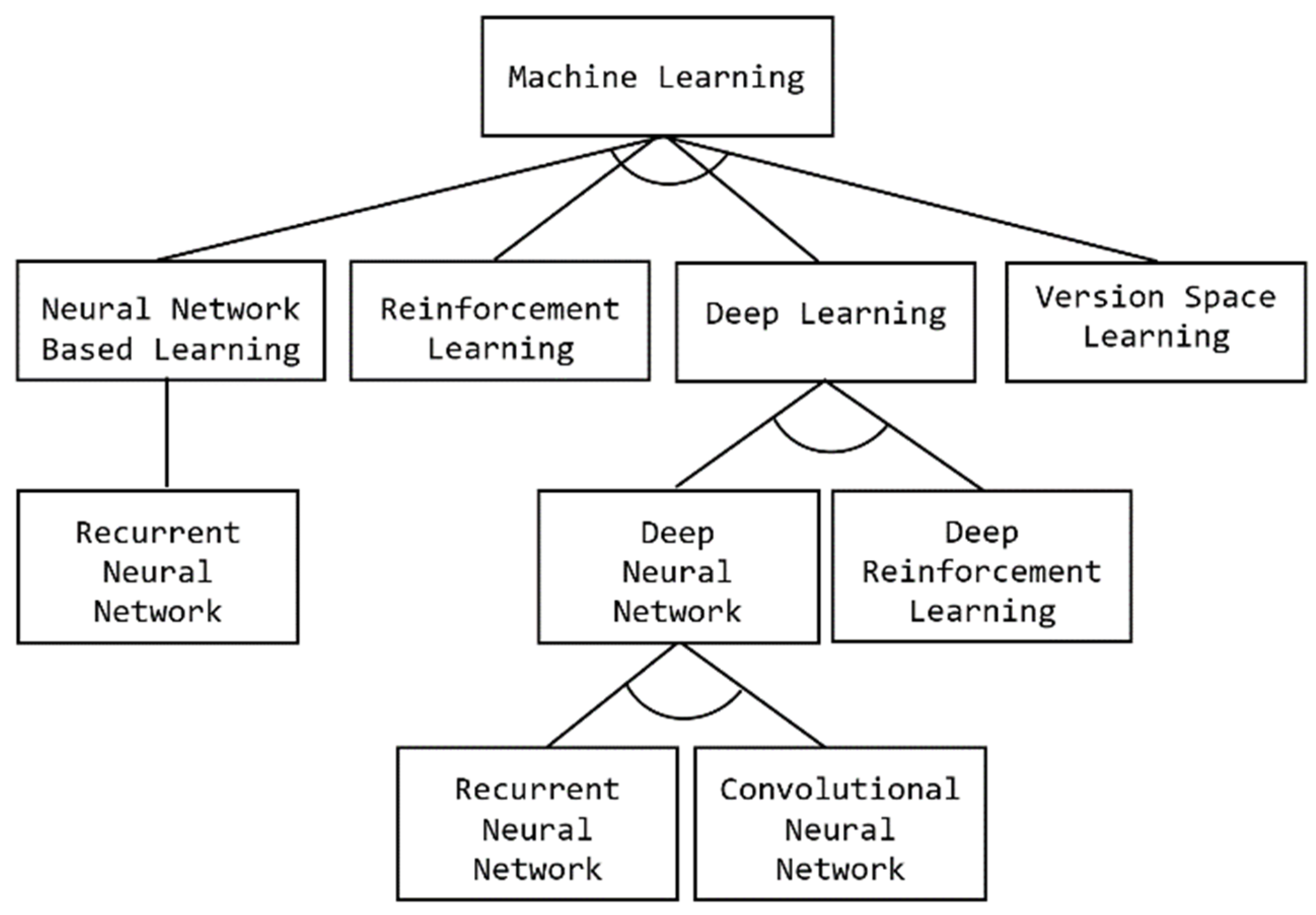
- Machine Learning: Machine learning (ML) is an application of the artificial intelligence (AI) branch of computer science that enables the machine to learn from a massive amount of data without being explicitly programmed. In the context of software engineering, ML techniques have brought great advances in program synthesis, in which they may be used to create automated tools with better code comprehension ability to help developers to understand and modify their code using knowledge extraction or recognition techniques [81]. Thus, the synthesis problem is introduced here as a machine learning problem. Developers who are interested in following this approach to solve the synthesis problem find themselves faced with a variety of independent choices, expressed in FD 17 by some optional notations. Different learning techniques are used to guide the synthesis search and automatically decompose the problem synthesis, such as deep learning, neural networks, reinforcement learning, and version space learning. These learning styles are illustrated in Figure 18.
- ○
- Version Space Learning: Version Space Learning is commonly used in programming-by demonstration (PBD) synthesis applications. In the PBD approach, a programmer demonstrates how to perform a task, and the system learns an appropriate representation of the procedure of that task. Version Space is considered to be a logical approach to machine learning where the concepts of learning are described using some logical language.
- ○
- Reinforcement Learning: Reinforcement learning (RL) is considered to be a subfield of machine learning that aims to teach an agent how to perform a specific task and achieve a goal in an uncertain, potentially complex environment. Many RL applications have been emerging with the rapid advancement in the domain of games technology and robotics. In the context of program synthesis, reinforcement learning algorithms are applied within various frameworks to maximize the likelihood of generating semantically correct programs, as well as to tackle program aliasing issues when different programs may satisfy a given specification [19,139].
- ○
- Neural-Network-Based Learning: A neural network can be defined as an interconnected group of artificial neurons that use a mathematical or computational model for information processing. They are used to solve AI problems through building classification and prediction systems to make predictions. According to the domain analysis, neural-network-based approaches to program synthesis have gained greater attention from the software engineering research community. This is reflected in the popularity of NNs for machine learning in recent years. Several recent research works have introduced neural-network-based frameworks and approaches to program synthesis from I/O examples [57].
- ○
- Deep Learning: As mentioned earlier in this paper, deep learning (DL) can be defined as a branch of machine learning where the architecture of a learning approach consists of multiple layers of data processing units. There is a variety of synthesis frameworks that adopt deep learning techniques, such as deep neural networks (Convolutional and Recurrent NNs) and deep reinforcement learning [116]. The RobustFill framework [82], for instance, is a neural program synthesis framework based on RNN that allows variable-length sets of input/output examples (pairs) to be encoded.
- ○
- Domain Specific Language (DSL) is used in RobustFill to express the collection of transformation rules of different textual operations, such as substring extractions, constant strings, and text conversions. The adopted DSL has the ability to express complex textual expressions (strings) by employing an effective regular expression extraction technique. The DSL takes a given string as the input and returns another string as the output. The synthesis system is trained with a number of I/O examples and has been shown to achieve 92% accuracy. It is worth mentioning that during the conducted domain analysis, we found various deep learning techniques adopted in different program synthesis applications, such as DeepCom [126] and CRAIC [127] for code comment, the CDE-Model [118] for code summarization, DeepRepair [156] for code repair, and RobustFill [82] and DLPaper2Code [145] for code translation and generation.
7. Applications of Program Synthesis
8. Architectural Design of a Suggested Code Generation Framework
8.1. Concepts
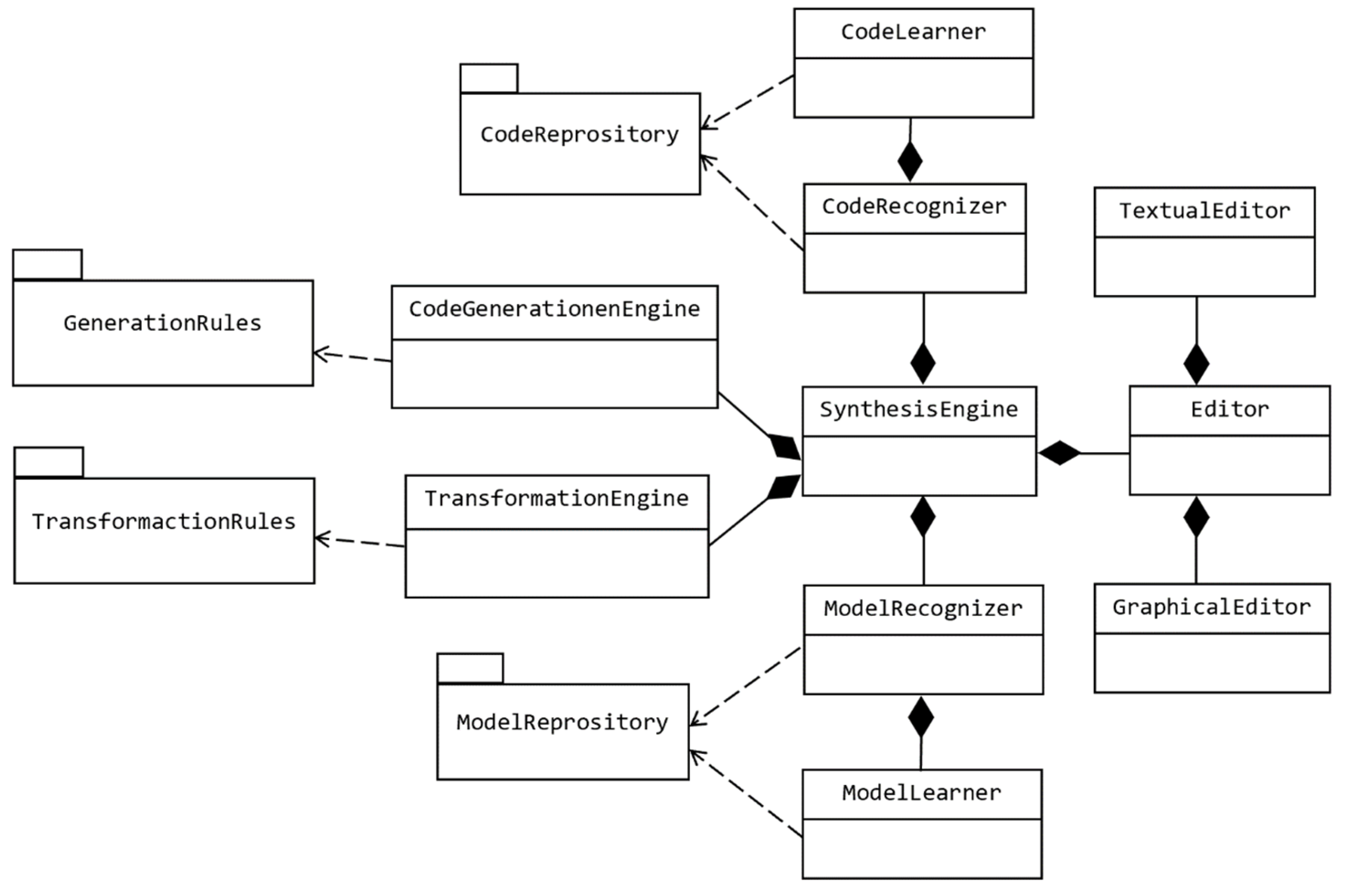
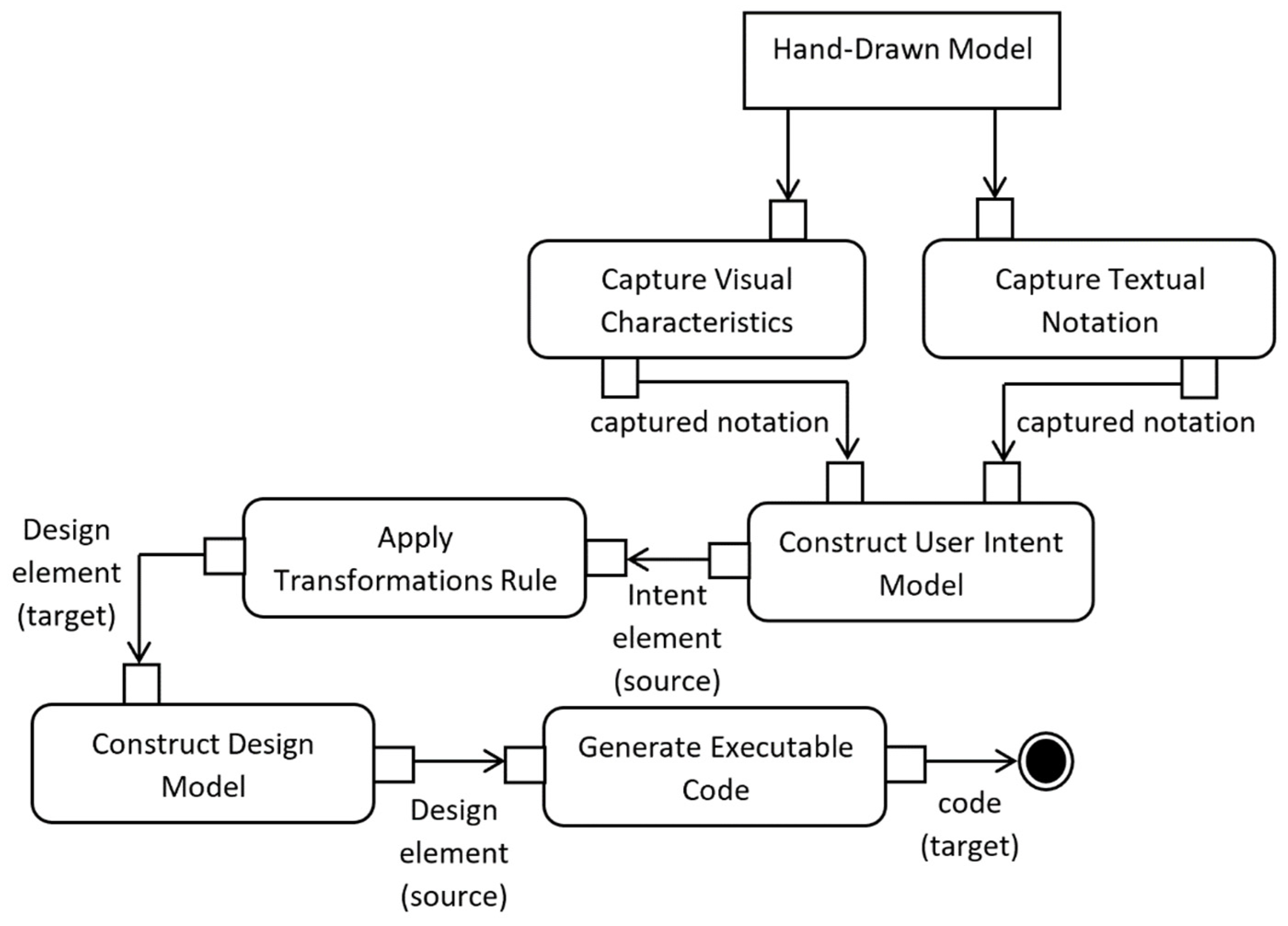
8.2. Architecture of the Synthesis Engine
8.3. Recommended Search Technique
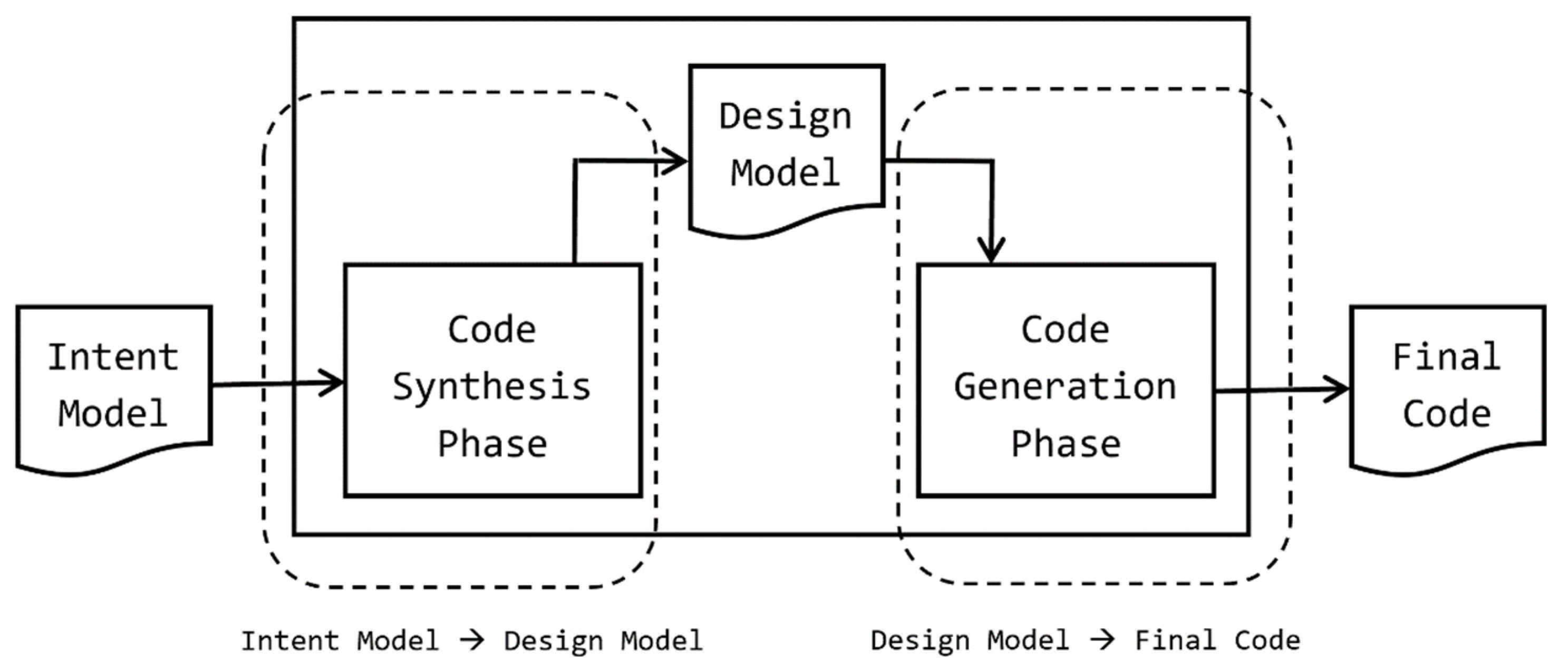
8.4. Language Model (Program Space)
8.4.1. Intent Model
|
8.4.2. Design Model
|
8.5. Transformations Engine
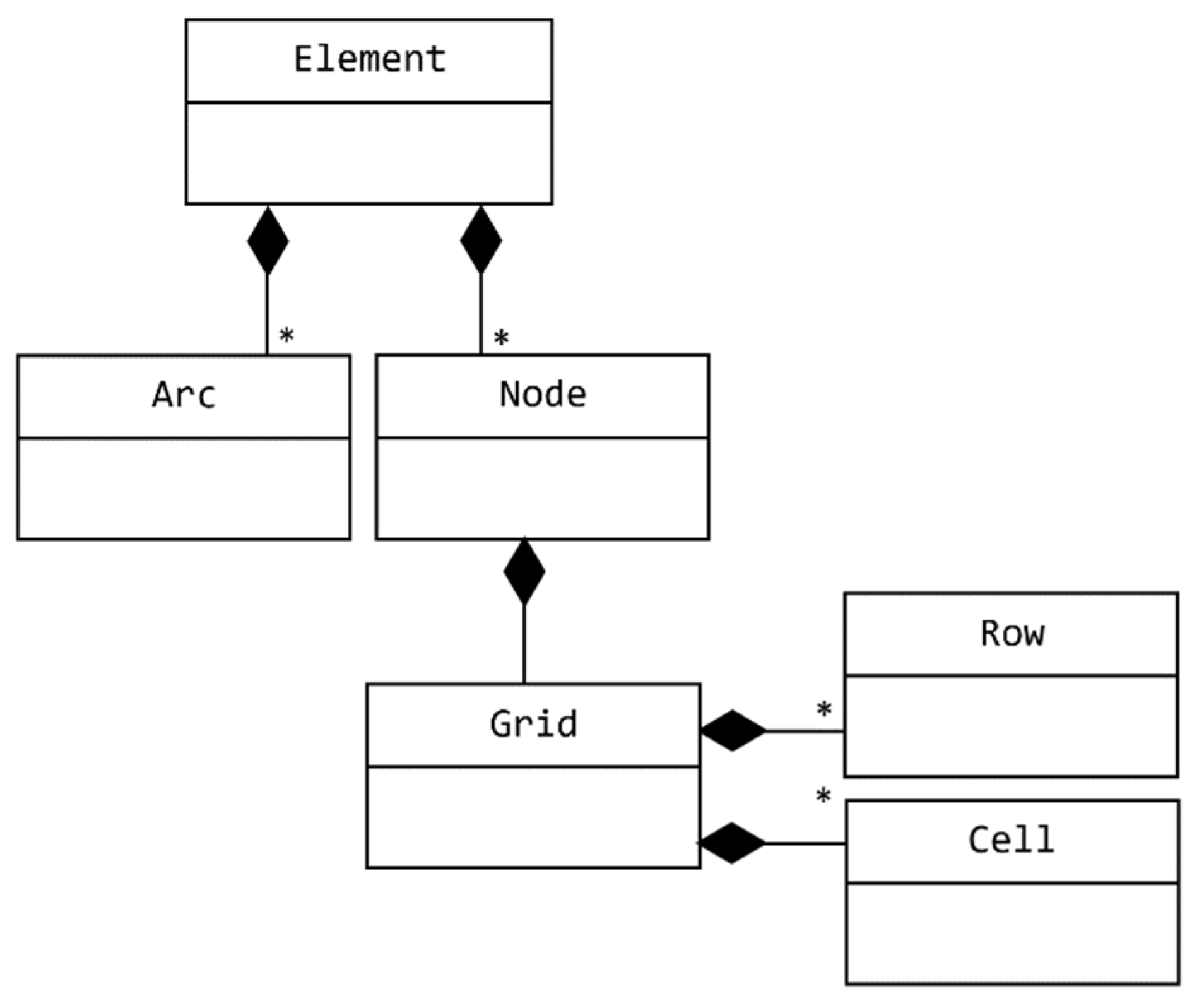
- Detecting Table: This transformation agent is responsible for transforming the captured hand-drawn grid shapes from the Intent model into a platform-independent table structure. This transformation step ensure that every transformed table has a unique name, even if the source grid has no name. The following First-Order Predicate Logic (FOPL) rule expresses the mapping between a grid element in the Intent model and a table element in the Design model.
- Detecting Column: This transformation agent is responsible for transforming the captured hand-drawn cell of a grid from the Intent model into a platform-independent column structure. This transformation step includes deciding whether the captured column is a primary key or not. The mapping rule between a cell element and a column one can be expressed using the following logical formula as
- Detecting Record Instance: This transformation agent is responsible for transforming the captured hand-drawn rows of a grid from the Intent model into a platform-independent recorded instance. The mapping rule between row and recorded elements can be expressed using the following FOPL logical formula as
8.6. Code Generation Engine
9. Conclusions
Funding
Conflicts of Interest
References
- Visser, E. A survey of rewriting strategies in program transformation systems. Electron. Notes Theor. Comput. Sci. 2001, 57, 109–143. [Google Scholar] [CrossRef]
- Cristina, D.; Pascal, K.; Daniel, K.; Matt, L. Program Synthesis for Program Analysis. ACM Trans. Program. Lang. Syst. 2018, 40, 45. [Google Scholar] [CrossRef]
- Church, A. Logic, arithmetic and automata. In Proceedings of the International Congress of Mathematicians, Institut Mittag-Leffler, Djursholm, Sweden, 15–22 August 1962; Volume 1962, pp. 23–35. [Google Scholar]
- Bodik, R.; Jobstmann, B. Algorithmic Program Synthesis: Introduction; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Buchi, J.R.; Landweber, L.H. Solving Sequential Conditions by Finite State Strategies; Springer: New York, NY, USA, 1967. [Google Scholar]
- Rabin, M.O. Automata on infinite objects and Church’s problem. Am. Math. Soc. 1972, 13, 6–24. [Google Scholar]
- Summers, P.D. A methodology for LISP program construction from examples. J. ACM 1977, 24, 161–175. [Google Scholar] [CrossRef]
- Pnueli, A. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (sfcs 1977), October 1977; IEEE: Piscataway Township, NJ, USA, 1977; pp. 46–57. [Google Scholar]
- Emerson, E.A.; Clarke, E.M. Using branching time temporal logic to synthesize synchronization skeletons. Sci. Comput. Program. 1982, 2, 241–266. [Google Scholar] [CrossRef]
- Manna, Z.; Wolper, P. Synthesis of communicating processes from temporal logic specifications. In Workshop on Logic of Programs; Springer: Berlin/Heidelberg, Germany, 1981; pp. 253–281. [Google Scholar]
- Manna, Z.; Pnueli, A. The Temporal Logic of Reactive and Concurrent Systems: Specification; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kupferman, O.; Vardi, M.Y.; Wolper, P. An automata-theoretic approach to branching-time model checking. J. ACM 2000, 47, 312–360. [Google Scholar] [CrossRef]
- Mens, T.; Van Gorp, P. A taxonomy of model transformation. Electron. Notes Theor. Comput. Sci. 2006, 152, 125–142. [Google Scholar] [CrossRef]
- Czarnecki, K.; Helsen, S. Feature-based survey of model transformation approaches. IBM Syst. J. 2006, 45, 621–645. [Google Scholar] [CrossRef]
- Lin, X.V.; Wang, C.; Pang, D.; Vu, K.; Ernst, M.D. Program Synthesis from Natural Language Using Recurrent Neural Networks; Tech. Rep. UW-CSE-17-03-01; University of Washington Department of Computer Science and Engineering: Seattle, WA, USA, 2017. [Google Scholar]
- Manshadi, M.H.; Gildea, D.; Allen, J.F. Integrating programming by example and natural language programming. In Proceedings of the Twenty-Seventh AAAI Conference on Artificial Intelligence, Washington, DC, USA, 14–18 July 2013. [Google Scholar]
- Locascio, N.; Narasimhan, K.; DeLeon, E.; Kushman, N.; Barzilay, R. Neural generation of regular expressions from natural language with minimal domain knowledge. arXiv 2016, arXiv:1608.03000. [Google Scholar]
- Kushman, N.; Barzilay, R. Using semantic unification to generate regular expressions from natural language. In Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Atlanta, Georgia, 9–14 June 2013; pp. 826–836. [Google Scholar]
- Guu, K.; Pasupat, P.; Liu, E.Z.; Liang, P. From language to programs: Bridging reinforcement learning and maximum marginal likelihood. arXiv 2017, arXiv:1704.07926. [Google Scholar]
- Krishnamurthy, J.; Mitchell, T.M. Weakly supervised training of semantic parsers. In Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Jeju Island, Korea, 12–14 July 2012; pp. 754–765. [Google Scholar]
- Rabinovich, M.; Stern, M.; Klein, D. Abstract syntax networks for code generation and semantic parsing. arXiv 2017, arXiv:1704.07535. [Google Scholar]
- Zhong, V.; Xiong, C.; Socher, R. Seq2sql: Generating structured queries from natural language using reinforcement learning. arXiv 2017, arXiv:1709.00103. [Google Scholar]
- Sun, Y.; Tang, D.; Duan, N.; Ji, J.; Cao, G.; Feng, X.; Zhou, M. Semantic parsing with syntax-and table-aware sql generation. arXiv 2018, arXiv:1804.08338. [Google Scholar]
- Murali, V.; Qi, L.; Chaudhuri, S.; Jermaine, C. Neural sketch learning for conditional program generation. arXiv 2017, arXiv:1703.05698. [Google Scholar]
- Samimi, H.; Rajan, K. Specification-based sketching with Sketch. In Proceedings of the 13th Workshop on Formal Techniques for Java-Like Programs, July 2011; ACM: New York, NY, USA, 2011; p. 3. [Google Scholar]
- Solar-Lezama, A.; Tancau, L.; Bodik, R.; Seshia, S.; Saraswat, V. Combinatorial sketching for finite programs. ACM Sigplan Notices 2006, 41, 404–415. [Google Scholar] [CrossRef]
- Solar-Lezama, A. Program sketching. Int. J. Softw. Tools Technol. Transf. 2013, 15, 475–495. [Google Scholar] [CrossRef]
- Hua, J.; Zhang, Y.; Zhang, Y.; Khurshid, S. EdSketch: Execution-driven sketching for Java. Int. J. Softw. Tools Technol. Transf. 2019, 21, 249–265. [Google Scholar] [CrossRef]
- Raza, M.; Gulwani, S.; Milic-Frayling, N. Compositional program synthesis from natural language and examples. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Subahi, A.F.; Alotaibi, Y. A New Framework for Classifying Information Systems Modelling Languages. JSW 2018, 13, 18–42. [Google Scholar] [CrossRef]
- Polozov, O.; Gulwani, S. PROSE: Inductive Program Synthesis for the Mass Markets; University of California: Berkeley, CA, USA, 2017. [Google Scholar]
- Polozov, O.; Gulwani, S. FlashMeta: A framework for inductive program synthesis. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2015; Volume 50, pp. 107–126. [Google Scholar]
- Torlak, E.; Bodik, R. A lightweight symbolic virtual machine for solver-aided host languages. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2014; Volume 49, pp. 530–541. [Google Scholar]
- Wang, C.; Cheung, A.; Bodik, R. Synthesizing highly expressive SQL queries from input-output examples. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2017; Volume 52, pp. 452–466. [Google Scholar]
- So, S.; Oh, H. Synthesizing imperative programs from examples guided by static analysis. In International Static Analysis Symposium; Springer: Cham, Switzerland, 2017; pp. 364–381. [Google Scholar]
- Singh, R.; Gulwani, S. Synthesizing number transformations from input-output examples. In Proceedings of the International Conference on Computer Aided Verification, July 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 634–651. [Google Scholar]
- Chen, X.; Liu, C.; Song, D. Towards synthesizing complex programs from input-output examples. arXiv 2017, arXiv:1706.01284. [Google Scholar]
- Zhang, L.; Rosenblatt, G.; Fetaya, E.; Liao, R.; Byrd, W.E.; Urtasun, R.; Zemel, R. Leveraging Constraint Logic Programming for Neural Guided Program Synthesis. In Proceedings of the Sixth International Conference on Learning Representations, Vancouver Convention Center, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Raza, M.; Gulwani, S. Disjunctive Program Synthesis: A Robust Approach to Programming by Example. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Gulwani, S.; Harris, W.R.; Singh, R. Spreadsheet data manipulation using examples. Commun. ACM 2012, 55, 97–105. [Google Scholar] [CrossRef]
- Peleg, H.; Shoham, S.; Yahav, E. Programming not only by example. In 2018 IEEE/ACM 40th International Conference on Software Engineering (ICSE), May 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1114–1124. [Google Scholar]
- Kalyan, A.; Mohta, A.; Polozov, O.; Batra, D.; Jain, P.; Gulwani, S. Neural-guided deductive search for real-time program synthesis from examples. arXiv 2018, arXiv:1804.01186. [Google Scholar]
- Subhajit, R. From concrete examples to heap manipulating programs. In International Static Analysis Symposium; Springer: Berlin/Heidelberg, Germany, 2013; pp. 126–149. [Google Scholar]
- Le, V.; Gulwani, S. FlashExtract: A framework for data extraction by examples. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2014; Volume 49, pp. 542–553. [Google Scholar]
- Lee, M.; So, S.; Oh, H. Synthesizing regular expressions from examples for introductory automata assignments. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2016; Volume 52, pp. 70–80. [Google Scholar]
- Bartoli, A.; Davanzo, G.; De Lorenzo, A.; Mauri, M.; Medvet, E.; Sorio, E. Automatic generation of regular expressions from examples with genetic programming. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, July 2012; ACM: New York, NY, USA, 2012; pp. 1477–1478. [Google Scholar]
- Gulwani, S. Automating string processing in spreadsheets using input-output examples. In ACM Sigplan Notices; ACM: New York, NY, USA, 2011; Volume 46, pp. 317–330. [Google Scholar]
- Torlak, E.; Bodik, R. Growing solver-aided languages with rosette. In Proceedings of the 2013 ACM International Symposium on New Ideas, New Paradigms, and Reflections on Programming & Software, October 2013; ACM: New York, NY, USA, 2013; pp. 135–152. [Google Scholar]
- Albarghouthi, A.; Gulwani, S.; Kincaid, Z. Recursive program synthesis. In International Conference on Computer Aided Verification, July 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 934–950. [Google Scholar]
- Zamani, M.; Esfahani, P.M.; Majumdar, R.; Abate, A.; Lygeros, J. Symbolic control of stochastic systems via approximately bisimilar finite abstractions. IEEE Trans. Autom. Control 2014, 59, 3135–3150. [Google Scholar] [CrossRef]
- Malik, S.; Weissenbacher, G. Boolean satisfiability solvers: Techniques & extensions. In Software Safety & Security Tools for Analysis and Verification; IOS Press: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Osera, P.M.; Zdancewic, S. Type-and-example-directed program synthesis. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2015; Volume 50, pp. 619–630. [Google Scholar]
- Balog, M.; Gaunt, A.L.; Brockschmidt, M.; Nowozin, S.; Tarlow, D. Deepcoder: Learning to write programs. arXiv 2016, arXiv:1611.01989. [Google Scholar]
- Amodio, M.; Chaudhuri, S.; Reps, T. Neural attribute machines for program generation. arXiv 2017, arXiv:1705.09231. [Google Scholar]
- Udupa, A.; Raghavan, A.; Deshmukh, J.V.; Mador-Haim, S.; Martin, M.M.; Alur, R. TRANSIT: Specifying protocols with concolic snippets. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2013; Volume 48, pp. 287–296. [Google Scholar]
- Liu, E.Z.; Guu, K.; Pasupat, P.; Shi, T.; Liang, P. Reinforcement learning on web interfaces using workflow-guided exploration. arXiv 2018, arXiv:1802.08802. [Google Scholar]
- Shin, R.; Polosukhin, I.; Song, D. Improving neural program synthesis with inferred execution traces. In Proceedings of the Advances in Neural Information Processing Systems, Palais des Congrès de Montréal, Montréal, QC, Canada, 3–8 December 2018; pp. 8917–8926. [Google Scholar]
- Ellis, K.; Ritchie, D.; Solar-Lezama, A.; Tenenbaum, J. Learning to infer graphics programs from hand-drawn images. In Proceedings of the Advances in Neural Information Processing Systems, Palais des Congrès de Montréal, Montréal, QC, Canada, 3–8 December 2018; pp. 6059–6068. [Google Scholar]
- Ganin, Y.; Kulkarni, T.; Babuschkin, I.; Eslami, S.M.; Vinyals, O. Synthesizing programs for images using reinforced adversarial learning. arXiv 2018, arXiv:1804.01118. [Google Scholar]
- Srivastava, S.; Gulwani, S.; Foster, J.S. From program verification to program synthesis. In ACM Sigplan Notices; ACM: New York, NY, USA, 2010; Volume 45, pp. 313–326. [Google Scholar]
- Heule, S.; Schkufza, E.; Sharma, R.; Aiken, A. Stratified synthesis: Automatically learning the x86–64 instruction set. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2016; Volume 51, pp. 237–250. [Google Scholar]
- Lau, T.; Domingos, P.; Weld, D.S. Learning programs from traces using version space algebra. In Proceedings of the 2nd International Conference on Knowledge Capture, October 2003; ACM: New York, NY, USA, 2003; pp. 36–43. [Google Scholar]
- Zhang, X.; Gupta, R. Whole execution traces and their applications. ACM Trans. Archit. Code Optim. 2005, 2, 301–334. [Google Scholar] [CrossRef]
- Bhansali, S.; Chen, W.K.; De Jong, S.; Edwards, A.; Murray, R.; Drinić, M.; Chau, J. Framework for instruction-level tracing and analysis of program executions. In Proceedings of the 2nd International Conference on Virtual Execution Environments, June 2006; ACM: New York, NY, USA, 2006; pp. 154–163. [Google Scholar]
- Wang, X.; Dillig, I.; Singh, R. Program synthesis using abstraction refinement. Proc. ACM Program. Lang. 2017, 63, 1–30. [Google Scholar] [CrossRef]
- Reyna, J. From program synthesis to optimal program synthesis. In Proceedings of the 2011 Annual Meeting of the North American Fuzzy Information Processing Society, March 2011; IEEE: Piscataway Township, NJ, USA, 2011; pp. 1–6. [Google Scholar]
- Bornholt, J.; Torlak, E.; Ceze, L.; Grossman, D. Approximate Program Synthesis. In Proceedings of the Workshop on Approximate Computing Across the Stack (WAX w/PLDI), Portland, OR, USA, 13 June 2015. [Google Scholar]
- Lee, V.T.; Alaghi, A.; Ceze, L.; Oskin, M. Stochastic Synthesis for Stochastic Computing. arXiv 2018, arXiv:1810.04756. [Google Scholar]
- Lee, W.; Heo, K.; Alur, R.; Naik, M. Accelerating search-based program synthesis using learned probabilistic models. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, June 2018; ACM: New York, NY, USA, 2018; pp. 436–449. [Google Scholar]
- Itzhaky, S.; Singh, R.; Solar-Lezama, A.; Yessenov, K.; Lu, Y.; Leiserson, C.; Chowdhury, R. Deriving divide-and-conquer dynamic programming algorithms using solver-aided transformations. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2016; Volume 51, pp. 145–164. [Google Scholar]
- Pu, Y.; Bodik, R.; Srivastava, S. Synthesis of first-order dynamic programming algorithms. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2011; Volume 46, pp. 83–98. [Google Scholar]
- Färm, P.; Dubrova, E.; Kuehlmann, A. Integrated logic synthesis using simulated annealing. In Proceedings of the 21st Edition of the Great Lakes Symposium on Great Lakes Symposium on VLSI, May 2011; ACM: New York, NY, USA, 2011; pp. 407–410. [Google Scholar]
- Forstenlechner, S.; Fagan, D.; Nicolau, M.; O’Neill, M. Towards understanding and refining the general program synthesis benchmark suite with genetic programming. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), July 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Oliveira, C.A.; Pardalos, P.M. A survey of combinatorial optimization problems in multicast routing. Comput. Oper. Res. 2005, 32, 1953–1981. [Google Scholar] [CrossRef]
- Torlak, E.; Vaziri, M.; Dolby, J. MemSAT: Checking axiomatic specifications of memory models. ACM Sigplan Notices 2010, 45, 341–350. [Google Scholar] [CrossRef]
- Inala, J.P.; Gao, S.; Kong, S.; Solar-Lezama, A. REAS: Combining Numerical Optimization with SAT Solving. arXiv 2018, arXiv:1802.04408. [Google Scholar]
- De Moura, L.; Bjørner, N. Z3: An efficient SMT solver. In Proceedings of the International conference on Tools and Algorithms for the Construction and Analysis of Systems, March 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–340. [Google Scholar]
- Reynolds, A.; Tinelli, C. SyGuS Techniques in the Core of an SMT Solver. arXiv 2017, arXiv:1711.10641. [Google Scholar] [CrossRef]
- Marić, F. Formalization and implementation of modern SAT solvers. J. Autom. Reason. 2009, 43, 81–119. [Google Scholar] [CrossRef]
- Alexandru, C.V. Guided code synthesis using deep neural networks. In Proceedings of the 2016 24th ACM SIGSOFT International Symposium on Foundations of Software Engineering, November 2016; ACM: New York, NY, USA, 2016; pp. 1068–1070. [Google Scholar]
- Alexandru, C.V.; Panichella, S.; Gall, H.C. Replicating parser behavior using neural machine translation. In Proceedings of the 25th International Conference on Program Comprehension, May 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 316–319. [Google Scholar]
- Devlin, J.; Uesato, J.; Bhupatiraju, S.; Singh, R.; Mohamed, A.R.; Kohli, P. Robustfill: Neural program learning under noisy I/O. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 990–998. [Google Scholar]
- Ke, Y.; Stolee, K.T.; Le Goues, C.; Brun, Y. Repairing programs with semantic code search (t). In Proceedings of the 2015 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), November 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 295–306. [Google Scholar]
- Yang, Y.; Jiang, Y.; Gu, M.; Sun, J.; Gao, J.; Liu, H. A language model for statements of software code. In Proceedings of the 32nd IEEE/ACM International Conference on Automated Software Engineering (ASE), October 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 682–687. [Google Scholar]
- Alur, R.; Bodik, R.; Juniwal, G.; Martin, M.M.; Raghothaman, M.; Seshia, S.A.; Udupa, A. Syntax-guided synthesis. In Proceedings of the 2013 Formal Methods in Computer-Aided Design, October 2013; IEEE: Piscataway Township, NJ, USA, 2013; pp. 1–8. [Google Scholar]
- Rolim, R.; Soares, G.; D’Antoni, L.; Polozov, O.; Gulwani, S.; Gheyi, R.; Hartmann, B. Learning syntactic program transformations from examples. In Proceedings of the 39th International Conference on Software Engineering, May 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 404–415. [Google Scholar]
- Wang, X.; Anderson, G.; Dillig, I.; McMillan, K.L. Learning Abstractions for Program Synthesis. In Proceedings of the International Conference on Computer Aided Verification, July 2018; Springer: Cham, Switzerland, 2018; pp. 407–426. [Google Scholar]
- Srivastava, S.; Gulwani, S.; Foster, J.S. Template-based program verification and program synthesis. Int. J. Softw. Tools Technol. Transf. 2013, 15, 497–518. [Google Scholar] [CrossRef]
- Abid, N.; Dragan, N.; Collard, M.L.; Maletic, J.I. The evaluation of an approach for automatic generated documentation. In Proceedings of the 2017 IEEE International Conference on Software Maintenance and Evolution (ICSME), September 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 307–317. [Google Scholar]
- Castrillon, J.; Sheng, W.; Leupers, R. Trends in embedded software synthesis. In Proceedings of the 2011 International Conference on Embedded Computer Systems: Architectures, Modeling and Simulation, July 2011; IEEE: Piscataway Township, NJ, USA, 2011; pp. 347–354. [Google Scholar]
- Kitzelmann, E.; Schmid, U. Inductive synthesis of functional programs: An explanation based generalization approach. J. Mach. Learn. Res. 2006, 7, 429–454. [Google Scholar]
- Liang, Z.; Tsushima, K. Component-based Program Synthesis in OCaml. 2017. [Google Scholar]
- Feng, Y.; Martins, R.; Wang, Y.; Dillig, I.; Reps, T.W. Component-based synthesis for complex APIs. ACM SIGPLAN Notices 2017, 52, 599–612. [Google Scholar] [CrossRef]
- Jha, S.; Gulwani, S.; Seshia, S.A.; Tiwari, A. Oracle-guided component-based program synthesis. In Proceedings of the 32nd ACM/IEEE International Conference on Software Engineering, May 2010; ACM: New York, NY, USA, 2010; Volume 1, pp. 215–224. [Google Scholar]
- Jha, S.; Seshia, S.A. A theory of formal synthesis via inductive learning. Acta Inform. 2017, 54, 693–726. [Google Scholar] [CrossRef]
- Kitzelmann, E. Inductive programming: A survey of program synthesis techniques. In Proceedings of the International Workshop on Approaches and Applications of Inductive Programming, September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 50–73. [Google Scholar]
- Gulwani, S.; Hernández-Orallo, J.; Kitzelmann, E.; Muggleton, S.H.; Schmid, U.; Zorn, B. Inductive programming meets the real world. Commun. ACM 2015, 58, 90–99. [Google Scholar] [CrossRef]
- Goffi, A.; Gorla, A.; Mattavelli, A.; Pezzè, M.; Tonella, P. Search-based synthesis of equivalent method sequences. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, November 2014; ACM: New York, NY, USA, 2014; pp. 366–376. [Google Scholar]
- Korukhova, Y. An approach to automatic deductive synthesis of functional programs. Ann. Math. Artif. Intell. 2007, 50, 255–271. [Google Scholar] [CrossRef]
- Hofmann, M.; Kitzelmann, E.; Schmid, U. A unifying framework for analysis and evaluation of inductive programming systems. In Proceedings of the Second Conference on Artificial General Intelligence, Atlantis, Catalonia, Spain, 16–22 July 2009; pp. 55–60. [Google Scholar]
- Gulwani, S. Dimensions in program synthesis. In Proceedings of the 12th international ACM SIGPLAN Symposium on Principles and Practice of Declarative Programming, July 2010; ACM: New York, NY, USA, 2010; pp. 13–24. [Google Scholar]
- Gulwani, S.; Polozov, O.; Singh, R. Program synthesis. Found. Trends Program. Lang. 2017, 4, 1–119. [Google Scholar] [CrossRef]
- Allamanis, M.; Barr, E.T.; Bird, C.; Sutton, C. Learning natural coding conventions. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, November 2014; ACM: New York, NY, USA, 2014; pp. 281–293. [Google Scholar]
- Li, J.; Wang, Y.; Lyu, M.R.; King, I. Code completion with neural attention and pointer networks. arXiv 2017, arXiv:1711.09573. [Google Scholar]
- Bhoopchand, A.; Rocktäschel, T.; Barr, E.; Riedel, S. Learning python code suggestion with a sparse pointer network. arXiv 2016, arXiv:1611.08307. [Google Scholar]
- Dam, H.K.; Tran, T.; Pham, T. A deep language model for software code. arXiv 2016, arXiv:1608.02715. [Google Scholar]
- Liu, C.; Wang, X.; Shin, R.; Gonzalez, J.E.; Song, D. Neural Code Completion. In Proceedings of the International Conference on Learning Representations (ICLR) 2016, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Han, S.; Wallace, D.R.; Miller, R.C. Code completion from abbreviated input. In Proceedings of the 2009 IEEE/ACM International Conference on Automated Software Engineering, November 2009; IEEE: Piscataway Township, NJ, USA, 2009; pp. 332–343. [Google Scholar]
- Raychev, V.; Bielik, P.; Vechev, M. Probabilistic model for code with decision trees. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2016; Volume 51, pp. 731–747. [Google Scholar]
- Raychev, V.; Bielik, P.; Vechev, M.; Krause, A. Learning programs from noisy data. In ACM SIGPLAN Notices; ACM: New York, NY, USA, 2016; Volume 51, pp. 761–774. [Google Scholar]
- Yamamoto, T. Code suggestion of method call statements using a source code corpus. In Proceedings of the 2017 24th Asia-Pacific Software Engineering Conference (APSEC), December 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 666–671. [Google Scholar]
- Ichinco, M. A Vision for Interactive Suggested Examples for Novice Programmers. In 2018 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC), October 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 303–304. [Google Scholar]
- Tu, Z.; Su, Z.; Devanbu, P. On the localness of software. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, November 2014; ACM: New York, NY, USA, 2014; pp. 269–280. [Google Scholar]
- White, M.; Vendome, C.; Linares-Vásquez, M.; Poshyvanyk, D. Toward deep learning software repositories. In Proceedings of the 12th Working Conference on Mining Software Repositories, May 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 334–345. [Google Scholar]
- Franks, C.; Tu, Z.; Devanbu, P.; Hellendoorn, V. Cacheca: A cache language model based code suggestion tool. In Proceedings of the 37th International Conference on Software Engineering, May 2015; IEEE: Piscataway Township, NJ, USA, 2015; Volume 2, pp. 705–708. [Google Scholar]
- Wan, Y.; Zhao, Z.; Yang, M.; Xu, G.; Ying, H.; Wu, J.; Yu, P.S. Improving automatic source code summarization via deep reinforcement learning. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, September 2018; ACM: New York, NY, USA, 2018; pp. 397–407. [Google Scholar]
- Hu, X.; Li, G.; Xia, X.; Lo, D.; Lu, S.; Jin, Z. Summarizing source code with transferred api knowledge. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden, 13–19 July 2018; pp. 2269–2275. [Google Scholar]
- Zeng, L.; Zhang, X.; Wang, T.; Li, X.; Yu, J.; Wang, H. Improving code summarization by combining deep learning and empirical knowledge (S). In Proceedings of the SEKE, Redwood City, CA, USA, 1–3 July 2018. [Google Scholar]
- Rai, S.; Gaikwad, T.; Jain, S.; Gupta, A. Method Level Text Summarization for Java Code Using Nano-Patterns. In Proceedings of the 2017 24th Asia-Pacific Software Engineering Conference (APSEC), December 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 199–208. [Google Scholar]
- Ghofrani, J.; Mohseni, M.; Bozorgmehr, A. A conceptual framework for clone detection using machine learning. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), December 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 0810–0817. [Google Scholar]
- Panichella, S. Summarization techniques for code, change, testing, and user feedback. In Proceedings of the 2018 IEEE Workshop on Validation, Analysis and Evolution of Software Tests (VST), March 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Malhotra, M.; Chhabra, J.K. Class Level Code Summarization Based on Dependencies and Micro Patterns. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), April 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1011–1016. [Google Scholar]
- Hassan, M.; Hill, E. Toward automatic summarization of arbitrary java statements for novice programmers. In Proceedings of the 2018 IEEE International Conference on Software Maintenance and Evolution (ICSME), September 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 539–543. [Google Scholar]
- Decker, M.J.; Newman, C.D.; Collard, M.L.; Guarnera, D.T.; Maletic, J.I. A Timeline Summarization of Code Changes. In Proceedings of the 2018 IEEE Third International Workshop on Dynamic Software Documentation (DySDoc3), September 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 9–10. [Google Scholar]
- Iyer, S.; Konstas, I.; Cheung, A.; Zettlemoyer, L. Summarizing source code using a neural attention model. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Berlin, Germany, 7–12 August 2016; pp. 2073–2083. [Google Scholar]
- Hu, X.; Li, G.; Xia, X.; Lo, D.; Jin, Z. Deep code comment generation. In Proceedings of the 26th Conference on Program Comprehension, May 2018; ACM: New York, NY, USA, 2018; pp. 200–210. [Google Scholar]
- Amodio, M.; Chaudhuri, S.; Reps, T.W. Neural Attribute Machines for Program Generation. CoRR abs/1705.09231. arXiv 2017, arXiv:1705.09231. [Google Scholar]
- Sulír, M.; Porubän, J. Source code documentation generation using program execution. Information 2017, 8, 148. [Google Scholar] [CrossRef]
- Le Moulec, G.; Blouin, A.; Gouranton, V.; Arnaldi, B. Automatic production of end user documentation for DSLs. Comput. Lang. Syst. Struct. 2018, 54, 337–357. [Google Scholar] [CrossRef]
- Louis, A.; Dash, S.K.; Barr, E.T.; Sutton, C. Deep learning to detect redundant method comments. arXiv 2018, arXiv:1806.04616. [Google Scholar]
- Wong, E.; Liu, T.; Tan, L. Clocom: Mining existing source code for automatic comment generation. In Proceedings of the 2015 IEEE 22nd International Conference on Software Analysis, Evolution, and Reengineering (SANER), Montreal, QC, Canada, 2–6 March 2015; pp. 380–389. [Google Scholar]
- Thayer, K. Using Program Analysis to Improve API Learnability. In Proceedings of the 2018 ACM Conference on International Computing Education Research, August 2018; ACM: New York, NY, USA, 2018; pp. 292–293. [Google Scholar]
- Newman, C.; Dragan, N.; Collard, M.L.; Maletic, J.; Decker, M.; Guarnera, D.; Abid, N. Automatically Generating Natural Language Documentation for Methods. In Proceedings of the 2018 IEEE Third International Workshop on Dynamic Software Documentation (DySDoc3), September 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–2. [Google Scholar]
- Ishida, Y.; Arimatsu, Y.; Kaixie, L.; Takagi, G.; Noda, K.; Kobayashi, T. Generating an interactive view of dynamic aspects of API usage examples. In Proceedings of the 2018 IEEE Third International Workshop on Dynamic Software Documentation (DySDoc3), September 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 13–14. [Google Scholar]
- Yildiz, E.; Ekin, E. Creating Important Statement Type Comments in Autocomment: Automatic Comment Generation Framework. In Proceedings of the 2018 3rd International Conference on Computer Science and Engineering (UBMK), September 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 642–647. [Google Scholar]
- Beltramelli, T. pix2code: Generating code from a graphical user interface screenshot. In Proceedings of the ACM SIGCHI Symposium on Engineering Interactive Computing Systems, June 2018; ACM: New York, NY, USA, 2018; p. 3. [Google Scholar]
- Cummins, C.; Petoumenos, P.; Wang, Z.; Leather, H. Synthesizing benchmarks for predictive modeling. In Proceedings of the 2017 IEEE/ACM International Symposium on Code Generation and Optimization (CGO), February 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 86–99. [Google Scholar]
- Chen, X.; Liu, C.; Song, D. Tree-to-tree neural networks for program translation. In Proceedings of the Advances in Neural Information Processing Systems, Palais des Congrès de Montréal, Montréal, QC, Canada, 3–8 December 2018; pp. 2547–2557. [Google Scholar]
- Bunel, R.; Hausknecht, M.; Devlin, J.; Singh, R.; Kohli, P. Leveraging grammar and reinforcement learning for neural program synthesis. arXiv 2018, arXiv:1805.04276. [Google Scholar]
- Barone, A.V.M.; Sennrich, R. A parallel corpus of Python functions and documentation strings for automated code documentation and code generation. arXiv 2017, arXiv:1707.02275. [Google Scholar]
- Aggarwal, K.; Salameh, M.; Hindle, A. Using Machine Translation for Converting Python 2 to Python 3 Code (No. e1817). Available online: https://peerj.com/preprints/1459.pdf (accessed on 3 April 2020).
- Yin, P.; Neubig, G. A syntactic neural model for general-purpose code generation. arXiv 2017, arXiv:1704.01696. [Google Scholar]
- Puschel, M.; Moura, J.M.; Johnson, J.R.; Padua, D.; Veloso, M.M.; Singer, B.W.; Chen, K. SPIRAL: Code generation for DSP transforms. Proc. IEEE 2005, 93, 232–275. [Google Scholar] [CrossRef]
- Strecker, M. Formal verification of a Java compiler in Isabelle. In Proceedings of the International Conference on Automated Deduction, Copenhagen, Denmark, 27–30 July 2002; pp. 63–77. [Google Scholar]
- Sethi, A.; Sankaran, A.; Panwar, N.; Khare, S.; Mani, S. DLPaper2Code: Auto-generation of code from deep learning research papers. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Subahi, A.F.; Simons, A.J. A multi-level transformation from conceptual data models to database scripts using Java agents. In Proceedings of the 2nd Workshop of Composition of Model Transformations, Kings Collage London, London, UK, 30 September 2011; pp. 1–7. [Google Scholar]
- Alhefdhi, A.; Dam, H.K.; Hata, H.; Ghose, A. Generating Pseudo-Code from Source Code Using Deep Learning. In Proceedings of the 2018 25th Australasian Software Engineering Conference (ASWEC), November 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 21–25. [Google Scholar]
- Durieux, T.; Monperrus, M. Dynamoth: Dynamic code synthesis for automatic program repair. In Proceedings of the 2016 IEEE/ACM 11th International Workshop in Automation of Software Test (AST), May 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 85–91. [Google Scholar]
- Campbell, J.C.; Hindle, A.; Amaral, J.N. Syntax errors just aren’t natural: Improving error reporting with language models. In Proceedings of the 11th Working Conference on Mining Software Repositories, May 2014; ACM: New York, NY, USA, 2014; pp. 252–261. [Google Scholar]
- Nguyen, T.; Weimer, W.; Kapur, D.; Forrest, S. Connecting program synthesis and reachability: Automatic program repair using test-input generation. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, April 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 301–318. [Google Scholar]
- Wang, K.; Singh, R.; Su, Z. Dynamic neural program embedding for program repair. arXiv 2017, arXiv:1711.07163. [Google Scholar]
- Shin, R.; Polosukhin, I.; Song, D. Towards Specification-Directed Program Repair. In Proceedings of the Sixth International Conference on Learning Representations (ICLR), Vancouver Convention Center, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bhatia, S.; Singh, R. Automated correction for syntax errors in programming assignments using recurrent neural networks. arXiv 2016, arXiv:1603.06129. [Google Scholar]
- Qi, Y.; Mao, X.; Lei, Y.; Dai, Z.; Wang, C. The strength of random search on automated program repair. In Proceedings of the 36th International Conference on Software Engineering, May 2014; ACM: New York, NY, USA, 2014; pp. 254–265. [Google Scholar]
- De Souza, E.F.; Goues, C.L.; Camilo-Junior, C.G. A novel fitness function for automated program repair based on source code checkpoints. In Proceedings of the Genetic and Evolutionary Computation Conference, July 2018; ACM: New York, NY, USA, 2018; pp. 1443–1450. [Google Scholar]
- White, M.; Tufano, M.; Martinez, M.; Monperrus, M.; Poshyvanyk, D. Sorting and transforming program repair ingredients via deep learning code similarities. In Proceedings of the 2019 IEEE 26th International Conference on Software Analysis, Evolution and Reengineering (SANER), February 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 479–490. [Google Scholar]
- Martinez, M.; Monperrus, M. Astor: Exploring the design space of generate-and-validate program repair beyond GenProg. J. Syst. Softw. 2019, 151, 65–80. [Google Scholar] [CrossRef]
- Hill, A.; Pasareanu, C.; Stolee, K. Poster: Automated Program Repair with Canonical Constraints. In Proceedings of the 2018 IEEE/ACM 40th International Conference on Software Engineering: Companion (ICSE-Companion), May 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 339–341. [Google Scholar]
- Martinez, M.; Monperrus, M. Astor: A program repair library for java. In Proceedings of the 25th International Symposium on Software Testing and Analysis, July 2016; ACM: New York, NY, USA, 2016; pp. 441–444. [Google Scholar]
- D’Antoni, L.; Samanta, R.; Singh, R. Qlose: Program repair with quantitative objectives. In Proceedings of the International Conference on Computer Aided Verification, July 2016; Springer: Cham, Switzerland, 2016; pp. 383–401. [Google Scholar]
- Krawiec, K.; Błądek, I.; Swan, J.; Drake, J.H. Counterexample-driven genetic programming: Stochastic synthesis of provably correct programs. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Vienna, Austria, 13–19 July 2018; pp. 5304–5308. [Google Scholar]
- Von Essen, C.; Jobstmann, B. Program repair without regret. Form. Methods Syst. Des. 2015, 47, 26–50. [Google Scholar] [CrossRef]
- Le, X.B.D.; Chu, D.H.; Lo, D.; Le Goues, C.; Visser, W. S3: Syntax-and semantic-guided repair synthesis via programming by examples. In Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering, August 2017; ACM: New York, NY, USA, 2017; pp. 593–604. [Google Scholar]
- Nguyen, H.D.T.; Qi, D.; Roychoudhury, A.; Chandra, S. Semfix: Program repair via semantic analysis. In Proceedings of the 2013 35th International Conference on Software Engineering (ICSE), May 2013; IEEE: Piscataway Township, NJ, USA, 2013; pp. 772–781. [Google Scholar]
- Mechtaev, S.; Nguyen, M.D.; Noller, Y.; Grunske, L.; Roychoudhury, A. Semantic program repair using a reference implementation. In Proceedings of the 40th International Conference on Software Engineering, May 2018; ACM: New York, NY, USA, 2018; pp. 129–139. [Google Scholar]
- Le, X.B.D.; Chu, D.H.; Lo, D.; Le Goues, C.; Visser, W. JFIX: Semantics-based repair of Java programs via symbolic PathFinder. In Proceedings of the 26th ACM SIGSOFT International Symposium on Software Testing and Analysis, July 2017; ACM: New York, NY, USA, 2017; pp. 376–379. [Google Scholar]
- Kneuss, E.; Koukoutos, M.; Kuncak, V. Deductive program repair. In Proceedings of the International Conference on Computer Aided Verification, July 2015; Springer: Cham, Switzerland, 2015; pp. 217–233. [Google Scholar]
- Ghanbari, A.; Zhang, L. ‘PraPR: Practical Program Repair via Bytecode Mutation’. In Proceedings of the 2019 34th IEEE/ACM International Conference on Automated Software Engineering (ASE), Automated Software Engineering (ASE), San Diego, CA, USA, 11– 15 November 2019; pp. 1118–1121. [Google Scholar]
- Liu, K.; Koyuncu, A.; Kim, K.; Kim, D.; Bissyandé, T.F. LSRepair: Live search of fix ingredients for automated program repair. In Proceedings of the 2018 25th Asia-Pacific Software Engineering Conference (APSEC), December 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 658–662. [Google Scholar]
- Kaleeswaran, S.; Tulsian, V.; Kanade, A.; Orso, A. Minthint: Automated synthesis of repair hints. In Proceedings of the 36th International Conference on Software Engineering, May 2014; ACM: New York, NY, USA, 2014; pp. 266–276. [Google Scholar]
- Lee, J.; Song, D.; So, S.; Oh, H. Automatic diagnosis and correction of logical errors for functional programming assignments. Proc. ACM Program. Lang. 2018, 158, 1–30. [Google Scholar] [CrossRef]
- Roychoudhury, A. SemFix and beyond: Semantic techniques for program repair. In Proceedings of the International Workshop on Formal Methods for Analysis of Business Systems, September 2016; ACM: New York, NY, USA, 2016; p. 2. [Google Scholar]
- Mechtaev, S.; Yi, J.; Roychoudhury, A. Directfix: Looking for simple program repairs. In Proceedings of the 37th International Conference on Software Engineering, May 2015; IEEE: Piscataway Township, NJ, USA, 2015; Volume 1, pp. 448–458. [Google Scholar]
- Dershowitz, N.; Reddy, U.S. Deductive and inductive synthesis of equational programs. J. Symb. Comput. 1993, 15, 467–494. [Google Scholar] [CrossRef]
- Uchihira, N.; Matsumoto, K.; Honiden, S.; Nakamura, H. Mendels: Concurrent program synthesis system using temporal logic. In Logic Programming ’87. LP, Lecture Notes in Computer Science; Furukawa, K., Tanaka, H., Fujisaki, T., Eds.; Springer: Berlin, Heidelberg, Germany, 2005; Volume 315. [Google Scholar]
- Manna, Z.; Waldinger, R. Fundamentals of deductive program synthesis. IEEE Trans. Softw. Eng. 1992, 18, 674–704. [Google Scholar] [CrossRef]
- Manna, Z.; Waldinger, R. A deductive approach to program synthesis. In Readings in Artificial Intelligence and Software Engineering; Morgan Kaufmann: Burlington, MA, USA, 1986; pp. 3–34. [Google Scholar]
- Shi, K.; Steinhardt, J.; Liang, P. FrAngel: Component-based synthesis with control structures. Proc. ACM Program. Lang. 2019, 73, 1–29. [Google Scholar] [CrossRef]
- Alur, R.; Fisman, D.; Singh, R.; Solar-Lezama, A. Sygus-comp 2017: Results and analysis. arXiv 2017, arXiv:1711.11438. [Google Scholar] [CrossRef]
- Lau, T.A.; Domingos, P.M.; Weld, D.S. Version Space Algebra and its Application to Programming by Demonstration. In Proceedings of the Seventeenth International Conference on Machine Learning (ICML 2000), Stanford University, Stanford, CA, USA, 29 June–2 July 2000; pp. 527–534. [Google Scholar]
- Subahi, A.F. Edge-Based IoT Medical Record System: Requirements, Recommendations and Conceptual Design. IEEE Access 2019, 7, 94150–94159. [Google Scholar] [CrossRef]





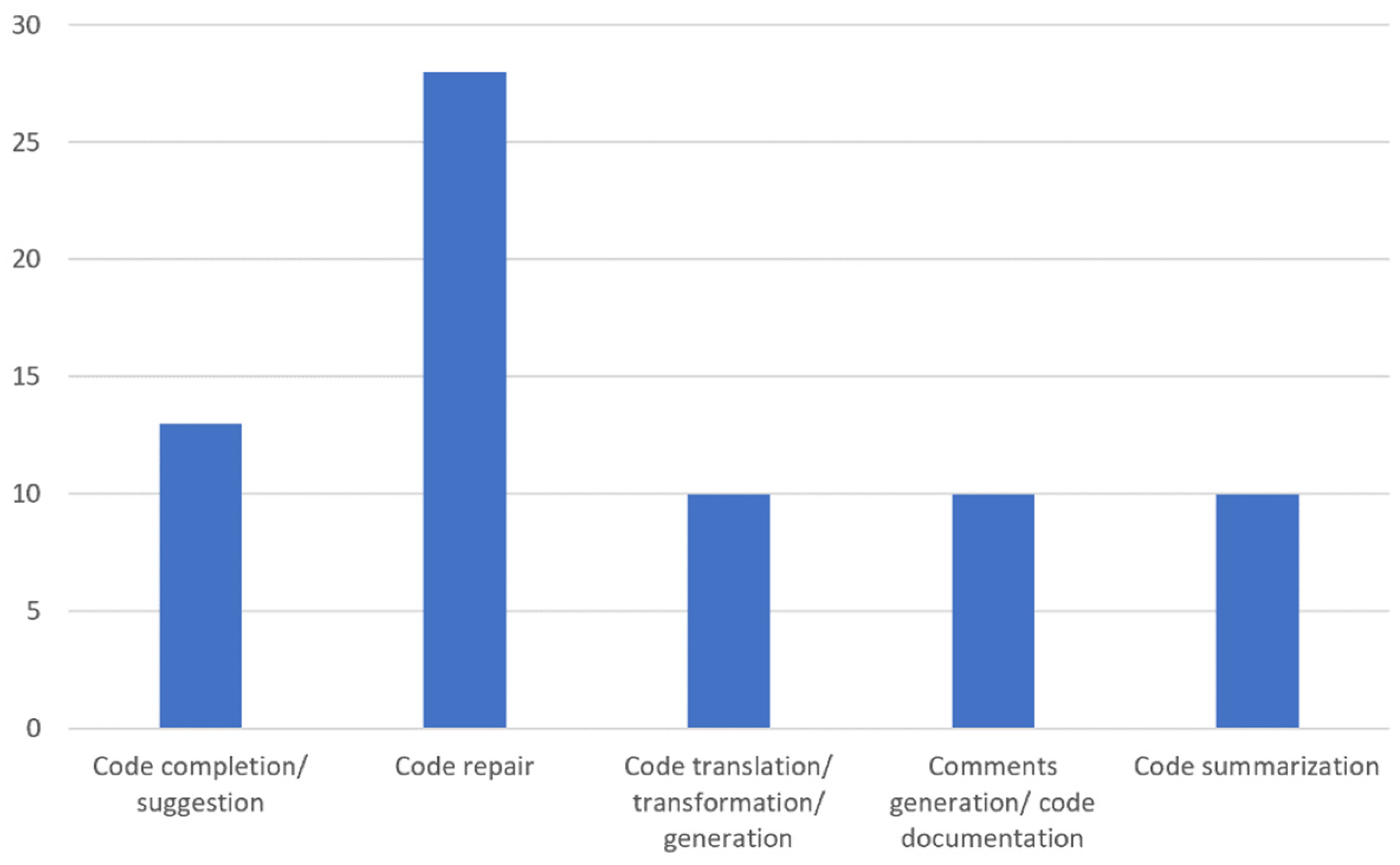
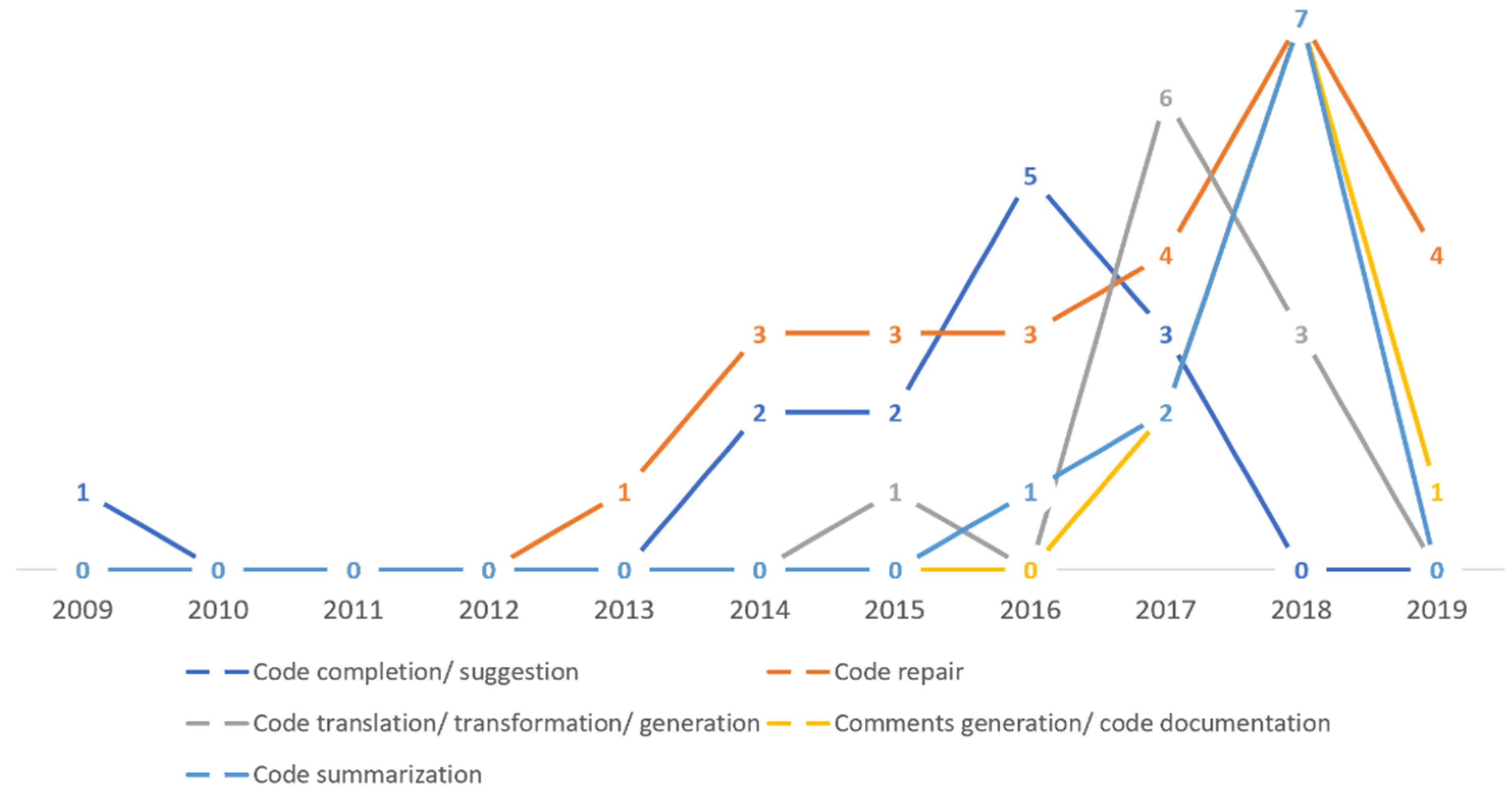
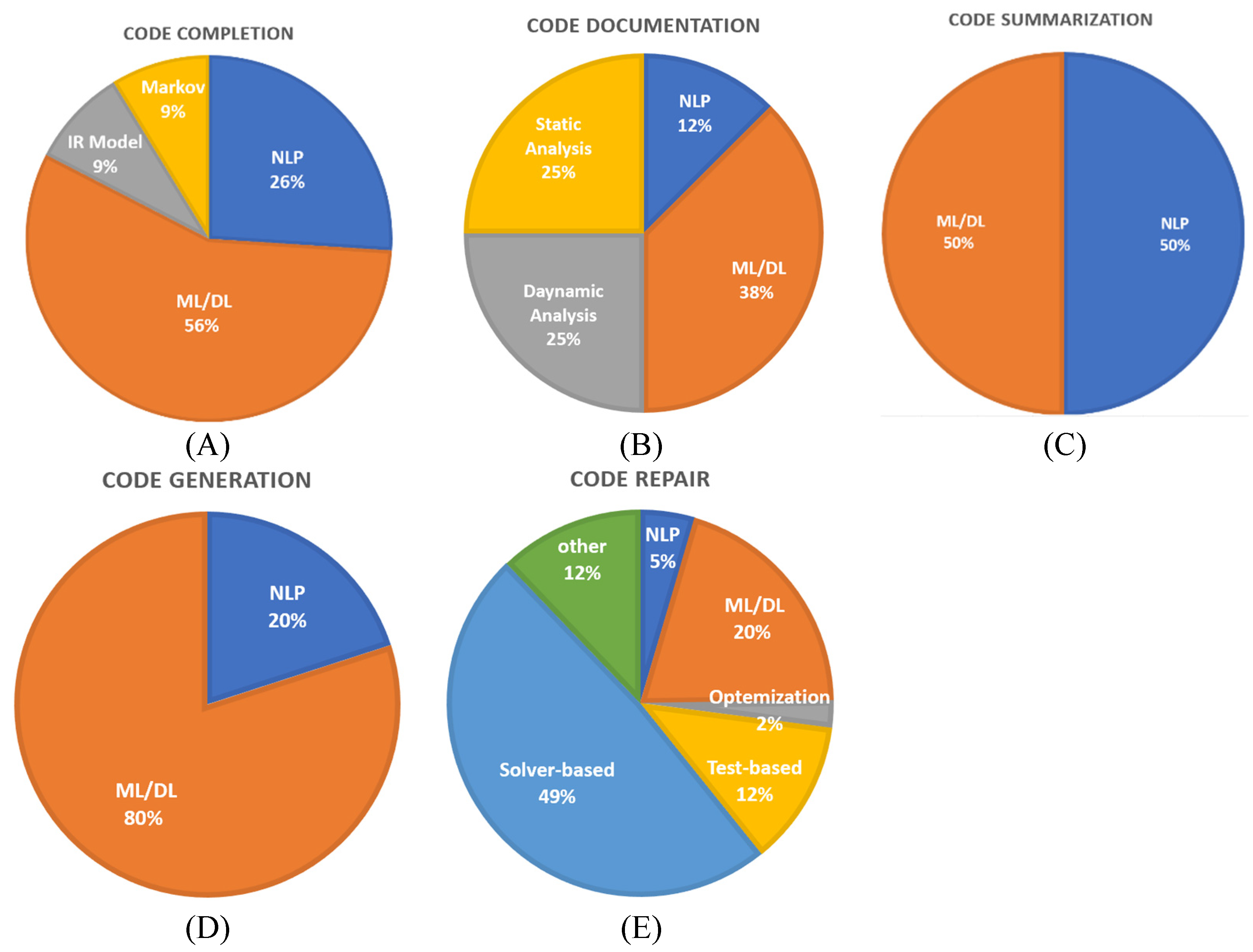

| Search Focus | Strings and Keywords |
|---|---|
| Program Synthesis Approaches and Techniques | (code OR program) AND synthesis |
| (inductive OR deductive) AND (code OR program) AND synthesis | |
| Example-based AND (programming OR coding) | |
| (programming OR coding) AND by (examples OR demonstration OR sketching) | |
| (program OR code) AND (synthesis from examples) | |
| (Syntax OR Semantics OR Symbolic) AND-based AND (code OR Program) Synthesis | |
| Applications of program synthesis | (program OR code) AND (suggestion OR completion OR repair OR correction OR recommendation OR comment OR documentation OR summarization OR generation OR transformation OR translation) |
| Aspect | Categories |
|---|---|
| Paradigms of Program synthesis | inductive paradigm, deductive paradigm |
| Features/Techniques of Program Synthesis | user intent specifications, program search space, search technique |
| Applications of program synthesis | program repair, program summarization, program transformation (including code generation), program documentation and code completion |
| Group ID | Reference No. | Techniques | Aspects |
|---|---|---|---|
| 1 | [15,16,17,18,19,20,21,22,23] | Recurrent Neural Networks (RNNs) and (deep) reinforcement learning with Natural Language Processing (NLP)-based user intent | Features and Techniques |
| 2 | [24,25,26,27,28] | Different sketching synthesis techniques for expressing user intent with annotated programs, e.g., execution-driven SAT/SMT-based and domain-specific rule sketching. User intent is expressed using a program sketch with some holes. | |
| 3 | [29,30,31,32,33] | Deductive reasoning, solver-based and programming-by-example with user intent expressed using domain specific languages (DSLs). | |
| 4 | [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] | Debugging information, programming-by-example with input/output (I/O) examples for expressing user intent. | |
| 5 | [49] | Counterexamples with oracle-guided inductive synthesis technique. | |
| 6 | [50,51] | These publications use logic formulas, the symbolic logic technique, weighted (tree) and context-free grammar for expressing user intent with SAT/SMT solving technique, statistical model. | |
| 7 | [52,53,54] | Constraints expressed using attribute grammar and refinement trees with RNNs, SMT-based solver | |
| 8 | [55] | Symbolic execution and extended finite-state-machine | |
| 9 | [37,56,57,58,59,60] | Execution traces with (RNNs), 2D drawing with convolutional neural networks (CNNs) and images with reinforced adversarial learning technique | |
| 10 | [61,62,63,64] | Execution traces for expressing user intent with different synthesis techniques such as the version space algebra and stochastic synthesizing | |
| 11 | [65] | Verification approach to solve the synthesis problem, specifications of atomic operations are used as input/output intent. Abstract finite tree automata used for expressing an initial program. | |
| 12 | [66,67] | Logic with approximation approaches to solve the synthesis problem. | |
| 13 | [68,69,70,71,72,73] | Optimization approaches are used to solve the synthesis problem. | |
| 14 | [33,48,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79] | Constraint solving approach, SAT/SMT-based techniques to solve the synthesis problem. | |
| 15 | [80,81,82,83] | Neural networks, deep learning, machine leaning and its related techniques to solve the synthesis problem. | |
| 16 | [84,85,86,87,88,89] | Template-based technique to express the program space. | |
| 17 | [90,91,92,93,94,95,96,97,98,99,100,101,102] | Paradigms of program synthesis. | Paradigms |
| 18 | [84,103,104,105,106,107,108,109,110,111,112,113,114,115] | Code completion and suggestion. | Applications |
| 19 | [116,117,118,119,120,121,122,123,124,125] | Code summarization. | |
| 20 | [126,127,128,129,130,131,132,133,134,135] | Code documentation and comments generation. | |
| 21 | [136,137,138,139,140,141,142,143,144,145,146,147] | Code compilation, generation, translation and transformation. | |
| 22 | [148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173] | Domain of code repair and correction. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subahi, A.F. Cognification of Program Synthesis—A Systematic Feature-Oriented Analysis and Future Direction. Computers 2020, 9, 27. https://doi.org/10.3390/computers9020027
Subahi AF. Cognification of Program Synthesis—A Systematic Feature-Oriented Analysis and Future Direction. Computers. 2020; 9(2):27. https://doi.org/10.3390/computers9020027
Chicago/Turabian StyleSubahi, Ahmad F. 2020. "Cognification of Program Synthesis—A Systematic Feature-Oriented Analysis and Future Direction" Computers 9, no. 2: 27. https://doi.org/10.3390/computers9020027
APA StyleSubahi, A. F. (2020). Cognification of Program Synthesis—A Systematic Feature-Oriented Analysis and Future Direction. Computers, 9(2), 27. https://doi.org/10.3390/computers9020027





