Implementation of a PSO-Based Security Defense Mechanism for Tracing the Sources of DDoS Attacks †
Abstract
1. Introduction
- To identify the most probable attack route for assisting the defenders’ design of DoS attack resistant systems, and a new tracing route-based IP traceback model with a revised PSO scheme by reconstructing the collected network packets to defend DDoS attacks.
- An improvement to the strategies of PSO in the optimal route searching process was proposed to prevent the PSO algorithm from converging prematurely to a local, sub-optimal solution in a big search space.
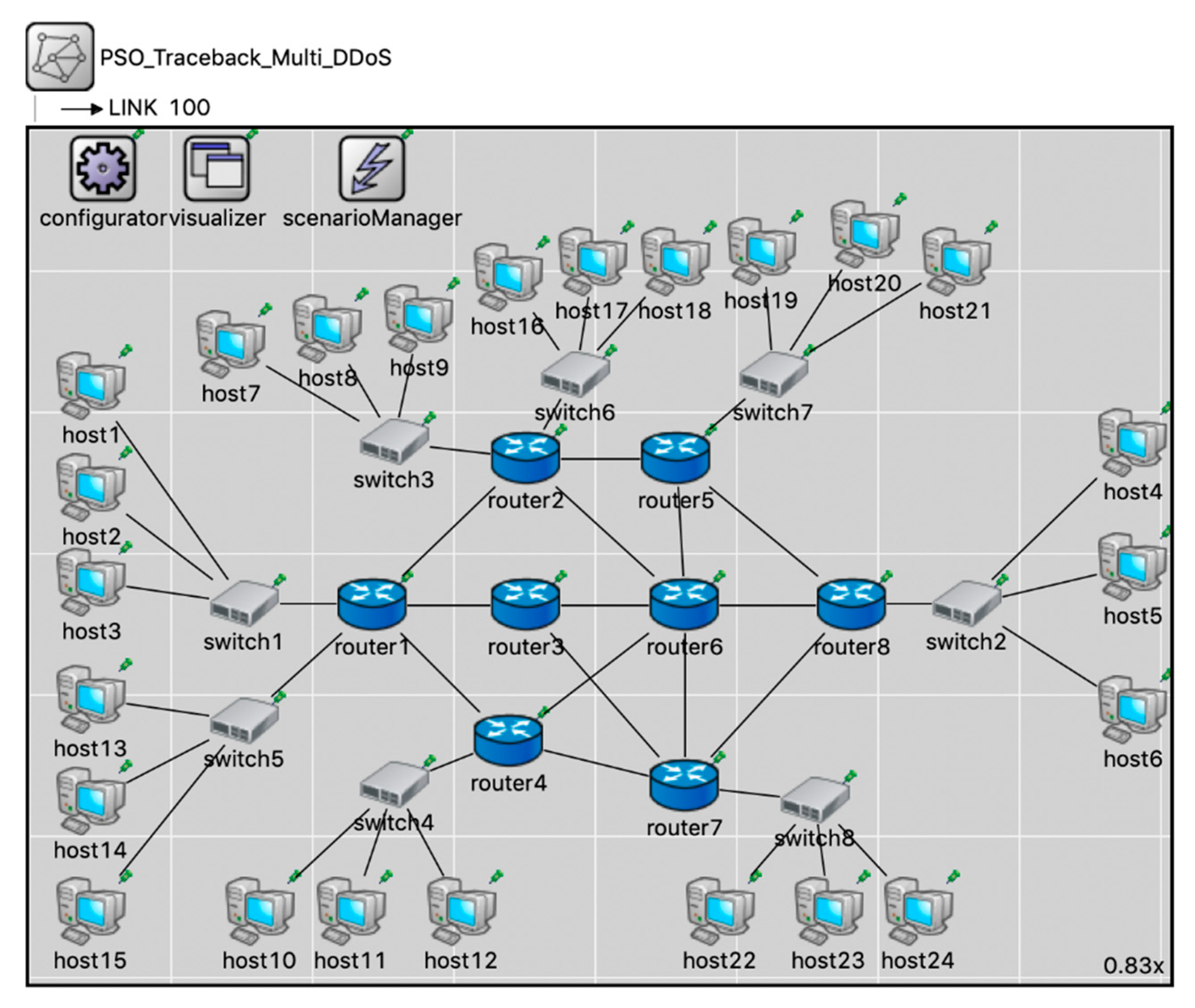
- The performance of the PSO-IPTBK algorithm in reconstructing the attack route was investigated through a series of simulations using a Monte Carlo model with OMNeT++ 5.5.1 and the INET 4 Framework to predict the accuracy of the proposed model.
- The experimental results revealed that the PSO-IPTBK accuracy is 98.33% for the attack scenarios in the experimental network (node = 24) and 94.64% for network topology (node = 40).
2. Preliminary Work
2.1. Techniques for the IP Traceback Problem
2.2. Particle Swarm Optimization Algorithms
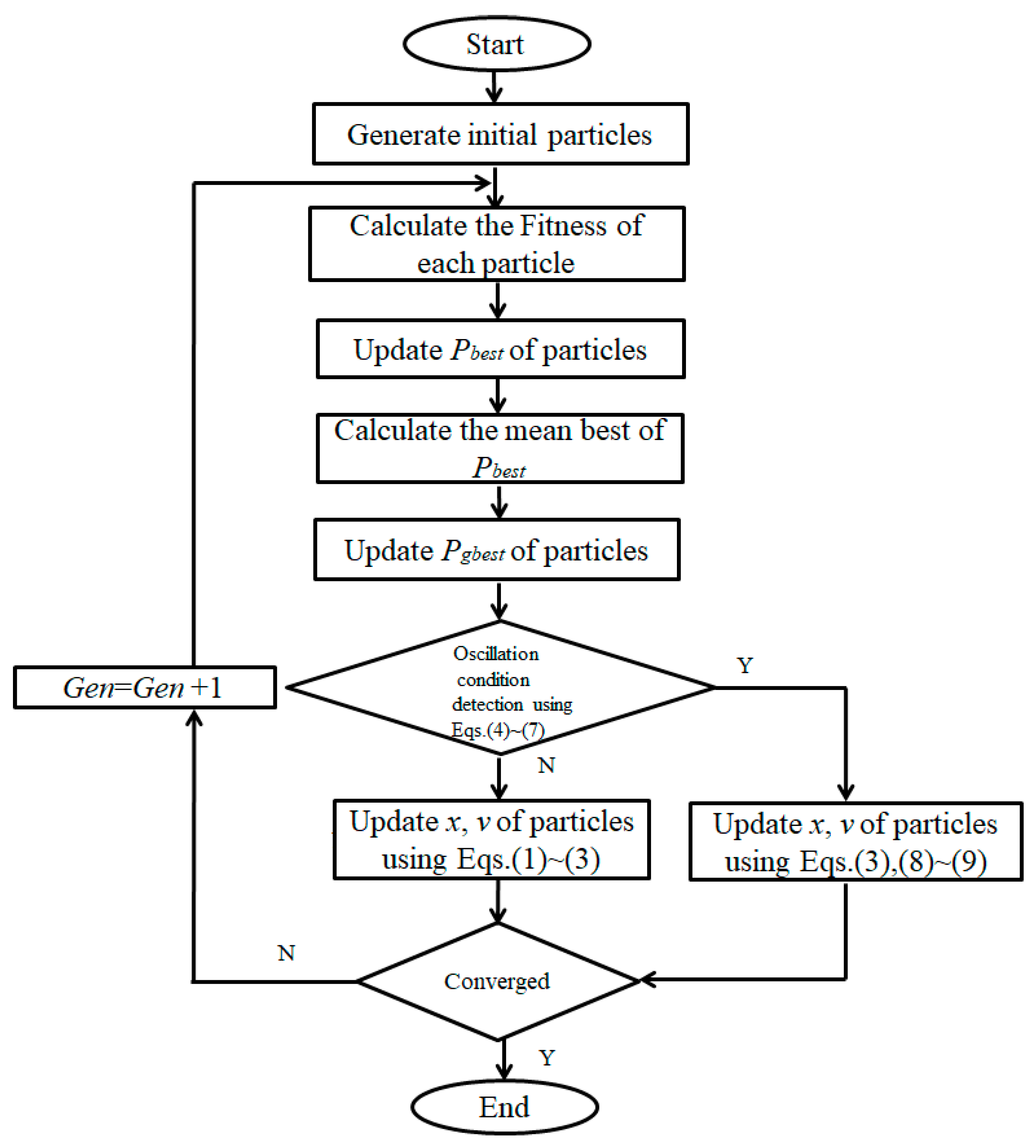
3. Proposed PSO Heuristic Models for IP Traceback Problem
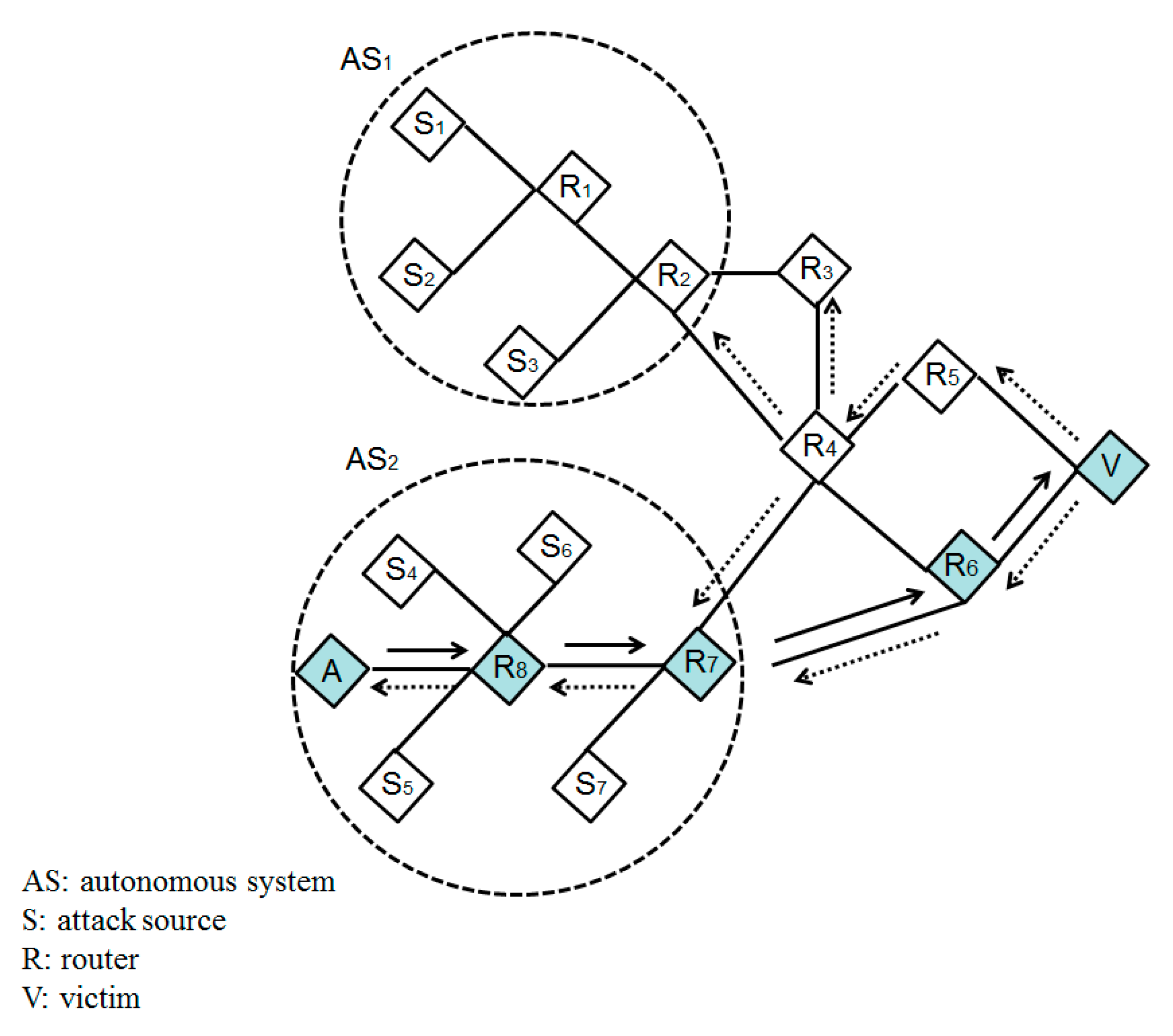
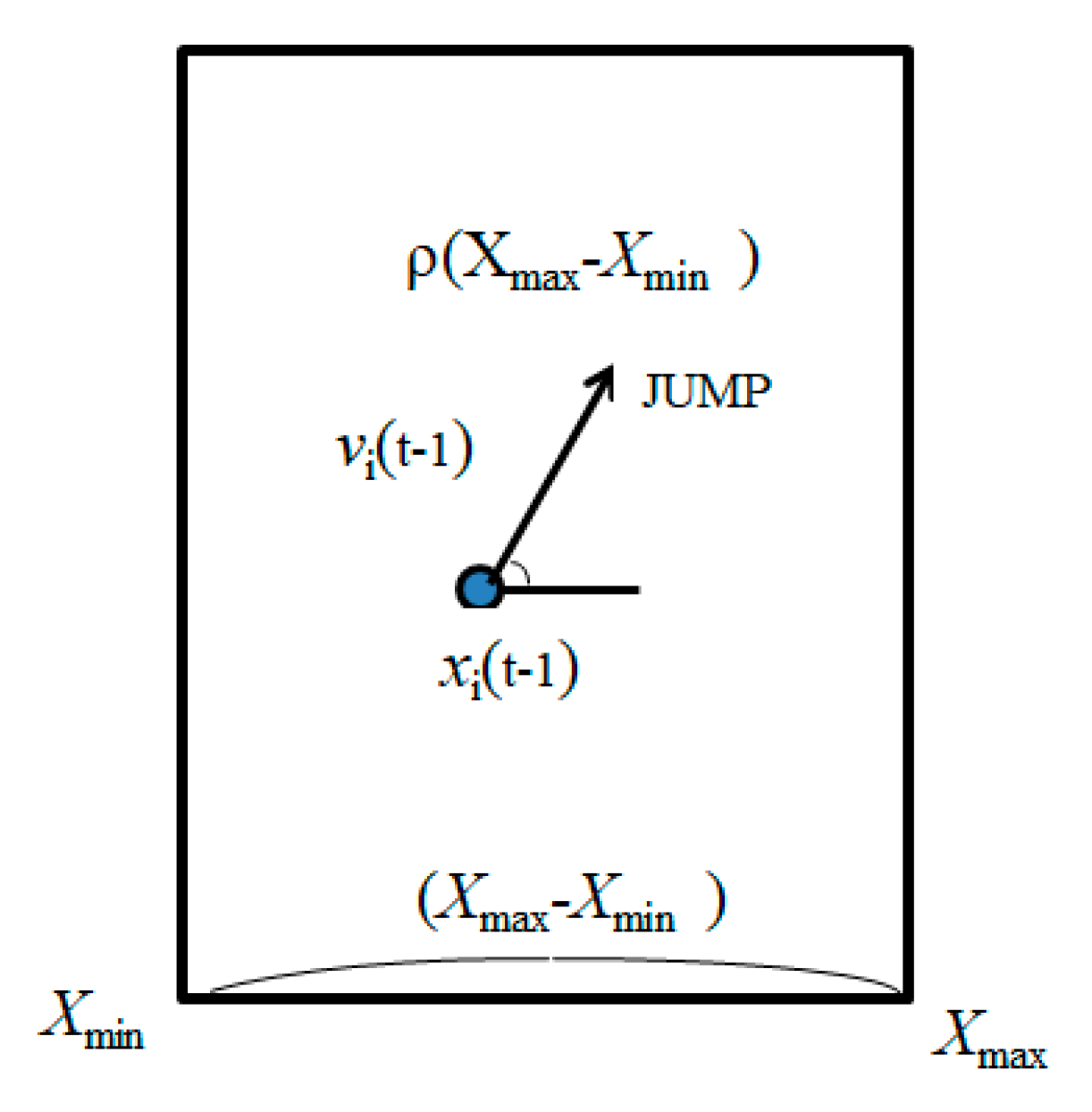
3.1. Basic Concept
3.2. Application of PSO to the IP Traceback Problem
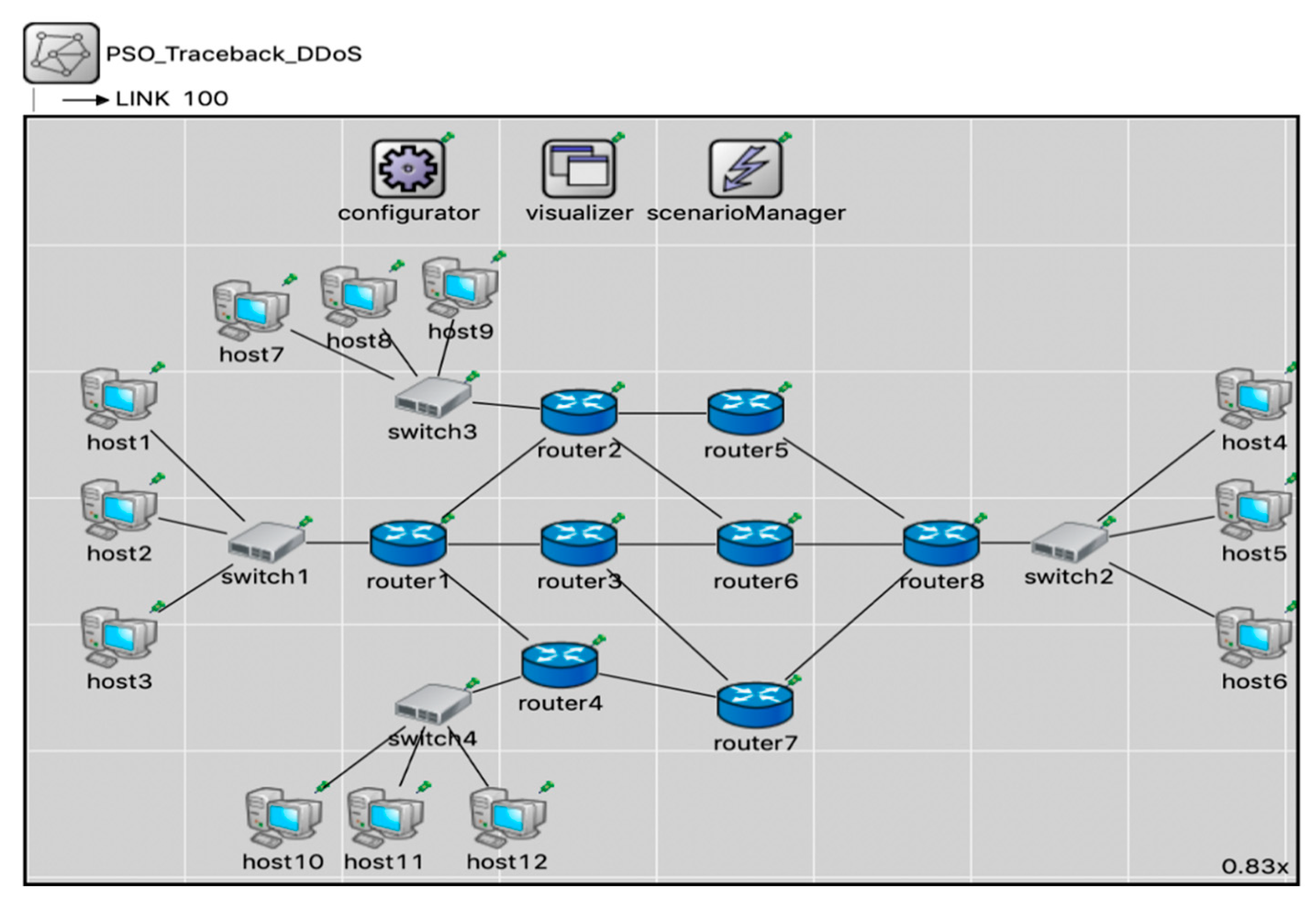
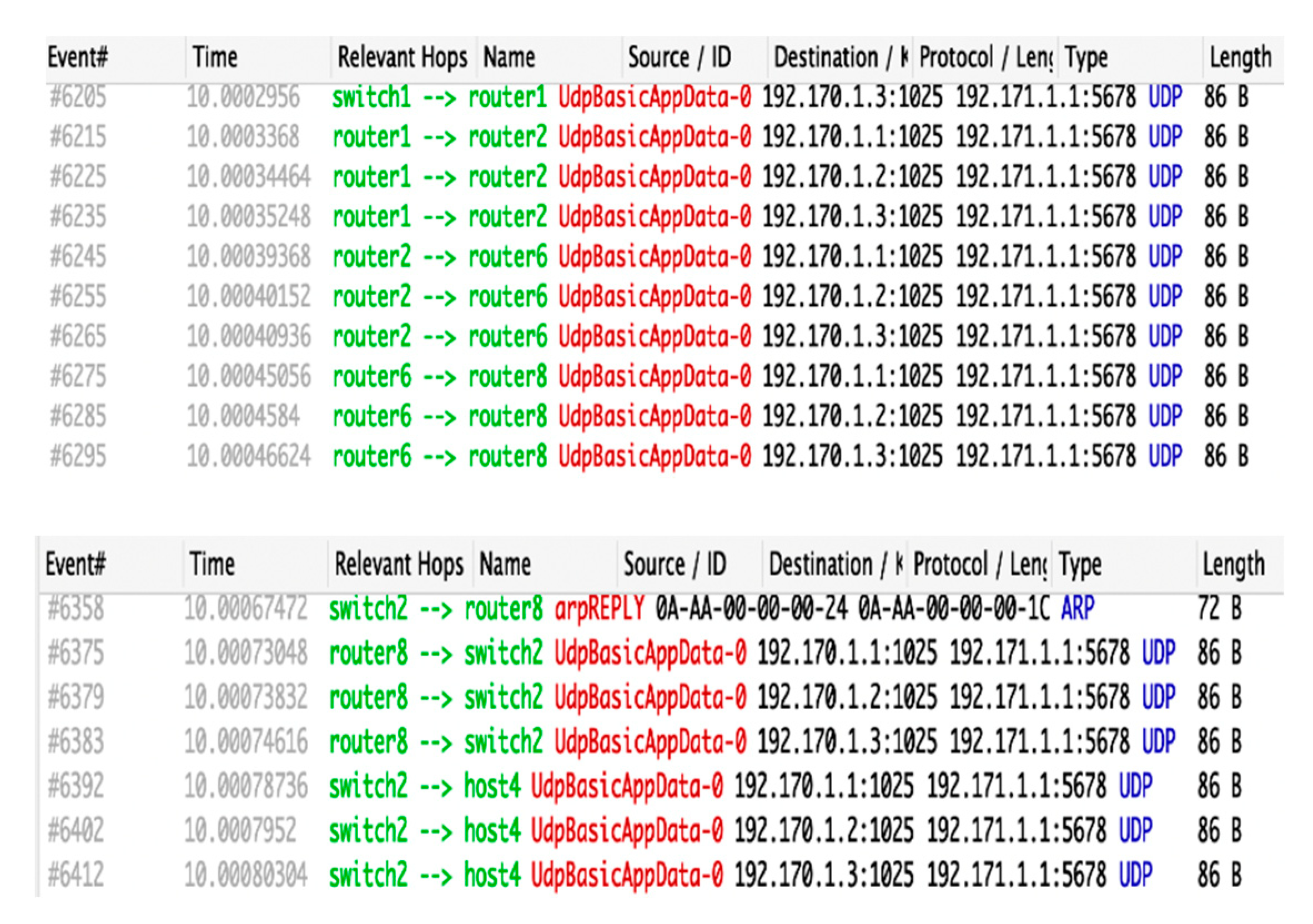
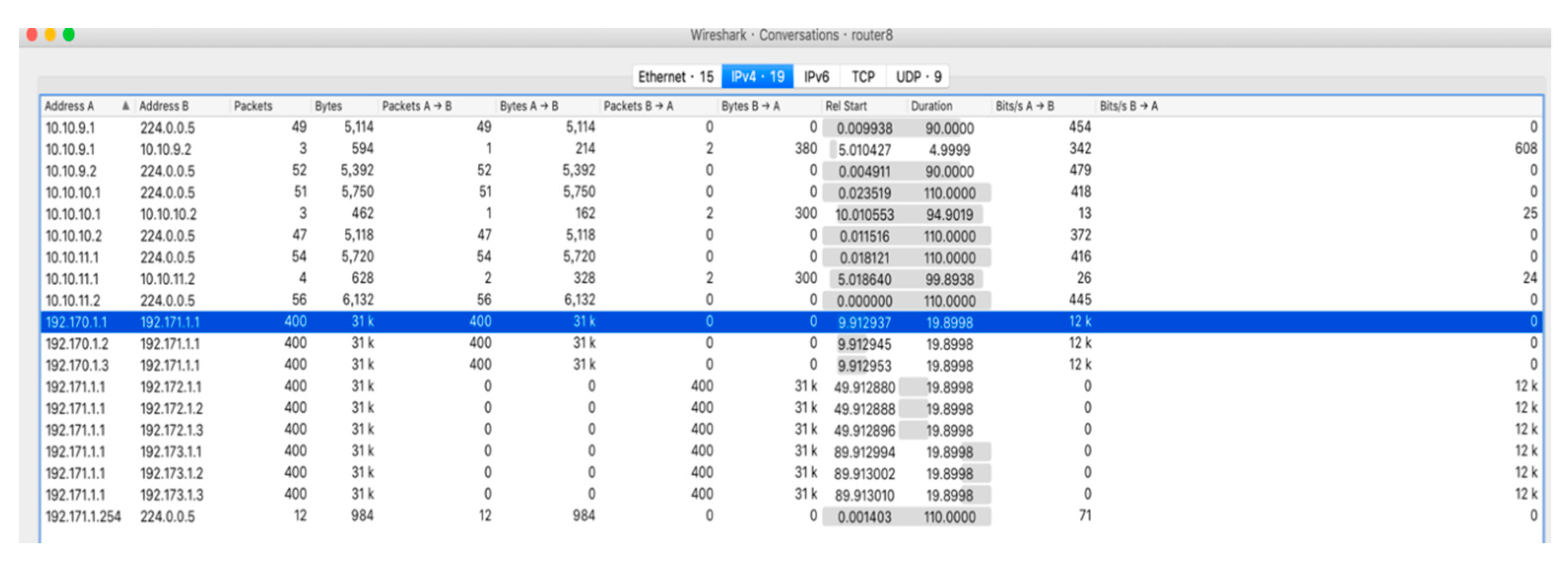
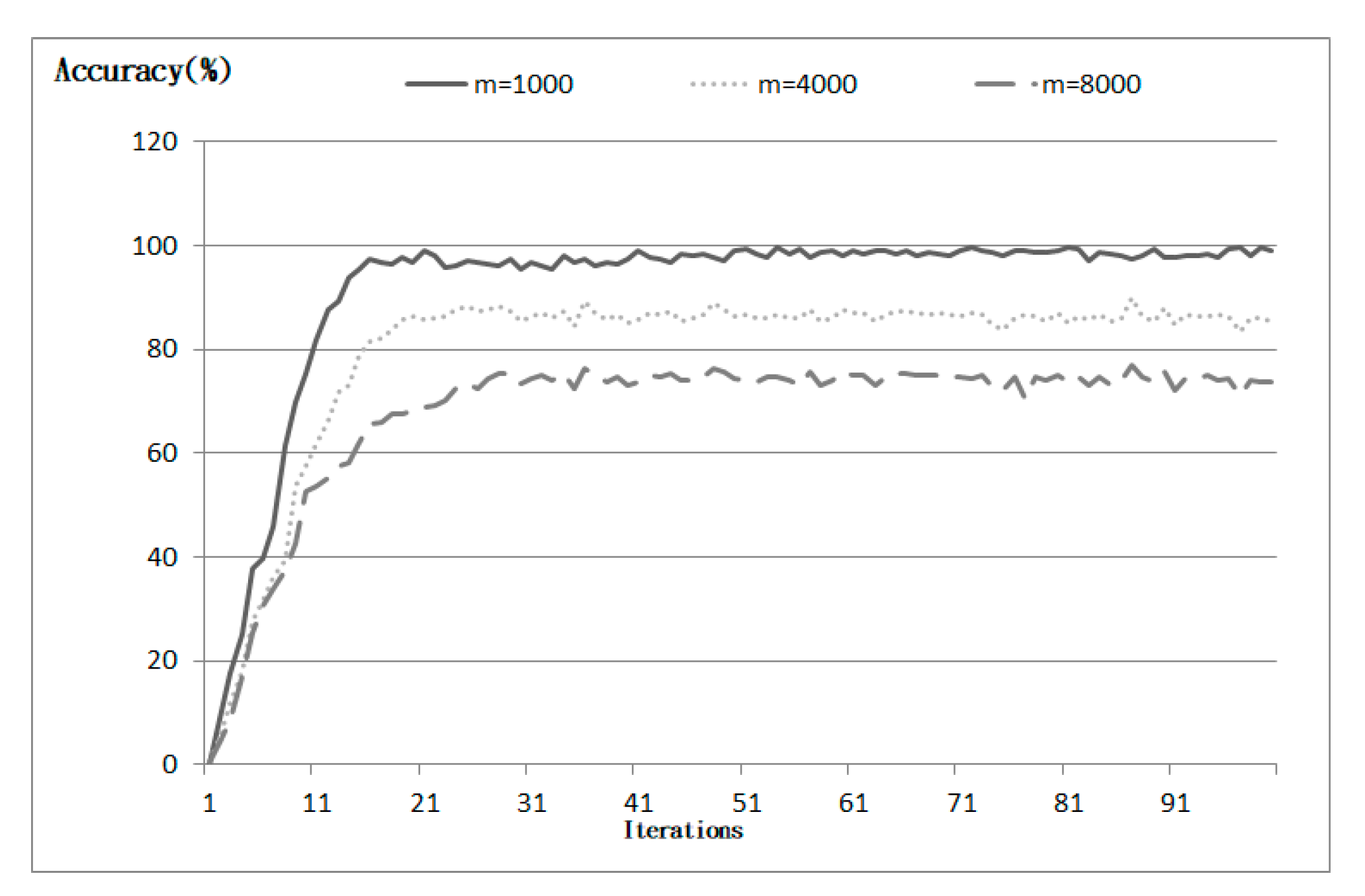
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amin, F.; Ahmad, A.; Sang Choi, G. Towards trust and friendliness approaches in the social Internet of things. Appl. Sci. 2019, 9, 166. [Google Scholar] [CrossRef]
- Amin, F.; Ahmad, A.; Choi, G.S. Community detection and mining using complex networks tools in social Internet of things. In Proceedings of the IEEE 10th Region Conference (TENCON 2018), Jeju, Korea, 28–31 October 2018; pp. 2086–2091. [Google Scholar] [CrossRef]
- Lin, S.; Chiueh, T.C. A Survey on Solutions to Distributed Denial of Service Attacks; Technical Report; Department of Computer Science, Stony Brook University: New York, NY, USA, 2013.
- Miller, C. RIPng the Forgotten Routing Protocol. December 2017. Available online: http://www.makikiweb.com/ipv6/ripng.html (accessed on 29 November 2019).
- Wang, P.; Lin, H.T.; Wang, T.S. An Improved Ant Colony System Algorithm for Solving the IP Traceback Problem; Information Sciences; Elsevier: Amsterdam, The Netherlands, 2016; pp. 172–187. [Google Scholar]
- Song, D.X.; Perrig, A. Advanced and Authenticated Marking Schemes for IP Traceback. In Proceedings of the 20th Conference on Computer Communications, Scottsdale, AZ, USA, 15–17 October 2001; pp. 878–886. [Google Scholar]
- Belenky, A.; Ansari, N. IP Traceback with Deterministic Packet Marking. IEEE Commun. Lett. 2003, 7, 162–164. [Google Scholar] [CrossRef]
- Paruchuri, V.; Durresi, A. On the (in)Effectiveness of Probabilistic Marking for IP Traceback Under DDoS Attacks. In Proceedings of the IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007; pp. 1965–1970. [Google Scholar]
- Moghaddam, B.F.; Ruizb, R.; Sadjadic, S.J. Vehicle routing problem with uncertain demands: An advanced particle swarm algorithm. Comput. Ind. Eng. 2012, 62, 306–317. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiah, A.K.; Kim, H.J. An Improved Routing Schema with Special Clustering Using PSO Algorithm for Heterogeneous Wireless Sensor Network. Sensors 2019, 3, 671. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Cao, J.; He, J.; Li, S. A Novel IP Traceback Scheme to Detect DDoS. In Proceedings of the 3rd International Conference on Instrumentation, Measurement, Computer, Communication and Control (IMCCC ’13), Washington, DC, USA, 21–23 September 2013; pp. 1077–1080. [Google Scholar]
- Umarani, R.; Selvi, V. Particle Swarm Optimization-evolution, Overview and Applications. Int. J. Eng. Sci. Technol. 2010, 2, 2802–2806. [Google Scholar]
- Bai, Q. Analysis of Particle Swarm Optimization Algorithm. Comput. Inf. Sci. 2010, 3, 180–184. [Google Scholar] [CrossRef]
- Snoeren, A.C.; Partridge, C.; Sanchez, L.A.; Jones, C.E. Hash-based IP traceback. In Proceedings of the Special Interest Group on Data Communication (SIGCOMM), San Francisco, CA, USA, 1–2 November 2001; pp. 27–31. [Google Scholar]
- Savage, S.; Wetherall, D.; Karlin, A.; Anderson, T. Network support for IP traceback. IEEE/ACM Trans. Netw. 2001, 9, 226–237. [Google Scholar] [CrossRef]
- Bellovin, S.; Leech, M.; Taylor, T. ICMP Traceback Messages. 2001. Available online: http://tools.ietf.org/id/draft-ietf-itrace-04.txt (accessed on 29 November 2019).
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Angeline, P.J. Evolutionary Optimization versus Particle Swarm Optimization: Philosophy and Performance Difference. In Proceedings of the 7th Annual Conference on Evolutionary Programming, International Conference on Evolutionary Computation Proceedings, San Diego, CA, USA, 25–27 March 1998; pp. 69–73. [Google Scholar]
- Lin, H.C.; Wang, P.; Lin, W.H. A Revised Particle Swarm Optimization Scheme for Discovering Attack Vectors of IPv6 Security by Spoofed IP Attacks. In Proceedings of the IEEE Eurasia Conference on IOT, Communication and Engineering (IEEE ECICE 2019), Yunlin, Taiwan, 3–6 October 2019. [Google Scholar]
- Waxman, B. Routing of Multipoint Connections. IEEE J. Sel. Areas Commun. 1988, 6, 1617–1622. [Google Scholar] [CrossRef]



| Approach | Features | Advantages | Disadvantages |
|---|---|---|---|
| Pro-active |
|
|
|
| Passive |
|
|
|
| Attack Route | Packets Collected | Coverage Percentage (%) |
|---|---|---|
| router1(1)-router2(0)-router2(1)-router5(0)-router5(1)-router8(1) | 570 | 31.67% |
| router2(1)-router5(0)-router5(1)-router8(1) | 600 | 33.33% |
| router4(0)-router1(3)-router1(2)-router3(0)-router3(1)-router6(0)-router6(1)-router8(2) | 600 | 33.33% |
| router1(2)-router3(0)-router3(1)-router6(0)-router6(1)-router8(2) | 30 | 1.67% |
| Total | 1800 | 100.0% |
| Attack Route | Packets Collected | Coverage Percentage (%) |
|---|---|---|
| router7(4)-router7(2)-router8(3) | 1200 | 14.286% |
| router5(3)-router5(2)-router6(4)-router6(2)-router8(3) | 1200 | 14.286% |
| router2(3)-router2(1)-router5(0)-router5(1)-router8(1) | 1200 | 14.286% |
| router(0)-router1(1)-router2(0)-router2(1)-router5(0)-router5(1)-router8(1) | 1050 | 12.50% |
| router4(2)-router4(1)-router7(1)-router7(2)-router8(3) | 1050 | 12.50% |
| router1(0)-router1(2)-router3(0)-router3(1)-router6(0)-router6(1)-router8(2) | 300 | 3.571% |
| router4(2)-router4(3)-router6(3)-router6(2)-router8(3) | 150 | 1.786% |
| Total | 8400 | 100.0% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.-C.; Wang, P.; Lin, W.-H. Implementation of a PSO-Based Security Defense Mechanism for Tracing the Sources of DDoS Attacks. Computers 2019, 8, 88. https://doi.org/10.3390/computers8040088
Lin H-C, Wang P, Lin W-H. Implementation of a PSO-Based Security Defense Mechanism for Tracing the Sources of DDoS Attacks. Computers. 2019; 8(4):88. https://doi.org/10.3390/computers8040088
Chicago/Turabian StyleLin, Hsiao-Chung, Ping Wang, and Wen-Hui Lin. 2019. "Implementation of a PSO-Based Security Defense Mechanism for Tracing the Sources of DDoS Attacks" Computers 8, no. 4: 88. https://doi.org/10.3390/computers8040088
APA StyleLin, H.-C., Wang, P., & Lin, W.-H. (2019). Implementation of a PSO-Based Security Defense Mechanism for Tracing the Sources of DDoS Attacks. Computers, 8(4), 88. https://doi.org/10.3390/computers8040088




