Lithuanian Speech Recognition Using Purely Phonetic Deep Learning
Abstract
1. Introduction
2. Methods
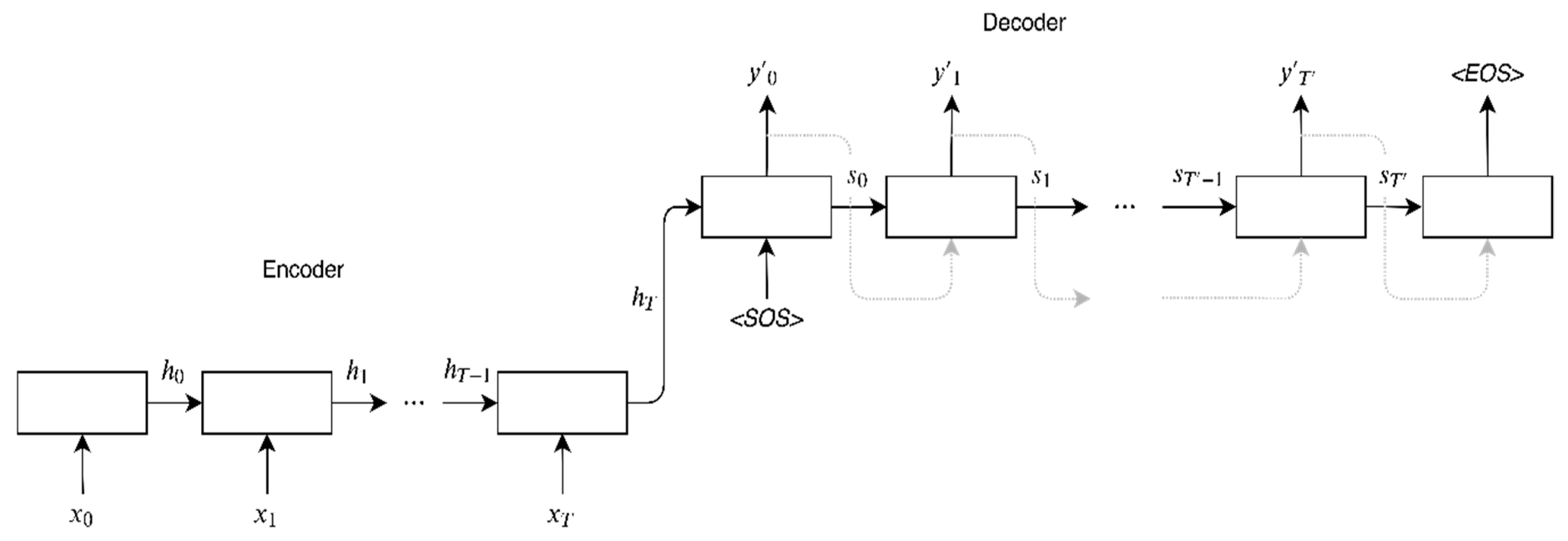
2.1. Sequence-To-Sequence (Seq2Seq) Encoder-Decoder Models
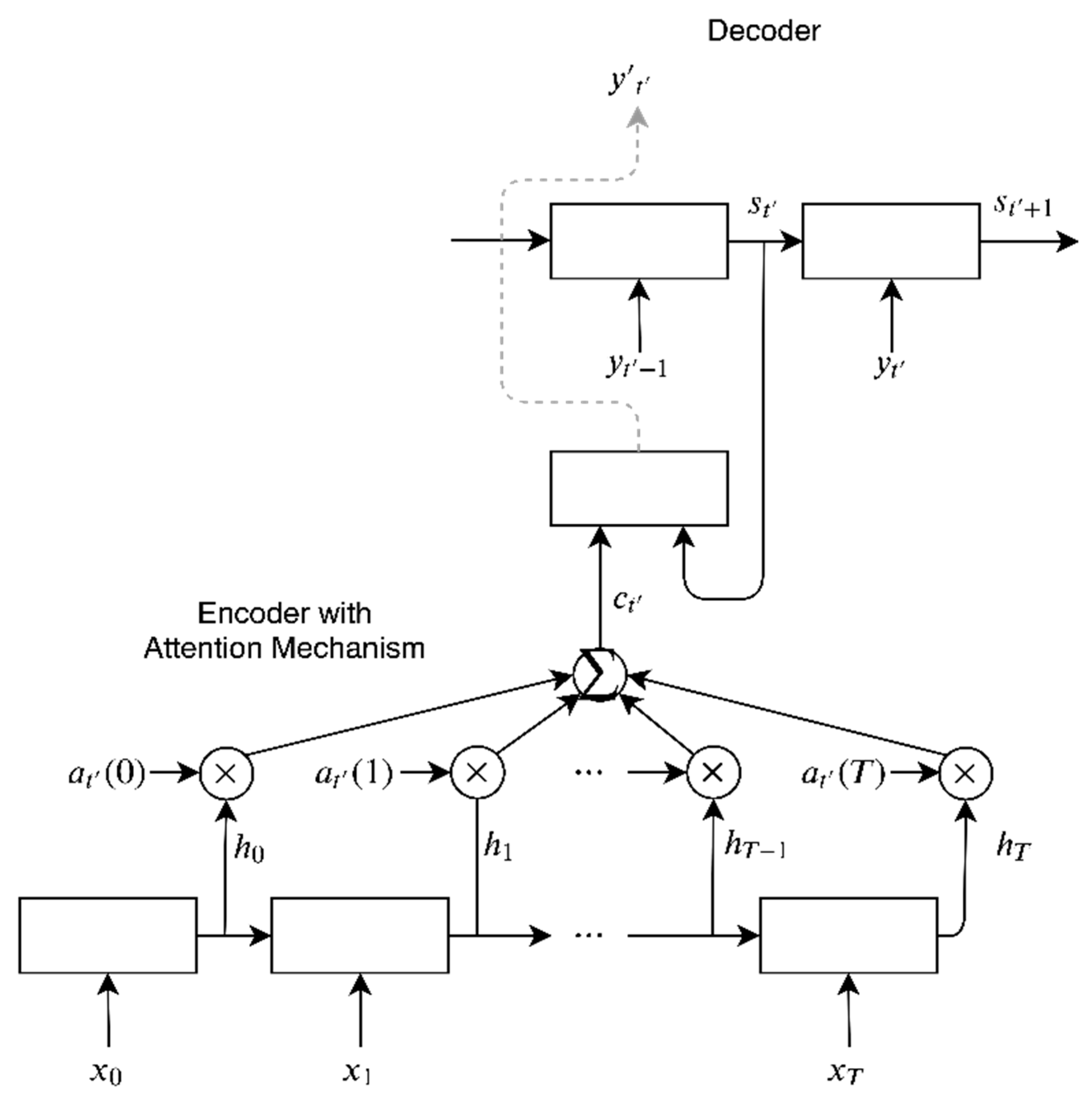
2.2. Attention Encoder–Decoder Models
2.3. Computational Complexity Analysis
2.4. Evaluation of Models
3. Experiments and Results
3.1. Dataset
3.2. Isolated Speech Experiments
3.3. Recognition of Long Phrases
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Badenhorst, J.; de Wet, F. The Usefulness of Imperfect Speech Data for ASR Development in Low-Resource Languages. Information 2019, 10, 268. [Google Scholar] [CrossRef]
- Nassif, A.B.; Shahin, I.; Attili, I.; Azzeh, M.; Shaalan, K. Speech recognition using deep neural networks: A systematic review. IEEE Access 2019, 7, 19143–19165. [Google Scholar] [CrossRef]
- Wang, D.; Wang, X.; Lv, S. End-to-End Mandarin Speech Recognition Combining CNN and BLSTM. Symmetry 2019, 11, 644. [Google Scholar] [CrossRef]
- Panayotov, V.; Chen, G.; Povey, D.; Khudanpur, S. Librispeech: An ASR corpus based on public domain audio books. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 5206–5210. [Google Scholar]
- Bu, H.; Du, J.; Na, X.; Wu, B.; Zheng, H. AIShell-1: An open-source Mandarin speech corpus and a speech recognition baseline. In Proceedings of the 20th Conference of the Oriental Chapter of the International Coordinating Committee on Speech Databases and Speech I/O Systems and Assessment (O-COCOSDA), Seoul, Korea, 1–3 November 2017; pp. 1–5. [Google Scholar]
- Watanabe, S.; Hori, T.; Karita, S.; Hayashi, T.; Nishitoba, J.; Unno, Y.; Soplin, N.E.Y.; Heymann, J.; Wiesner, M.; Chen, N.; et al. ESPnet: End-to-End Speech Processing Toolkit. arXiv 2018, arXiv:1804.00015. [Google Scholar]
- Tamazin, M.; Gouda, A.; Khedr, M. Enhanced Automatic Speech Recognition System Based on Enhancing Power-Normalized Cepstral Coefficients. Appl. Sci. 2019, 9, 2166. [Google Scholar] [CrossRef]
- Besacier, L.; Barnard, E.; Karpov, A.; Schultz, T. Automatic speech recognition for under-resourced languages: A survey. Speech Commun. 2014, 56, 85–100. [Google Scholar] [CrossRef]
- Zhang, Z.; Geiger, J.; Pohjalainen, J.; Mousa, A.E.; Jin, W.; Schuller, B. Deep learning for environmentally robust speech recognition: An overview of recent developments. ACM Trans. Intell. Syst. Technol. 2018, 9. [Google Scholar] [CrossRef]
- Yu, C.; Chen, Y.; Li, Y.; Kang, M.; Xu, S.; Liu, X. Cross-Language End-to-End Speech Recognition Research Based on Transfer Learning for the Low-Resource Tujia Language. Symmetry 2019, 11, 179. [Google Scholar] [CrossRef]
- Lipeika, A.; Lipeikienė, J.; Telksnys, L. Development of Isolated Word Speech Recognition System. Informatica 2002, 13, 37–46. [Google Scholar]
- Raškinis, G.; Raškinienė, D. Building Medium-Vocabulary Isolated-Word Lithuanian HMM Speech Recognition System. Informatica 2003, 14, 75–84. [Google Scholar]
- Filipovič, M.; Lipeika, A. Development of HMM/Neural Network-Based Medium-Vocabulary Isolated-Word Lithuanian Speech Recognition System. Informatica 2004, 15, 465–474. [Google Scholar]
- Dovydaitis, L.; Rudžionis, V. Identifying Lithuanian native speakers using voice recognition. In Business Information Systems Workshops; Springer International Publishing: Berlin, Germany, 2017; pp. 79–84. [Google Scholar]
- Ivanovas, E.; Navakauskas, D. Towards speaker identification system based on dynamic neural network. Electron. Electr. Eng. 2012, 18, 69–72. [Google Scholar] [CrossRef][Green Version]
- Korvel, G.; Treigys, P.; Tamulevičius, G.; Bernatavičienė, J.; Kostek, B. Analysis of 2D feature spaces for deep learning-based speech recognition. AES J. Audio Eng. Soc. 2018, 66, 1072–1081. [Google Scholar] [CrossRef]
- Salimbajevs, A.; Kapociute-Dzikiene, J. General-Purpose Lithuanian Automatic Speech Recognition System. In Proceedings of the 8th International Conference, Baltic HLT, Tartu, Estonia, 27–29 September 2018; pp. 150–157. [Google Scholar]
- Povey, D.; Peddinti, V.; Galvez, D.; Ghahremani, P.; Manohar, V.; Na, X.; Wang, Y.; Khudanpur, S. Purely Sequence-Trained Neural Networks for ASR Based on Lattice-Free MMI. In Proceedings of the Interspeech, San Francisco, CA, USA, 8–12 September 2016; pp. 2751–2755. [Google Scholar]
- Yajie, M.; Zhang, H.; Metze, F. Towards speaker adaptive training of deep neural network acoustic models. In Proceedings of the Fifteenth Annual Conference of the International Speech Communication Association, Singapore, 14–18 September 2014. [Google Scholar]
- Šilingas, D.; Laurinčiukaitė, S.; Telksnys, L. Towards Acoustic Modeling of Lithuanian Speech. In Proceedings of the 2004 International Conference on Speech and Computer (SPECOM), Saint-Petersburg, Russia, 20–22 September 2004; pp. 326–333. [Google Scholar]
- Lipeika, A.; Laurinčiukaitė, S. Framework for Choosing a Set of Syllables and Phonemes for Lithuanian Speech Recognition. Informatica 2007, 18, 395–406. [Google Scholar]
- Laurinčiukaitė, S.; Lipeika, A. Syllable-Phoneme based Continuous Speech Recognition. Electr. Eng. 2006, 6, 10–13. [Google Scholar]
- Lileikyte, R.; Gorin, A.; Lamel, L.; Gauvain, J.L.; Fraga-Silva, T. Lithuanian Broadcast Speech Transcription Using Semi-supervised Acoustic Model Training. Proc. Comput. Sci. 2016, 81, 107–113. [Google Scholar] [CrossRef]
- Alumäe, T.; Tilk, O. Automatic speech recognition system for Lithuanian broadcast audio. Front. Artif. Intell. Appl. 2016, 289, 39–45. [Google Scholar] [CrossRef]
- Lileikytė, R.; Lamel, L.; Gauvain, J.-L.; Gorin, A. Conversational telephone speech recognition for Lithuanian. Comput. Speech Lang. 2018, 49, 71–82. [Google Scholar] [CrossRef]
- Gales, M.J.F.; Knill, K.M.; Ragni, A. Unicode-based graphemic systems for limited resource languages. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 5186–5190. [Google Scholar]
- Maskeliunas, R.; Rudžionis, A.; Ratkevičius, K.; Rudžionis, V. Investigation of foreign languages models for lithuanian speech recognition. Electron. Electr. Eng. 2009, 3, 15–20. [Google Scholar]
- Rudzionis, V.; Maskeliunas, R.; Rudzionis, A.; Ratkevicius, K. On the adaptation of foreign language speech recognition engines for Lithuanian speech recognition. Lect. Notes Bus. Inf. Process 2009, 37, 113–118. [Google Scholar] [CrossRef]
- Rudzionis, V.; Raskinis, G.; Maskeliunas, R.; Rudzionis, A.; Ratkevicius, K. Comparative analysis of adapted foreign language and native Lithuanian speech recognizers for voice user interface. Electron. Electr. Eng. 2013, 19, 90–93. [Google Scholar] [CrossRef][Green Version]
- Rasymas, T.; Rudžionis, V. Combining multiple foreign language speech recognizers by using neural networks. Front. Artif. Intell. Appl. 2014, 268, 33–39. [Google Scholar] [CrossRef]
- Rudzionis, A.; Rudzionis, V. Phoneme recognition in fixed context using regularized discriminant analysis. In Proceedings of the Sixth European Conference on Speech Communication and Technology (EUROSPEECH’99), Budapest, Hungary, 5–9 September 1999. [Google Scholar]
- Driaunys, K.; Rudžionis, V.; Žvinys, P. Averaged Templates Calculation and Phoneme Classification. Inf. Technol. Control. 2007, 36. [Google Scholar] [CrossRef]
- Rudzionis, A.; Rudzionis, V. Lithuanian Speech Database LTDIGITS. In Proceedings of the Third International Conference on Language Resources and Evaluation (LREC’02), Las Palmas, Canary Islands, Spain, 29–31 May 2002. [Google Scholar]
- Vaičiūnas, A.; Kaminskas, V.; Raskinis, G. Statistical Language Models of Lithuanian Based on Word Clustering and Morphological Decomposition. Informatica 2004, 15, 565–580. [Google Scholar]
- Karpov, A.; Markov, K.; Kipyatkova, I.; Vazhenina, D.; Ronzhin, A. Large vocabulary Russian speech recognition using syntactico-statistical language modeling. Speech Commun. 2014, 56, 213–228. [Google Scholar] [CrossRef]
- Kipyatkova, I.S.; Karpov, A.A. A study of neural network Russian language models for automatic continuous speech recognition systems. Autom. Remote Control 2017, 78, 858–867. [Google Scholar] [CrossRef]
- Jadczyk, T. Audio-visual speech-processing system for Polish applicable to human-computer interaction. Comput. Sci. 2018, 19, 41–64. [Google Scholar] [CrossRef]
- Pakoci, E.; Popović, B.; Pekar, D. Improvements in Serbian speech recognition using sequence-trained deep neural networks. SPIIRAS Proc. 2018, 3, 53–76. [Google Scholar] [CrossRef][Green Version]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Luong, M.-T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Fayek, H.M.; Lech, M.; Cavedon, L. Evaluating deep learning architectures for Speech Emotion Recognition. Neur. Netw. 2017, 92, 60–68. [Google Scholar] [CrossRef]
- Hannun, A. Sequence Modeling with CTC. Distill 2017, 2. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. Proceedings of International Conference on Learning Representations (ICLR), San Diego, CA, USA, 8–9 May 2015. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Zeyer, A.; Doetsch, P.; Voigtlaender, P.; Schluter, R.; Ney, H. A comprehensive study of deep bidirectional LSTM RNNS for acoustic modeling in speech recognition. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Xie, Z.; Huang, Y.; Zhu, Y.; Jin, L.; Liu, Y.; Xie, L. Aggregation Cross-Entropy for Sequence Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 6538–6547. [Google Scholar]
- Graves, A. Supervised Sequence Labelling; Springer: Berlin, Germany, 2012. [Google Scholar]
- Liepa Corpora. Interactive Repository Link. Available online: https://www.xn--ratija-ckb.lt/liepa (accessed on 17 October 2019).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sipavičius, D.; Maskeliūnas, R. “Google” Lithuanian Speech Recognition Efficiency Evaluation Research. In Proceedings of the International Conference on Information and Software Technologies, Druskininkai, Lithuania, 13–15 October 2016; pp. 602–612. [Google Scholar]
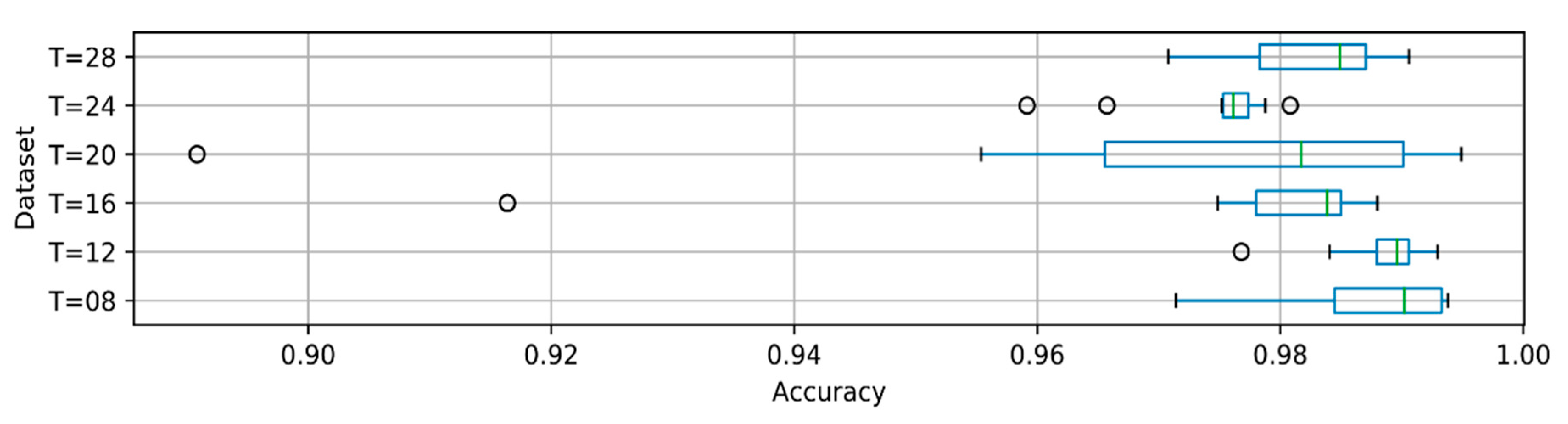
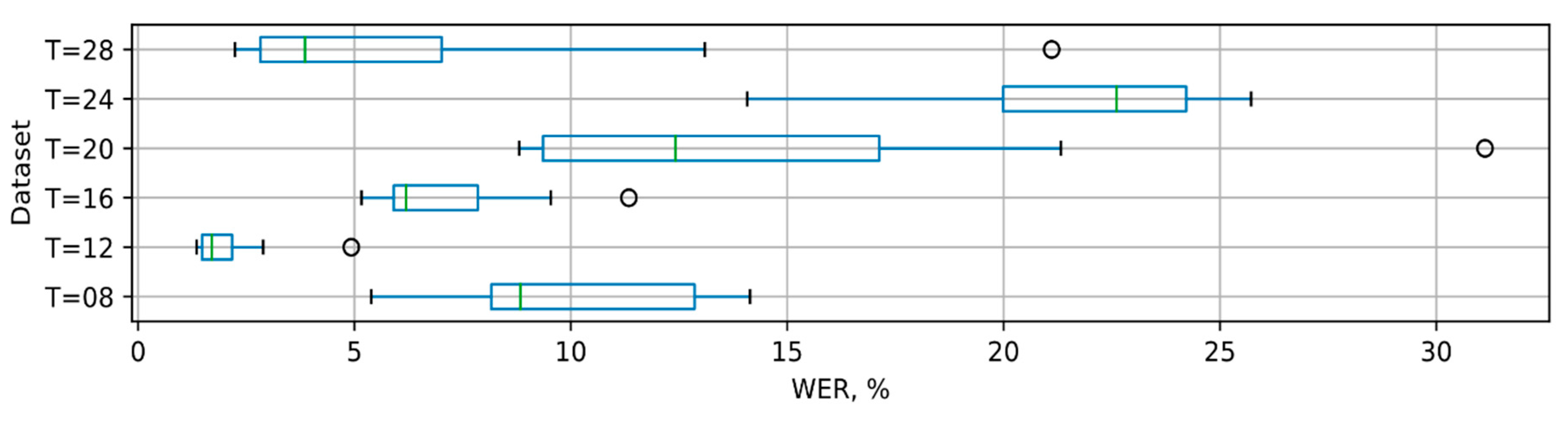
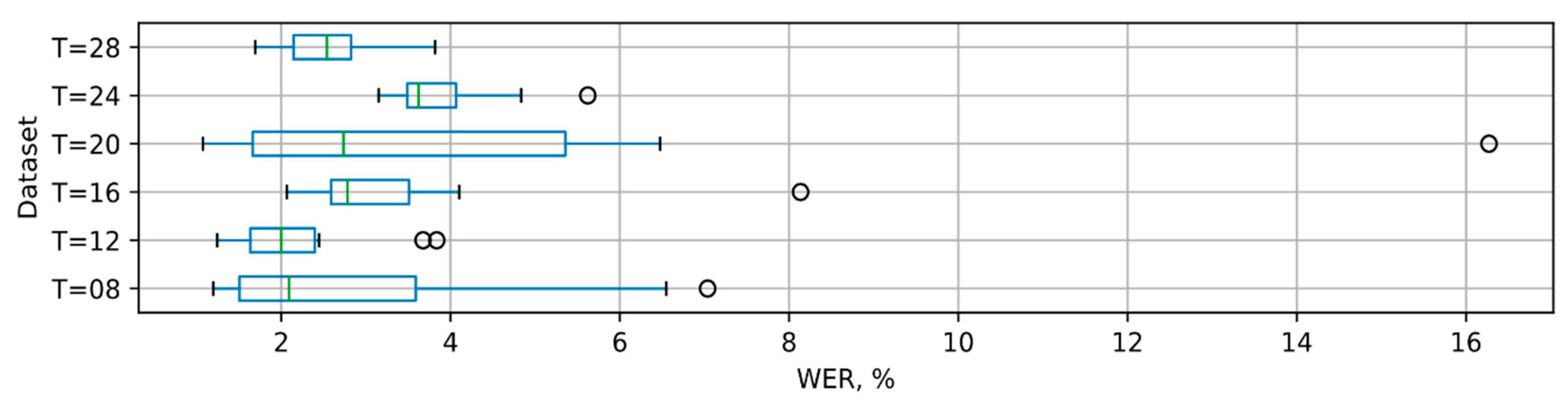
| Max Length of Phonemes | T = 8 | T = 12 | T = 16 | T = 20 | T = 24 | T = 28 |
|---|---|---|---|---|---|---|
| Number of words | 417,935 | 765,845 | 1,273,983 | 1,821,439 | 2,473,073 | 3,151,933 |
| Number of sequences | 367,989 | 570,321 | 782,680 | 96,5211 | 1,145,086 | 1,304,801 |
| Model | Number of Hidden Layers | Number of Epochs Trained | Training Loss | Training Accuracy | Testing Loss | Testing Accuracy |
|---|---|---|---|---|---|---|
| Seq2Seq-2x32 | 2 | 8 | 1.709 | 0.991 | 0.702 | 0.976 |
| Seq2Seq-2x64 | 2 | 10 | 1.703 | 0.994 | 0.625 | 0.986 |
| Seq2Seq-2x128 | 2 | 9 | 1.701 | 0.995 | 0.534 | 0.991 |
| Seq2Seq-2x256 | 2 | 3 | 1.711 | 0.990 | 0.703 | 0.973 |
| Seq2Seq-3x32 | 3 | 8 | 1.713 | 0.989 | 0.714 | 0.960 |
| Seq2Seq-3x64 | 3 | 10 | 1.709 | 0.991 | 0.596 | 0.982 |
| Seq2Seq-3x128 | 3 | 9 | 1.711 | 0.990 | 0.612 | 0.978 |
| Seq2Seq-3x256 | 3 | 10 | 1.785 | 0.954 | 2.350 | 0.778 |
| Seq2Seq-4x32 | 4 | 8 | 1.770 | 0.964 | 0.995 | 0.897 |
| Seq2Seq-4x64 | 4 | 10 | 1.783 | 0.955 | 2.047 | 0.810 |
| Seq2Seq-4x128 | 4 | 7 | 1.732 | 0.980 | 0.940 | 0.939 |
| Seq2Seq-4x256 | 4 | 8 | 1.966 | 0.812 | 4.041 | 0.451 |
| Seq2Seq-5x32 | 5 | 8 | 1.745 | 0.974 | 0.989 | 0.920 |
| Seq2Seq-5x64 | 5 | 7 | 1.806 | 0.943 | 1.657 | 0.812 |
| Seq2Seq-5x128 | 5 | 7 | 2.175 | 0.685 | 6.832 | 0.217 |
| Seq2Seq-5x256 | 5 | 7 | 3.153 | 0.172 | 2.939 | 0.180 |
| Model | Number of Hidden Layers | Number of Epochs Trained | Training Loss | Training Accuracy | Testing Loss | Testing Accuracy |
|---|---|---|---|---|---|---|
| Attention-2x32 | 2 | 8 | 1.701 | 0.994 | 0.552 | 0.989 |
| Attention-2x64 | 2 | 2 | 1.710 | 0.990 | 0.514 | 0.993 |
| Attention-2x128 | 2 | 1 | 1.759 | 0.959 | 0.530 | 0.989 |
| Attention-2x256 | 2 | 1 | 2.438 | 0.654 | 7.113 | 0.111 |
| Attention-3x32 | 3 | 5 | 1.703 | 0.994 | 0.527 | 0.985 |
| Attention-3x64 | 3 | 3 | 1.707 | 0.992 | 0.538 | 0.988 |
| Attention-3x128 | 3 | 1 | 1.787 | 0.942 | 0.523 | 0.990 |
| Attention-3x256 | 3 | 5 | 1.832 | 0.959 | 0.691 | 0.969 |
| Attention-4x32 | 4 | 6 | 1.702 | 0.994 | 0.605 | 0.965 |
| Attention-4x64 | 4 | 6 | 1.706 | 0.992 | 0.820 | 0.949 |
| Attention-4x128 | 4 | 4 | 1.711 | 0.990 | 0.508 | 0.990 |
| Attention-4x256 | 4 | 4 | 3.170 | 0.311 | 2.523 | 0.302 |
| Attention-5x32 | 5 | 6 | 1.707 | 0.992 | 0.630 | 0.967 |
| Attention-5x64 | 5 | 5 | 1.706 | 0.992 | 0.608 | 0.976 |
| Attention-5x128 | 5 | 3 | 1.750 | 0.973 | 0.797 | 0.921 |
| Attention-5x256 | 5 | 5 | 2.588 | 0.496 | 2.297 | 0.457 |
| Model | Loss Value | Accuracy | Mean Levenshtein | Median Levenshtein |
|---|---|---|---|---|
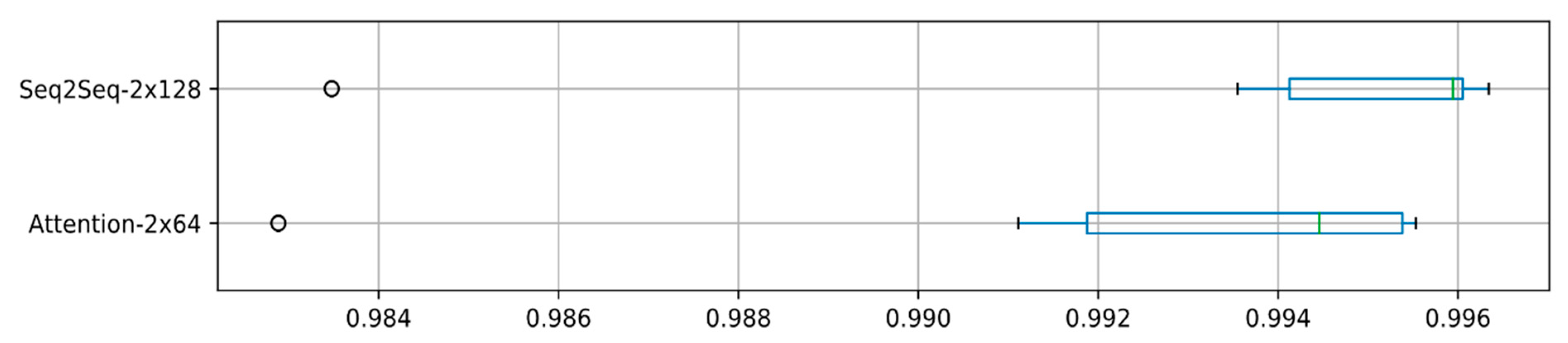
| Seq2Seq-2x128 | 0.536 | 0.991 | 0.043 | 0 |
| Attention-2x64 | 0.515 | 0.993 | 0.028 | 0 |
| Model | Longest Phoneme Sequence in the Dataset | Number of Epochs Trained | Training Accuracy | Validation Accuracy | Test Accuracy |
|---|---|---|---|---|---|
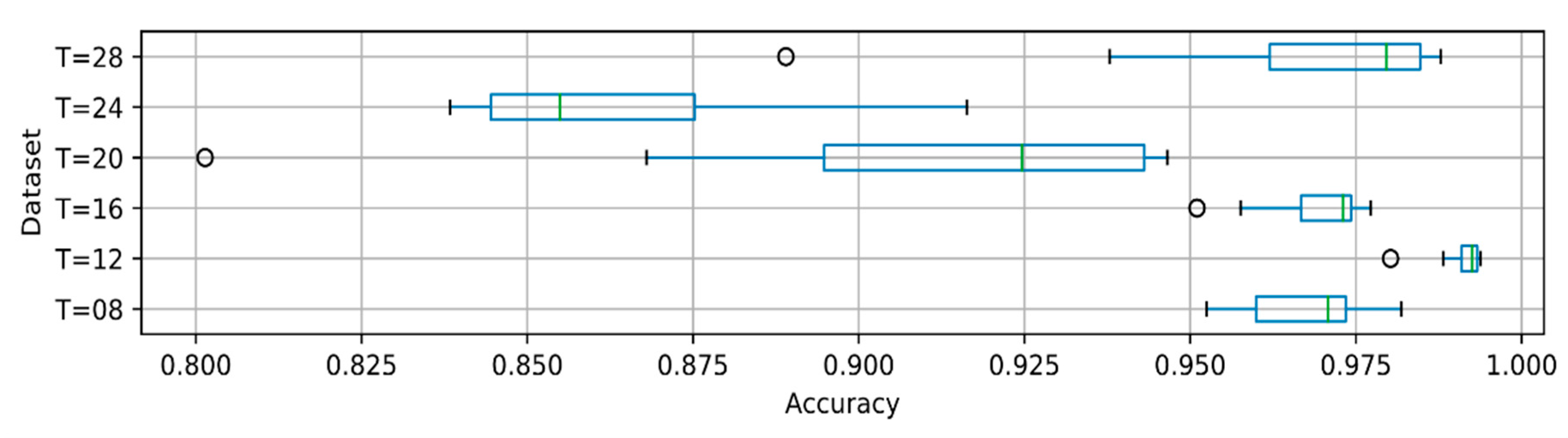
| Seq2Seq-2x128 | 8 | 18 | 0.996 | 0.992 | 0.875 |
| Seq2Seq-2x128 | 12 | 19 | 0.997 | 0.922 | 0.920 |
| Seq2Seq-2x128 | 16 | 19 | 0.997 | 0.982 | 0.985 |
| Seq2Seq-2x128 | 20 | 13 | 0.997 | 0.966 | 0.960 |
| Seq2Seq-2x128 | 24 | 20 | 0.998 | 0.956 | 0.953 |
| Seq2Seq-2x128 | 28 | 20 | 0.998 | 0.849 | 0.990 |
| Attention-2x64 | 8 | 16 | 0.996 | 0.914 | 0.858 |
| Attention-2x64 | 12 | 19 | 0.997 | 0.975 | 0.975 |
| Attention-2x64 | 16 | 20 | 0.998 | 0.963 | 0.951 |
| Attention-2x64 | 20 | 17 | 0.998 | 0.993 | 0.992 |
| Attention-2x64 | 24 | 18 | 0.998 | 0.930 | 0.874 |
| Attention-2x64 | 28 | 20 | 0.999 | 0.993 | 0.988 |
| Model | Longest Phoneme Sequence in the Dataset | Validation WER | Test WER |
|---|---|---|---|
| Seq2Seq-2x128 | 8 | 2.086 | 24.692 |
| Seq2Seq-2x128 | 12 | 13.953 | 14.057 |
| Seq2Seq-2x128 | 16 | 2.905 | 2.394 |
| Seq2Seq-2x128 | 20 | 5.097 | 5.693 |
| Seq2Seq-2x128 | 24 | 6.142 | 6.362 |
| Seq2Seq-2x128 | 28 | 20.039 | 1.524 |
| Attention-2x64 | 8 | 10.406 | 20.887 |
| Attention-2x64 | 12 | 3.104 | 3.150 |
| Attention-2x64 | 16 | 4.071 | 5.239 |
| Attention-2x64 | 20 | 1.087 | 1.303 |
| Attention-2x64 | 24 | 7.098 | 12.989 |
| Attention-2x64 | 28 | 1.098 | 1.583 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pipiras, L.; Maskeliūnas, R.; Damaševičius, R. Lithuanian Speech Recognition Using Purely Phonetic Deep Learning. Computers 2019, 8, 76. https://doi.org/10.3390/computers8040076
Pipiras L, Maskeliūnas R, Damaševičius R. Lithuanian Speech Recognition Using Purely Phonetic Deep Learning. Computers. 2019; 8(4):76. https://doi.org/10.3390/computers8040076
Chicago/Turabian StylePipiras, Laurynas, Rytis Maskeliūnas, and Robertas Damaševičius. 2019. "Lithuanian Speech Recognition Using Purely Phonetic Deep Learning" Computers 8, no. 4: 76. https://doi.org/10.3390/computers8040076
APA StylePipiras, L., Maskeliūnas, R., & Damaševičius, R. (2019). Lithuanian Speech Recognition Using Purely Phonetic Deep Learning. Computers, 8(4), 76. https://doi.org/10.3390/computers8040076





