1. Introduction
Localization is a problem for mobile robots to localize themselves in the environment with sensory information from their embedded sensors. A reliable solution to this problem is the prerequisite and foundation for achieving high level applications, such as tracking, path planning, security alerts, environmental survey, etc. A vast number of works dedicated to the localization problems utilize the probabilistic method, which is based on the propagation of probabilistic distributions of the sensor noise and the unknown parameters (the robot pose state). While some others get rid of dealing with the uncertainty probability distributions, they assumed that noise is unknown but bounded by real intervals. Those methods provide solutions presented by a set of bounded configurations in which the robot is guaranteed to be, and they are classified as deterministic methods.
Probabilistic techniques have long been used in solving robotic localization and mapping issues. The most commonly used methods are Kalman filtering and Particle filtering [
1,
2,
3]. However, these methods suffer inconsistency problems in some scenarios. This shortcomings have long been noticed by the research community [
4,
5,
6,
7,
8]. An interval analysis based method is another type of method. Different from probabilistic methods, which make hypotheses on the probability distribution, these methods take a soft assumption that all the noise is bounded within known limits. This is a realistic representation because many manufacturers provide the maximum and minimum errors for the sensors they produce. These maximum and minimum error values can be regarded as the error bounds. Based on these error bounds, interval analysis based methods can recursively propagate such bounded errors by using consistency techniques and systematic search methods. Contrary to probabilistic methods, interval analysis based methods calculate guaranteed sets to enclose the real solutions, without losing any feasible values.
Interval analysis based methods have achieved applications successfully such as parameter and state estimation [
9,
10] as well as the robotic localization and mapping field. Seignez [
11] presents their simulation results of a mobile robot navigating in an indoor environment. The ability of an interval analysis method to cope with erroneous data and to obtain consistent estimations of the robot pose was demonstrated. Lambert [
12] extended such work for an outdoor vehicle equipped with two proprioceptive sensors and a GPS receiver. Comparison was made with the Particle Filter localization, showing the better performance of an interval based method in terms of consistency issues. Gning [
13] and Kueviakoe [
14] deal with the outdoor localization problem in the framework of an Interval Constraint Satisfaction Problem (ICSP). Those works used interval constraint propagation techniques to fuse the redundant data of sensors [
9]. Drevelle [
15] proposed a relaxed constraint propagation approach to deal with erroneous GPS measurements. Bonnifait [
16] combined constraint propagation and set inversion techniques and presented a cooperative localization method with significant enhancement in terms of accuracy and confidence domains. Experimental results illustrate that the precision obtained is very good with a consistent localization, and the constraint propagation techniques are well adapted to real time implementation.
The main advantage of interval analysis based localization over Kalman filtering or Bayesian methods is that they provide guaranteed solutions without the need to linearize the robot motion or the sensoring models, unlike the probabilistic counterparts that require linearization to facilitate the propagation of uncertainties. Moreover, interval methods do not assume any noise probability distribution in the system; they just require a soft assumption about the support of the noise, i.e., it is bounded by real intervals. Thus, they can provide guaranteed and consistent results.
We present, in this paper, a dynamic ICSP graph optimization based methodology for solving outdoor robotic localization problems. We put forward a two-stage framework: visual teach and repeat. Closer approaches have already been proposed by different researchers [
17,
18,
19], which all involve a visual learning step to reconstruct a map of the environment, and then use this map for localization and navigation tasks. Royer [
17] uses bundle adjustment in the mapping step and the localization results are obtained via a Newton iteration method. Lim [
19] uses structure from a motion (SFM) algorithm to reconstruct the 3D environment; then, in the localization step, two discrete Kalman filters are employed to estimate the camera trajectory. Courbon’s method [
18] doesn’t involve the 3D reconstruction procedure during the map building step; instead, it records some key views and the performed path as references and uses them for future navigation missions. Our proposed method uses totally different theory and techniques from these approaches; we use a bounded-error model to parameterize landmarks detected by a monocular camera and cast the landmark estimation process as an ICSP. The ICSP graph architecture is put forward for intensively interval domain contraction. By using consistent techniques (ICP) to search for all possible solutions, a consistent real-time localization result is obtained. This result could be further improved by performing global optimization over the ICSP graph.
The paper is organized as follows:
Section 2 introduces the basics of interval analysis and constraint propagation.
Section 3 presents the formulation of ICSP based landmark estimation, and details the construction and resolution of the ICSP graph. The real-time localization process is introduced in
Section 4. Numerical and experimental results are given in
Section 5.
Section 6 concludes the paper and proposes the perspective of future work.
2. Overview of Interval Analysis
Interval analysis and the constraints satisfaction problem are the two main mathematical theories on which our work are based. In this section, we give a brief description of the fundamental knowledge that are used in our work.
2.1. Principle of Interval
Interval analysis [
20,
21] was developed in the 1960s in order to deal with approximation problems encountered during calculation. It is a numerical method which puts bounds on rounding or measurements errors during mathematical computations in order to get reliable results.
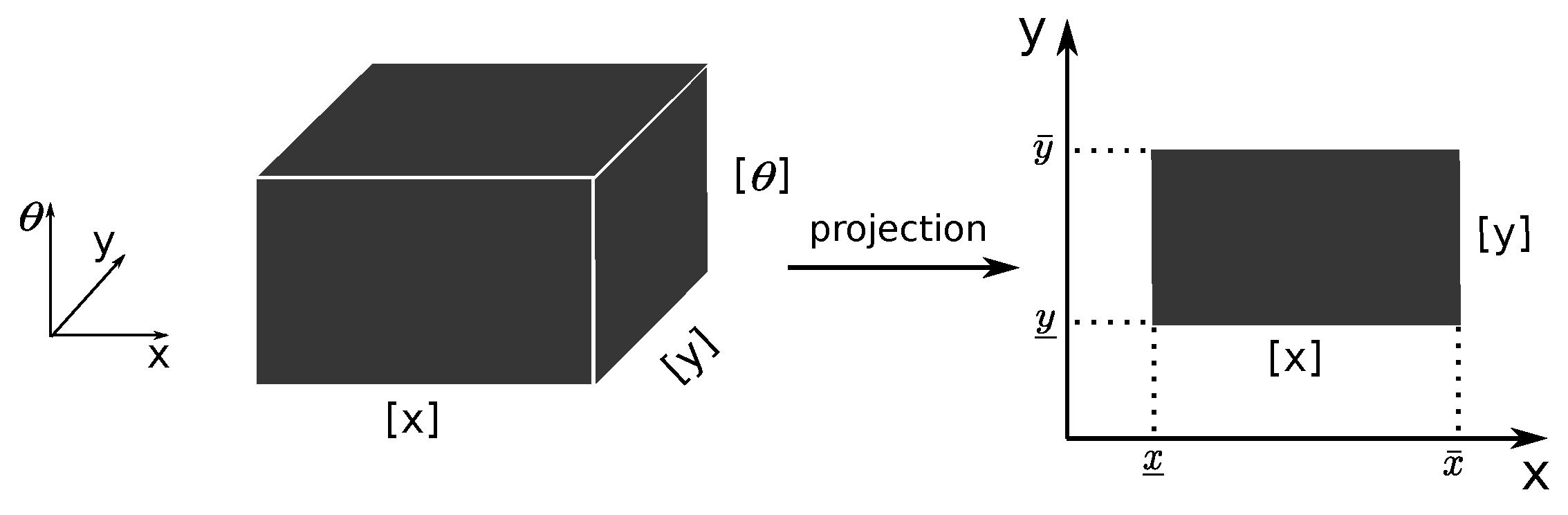
An interval is a connected subset of , defined as , where and are respectively the lower and upper bound of , . , , are some interval examples. The empty set ∅ is also considered as an interval since it can be used to represent the null solution to a problem. The width of is computed by . The set of intervals is denoted by .
An interval vector (or box) is a generalization of the interval concept. It is a vector whose components are intervals.
(
) is an
n-dimensional interval vector defined as the Cartesian product of
n intervals:
where the
interval
(
) is the projection of
on to the
axis. The volume of the interval vector is then computed via
The volume of the interval box is usually used to evaluate the uncertainty of
[
22].
For instance, the configuration of a vehicle’s pose usually contains three parameters: position
x, position
y and heading angle
. Consequently, for vehicle localization, the solution is a three-dimensional box:
. When projected on the
plane, it decreases to a two-dimensional box, which gives the position region of the vehicle. The projection on the
x axis and
y axis then gives the
x position and
y position of the vehicle separately—see the illustration on
Figure 1.
2.2. Operations of Interval Arithmetic
Rules have been defined to apply the basic arithmetical operations on intervals. Consider two intervals
and
and a binary operator
, the smallest interval which contains all feasible values for
is defined as:
⋄ is a complete operator as it returns all the possible solutions for the computations between the two intervals. The resulting solutions are thus guaranteed. For example,
,
.
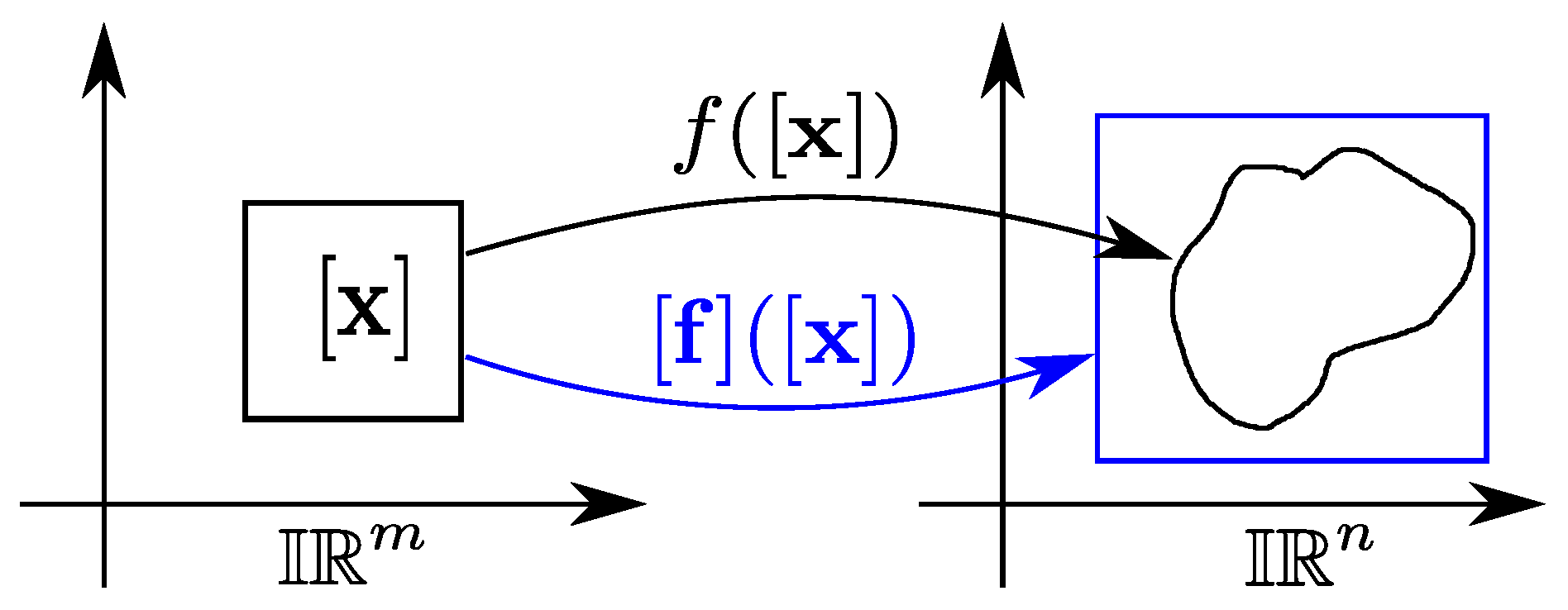
The image of a vector function
(defined by arithmetical operators and elementary functions), over an interval box
can be evaluated by its inclusion function
, whose output contains all possible values taken by
over
:
The image set of
may have any shape; the inclusion function
of
makes it possible to compute a box that is guaranteed to contain the entire image set (see
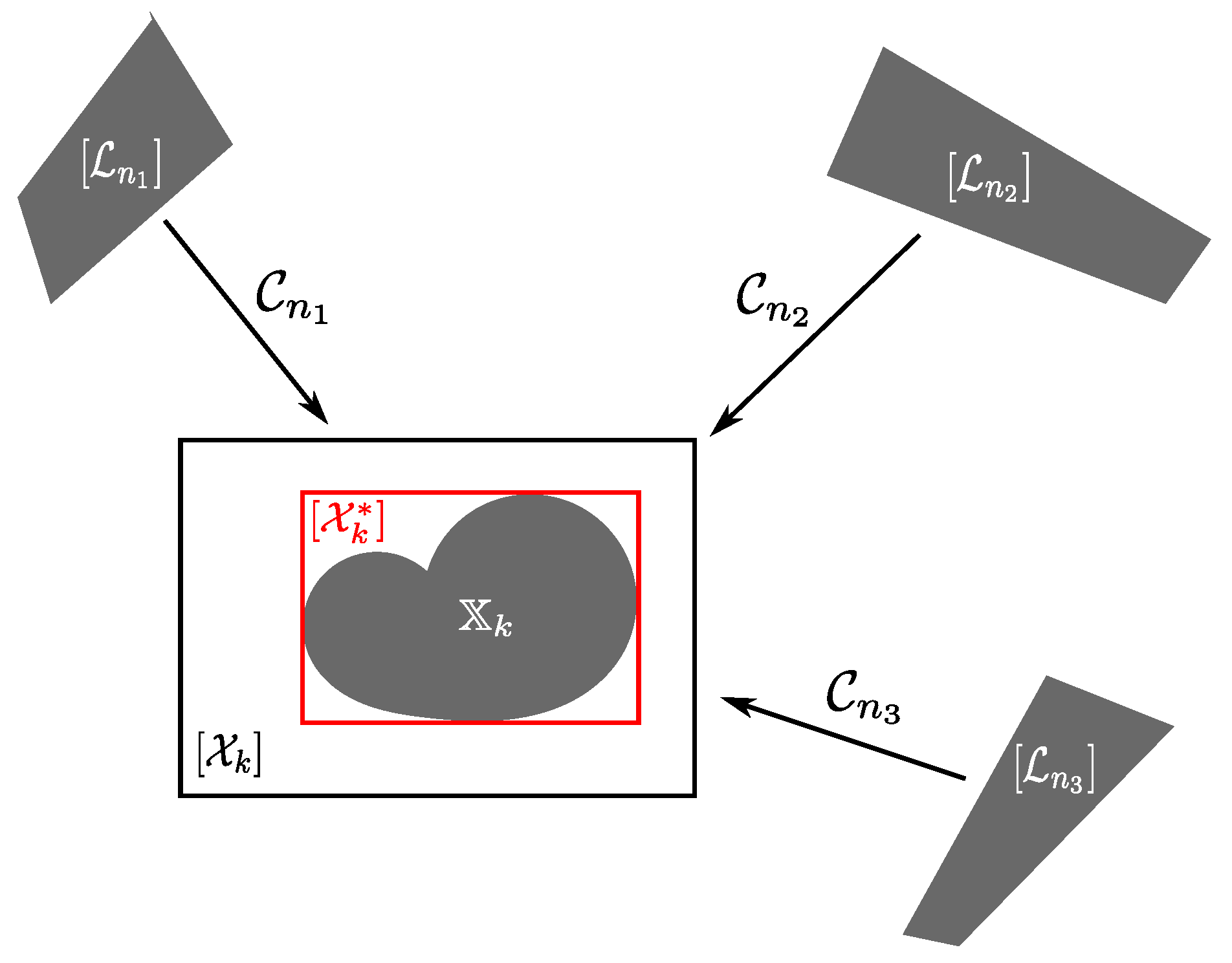
Figure 2). The inclusion function is one of the most important notions in interval analysis. It can be used to represent equations. Such equations, also called constraints, are the core of the Interval Constraint Satisfaction Problem.
2.3. Interval Constraint Satisfaction Problem (ICSP)
The Constraint Satisfaction Problem (CSP) is a mathematical problem of finding a solution to a set of variables whose states should satisfy a number of constraints. The notion of an Interval Constraint Satisfaction Problem (ICSP) was introduced by Hyvoen [
23] in 1992. It is a certain form of CSP that deals with continuous variable domains represented by intervals. It is typically defined as a triple
:
a set V of n variables ,
a set D of n domains , such as for each variable , a domain with the possible values for that variable is given. could be an interval or union of intervals;
a set C of p constraints , each constraint defines a relationship over a subset variables of V, e.g., restricts the possible domains of , and .
ICSP is a mathematical problem of searching all the possible domains of the variables that satisfy all the constraints corresponding to the ICSP.
2.4. Contractor
The concept of contractor is directly inspired from the ubiquitous concept of filtering algorithms in constraint programming. Given a constraint
c relating a set of variables
, an algorithm
is called a contractor (or a filtering algorithm) if
returns a sub-domain of the input domain
and the resulting sub-domain
contains all the feasible values with respect to the constraint
c. Mathematically,
The first condition indicates the contractance property and the second one refer to the correctness. The concept has been formalized and intensively used in solving the constraint satisfaction problems. Contractor has been formalized and intensively used in solving ICSP, such as Forward/Backward, HC4, etc.
2.5. Interval Consistency
The notion of consistency is the fundamental and underlying concept to the domain contraction for the Interval Constraint Satisfaction Problem.
Local consistency: When an algorithm locally computes the domain of variables, considering only one constraint at a time, then we say the algorithm is local consistency (related to the constraint). Since it doesn’t take into account the whole constraint system, it may not achieve the optimal solution for all the variables. The Forward/Backward contractor is a classical local consistency algorithm since it calculates the primitive constraints one by one. The strength of local consistency algorithm is their good performance in computing time. Due to the simple calculation (one constraint at a time), the local consistency algorithm always surpasses the global ones in the comparison of computing time.
Global consistency: An algorithm is said to have global consistency if it takes into account of all the constraints of the system when performing domain contractions. Consider an
with
n variables (
) and
p constraints (
). Denote each constraint by
, where
is a subset of
V with
. The domain of
is global consistent if the following condition is satisfied:
such that
. If the domain of all variables reaches global consistency, then the contraction algorithm is said to be a global one. A global consistency algorithm seeks the strength of the domain contractions rather than the shortness of computation time.
3. Visual Teach Mapping
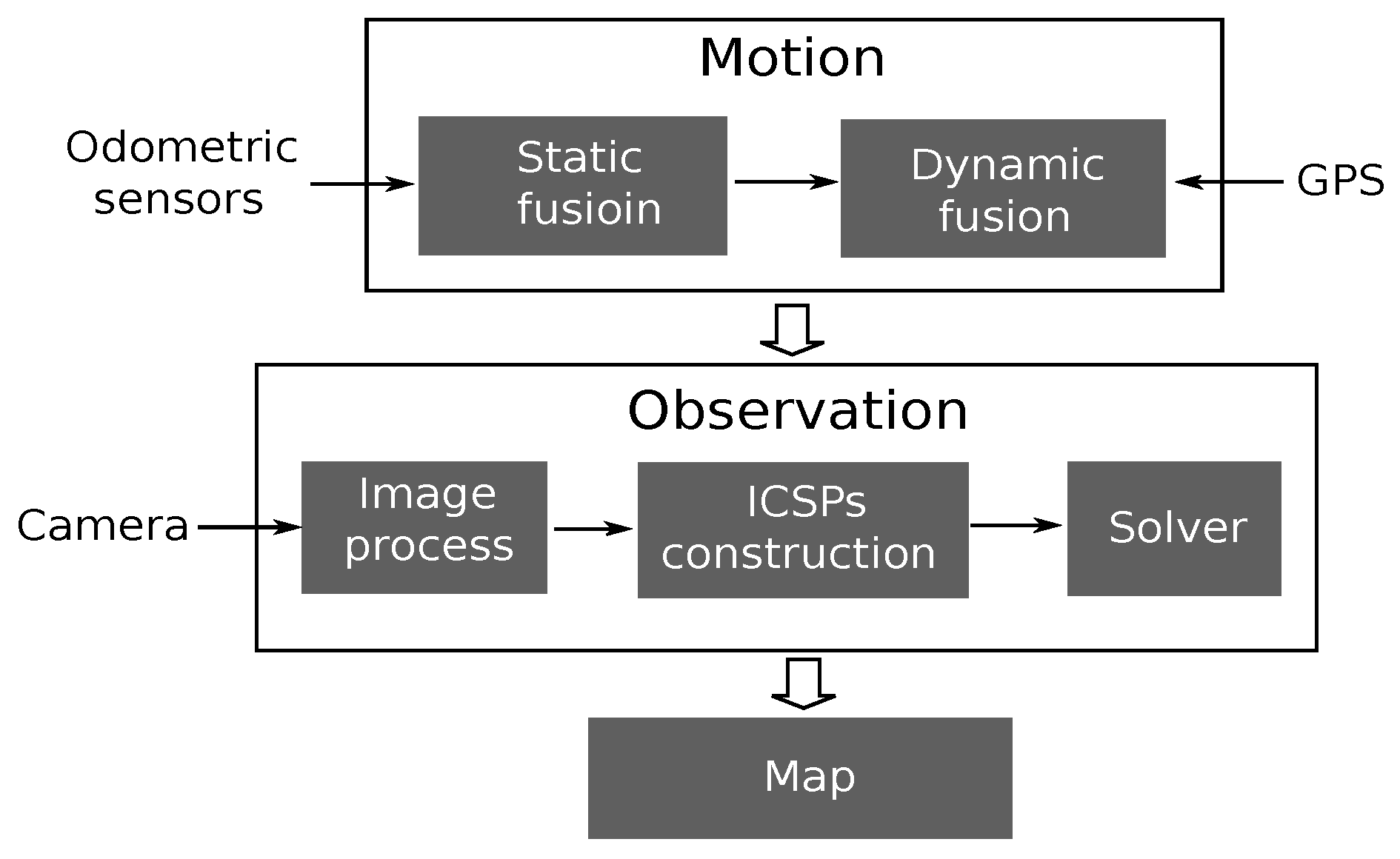
3.1. Framework of Visual Teach
The objective of the visual teach phase is to construct a map of the surrounding environment. The general framework of our proposed visual teach is described in
Figure 3. It includes two main processes: motion estimation and observation processing. The two processes are conducted at each timestep. In the motion estimation process, the preliminary pose of the robot is estimated by fusing the measurements of odometric sensors and GNSS receivers; then, in the observation process, the measurement (new captured image) from the camera is processed. By constructing and solving the ICSPs successively, the position of each landmark can be estimated.
3.2. Motion Estimation
The motion estimation process integrates the odometric measurements and GNSS data to determine the current robot pose given the previous pose and the sensor data collected during the instant and k. It is a dynamic nonlinear state estimation problem. Based on the definition of ICSP, we can cast the motion estimation process as an ICSP. At timestep k, the new ICSP(, , ) is generated and defined as
a set of variables,
:
a set of constraints,
:
represents the set of constraints; it is the robotic kinematic model defined by Seignez [
11].
Once the ICSP is generated, the robot pose
can be estimated by applying the ICP algorithms over the constraints deduced from the kinematic model.
Table 1 gives the equations that are obtained from a Forward/Backward propagation. Interval analysis is a pessimistic method maintaining all possible solutions; the cumulative odometric errors will result in interval expansion, i.e., the width (or uncertainty) of
will become larger and larger. This would be a hindrance to pursuing a precise map. To deal with such problem, GPS measurement
is used to initialize the priori domains of
.
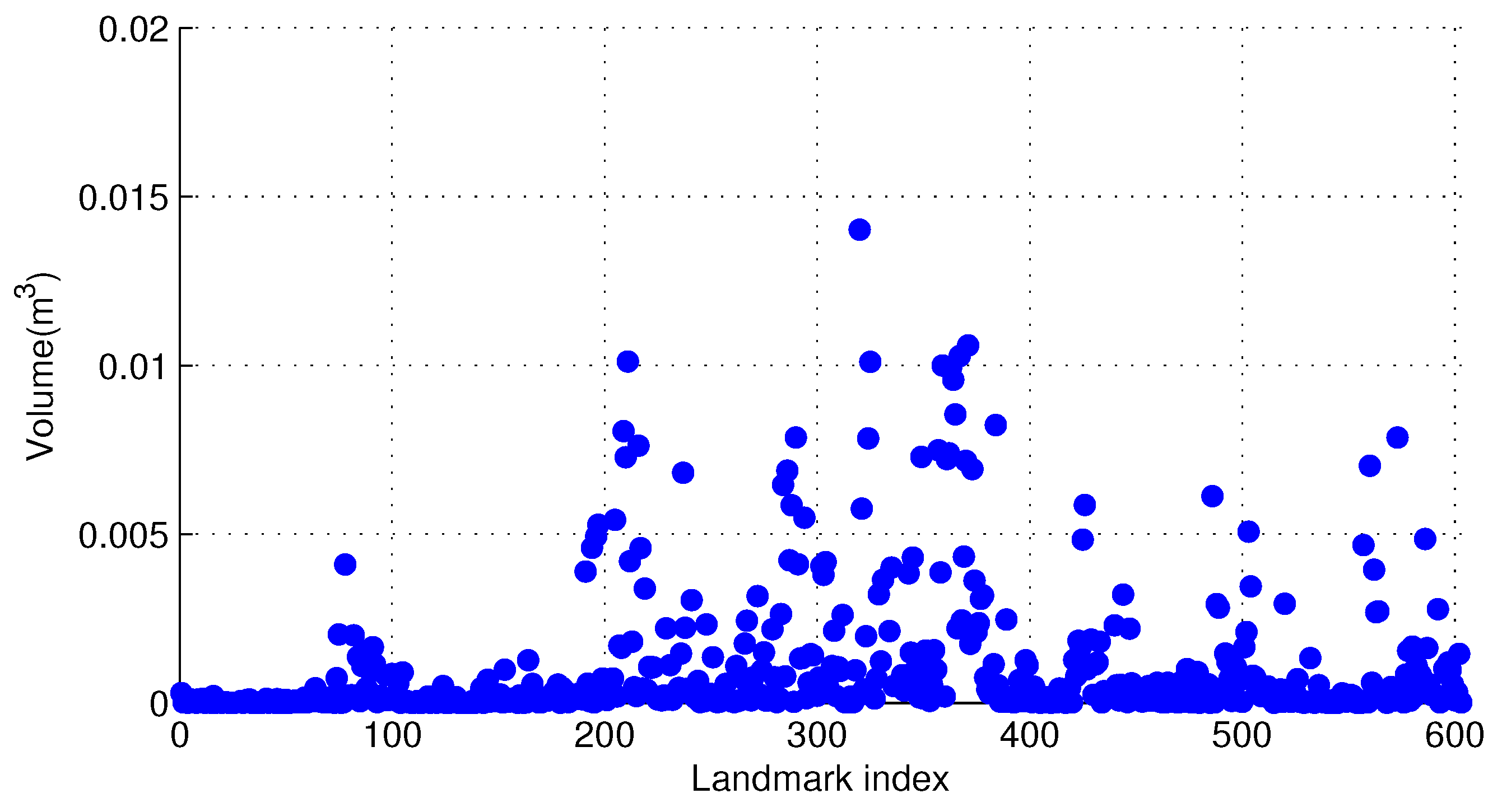
3.3. Bounded-Error Landmark Parameterization
A landmark (or feature point) is a 3D point in the global world. The map of the environment thus can be represented by
n stationary landmarks:
. Drocourt [
24] proposed a parameterization method in the context of interval analysis by representing the landmark with a 3D interval box (
). However, this representation turns out to suffer the envelope problem [
25]. To improve the mapping result, we make an extension of the inverse depth parameterization [
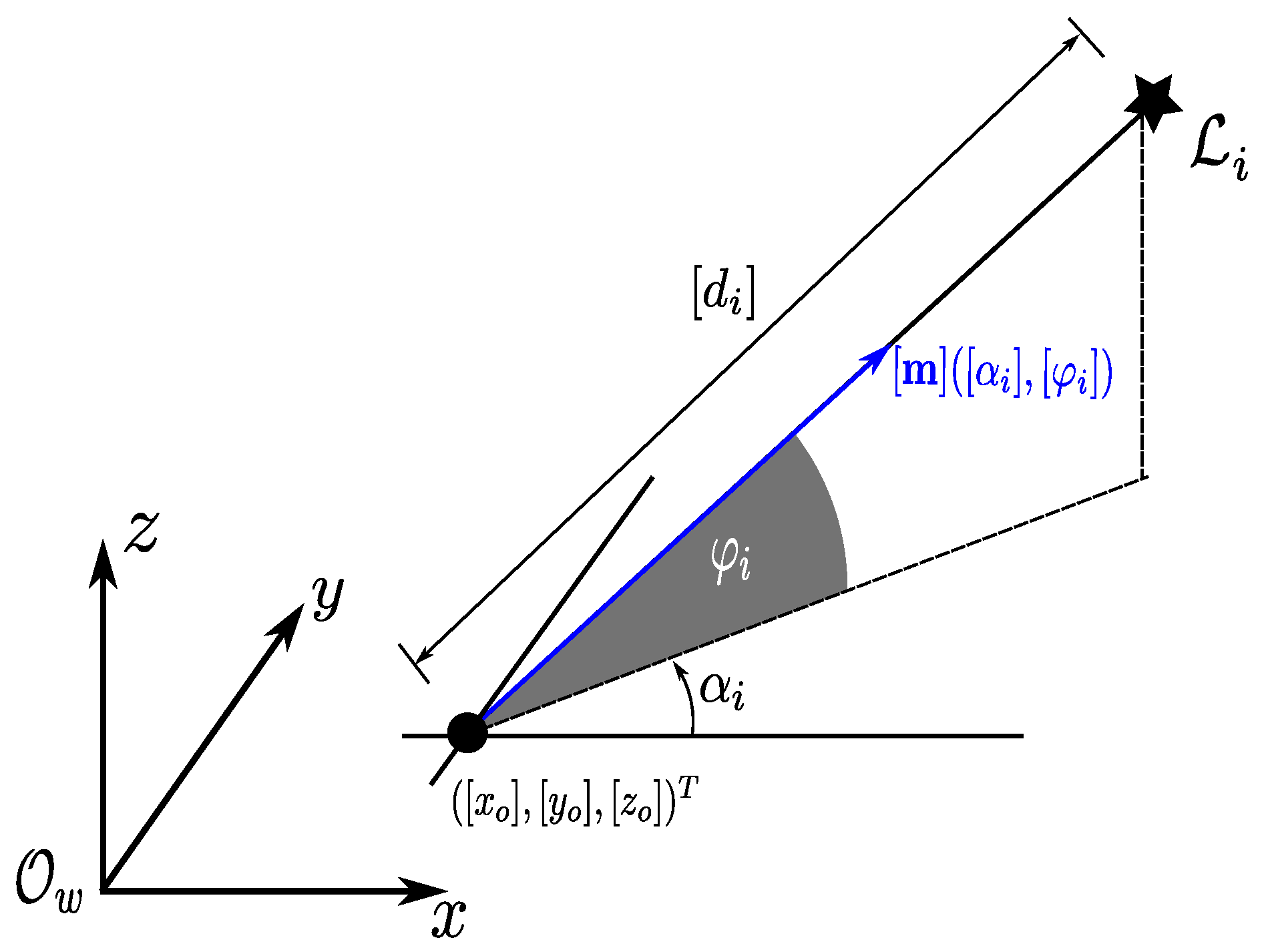
26] to obtain an bounded-error model to parameterize the landmark. Each landmark
is defined as a six-dimensional interval vector:
, which models the estimated landmark position at:
where
is the unknown depth of the landmark. The coordinate
,
,
represents the position of the optical center in the world frame when the landmark was seen for the first time;
,
represent respectively the azimuth and elevation angle for the ray that traces the landmark and
is the depth of the landmark.
is a unitary vector pointing from the optical center to the landmark
, see illustration in
Figure 4.
Since all the parameters are represented by intervals, and
can be initialized as
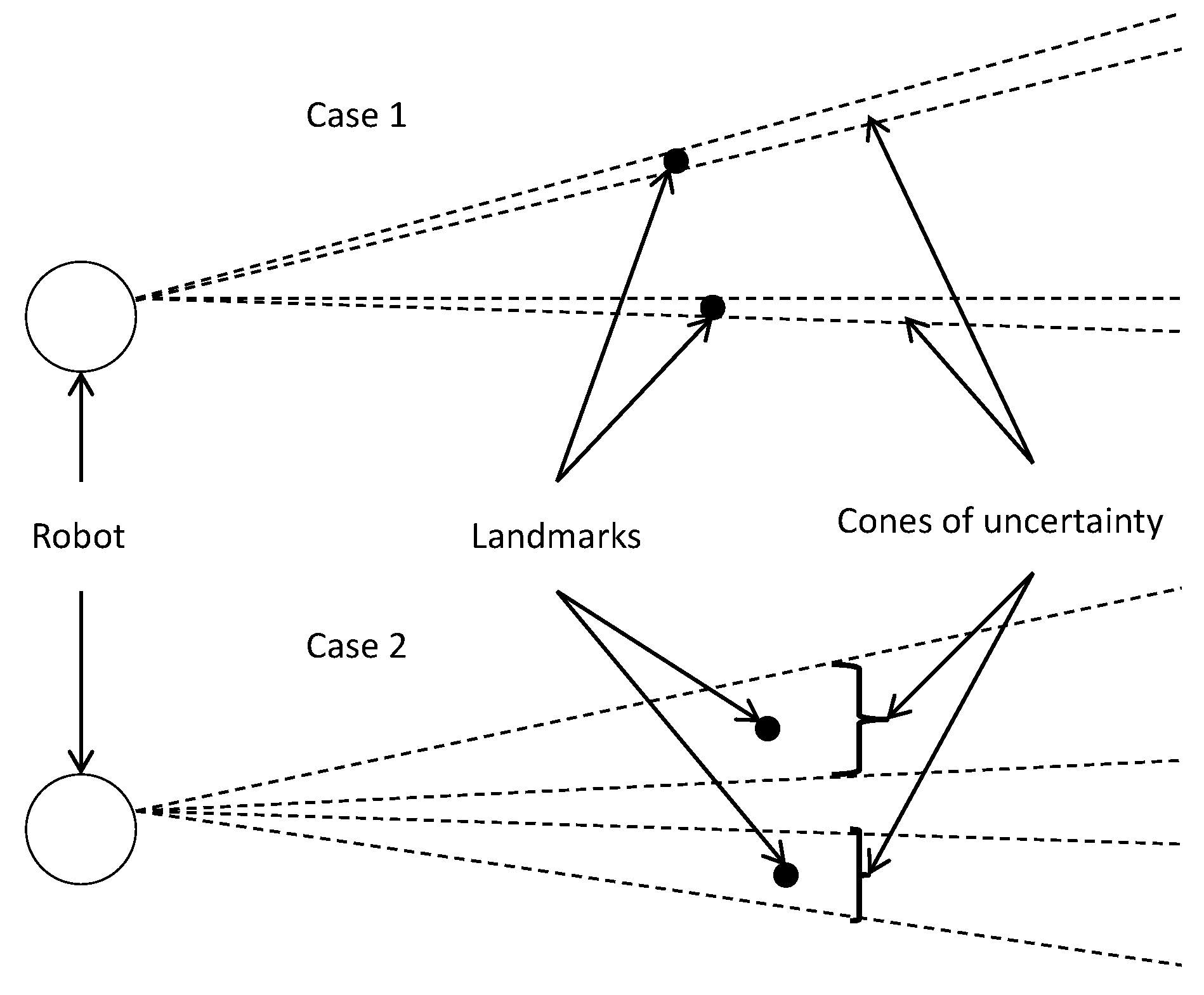
, the landmark’s uncertainty is modeled as an infinite cone (
Figure 5 shows the initialization of two landmarks with different cone uncertainty). It is a realistic representation for the monocular vision uncertainty. The major advantage is that the initialization of
is undelayed, guaranteed and efficient for landmarks over a wide range as it always includes all possible values without any a priori information.
3.4. ICSP Based Estimation
The observation of a landmark is the coordinates of the pixel on the image. Although the depth information is lacking, each of the landmark’s position can be estimated through multiple parallax observations. To achieve the estimation, we form the estimation process as the problem of solving ICSP. Considering the
ith observed landmark
, due to its position uncertainty, its projection on the current image plane is no longer a feature point but an area that can be computed via a pin-hole camera model [
27]:
The resulting projection
is a bounding area, which is assumed to contain the observed feature point related to the landmark. On this bounding area, we can search for the matching candidates. Probabilistic methods work in the same manner but with an uncertainty ellipsoid. We adopt Dan’s method [
28], which performs a two-stage matching process (considering both the Euclidean distance and dominant orientation information of feature descriptors) to achieve robust and accuracy matching results. A failure counter and a Zero Normalized Cross Correlation (ZNCC) [
29] score are assigned to each landmark to evaluate the stability of the landmark. When the matching candidate is found, a link between the prediction and observation data are built, which can be expressed as an interval domain intersection:
Based on these two top level constraints, we can establish an ICSP that contains a set of nine variables (e.g., , and ). By solving the ICSP, the robot pose and landmark’s position can be contracted. The ICSP is defined as follows:
A set of two top level constraints:
Such ICSP can be generated for each matched landmark, and can be independently solved by a local consistency ICP algorithm. After multiple observations from different parallaxes at different times, the ICSP building and solving process will be repeatedly performed. The position of each landmark thus can be estimated.
3.5. Dynamic ICSP Graph (DIG) Optimization
The notion of graph optimization has been widely used in a Simultaneous Localization and Mapping (SLAM) area. In this section, we will present our proposed graph optimization method in the context of interval analysis.
3.5.1. Graph Architecture
As we presented in our previous study [
30], the generated ICSPs can be solved independently by local consistency ICP algorithms (Forward/Backward, HC3, HC4, etc.). However, we note that, at each timestep
k, the generated ICSPs associated with each observed landmark are linked together by two links. The first one is the spatial link; at each timestep, the generated ICSPs are linked together by the variables
,
,
(the current robot pose state). Another one is the time link between the robot pose state at different timesteps. Based on these two links, an ICSP graph can be built. In order to be consistent with the traditional graph notion, which consists of vertices and edges, in our proposed ICSP graph, the vertex represents the robot pose or landmark position while the edge represents the constraints of the ICSP imposed on the connected vertices.
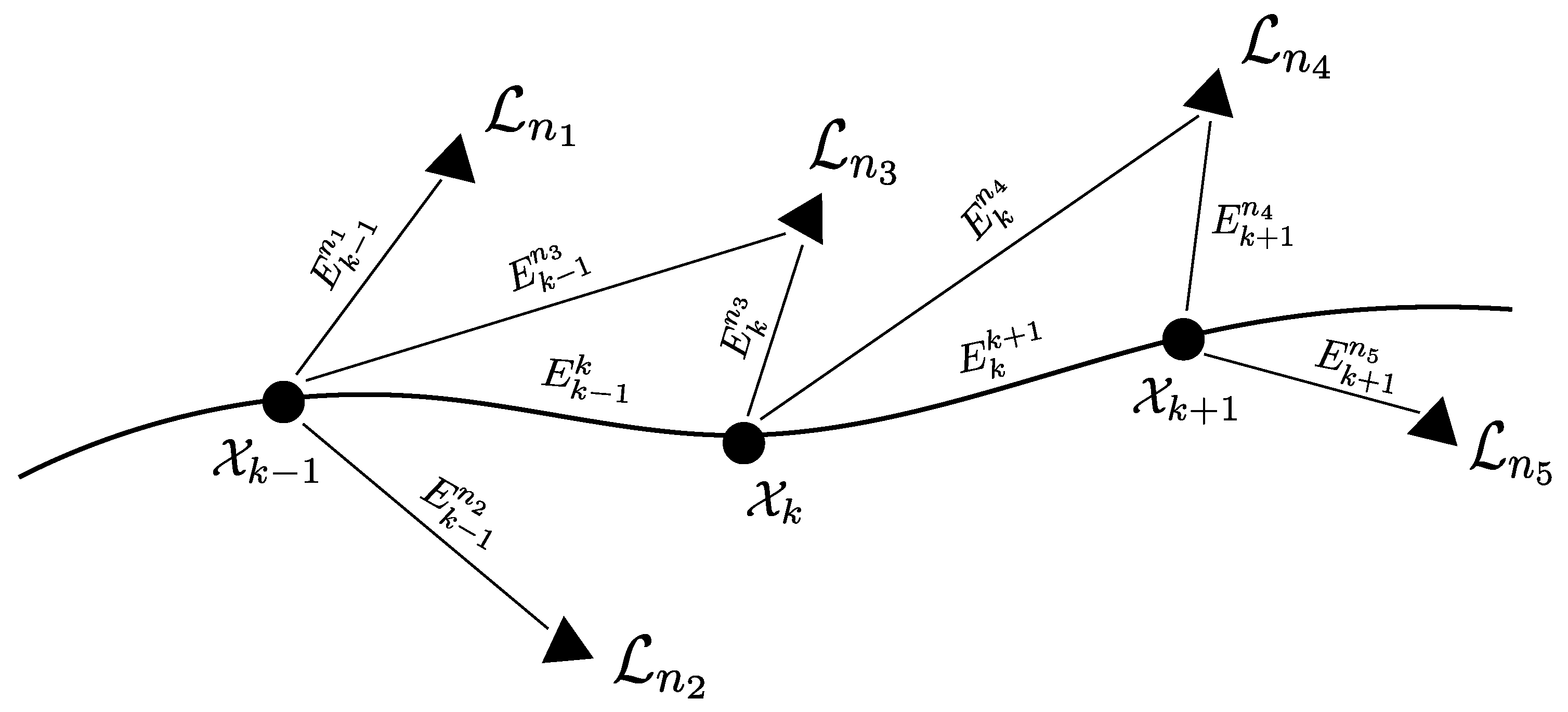
Figure 6 gives a simplified illustration of the ICSP graph. Denote the ICSP graph by
; each edge is given by
where
is the index of landmark and
k is the timestep.
denotes the generated ICSP corresponding to the observation of landmark
at timestep
k, while
denotes the ICSP generated in the motion estimation process. By constructing the ICSP graph, the domains of all the variable are connected together. Our idea is that an improvement of one vertex’s domain estimation due to new observations can be propagated to contract the other vertex’s domain via the graph architecture, and this could be a bi-directional process since ICP algorithms always work in a forward and backward propagation manner.
To the best of our knowledge, this is the first time that the notion of an ICSP graph is proposed to solve the robotic localization and mapping problem. The ICSP graph can be used for global and intensive domain contraction, as it brings together all of the measurement information. At each timestep, when new observation has been processed, the corresponding ICSPs are added to the graph and old ones will be removed.
3.5.2. Graph Operation: Augmentation and Depletion
The augmentation and deletion actions of the ICSP graph actually work on the variables and constraints. The union of an ICSP
and a constraint
K (which only contains variables that are already presented in
P) is defined by:
Similarly, the union of an ICSP
and another ICSP
is achieved by union the variable, domain and constraint sets:
The union operation of ICSPs can be directly used to make augmentation to the ICSP graph. The depletion of an ICSP from the ICSP graph is a bit different. Denote the ICSP network by
; to remove the ICSP
from
, one should delete the constraint set
and the variables
that only appear in
(
and
).
can be calculated by
Then, the new ICSP graph
is given by
3.5.3. Dynamic Graph Optimization
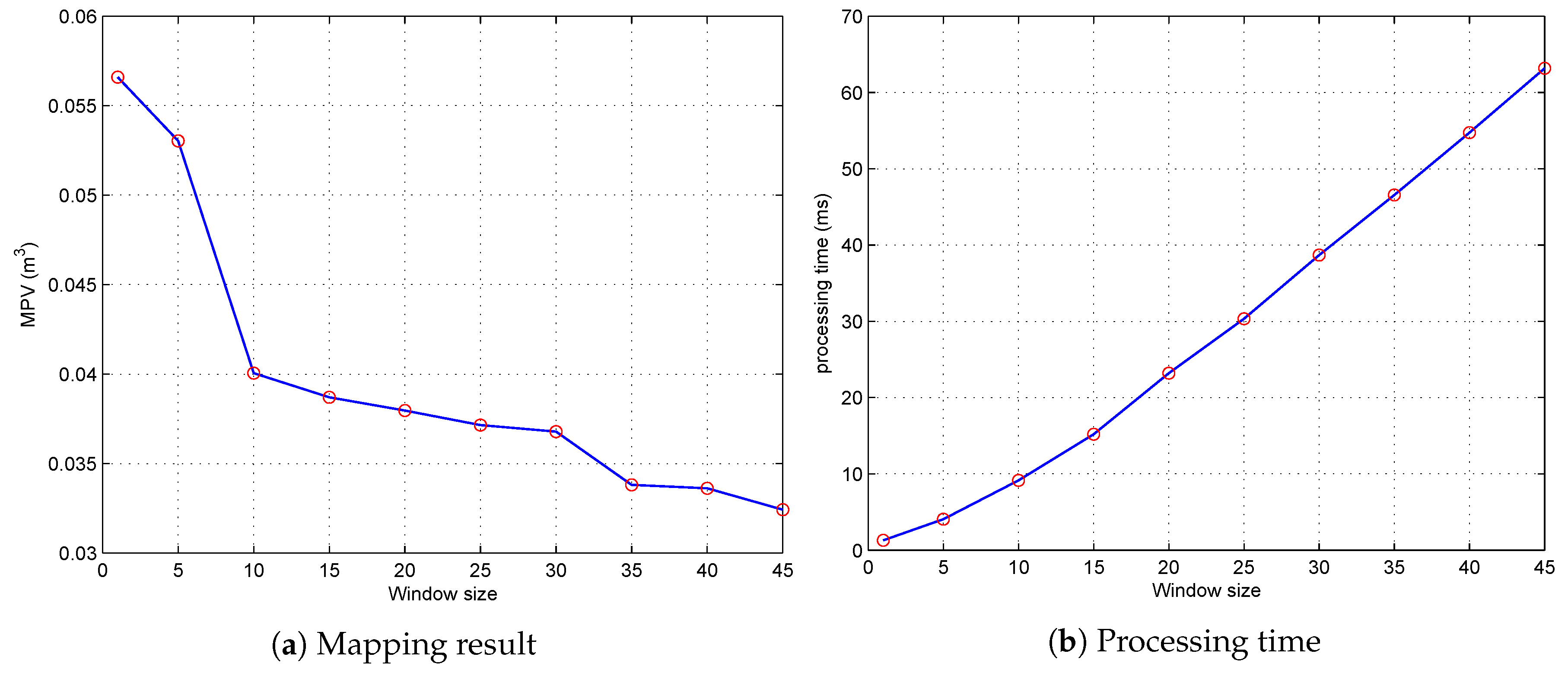
The entire ICSP graph can be regarded as a stack of ICSPs which can be solved by Interval Constraint Propagation Algorithms (in our case, we use the HC4 algorithm). However, solving the entire graph at each timestep is a complex and time consuming task. To maintain the real time adaptability, we propose to solve the ICSP graph in a sliding window
: at each timestep
k; only the sub-graph
is taken into computation. When
, it is equivalent to solve the multiple ICSP:
where
and
are respectively the index set of the observed landmarks at timestep
and
k. By solving the
, a better estimation of the landmark’s parameters could be achieved. This can be viewed as a graph optimization process, which we named the Dynamic ICSP Graph Optimization (DIGO).