A Sparse Analysis-Based Single Image Super-Resolution
Abstract
1. Introduction
1.1. Background
1.2. Prior Work
1.3. Contribution
- a novel SR technique is proposed for mapping between HR–LR patches based on HR–LR sparse analysis operators;
- a new sparse operator learning method is proposed in the patch selection stage that considers image texture complexity;
- the computational complexity of the algorithm is less than in previous approaches;
1.4. Organization
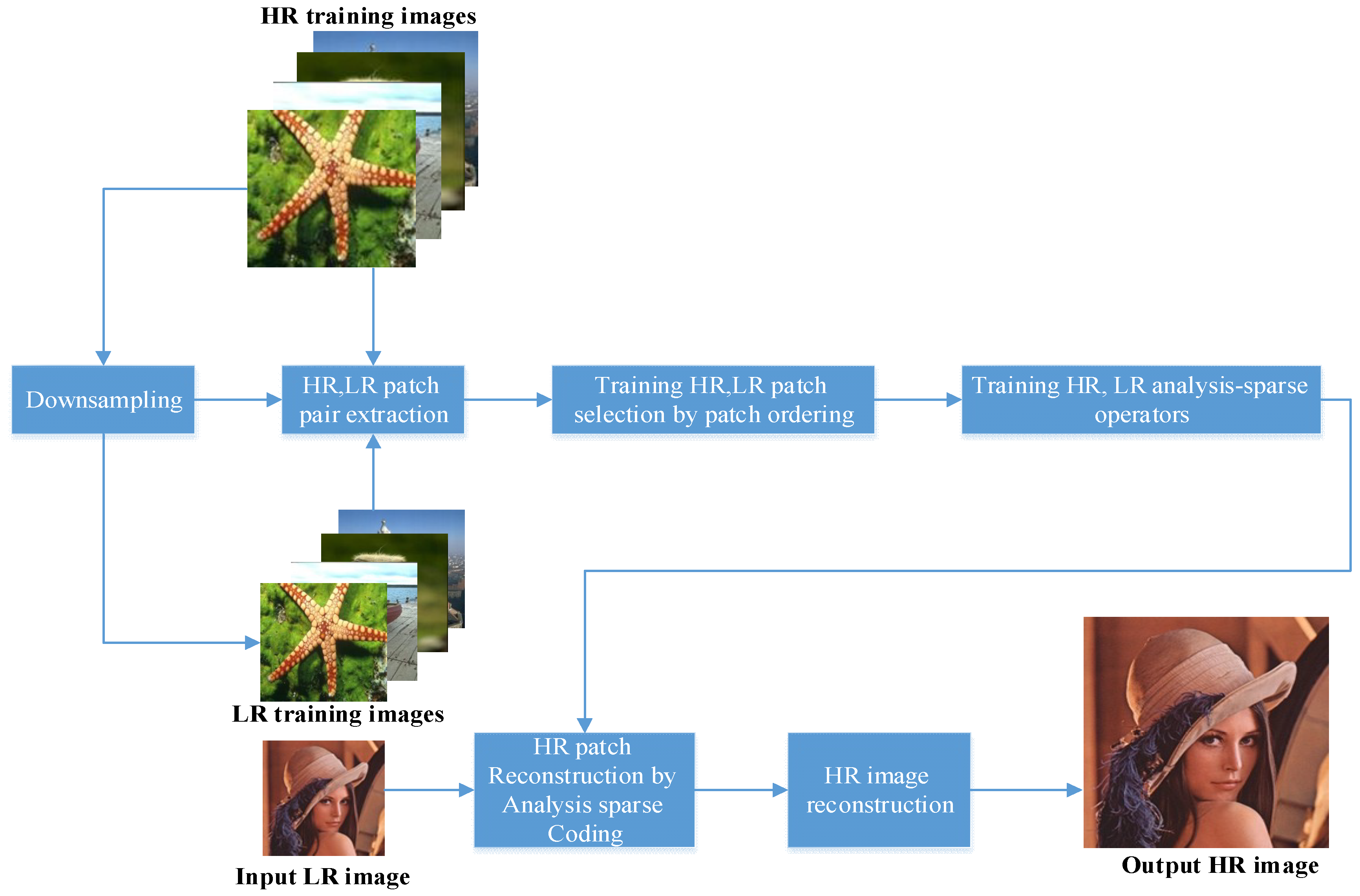
2. Proposed Sparse Analysis-Based SR Algorithm (SASR)
2.1. Sparse Analysis Model
2.2. Image SR Using Coupled Sparse Analysis Operators
2.2.1. Coupled Sparse Analysis Operator Learning
| Algorithm 1: Proposed patch ordering based on structural similarity |
| Task: Reorder the image patches Parameters: We are given image patches and distance function ω. Let be the set of indices of all overlapping patches extracted from the image. Initialization: Choose random index . Set , . Main iteration: For Find as the nearest neighbor to If and Set Otherwise: Find as the nearest neighbor to such that . Set . Output: Set Ω holds the proposed patch-based patch ordering. |
2.2.2. HR Image Reconstruction
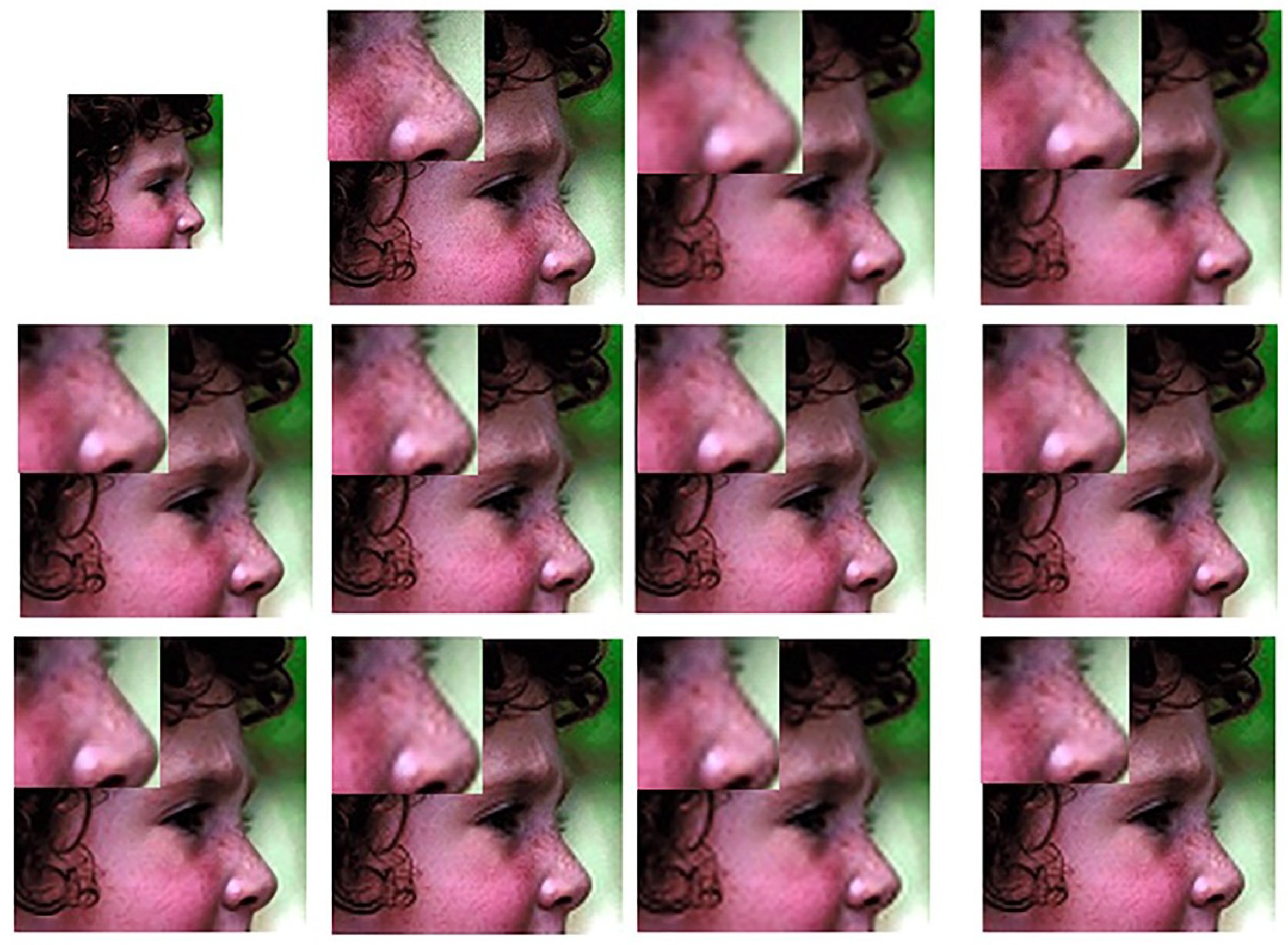
3. Experimental Results
3.1. Test Setup
3.2. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, S.; Han, M.; Xu, W.; Wu, Y.; Gong, Y. Soft edge smoothness prior for alpha channel super resolution. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Sun, J.; Xu, Z.; Shum, H. Image super-resolution using gradient profile prior. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Farsiu, S.; Robinson, M.D.; Elad, M.; Milanfar, P. Fast and robust multi-frame super resolution. IEEE Trans. Image Process. 2004, 13, 1327–1344. [Google Scholar] [CrossRef] [PubMed]
- Hardie, R.C.; Barnard, K.J.; Armstrong, E.E. Joint MAP registration and high-resolution image estimation using a sequence of under sampled images. IEEE Trans. Image Process. 1997, 6, 1621–1633. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Hu, R.; Han, Z.; Lu, T. Efficient single image super-resolution via graph-constrained least squares regression. Multimed. Tools Appl. 2014, 72, 2573–2596. [Google Scholar] [CrossRef]
- Suresh, K.V.; Rajagopalan, A. A discontinuity adaptive method for super-resolution of license plates. In Computer Vision, Graphics and Image Processing; Kalra, P.K., Peleg, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2006; Volume 4338, pp. 25–34. [Google Scholar]
- Chen, H.; Jiang, B.; Chen, B. Image super-resolution based on patches structure. In Proceedings of the 2011 IEEE International Congress Image and Signal Processing, Shanghai, China, 15–17 October 2011; pp. 1076–1080. [Google Scholar]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, K.; Tao, D.; Li, X. Image super-resolution with sparse neighbor embedding. IEEE Trans. Image Process. 2012, 21, 3194–3205. [Google Scholar] [PubMed]
- Yang, J.; Wang, Z.; Lin, Z.; Cohen, S.; Huang, T. Coupled dictionary training for image super-resolution. IEEE Trans. Image Process. 2012, 21, 3467–3478. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the 7th International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2010; Volume 6920, pp. 711–730. [Google Scholar]
- Zhang, J.; Zhao, C.; Xiong, R.; Ma, S. Image super-resolution via dual-dictionary learning and sparse representation. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 1688–1691. [Google Scholar]
- Yeganli, F.; Nazzal, M.; Unal, M.; Ozkaramanli, H. Image super-resolution via sparse representation over coupled dictionary learning based on patch sharpness. In Proceedings of the 2012 IEEE European Modelling Symposium, Pisa, Italy, 21–23 October 2014; pp. 203–208. [Google Scholar]
- Wang, S.; Zhang, L.; Liang, Y.; Pan, Q. Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2216–2223. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. A K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G.; LI, X. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2013, 22, 1620–1630. [Google Scholar] [CrossRef] [PubMed]
- Timofte, R.; De Smet, V.; Van Gool, L. Anchored neighborhood regression for fast example-based super-resolution. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1920–1927. [Google Scholar]
- Zhang, H.; Liu, W.; Liu, J.; Liu, C.; Shi, C. Sparse representation and adaptive mixed samples regression for single image super-resolution. Signal Process Image Commun. 2018, 67, 79–89. [Google Scholar] [CrossRef]
- Lu, W.; Sun, H.; Wang, R.; He, L.; Jou, M.; Syu, S.; Li, J. Single image super resolution based on sparse domain selection. Neurocomputing 2017, 269, 180–187. [Google Scholar] [CrossRef]
- Naderahmadian, Y.; Beheshti, S.; Tinati, M.A. Correlation based online dictionary learning algorithm. IEEE Trans. Signal Process. 2016, 64, 592–602. [Google Scholar] [CrossRef]
- Zhu, X.; Tao, J.; Li, B.; Chen, X.; Li, Q. A novel image super-resolution reconstruction method based on sparse representation using classified dictionaries. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 776–780. [Google Scholar]
- Yang, W.; Yuan, T.; Wang, W.; Zhao, F.; Liao, Q. Single-Image Super-Resolution by Subdictionary Coding and Kernel Regression. IEEE Trans. Syst. Man Cybern. 2017, 47, 2478–2488. [Google Scholar] [CrossRef]
- Juefei-Xu, F.; Savvides, M. Single face image super-resolution via solo dictionary learning. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 2239–2243. [Google Scholar]
- Elad, M.; Milanfar, P.; Rubinstein, R. Analysis versus synthesis in signal priors. Inverse Problems 2007, 23, 947–953. [Google Scholar] [CrossRef]
- Rubinstein, R.; Peleg, T.; Elad, M. Analysis K-SVD: A dictionary-learning algorithm for the analysis sparse model. IEEE Trans. Signal Process. 2013, 61, 661–677. [Google Scholar] [CrossRef]
- Dong, J.; Wang, W.; Dai, W. Analysis SimCO algorithms for sparse analysis model based dictionary learning. IEEE Trans. Signal Process. 2016, 64, 417–431. [Google Scholar] [CrossRef]
- Seibert, M.; Wörmann, J.; Gribonval, R. Learning co-sparse analysis operators with separable structures. IEEE Trans. Signal Process. 2016, 64, 120–130. [Google Scholar] [CrossRef]
- Ning, Q.; Chen, K.; Yi, L. Image super-resolution via analysis sparse prior. IEEE Signal Process. Letters 2013, 20, 399–402. [Google Scholar] [CrossRef]
- Hawe, S.; Kleinsteuber, M.; Diepold, K. Analysis operator learning and its application to image reconstruction. IEEE Trans. Image Process. 2013, 22, 2138–2150. [Google Scholar] [CrossRef] [PubMed]


| Image | Total Variation | Sampling Step | Number of Extracted Patches |
|---|---|---|---|
| Penguin | 940 | 13 | 5044 |
| Boats | 1248 | 10 | 6696 |
| Old woman | 1672 | 7 | 8974 |
| Ladybird | 1047 | 12 | 5621 |
| Girls | 4409 | 3 | 23,662 |
| Lena | Barbara | Zebra | Butterfly | Cat | Sails | Coastguard | Parrot | Pool | Face | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bicubic | 29.80 | 26.91 | 21.56 | 24.58 | 23.33 | 25.72 | 26.79 | 30.69 | 33.62 | 33.88 | 27.68 |
| SRSC [12] | 30.87 | 27.40 | 23.13 | 25.48 | 23.77 | 26.38 | 26.80 | 30.94 | 34.85 | 34.31 | 28.39 |
| SISU [13] | 31.04 | 27.86 | 23.16 | 25.60 | 23.89 | 26.44 | 27.30 | 31.20 | 35.28 | 34.85 | 28.66 |
| GR [19] | 30.56 | 27.54 | 23.14 | 25.61 | 23.97 | 26.33 | 27.15 | 31.00 | 34.61 | 34.72 | 28.46 |
| ANR [19] | 31.11 | 27.83 | 23.28 | 25.77 | 23.93 | 26.52 | 27.23 | 31.20 | 35.32 | 34.94 | 28.71 |
| NE + LS [19] | 31.08 | 27.73 | 23.14 | 25.65 | 23.86 | 26.40 | 27.24 | 30.14 | 35.38 | 34.80 | 28.54 |
| GOAL [29] | 31.22 | 27.79 | 23.18 | 25.83 | 24.10 | 26.55 | 27.27 | 31.30 | 35.47 | 34.89 | 28.76 |
| AMSRR [20] | 31.47 | 27.85 | 23.27 | 25.82 | 24.12 | 26.56 | 27.11 | 30.91 | 35.39 | 34.65 | 28.71 |
| SDS [21] | 31.60 | 27.80 | 23.21 | 25.72 | 23.98 | 26.51 | 27.09 | 30.88 | 34.78 | 34.66 | 28.62 |
| Proposed SASR | 31.68 | 27.87 | 23.24 | 25.92 | 24.19 | 26.47 | 27.13 | 31.16 | 34.96 | 34.69 | 28.83 |
| Lena | Barbara | Zebra | Butterfly | Cat | Sails | Coastguard | Parrot | Pool | Face | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bicubic | 8.24 | 11.49 | 19.98 | 15.04 | 17.37 | 13.19 | 11.66 | 7.44 | 5.31 | 5.15 | 11.48 |
| SRSC [12] | 7.28 | 10.86 | 17.77 | 13.55 | 16.51 | 12.23 | 11.66 | 7.23 | 4.61 | 4.90 | 10.66 |
| SISU [13] | 7.15 | 10.31 | 17.71 | 13.37 | 16.28 | 12.14 | 11.00 | 7.01 | 4.38 | 4.60 | 10.39 |
| GR [19] | 7.55 | 10.69 | 17.75 | 13.35 | 16.14 | 12.29 | 11.19 | 7.17 | 4.73 | 4.67 | 10.55 |
| ANR [19] | 7.09 | 10.34 | 17.46 | 13.11 | 16.21 | 12.02 | 11.08 | 7.87 | 4.36 | 4.56 | 10.41 |
| NE + LS [19] | 7.11 | 10.46 | 17.75 | 13.30 | 16.33 | 12.20 | 11.07 | 7.02 | 4.33 | 4.63 | 10.42 |
| GOAL [29] | 7.00 | 10.39 | 17.67 | 13.02 | 15.89 | 11.98 | 11.27 | 6.93 | 4.29 | 4.58 | 10.30 |
| AMSRR [20] | 6.95 | 10.59 | 17.51 | 13.00 | 15.86 | 12.20 | 11.07 | 7.27 | 4.32 | 4.70 | 10.34 |
| SDS [21] | 6.71 | 10.52 | 17.58 | 13.11 | 16.20 | 12.22 | 11.16 | 7.30 | 4.50 | 4.71 | 10.40 |
| Proposed SASR | 6.64 | 9.27 | 17.54 | 12.88 | 15.72 | 12.09 | 11.21 | 7.04 | 4.55 | 4.69 | 10.16 |
| Lena | Barbara | Zebra | Butterfly | Cat | Sails | Coastguard | Parrot | Pool | Face | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bicubic | 0.8422 | 0.7737 | 0.6914 | 0.8412 | 0.7023 | 0.6603 | 0.6064 | 0.8612 | 0.9540 | 0.8477 | 0.7780 |
| SRSC [12] | 0.8581 | 0.7976 | 0.7426 | 0.8716 | 0.7491 | 0.7060 | 0.6194 | 0.8607 | 0.9597 | 0.8490 | 0.8014 |
| SISU [13] | 0.8699 | 0.8144 | 0.7501 | 0.8749 | 0.7499 | 0.7101 | 0.6422 | 0.8751 | 0.9655 | 0.8678 | 0.8120 |
| GR [19] | 0.8592 | 0.7964 | 0.7549 | 0.8761 | 0.7629 | 0.7109 | 0.6428 | 0.8726 | 0.9585 | 0.8689 | 0.8103 |
| ANR [19] | 0.8720 | 0.8124 | 0.7557 | 0.8793 | 0.7564 | 0.7160 | 0.6424 | 0.8790 | 0.9652 | 0.8706 | 0.8149 |
| NE + LS [19] | 0.8701 | 0.8087 | 0.7478 | 0.8748 | 0.7485 | 0.7160 | 0.6397 | 0.8761 | 0.9656 | 0.8665 | 0.8114 |
| GOAL [29] | 0.8745 | 0.8098 | 0.7510 | 0.8807 | 0.7627 | 0.7141 | 0.6342 | 0.8782 | 0.9651 | 0.8695 | 0.8139 |
| AMSRR [20] | 0.8701 | 0.8291 | 0.7546 | 0.8808 | 0.7659 | 0.7165 | 0.6427 | 0.8725 | 0.9656 | 0.8611 | 0.8159 |
| SDS [21] | 0.8698 | 0.8292 | 0.7541 | 0.8794 | 0.7564 | 0.7156 | 0.6423 | 0.8720 | 0.9556 | 0.8668 | 0.8141 |
| Proposed SASR | 0.8807 | 0.8296 | 0.7470 | 0.8743 | 0.7669 | 0.7093 | 0.6588 | 0.8731 | 0.9598 | 0.8660 | 0.8166 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anari, V.; Razzazi, F.; Amirfattahi, R. A Sparse Analysis-Based Single Image Super-Resolution. Computers 2019, 8, 41. https://doi.org/10.3390/computers8020041
Anari V, Razzazi F, Amirfattahi R. A Sparse Analysis-Based Single Image Super-Resolution. Computers. 2019; 8(2):41. https://doi.org/10.3390/computers8020041
Chicago/Turabian StyleAnari, Vahid, Farbod Razzazi, and Rasoul Amirfattahi. 2019. "A Sparse Analysis-Based Single Image Super-Resolution" Computers 8, no. 2: 41. https://doi.org/10.3390/computers8020041
APA StyleAnari, V., Razzazi, F., & Amirfattahi, R. (2019). A Sparse Analysis-Based Single Image Super-Resolution. Computers, 8(2), 41. https://doi.org/10.3390/computers8020041




