An Efficient Multicore Algorithm for Minimal Length Addition Chains
Abstract
1. Introduction
- , where is the length in bits for the given number m [5].
- Given m as a binary representation, v(m) is the number of 1s in m.
- The step in the chain is called
- The number of small steps in the chain up to sk is denoted by S(s0, s1, …, sk) and the number of big steps is .
- The length of AC, l, for m can be written in terms of the number of small steps and as follows.
- If l is minimal then the chain is called the minimal length addition chain (MLAC) or the shortest addition chain and the length of the chain is denoted by Otherwise, the chain is called a short addition chain (SAC).
2. The Best Known Sequential AC Algorithm
- Step 1:
- Compute the lower bound of l(m), say Lb.
- Step 2:
- Loop the following:
- 2.1:
- Compute the bounding sequences, Bs.
- 2.2:
- Initialize the two stacks T1 and T2 by pushing the elements s0 = 1 and s1 = 2 on T1 and the levels 0 and 1 on T2. Also, initialize the current level with 1, k = 1.
- 2.3:
- Repeat
- Push on T1 all possible elements (star and non-star) sk+1, after applying pruning conditions for sk.
- Push on T2 the levels, k + 1, of all elements pushed in the previous step.
- Pop the stack T2 and assign the top to k.
- Pop the stack T1 and assign it to the current element sk.
- If the current element sk equals the goal m then return the minimal length chain s0 s1 …sk.Until k < 2.
- 2.4:
- Increase the lower bound by 1, Lb = Lb + 1.
- For vertical bounds, if for some apply for Vbs, while if for any apply for Vbs.
- For slant bounds, if then apply for Sbs, while if then apply for Sbs.
3. Methodology
3.1. Main Stages
- Step 1:
- Compute the lower bound of l(m), say Lb.
- Step 2:
- Compute the vertical and slant bounding sequences.
- Step 3:
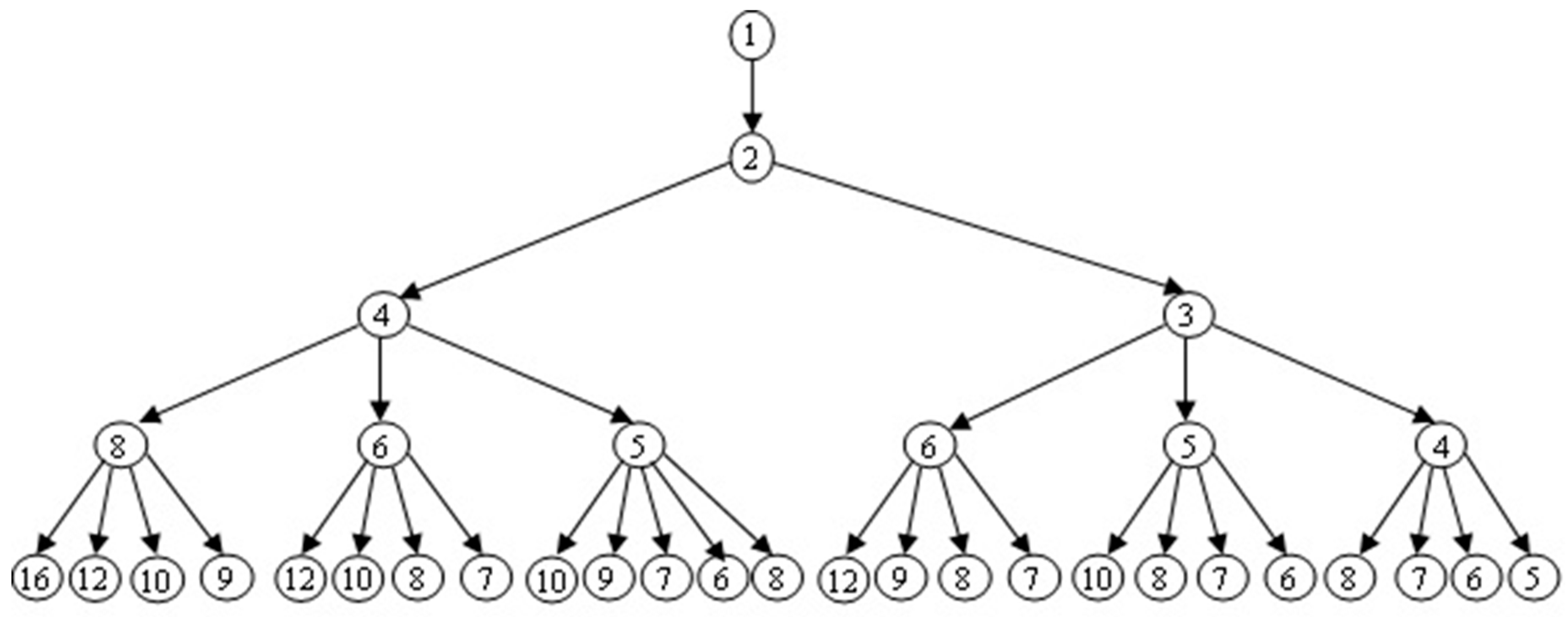
- Generate the breadth tree until level α and assign it to a queue Q.
- Step 4:
- Each core will assign one element e from the queue Q, and then we use the best known B&B algorithm to find the goal m.
- Step 5:
- If one core finds the goal then terminate the process of searching. Otherwise, repeat Step 4 on a new element from the queue if not empty.
- Step 6:
- If the queue is empty then increase the lower bound by one and repeat Steps 2–5.
3.2. Implementation Details
- Use critical directive to update the counter for while-loop and make a private copy of it to the thread.
- Threads execute the B&B algorithm in parallel and store the result in a private variable Exist.
- If Exist equals true then we use the critical section to update the value of global variable ACExist with true.
- The while-loop is terminated if ACExist equal to true or the counter of while-loop equals the number of element in the queue -1.
4. Results and Discussion
- It does not follow necessarily that if two integers m1 and m2 have the same number of bits and v(m1) < v(m2) then the running time of the proposed algorithm for m1 is less than for m2. For example, m1 = 131,560 = (100000000111101000)2 and m2 = 238,368 = (111010001100100000)2. The running times of the proposed algorithm on m1 and m2 are 2.067 and 0.297 s, respectively, using four threads.
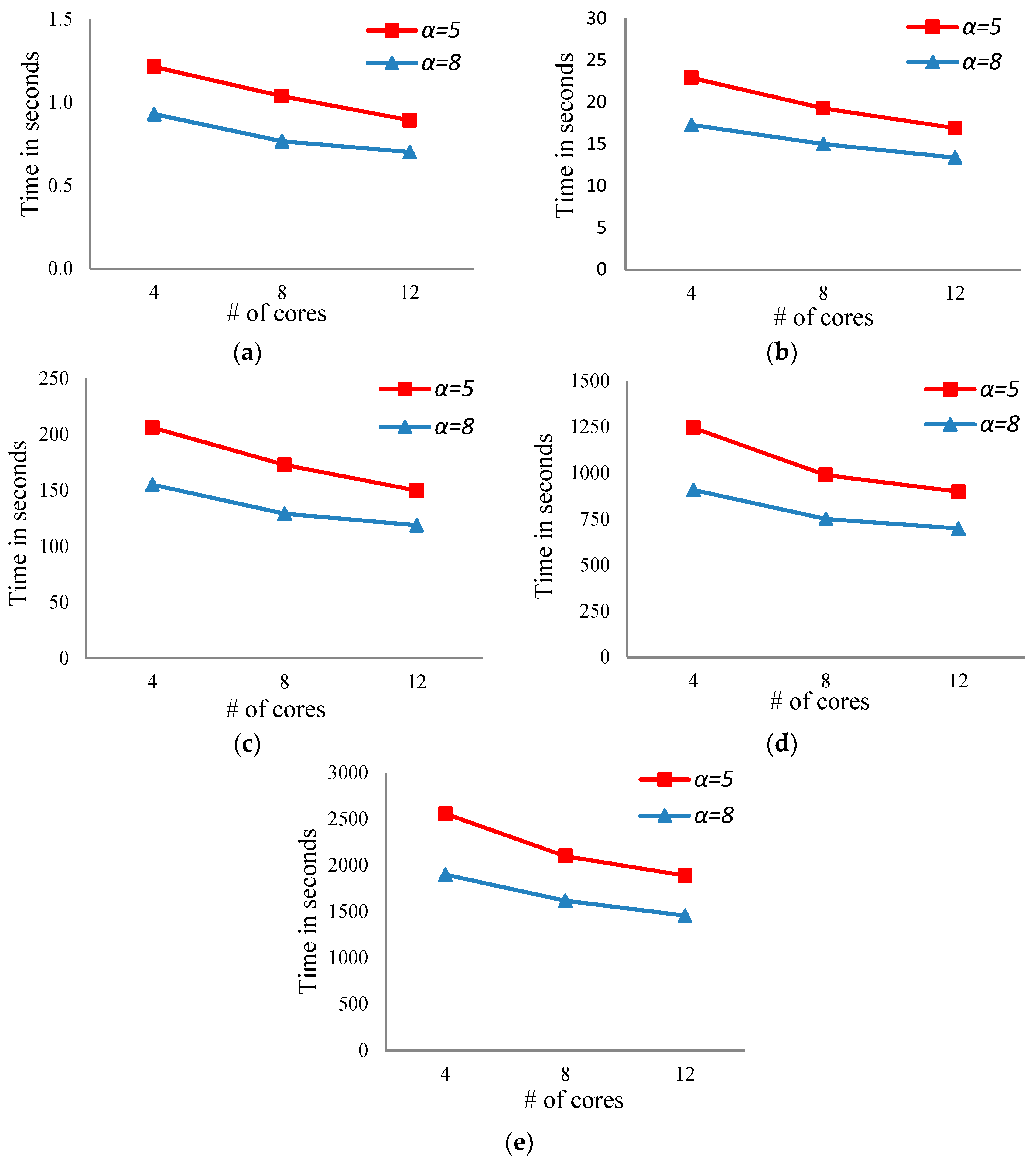
- For a fixed number of bits, the running time of the proposed algorithm decreases with increasing the number of cores (see Figure 3a–e).
- For a fixed number of bits, increasing the number of levels in the case of the breadth search will reduce the running time (see Figure 3a–e in both cases, α = 5 and 8).
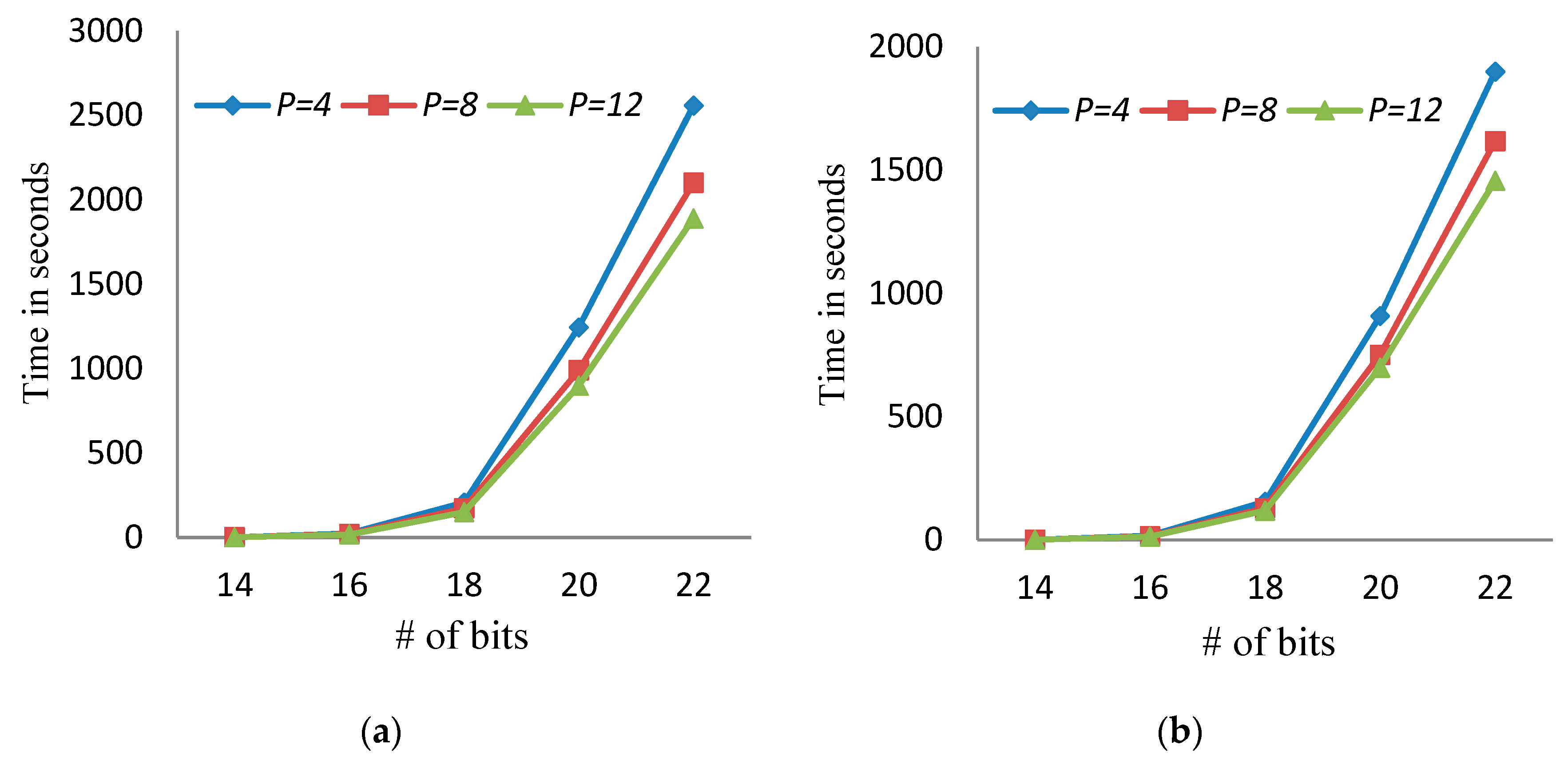
- The running time of the proposed algorithm increases with increasing the number of bits (see Figure 4).
- Increasing the number of threads is effective when the number of bits is large. For example, in the case of 20 bits, the running time of the proposed algorithm using 4, 8, and 12 threads is 1245.4, 989.2, and 899.0 s, respectively, when α = 5.
- The time spent in the BF stage in the proposed algorithm is very small compared to the total running time. In the case of α = 5, the average time for breadth stage tends to zero, while in the case of α = 8, the average time for the breadth stage equals 0.03 s.
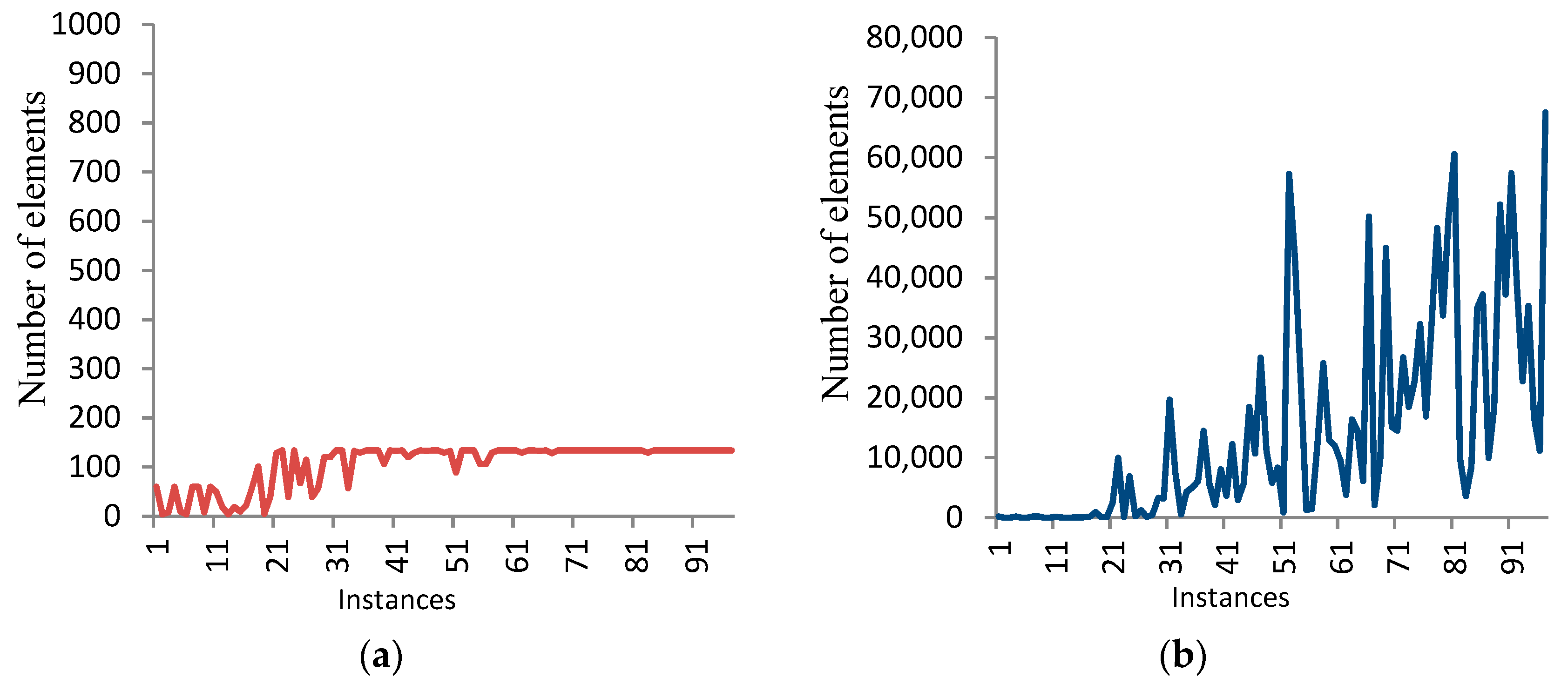
- The storage required by the BF stage increases when increasing the level α. Figure 5 shows the number of elements generated by the DF stage in the case of α = 5 and 8 for 100 numbers, each of 14 bits.
- The storage required by the DF stage increases with the increase of the number of bits in the average cases. Table 1 shows this behavior in the average case. On the other side, the storage required by the DF stage decreases with the increase of the level α in the BF stage.
- The expected amount of memory required by the proposed algorithm is (|Qα|(α + 1)) + Size(T) p, where Qα is the queue that represents the list of all elements at level α, and T is the stack that represents the list of all elements in the DF search from level α+1 to Lb. The term (α + 1) represents the number of elements of the chain from level 0 to level α, while the term Size (T)p represents the size of stacks for all threads.
- The term (|Qα| (α + 1)) is very large compared to the term Size (T)p, so the storage required by the proposed algorithm increases with the increase of the level α in the average case.
- In some cases, we found that the running time of the sequential algorithm is less than or equal to the running time of the proposed algorithm when the number of 1s is very small or the goal exists in the left of the search space and the length of a minimal length chain is equal to the initial lower bound. For example, let m = 148,544 = (100100010001000000)2. The running time of the sequential and proposed algorithms on m is 0.015 s. In addition, the running time for the sequential and proposed algorithms on m = 164560 = (101000001011010000)2 is 0.015 and 0.031 s, respectively, using four threads in the case of parallelism.
- In general, the behavior of traversing the search tree is unsystematic in the sense that the running times for different numbers of the same size have a significant difference in some instances. For example, the running times for three different instances, each of 18 bits, are 23.75, 175.94, and 834.2 s. Also, the same behavior occurs for the memory consumed (see Figure 5).
- Table 2 shows the running time for the best known sequential algorithm to generate the MLAC using the same datasets. It is clear, from Table 2 and Figure 3, that the running time of the parallel proposed algorithm is faster than that of the sequential algorithm. For example, the running time for the best known sequential algorithm when m = 16 is 25.2 s, while the parallel proposed algorithm’s running time equals 22.9, 19.3, and 16.9 using p = 4, 8, and 12, respectively, in the case of α = 5. Additionally, for the same dataset, the running time for the proposed parallel algorithm decreases to 17.3, 15, and 13.3 using p = 4, 8, and 12, respectively, in the case of α = 8.
- Table 3 represents the speedup of the proposed algorithm, where the speedup of a parallel algorithm equals the ratio between the running time of the fastest sequential algorithm and the running time of the parallel algorithm.
- From Table 3, we observe that the speedup of the proposed algorithm increases in the following cases.Case 1: the number of threads and levels are fixed, while the number of bits is changed. For example, the speedup of the proposed algorithm for the number of bits 14 and 16 is 1.05 and 1.10, respectively, using the number of threads and levels equal to 4 and 5, respectively.Case 2: the number of bits and levels are fixed, while the number of threads is changed. For example, the speedup of the proposed algorithm using the number of threads 4, 8, and 12 is 1.37, 1.67, and 1.82, respectively, using the number of bits and levels equal to 14 and 8, respectively.Case 3: the number of threads and bits are fixed, while the number of levels is changed. For example, the speedup of the proposed algorithm using the number of levels 4 and 8 is 1.57 and 2.07, respectively, using the number of bits and threads equal to 20 and 8, respectively.
- There are many factors that affect the values of the scalability for the proposed parallel algorithm. These factors are:(i) In some instances, for a fixed number of bits, the running time of the sequential algorithm is less than that of the proposed algorithm due to the existence of the goal at the beginning of the search tree (the left of the tree).(ii) When the first thread finds the MLAC, it exits the loop after activating the cancellation. The remaining threads will not exit the loop immediately. They exit the loop after finishing their tasks. This case will increase the running time of the proposed algorithm.Clearly, doubling or tripling the numbers of processors will not necessarily cut the run time by 2 or 3, respectively, and so on.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Knuth, D.E. The Art of Computer Programming: Seminumerical Algorithms; Addison-Wesley: Boston, MA, USA, 1973; Volume 2. [Google Scholar]
- Gordon, D.M. A Survey of fast exponentiation methods. J. Algorithms 1998, 27, 129–146. [Google Scholar] [CrossRef]
- Rivest, R.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Yen, S.M. Cryptanalysis of secure addition chain for SASC applications. Electron. Lett. 1993, 31, 175–176. [Google Scholar] [CrossRef]
- Bahig, H. Improved generation of minimal addition chains. Computing 2006, 78, 161–172. [Google Scholar] [CrossRef]
- Bahig, H. Star reduction among minimal length addition chains. Computing 2011, 91, 335–352. [Google Scholar] [CrossRef]
- Bahig, H. A fast optimal parallel algorithm for a short addition chain. J. Supercomput. 2018, 74, 324–333. [Google Scholar] [CrossRef]
- Bergeron, F.; Berstel, J.; Brlek, S. Efficient computation of addition chains. J. Théorie Nr. Bordx. 1994, 6, 21–38. [Google Scholar] [CrossRef]
- Bergeron, F.; Berstel, J.; Brlek, S.; Duboc, C. Addition chains using continued fractions. J. Algorithms 1989, 10, 403–412. [Google Scholar] [CrossRef]
- Clift, N. Calculating optimal addition chains. Computing 2011, 91, 265–284. [Google Scholar] [CrossRef]
- Cruz-Cortés, N.; Rodríguez-Henríquez, F.; Juárez-Morales, R.; Coello Coello, C.A. Finding Optimal Addition Chains Using a Genetic Algorithm Approach. In Computational Intelligence and Security. CIS 2005. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3801, pp. 208–215. [Google Scholar]
- Flammenkamp, A. Integers with a small number of minimal addition chains. Discret. Math. 1999, 205, 221–227. [Google Scholar] [CrossRef]
- Scholz, A. Jahresbericht: Deutsche Mathematiker Vereinigung. Aufgabe 1937, 47, 41–42. [Google Scholar]
- Thurber, E. Addition chains—An erratic sequence. Discret. Math. 1993, 122, 287–305. [Google Scholar] [CrossRef]
- Thurber, E. Efficient generation of minimal length addition chains. SIAM J. Comput. 1999, 28, 1247–1263. [Google Scholar] [CrossRef]
- Bleichenbacher, D.; Flammenkamp, A. An Efficient Algorithm for Computing Shortest Addition Chains. unpublished. Available online: http://www.homes.uni-bielefeld.de/achim/addition_chain.html (accessed on 21 May 2018).
- Chin, Y.; Tsai, Y. Algorithms for finding the shortest addition chain. In Proceedings of the National Computer Symposium, Kaoshiung, Taiwan, 20–22 December 1985; pp. 1398–1414. [Google Scholar]
- Fathy, K.; Bahig, H.; Bahig, H.; Ragb, A. Binary addition chain on EREW PRAM. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing (ICA3PP 2011), Melbourne, Australi, 24–26 October 2011; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7017, pp. 321–330. [Google Scholar]
- Schonhage, A.; Strassen, V. Schnelle multiplikation GroBer Zahlen. Computing 1971, 7, 281–292. [Google Scholar] [CrossRef]

| α | Number of Bits | ||||
|---|---|---|---|---|---|
| 14 | 16 | 18 | 20 | 22 | |
| 5 | 45 | 57 | 66 | 78 | 89 |
| 8 | 37 | 48 | 59 | 70 | 81 |
| Number of bits | 14 | 16 | 18 | 20 | 22 |
| Time in seconds | 1.3 | 25.2 | 243.4 | 1556.8 | 3581.6 |
| Number of Bits | α = 5 | α = 8 | ||||
|---|---|---|---|---|---|---|
| p = 4 | p = 8 | p = 12 | p = 4 | p = 8 | p = 12 | |
| 14 | 1.05 | 1.23 | 1.43 | 1.37 | 1.67 | 1.82 |
| 16 | 1.10 | 1.31 | 1.49 | 1.46 | 1.68 | 1.89 |
| 18 | 1.18 | 1.41 | 1.62 | 1.57 | 1.88 | 2.05 |
| 20 | 1.25 | 1.57 | 1.73 | 1.71 | 2.07 | 2.23 |
| 22 | 1.40 | 1.71 | 1.90 | 1.89 | 2.21 | 2.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahig, H.M.; Kotb, Y. An Efficient Multicore Algorithm for Minimal Length Addition Chains. Computers 2019, 8, 23. https://doi.org/10.3390/computers8010023
Bahig HM, Kotb Y. An Efficient Multicore Algorithm for Minimal Length Addition Chains. Computers. 2019; 8(1):23. https://doi.org/10.3390/computers8010023
Chicago/Turabian StyleBahig, Hazem M., and Yasser Kotb. 2019. "An Efficient Multicore Algorithm for Minimal Length Addition Chains" Computers 8, no. 1: 23. https://doi.org/10.3390/computers8010023
APA StyleBahig, H. M., & Kotb, Y. (2019). An Efficient Multicore Algorithm for Minimal Length Addition Chains. Computers, 8(1), 23. https://doi.org/10.3390/computers8010023





