Abstract
Numerous computational algorithms are used to obtain a high performance in solving mathematics, engineering and statistical complexities. Recently, an attractive bio-inspired method—namely the Artificial Bee Colony (ABC)—has shown outstanding performance with some typical computational algorithms in different complex problems. The modification, hybridization and improvement strategies made ABC more attractive to science and engineering researchers. The two well-known honeybees-based upgraded algorithms, Gbest Guided Artificial Bee Colony (GGABC) and Global Artificial Bee Colony Search (GABCS), use the foraging behavior of the global best and guided best honeybees for solving complex optimization tasks. Here, the hybrid of the above GGABC and GABC methods is called the 3G-ABC algorithm for strong discovery and exploitation processes. The proposed and typical methods were implemented on the basis of maximum fitness values instead of maximum cycle numbers, which has provided an extra strength to the proposed and existing methods. The experimental results were tested with sets of fifteen numerical benchmark functions. The obtained results from the proposed approach are compared with the several existing approaches such as ABC, GABC and GGABC, result and found to be very profitable. Finally, obtained results are verified with some statistical testing.
1. Introduction
In recent years, bio-inspired attractive algorithms have become a research interest for a different domain of researchers for solving complex problems in science, engineering, management and financial real applications. Scientific researchers in particular are interested in developing new bio-inspired techniques based on the nature collections such as bee colony, multiple gbest and some other hybrid namely monarch butterfly optimization, phase transition-based optimization, hybrid PSO, whale optimization algorithm and metaheuristic algorithms [1,2,3,4,5,6]. To increase the performance of the standard Artificial Bee Colony (ABC) algorithm in exploration and exploitation procedures, researchers improved the standard ABC by using different strategies like hybridization with local and global search methods, modification, gbest, global best, guided by best so far, globally guided and other recent powerful searching and selecting meta heuristic strategies [7,8,9,10,11].
The success story of the ABC algorithm started with classification, optimization, scheduling, clustering, engineering, science, machine learning, medicine, transportation, social science, various management problems, ANFIS training, risk assessment, Vehicle route selection, traveling salesman problems, decision making, applications in management and engineering, economic order quantity and so on., [12,13,14,15].
Based on previous literature, various computational intelligence methods have been used to solve complex numerical function optimization problems, which include particle Swarm Optimization (PSO), Cuckoo Search (CS), African Buffalo Search (ABS), Improved and Hybrid particle Swarm Optimization, Improved and Hybrid Cuckoo Search methods, Chicken Swarm Optimization (CSO) and their hybrid and improved versions, Butterfly Optimization and their hybrid and updated methods, Bacterial Foraging Inspired Hybrid Artificial Bee Colony algorithm, Artificial Bee Colony (ABC) and their improved and hybrid versions, along with other local, global search methods and so on [16,17,18,19,20,21,22]. These algorithms are called meta-heuristics algorithms, which have unique properties such as the ability to rapidly converge to the global optimum solution of the related objective function, acceptable simulation time towards reaching the global minimizer, fewer control parameters and easy adoption of various complex problems. Although these algorithms are famous and effective for a large number of complex problems; however, sometimes it is trapped in local minima, slow convergence speed, un-optimal results, low success rate, wrong selection of stopping criteria and a long duration of execution for some problems. These problems occur due to reasons such as non consistency in exploration and exploitation, repletion of searching strategies, no proper guidance on searching methods, difficulty finding suitable parameter values and sometimes a low success rate due to the random way of finding the optimal solution [6,18,23,24,25,26,27].
In this paper, we concentrate on the improved versions of typical ABC algorithms, developed by References [24,28,29] based on guided, gbest and global foraging behaviors of honey bee swarms. The previous study shows that the typical ABC, GABC and GGABCS are competitive with other population-based algorithms with an advantage of employing fewer control parameters and enough exploration and exploitation processes for solving numerical function optimization problems [30]. Furthermore, these algorithms have shown their strength towards optimal solutions in various science and engineering complex problems.
However, comparable to other bio-inspired algorithms, the typical and the improved versions of ABC based algorithms also face some stimulating problems, which have motivated various field researchers. These include the tired convergence speed when compared to Particle Swarm Optimization (PSO) and differential evolution (DE) during the simulation of solving unimodal problems [31,32,33,34], due to both the poor exploration and exploitation processes through the repeated way of searching and selection. Also, the typical ABC lacks the use of secondary information and a higher number of objective function evaluations as well.
For finding optima for numerical function optimization problems, with a high efficiency rate, a stable amount of exploration and exploration processes, the two global algorithms—Gbest Guided Artificial Bee Colony (GGABC) and Global Artificial Bee Colony (GABC)—compose the hybrid 3G-ABC algorithm. In this research, the performance of the proposed 3G-ABC algorithm and four standard algorithms ABC, GABC and GGABC were compared in fifteen benchmark numerical functions [22,24]. The proposed hybrid method obtained the global optima of the benchmarked numerical function optimization problems through the fast exploitation and effective exploration processes with the cooperative gbest guided and global bees.
The rest of the manuscript is organized as follows: In Section 2, we present the concept of the typical ABC and the improved ABC algorithms. In Section 3, we present the concepts of the proposed 3G-ABC algorithm to effectively solve the optimization problem through multiple guided strategies. In Section 4, we illustrate the presented approach, test it on the benchmarked function and discuss the results. Finally, a conclusion and future work are stated in Section 5.
2. Artificial Bee Colony Algorithm
Initially, ABC was proposed for optimization, classification and Neural Networks (NNs) problem solution based on the intelligent foraging behavior of honeybee swarms [22,35,36]. The ABC algorithm provides solutions in an organized form by dividing the bee objects into different tasks such as employed bees, onlooker bees and scout bees. These three bees/tasks determine the objects of problems by sharing information with other bees. The common duties of these artificial bees are as follows: the first half of the colony consists of the employed bees and the second includes the unemployed. The different numerical and statistical performance measures demonstrate that the ABC algorithm is competitive with other types of meta-heuristic and typical algorithms. The technical duties of the employed and unemployed artificial bees are given in detail.
Each employed bee searches around the food source, gathering the required information about its quality and position of the onlookers. Then, they carry the information about the position of food source back to the hive and share this information with artificial onlooker bees by dancing in the nearby hive. Onlooker bees: the onlookers tend to choose the best food sources to further exploit, based on information communicated by the employed bees through their dances. Therefore, good food sources attract more onlooker bees compared to the bad ones. The artificial onlooker bees choose the best food source with better quality based on information communicated from those found by employing bees using different ways, such as a probability selection mechanism, greedy selection, fitness function as a proportional of the quality of the food source [36]. The last bee processes are managing by the scout bee group, which is responsible for the exploration process, randomly choosing a new good food source to replace the old one. The number of food sources (based on position and quality) which represent a possible solution to the optimization problem and fitness of the associated solution is equal to the number of employed bees, which is also equal to the number of onlooker bees. The employed onlooker bees used for the exploitation process for a given problem towards the best solution space given in Equation (1), while scout bees use Equation (2) for the exploration process
where is a new solution in the neighborhood of for the employed bees, is a solution in the neighborhood of , is a random number in the range [−1, 1].
Although typical ABC is famous due to its robustness and high efficiency for clustering, classification and numerical function optimization problems; however, due to the same and the random searching approach of exploitation it cannot guarantee finding the best food position, also sometimes it is trapped in local minima. The researchers improved the typical ABC algorithm with different strategies such as best so far, discrete, hybrid, gbest guided and quick within employed, onlookers and scout bees.
2.1. Gbest Guided Artificial Bee Colony Algorithm
Bio-inspired methods are famous due to their unique way of searching, discovering and utilization which go beyond the cooperation of individual and society nature agents as well. A stable and sufficient amount of exploration and exploitation mean these methods are robust for finding a solution to a given problem [23,37,38,39,40,41,42,43,44,45,46]. Exploration includes things captured by terms such as search, variation, risk taking, experimentation, play, flexibility, discovery, innovation, while exploitation includes such things as refinement, choice, production, efficiency, selection, implementation, execution. To improve the exploration process, a typical ABC algorithm is upgraded with existing techniques. One of the famous methods used to increase the performance of typical ABC method is called the Gbest Guided Artificial Bee Colony [24]. The proposed method is used to obtain the new candidate solutions of both agents, guided employed and onlookers are generated by moving the old solution towards (or away from) another solution selected randomly from the population. Here the guided employed bee section of the standard ABC has been modified for improving the exploitation procedure as:
The GGABC method has proven its efficiency through the guided employed and onlooker bees phase. However, the modifying Equation (3) increases the exploitation of a typical ABC algorithm, while the exploration is still not enough and the balance through the random way as given in Equation (2) [37] Therefore, the exploration process can be improved through the hybridization or enhancement of ways for complex and large dataset problems.
2.2. Global Artificial Bee Colony Search Algorithm
The Global Artificial Bee Colony (GABC) Search algorithm is the updated version of typical ABC, which used to collect the properties of exploration and exploitation with intelligent behavior artificial honeybees agents [28]. The GABC algorithm is used to update the solution step and convert it to the best solution based on neighborhood values through employed, onlooker and scout bees sections. Usually, in bee swarm, the experienced foragers can use previous knowledge of position and the nectar quantity of a food source to regulate their group directions in the search space. Therefore, GABC agents employed scout and onlookers have improved their optimality by their best food source. The GABC algorithm used the following methods to enhance the exploration and exploitation process of the typical ABC algorithm. The GABC used Equations (3) and (4) to enhance the employed onlooker bees capabilities and quality as:
where shows best food source position, and are two constant values, is the j-th element of the global best solution found so far, is the j-th element of the best solution in the current iteration, is a uniformly distributed real random number in the range [−1, 1]. The scout bee section of the typical ABC is updated as:
if , then
else
Then, comparing the fitness value of random generated solution and the mutation solution the better one is chosen as a new food source, where b is a scaling parameter. The GABC method successfully applied to some complex optimization problems such as classification, clustering and numerical function optimizations function optimizations as well [28,29]. However, it cannot prove the effectiveness capabilities to get the exact desired optimal values for all given complex problems due to the same and random searching strategies used by employed and onlooker’s bees sections. In other words, the GABC algorithm used the single strategy in different bee phases which cannot achieve the balance and optimal exploitation process.
3. The Proposed 3G-ABC Algorithm
Based on recently published research, the GABC algorithm has a global ability to find a globally optimistic result through a strong exploration process in various applications with different variables and dynamics control parameters [28]. On the other side, the GGABC algorithm has ability to discover the exit solution space through the efficient onlooker and employed bees phases in a balance way through the parameter c and gbest process [24]. Combining the step of GABC with GGABC, a new hybrid algorithm is proposed called 3G-ABC for solving the nonlinear optimization problems as mention in the next section. The key point of this proposed 3G-ABC algorithm is that the GGABC is used at the initial stage of searching for the optimum using global best methods with enough amount of exploitation process and then the global search method used to cover the best area for exploration purpose. The parameter c, gbest guided employed, global gbest onlooker and typical scout bees along with max fitness evaluations method will balance and increase the amount of exploration and exploitation process [42,43,47]. The pseudocode of the proposed 3G-ABC algorithm detailed as:
Set the control Parameters (Colony Size (Gbest Guided Employed bees + Guided Onlooker Bees), Limit, Upper Bound, Lower Bound, Dimension, number of runs, maximum number of fitness evaluations and Max Cycle Numbers)
Start
// Initialization
Initialize the food source positions;
Evaluate the nectar amount (fitness) of food sources; /* by using the following equation*/
While (the termination conditions are not met) /*if the error goal reach to the defined maximum number of fitness evaluations stop otherwise continue until Max Cycle Numbers = 100,000) */
/*Gbest Guided Employed Bees’ Phase*/
FOR (each gbest guided employed bee)
Produce a new food source following the Equation (3);
Evaluate the fitness of the new food source by Equation (9).
Apply greedy selection on the new food source and the old one;
If the num_eval == maximum fitness evaluations then
Memorize the best solution of Gbest Guided Employed Bee So far; and Exit
End IF
END FOR.
Calculate the probability P for each food source following the Equation (10);
/*Global Onlooker Bees’ Phase*/
FOR (each global onlooker bee)
Send global onlooker bees to food sources depending on P;
Produce a new food source following the Equations (4) and (5);
Evaluate the fitness of the new food source;
Apply greedy selection on the new food source and the old one;
If the num_eval == maximum fitness evaluations then
Memorize the best solution of Global Onlooker Bee So far; and Exit
End IF
END FOR
/*Global Scout Bees’ Phase*/
IF (an gbest guided employed bee becomes into a global scout bee)
Send the global scout bee to a new randomly produced food source;
END IF
END WHILE
Determine the abandoned solution (source), if exists, replace it with a new randomly produced solution for the scout bee using the Equation (2)
If the Num_Eval == maximum fitness evaluations then
Then memorize the best solution of Scout Bee So far; and Exit
End IF
Memorize the best solution achieved so far
If num_eval ~= maximum fitness evaluations
then continue Maximum Cycle Number
End
End
Based on the existence of the GGABC and GABCS algorithms, the exploitation and exploration process are enhanced through Equations (3)–(7), which have been hybrid in the proposed 3G-ABC algorithm. The values of , C1 and C2 have an important role for obtaining the high amount of exploitation and exploration through the gbest guided employed bees, global onlookers and scout bees with the guided and gbest strategies. Here, the various values are selected for C1 and C2 for the given problems. The proposed 3G-ABC algorithm can be easily applied to complex optimization problems including benchmarked numerical function to obtain a fast convergence speed with global optima as well. The randomization procedures are replaced by incorporating the bees’ best food position through the effective candidates and tested strategies (Gbest Guided Employed Bees, Global Best Onlooker bees and typical Scout Bees).
Most of the researchers have used the typical ABC algorithm as well as their improved and hybrid versions with local and global search methods with the termination criteria Maximum Cycle Number. According to Reference [42], using MCN as the termination criteria cannot reach the global minima and the comparison is also not valid with other meta-heuristic methods. Therefore, here the proposed method has been implemented with the termination criteria of the maximum fitness evaluation function instead of MCN which is 2*SN (SN employed bees + SN onlooker bees)*MCN. Here, all algorithms ABC, GABC, GGABC and 3G-ABC were terminated after 100,000 FEs, where FEs ≤ (SN + SN + 1) ⁄ MCN + SN. So in each iteration there are SN gbest guided employed bees, SN global onlooker bees and at most 1 scout bee of the typical ABC. The FEs will be counting dynamically through the fitness function of all sections during execution. Also, achieving an employed bee (by using the gbest guided strategy) that will become a scout bee does not consume a fitness evaluation in the employed bee phase again as the solution is going to be replaced by a random solution anyway. In such an implementation, there will be exactly SN*2 fitness evaluations per cycle. It has really changed the simulation results in terms of the exploration and exploitation process with a balanced quantity as well as saving the execution time. Also, these processes will continue until reaching the maximum fitness evaluation function until MCN.
4. Simulation Results and Discussion
In order to evaluate the performance of the proposed 3G-ABC for global optimization problems, simulation experiments were performed on Intel Core i7-3612QM @ 2.1Ghz, 6 MB L3 Cache Intel HM76 with 4 GB RAM using Matlab 2014b software. Fifteen well-known benchmark functions are used to compare the performance of the 3G-ABC algorithm with standard algorithms. These functions contain one unimodal variable-separable function, two unimodal non-separable functions, two multimodal variable separable functions and two multimodal non-separable functions. These bechmarked functions are Rosenbrock, Sphere, Rastrigin, Schwefel, Ackley, Griewank, Quartic, Zakharov, Weierstrass and Himmelblau and so forth.
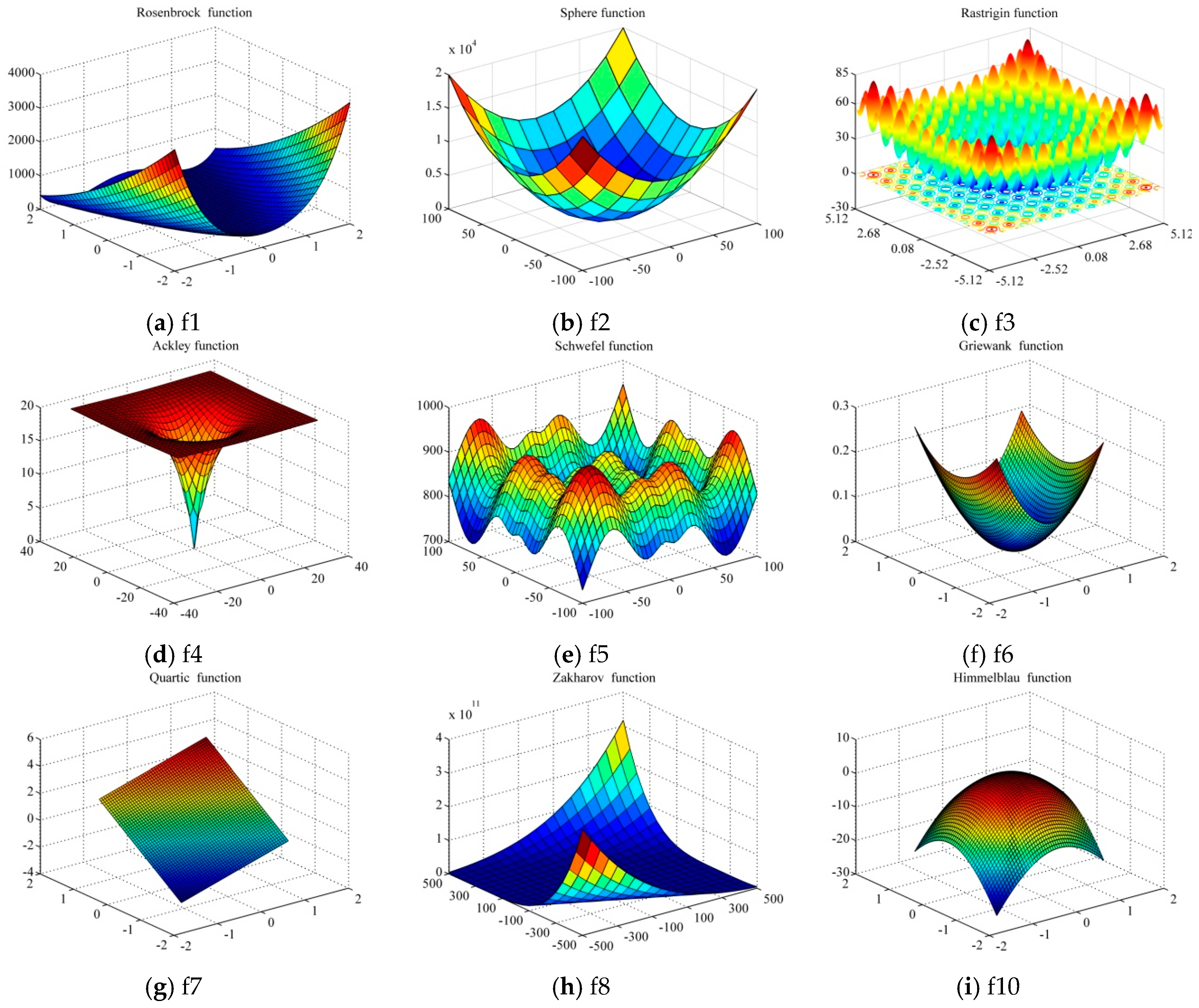
The first benchmark is Rosenbrock a unimodal with the nonseparable variables function used for simulation, whose global minimum value is 0 at (1, 1 … 1).The second benchmark function is Sphere, a unimodal function with separable variables used for simulation, whose global minimum value is 0 at (0, 0, … ,0). The third benchmark function is Rastrigin, based on the second function used for simulation, the global minimum value of which is 0 at (0, 0, … ,0). This function is based on Sphere function with the addition of cosine modulation to produce many local minima. The 4th benchmark is Ackley a multimodal function whose global minimum value is 0 at (0, 0, … ,0) is non-separable variables. The fifth benchmark function is Schwefel a multimodal and separable function used for simulation, whose global minimum value is 0 at (420.9867, 420.9867 …, 420.9867). The function has a second best minimum far from the global minimum where many search algorithms are trapped. The 6th benchmark function is Griewank also a multimodal function with non-separable variables function whose global minimum value is 0 at (0, 0 … ,0). Griewank function has a product term that introduces interdependence among the variables. Seventh to fifteen functions are: Quartic (noisy), Zakharov (Unimodal), Weierstrass (continuous but differentiable only on a set of points of measure zero) and Himmelblau (multi-modal function) functions. Initialization range for these functions are [−2.048, 2.048], [−100, 100], [−5.12, 5.12], [−500, 500], [−32, 32], [−600, 600], (−1.28, 1.28), (−1.28, 1.28), (−1.28, 1.28) and (−1.28, 1.28) respectively. The rotated and shifted functions of these algorithms such as Shifted Rotated High Conditioned Elliptic, Shifted Rotated Expanded Scaffer’s, Shifted Rastrigin’s, Shifted Rosenbrock’s and Shifted Rotated Griewank’s functions also used. Mathematically these functions are shown as below.
with
The values of f_bias3, f_bias6, bias7 and f_bias9 are −450, 390, −180 and −330 respectively. Here, all the selected benchmarked functions were tested with 10, 20 and 30 dimensions and run for 30 times randomly with various numbers of control parameters (as mentioned in Table 1, Table 2, Table 3 and Table 4 of the proposed and typical bees based algorithms as mentioned after Figure 1. In the proposed and standard algorithms, the numbers of global employed and global onlooker bees were half of the population size and the number of guided scout bees was selected as one. The abandon limit selected 10, 20 and 30 for the above benchmark function optimization. The standard ABC algorithm was used in this experiment for the optimization task. The comparison of proposed 3G-ABC with GGABC, GABC and ABC algorithms are discussed based on the simulation results.

Table 1.
Fifteen Benchmark Numerical Functions and their details (D is dimension of the problem).

Table 2.
Average Results obtained by ABC, GABC, GGABC and 3G-ABC for Numerical Function Optimization (Colony Size = 30, Limit = 30, C1 and C2 = 1.5, D = 10).

Table 3.
Average Results obtained by ABC, GABC, GGABC and 3G-ABC for Numerical Function Optimization (Colony Size = 20, limit = 20, C1, C2 = 1.2 and D = 20).

Table 4.
Average Results obtained by ABC, GABC, GGABC and 3G-ABC for Numerical Function Optimization (Colony Size = 10, limit = 10, C1, C2 = 1.1 and D = 30).
Figure 1.
Some graphical representation of numerical functions.
Table 2, Table 3 and Table 4 show the simulation results in terms of MSE and Std of the above mentioned fifteen benchmarked functions with various values of control parameters such as Colony Size, Limit, C1, C2 values and D as well, with standard and proposed algorithms. One of the big challenges of using bio-inspired particularly artificially based algorithms is the selection of the suitable values of control parameters. It is because the inappropriate parameter values can trapped and fail the method for any solving various complex problems. On the other hand, the proper selection of colony size, values of C1, C2, limit and D can make these algorithms effective than other methods.
The 3G-ABC algorithm plays a significant role in improving and balancing the exploration and exploitation procedures. The average result obtained by 3G-ABC is outstanding compared to other ABC, GABC and GGABC algorithms with 10, 30 and 50 dimensions are mentioned in Table 2, Table 3 and Table 4 respectively. The colony size put 30, 20 and 10 for average results respectively, food sources half of the colonies, various values of C1 and C2 were, cycle numbers 100,000 of ABC, GABC, GGABC and 3G-ABC algorithms. For typical ABC, GABC, GGABC and proposed 3G-ABC algorithms the percentage of employed and onlooker bees, gbest guided employed and gbest guided onlooker bees, global employed and global onlooker bees and gbest guided employed and global onlookers bees are set 50% of the colony.
The best average simulation results with different topologies, initial food sources values and various numbers of control parameters of the proposed and existence methods were used for fifteen benchmarked numerical function optimization task. Every setting of Table 1, Table 2 and Table 3 were run with 30 trials and the average of runs were calculated with MSE and Std. Dev, along with convergence curves for finding the efficiency of each algorithm. The average MSE and Std dev obtained by the proposed and existence algorithms show that the proposed method achieved the high efficiency, optimal results and optima for the abovementioned functions.
Based on the various control parameters values, the simulation results is effecting for each problem, such as: the size of colony can affect the speed during the solution so large colony may good towards the best foods source but wasting a lot of time and resources. In addition, the simulation results is affecting through the inappropriate values of limit and upper and lower bounds as well. Furthermore, the positive constant values of C1 and C2 having an important role towards achieving the global optima. He results can be analyzed from Table 2, Table 3 and Table 4 as in most of the cases the performance is increased in 3,4 topologies. The simulation results obtained by the proposed 3G-ABC and GABC algorithm are outstanding when compare with GGABC and ABC.
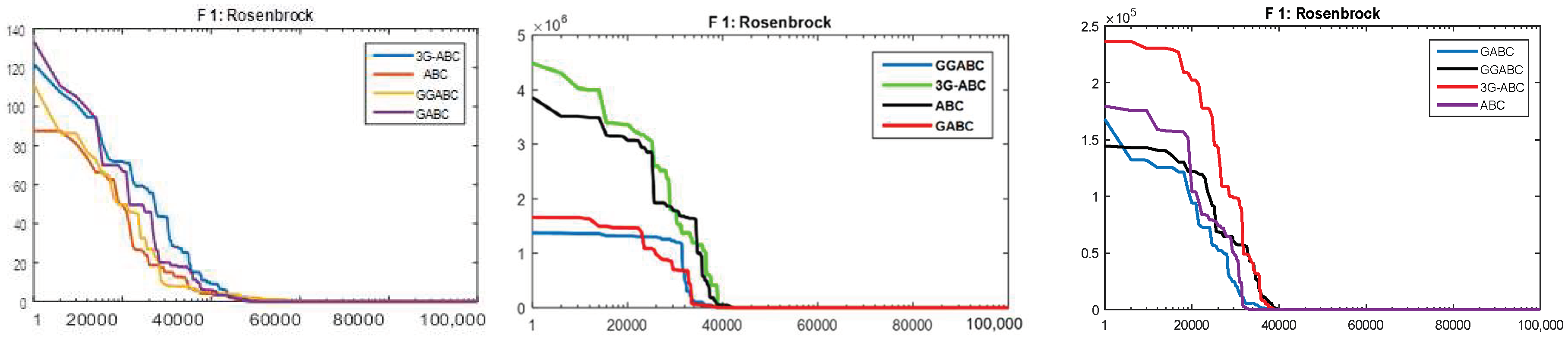
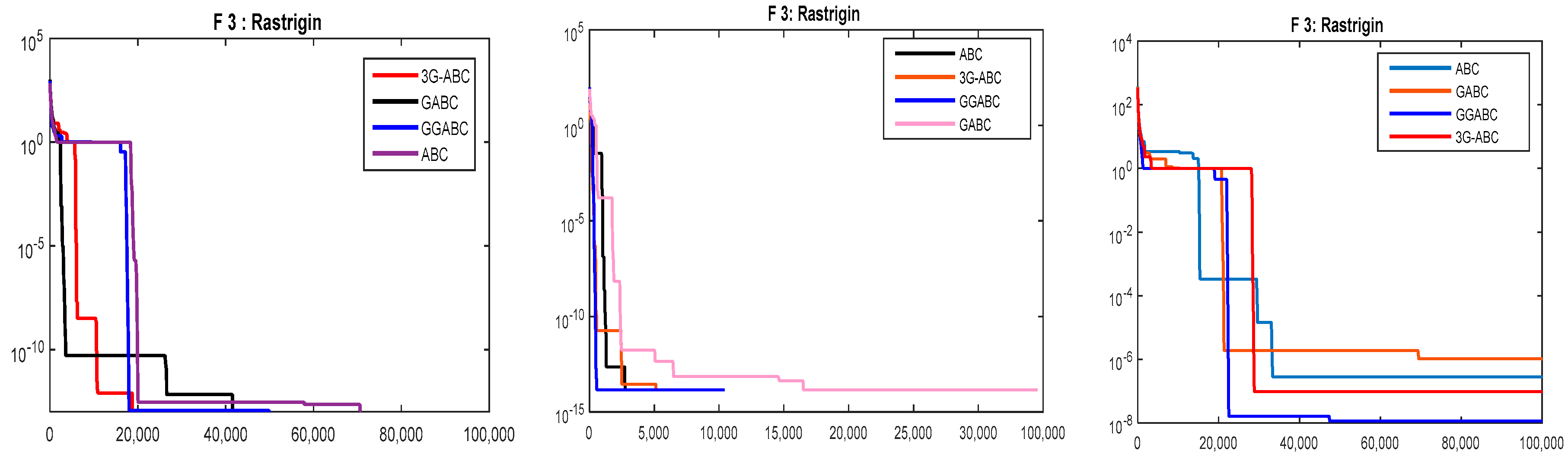
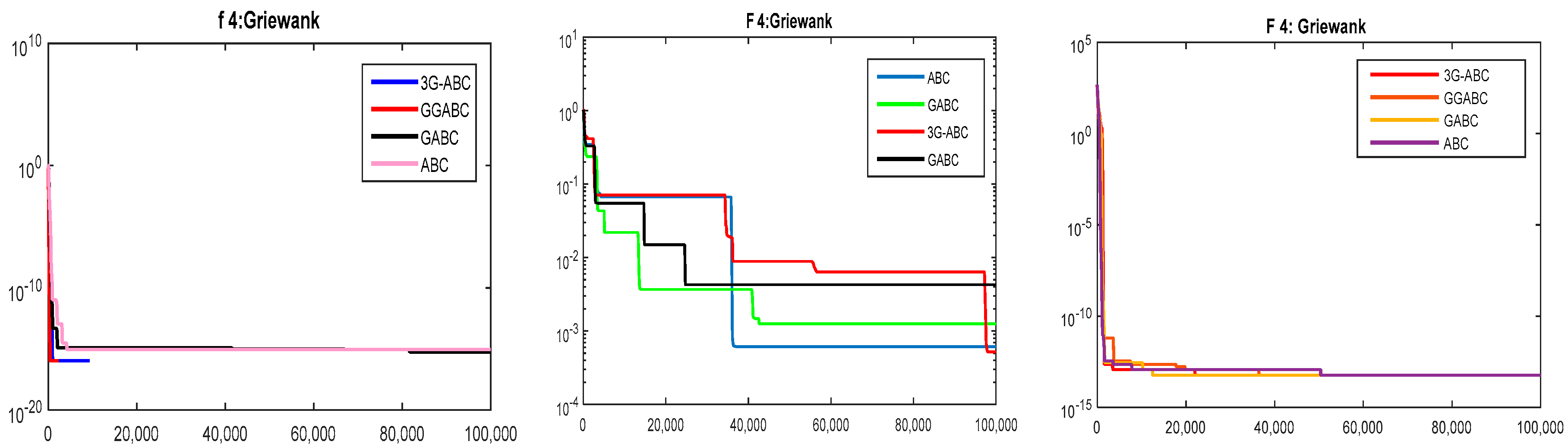
The curves obtained by the newly hybrid proposed and ABC, GABC and GGABC algorithms for first four benchmarked functions are given in Figure 2, Figure 3, Figure 4 and Figure 5 for the first 4 functions respectively. These functions are: Rosenbrock, Sphere, Rastrigin and Schwefel functions were simulated 30 runs with the maximum fitness evaluations through the various values of control parameters that are mentioned with each figure.

Figure 2.
Average convergence curves for Rosenbrock functions (Colony Size = 30, Limit = 30, C1, C2 = 1.5, D = 10), (Colony Size = 20, limit = 20, C1 C2 = 1.2 and D = 30) and (Colony Size = 100, limit = 10, C1, C2 = 1.1 and D = 50) from left to right respectively.

Figure 3.
Average convergence curves for Sphere functions (Colony Size = 100, Limit = 30, C1, C2 = 1.5, D = 10), (Colony Size = 50, limit = 20, C1 C2 = 1.2 and D = 30) and (Colony Size = 10, limit = 10, C1, C2 = 1.1 and D = 50) from left to right respectively.
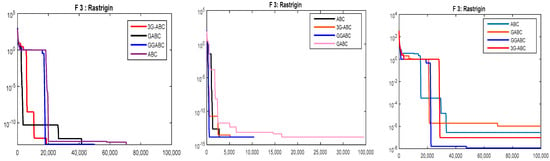
Figure 4.
Average convergence curves for Rastrigin function (Colony Size = 30, Limit = 30, C1, C2 = 1.5, D = 10), (Colony Size = 20, limit = 30, C1, C2 = 1.2 and D = 30) and (Colony Size = 10, limit = 10, C1, C2 = 1.1 and D = 50) from left to right respectively.

Figure 5.
Average convergence curves for the Griewank function (Colony Size = 30, Limit = 30, C1, C2 = 1.5, D = 10), (Colony Size = 20, limit = 20, C1, C2 = 1.2 and D = 30) and (Colony Size = 10, limit = 10, C1, C2 = 1.1 and D = 50) from left to right respectively.
Results obtained through the mentioned (proposed and typical) algorithms are not very stable when its use for Rosenbrock function even with the colony size of 100 as shown in the above Figure 2 (right most).
Using the max fitness evaluations as the stopping criteria has increased the efficiency of the abovementioned logarithm from the typical implementation method. From the above Figure 3, it is clear that 3G-ABC algorithm reach to obtain the best result for Sphere functions with colony size 30 and 10, however GGABC algorithm got the best results when the colony size was 20. Also the others such as ABC and Global ABC also have an enough average results in the cases. Using the proposed and typical meta-heuristic methods for Rastrigin function, FEs as the stopping criteria the GGABC and 3G-ABC are very close, also the results obtained by GABC and ABC are outstanding as well as shown in Figure 4. The best results obtained with various colony sizes (30, 20 and 10) through all the above mentioned methods.
In Figure 3, the average convergence curves for Sphere functions with (Colony Size = 30, Limit = 30, C1, C2 = 1.5, D = 10), (Colony Size = 20, limit = 20, C1 C2 = 1.2 and D = 30) and (Colony Size = 10, limit = 10, C1, C2 = 1.1 and D = 50) shows that the proposed 3G-ABC algorithm outperformed than others methods, also GGABC algorithm is performed better than ABC and Guided ABC algorithms with various values of control parameters. The difference in mean and std dev rankings achieved by ABC, GABC is especially large for 30-dimensional maximization problems (see Table 2 and Table 3) but also clear for 10- and 50-dimensional ones. According to the mean-based ranking obtained for 10 and 30-dimensional problems, these methods are very close to each other’s. It can be noted that the C1 and C2 with value 1.2 outperformed than 1.5 values.
The average convergence curves of 30 runs for the first four functions are presented from Figure 2, Figure 3, Figure 4 and Figure 5 shows that the, in case of Rastrigin, Schwefel and ackely functions, the results obtained by GABC algorithm are very close to the proposed one.
Here, the proposed 3G-ABC generates the best solutions on first eight benchmarked function out of fifteen while for GGABC, GABC, optimum solutions obtained for first three functions only. For the average solution, the proposed 3G-ABC can come up with the best solutions on all the fifteen selected benchmarked functions. The results in Table 2, Table 3 and Table 4 indicate that 3G-ABC and GABC exhibits the best performance among four typical methods discussed here.
To make sure that the proposed algorithm is outperformed efficiently than standard algorithms, to see the stability and to calculate the Analysis of variance ANOVA test used to find the estimation procedures (such as the “variation” among and between ABC, GABC, GGABC and 3G-ABC algorithms) to analyze the differences among various algorithm. The test has been used based on the mean square error values of first 10,000 FEs for solving the abovementied benchmarked function optimization task. Here, the difference using ANOVA with single factor has been presented in Table 5 of Sphere functions.

Table 5.
ANOVA test of ABC, GABC, GGABC and 3G-ABC algorithms based on Table 2 parameters for Sphere function based on first 10,000 fitness evaluations.
From Table 5, we can see that the F-value is greater than the F-critical value for the alpha level selected (0.05). Therefore, we have evidence to reject the null hypothesis and say that at least one of the four samples have significantly different means and thus belong to entirely different values. From we can see that the F-value is greater than the F-critical value for the alpha level selected (0.05). We can see that the significance value is 2.605131, which is much below than 0.05, and, therefore, there is a statistically significant difference in the mean length to solve Sphere function problem through the different algorithms used here.
Based on the statistical test there is an enough difference between proposed and typical algorithms during the solving benchmarked function optimization problems. Furthermore, in most of the cases, the proposed method has outperformed in convergence and reaching to max fitness numbers through the cooperation of guided and global honey bees, the global optima can easily obtained with fast convergence and minimum error. The GABC algorithm got the second rank after the proposed 3G-ABC algorithm especially with the colony Size = 20, limit = 20, C1, C2 = 1.2 and D = 20). In some cases, the GGABC got outstanding results from proposed and typical algorithms. Overall, the exploitation and exploration strategies have been improved and enhanced in the proposed and typical methods with the maximum fitness evaluation implementation method.
5. Conclusions
This paper presents a new hybridized ABC algorithm called 3G-ABC, where the global ABC and Gbest Guided ABC were introduced together to improve the searching and selecting performance of the typical ABC. To effectively validate the optimization performance of the new proposed 3G-ABC algorithm, we compared it with the classical ABC, GABC and GGABC algorithms on fifteen benchmark numerical functions. The results corresponding to these benchmark problems are computed and compared their performance with several existing algorithms and their results are summarized in the form of their Tables and Figures. Further, the convergence speed as well the statistical test is investigated to show the validity of the proposed approach. From these computed results, it is reveals that in most of the cases, the proposed approach shows a statistically significant and hence the proposed algorithm work is more reliable to find the global solution. Also, the performance of the GABC and GGABC algorithms also improved sufficiently based on the max fitness evaluation method rather than stopping criteria MCN. In other words, it is clearly presenting the hybridization objectives to improve the exploration and exploitation processes which are mainly the advantages of the two bees inspired algorithms GABC and GGABC. It is also clear that the 3G-ABC had the capability of fast convergence and to efficiently escape trapping at the local minimum and easily reached to global optima. Based on the high efficiency for optimization task, the proposed method can be suggested in the future for data-clustering and Neural Networks training purpose for solving complex time series problems. Also, the improved algorithms of the ABC will be improved and analysis with the new implementation strategy where the termination criteria will be max fitness evaluation values instead of MCN, which will be applied to solve various other benchmark optimization problems in an effective way. In the future, we shall test the performance of the proposed algorithm to solve other domain such as reliability optimization, decision-theory etc. [48,49,50,51].
Author Contributions
conceptualization, H.S, N.T., and R.G.; methodology, H.S, N.T., and R.G.; validation, H.S, N.T., and R.G.; formal analysis, H.S, N.T., and R.G.; investigation, H.S, N.T., H.G., and R.G.; writing—original draft preparation, H.S, N.T., and R.G.; writing—review and editing, H.S, N.T., and H.G.; funding acquisition, H.S, N.T., and R.G..
Funding
This research was funded by King Khalid University, Saudi Arabia.
Acknowledgments
The authors would like to thanks Deanship of Scientific Research, King Khalid University, Abha Saudi Arabia for supporting this research under the project number 525 (1438).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shah, H.; Tairan, N.; Garg, H.; Ghazali, R. A quick gbest guided artificial bee colony algorithm for stock market prices prediction. Symmetry 2018, 10, 292. [Google Scholar] [CrossRef]
- Tairan, N.; Algarni, A.; Varghese, J.; Jan, M.A. Population-based guided local search for multidimensional knapsack problem. In Proceedings of the 2015 Fourth International Conference on Future Generation Communication Technology (FGCT), Luton, UK, 29–31 July 2015; pp. 1–5. [Google Scholar]
- Faris, H.; Aljarah, I.; Mirjalili, S. Improved monarch butterfly optimization for unconstrained global search and neural network training. Appl. Intell. 2018, 48, 445–464. [Google Scholar] [CrossRef]
- Shah, H.; Ghazali, R.; Herawan, T.; Khan, N.; Khan, M.S. Hybrid guided artificial bee colony algorithm for earthquake time series data prediction. In International Multi Topic Conference; Springer: Cham, Switzerland, 2013; pp. 204–215. [Google Scholar]
- Shah, H.; Herawan, T.; Naseem, R.; Ghazali, R. Hybrid guided artificial bee colony algorithm for numerical function optimization. In International Conference in Swarm Intelligence; Springer: Cham, Switzerland, 2014; pp. 197–206. [Google Scholar]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Guo, J.; Sun, Z.; Tang, H.; Jia, X.; Wang, S.; Yan, X.; Ye, G.; Wu, G. Hybrid optimization algorithm of particle swarm optimization and cuckoo search for preventive maintenance period optimization. Discret. Dyn. Nat. Soc. 2016, 2016, 1516271. [Google Scholar] [CrossRef]
- Wu, B.; Qian, C.; Ni, W.; Fan, S. Hybrid harmony search and artificial bee colony algorithm for global optimization problems. Comput. Math. Appl. 2012, 64, 2621–2634. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Li, H. Artificial bee colony algorithm and pattern search hybridized for global optimization. Appl. Soft Comput. 2013, 13, 1781–1791. [Google Scholar] [CrossRef]
- Shah, H.; Tairan, N.; Mashwani, W.K.; Al-Sewari, A.A.; Jan, M.A.; Badshah, G. Hybrid global crossover bees algorithm for solving boolean function classification task. In International Conference on Intelligent Computing; Springer: Cham, Switzerland, 2017; pp. 467–478. [Google Scholar]
- Duan, H.B.; Xu, C.F.; Xing, Z.H. A hybrid artificial bee colony optimization and quantum evolutionary algorithm for continuous optimization problems. Int. J. Neural Syst. 2010, 20, 39–50. [Google Scholar] [CrossRef]
- Pamucar, D.; Ljubojevic, S.; Kostadinovic, D.; órovic, B. Cost and risk aggregation in multi-objective route planning for hazardous materials transportation—A neuro-fuzzy and artificial bee colony approach. Expert Syst. Appl. 2016, 65, 1–15. [Google Scholar] [CrossRef]
- Xu, J.; Gang, J.; Lei, X. Hazmats transportation network design model with emergency response under complex fuzzy environment. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Sremac, S.; Tanackov, I.; Kopic, M.; Radovic, D. ANFIS model for determining the economic order quantity. Decis. Making Appl. Manag. Eng. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Pamucar, D.; Círovic, G. Vehicle route selection with an adaptive neuro fuzzy inference system in uncertainty conditions. Decis. Making: Appl. Manag. Eng. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Yan, Y.; Li, Z. PS–ABC: A hybrid algorithm based on particle swarm and artificial bee colony for high-dimensional optimization problems. Expert Syst. Appl. 2015, 42, 8881–8895. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver press: Frome, UK, 2010. [Google Scholar]
- Long, W.; Liang, X.; Huang, Y.; Chen, Y. An effective hybrid cuckoo search algorithm for constrained global optimization. Neural Comput. Appl. 2014, 25, 911–926. [Google Scholar] [CrossRef]
- Wu, D.; Kong, F.; Gao, W.; Shen, Y.; Ji, Z. Improved chicken swarm optimization. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 681–686. [Google Scholar]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2015, 1–20. [Google Scholar] [CrossRef]
- Qi, X.; Zhu, Y.; Zhang, H. A new meta-heuristic butterfly-inspired algorithm. J. Comput. Sci. 2017, 23, 226–239. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Garg, H. A hybrid GSA-GA algorithm for constrained optimization problems. Inf. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Uymaz, S.A.; Tezel, G.; Yel, E. Artificial algae algorithm (AAA) for nonlinear global optimization. Appl. Soft Comput. 2015, 31, 153–171. [Google Scholar] [CrossRef]
- Abraham, A.; Pedrycz, W. Hybrid artificial intelligence systems. In Innovations in Hybrid Intelligent; Systems, E., Corchado, J.M., Abraham, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Crepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. (CSUR) 2013, 45, 35. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, W.; Liang, J. Global artificial bee colony search algorithm for numerical function optimization. In Proceedings of the 2011 Seventh International Conference on Natural Computation (ICNC), Shanghai, China, 26–28 July 2011; Volume 3, pp. 1280–1283. [Google Scholar]
- Sharma, H.; Bansal, J.C.; Arya, K.; Deep, K. Dynamic swarm artificial bee colony algorithm. Int. J. Appl. Evol. Comput. (IJAEC) 2012, 3, 19–33. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Gao, W.; Liu, S. Improved artificial bee colony algorithm for global optimization. Inf. Process. Lett. 2011, 111, 871–882. [Google Scholar] [CrossRef]
- Garg, H.; Sharma, S.P. Multi-objective reliability-redundancy allocation problem using particle swarm optimization. Comput. Ind. Eng. 2013, 64, 247–255. [Google Scholar] [CrossRef]
- Karabogă, D.; Ökdem, S. A simple and global optimization algorithm for engineering problems: Differential evolution algorithm. Turk. J. Electr. Eng. Comput. Sci. 2004, 12, 53–60. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Ozturk, C.; Karaboga, D. Hybrid artificial bee colony algorithm for neural network training. In Proceedings of the 2011 IEEE Congress on Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 84–88. [Google Scholar]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Kar, A.K. Bio inspired computing–a review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Garg, H. Multi-objective optimization problem of system reliability under intuitionistic fuzzy set environment using cuckoo search algorithm. J. Intell. Fuzzy Syst. 2015, 29, 1653–1669. [Google Scholar] [CrossRef]
- Mashwani, W.K. Comprehensive survey of the hybrid evolutionary algorithms. Int. J. Appl. Evol. Comput. (IJAEC) 2013, 4, 1–19. [Google Scholar] [CrossRef]
- Garg, H. Solving structural engineering design optimization problems using an artificial bee colony algorithm. J. Ind. Manag. Optim. 2014, 10, 777–794. [Google Scholar] [CrossRef]
- Mernik, M.; Liu, S.-H.; Karaboga, D.; Crepinšek, M. On clarifying misconceptions when comparing variants of the artificial bee colony algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Crepinšek, M.; Liu, S.-H.; Mernik, L.; Mernik, M. Is a comparison of results meaningful from the inexact replications of computational experiments? Soft Comput. 2016, 20, 223–235. [Google Scholar] [CrossRef]
- Garg, H. A Hybrid GA—GSA Algorithm for Optimizing the Performance of an Industrial System by Utilizing Uncertain Data. In Handbook of Research on Artificial Intelligence Techniques and Algorithms; Vasant, P., Ed.; IGI Global: Hershey, PA, USA, 2015; pp. 620–654. [Google Scholar]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Shastri, A.S.; Kulkarni, A.J. Multi-cohort intelligence algorithm: An intra-and inter-group learning behaviour based socio-inspired optimisation methodology. Int. J. Parallel Emerg. Distrib. Syst. 2018, 33, 675–715. [Google Scholar] [CrossRef]
- Karaboga, D.; Ozturk, C. A novel clustering approach: Artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2011, 11, 652–657. [Google Scholar] [CrossRef]
- Garg, H. Performance analysis of an industrial systems using soft computing based hybridized technique. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1441–1451. [Google Scholar] [CrossRef]
- Garg, H. An efficient biogeography based optimization algorithm for solving reliability optimization problems. Swarm Evol. Comput. 2015, 24, 1–10. [Google Scholar]
- Garg, H.; Rani, M.; Sharma, S.P.; Vishwakarma, Y. Bi-objective optimization of the reliability-redundancy allocation problem for series-parallel system. J. Manuf. Syst. 2014, 33, 353–367. [Google Scholar] [CrossRef]
- Garg, H.; Rani, M.; Sharma, S.P.; Vishwakarma, Y. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment. Expert Syst. Appl. 2014, 41, 3157–3167. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).