Abstract
The paper presents a Non-Uniform Memory Access (NUMA)-aware compiler optimization for task-level parallel code. The optimization is based on Non-Uniform Memory Access—Balanced Task and Loop Parallelism (NUMA-BTLP) algorithm Ştirb, 2018. The algorithm gets the type of each thread in the source code based on a static analysis of the code. After assigning a type to each thread, NUMA-BTLP Ştirb, 2018 calls NUMA-BTDM mapping algorithm Ştirb, 2016 which uses PThreads routine pthread_setaffinity_np to set the CPU affinities of the threads (i.e., thread-to-core associations) based on their type. The algorithms perform an improve thread mapping for NUMA systems by mapping threads that share data on the same core(s), allowing fast access to L1 cache data. The paper proves that PThreads based task-level parallel code which is optimized by NUMA-BTLP Ştirb, 2018 and NUMA-BTDM Ştirb, 2016 at compile-time, is running time and energy efficiently on NUMA systems. The results show that the energy is optimized with up to 5% at the same execution time for one of the tested real benchmarks and up to 15% for another benchmark running in infinite loop. The algorithms can be used on real-time control systems such as client/server based applications which require efficient access to shared resources. Most often, task parallelism is used in the implementation of the server and loop parallelism is used for the client.
1. Introduction
Non-Uniform Memory Access (NUMA) systems overcome the drawbacks of the Uniform Memory Access (UMA) systems such as lack of performance with increasing the number of processing units and need for synchronization barriers to ensure the correctness of the shared memory accesses [1]. NUMA systems have a memory subsystem for each CPU, considering that the CPU is placed on the last level in the tree-based memory hierarchy [2]. While the number of processing units is continuously growing, NUMA systems avoid congested data traffic, which is one of the main factors that influence performance.
Thread mapping algorithms have been developed to benefit from the advantage of NUMA systems of allowing the more cost effective local accesses, instead of the remote accesses [3]. Thread mapping is defined as the association between the thread and the cores on which the thread runs, also defined as CPU affinity. Improved thread mapping requires several threads to access efficiently the same data [4]. Efficient access requires using the cache and the interconnection so that performance and energy consumption is improved [3].
The paper presents Non-Uniform Memory Access—Balanced Task and Loop Parallelism (NUMA-BTLP) [5], a compiler optimization for NUMA systems which is applied to C parallel code which uses PThreads Library so that the code runs with balanced data locality. NUMA-BTLP [5] classifies threads based on the several static criteria into autonomous, side-by-side and postponed [5]. The resulting thread-type associations for each thread are given as input data to Non-Uniform Memory Access—Balanced Thread and Data Mapping (NUMA-BTDM) mapping algorithm [6] that computes the CPU affinities of the threads, mapping the threads uniformly to cores on which other threads with which they shared data are mapped already [5]. NUMA-BTLP [5] and NUMA-BTDM [6] achieve application dependent balanced data locality which means that the application controls the thread mapping instead of the operating system. Thread mapping is performed by the compiler optimization by inserting PThreads routine pthread_setaffinity_np in the source code [5].
The second section of the paper presents state-of-the-art techniques to improve parallel application though efficient thread mapping. Section 3 describes the NUMA-BTLP algorithm [5] and explains how the design of the algorithm contributes to performance and energy consumption improvements. Section 4 compares NUMA-BTLP algorithm [5] with other related work. Section 5 presents the materials and methods for the experiments and Section 6 includes the experimental results on two case studies on real benchmarks which use PThreads Library. Section 7 discusses the results. Section 8 concludes on the findings and the limitations of NUMA-BTLP [5] and NUMA-BTDM [6] algorithms based on the experimental results and Section 9 summarizes the conclusions.
2. State-of-the-Art Thread Mapping Techniques
2.1. Thread Mapping Overview
Mapping threads requires knowing the communication behavior (i.e., the data that the threads share and the amount of it per thread) and the information about the hardware hierarchy, such as the number of processors, cores, and cache levels [3], which can be obtained using specialized tools like hwloc [7]. For instance, a type of communication pattern is the nearest-neighbor communication pattern [3]. In this case, the newly created threads are bound to cores through system calls such as the Linux system call sched_setaffinity, so that threads that have neighboring identifiers are placed on cores that are nearby in the memory hierarchy in order to take advantage of the shared cache [3].
Thread mapping can be based on different policies depending on whether it takes into account or not the dynamic behavior changes. Such mapping is the affinity-based thread mapping, which uses the allocation and the migration policies. In the allocation policy, each thread is assigned to a particular core by the operating system and remains on the core until the end of execution causing no runtime overhead. However, the application cannot react when its behavior changes during execution. The second policy, migration policy, moves the execution of threads from one core to another at runtime following the dynamic behavior changes [3]. The migration causes a runtime overhead, mostly due to an increase in the number of cache misses [8], apart from the overhead of calling the migration functions themselves.
Depending on the number of threads assigned once, thread mapping could be a global or a non-global operation. A global mapping operation requires setting the CPU affinities of all threads once. Such operation does not involve high costs for a small number of threads in case of the majority of the mapping algorithms [9].
2.2. Thread Mapping Algorithms
The traditional scheduler used currently by Linux, Completely Fair Scheduler [10], focuses on load balancing and fairness [11,12] and has no information related to memory access behavior of the application. Thread mapping algorithms are needed to overwrite the mapping performed by the operating system [3].
Thread mapping is often a NP-Hard problem [9] requiring an efficient mapping algorithm [13] and induces extra runtime overhead if performed dynamically. The overhead is due to the work done with reassigning threads to processing units [14]. However, because of the overhead, most algorithms use approximations to reduce their complexity to polynomial [9].
2.2.1. Classification of Thread Mapping Algorithms
Thread mapping algorithms can be classified based on different criteria:
- The moment of mapping:
- ○
- Static mapping algorithms: Limited Best Assignment (LBA) [15] and other Greedy algorithms described in [15], SCOTCH [16] and NUMA-BTDM [6]
- ○
- Dynamic mapping algorithms: Opportunistic Load Balancing (OLB) [15], METIS [17,18], and the mapping algorithm part of Zoltan Toolkit [19]
- The mapping method:
- ○
- algorithms which use a communication matrix to perform the mapping: Compact mapping algorithm which uses the nearest-neighbor communication pattern [3]
- ○
- algorithms which use partitioning technique of the communication graph: SCOTCH [16], METIS [17,18], the mapping algorithm part of Zoltan toolkit [19]
- ○
- algorithms that use pattern matching in matching the communication pattern with the hardware architecture: Treematch [20]
- ○
- algorithms that use a communication tree to determine the CPU affinities of the threads: NUMA-BTDM [6]
- Awareness of the underlying hardware architecture:
- ○
- algorithms that does not take into account the hardware architecture that the application is running on: OLB [15], SCOTCH [16], METIS [17,18], and the mapping algorithm part of Zoltan Toolkit [19]
- ○
- algorithms that take into account the hardware architecture that the application is running on: Treematch [9,20], EagerMap [21], NUMA-BTDM [6]
State-of-the-art thread mapping algorithms use graph representations of the communication behavior and of the hardware hierarchy and techniques such as graph partitioning or graph matching [3].
2.2.2. Description of Thread Mapping Algorithms
The algorithms above will be described in the following.
1. Naive mapping algorithms: OLB [15], LBS [15]
OLB [15] algorithm places each jobs as it is created, to the processing unit which is available. LBA [15] assigns the job to the processing unit which is expected to execute the job the fastest, without being aware of the load of the core, nor of the load caused by the assignment of the job to the core.
2. Mapping algorithms based on graph partitioning techniques: SCOTCH [16], METIS [17], and the mapping algorithm part of Zoltan Toolkit [19]
SCOTCH [16] is a static mapping algorithm based on recursive bipartition of the communication graph and of the processing unit graph. Mapping in this case involves minimizing the communication cost by mapping the threads that communicate intensely on processing units close to one another, while taking into account the load of the processing units caused by other applications that are running in parallel.
METIS [17] algorithm uses an unstructured graph partitioning technique to perform the mapping. The algorithm is composed of 3 operations: repeated coarsening until a graph of p partitions is obtained, bipatitioning the coarse graph and repeated bipartitioning of finer graphs until a bipartition of the initial graph is obtained (the reverse operation of the coarsening operation).
Coarsening in case of METIS algorithm [17] results in p partitions with different number of nodes, provided that the number of edges which connect nodes from different partitions is minim. Coarsening in this case requires finding the minimum spanning tree by selecting each time a node that connects with a node from the partition that was previously formed through an edge that has the biggest cost of all edges and by grouping the two nodes together into a single node that has the weight equal to the sum of the weights of the two nodes, forming each time a new partition. The weight of the edge that connects the selected node with the minimum spanning tree regarded as a single node is assigned with the difference between the sum of the weights of the edges that connect the node with the nodes from the spanning tree and the weight of the edge with the biggest cost selected before. The result of this step is a tree with less nodes and edges compared to the initial graph.
The second step of METIS algorithm [17] consists of partitioning the graph obtained in first step into two partitions having both the sum of the weights of all nodes in the partition close to the sum of the weights of all nodes in the graph divided by 2. The partitions are formed so as the cost of edge cutting required to form the two partitions is minimum [17].
The third step of METIS [17] is the reverse of first step and the output is a bipartition of the initial graph.
Another mapping algorithm, which is part of Zoltan Toolkit [19], is based on a multilevel hypergraph partitioning technique. The algorithm consists of 3 operations [19]: coarsening to k partitions (k is considered equal to the number of processors in this case), hyperedge cutting and expansion of the resulted hypergraph.
Coarsening is performed in steps similar to coarsening operation in case of METIS [17].
A hyperedge is defined as a subset of nodes [19]. Hyperedge cutting involves eliminating the nodes from each partition which are connected the most with nodes from other partitions so as to obtain the hypergraph which is the densest of all variants [19]. The result of coarsening and hyperedge cutting is a set of smaller hypergraphs which are an approximation of the initial hypergraph.
3. Hardware architecture-aware mapping algorithms which use tree representations: Treematch [9,20], EagerMap [21]
Most of the algorithms that use tree representations are more efficient than those using graph representations [20,22].
In case of Treematch algorithm [20], mapping is done between the communication pattern and the NUMA architecture. The algorithm uses a communication matrix where the rows and columns indicate the processes and elements (i,j) represent the amount of communication between processes i and j [20]. Processes are grouped into groups of two processes and a graph is formed in which the nodes are all possible groups of two processes and the edges connect nodes that are incompatible [20]. Two nodes are incompatible if they share a common process [20].
Treematch algorithm [20] identifies a set of groups using a Greedy algorithm so that each process is contained within a single group and the processes within every group communicate with one another more than with any other process from another group. The Greedy algorithm in this case is an NP-problem and the complexity of it is simplified based on the heuristic in [20]: the value of a group is obtained by subtracting the amount communication between the two processes in the group from the sum of the amount of communication of each of the two processes with all other processes. To identify the set of groups, the Greedy algorithm orders descending the groups by their value and then it orders descending the groups by the mean of the values of the neighboring groups from the ordered list [20]. Based on the resulting set of groups, Treematch algorithm [20] constructs another communication matrix, where element (i,j) represents the sum of the amount of communication of each process from group i with each process from group j.
Treematch algorithm [20] uses a tree representation for representing the hardware architecture [20]. For instance, if the underlying architecture has 2 cache levels, the architecture is mapped to a 4-level tree as follows: the main memory is mapped to the root of the tree, which is placed on level 0, L2 cache nodes are mapped to the nodes on level 1, L1 cache nodes are mapped to nodes on level 2 and processing units are mapped to the leaves of the tree located all in level 4.
Finally, Treematch [20] assigns each process in a group to one core from a pair of cores that share the same cache, until all groups of processes are assigned.
EagerMap [21] is another architecture-aware mapping algorithm which uses a Greedy algorithm. The algorithm can be applied on symmetric hardware architectures only [21]. EagerMap [21] uses a communication matrix and a tree representation for the hardware architecture like in case of Treematch [20], except that EagerMap [21] maps the nodes in the tree to NUMA nodes, processors, cache memories, and processing units. The algorithm forms a number of groups of tasks which is equal to the number of cores and maps each group to a core [21]. The tasks are grouped using a Greedy algorithm so that each task within a group communicates the most with tasks from the same group [21]. On each step, the Greedy algorithm places in a group a new task that communicates the most with the tasks already added in the group [21].
4. Algorithms based on artificial intelligence: LBA [15] and the Greedy algorithms in [15] that perform the mapping based on the estimated time of running the threads on each core and the load of each core
The mapping algorithms which use artificial intelligence perform the mapping based on the history of previous runs of the application, which gives the estimated time of executing the threads on each of the cores. Such algorithms are LBA [15], which was mentioned before and the Greedy algorithms in [15]. The Greedy algorithms [15] use a matrix in which the rows are the jobs and the columns are the cores. Element (i,j) represents the estimated execution time of job i on core j [15].
The first Greedy algorithm [15] assigns each job on the core the job is expected to finish first its execution. The jobs are assigned in the order they are processed and the execution time matrix is updated each time there is a new assignment so the next assignment takes into account the previous ones [15].
The second Greedy algorithm [15] uses two nested Greedy algorithms to give the lowest estimated time to finish the execution and chooses the minimum from the two execution times given by the nested algorithms, on each assignment. The first nested algorithm [15] identifies each step a job that is not yet assigned and a core on which the job runs so that the selected job leads to finishing the execution of the jobs already assigned, including the job identified, the earliest. To comply with the condition, the job must not finish execution faster on any other core and any other unassigned job must not lead to finishing the execution faster than the one selected does [15]. The second nested algorithm [15] searches each step for the job that leads to the most unfavorable execution of the application and selects a core for mapping the job such that the execution of the already jobs assigned, including the selected job, finishes earliest.
2.2.3. Software Libraries for Thread Mapping
Most programming languages do not implement thread and data mapping algorithms that can be called from the source code [23]. Thus, the developer is required to know the implementation of the language or of the compiler to be able to map threads efficiently using specific routines [23]. The libraries that provide such routines are TBB-NUMA [23], QThreads [24] and PThreads.
TBB-NUMA [23] is designed as a portable and composable library for parallel computation. The library is derived from Intel Threading Blocks (TBB) and designed for developing parallel applications for NUMA systems [23]. TBB-NUMA [23] does not assign threads to cores randomly.
QThreads [24] provides ways to control thread mapping and can be extended with NUMA-aware optimizations.
PThreads is one of the most representative libraries used to perform thread mapping. It allows its users to explicitly control thread mapping using specialized routines such as [6]:
- pthread_setaffinity_np(pthread_t thread, size_t cpusetsize, const cpu_set_t *cpuset) —sets the CPU affinity of a thread if it does not have the affinity currently
- pthread_getaffinity_np(pthread_t thread, size_t cpusetsize, const cpu_set_t *cpuset)—gets the CPU affinity of a thread and stores it in the output parameters cpuset
3. NUMA-BTLP Algorithm
3.1. Improving the Accuracy of Static Predictions on Dynamic Behavior by Eliminating Dynamic Aspects from the Static Analysis
Parallel programs have static behavior and dynamic behavior [3].
Dynamic behavior can change from one execution to another depending on the following factors [3]:
- input data and their placement in memory
- the number of threads
Dynamic behaviour can change during execution depending on the following factors [3]:
- pipeline model
- work-stealing technique [25]
- thread creation and destruction
- memory allocation and deallocation
If none of the dynamic aspects from above occurs, than the behavior of the parallel program can be considered static [3].
NUMA-BTLP algorithm strives to eliminate the impact on the thread mapping of some of the factors above, such as the number of threads and the thread creation and destruction. To exemplify, two case studies are considered: in the first case, the threads are created in a loop with a number of dynamically established iterations and in the second case, the thread is created inside an “if” statement whose condition depends on dynamic aspects of the execution.
In the loop case, regardless of the number of threads that are created inside a loop, NUMA-BTLP assigns the threads the same type and maps all threads to the same core by inserting a pthread_setaffinity_np call inside the loop body, after the pthread_create call.
If a thread is created inside an if statement, the pthread_setaffinity_np call is inserted inside the if branch after the pthread_create call and the thread is mapped independent of the if condition, on the cores where other threads with which the thread shares data are mapped, if applicable, or on a separate core, if the thread does not share data with any thread, while ensuring the load balance.
3.2. Determining the Thread Type by Static Analysis
First step of NUMA-BTLP algorithm [5] is a static analysis on the source code which returns the type of each thread in the code. In this step, NUMA-BTLP algorithm uses the following classification to decide the type of each thread [5]:
- An autonomous thread is defined as a thread that shares no data with other threads at the same level in the thread creation hierarchy which are executed in parallel and should not benefit of the same core or of the same NUMA node as those other threads. Thus, autonomous threads can be assigned to cores as uniformly as possible. One of the criteria in achieving balanced data locality is not to exceed the average load per processing unit, which is ensured by the uniform mapping [26]
- A side-by-side thread is a thread sharing data with at least one other thread and should be mapped on every core where other threads with which the side-by-side thread shares data with are mapped. If the thread is of type side-by-side relative to the generating core, the side-by-side thread should be mapped as close as possible, e.g., on the same cores, to the generating thread and should benefit of the execution on the same core as the generating thread with priority from an autonomous thread. A thread is classified as side-by-side if:
- ○
- it executes a function that returns a value read by any other thread
- ○
- it executes a function with output parameters, which are input data of other threads
- ○
- it is created inside the body of a loop
- ○
- it contains nested threads created using pthread_create routine call
- A postponed thread is defined as a thread generated by another thread, not requiring to be executed immediately. Such threads are classified as so if they are not side-by-side relative to other threads at the same level in the thread creation hierarchy. Therefore, a postponed thread is an autonomous thread which computes non-critical data, relative to the threads at the same level in the creation hierarchy. However, it is side-by-side thread relative to the generating thread. Postponed threads meet at least one of the following criteria:
- ○
- they execute a function that returns a value not read by other threads which are currently running
- ○
- they execute a void or non-void function that has no output parameters read by threads which are currently running, or a non-void functions with previous property which, in addition, returns a value that is not used by other threads currently running
- ○
- usually the thread in not enclosed within a loop
Algorithm 1 presents the static analysis performed by NUMA-BTLP algorithm to obtain the type of each thread [5]. Autonomous threads share data with no other thread and they are independent threads relative to the threads at the same level in the thread creation hierarchy [5]. A thread is classified as side-by-side relative to the generating thread and to others at the same level in the thread creation hierarchy if the thread shares data with them [6]. If there is at least some data that two threads share, they are considered side-by-side relative to one another [5]. Postponed threads are independent threads relative to the threads at the same level in the thread creation hierarchy and side-by-side threads relative to the generating thread.
In PThreads, the relation between function calls and threads is one-to-one, thus, threads are given a function pointer when created [5]. The static analysis in Algorithm 1 is performed on the function argument of the pthread_create call [5]. The analysis applies to intermediate representation, which can be accessed in the optimization phase of the compiler. In this phase, modern compilers use classes that describe the instructions in the code, e.g., a class so-called Loop can be used to instantiate objects that each stores the information of a loops in the source code.
| Algorithm 1. NUMA-BTLP static analysis [5] |
for every pthread_create call identified in the code, associated with thread A:
|
3.3. Type-Aware Tree Representation of Threads
NUMA-BTLP algorithm uses a tree representation for the communication between threads. Each node in the tree stores the data of a thread, such as the type and its identifier. The tree is constructed based on the following rules:
- the root of the tree is assigned to the main thread
- a node on the i-th level of the tree which is assigned to thread ik is the child of the node on the j-th level which is assigned to thread jl, where j = i − 1, if thread ik uses the data read or written before by thread jl, ∀ i ≥ 1, ∀ 1 ≤ k ≤ ni, ∀ 1 ≤ l ≤ nj, where ni and nj are the number of nodes on level i and level j, respectively
- if both threads ik and jl use for the first time a data which is then used by the other (e.g., thread ik writes a data which is then read by thread jl and thread jl writes other data which is then read by thread ik) then the relation parent-child is established as follows: if thread ik is created first, then the thread will be the parent of thread jl and vice versa
3.4. NUMA-BTDM Algorithm
NUMA-BTDM [6] is a thread type-aware mapping algorithm which sets the CPU affinities of the threads using PThreads routine pthread_setaffinity_np and considers the thread type when mapping. The algorithm performs the mapping in a compile-time optimization and the mapping is kept until the end of the execution [5]. Therefore, NUMA-BTDM [6] is classified as a compile-time mapping algorithm [5], according to taxonomy in [3]. The algorithm prevents the operating system to apply randomly its scheduling policies, that is, without taking into account the characteristics of the application that runs in parallel and allows the running application to control the thread mapping [6]. Nevertheless, it does not cause runtime overhead, since there is no migration taking place at runtime [5].
Second step of NUMA-BTLP algorithm [5] consists of calling NUMA-BTDM algorithm [6]. Prior to NUMA-BTDM [6] call, NUMA-BTLP [5] inserts in the source code, code that detects the characteristics of the underlying architecture such as the number of cores or the number of logical cores per physical core, so as the analysis is performed online [5].
The input data of NUMA-BTDM algorithm [6] consists of the characteristics of the underlying architecture and the tree representation which stores in each node the type of the thread assigned to the node.
NUMA-BTDM algorithm performs the type-aware mapping as follows:
- Autonomous threads are scattered uniformly to processing units to improve balance [6]
- Side-by-side threads are mapped on the same cores to improve locality [6]. However, the side-by-side threads are mapped on other cores as well, if they share data with other threads as well [5].
- Postponed threads are mapped to the less loaded processing unit (considering the number of flops and iops is identified statically) [6], improving load balance. Postponed threads do not need to be executed immediately, so, mapping them on less loaded processing unit enables the possibility to apply Dynamic Voltage and Frequency Scaling(DVFS) to the unit without performance loss [5]
As a consequence of the mapping performed by NUMA-BTDM [6], balanced data locality is improved on NUMA systems due to the balanced manner of distribution of threads to cores and improved cache hit ensured by NUMA-BTLP [5] and NUMA-BTDM [6] algorithms.
3.5. Setting CPU Affinity
Next, NUMA-BTLP inserts in the program code after each pthread_create call, a call to pthread_setaffinity_np routine, which sets the CPU affinity of each thread, at runtime, immediately after its creation [5]. The insertions are done at compile-time part of the compiler optimization NUMA-BTLP [5].
3.6. Description of NUMA-BTLP Algorithm in Pseudo Code
In Algorithm 2, NUMA-BTLP [5] triggers the static analysis in Algorithm 1 and saves the output of it in the tree representation. Next, NUMA-BTDM algorithm [6] is called to calculate the CPU affinities of every thread based on the data in the communication tree. NUMA-BTDM is called once for all threads, performing a so-called global operation [3]. Finally, the insertion of pthread_setaffinity_np routines takes place for all threads once.
| Algorithm 2. NUMA-BTLP algorithm [5] |
|
4. Comparison of the NUMA-BTLP Algorithm and Other Work
Mapping side-by-side threads on the same cores minimizes the overall communication between cores. Another approach [27] which seeks to obtain the same, minimizes inter-core communication overhead by splitting the threads into clusters such that the amount of inter-communication between clusters is minimized, while the number of clusters must not exceed the number of cores. Authors [27] say it that mapping clusters of threads to cores instead of mapping individual threads to cores is more efficient because it is easier to minimize the amount of communication between clusters instead of threads.
The speedup obtained by mapping clusters of threads instead of threads, using the algorithm in [27], varies from 10.2% to 131.82% when compared to speedup obtained when mapping individual threads. However, when the threads are independent, mapping individual threads, as happens with NUMA-BTLP [5], is 10% more efficient in terms of execution time than mapping clusters, as happens with the algorithm in [27]. Similarly, applying NUMA-BTLP algorithm [5] on one of the benchmarks tested in this paper, which has threads of type autonomous only, results in a bigger optimization of power consumption, than the optimization obtained on another benchmark, which has threads of other types. Execution time results for the benchmark which has only autonomous threads could not be obtained because the benchmark runs in infinite loop.
However, a group of side-by-side threads can be considered as forming a cluster, but the difference is that a side-by-side thread can be part of multiple such clusters, taking into account that any two threads that share at least a data are considered side-by-side relative to one another and mapped on the same core. Therefore, a side-by-side thread is mapped to all the cores on which the threads with which it shares data are mapped and it is part of all so-called clusters of which those threads are part of.
Critical threads are delayed due to race conditions which degrades the power consumption with no performance loss [27]. Postponed threads can be considered autonomous threads relative to other threads at the same level in the thread creation hierarchy. Mapping postponed threads to less loaded core minimizes the number of race conditions to main memory because the data resides with higher probability in the L1 or L2 cache of the less loaded core compared to a higher loaded core and fetching the data, which might be locked, from main memory, is not required. Using the cache of the less loaded core with high probability, improves cache hit rate and reduces the race conditions, allowing critical threads to finish earlier.
Choosing each time the less loaded core for mapping a postponed thread to it can be compared to placing balls into bins. The problem of placing the balls into bins [28] requires a graph representation, where vertexes represent the bins and the weight of the vertexes is the load of the bin. To solve the problem, each time a ball is placed in a bin, an initial vertex is chosen and the edges are traversed until the vertex with the minimum current load is reached starting from the initial vertex [28]. Similar, the less loaded core is computed each time a postponed thread is detected, taking into account the load of each core so far, given by the threads already mapped statically.
Both the NUMA-BTLP algorithm [5] and the methodology in [27] that models the dynamic execution and partitions the application into clusters use intermediate representation for the data dependency analysis. As opposed to methodology in [27] which uses two graphs to obtain the mapping: a weighted dynamic application graph to model the data dependencies, where nodes represent instructions from the code in intermediate representation and another graph to represent the clusters, NUMA-BTLP [5] represents both the threads and the data dependencies between them using a tree, which is constructed according to rules already given and where the nodes represent the threads.
However, the limitation of NUMA-BTLP [5] is that it takes into account only the number of flops and iops when computing the load of each core, while the methodology in [27] takes into account the execution time when partitioning the threads into clusters so that clusters reach approximately equalized execution time.
As apposed to NUMA-BTLP [5], which aims to use all available cores for the execution while keeping the load balance, methodology in [27] shuts off the cores on which no cluster is executing, taking into account that a core can execute at most one cluster. This paper affirms that shutting off the cores might degrade the performance of other applications running in parallel.
The analysis performed by NUMA-BTLP [5] at compile-time is aimed to optimize thread mapping for NUMA systems by taking into account the characteristics of the hardware architecture when improving data locality. Similar analyses have been designed to optimize data mapping. Such an analysis [29] detects the memory references in a loop through a compiler pass and schedules each loop iteration to the processing unit owning the most frequent data used in the iteration.
The data distribution in [29] is aimed to improve applications running on a proposed abstraction of a NUMA system, in which the memory subsystems are placed in the chip above the processing units, minimizing and equalizing the interconnections between the processing units via memory. Instead of clustering side-by-side threads to execute on the same cores as NUMA-BTLP [5] does, the data distribution in [29] clusters the data with high locality into separate queues, one for each processing unit, and each iteration of the loop takes data from one or more queues [29].
To improve balanced data locality, each queue is mapped to the memory subsystem closest to the processing unit owning the queue and each iteration of the loop is mapped to the processing unit owning the queue which contains most of the data used by the iteration [29]. If the work still results to be unbalanced, neighbor idle processing units steal the work from the high loaded processor through work stealing techniques [29].
Therefore, the same as NUMA-BTLP [5], the data distribution in [29] relies on work relocation (static migration of postponed threads in case of NUMA-BTLP [5]) to improve balance. As opposed to NUMA-BTLP [5], when stealing work, data distribution in [29] does not take into account the load of the processing unit that steals the work, considering only its state (idle or active). Considering the load of the processing units, even determined statically, as in case of NUMA-BTLP [5], avoids the need for any work stealing analysis at runtime such as the one performed by the data distribution in [29]. Still, by comparing the data distribution in [29] with other dynamic scheduling policies, a speedup of 69% against the dynamic scheduling is obtained. In addition, a speedup of 50% against other data distributions for balanced loops is obtained [29].
5. Materials and Methods
Experimental results were obtained on a NUMA system running under Linux operating system (Ubuntu 17.10 artful) with the characteristics in Figure 1: 12-core Fujitsu Workstation which has 2 Intel Xeon E5-2630 v2 ivy bridge processors, where each processor is a NUMA node and each NUMA node has 6 cores, with 2 logical threads running on each core.
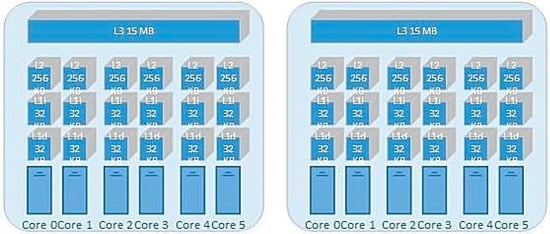
Figure 1.
Intel Xeon E5-2630 v2 sockets (CPUs) of Fujitsu Workstation Celsius r930 power.
The two levels of private cache in Figure 1 (6 × 32 KB 8-way set associative L1 instruction caches, 6 × 32 KB 8-way set associative L1 data caches, 6 × 256 KB 8-way set L2 associative caches) favor increasing cache hit rate of autonomous threads. The shared cache is the L3 cache (15 MB 20-way set associative L3 shared cache). Sharing a bigger dimension cache (L3 instead of L2) allows the side-by-side threads to share more data residing in the cache.
The power consumption of the CPU cores was obtained using turbostat software tool and the measurements were correlated with the measurements of power consumption of the entire system, which were obtained using a WattsUp specialized hardware device for measuring power consumption. turbostat software tool returns each second, in the form of a table, the following: the statistics for all CPU cores in the system in a single line, the statistics for each CPU core separately, written on a new line for each CPU core. PkgWatt column from the table refers to the power consumption of the entity. Using WattsUp specialized hardware device which has been connected to the computer, the power consumption measurements of the entire system were written in an output file every one second. The measurements were obtained with the monitor turned off.
All power consumption results in the paper refer to measurements obtained per second.
6. Results
Experimental results were obtained for CPU-X Benchmark and Context Switch Benchmark. Power consumption of each real benchmark was obtained by subtracting the idle power consumption of the CPU from the power consumption of the CPU with the benchmark running. The applications were run each separately with no other processes running in parallel.
6.1. Results for CPU-X Benchmark
6.1.1. Description of the Benchmark
CPU-X Benchmark uses a Graphical Uses Interface (GUI) to displays hardware parameters of the system each one second, such as memory configuration parameters, operating system parameters or CPU-X specific execution parameters. CPU-X uses PThreads Library to create threads. In the implementation, threads are created inside a loop. After applying a prototype of NUMA-BTLP [5] on the benchmark, threads are all set as side-by-side and mapped on the same core.
CPU-X runs in infinite loop, therefore, experimental results for execution time are not applicable in this case.
6.1.2. Experimental Power Consumption Results
To obtain the power consumption results, CPU-X Benchmark was run 5 times for 15 min for each number of threads in the range [1,12]. The number of threads is set at compile-time and it is kept throughout the execution.
Table 1 lists the power consumption results for CPU-X Benchmark when the benchmark runs with different number of threads which is set statically, without NUMA-BTLP algorithm [5] applied (second column) and with NUMA-BTLP algorithm [5] applied at compile-time (third column). The values in the fourth column are obtained by subtracting from the results in the third column and the results in the second column and they represents the optimization of power consumption expressed in Watt, which is achieved for CPU-X Benchmark when the benchmark is optimized using NUMA-BTLP algorithm [5]. The last column shows the same optimization, expressed in percentages. The results in the table show that the optimization is up to 15%, i.e., 0.3 Watt each second, in this case.

Table 1.
Power consumption optimization of CPU-X Benchmark running on Non-Uniform Memory Access (NUMA) system with different number of threads which is set at compile-time, when the benchmark is not optimized and when it is optimized using NUMA-BTLP. BTLP: Balanced Task and Loop Parallelism.
Figure 2 shows the power consumption of CPU-X Benchmark running on NUMA system with different number of threads which are set statically both when NUMA-BTLP algorithm [5] is applied and when the algorithm is not applied at compile-time. The figure illustrates comparatively the results in the second and third column, respectively, from Table 1.
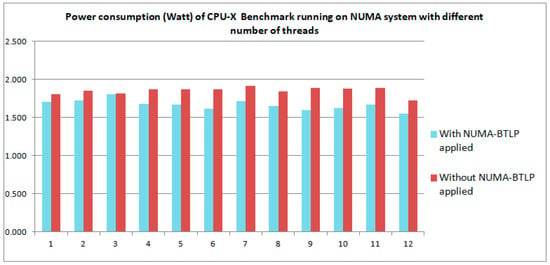
Figure 2.
Power consumption of CPU-X Benchmark running on NUMA system with different number of threads which is set statically, when NUMA-BTLP algorithm [5] is applied and when the algorithm is not applied at compile-time.
The power consumption is optimized by NUMA-BTLP [5], for small number of side-by-side threads, as seen in Figure 2.
Figure 3 shows the power consumption optimization which results from applying NUMA-BTLP [5] on CPU-X Benchmark which runs on NUMA system with different number of threads that is set statically. Figure 3a indicates the power consumption optimization in Watt and Figure 3b expresses the optimization in percentages.
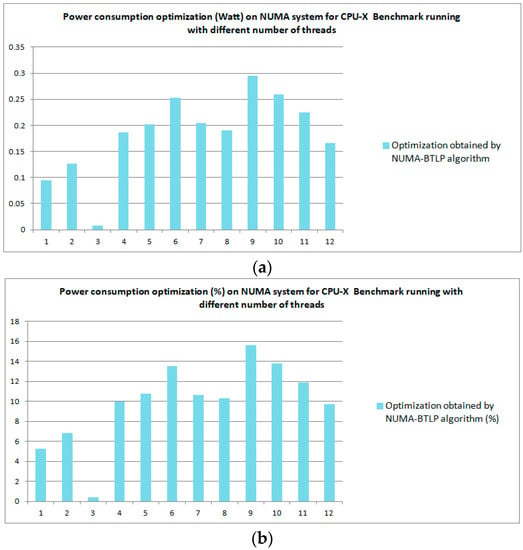
Figure 3.
Power consumption optimization obtained on NUMA system for CPU-X Benchmark running with different number of threads which are set statically: (a) Optimization expressed in Watt (b) Optimization expressed in %. NUMA-BTLP: Non-Uniform Memory Access—Balanced Task and Loop Parallelism.
The power consumption optimization increases non-linearly with the increase in the number of threads, for small number of side-by-side threads, as seen in Figure 3.
6.2. Results for Context Switch Benchmark
6.2.1. Description of the Benchmark
Context Switch is a benchmark used to quantify the cost of context switch. As such, the benchmark has two main programs. Both main programs create a thread which is considered of type autonomous, according to NUMA-BTLP [5].
6.2.2. Experimental Performance Results
Context Switch was run 40 times under the same conditions and the statistics of the execution time results for all 40 running rounds are shown in Table 2. The table contains statistics such as the minimum, the average and the maximum values over all rounds for the execution time, when NUMA-BTLP algorithm [5] is applied at compile-time and when the algorithm is not applied. In addition, Table 2 lists the average variance and standard deviation, for both cases.

Table 2.
Performance statistics of the 40 running rounds of Context Switch Benchmark on NUMA system, when NUMA-BTLP algorithm [5] is applied at compile-time and when the algorithm is not applied.
The results in Table 2 show that the average execution time when the algorithm is not applied is approximately equal to the average execution time when the algorithm is applied at compile-time for the 40 rounds.
6.2.3. Experimental Power Consumption Results
Context Switch was run 40 times under the same conditions to obtain the power consumption results. The statistics of the power consumption results for all running rounds of the benchmark are shown in Table 3. The table contains statistics such as the minimum, the average and the maximum values for power consumption over all rounds, when NUMA-BTLP algorithm [5] is applied at compile-time and when the algorithm is not applied. Table 3 presents also the average variance and standard deviation for all rounds, in both cases.

Table 3.
Statistics of power consumption for the 40 running rounds of Context Switch Benchmark on NUMA system, when NUMA-BTLP algorithm [5] is applied at compile-time and when the algorithm is not applied.
The results show that the average power consumption optimization obtained for 2 autonomous threads is 0.32 Watt each second. Another observation is that the power consumption measurements are closer to the mean when the algorithm is applied compared to when it is not applied, which results from the values of the variance and the standard deviation in Table 3.
Figure 4 shows the power consumption of Context Switch Benchmark which runs successively for a number of 40 times on the NUMA system, both when NUMA-BTLP algorithm [5] is applied at compile-time and when the algorithm is not applied on the benchmark.
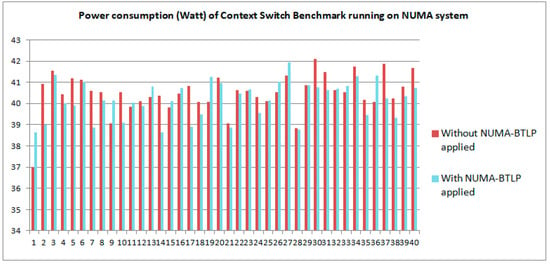
Figure 4.
Power consumption (Watt) for Context Switch Benchmark, obtained on 40 runningrounds of the application on NUMA system, both when NUMA-BTLP algorithm is applied at compile-time and when the algorithm is not applied.
The power consumption values obtained vary non-linear from one round to the next in the range [36.99, 42.09] in case the algorithm is not applied and they vary in the range [38.62, 41.94] in case the algorithm is applied.
Figure 5 shows the power consumption optimization for each round, which results from applying NUMA-BTLP [6] on Context Switch Benchmark. Figure 5a indicates the power consumption optimization in Watt and Figure 5b expresses the optimization in percentages.
Figure 5.
Power consumption optimization per round for Context Switch Benchmark running 40 times on NUMA system: (a) Optimization expressed in Watt (b) Optimization expressed in %.
In most rounds optimization is achieved and optimization is up to 5%, i.e., approximate 2 Watt.
7. Discussion
The results on proposed architecture show that the power consumption is optimized by NUMA-BTLP [5], for small number of side-by-side threads. The side-by-side threads that are spanned by CPU-X Benchmark are mapped on the same cores and they benefit from the same L1 cache, increasing the number of local accesses. The energy consumption optimization achieved by NUMA-BTLP [5] is due to increasing the number of local accesses to the detriment of remote accesses. The results show that for small number of threads, the more threads that benefit from common L1 cache data, the better the power consumption optimization, reaching the maximum value of 15%.
In case of Context Switch Benchmark, the average execution time is not improved by applying NUMA-BTLP algorithm [5]. The lack of performance optimization is due to the small number of threads that the benchmark uses, namely two autonomous threads that are mapped on different cores by NUMA-BTLP [5], and it is explained by the fact that the gain of the execution time obtained by running with two threads mapped according to NUMA-BTLP algorithm [5], is less than the execution time consumed with the actual mapping operations using pthread_setaffinity_np calls.
The power consumption results for Context Switch Benchmark show that the average power consumption optimization obtained for 2 autonomous threads, after applying NUMA-BTLP [5], is 0.32 Watt each one second, meaning that energy is optimized with up to 5% at the same execution time. A factor that leads to power consumption optimization is the reduction in the number of thread switching operations. However, if several autonomous threads are created in a loop (threads of such type can be created in loops if they execute loop-invariant code), NUMA-BTLP algorithm [5] does not take into account the overall number of threads created, which is given by the number of iterations, because the number of iterations is considered to belong to the dynamic behavior, while NUMA-BTLP [5] performs a static analysis. Not being aware at compile of the overall number of threads that are created by a loop affects load balance. To exemplify a case in which load is not balanced, 4 autonomous threads that are explicitly created inside the loops (using pthread_setaffinity calls) are considered. If NUMA-BTLP algorithm [5] were aware of the number of iterations, in case the number of threads exceeds the number of cores the algorithm would have used all the cores to map threads uniformly. Instead, the algorithm maps uniformly the 4 threads on separate cores as if they were a total of 4 threads. At runtime, there will be more than one thread per core, resulting 4 groups of threads, each group having a number of threads equal to the number of iterations. Threads in each group are mapped all to the same core, instead of being mapped uniformly to cores, which affects load balance.
As opposed to autonomous threads, an increased number of postponed threads might degrade the performance and energy consumption due to costly cache level traversal operations.
8. Findings and Limitations
NUMA-BTLP algorithm [5] is applied on intermediate representation at compile-time, which makes it independent of the instruction set of the processor and applicable for both heterogeneous and homogeneous architectures. One disadvantage of the NUMA-BTLP algorithm [5] is that the analysis performed by the algorithm does not take into account the dynamic characteristics of the processors such as the clock speed, which may differ from one processor to another on heterogeneous architectures. It rather considers the load of each core i.e., the number of flops and iops performed by all threads assigned to the core and maps postponed threads to less loaded cores.
Considering that each autonomous thread is mapped on a different core, ideally, the number of autonomous threads should be less or equal to the number of physical cores of the underlying architecture, 12 in this case, so that each autonomous thread to benefit only from the its core resources (L1 and L2 cache). The number of autonomous threads can extend up to the number of logical cores in the ideal case, if two collocated threads would not require more resources than provided while keeping the same performance as if the thread runs only on the core, i.e., autonomous threads can be collocated on the same core if the cache miss rate of each thread does not increase compared to the cache miss rate of the thread if it only runs on the core. Therefore, in most such cases, as the number of cores is higher, the performance of multi-threading applications is better.
In case of side-by-side threads, the underlying architecture has no impact on the performance of the mapping algorithm. Side-by-side threads run on the same cores, regardless of the number of cores or of the communication pattern, which improves cache hit rate.
Postponed threads are mapped on the less loaded cores and they are considered side-by-side relative to the generating thread and autonomous relative to the threads which are created at the same level in the thread creation hierarchy. Mapping of postponed threads can influence the performance of the mapping algorithm, since the less loaded core on which the postponed thread is mapped may be far away in terms of NUMA distance from the core on which the generating thread (requiring data computed by the postponed thread) is mapped. In this case, the data needs to traverse, in the worst case, all cache levels to get into the main memory and once in the main memory, to traverse backwards the cache levels to reach the L1 cache of the core on which the generating thread runs. The more the number of cores is, the worst case occurs with a higher probability. Therefore, a high number of postponed threads would be mapped efficiently to an architecture with has small number of cores, as opposed to autonomous threads.
However, so far tested, NUMA-BTLP algorithm [5] does not degrade, in either case, neither the performance nor the power consumption, although additional CPU affinity setting function calls were inserted in the source code for each thread.
9. Conclusions
NUMA-BTLP algorithm [5] is a compiler optimization which classifies threads into autonomous, side-by-side and postponed by static analysis of the source code and calls NUMA-BTDM algorithm [6] to set the CPU affinities of the threads based on their type. NUMA-BTDM algorithm [6] maps threads to cores uniformly, favoring balanced data locality on NUMA systems. The optimization is designed for C parallel code which uses PThreads Library [5]. The classification of the threads allows the threads to execute as close as possible in time and NUMA distance to the data they use [5] and to benefit from local accesses in the detriment of remote accesses.
The novelty in case of NUMA-BTLP [5] is that the algorithm allows the application to customize, control and optimize for NUMA the mapping of threads to core, overwriting the random mapping of the operating system.
The results show that the energy is optimized with up to 5% at the same execution time for one of the tested real benchmarks and up to 15% for another real benchmark running in infinite loop.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Introduction to Parallel Computing. Available online: https://computing.llnl.gov/tutorials/parallel_comp/ (accessed on 25 February 2018).
- Falt, Z.; Krulis, M.; Bednárek, D.; Yaghob, J.; Zavoral, F. Towards efficient locality aware parallel data stream processing. J. Univ. Comput. Sci. 2015, 21, 816–841. [Google Scholar]
- Diener, M.; Cruz, E.H.M.; Alves, M.A.Z.; Navaux, P.O.A.; Koren, I. Affinity-Based Thread and Data Mapping in Shared Memory Systems. ACM Comput. Surv. 2017, 49, 64. [Google Scholar] [CrossRef]
- Tam, D.; Azimi, R.; Stumm, M. Thread clustering: Sharing-aware scheduling on SMP-CMP-SMT multiprocessors. In Proceedings of the ACM SIGOPS Operating Systems Review, Lisbon, Portugal, 21–23 March 2007; Volume 41. [Google Scholar]
- Ştirb, I. NUMA-BTLP: A static algorithm for thread classification. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 882–887. [Google Scholar]
- Știrb, I. NUMA-BTDM: A thread mapping algorithm for balance data locality on NUMA systems. In Proceedings of the 2016 17th International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT), Guangzhou, China, 16–18 December 2016; pp. 317–320. [Google Scholar]
- Broquedis, F.; Clet-Ortega, J.; Moreaud, S.; Furmento, N.; Goglin, B.; Mercier, G.; Thibault, S.; Namyst, R. hwloc: A generic framework for managing hardware affinities in HPC applications. In Proceedings of the 2010 18th Euromicro Conference on Parallel, Distributed and Network-Based Processing, Pisa, Italy, 17–19 February 2010; pp. 180–186. [Google Scholar]
- Constantinou, T.; Sazeides, Y.; Michaud, P.; Fetis, D.; Seznec, A. Performance implications of single thread migration on a chip multi-core. ACM Sigarch Comput. Archit. News 2005, 33, 80–91. [Google Scholar] [CrossRef]
- Jeannot, E.; Mercier, G.; Tessier, F. Process placement in multicore clusters: Algorithmic issues and practical techniques. IEEE Trans. Parallel Dist. Syst. 2014, 25, 993–1002. [Google Scholar] [CrossRef]
- Wong, C.S.; Tan, I.; Kumari, R.D.; Wey, F. Towards achieving fairness in the linux scheduler. ACM Sigops Oper. Syst. Rev. 2008, 42, 34–43. [Google Scholar] [CrossRef]
- Li, T.; Baumberger, D.P.; Hahn, S. Efficient and scalable multiprocessor fair scheduling using distributed weighted round-robin. In Proceedings of the 14th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Raleigh, NC, USA, 14–18 February 2009; ACM: New York, NY, USA, 2009; pp. 65–74. [Google Scholar]
- Das, R.; Ausavarungnirun, R.; Mutlu, O.; Kumar, A.; Azimi, M. Application-to-core mapping policies to reduce memory system interference in multi-core systems. In Proceedings of the 2013 IEEE 19th International Symposium on High Performance Computer Architecture (HPCA), Shenzhen, China, 23–27 February 2013; pp. 107–118. [Google Scholar]
- Diener, M.; Cruz, E.H.; Pilla, L.L.; Dupros, F.; Navaux, P.O. Characterizing communication and page usage of parallel applications for thread and data mapping. Perform. Eval. 2015, 88, 18–36. [Google Scholar] [CrossRef]
- Ribic, H.; Liu, Y.D. Energy-efficient work-stealing language runtimes. ACM SIGARCH Comput. Archit. News 2014, 42, 513–528. [Google Scholar]
- Armstrong, R.; Hensgen, D.; Kidd, T. The relative performance of various mapping algorithms is independent of sizable variances in run-time predictions. In Proceedings of the Seventh Heterogeneous Computing Workshop (HCW’98), Orlando, FL, USA, 30 March 1988; pp. 79–87. [Google Scholar]
- Pellegrini, F.; Roman, J. Scotch: A software package for static mapping by dual recursive bipartitioning of process and architecture graphs. In High-Performance Computing and Networking. HPCN-Europe 1996. Lecture Notes in Computer Science; Liddell, H., Colbrook, A., Hertzberger, B., Sloot, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1067, pp. 493–498. [Google Scholar]
- Karypis, G.; Kumar, V. Parallel multilevel graph partitioning. In Proceedings of the International Conference on Parallel Processing, Honolulu, HI, USA, 15–19 April 1996; pp. 314–319. [Google Scholar]
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1988, 20, 359–392. [Google Scholar] [CrossRef]
- Devine, K.D.; Boman, E.G.; Heaphy, R.T.; Bisseling, R.H.; Catalyurek, U.V. Parallel hypergraph partitioning for scientific computing. In Proceedings of the 20th IEEE International Parallel & Distributed Processing Symposium, Rhodes Island, Greece, 25–29 April 2006. [Google Scholar]
- Jeannot, E.; Mercier, G. Near-optimal placement of MPI processes on hierarchical NUMA architectures. In Euro-Par 2010—Parallel Processing. Euro-Par 2010. Lecture Notes in Computer Science; D’Ambra, P., Guarracino, M., Talia, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6272, pp. 199–210. [Google Scholar]
- Cruz, E.H.; Diener, M.; Pilla, L.L.; Navaux, P.O. An efficient algorithm for communication-based task mapping. In Proceedings of the 2015 23rd Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, Turku, Finland, 4–6 March 2015; pp. 2017–2214. [Google Scholar]
- Traff, J.L. Implementing the MPI process topology mechanism. In Proceedings of the 2002 ACM/IEEE Conference on Supercomputing, Baltimore, MD, USA, 16–22 November 2002; p. 28. [Google Scholar]
- Majo, Z.; Gross, T.R. A library for portable and composable data locality optimizations for NUMA systems. ACM Trans. Parallel Comput. 2017, 3, 227–238. [Google Scholar] [CrossRef]
- Wheeler, K.B.; Murphy, R.C.; Thain, D. Qthreads: An API for programming with millions of lightweight threads. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing, Miami, FL, USA, 14–18 April 2008; pp. 1–8. [Google Scholar]
- Blumofe, R.D.; Leiserson, C.E. Scheduling multithreaded computations by work stealing. J. ACM 1999, 46, 720–748. [Google Scholar] [CrossRef]
- Diener, M.; Cruz, E.H.; Alves, M.A.; Alhakeem, M.S.; Navaux, P.O.; Heiß, H.-U. Locality and balance for communication-aware thread mapping in multicore systems. In Euro-Par 2015: Parallel Processing. Euro-Par 2015. Lecture Notes in Computer Science; Träff, J., Hunold, S., Versaci, F., Eds.; Spinger: Berlin/Heidelberg, Germany, 2015; Volume 9233, pp. 196–208. [Google Scholar]
- Xiao, Y.; Xue, Y.; Nazarian, S.; Bogdan, P. A load balancing inspired optimization framework for exascale multicore systems: A complex networks approach. In Proceedings of the 36th International Conference on Computer-Aided Design, Irvine, CA, USA, 13–16 November 2017; pp. 217–224. [Google Scholar]
- Bogdan, P.; Sauerwald, T.; Stauffer, A.; Sun, H. Balls into bins via local search. In Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 6–8 January 2013; pp. 16–34. [Google Scholar]
- Marongiu, A.; Burgio, P.; Benini, L. Vertical stealing: Robust, locality-aware do-all workload distribution for 3D MPSoCs. In Proceedings of the 2010 International Conference on Compilers, Architectures and Synthesis for Embedded Systems, Scottsdale, AZ, USA, 24–29 October 2010; pp. 207–216. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).