An Improvement on Remote User Authentication Schemes Using Smart Cards

Abstract

In 2010, Yeh et al. proposed two robust remote user authentication schemes using smart cards; their claims were such that their schemes defended against ID-theft attacks, reply attacks, undetectable on-line password guessing attacks, off-line password guessing attacks, user impersonation attack, server counterfeit attack and man-in-the-middle attack. In this paper, we show that Yeh et al.’s schemes are still vulnerable to ID-theft attack, off-line password guessing attacks, undetectable on-line password guessing attacks and user impersonation attack. Notably, problems remain in situations where the user lost a smart card or the malicious legal user. To remedy these flaws, this paper proposes an improvement on Yeh et al.’s remote user authentication schemes using smart cards.

1. Introduction

With the rapid growth of network technologies, it is extremely important to pay close attention to any developing security concerns. As such, password-based authentication has become one of the best practically applied techniques used to problem-solve regarding various applications in wireless environments and other remote authentication systems. In 1981, Lamport [1] proposed the first password-based remote authentication scheme for identifying a legal user using a hash-chain technique through insecure communication. In our scheme, all secret passwords are stored in a verifier’s table that is maintained by the remote server; in a situation such as this, there exists a potential threat such that all maintained records might be modified by attackers. In order to solve these problems, numerous undertakings in research [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] have been executed during recent years.

In 1990, Hwang et al. [12] proposed a non-interactive password authentication scheme without password tables using smart cards. Follow up research [3,6,16,18,23,24,30,31,32,33,34,35,36,37,38,39] has also been proposed. Because these schemes suffered from a susceptibility to ID-theft attack, an attacker could forge a legal user using an eavesdropped users’ identity documentation. Das et al. [6] proposed a dynamic ID-based remote user authentication scheme that has significant advantages; most notably, the remote server does not need to maintain a verifier’s table. However, in 2009, Wang et al. [25] pointed out that Das et al.’s scheme still exhibited several weaknesses. For example, it is susceptible to server counterfeit attack and provides poor password authentication. In the same year, Hsiang and Shih [11] proposed a remote user authentication scheme using smart cards claiming that their scheme provided many security features, such as: mutual authentication, the ability to freely change passwords and protection from masquerade attack.

Next, Yeh et al. [27] proposed two robust remote user authentication schemes using smart cards. Their schemes illustrated how Wang et al.’s scheme and Hsiang and Shih’s scheme were still susceptible to masquerade attack, off-line password guessing attacks and undetectable on-line password guessing attacks. Thus, Yeh et al. proposed two schemes to remedy these weaknesses that were more efficient than both Wang et al.’s scheme and Hsiang and Shih’s scheme. Nevertheless, according to our cryptanalysis, Yeh et al.’s schemes still have notable weaknesses to ID-theft attack, off-line password guessing attacks, undetectable on-line password guessing attacks and user impersonation attack. Moreover, the smart-card-based schemes [6,9,11,19,25,28] suffered in contexts involving a lost smart card. In fact, some researches [15,21] reveal the stored parameters of smart card. Therefore, we propose an improved scheme to overcome all of the security weaknesses mentioned above.

The security requirements of a remote user authentication scheme based on smart cards are listed as follows:

- Mutual authentication

In the information transmission process, the message receiver must be able to verify the identity legitimacy of the sender. Thus, each party must be able to verify the identity legitimacy of the other parties in a remote user authentication environment. If the two parties have confirmed each other’s identities, then mutual authentication is achieved.

- Lost smart card

If the user’s smart card is stolen by an attacker, the attacker may use the smart card for future malicious communications, or use it to obtain previous messages. A secure remote user authentication environment should avoid these situations, when the smart card is stolen by an attacker.

- ID-theft attack

Malicious attacks may also attempt to get a person’s identification by tracing their transmitted messages. Thus, a secure remote user authentication scheme must prevent such ID-theft attack.

- Server counterfeit attack and user impersonation attack

Any information transferred in an unencrypted network environment is vulnerable to malicious attack in the form of modification, where the message delivered to the receiver is not the original message transmitted by the sender. The attacker may pretend a legal server or a legal user. The legality of the transmitted parties must therefore be ensured and protected against tampering in transit.

- Replay attacks

Malicious attacks may also intercept the transmitted message between the user and the server and then impersonate a legitimate transmitter in order to send the same message to the intended receiver. This constitutes a serious breach of personal data security and must be prevented by a secure remote user authentication environment.

The rest of this paper is organized as follows. Section 2 provides a brief review of the weakness of Yeh et al.’s schemes. Section 3 provides details of the proposed scheme. Section 4 provides a security analysis of our scheme. Section 5 shows a security and performance comparison with related research. We provide conclusions in the last section.

2. Cryptanalysis of Yeh et al.’s Schemes

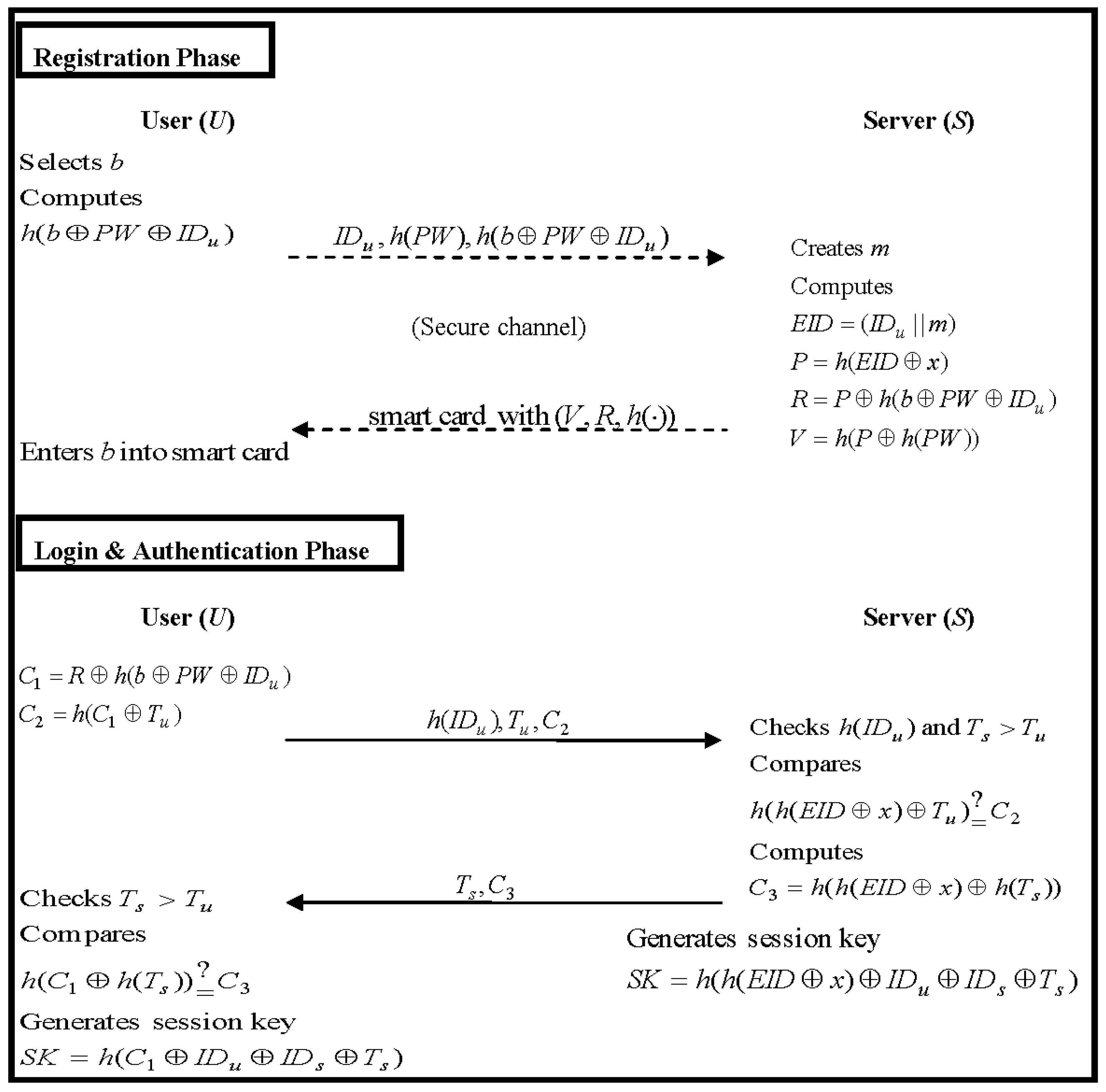
2.1. Review of Yeh et al.’s Timestamp Based Scheme

In this subsection, we briefly describe Yeh et al.’s timestamp based scheme [27], which consists of four phases: the registration phase, the login phase, the authentication phase and the password-change phase. The overview is described in Figure 1 and the notation of this scheme is listed as follows:

2.1.1. Registration Phase

In this phase, U initially registers, or re-registers, to S and the steps are described as follows:

• U selects a random number b and computes h(b ⊕ PW ⊕ ID_u). He or she then securely send ID_u, h(PW) and h(b ⊕ PW ⊕ ID_u) to S.
• S creates a new entry with a value m = 0 for U in the database or sets m = m + 1 in the existing entry. Here, m denotes the number of times of re-registering to S for each user U. Next, S computes EID, P, R and V:

  $$EID=(I{D}_u||m)$$

  (1)

  $$P=h(EID\oplus x)$$

  (2)

  $$R=P\oplus h(b\oplus PW\oplus I{D}_u)$$

  (3)

  $$V=h(P\oplus h(PW))$$

  (4)
  Then, S securely issues a smart card containing V, R, h(·) to U.
• Finally, U enters a random number b into his or her smart card.

2.1.2. Login Phase

When U wants to login S, the following steps will be performed:

• U inserts his or her smart card into the card reader and then enters the ID_u and PW.
• U’s smart card computes C₁, C₂ and sends the authentication request messages (h(ID_u), T_u, C₂) to S:

  $$C_1=R\oplus h(b\oplus PW\oplus I{D}_u)$$

  (5)

  $$C_2=h(C_1\oplus T_u)$$

  (6)

2.1.3. Authentication Phase

Upon receiving the request messages (h(ID_u), T_u, C₂), the remote server S and the smart card perform the following steps:

• S first checks the validity of h(ID_u) and T_s > T_u. If it does not hold, S rejects U’s login request; otherwise, S computes h(h(EID ⊕ x) ⊕ T_u) and compares it with C₂:

  $$h{(h(EID\oplus x)\oplus T_u)}_{=}^{?}{C}_2$$

  (7)

  If the Equation (7) holds, S accepts U’s login request and computes C₃:

  $$C_3=h(h(EID\oplus x)\oplus h(T_s))$$

  (8)

  otherwise, S rejects it. Continuously, S sends the response messages (T_s, C₃) to U and generates a session key SK for later secure communication:

  $$SK=h(h(EID\oplus x)\oplus I{D}_u\oplus I{D}_s\oplus T_s)$$

  (9)
• According the received messages (T_s, C₃), U’s smart card checks the validity of T_s > T_u. If it does not hold, U terminates the session; otherwise, U computes h(C₁ ⊕ h(T_s)) and compares it with C₃:

  $$h{(C_1\oplus h(T_s))}_{=}^{?}{C}_3$$

  (10)
  If the Equation (10) holds, U successfully authenticates S. Finally, U computes the same session key SK:

  $$SK=h(C_1\oplus I{D}_u\oplus I{D}_s\oplus T_s)$$

  (11)

  and then, U and S can use the session key SK to securely communicate with each other.

2.1.4. Password Change Phase

In this phase, U intends to exchange his or her password PW with a new one PW_new. The steps are described as follows:

• U inserts his or her smart card into the card reader, enters ID_u and PW and then requests a password change.
• U’s smart card computes P*, V* and compares V* with the stored V:

  $$P^{*}=R\oplus h(b\oplus PW\oplus I{D}_u)$$

  (12)

  $$V^{*}=h(P^{*}\oplus h(PW))$$

  (13)

  $$V^{*}{}_{=}^{?}V$$

  (14)
  If Equation (14) does not hold, the smart card rejects the request; if the number of login failures exceeds a predefined value, the smart card is locked immediately to prevent exhaustive password guessing attacks; otherwise, U inputs the new password PW_new. Afterward, U’s smart card computes R_new and V_new as follows:

  $$R_{new}=P*\oplus h(b\oplus P{W}_{new}\oplus I{D}_u)$$

  (15)

  $$V_{new}=h(P*\oplus h(PW))$$

  (16)

  then, replaces $R,V$ with R_new, V_new, respectively.

2.2. Weakness of Yeh et al.’s Timestamp Based Scheme

Although Yeh et al.’s timestamp based scheme was an improved version of Hsiang-Shih’s scheme [11], several security weaknesses still exist. These susceptibilities include: ID-theft attack, off-line password guessing attacks and undetectable on-line password guessing. We describe these attacks as follows.

2.2.1. ID-Theft Attack

In the login phase, an attacker A can intercept the login messages (h(ID_u), T_u, C₂) to compute the user’s identity ID_u as follows:

• A guesses an identity ID_A, computes a hashed value h(ID_A) and compares it with the intercepted h(ID_u).
• If the guessed hashed value is equal to h(ID_u), this indicates that A guessed the correct identity (i.e., h(ID_A) = h(ID_u)); otherwise, A retries Steps 1 and 2.

Therefore, A can easily obtain U’s identity; the relevant details will be discussed in the next subsection.

2.2.2. Off-Line Password Guessing Attacks

This involves a situation where a user’s smart card was stolen by an attacker A and where A uses the stolen smart card to extract the secret parameters b and R [15,21]. Continuously, A can use the previously eavesdropped messages (h(ID_u), T_u, C₂) or (T_s, C₃) to obtain U’s password PW according to the following steps:

• Following Section 2.2.1, the attacker A can obtain the real identity of U. Afterward, A guesses a password PW_A.
• A computes counterfeit messages C_A1 and C_A2 for comparison with the intercepted messages C₂ or C₃, as follows:

  $$C_{A1}=h(R\oplus (b\oplus P{W}_A\oplus I{D}_u)\oplus T_u)$$

  (17)

  $$C_{A1}{}_{=}^{?}{C}_2$$

  (18)

  or

  $$C_{A2}=h(R\oplus (b\oplus P{W}_A\oplus I{D}_u)\oplus h(T_s))$$

  (19)

  $$C_{A2}{}_{=}^{?}{C}_3$$

  (20)
• Since ID_u is revealed following Section 2.2.1, A can guess the correct ID_u and PW to change the user’s password. Refer to the password change phase of Section 2.1.4.

2.2.3. On-line Password Guessing Attacks

This refers to Section 2.2.2, where an attacker A is able to extract the secret parameters $b\mathrm{and}R$ through the stolen smart card. As with the previously eavesdropped messages (h(ID_u), T_u, C₂), A can guess the U’s password as follows:

• A guesses a possible password PW_A and computes a value following Equation (17) C_A1 with a timestamp T_A. A then computes counterfeit messages (h(ID_A), T_A, C_A1) to send to the server S.
• After receiving the messages, S first checks the timestamp T_s > T_u. Continuously, S computes h(h(EID ⊕ x) ⊕ T_A) to compare the received value C_A1. If both of them are equal, then PW_A is U’s correct password.
• Then, S accepts this login request and sends the messages (T_s, C₃) to A.
• According to the received messages, A can recognize that the correct password has been guessed; otherwise, A retries the above attack procedures until obtaining the correct password.

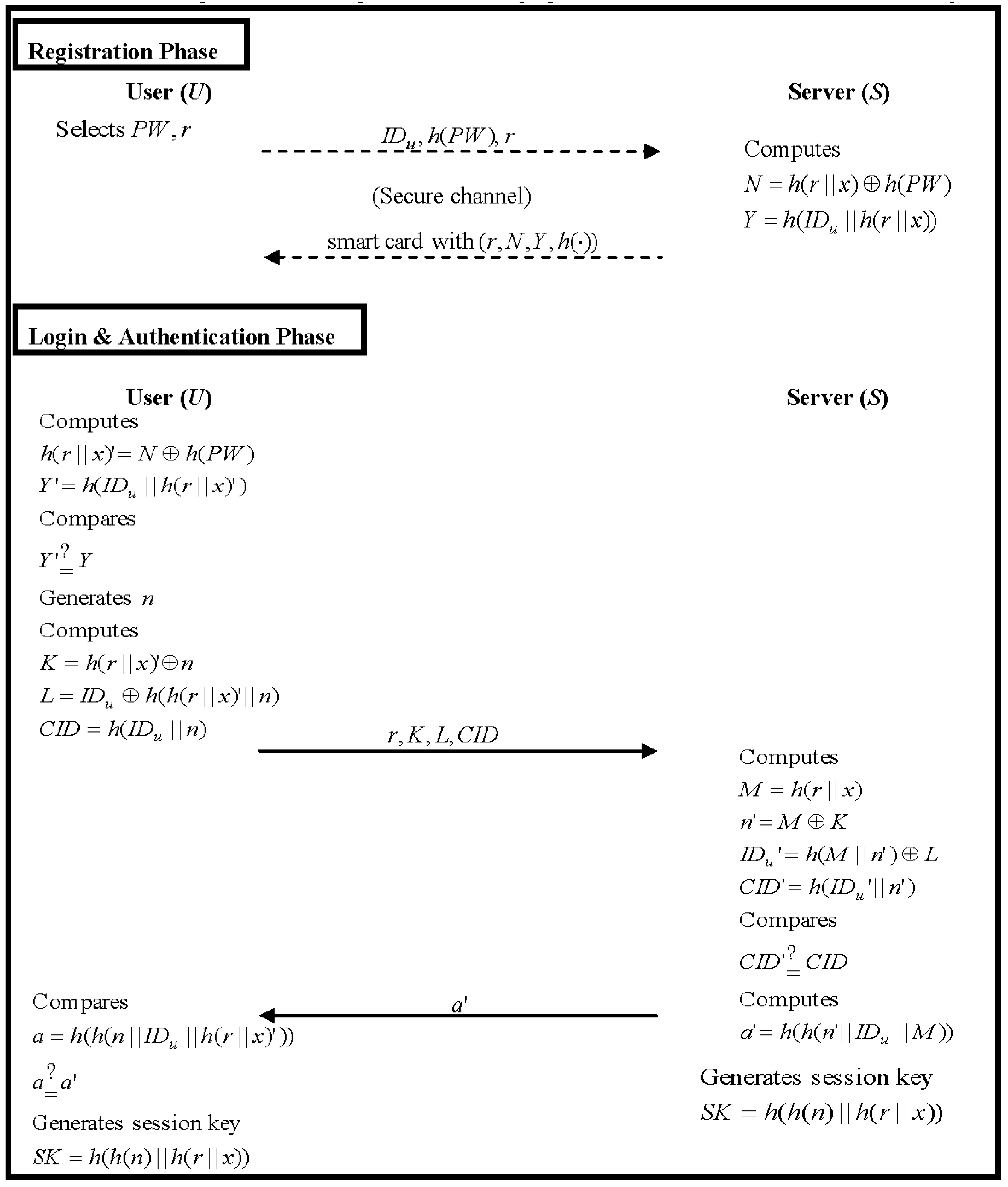
2.3. Review of Yeh et al.’s Nonce Based Scheme

Yeh et al.’s nonce based scheme [27] consists of four phases: the registration phase, the login phase, the authentication phase and the password change phase. The overview is described in Figure 2.

2.3.1. Registration Phase

When a user U wants to register to the remote server S, he or she has to perform the following steps:

• The user U first selects a password PW and a random number r. Then, U submits ID_u, h(PW) to the remote server S through a secure channel.
• When receiving the registration request messages from U, S first computes a hash value h(r||x). With h(r||x), ID_u and h(PW), S computes N and Y:

  $$N=h(r||x)\oplus h(PW)$$

  (21)

  $$Y=h(ID||h(r\left|\right|x))$$

  (22)
  Next, S initializes the smart card with r, N, Y, h(·) and sends it to U via a secure channel.

2.3.2. Login Phase

When U intends to login S, he or she first insert his or her own smart card into a card reader or the terminal. Next, U enters his or her identity ID_u and password PW. The smart card then performs the following steps:

• First, the smart card uses PW and N to derive the value h(r||x). Next, the smart card computes $Y\prime$:

  $$h(r||x)\prime =N\oplus h(PW)$$

  (23)

  $$Y\prime =h(I{D}_u||h(r\left|\right|x)\prime )$$

  (24)

  and compares Y′ with the stored Y; otherwise, the login request is rejected.
• Second, the smart card generates a nonce n and computes K, L and CID:

  $$K=h(r||x)\prime \oplus n$$

  (25)

  $$L=I{D}_u\oplus h(h(r\left|\right|x)\prime ||n)$$

  (26)

  $$CID=h(I{D}_u||n)$$

  (27)
• Third, the smart card sends login request messages (r, K, L, CID) to S.

2.3.3. Authentication Phase

After receiving the messages (r, K, L, CID), S performs the following steps to authenticate U:

• S uses the received value r and its secret x to compute the hashed value M:

  $$M=h(r||x)$$

  (28)
  Next, S computes n′, ID_u′ and CID′:

  $$n\prime =M\oplus K$$

  (29)

  $$I{D}_u\prime =h(M||n\prime )\oplus L$$

  (30)

  $$CID\prime =h(I{D}_u||n\prime )$$

  (31)
  After that, S checks whether CID′ is equal to CID or not. If it holds, S confirms that U is valid and replies a message a′ to U:

  $$a\prime =h(h(n\left|\right|I{D}_u\left|\right|M))$$

  (32)

  otherwise, S rejects the login request.
• Upon receiving message a′, U first calculates value a:

  $$a=h(h(n\left|\right|I{D}_u\left|\right|h(r||x)\prime )$$

  (33)

  and compares it with the received value a′. If both of these two values are identical, U confirms that S is valid. Since they already possess the current secret values h(r||x) and n, the session key SK will be securely agreed upon by S and U:

  $$SK=h(h(n)||h(r\left|\right|x))$$

  (34)

2.3.4. Password Change Phase

If U wants to change his or her password, the procedures are as follows:

• U first inserts his or her smart card into a card reader or the terminal and keys in the identity ID_u and the original password PW.
• Next, according to Equations (23) and (24), the smart card examines the validity of ID_u and PW and checks to see if Y′ = Y. If the verification holds, U is allowed to enter a new password PW_new; otherwise, the smart card rejects the password change request.
• Finally, the smart card calculates N′:

  $$N\prime =N\oplus h(PW)\oplus h(P{W}_{new})=h(r||x)\oplus h(P{W}_{new})$$

  (35)

  and replaces the old value N with the new one N′. Now, the password has been successfully changed without the participation of S.

2.4. Weakness of Yeh et al.’s Nonce Based Scheme

Within Yeh et al.’s nonce based scheme, a security flaw has presented. We will now describe the details of the weakness.

User Impersonation Attack

In this subsection, we assume that an attacker A, who is a malicious legal user, can use his or her smart card to extract their own secret parameters r, N and Y. A uses those parameters to impersonate the other user as follows:

• A uses his or her own PW and N to compute the hashed value h(r||x)′ (see Equation (23)).
  Continuously, A selects a nonce n and the same format of identity ID_i to compute the authentication message K, L and CID:

  $$K=h(r||x)\prime \oplus n$$

  (36)

  $$L=I{D}_i\oplus h(h(r\left|\right|x)\prime ||n)$$

  (37)

  $$CID=h(I{D}_i||n)$$

  (38)

  and then A sends (r, K, L, CID) to S.
• S uses the received value r and its secret x to compute the hashed value M (Refer to Equation (28)):
  Next, S computes n′ (Refer to Equation (29), ID_i′ and CID′:

  $$I{D}_i\prime =h(M||n\prime )\oplus L$$

  (39)

  $$CID\prime =h(I{D}_i||n\prime )$$

  (40)
  After that, S checks whether CID′ is equal to CID or not. If it holds, S confirms that A is valid and replies a message a′ to A:

  $$a\prime =h(h(n\left|\right|I{D}_i\left|\right|M))$$

  (41)
• After receiving message a′, A can confirm that he or she pass the authentication to impersonate the User i.

For this reason, if A is a malicious legal user, he or she can impersonate any legal user to communicate with remote user. Yeh et al.’s nonce based scheme is similar to a no identity authentication.

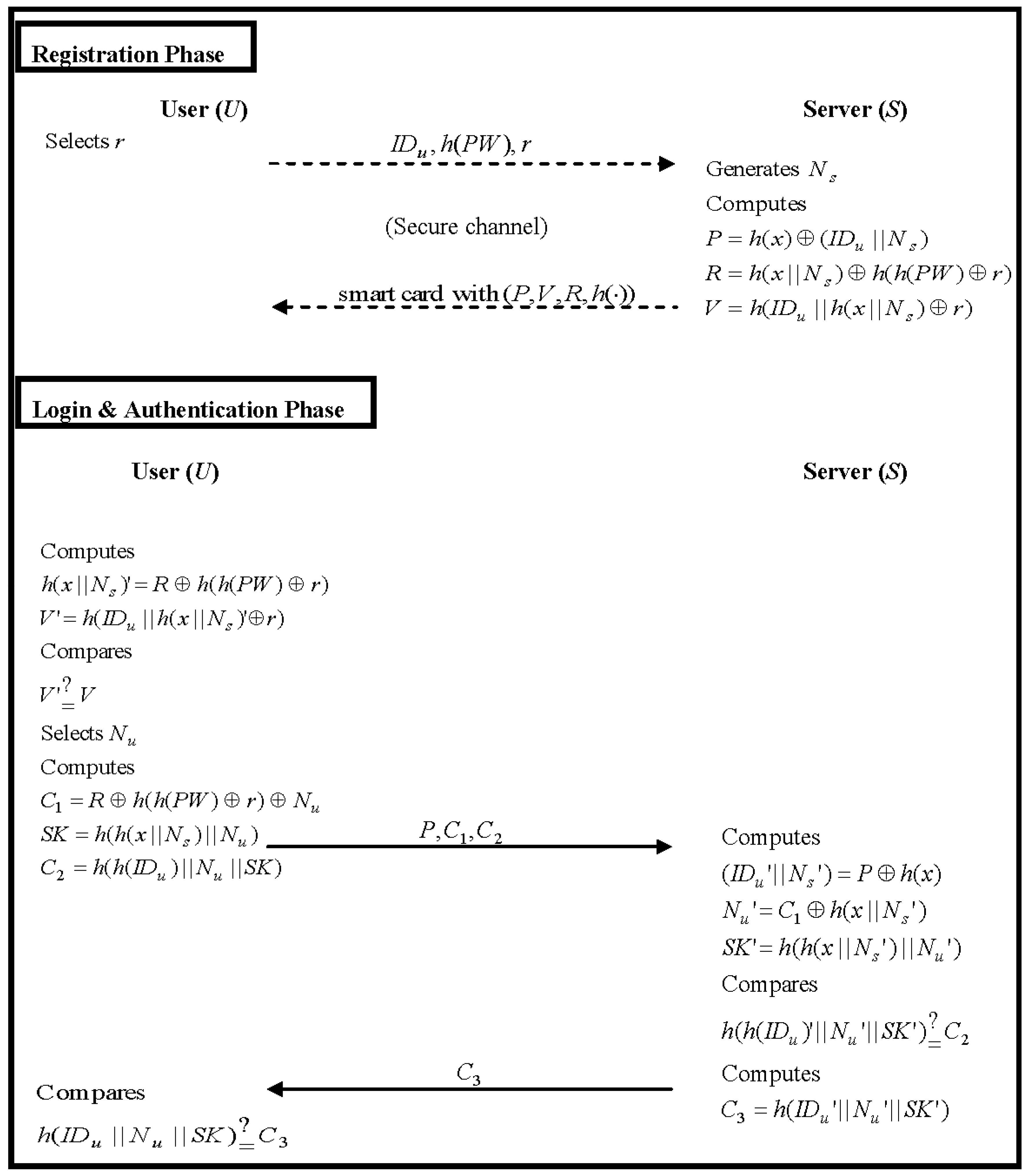
3. The Improved Scheme

In the context of Yeh et al.’s two user authentication schemes, there are some security flaws remaining. Therefore, we have designed a scheme with two unknown factors to protect each parameter in the smart card. Our remediable scheme consists of four phases: the registration phase, the login phase, the authentication phase and the password change phase. We describe these phases in the following subsection and an overview of our improved scheme is presented in Figure 3.

3.1. Registration Phase

• The user U chooses a password and selects a random number r, then submits the registration messages (ID_u, h(PW), r) to the remote server S via a secure channel.
• When S receives the registration messages from U, S first generates a nonce N_s and uses ID_u and h(PW) to compute three values P, R and V:

  $$P=h(x)\oplus (I{D}_u||N_s)$$

  (42)

  $$R=h(x||N_s)\oplus h(h(PW)\oplus r)$$

  (43)

  $$V=h(I{D}_u||h(x\left|\right|N_s)\oplus r)$$

  (44)
  Afterward, S issues the smart card with parameters P, R, V and h(·) to U through a secure channel.

3.2. Login Phase

If U wants to login S, he or she first insert his or her own smart card into a card reader or the terminal. Then, U enters his or her ID_u and PW. The smart card performs the following steps:

• The smart card uses random number r, PW and R to compute a value h(x||N_s)′ and calculate V′ to compare with V:

  $$h(x||N_s)\prime =R\oplus h(h(PW)\oplus r)$$

  (45)

  $$V\prime =h(I{D}_u||h(x\left|\right|N_s)\prime \oplus r)$$

  (46)

  $$V{\prime }_{=}^{?}V$$

  (47)
  If Equation (47) holds, the smart card generates a nonce N_u and computes messages C₁, SK and C₂; otherwise, the login request is rejected:

  $$C_1=R\oplus h(h(PW)\oplus r)\oplus N_u$$

  (48)

  $$SK=h(h(x\left|\right|N_s)||N_u)$$

  (49)

  $$C_2=h(h(I{D}_u)|\left|N_u\right||SK)$$

  (50)
• Finally, the smart card sends login request messages (P, C₁, C₂) to S.

3.3. Authentication Phase

Upon receiving the login request (P, C₁, C₂), S has to perform the following steps to authenticate U:

• S uses the received value P and its secret key x to obtain (ID_u′ and N_s′):

  $$(I{D}_u\prime ||N_s\prime )=P\oplus h(x)$$

  (51)
  Afterward, S computes N_u′ and SK′ to check if the authentication message C₂ is valid or not:

  $$N_u\prime =C_1\oplus h(x||N_s\prime )$$

  (52)

  $$SK\prime =h(h(x\left|\right|N_s\prime )||N_u\prime )$$

  (53)

  $$h{(h(I{D}_u\prime )||N_u\prime ||SK\prime )}_{=}^{?}{C}_2$$

  (54)
  If Equation (54) holds, S confirms that U is a legal user and responds a message C₃ to U:

  $$C_3=h(I{D}_u\prime ||N_u\prime ||SK\prime )$$

  (55)
  Otherwise, S rejects the login request.
• When receiving the response C₃, U first verifies whether the message is valid or not:

  $$h{(I{D}_u|\left|N_u\right||SK\prime )}_{=}^{?}{C}_3$$

  (56)
  If the Equation (56) holds, U confirms that S is valid. Afterward, U and S can use the same session key SK to securely communicate with each other.

3.4. Password Change Phase

In this phase, if a U wants to change his or her password, he or she will perform the following steps:

• First, U inserts his or her smart card into a card reader or the terminal and enters the ID_u and the original PW.
• Second, according to Equations (46) and (47), the smart card examines the validity of ID_u and PW and compares V′ with the stored V. If this holds, U is allowed to key in a new password PW_new; otherwise, the smart card rejects the password change request.
• Third, the smart card calculates $R\prime$:

  $$R\prime =R\oplus h(PW)\oplus h(P{W}_{new})=h(x||N_s)\oplus h(P{W}_{new})$$

  (57)

  and replaces the old value R with the new R′. Thus, the password has been successfully changed without the participation of remote server S.

4. Security Analysis

In this section, we will discuss the security of our improved scheme and demonstrate how it is more secure than previous schemes.

4.1. Mutual Authentication

In the proposed scheme, when the personal reader wants to communicate with the medical reader, they must authenticate each other. In this subsection, we use the Burrows–Abadi–Needham (BAN) logic model [40] to proof the correctness of our improved scheme. Recently, many authentication schemes [41,42,43] have applied BAN logic to proof the correctness of an authentication and key establishment. The symbols N_s and N_u are nonces; h(x), h(x||N_s) and SK denotes the secret keys; the notation of Ban logic is described as follows:

$P|\equiv X$	P believes X, or P would be entitled to believe X.
$P⊲X$	P sees X. Someone has sent a message containing X to P, who can read and repeat X.
$P|~X$	P once said X. P at some time sent a message including X.
$P|\Rightarrow X$	P has jurisdiction over X. P is an authority on X and should be trusted on this matter.
$<X{>}_Y$	This represents X combined with Y.
$\#(X)$	The formula X is fresh, that is, X has not been sent in a message at any time before the current run of the protocol.
$P\stackrel{K}{\leftrightarrow }Q$	P and Q may use the shared key K to communicate.
$P\stackrel{S}{\iff }Q$	The formula S is a secret known only to P and Q and possibly to principals trusted by them.

The main goal of our scheme is to authenticate the session key establishment between a user U and the remote server S.

G1	$U|\equiv U\stackrel{SK}{\leftrightarrow }S$
G2	$U|\equiv S|\equiv U\stackrel{SK}{\leftrightarrow }S$
G3	$S|\equiv U\stackrel{SK}{\leftrightarrow }S$
G4	$S|\equiv U|\equiv U\stackrel{SK}{\leftrightarrow }S$
G5	$S|\equiv I{D}_u$
G6	$S|\equiv U|\equiv I{D}_u$

According to our authentication phase, we use BAN logic to produce an idealized form as follows:

M1	$(<I{D}_u||N_s{>}_{h(x)},<N_u{>}_{h(x||N_s)},<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$
M2	$(<U\stackrel{SK}{\leftrightarrow }S{>}_{h(I{D}_u||N_u)})$

To analyze our improved scheme, we make the following assumptions:

A1	$U|\equiv \#(N_u)$
A2	$S|\equiv \#(N_u)$
A3	$U|\equiv U\stackrel{h(x||N_s)}{\iff }S$
A4	$S|\equiv U\stackrel{h(x||N_s)}{\iff }S$
A5	$U|\equiv S|\Rightarrow U\stackrel{SK}{\leftrightarrow }S$
A6	$S|\equiv U|\Rightarrow U\stackrel{SK}{\leftrightarrow }S$
A7	$S|\equiv U|\Rightarrow I{D}_u$

According to those assumptions and the rules of BAN logic, we show the main proof of our authentication phase as follows:

• Server S authenticates user U.
  By M1 and the seeing rule, we can derive:

  $$S⊲(<I{D}_u||N_s{>}_{h(x)},<N_u{>}_{h(x||N_s)},<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 1)
  By A2 and the freshness rule, we can derive:

  $$S|\equiv \#(<I{D}_u||N_s{>}_{h(x)},<N_u{>}_{h(x||N_s)},<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 2)
  By (Statement 1), A4 and the message meaning rule, we can derive:

  $$S|\equiv U|~(<I{D}_u||N_s{>}_{h(x)},<N_u{>}_{h(x||N_s)},<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 3)
  By (Statement 2), (Statement 3) and the nonce verification rule, we can derive:

  $$S|\equiv U|\equiv (<I{D}_u||N_s{>}_{h(x)},<N_u{>}_{h(x||N_s)},<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 4)
  By (Statement 4) and the belief rule, we can derive:

  $$S|\equiv U|\equiv U\stackrel{SK}{\leftrightarrow }S$$

  (Statement 5)
  By (Statement 5), A6 and the jurisdiction rule, we can derive:

  $$S|\equiv U\stackrel{SK}{\leftrightarrow }S$$

  (Statement 6)
  By (Statement 6) and the belief rule, we can derive:

  $$S|\equiv U|\equiv I{D}_u$$

  (Statement 7)
  By (Statement 7), A7 and the jurisdiction rule, we can derive:

  $$S|\equiv I{D}_u$$

  (Statement 8)
• User U authenticates server S.
  By M2 and the seeing rule, we can derive:

  $$U⊲(<U\stackrel{SK}{\leftrightarrow }S{>}_{h(I{D}_u||N_u)})$$

  (Statement 9)
  By A1 and the freshness rule, we can derive:

  $$U|\equiv \#(<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 10)
  By (Statement 9), A3 and the message meaning rule, we can derive:

  $$U|\equiv S|~(<U\stackrel{SK}{\leftrightarrow }S{>}_{h(h(I{D}_u)||N_u)})$$

  (Statement 11)
  By (Statement 10), (Statement 11) and the message meaning rule, we can derive:

  $$U|\equiv S|\equiv U\stackrel{SK}{\leftrightarrow }S$$

  (Statement 12)
  By (Statement 12), A5 and the jurisdiction rule, we can derive:

  $$U|\equiv U\stackrel{SK}{\leftrightarrow }S$$

  (Statement 13)

By (Statement 5) to (Statement 8), (Statement 12) and (Statement 13), we can proof our improved scheme such that user U and the remote server S authenticate each other. Moreover, we are also able to prove that the improved scheme can establish a session key between the user U and the remote server S.

In our improved scheme, the server authenticates the user by checking the message C₂. If server’s computed value h(h(ID_u′)||N_u′||SK′) is equal to C₂, the server proves that the user is valid. Then, server sends message C₃ to the user. The user also compares C₃ with his or her computation value h(ID_u||N_u||SK′). If both of them are equal, the user confirms that the server is legitimate. Since the secret value h(x||N_s) is shared between user and server, they can authenticate each other with the login messages (P, C₁, C₂) and the reply message C₃. Hence, mutual authentication obtains in our improved scheme.

Scenario:

A malicious attacker uses an illegal server to authenticate a legal user.

Analysis:

The attacker will not succeed because the legal user has not been registered to the illegal server and the illegal server cannot calculate the correct session key SK. Thus, it will fail when the legal user attempts to authenticate the illegal server. In the proposed scheme, the attacker cannot achieve their purpose using an illegal server. In the same scenario, the proposed scheme can also defend against a malicious attack using an illegal user to connect to a legal server. This is why the illegal user has not been registered to the legal server and the illegal user cannot calculate the correct session key SK. Thus, the attack will fail when the legal server attempts to authenticate the illegal user.

4.2. Lost Smart Card

According to our improved scheme, if an attacker A obtains a legal user U’s smart card somehow, they cannot obtain any parameter without the user’s password; even if A extracts the parameters P, R and V (see Equations (42)–(44)) from the smart card, they still cannot obtain any sensitive information (such as ID_u, PW, N_s or the server’s secret key x) with those parameters. Notably, A does not know U’s correct password and each parameter is always protected by two unknown factors of the smart card. Therefore, no one can use the stolen smart card to obtain authentication without U’s correct password and identity.

4.3. ID-Theft Attack

As regards the login and authentication phases of our improved scheme, U’s ID_u is always protected by P and C₂; it is impossible for an attacker A to acquire it from P and C₂. Notably, it is difficult to reveal ID_u from P without the server’s secret key x and the nonce N_s. Additionally, A cannot obtain ID_u from C₂ without the nonce N_u. Therefore, ID_u cannot be known by the attacker.

4.4. Password Guessing Attacks

This situation involves an attacker A obtaining the U’s smart card and intercepting previous messages. In this case, A intends to guess the U’s PW from the stored parameter R of the smart card and must know the secret key x and the nonce N_s to compute similar parameters for comparison with parameter R. On the other hand, A can use R and the intercepted P to compute similar messages (P, C₁′, C₂′) and send it to S in an attempt to guess U’s PW. As A has two unknown values, ID_u and PW, it is difficult to successfully complete this password guessing attack.

4.5. Server Counterfeit Attack and User Impersonation Attack

Notably, Yeh et al.’s schemes will compromise the server’s secret key x in the context of a malicious legal user, allowing forgery of another legal user and a remote server. Hence, in the registration phase of our improved scheme (see Equation (42)), the remote server S generates a nonce value N_s to compute parameter P with U’s identity ID_u and its secret key x, where the nonce value N_s is different for each user. So, the malicious legal user cannot guess x with an unknown value N_s. As such, these two attacks will be prevented.

4.6. Replay Attack

In our improved scheme, we use a nonce mechanism to prevent the replay attack and to solve the synchronization problem. When an attacker intends to replay the previous messages (P, C₁, C₂) to achieve authentication, they cannot as the nonce value N_u is different in each session. For this reason, the attacker cannot achieve authentication using previous messages.

Scenario:

A malicious attacker intercepts the transmitted message between the user and the server and sends the same message again to the user or the server.

Analysis:

The attacker will not succeed because the legal user uses the nonce value N_u in each session. The attacker cannot get the correct nonce value N_u. Thus, the attack will fail when the legal server authenticates the received message. In the proposed scheme, the attackers cannot achieve their purpose by sending the same message again to the user or to the server. Therefore, attackers cannot achieve their purpose by replay attack.

5. Performance Analysis

In this section, we compare the security requirements and computation costs with other related proposals in the literature [9,11,27] in

Table 1. Security comparison between other related researches and ours.

	Hsiang and Shih’s Scheme (2009)	Wang et al.’s Scheme (2009)	Yeh et al.’s Timestamp-Based Scheme (2010)	Yeh et al.’s Nonce-Based Scheme (2010)	Ours
Mutual authentication	Yes	Yes	Yes	Yes	Yes
Freely change password	Yes	Yes	Yes	Yes	Yes
Solve clock synchronization problem	No	No	No	Yes	Yes
Lost smart card	No	No	No	Yes	Yes
Prevention of ID-theft attack	No	No	No	Yes	Yes
Prevention of undetectable on-line password guessing attacks	No	No	No	Yes	Yes
Prevention of off-line password guessing attacks	No	No	No	Yes	Yes
Prevention of user impersonation attack	No	No	Yes	No	Yes
Prevention of server counterfeit attack	No	No	Yes	Yes	Yes
Prevention of man-in-the-middle attack	No	No	Yes	Yes	Yes
Prevention of replay attack	No	No	Yes	Yes	Yes
Prevention of session parallel attack	Yes	Yes	Yes	Yes	Yes

and

Table 2. Performance comparison between other related researches and ours.

	Hsiang and Shih’s Scheme (2009)	Wang et al.’s Scheme (2009)	Yeh et al.’s Timestamp-Based Scheme (2010)	Yeh et al.’s Nonce-Based Scheme (2010)	Ours
Registration phase	4H + 4Xor	2H + 2Xor	4H + 5Xor	3H + 1Xor	4H + 2Xor
Login & authentication phase	8H + 7Xor	6H + 13Xor	11H + 14Xor	15H + 5Xor	12H + 4Xor
Password change phase	6H + 6Xor	2H + 2Xor	6H + 6Xor	3H + 2Xor	3H + 2Xor
Total	18H + 17Xor	10H + 17Xor	21H + 25Xor	21H + 8Xor	19H + 8Xor

H denotes one way hash operation; Xor denotes bitwise exclusive operation.

, respectively. Recent research [6,9,11,19,25,27,28] has generally only considered one unknown factor for each parameter; this is why their schemes were compromised and have become susceptible to various attacks. However, our improved scheme always consists of two unknown factors within each communication to meet more stringent security requirements. It can be clearly observed that our scheme is more secure than those proposed by others. From Table 2, the proposed scheme’s computation costs for our scheme and previous researchers’ schemes in each phase are analyzed. For the highest computation cost in the login & authentication phase, Hsiang and Shih’s scheme needs eight hash function operations and seven exclusive-or operations. Wang et al.’s scheme needs six hash function operations and thirteen exclusive-or operations. Yeh et al.’s timestamp-based scheme needs eleven hash function operations and fourteen exclusive-or operations. Yeh et al.’s nonce-based scheme needs fifteen hash function operations and five exclusive-or operations. Our scheme needs twelve hash function operations and four exclusive-or operations. Generally speaking, the computation cost of our scheme is comparable to Yeh et al.’s scheme and inferior to Hsiang and Shih’s scheme. However, our scheme can defend against all of the attacks discussed herein more effectively than all previous attempts.

6. Conclusions

In this paper, we first reviewed Yeh et al.’s two remote user authentication schemes using smart cards. They claimed that their schemes could defend against known attacks more effectively and more efficiently than previous related research. However, in our cryptanalysis, we find that Yeh et al.’s claims allow for further improvements and that their proposals exhibit serious security flaws, i.e., susceptibility to ID-theft attacks, off-line password guessing attacks, undetectable on-line password guessing attacks and user impersonation attacks. Moreover, based on other related researches [15,21], if an attacker can obtain a legal user’s smart card, they can extract the secret parameters from the smart card to successfully complete password guessing attacks. Additionally, in cases where an attacker is a malicious legal user, the attacker can use their smart card to impersonate any legal user. This factor results in the security flaws we discussed above; hence, many schemes will be insecure.

To remedy the specific security problems detailed in this paper, we have proposed an improved scheme. The proposed scheme consistently protects each secret parameter with two unknown factors in the smart card; thus, an attacker cannot obtain any sensitive information, even if he or she is a malicious legal user. Most notably, our scheme not only addresses more stringent security requirements and protects against known types of attacks, it also reduces computation costs more effectively than Yeh et al.’s scheme. Therefore, our scheme holds substantial value in the context of numerous applications in various network environments.