Quantum Genetic Algorithms for Computer Scientists
Abstract
:1. Introduction
2. What is Quantum Computing?
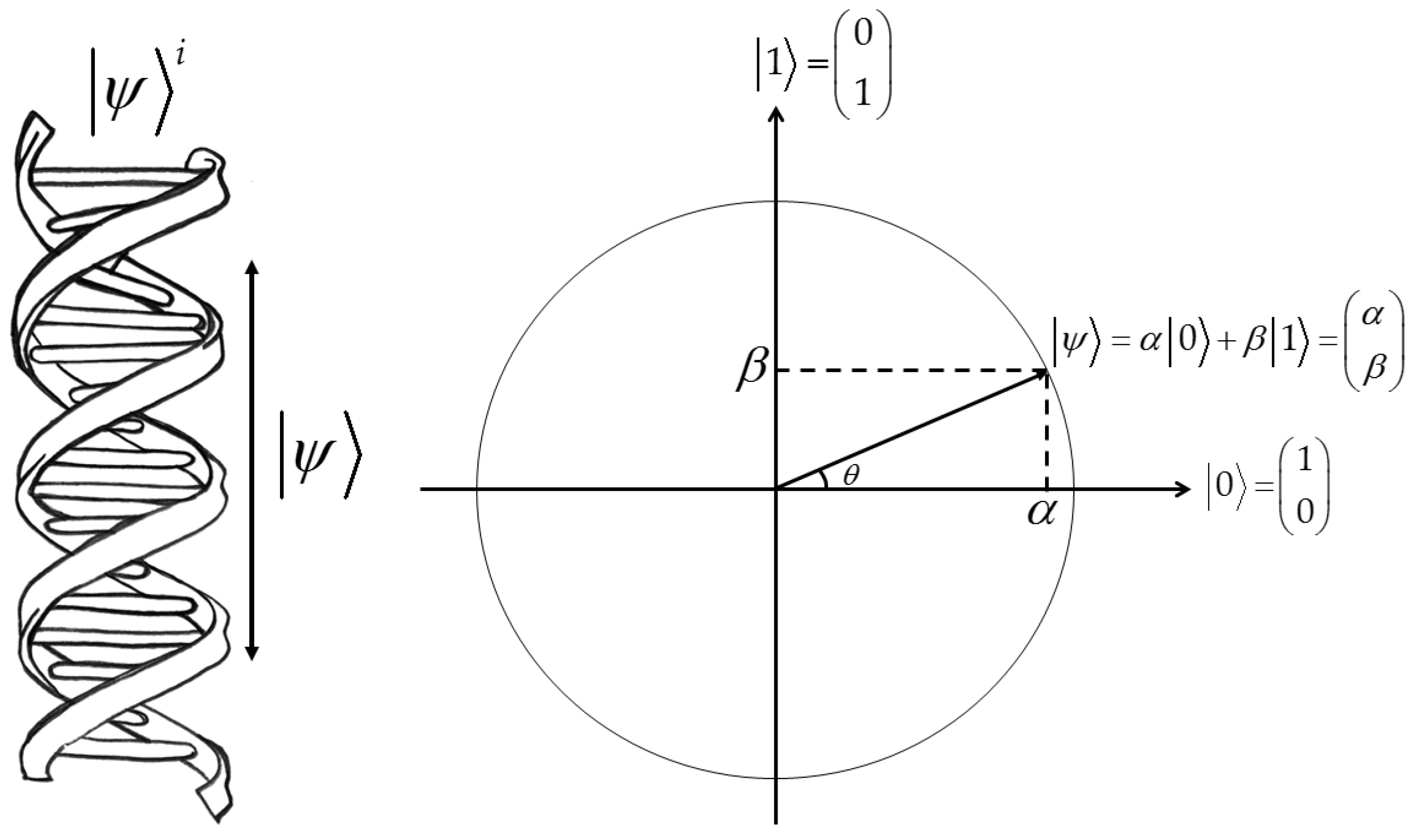
2.1. Quantum Information
2.2. Quantum Gates
2.3. Quantum Algorithms and Quantum Circuits
2.4. Quantum Computing in Practice
2.4.1. Q-Circuit Simulators
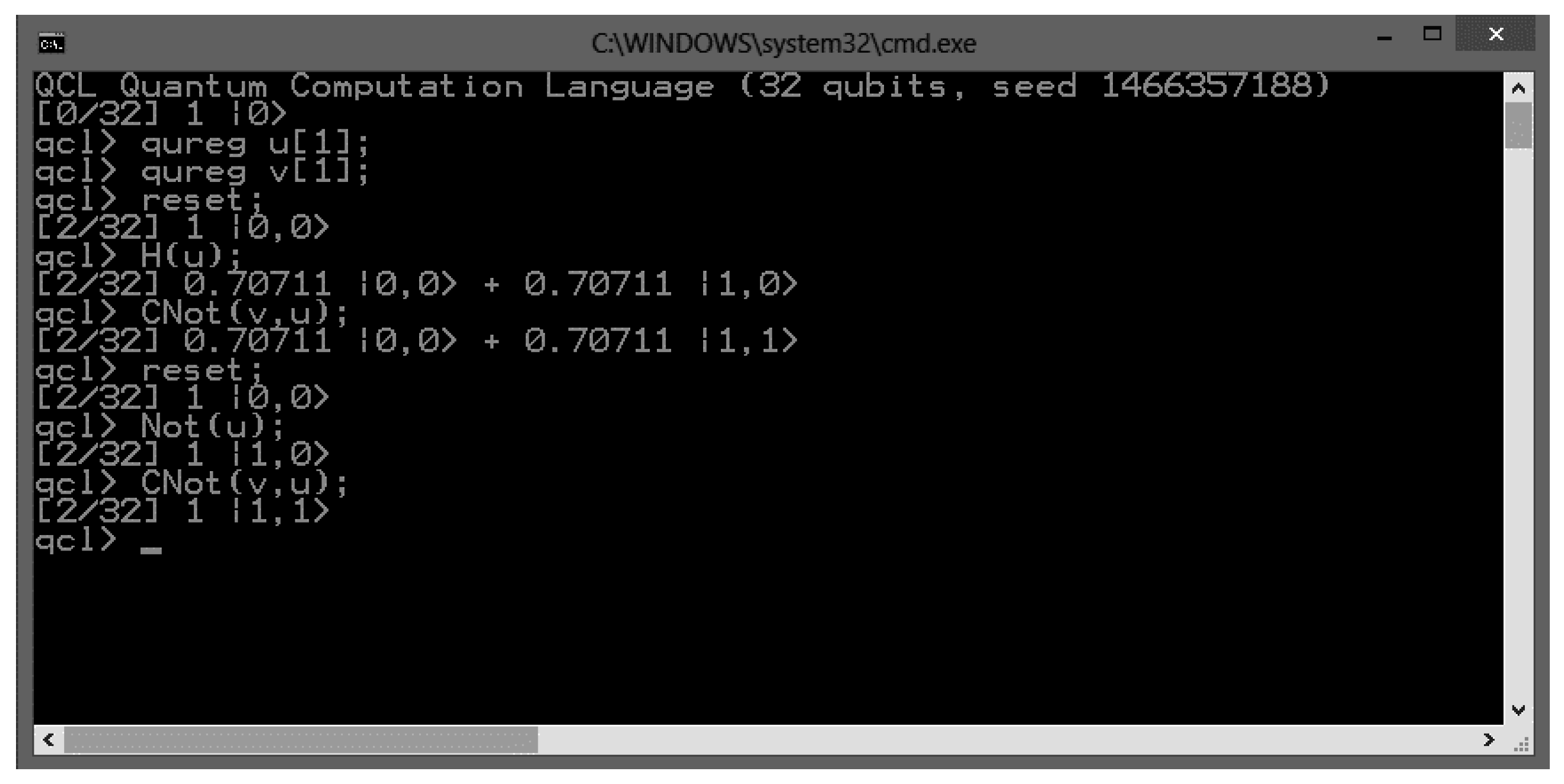
2.4.2. Q-Programming Languages
2.4.3. Simulated Q-Computer
2.4.4. Do-It-Yourself: Quantum Computing with Python
3. Quantum Computing and Quantum Evolutionary Algorithms
3.1. Quantum Genetic Operators
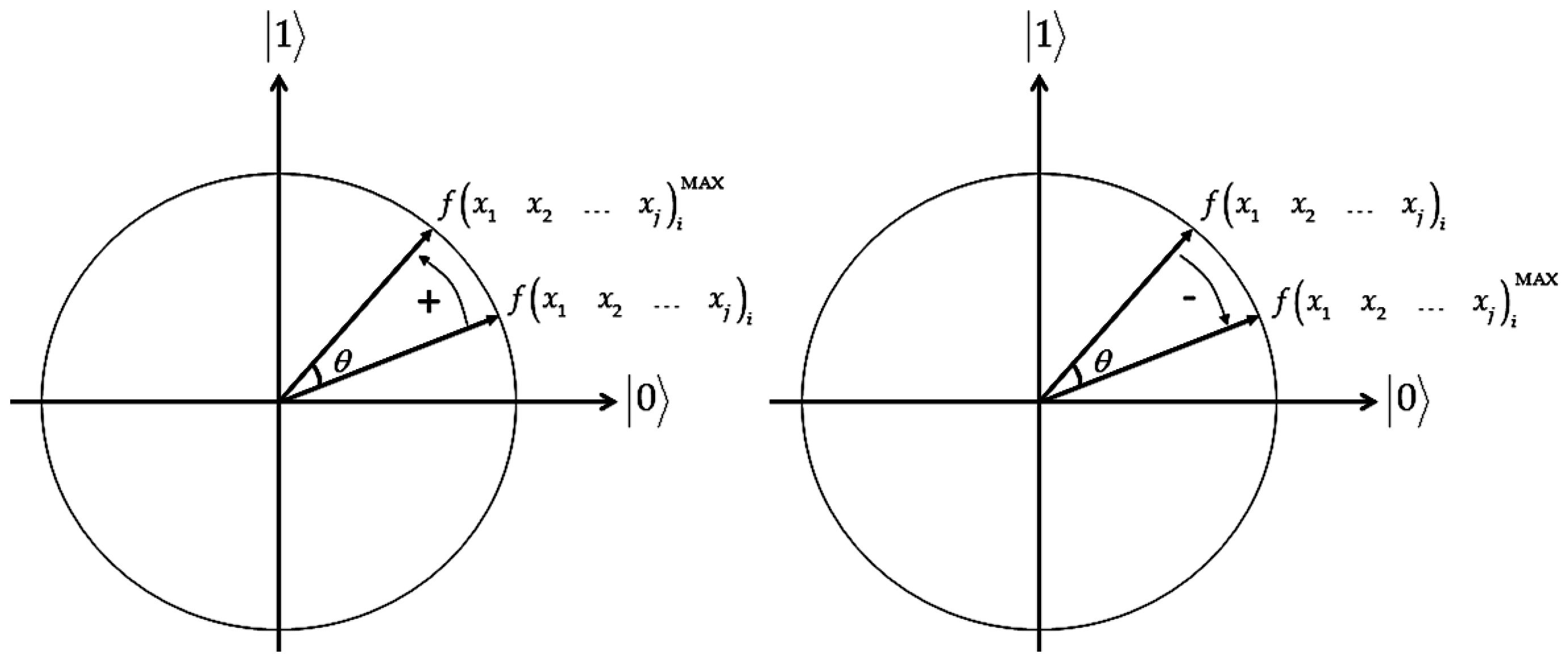
3.1.1. Qubit (Interference) Rotation Gate
3.1.2. Quantum Mutation (Inversion) Gate
3.1.3. Quantum Mutation (Insertion) Gate
3.1.4. Quantum Crossover (Classical) Gate
3.1.5. Quantum Crossover (Interference) Gate
3.2. A Canonical Classification of Quantum Evolutionary Algorithms
4. Towards True Quantum Evolutionary Algorithms
5. Simulation Experiments
6. Results
7. Future Directions
8. Conclusions
Acknowledgments
Conflicts of Interest
References
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989; pp. 1–432. [Google Scholar]
- Lahoz-Beltra, R. Bioinformática: Simulación, Vida Artificial e Inteligencia Artificial; Ediciones Díaz de Santos: A Coruña, Spain, 2004; pp. 237–323. (In Spanish) [Google Scholar]
- Perales-Gravan, C.; Lahoz-Beltra, R. An AM radioreceiver designed with a genetic algorithm based on a bacterial conjugation genetic operator. IEEE Trans. Evolut. Comput. 2008, 12, 129–142. [Google Scholar] [CrossRef]
- Ribeiro Filho, J.L.; Treleaven, P.C.; Alippi, C. Genetic-algorithm programming environments. IEEE Comput. 1994, 24, 28–43. [Google Scholar] [CrossRef]
- Calvin, W.H. The brain as a Darwin machine. Nature 1987, 330, 33–34. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Fraser, A.S. Simulation of genetic systems by automatic digital computers. Aust. J. Biol. Sci. 1957, 10, 484–491. [Google Scholar] [CrossRef]
- Han, K.-H.; Kim, J.-H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evolut. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Ying, M. Quantum computation, quantum theory and AI. Artif. Intell. 2010, 174, 162–176. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R.; University of Stirling, Computing Science and Mathematics School of Natural Sciences, Stirling, Scotland, United Kingdom. Quantum Genetic Algorithms for Computer Scientists. Computing Science Seminars, Spring 2015, 26 June. Personal communication, 2015. [Google Scholar]
- Susskind, L.; Friedman, A. Quantum Mechanics: The Theoretical Minimum; Penguin Books: London, UK, 2015; pp. 1–364. [Google Scholar]
- Boghosian, B.M.; Taylor, W., IV. Simulating quantum mechanics on a quantum computer. Phys. D 1998, 120, 30–42. [Google Scholar] [CrossRef]
- Alfonseca, M.; Ortega, A.; de La Cruz, M.; Hameroff, S.R.; Lahoz-Beltra, R. A model of quantum-von Neumann hybrid cellular automata: Principles and simulation of quantum coherent superposition and decoherence in cytoskeletal microtubules. Quantum Inf. Comput. 2015, 15, 22–36. [Google Scholar]
- Zeiter, D. A Graphical Development Environment for Quantum Algorithms. Master’s Thesis, Department of Computer Science, ETH Zurich, Zürich, Switzerland, 3 September 2008. [Google Scholar]
- Quantum Computing. How D-Wave Systems Work. Available online: http://www.dwavesys.com/quantum-computing (accessed on 1 July 2016).
- Quantum Circuit Simulator. Available online: http://www.davyw.com/quantum/ (accessed on 25 April 2016).
- QCAD: GUI Environment for Quantum Computer Simulator. Available online: http://qcad.osdn.jp/ (accessed on 25 April 2016).
- jQuantum—Quantum Computer Simulation Applet. Available online: http://jquantum.sourceforge.net/jQuantumApplet.html (accessed on 25 April 2016).
- Hayes, B. Programming your quantum computer. Am. Sci. 2014, 102, 22–25. [Google Scholar] [CrossRef]
- QCL—A Programming Language for Quantum Computers. Available online: http://tph.tuwien.ac.at/~oemer/qcl.html (accessed on 25 April 2016).
- Al Daoud, E. Quantum computing for solving a system of nonlinear equations over GF(q). Int. Arab J. Inf. Technol. 2007, 4, 201–205. [Google Scholar]
- Arustei, S.; Manta, V. QCL implementation of the Bernstein-Vazirani algorithm. Bul. Inst. Politech. Din Iasi 2008, 54, 35–44. [Google Scholar]
- Glendinning, I.; Ömer, B. Parallelization of the General Single Qubit Gate and CNOT for the QC-lib Quantum Computer Simulator Library. In Proceedings of the PPAM 2003, Czestochowa, Poland, 7–10 September 2003; Wyrzykowski, R., Dongarra, J., Paprzycki, M., Wasniewski, J., Eds.; Volume 3019, pp. 461–468.
- Ray, P. Quantum simulation of Dijkstra’s algorithm. Int. J. Adv. Res. Comput. Sci. Manag. Stud. 2014, 2, 30–43. [Google Scholar]
- Yingchareonthawornchai, S.; Aporntewan, C.; Chongstitvatana, P. An Implementation of Compact Genetic Algorithm on a Quantum Computer. In Proceedings of the 2012 International Joint Conference on Computer Science and Software Engineering (JCSSE), Bangkok, Thailand, 30 May–1 June 2012; pp. 131–135.
- Introduction to Quantum Computing. A Guide to Solving Intractable Problems Simply. Available online: http://www.ibm.com/developerworks/library/l-quant/ (accessed on 24 February 2016).
- Quantum Programming Language. Available online: https://quantiki.org/wiki/quantum-programming-language (accessed on 24 February 2016).
- Adam Miszczak, J. High-Level Structures for Quantum Computing; Morgan & Claypool: San Rafael, CA, USA, 2012. [Google Scholar]
- Rüdiger, R. Quantum programming languages: An introductory overview. Comput. J. 2007, 50, 134–150. [Google Scholar] [CrossRef]
- Google’s Quantum Computing Playground. Available online: www.quantumplayground.net (accessed on 26 April 2016).
- Quantum in the Cloud. Available online: http://cnotmz.appspot.com/ (accessed on 26 April 2016).
- Quantum Computing Simulation in Pure Python. Available online: https://code.google.com/archive/p/pyqu/ (accessed on 26 April 2016).
- Qitensor: A Quantum Information Module for Python. Available online: https://github.com/dstahlke/qitensor (accessed on 26 April 2016).
- QuTiP: Quantum Toolbox in Python. Available online: http://qutip.org/ (accessed on 26 April 2016).
- Cugini, A. Quantum Mechanics, Quantum Computation, and the Density Operator in SymPy. Available online: http://digitalcommons.calpoly.edu/physsp/38/ (accessed on 26 April 2016).
- Han, K-H. Quantum-inspired evolutionary algorithms with a new termination criterion, gate, and two-phase scheme. IEEE Trans. Evolut. Comput. 2004, 8, 156–169. [Google Scholar]
- Zhang, G. Quantum-inspired evolutionary algorithms: A survey and empirical study. J. Heuristics 2011, 17, 303–351. [Google Scholar] [CrossRef]
- Roy, U.; Roy, S.; Nayek, S. Optimization with quantum genetic algorithm. Int. J. Comput. Appl. 2014, 102, 1–7. [Google Scholar]
- Sun, Y.; Xiong, H. Function optimization based on quantum genetic algorithm. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 144–149. [Google Scholar]
- Zhifeng, Z.; Hongjian, Q. A New Real-Coded Quantum Evolutionary Algorithm. In Proceedings of the 8th WSEAS International Conference on Applied Computer and Applied Computational Science, Hangzhou, China, 20–22 May 2009; pp. 426–429.
- Wang, H.; Li, L.; Liu, J.; Wang, Y.; Fu, C. Improved quantum genetic algorithm in application of scheduling engineering personnel. Abstr. Appl. Anal. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Lee, J.-C.; Lin, W.-M.; Liao, G.-C.; Tsao, T.-P. Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system. Electr. Power Energy Syst. 2011, 33, 189–197. [Google Scholar] [CrossRef]
- Talbi, H.; Draa, A.; Batouche, M. A novel quantum-inspired evolutionary algorithm for multi-sensor image registration. Int. Arab J. Inf. Technol. 2006, 3, 9–15. [Google Scholar]
- Hu, W. Cryptanalysis of TEA using quantum-inspired genetic algorithms. J. Softw. Eng. Appl. 2010, 3, 50–57. [Google Scholar] [CrossRef]
- Han, K.-H.; Kim, J.-H. Introduction of Quantum-Inspired Evolutionary Algorithm. In Proceedings of the 2002 FIRA Robot World Congress, Seoul, Korea, 26–28 May 2002; pp. 243–248.
- Laboudi, Z.; Chikhi, S. A Retroactive Quantum-Inspired Evolutionary Algorithm. In Proceedings of the Arab Conference on Information and Technology ACIT 2010, Benghazi, Lybia, 15–17 December 2010.
- Laboudi, Z.; Chikhi, S. Comparison of genetic algorithm and quantum genetic algorithm. Int. Arab J. Inf. Technol. 2012, 9, 243–249. [Google Scholar]
- Han, K.-H.; Kim, J.-H. Genetic Quantum Algorithm and Its Application to Combinatorial Optimization Problem. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 1354–1360.
- Ma, S.; Jin, W. A New Parallel Quantum Genetic Algorithm with Probability-Gate and Its Probability Analysis. In Proceedings of the 2007 International Conference on Intelligent Systems and Knowledge Engineering (ISKE 2007), Chengdu, China, 15–16 October 2007.
- Junan, Y.; Bin, L.; Zhenquan, Z. Research of quantum genetic algorithm and its application in blind source separation. J. Electron. 2003, 20, 62–68. [Google Scholar]
- Hang, B.; Jiang, J.; Gao, Y.; Ma, Y. A Quantum Genetic Algorithm to Solve the Problem of Multivariate. In Information Computing and Applications, Proceedings of the Second International Conference ICICA 2011, Qinhuangdao, China, 28–31 October 2011; Liu, C., Chang, J., Yang, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 308–314. [Google Scholar]
- Xiao, J.; Yan, Y.; Lin, Y.; Yuan, L.; Zhang, J. A Quantum-Inspired Genetic Algorithm for Data Clustering. In Proceedings of the IEEE World Congress on Computational Intelligence Evolutionary Computation, 2008, CEC 2008, Hong Kong, 1–6 June 2008; pp. 1513–1519.
- Shu, W.; He, B. A Quantum Genetic Simulated Annealing Algorithm for Task Scheduling. In Advances in Computation and Intelligence, Proceedings of the Second International Symposium ISICA 2007, Wuhan, China, 21–23 September 2007; Kang, L., Liu, Y., Zeng, S., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2007; Volume 4683, pp. 169–176. [Google Scholar]
- SaiToh, A.; Rahimi, R.; Nakahara, M. A quantum genetic algorithm with quantum crossover and mutation operations. Quantum Inf. Process. 2014, 13, 737–755. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Zhi, J.; Fu, C. The improvement of quantum genetic algorithm and its application on function optimization. Math. Probl. Eng. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Mohammed, A.M.; Elhefnawy, N.A.; El-Sherbiny, M.M.; Hadhoud, M.M. Quantum Crossover Based Quantum Genetic Algorithm for Solving Non-Linear Programming. In Proceedings of the 8th International Conference on INFOrmatics and Systems (INFOS2012), Cairo, Egypt, 14–16 May 2012; pp. 145–153.
- Layeb, A. A novel quantum inspired cuckoo search for Knapsack problems. Int. J. Bio-Inspir. Comput. 2011, 3, 297–305. [Google Scholar] [CrossRef]
- Yu, Y.; Hui, Li. Improved quantum crossover based genetic algorithm for solving traveling salesman problem. Int. J. Adv. Comput. Technol. 2013, 5, 651–658. [Google Scholar]
- Sofge, D.A. Prospective Algorithms for Quantum Evolutionary Computation. In Proceedings of the Second Quantum Interaction Symposium (QI-2008), College Publications, Oxford, UK, 26–28 March 2008.
- Udrescu, M.; Prodan, L.; Vladutiu, M. Implementing Quantum Genetic Algorithms: A Solution Based on Grover’s Algorithm. In Proceedings of the 3rd conference on Computing frontiers, Ischia, Italy, 3–5 May 2006; pp. 71–82.
- Goswami, D.; Kumar, N. Quantum algorithm to solve a maze: Converting the maze problem into a search problem. 2013; arXiv:1312.4116. [Google Scholar]
- Malossini, A.; Blanzieri, E.; Calarco, T. Quantum genetic optimization. IEEE Trans. Evolut. Comput. 2008, 12, 231–241. [Google Scholar] [CrossRef]
- Ahuja, A.; Kapoor, S. A quantum algorithm for finding the maximum. 1999; arXiv: quant-ph/9911082. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on the Theory of Computing (STOC), Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219.
- Lahoz-Beltra, R. Quantum genetic algorithm (QGA). Figshare 2016. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R. Hybrid genetic algorithm (HGA). Figshare 2016. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R. Reduced quantum genetic algorithm (RQGA). Figshare 2016. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R. Simple genetic algorithm (SGA). Figshare 2016. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R.; Perales-Gravan, C. A survey of nonparametric tests for the statistical analysis of evolutionary computational experiments. Int. J. Inf. Theor. Appl. 2010, 17, 49–61. [Google Scholar]
- Zhang, J.; Zhou, J.; He, K.; Gong, M. An improved quantum genetic algorithm for image segmentation. J. Comput. Inf. Syst. 2011, 7, 3979–3985. [Google Scholar]
- Zhao, Z.; Peng, X.; Peng, Y.; Yu, E. An Effective Repair Procedure Based on Quantum-Inspired Evolutionary Algorithm for 0/1 Knapsack Problems. In Proceedings of the 5th WSEAS International Conference on Instrumentation, Measurement, Circuits and Systems, Hangzhou, China, 16–18 April 2006; pp. 203–206.
- Huo, H.; Xie, Q.; Shen, X.; Stojkovic, V. A probabilistic coding based quantum genetic algorithm for multiple sequence alignment. Comput. Syst. Bioinf. Conf. 2008, 7, 15–26. [Google Scholar]
- Zhaokai, L.; Xiaomei, L.; Nanyang, X.; Jiangfeng, D. Experimental realization of quantum artificial intelligence. 2014; arXiv:1410.1054. [Google Scholar]
- Veldhorst, M.; Yang, C.H.; Hwang, J.C.C.; Huang, W.; Dehollain, J.P.; Muhonen, J.T.; Simmons, S.; Laucht, A.; Hudson, F.E.; Itoh, K.M.; et al. A two-qubit logic gate in silicon. Nature 2015, 526, 410–414. [Google Scholar] [CrossRef] [PubMed]
- IBM Makes Quantum Computing Available on IBM Cloud to Accelerate Innovation. Available online: https://www-03.ibm.com/press/us/en/pressrelease/49661.wss (accessed on 30 June 2016).
- Nowotniak, R.; Kucharski, J. Higher-Order Quantum-Inspired Genetic Algorithms. In Proceedings of the 2014 Federated Conference on Computer Science and Information Systems, Warsaw, Poland, 7–10 September 2014; pp. 465–470.
- Choy, C.K.; Nguyen, K.Q.; Thawonmas, R. Quantum-Inspired Genetic Algorithm with Two Search Supportive Schemes and Artificial Entanglement. In Proceedings of the 2014 IEEE Symposium on Foundations of Computational Intelligence (FOCI), Orlando, FL, USA, 9–12 December 2014; pp. 17–23.
- Duan, H.B.; Xu, C.-F.; Xing, Z.-H. A hybrid artificial bee colony optimization and quantum evolutionary algorithm for continuous optimization problems. Int. J. Neural Syst. 2010, 20, 39–50. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D. From Cbits to Qbits: Teaching computer scientists quantum mechanics. Am. J. Phys. 2003, 71, 23–30. [Google Scholar] [CrossRef]
- Sardana, M.; Agrawal, R.K.; Kaur, B. Clustering in Conjunction with Quantum Genetic Algorithm for Relevant Genes Selection for Cancer Microarray Data. In Trends and Applications in Knowledge Discovery and Data Mining; Li, J., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7867, pp. 428–439. [Google Scholar]
- Mani, A.; Patvardhan, C. An adaptative quantum evolutionary algorithm for engineering optimization problems. Int. J. Comput. Appl. 2010, 1, 43–48. [Google Scholar]
- Draa, A.; Meshoul, S.; Talbi, H.; Batouche, M. A Quantum-inspired differential evolution algorithm for solving the N-Queens problem. Int. Arab J. Inf. Technol. 2010, 7, 21–27. [Google Scholar]
- Alvarez-Rodriguez, U.; Sanz, M.; Lamata, L.; Solano, E. Artificial life in quantum technologies. 2016; arXiv:1505.03775. [Google Scholar]
- Lahoz-Beltra, R. ¿Juega Darwin a Los Dados? Simulando la Evolución en el Ordenador; Nivola: Madrid, Spain, 2008; pp. 1–157. (In Spanish) [Google Scholar]
- Montiel, O.; Rivera, A.; Sepulveda, R. Design and Acceleration of a Quantum Genetic Algorithm through the Matlab GPU Library. In Design of Intelligent Systems Based on Fuzzy Logic, Neural Networks and Nature-Inspired Optimization. Studies in Computational Intelligence; Melin, P., Ed.; Springer: Basel, Switzerland, 2015; Volume 601, pp. 333–345. [Google Scholar]


| Step | |
|---|---|
| 1 | Randomly initialize a population P(0) |
| 2 | Evaluate P(0) |
| 3 | while (not termination condition) do |
| 4 | begin |
| 5 | t ← t + 1 |
| 6 | Selection of parents from population P(t) |
| 7 | Crossover |
| 8 | Mutation |
| 9 | Evaluate P(t) |
| 10 | end |
| Q1 | Q2 | Q1 | * Q2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
| Q1 | Q2 | Q3 | * Q3 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| Step | |
|---|---|
| 1 | Prepare an input state |
| 2 | Apply quantum parallelism |
| 3 | Performs quantum information processing |
| 4 | Use interference to exploit the parallelism |
| 5 | Make a measure |
| Quantum Circuit Example | Symbol | Input → Output * |
|---|---|---|
 |  | |
 |  | |
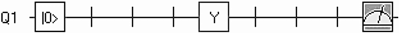 |  | |
 |  | |
 |  | |
 | 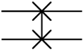 | |
 | 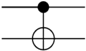 | |
 |  |
| Step | Quantum Computing | Classical Computing |
|---|---|---|
| 1 | Initialize a quantum population Q(0) | |
| 2 | Make P(0), measure of every individual Q(0) → P(0) | |
| 3 | Evaluate P(0) | |
| 4 | while (not termination condition) do | |
| 5 | begin | |
| 6 | t ← t + 1 | |
| 7 | Update Q(t) applying Q-gates: Q(t + 1) = U(t).Q(t) | |
| 8 | Make P(t), measure of every individual Q(t) → P(t) | |
| 9 | Evaluate P(t) | |
| 10 | end |
| 0 0 | False | 0 | - | - | - | - |
| 0 0 | True | 0 | - | - | - | - |
| 0 1 | False | +1 | −1 | 0 | 1 | |
| 0 1 | True | −1 | +1 | 1 | 0 | |
| 1 0 | False | −1 | +1 | 1 | 0 | |
| 1 0 | True | +1 | −1 | 0 | 1 | |
| 1 1 | False | 0 | - | - | - | - |
| 1 1 | True | 0 | - | - | - | - |
| Step | Quantum Computing | Classical Computing |
|---|---|---|
| 1 | Initialize a quantum population Q(0) | |
| 2 | Make P(0), measure of every individual Q(0) P(0) | |
| 3 | Evaluate P(0) | |
| 4 | while (not termination condition) do | |
| 5 | begin | |
| 6 | t t + 1 | |
| 7 | Rotation Q-gate | |
| 8 | Mutation Q-gate | |
| 9 | Make a measure Q(t) P(t) | |
| 10 | Evaluate P(t) | |
| 11 | end |
| Step | Quantum Computing | Classical Computing |
|---|---|---|
| 1 | Initialize a quantum population Q(0) | |
| 2 | Make P(0), measure of every individual Q(0) P(0) | |
| 3 | Evaluate P(0) | |
| 4 | while (not termination condition) do | |
| 5 | begin | |
| 6 | t t + 1 | |
| 7 | Rotation Q-gate | |
| 8 | Crossover operator | |
| 9 | Mutation Q-gate | |
| 10 | Make a measure Q(t) P(t) | |
| 11 | Evaluate P(t) | |
| 12 | end |
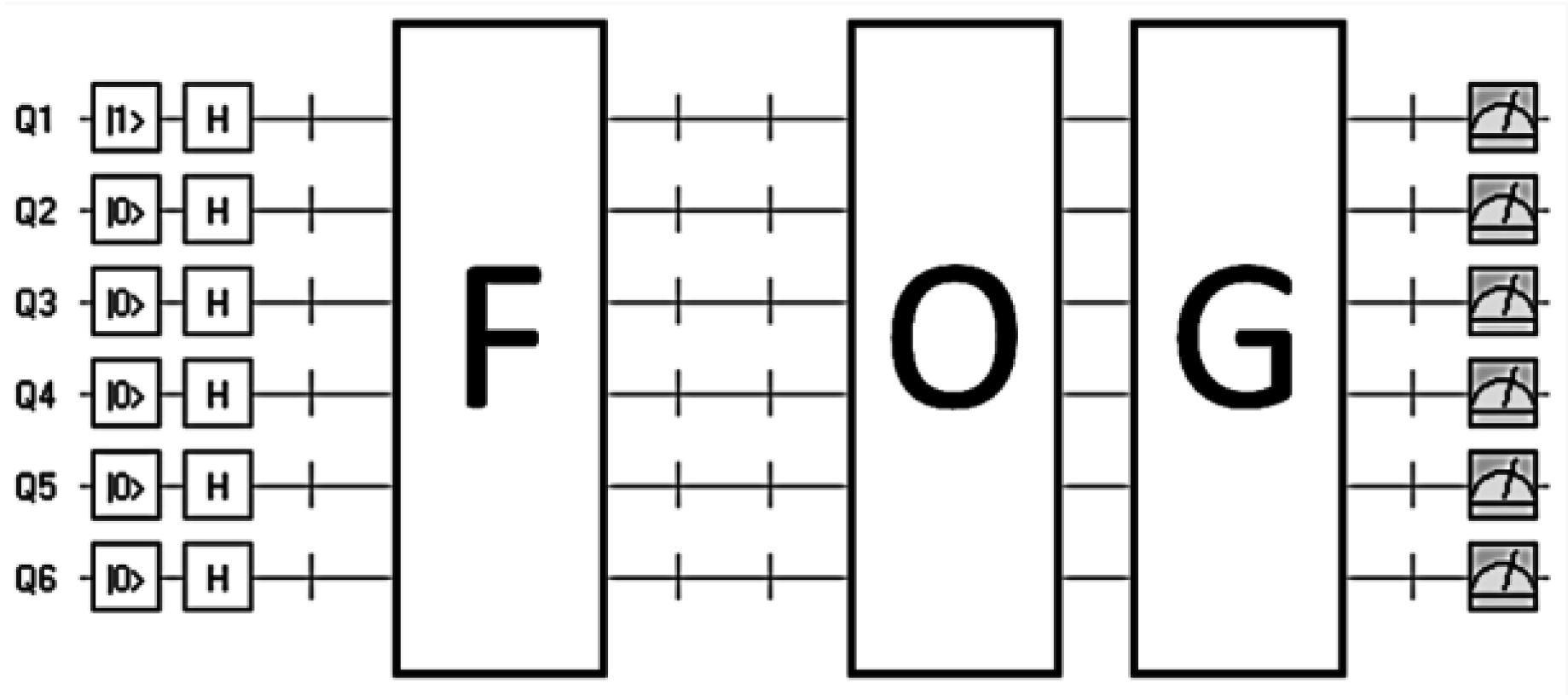
| Step | Quantum Computing |
|---|---|
| 1 | Initialize a superposition of all possible chromosomes |
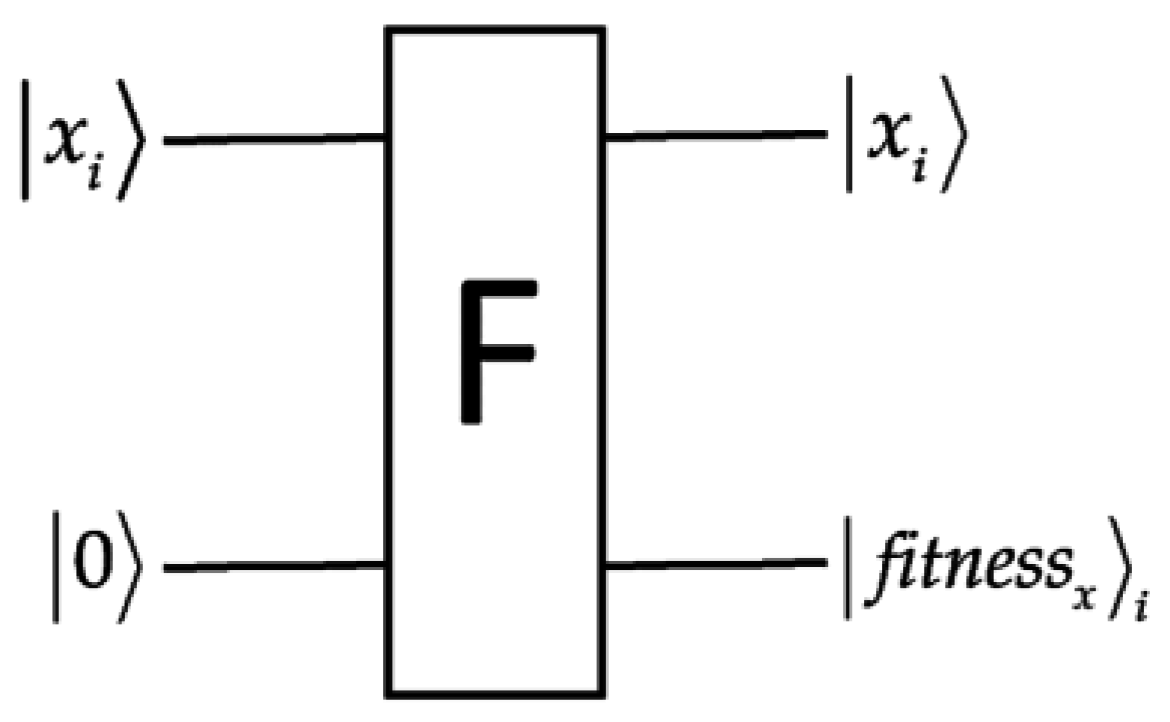
| 2 | Evaluates fitness with operator F |
| 3 | Apply Grover’s algorithm |
| 4 | Ask to the oracle O |
| 5 | Apply Grover’s diffusion operator G |
| 6 | Make a measure |
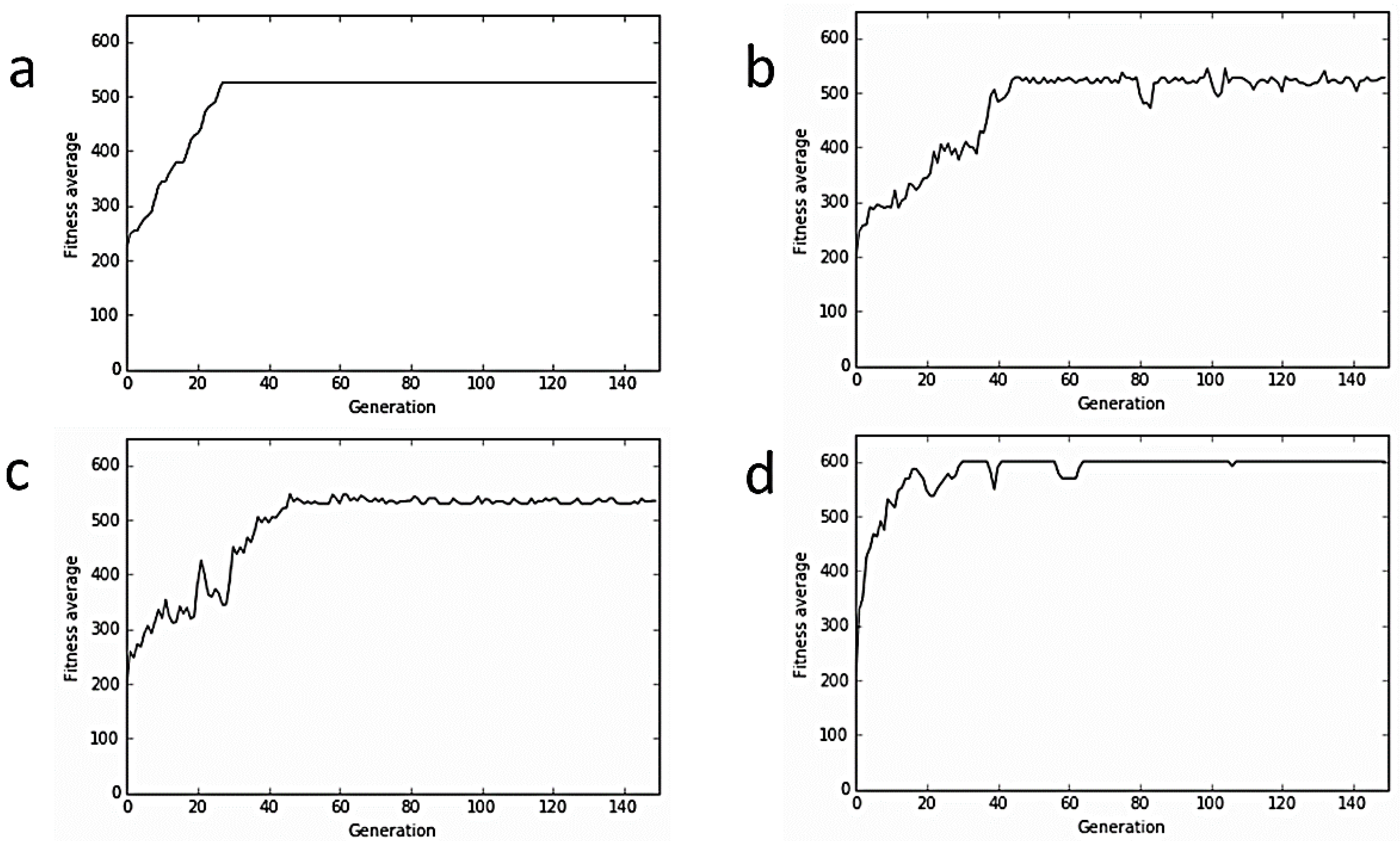
| Algorithm | Sample Size | Mean Rank |
|---|---|---|
| SGA | 50 | 325.5 |
| HGA1 | 50 | 119.12 |
| HGA2 | 50 | 111.52 |
| HGA3 | 50 | 202.98 |
| QGA1 | 50 | 151.3 |
| QGA2 | 50 | 184.38 |
| QGA3 | 50 | 133.7 |
| State | ||
|---|---|---|
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahoz-Beltra, R. Quantum Genetic Algorithms for Computer Scientists. Computers 2016, 5, 24. https://doi.org/10.3390/computers5040024
Lahoz-Beltra R. Quantum Genetic Algorithms for Computer Scientists. Computers. 2016; 5(4):24. https://doi.org/10.3390/computers5040024
Chicago/Turabian StyleLahoz-Beltra, Rafael. 2016. "Quantum Genetic Algorithms for Computer Scientists" Computers 5, no. 4: 24. https://doi.org/10.3390/computers5040024
APA StyleLahoz-Beltra, R. (2016). Quantum Genetic Algorithms for Computer Scientists. Computers, 5(4), 24. https://doi.org/10.3390/computers5040024





