A New Scalable, Distributed, Fuzzy C-Means Algorithm-Based Mobile Agents Scheme for HPC: SPMD Application
Abstract
:1. Introduction
- We provide the model of parallel and distributed computing where the distributed DFCM method is assigned to be implemented (Section 3).
2. Background
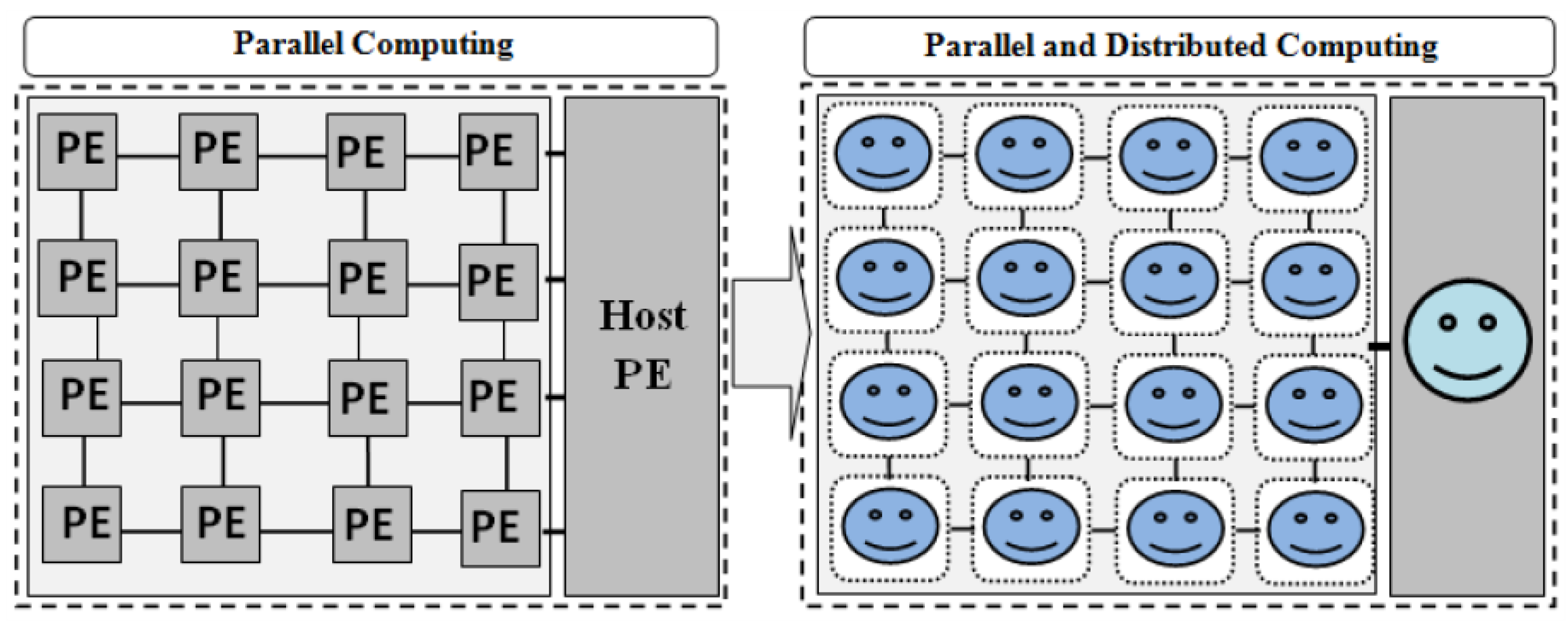
3. Parallel and Distributed Computational Model
3.1. Model Overview
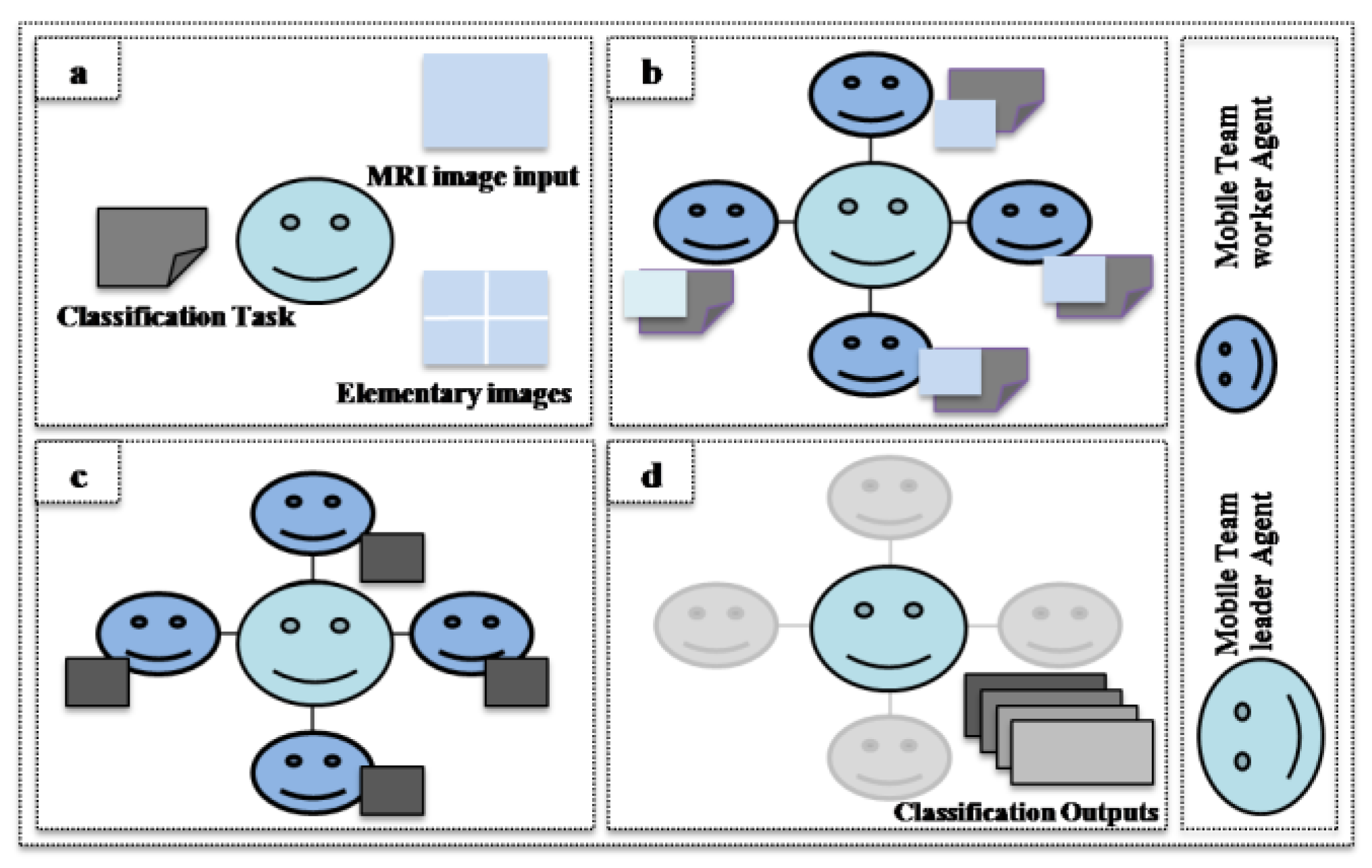
3.2. Cooperative Mobile Agent Virtual Element (AVPE) Model
4. Distributed Clustering Algorithm
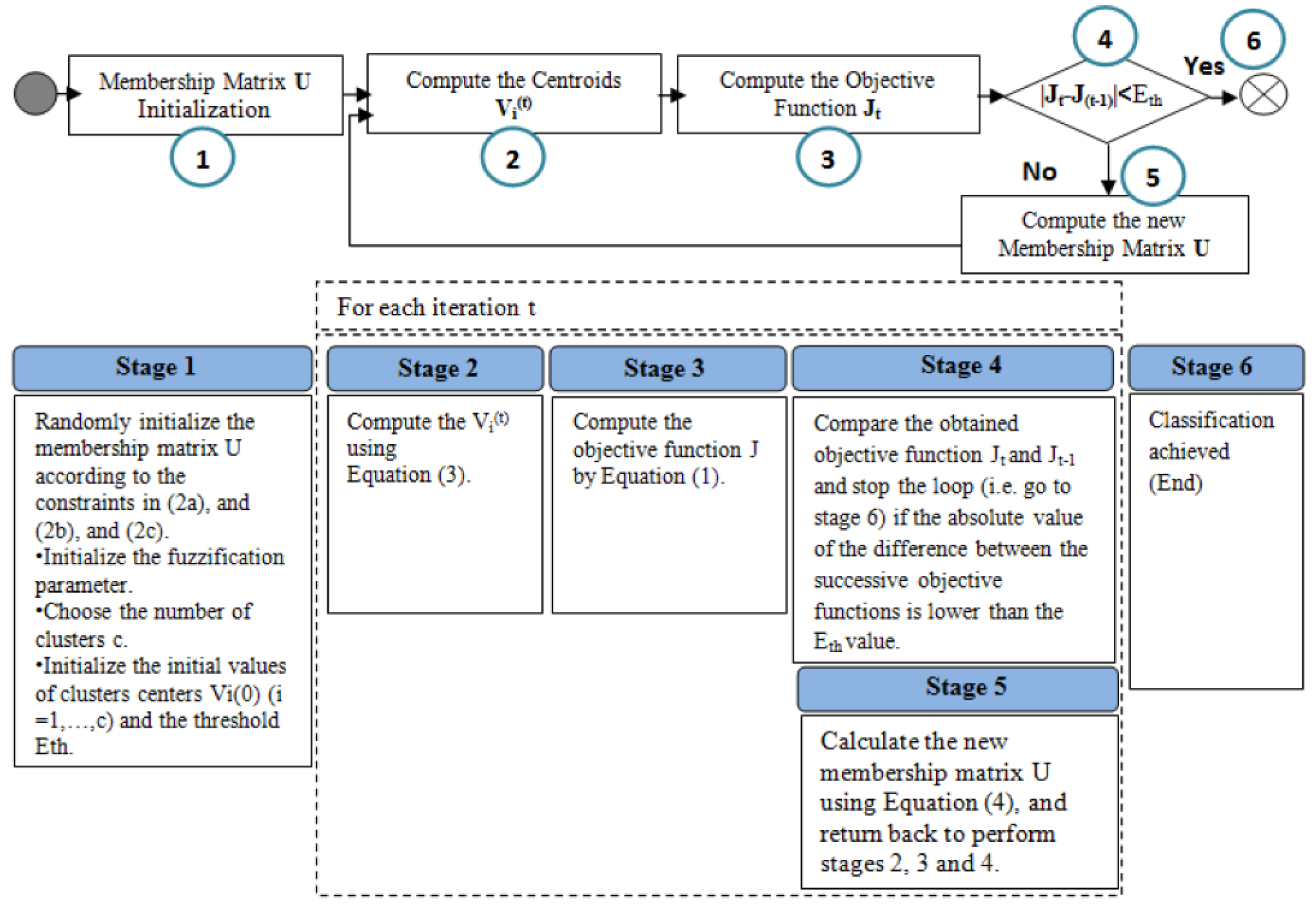
4.1. Standard Fuzzy C-Means Algorithm
- Membership of data xj in the cluster Vi.
- Vi Centroid of the cluster i.
- Euclidian distance between centroid (Vi) and data point xj.
- Fuzzification parameter generally equals 2.
- N Number of data.
- c Number of clusters 2 ≤ c < N.
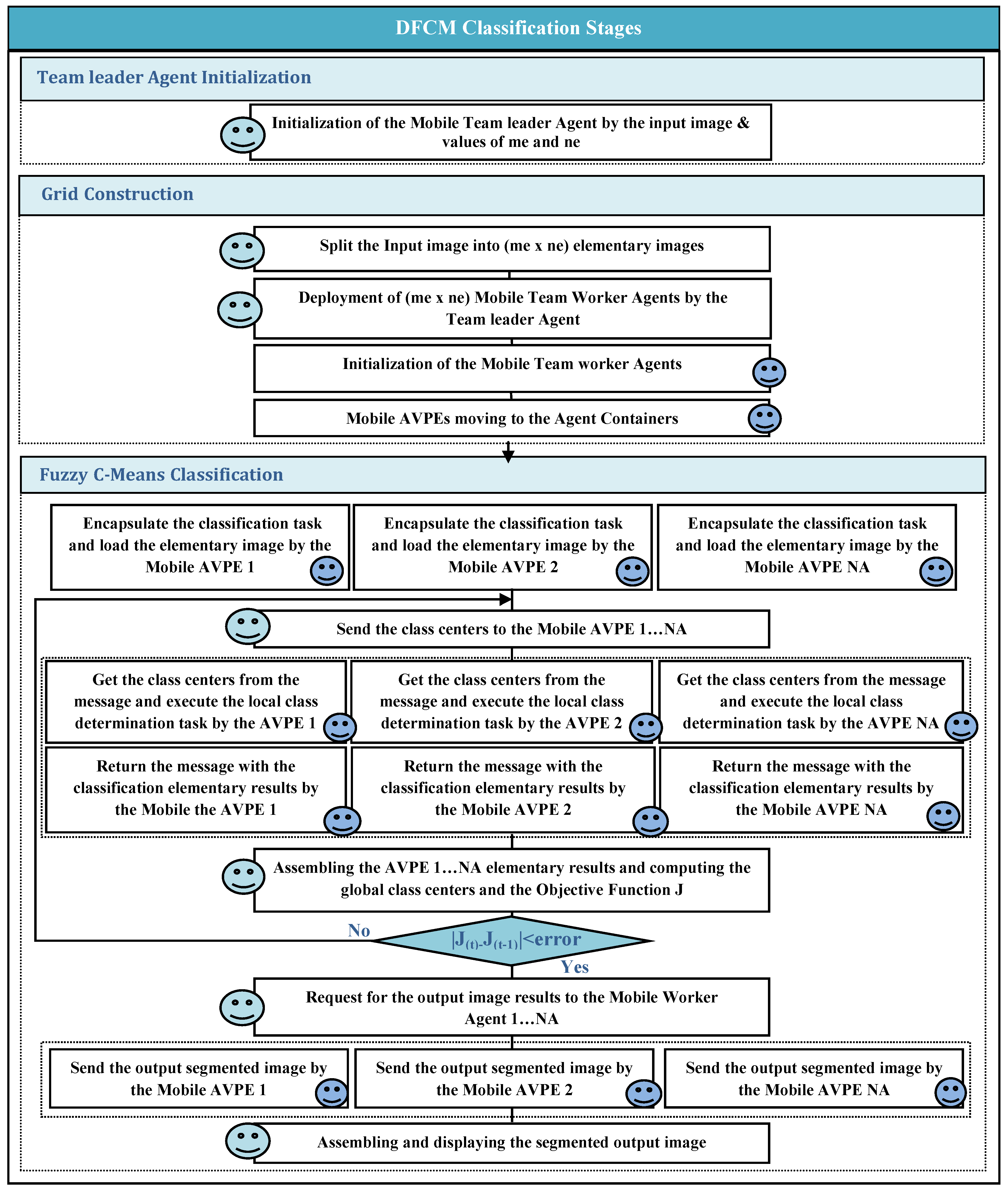
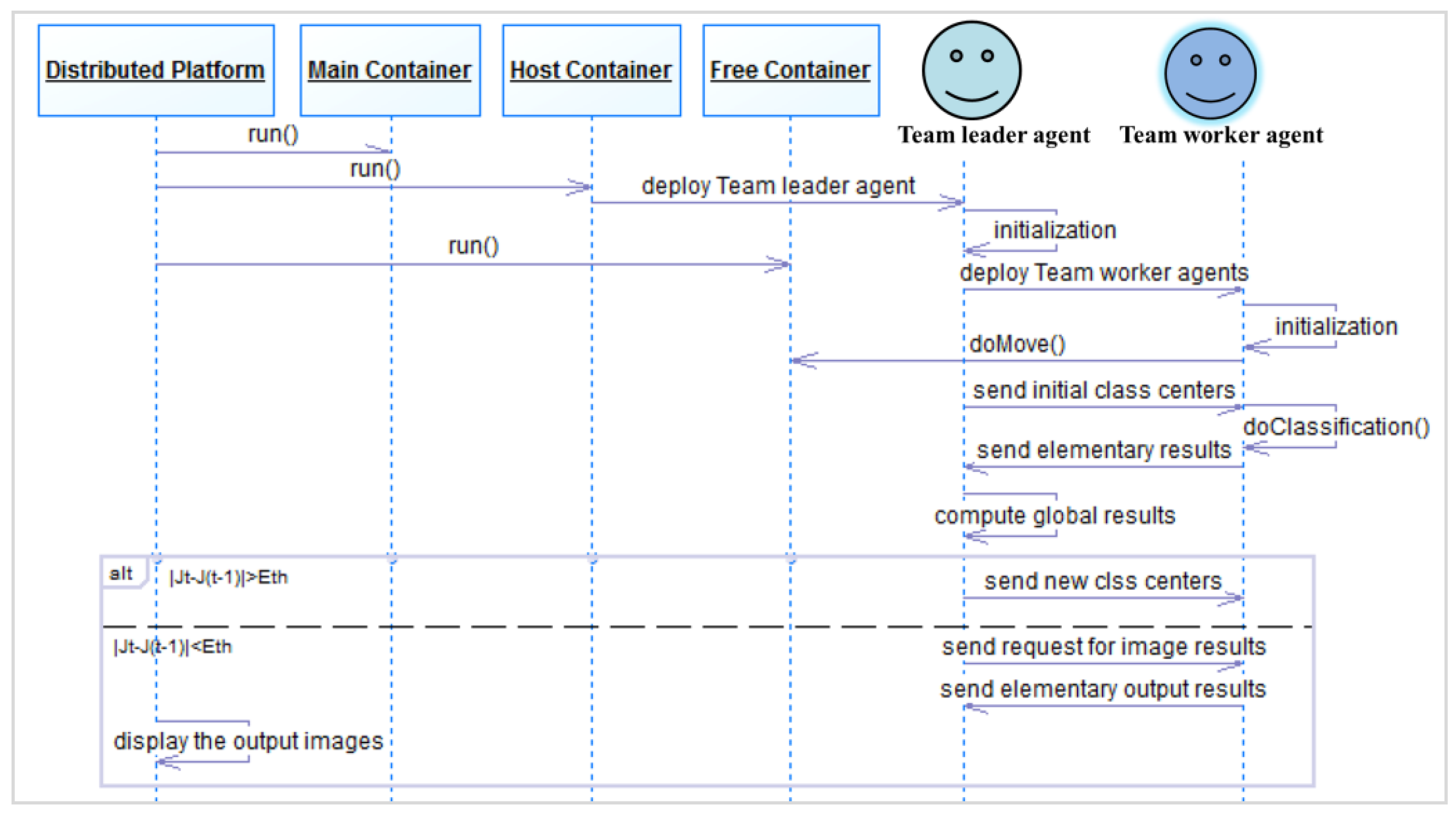
4.2. Distributed Fuzzy C-Means Algorithm
- Step 1.
- Mobile Team Leader Agent Initialization
- Step 2.
- Grid Construction
- Step 3.
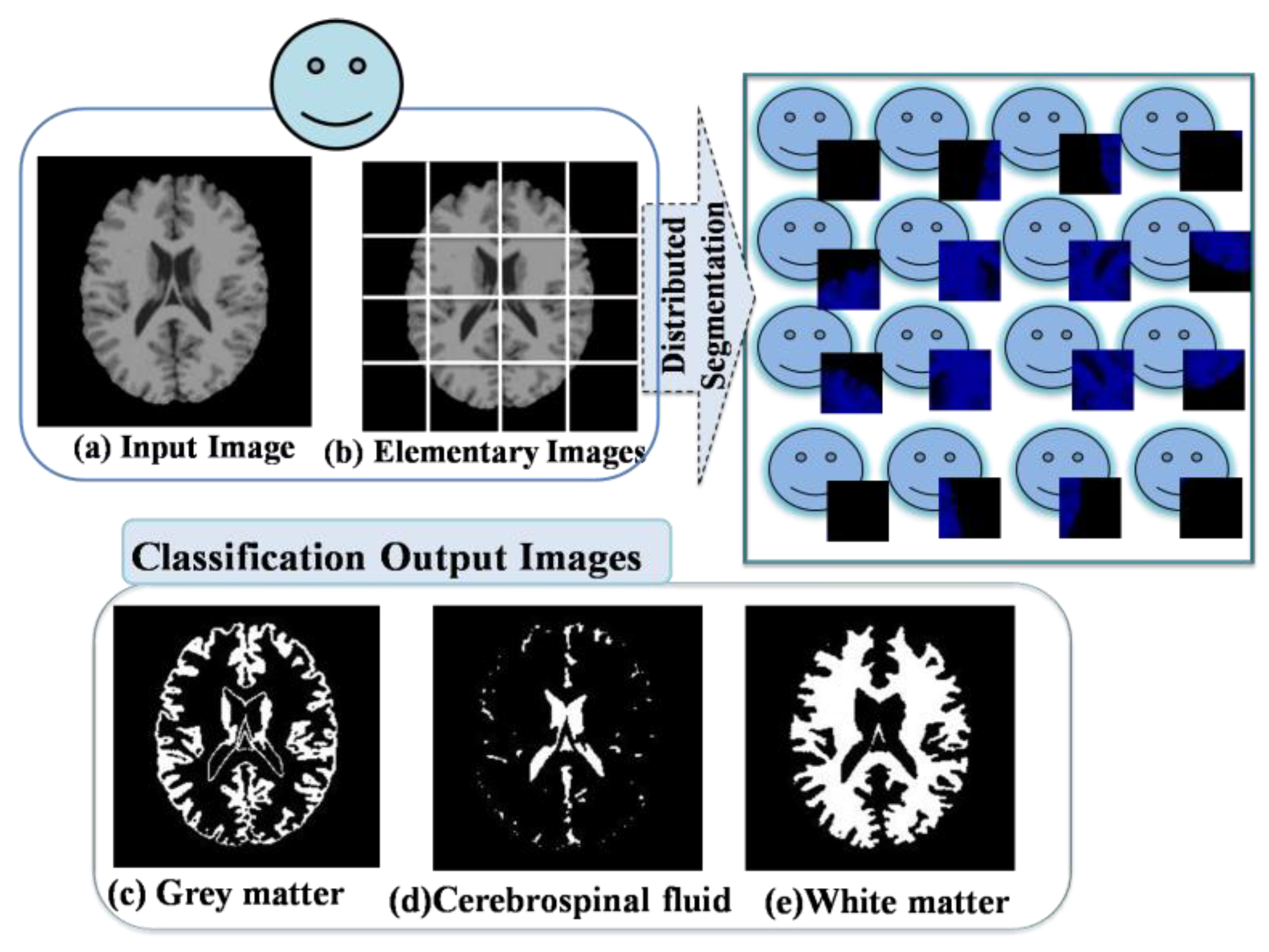
- Fuzzy C-Means Classification
- •
- Each AVPE(a) encapsulates the task and load its elementary image.
- •
- For each iteration t
- {
- The Team Leader agent sends the class centers to all the AVPEs.
- Each AVPE(a) gets the class centers from the message and executes the local class determination task.
- Each AVPE(a) returns its classification elementary results, which consist of the following terms: TE1(a,i), TE2(a,i), TE3(a), and Cardinal(a,i).where:
- ○
- TE1(a,i) contains the result of the sum of (Um × data) computed for each class center i. This term is computed by:
- ○
- TE2(a,i) contains the result of the sum of (Um) computed for each class center i computed by:
- ○
- TE3(a) contains the result of the sum of (Um × distance²) computed for all classes. This term is computed by:
- ○
- Cardinal(a,i) contains the result of the sum of pixel membership for each class center i. This term is computed by:
- ○
- pi: Number of pixels of the elementary image of the AVPE(a).
- The Team Leader agent performs these three sub tasks: assembling the elementary results, computing the new class centers, and computing the objective function Jt.
- ○
- Assembling the elementary resultsThe Team Leader agent receives the elementary results (TE1(a,i), TE2(a,i), TE3(a), Cardinal(a,i)) from each AVPE(a) and assembles them in order to compute the global values (GTE1(i), GTE2(i), GTE3(i), GC(i)), respectively, by the given equations:where:
- ■
- GTE1(i) is the global value of TE1(a,i) over the AVPEs of the grid.
- ■
- GTE2(i) is the global value of TE2(a,i) over the AVPEs of the grid.
- ■
- GTE3(i) is the global value of TE3(a) over the AVPEs of the grid.
- ■
- GC(i) is the global value of Cardinal(a,i) over the AVPEs of the grid.
- ○
- Computing the global class centersThe Team Leader agent gets the computed global values (GTE1(i), GTE2(i)) to compute the new class centers Vi by the following equation:
- ○
- Computing the objective function Jt:The Team leader agentgets the global value of GTE3(i) to compute the objective function given by the following equation:
- The Team Leader agent tests the condition of the algorithm convergence (|Jt − J(t−1)|<Eth).
- }
- // End of iteration t
- •
- The Team Leader agent requests to each AVPE(a) the segmented elementary image.
- •
- Each AVPE(a) sends the segmented elementary image result to the Team Leader agent.
- •
- The Team Leader agent assembles the segmented elementary images and displays the segmented output image.
5. Distributed Environment and Results
5.1. Distributed Environment Communication Mechanisms
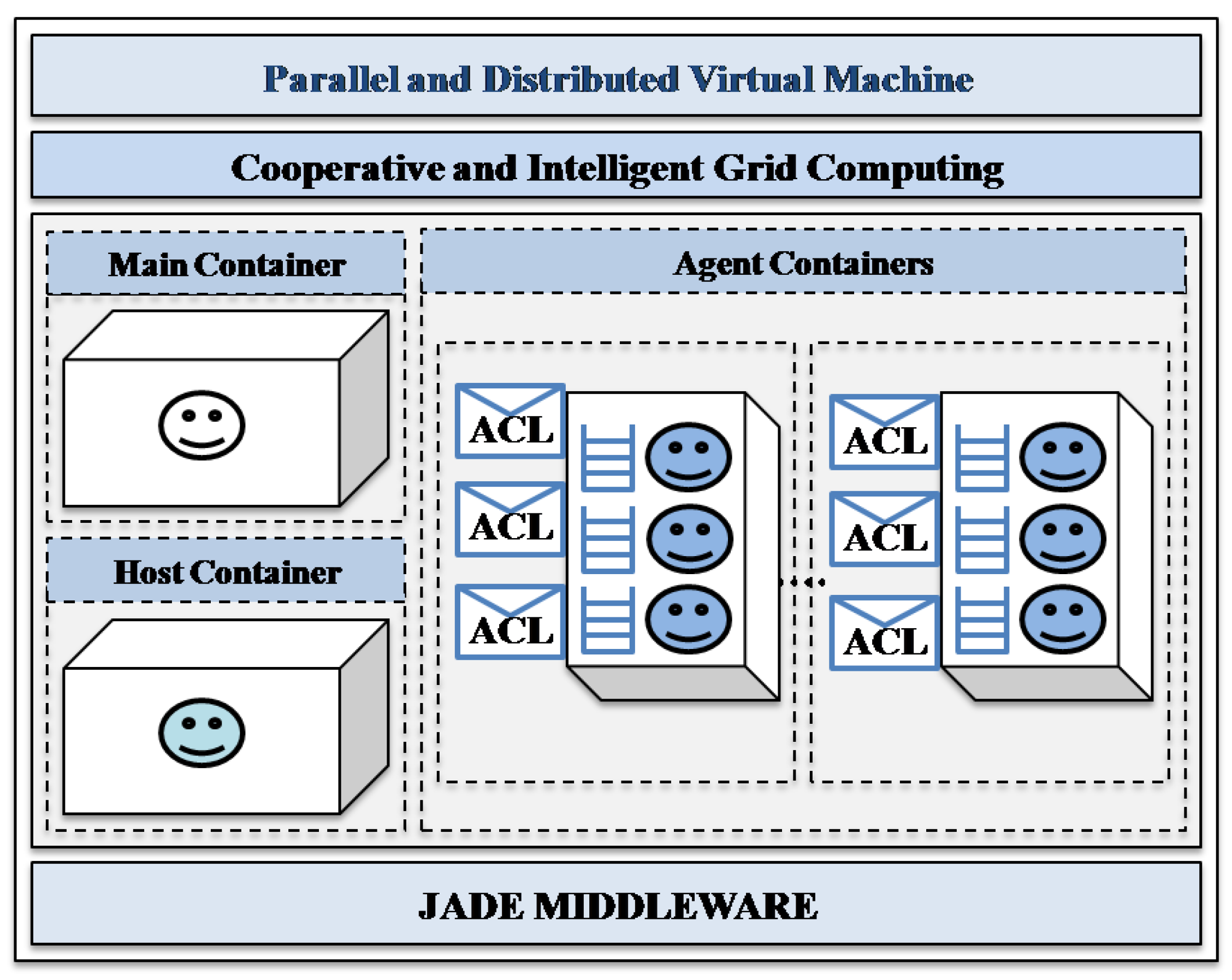
5.2. Cooperative Multi-Agent Middleware
- (1)
- The host container: this is the second container which is started in the platform after the main container, where the mobile team leader agent is deployed in order to perform its tasks in the grid.
- (2)
- The agent containers: these are the containers that are started in the platform, where the mobile team worker agents will move to perform their tasks.
5.3. Implementation and Results
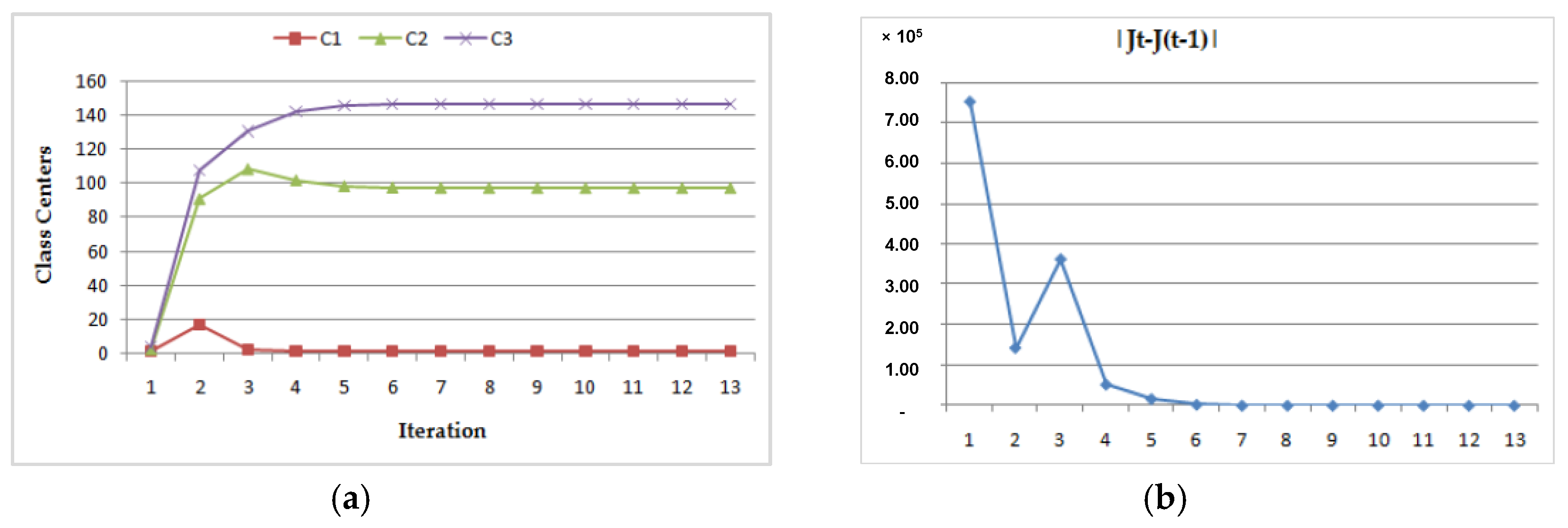
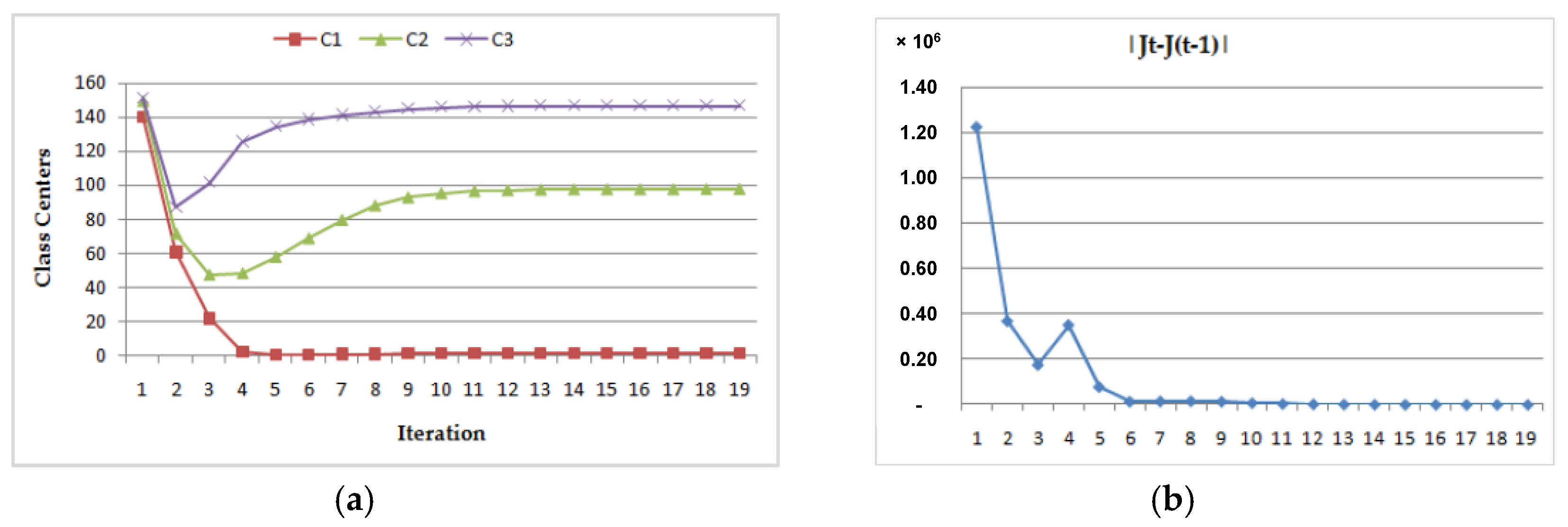
- (1)
- Dynamic convergence of this program for the MRI image (Img1) with two different class center initializations:
- (a)
- (b)
- (2)
- Dynamic convergence of this program for the MRI image (Img2) with two different class center initializations:
- (a)
- (b)
- (3)
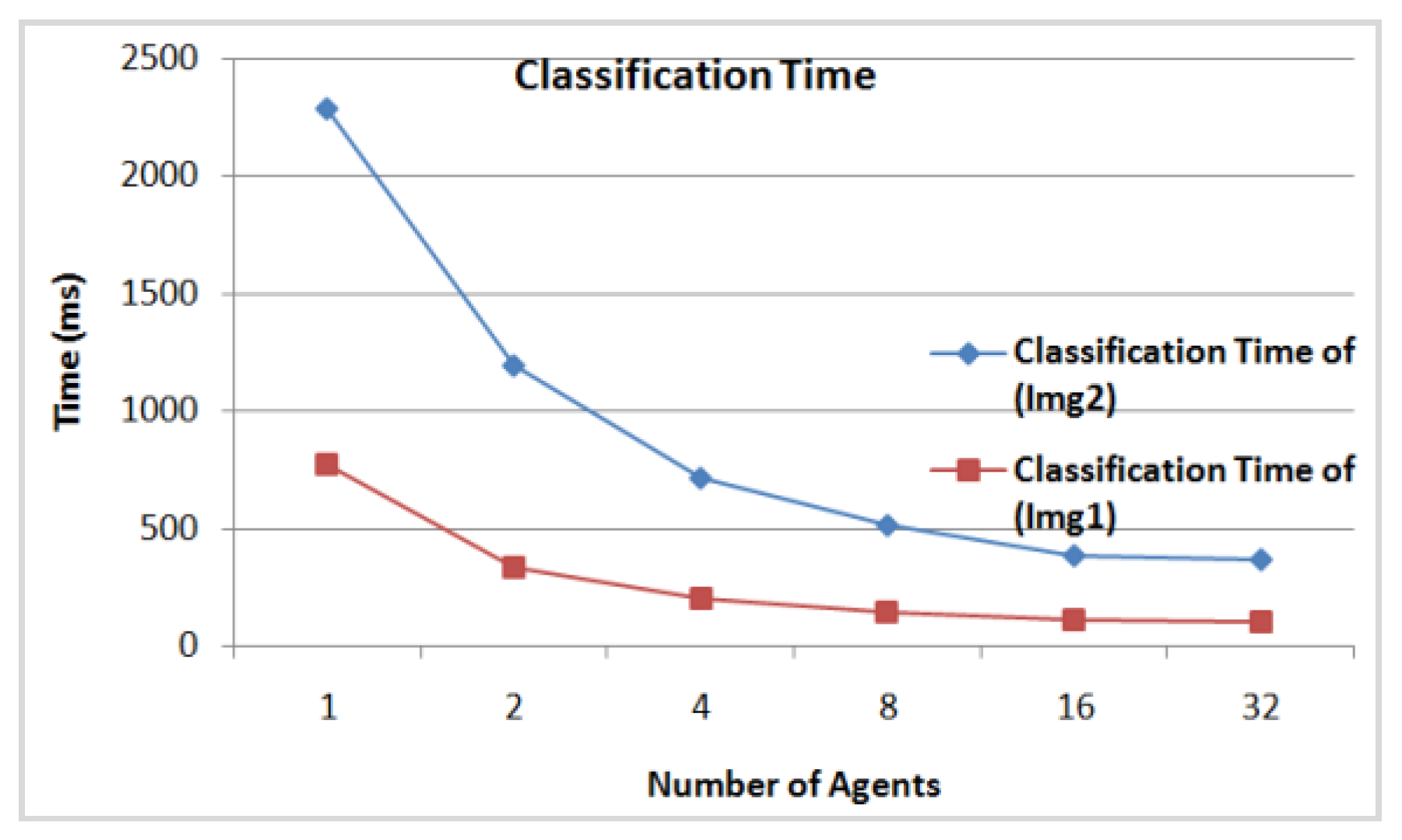
- The DFCM classification time according to the number of agents involved in the classification for the initial class centers (c1, c2, c3, c4, c5) = (1.5, 2.2, 3.8, 5.2, 8.6) for Img1, and (c1, c2, c3, c4, c5) = (1.5, 2.2, 3.8, 5.2, 8.6) for Img2. In Figure 14 we see clearly that from 16 agents the classification time of the two images achieves minimum values of 108 ms for Img1 and of 278 ms for Img2. Thus, it is considered as the appropriate number of agents needed to classify these images.
- (4)
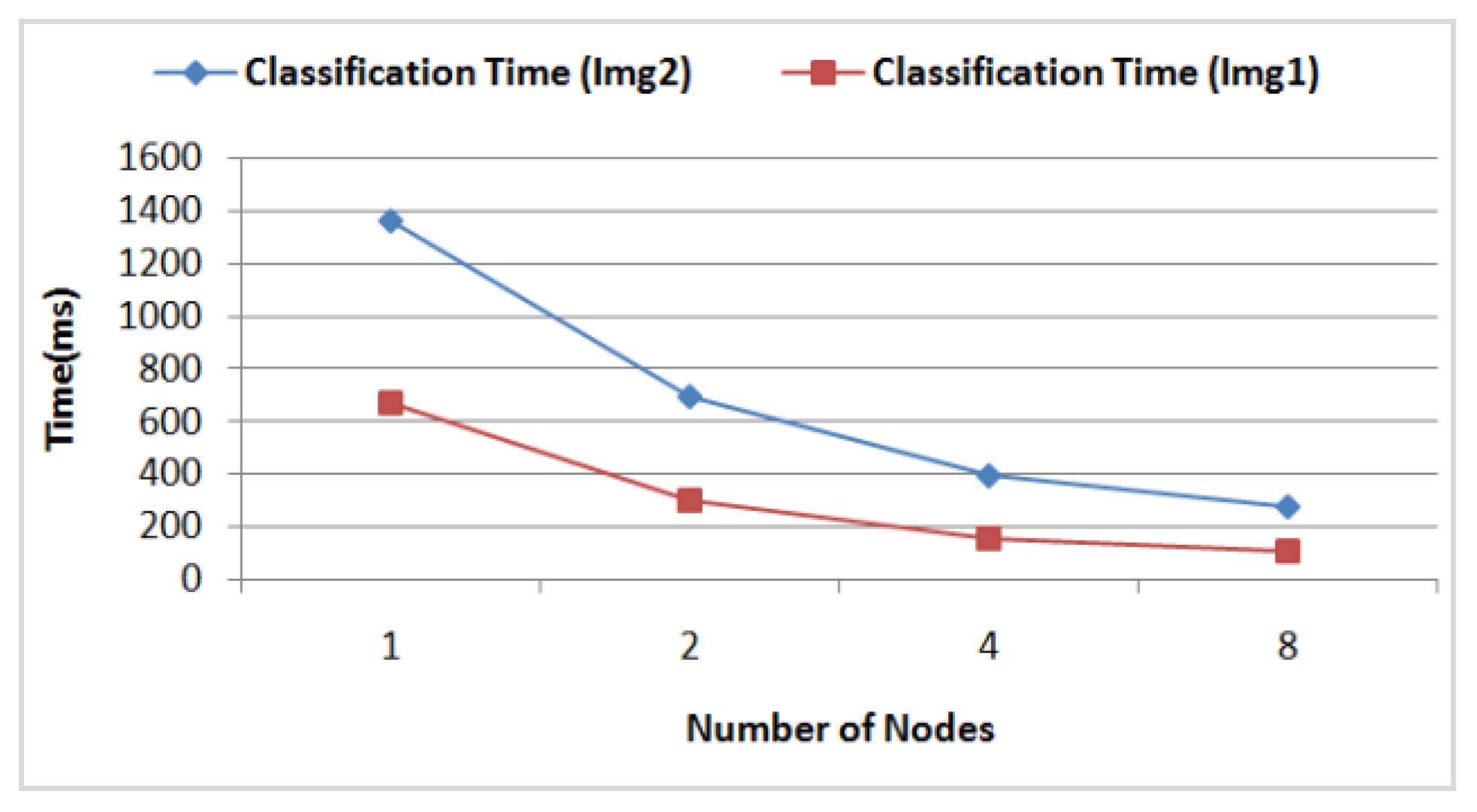
- The DFCM classification time according to the number of nodes in the grid computing by considering 16 AVPEs for the two images (Img1) and (Img2). In Figure 15, we see clearly that for both images the classification time achieves a gain of time of about 78% using eight nodes, compared to using just one. The corresponding classification data size for each node is illustrated in Figure 16.
- (5)
- The speedup S(DFCM), its relative speedup SR(DFCM), and the efficiency of the DFCM classification method are presented, respectively, in Figure 17 and Figure 18, compared to the sequential FCM method. We perform interesting maximum relative speedups of 86.760% for Img1, which corresponds to again of 7.55, and of 82.372% for Img2, which corresponds to again of 5.67, by using 32 AVPEs. The speedup S(DFCM) and the relative speedup SR(DFCM) are illustrated in Table 4 and computed, respectively, by the following equations:
- ○
- T(FCM)is the classification time of the FCM method which corresponds to one agent; and
- ○
- T(DFCM) is the classification time of the DFCM method which corresponds to the number NA of agents.
6. Related Work
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Rahimi, S.; Zargham, M.; Thakre, A.; Chillar, D. A Parrallel Fuzzy C-Mean Algorithm for Image Segmentation. In Proceedings of the IEEE Annual Meeting of the Fuzzy Information, Banff, AB, Canada, 27–30 June 2004; pp. 234–237.
- Bellifemine, F.L.; Caire, G.; Greenwood, D. Developing Multi-Agent Systems with JADE; Wiley: West Sussex, UK, 2007. [Google Scholar]
- Depuru, S.S.S.R.; Wang, L.; Devabhaktuni, V.; Green, R.C. High performance computing for detection of electricity theft. ELSEVIER Electr. Power Energy Syst. 2013, 147, 21–30. [Google Scholar] [CrossRef]
- Coria, J.A.G.; Castellanos-Garzón, J.A.; Corchado, J.M. Intelligent business processes composition based on multi-agent systems. ELSEVIER Expert Syst. Appl. 2014, 41, 1189–1205. [Google Scholar] [CrossRef]
- Isern, D.; Moreno, A.; Sánchez, D.; Hajnal, A.; Pedone, G.; Varga, L.Z. Agent-based execution of personalised home care treatments. Appl. Intell. 2011, 34, 155–180. [Google Scholar] [CrossRef]
- Sánchez, D.; Isern, D.; Rodríguez-Rozas, A.; Moreno, A. Agent-based platform to support the execution of parallel tasks. ELSEVIER Expert Syst. Appl. 2011, 38, 6644–6656. [Google Scholar] [CrossRef]
- Rodríguez-González, A.; Torres-Niño, J.; Hernández-Chan, G.; Jiménez-Domingo, E.; Alvarez-Rodríguez, J.M. Using agents to parallelize a medical reasoning system based on ontologies and description logics as an application case. ELSEVIER Expert Syst. Appl. 2012, 39, 13085–13092. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Benchara, F.Z.; Youssfi, M.; Bouattane, O.; Ouajji, H.; Bensalah, M.O. Distributed C-Means Algorithm for Big Data Image Segmentation on a Massively Parallel and Distributed Virtual Machine Based on Cooperative Mobile Agents. JSEA 2015, 8, 103–113. [Google Scholar] [CrossRef]
- Kwok, T.; Smith, K.; Lozano, S.; Taniar, D. Parallel Fuzzy C-means Clustering for Large Data Sets. In Euro-Par 2002 Parallel Processing, Proceedings of the 8th International Euro-Par Conference on Parallel Processing, Paderborn, Germany, 27–30 August 2002; Monien, B., Feldman, R., Eds.; Lecture Notes in Computer Science. Springer Verlag: Heidelberg, Germany, 2002; Volume 2400, pp. 365–374. [Google Scholar]
- Kubota, K.; Nakase, A.; Sakai, H.; Oyanagi, S. Parallelization of decision tree algorithm and its performance evaluation. In Proceedings of the Fourth International Conference on High Performance Computing in the Asia-Pacific Region, Beijing, China, 14–17 May 2000; Volume 2, pp. 574–579.
- Kim, M.W.; Lee, J.G.; Min, C. Efficient fuzzy rule generation based on fuzzy decision tree for data mining. In Proceedings of the IEEE International Fuzzy Systems Conference FUZZ-IEEE ’99, Seoul, Korea, 22–25 August 1999; pp. 1223–1228.
- Evsukoff, A.; Costa, M.C.A.; Ebecken, N.F.F. Parallel Implementation of Fuzzy Rule Based Classifier. In Proceedings of the VECPAR’2004, Valencia, Spain, 28–30 June 2004; Volume 2, pp. 443–452.
- Phua, P.K.H.; Ming, D. Parallel nonlinear optimization techniques for training neural networks. IEEE Trans. Neural Netw. 2003, 14, 1460–1468. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.C.A.; Ebecken, N.F.F. A Neural Network Implementation for Data Mining High Performance Computing. In Proceedings of the V Brazilian Conference on Neural Networks, Granada, Spain, 13–15 June 2001; pp. 139–142.
- Boutsinas, B.; Gnardellis, T. On distributing the clustering process. Pattern Recognit. Lett. 2002, 23, 999–1008. [Google Scholar] [CrossRef]
- El-Rewini, H.; Abd-El-Barr, M. Advanced Computer Architecture and Parallel Processing; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bouattane, O.; Cherradi, B.; Youssfi, M.; Bensalah, M.O. Parallel c-means algorithm for image segmentation on a reconfigurable mesh computer. ELSEVIER Parallel Comput. 2011, 37, 230–243. [Google Scholar] [CrossRef]







| Case | Initial Class Centers | Final Class Centers | Number of Iteration | ||||
|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C1 | C2 | C3 | ||
| CASE 1 | 1.1 | 2.5 | 3.8 | 1.100 | 97.667 | 146.569 | 13 |
| CASE 2 | 140.1 | 149.5 | 150.8 | 1.100 | 97.661 | 146.566 | 20 |
| Initial Class Centers | Final Class Centers | Number of Iteration | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | C1 | C2 | C3 | C4 | C5 | C1 | C2 | C3 | C4 | C5 | |
| CASE 1 | 1.5 | 2.2 | 3.8 | 5.2 | 8.6 | 1.742 | 67.587 | 101.709 | 238.983 | 170.040 | 35 |
| CASE 2 | 140.5 | 149.5 | 150.5 | 220.5 | 250.5 | 1.764 | 67.967 | 101.858 | 239.140 | 170.560 | 26 |
| FCM Method | DFCM Method | |||
|---|---|---|---|---|
| Classification Time (Img1) (ms) | Classification Time (Img2) (ms) | Number of Agents | Classification Time (Img1) (ms) | Classification Time (Img2) (ms) |
| 778 | 1509 | 1 | 778 | 1509 |
| - | - | 2 | 334 | 860 |
| - | - | 4 | 200 | 516 |
| - | - | 8 | 144 | 371 |
| - | - | 16 | 108 | 278 |
| - | - | 32 | 103 | 266 |
| Number of Agents | SR(DFCM) (Img1) (%) | S(DFCM) (Img1) | SR(DFCM) (Img2) (%) | S(DFCM) (Img2) |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 |
| 2 | 57.069 | 2.32 | 43.008 | 1.75 |
| 4 | 74.293 | 3.89 | 65.805 | 2.92 |
| 8 | 81.491 | 5.4 | 75.414 | 4.06 |
| 16 | 86.118 | 7.2 | 81.577 | 5.42 |
| 32 | 86.76 | 7.55 | 82.372 | 5.67 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benchara, F.Z.; Youssfi, M.; Bouattane, O.; Ouajji, H. A New Scalable, Distributed, Fuzzy C-Means Algorithm-Based Mobile Agents Scheme for HPC: SPMD Application. Computers 2016, 5, 14. https://doi.org/10.3390/computers5030014
Benchara FZ, Youssfi M, Bouattane O, Ouajji H. A New Scalable, Distributed, Fuzzy C-Means Algorithm-Based Mobile Agents Scheme for HPC: SPMD Application. Computers. 2016; 5(3):14. https://doi.org/10.3390/computers5030014
Chicago/Turabian StyleBenchara, Fatéma Zahra, Mohamed Youssfi, Omar Bouattane, and Hassan Ouajji. 2016. "A New Scalable, Distributed, Fuzzy C-Means Algorithm-Based Mobile Agents Scheme for HPC: SPMD Application" Computers 5, no. 3: 14. https://doi.org/10.3390/computers5030014
APA StyleBenchara, F. Z., Youssfi, M., Bouattane, O., & Ouajji, H. (2016). A New Scalable, Distributed, Fuzzy C-Means Algorithm-Based Mobile Agents Scheme for HPC: SPMD Application. Computers, 5(3), 14. https://doi.org/10.3390/computers5030014





