Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation
Abstract
:1. Introduction
2. Learning in Shop Scheduling: A Concise Review
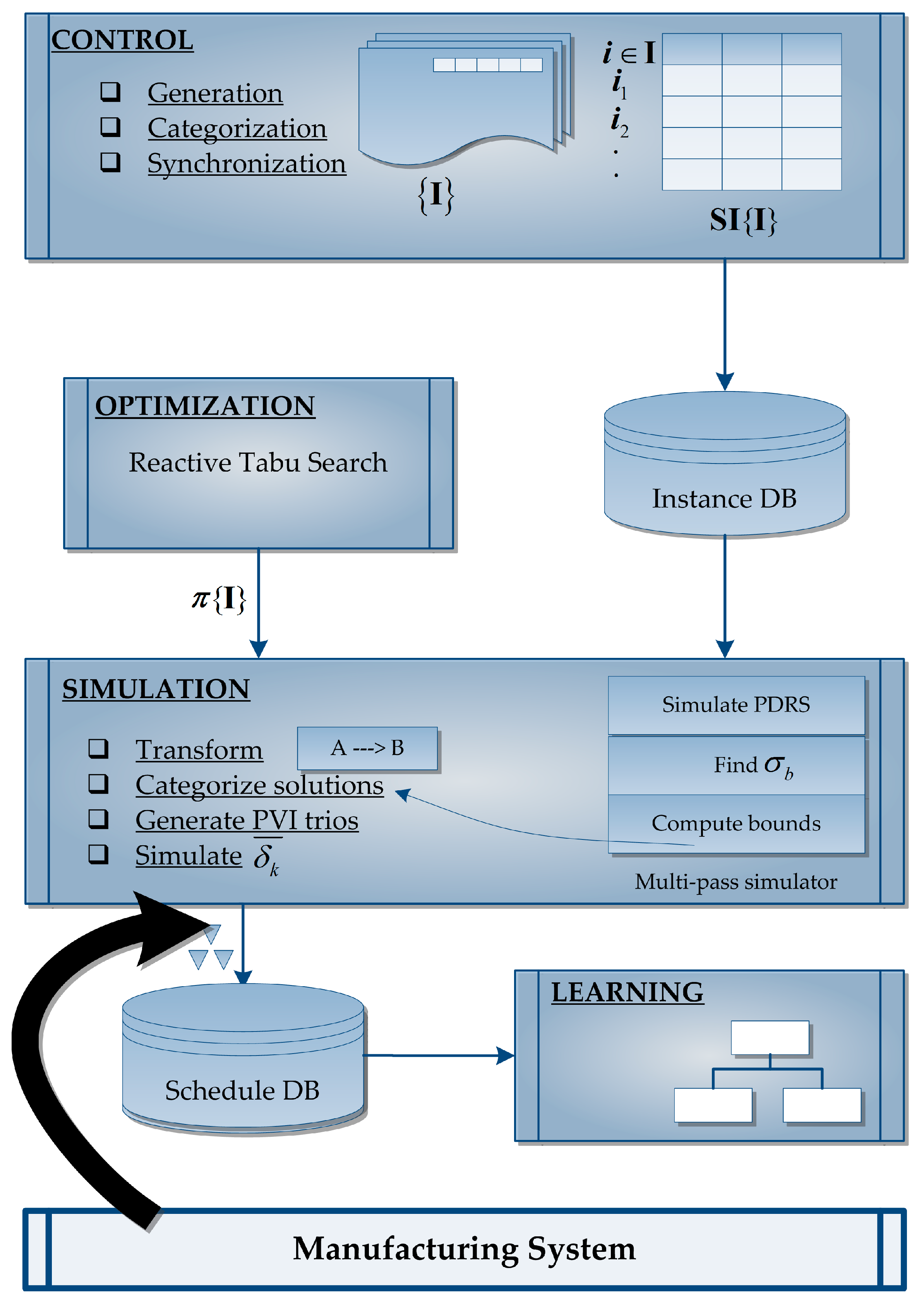
3. Proposed Methodology
3.1. Control Module
3.2. Optimization Module
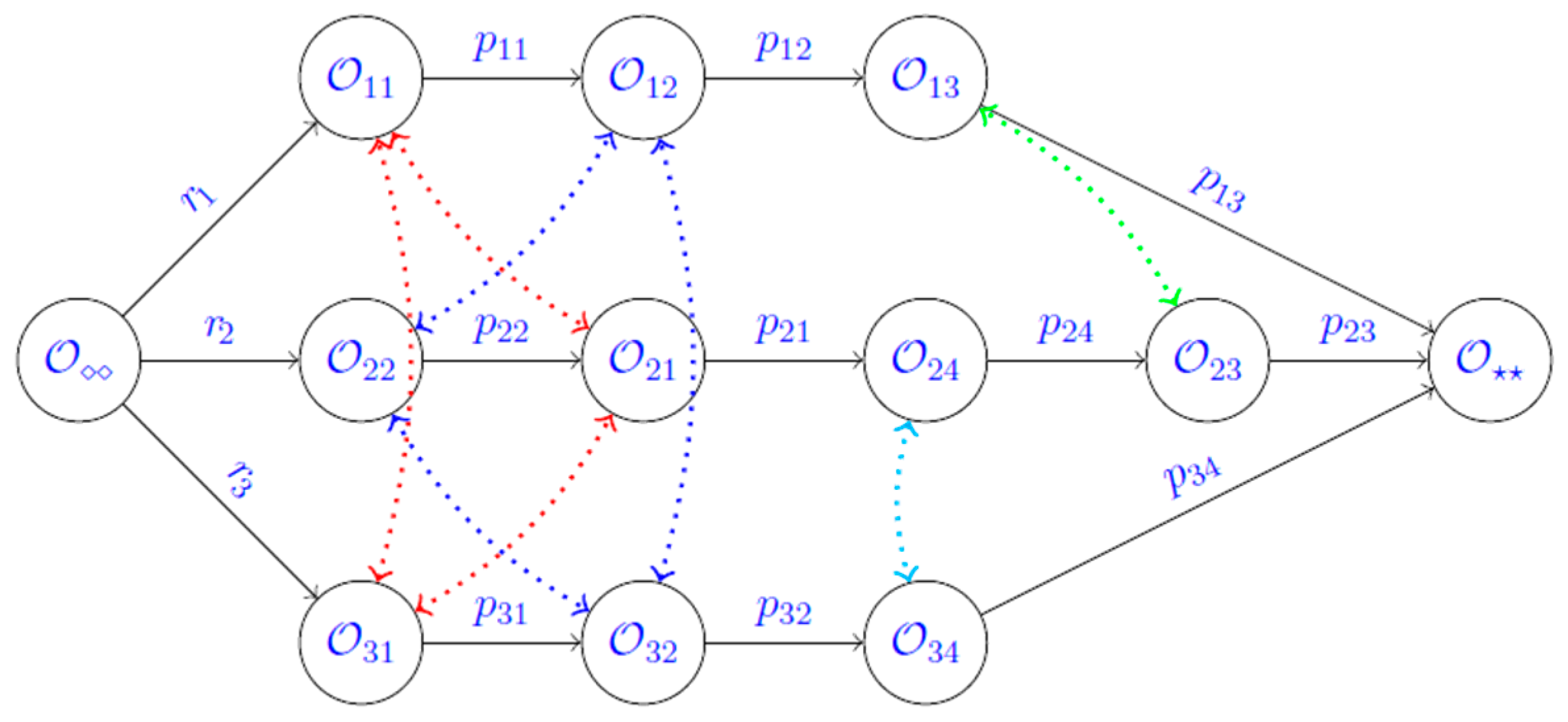
3.3. Simulation Module
3.4. Learning Module
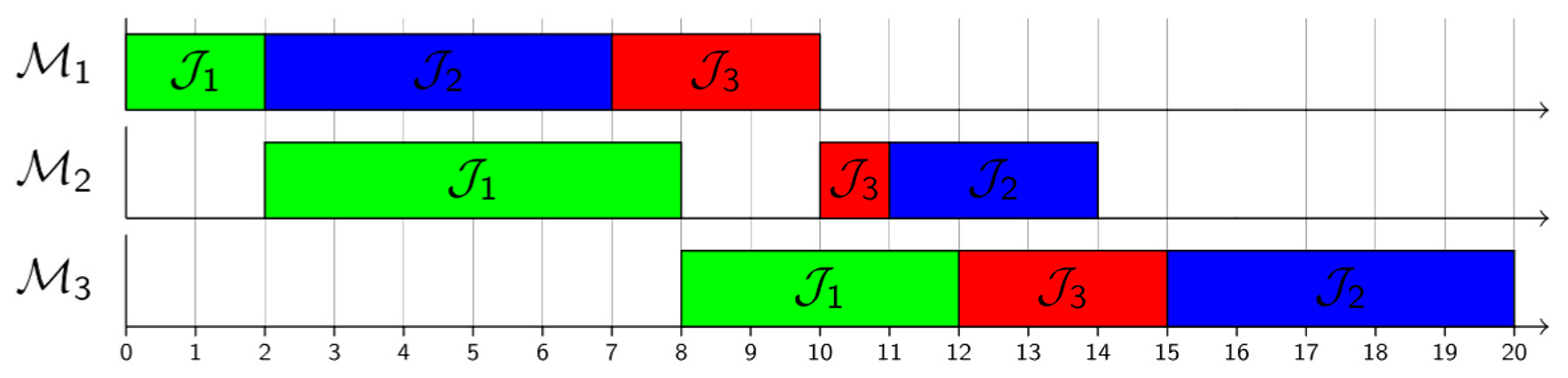
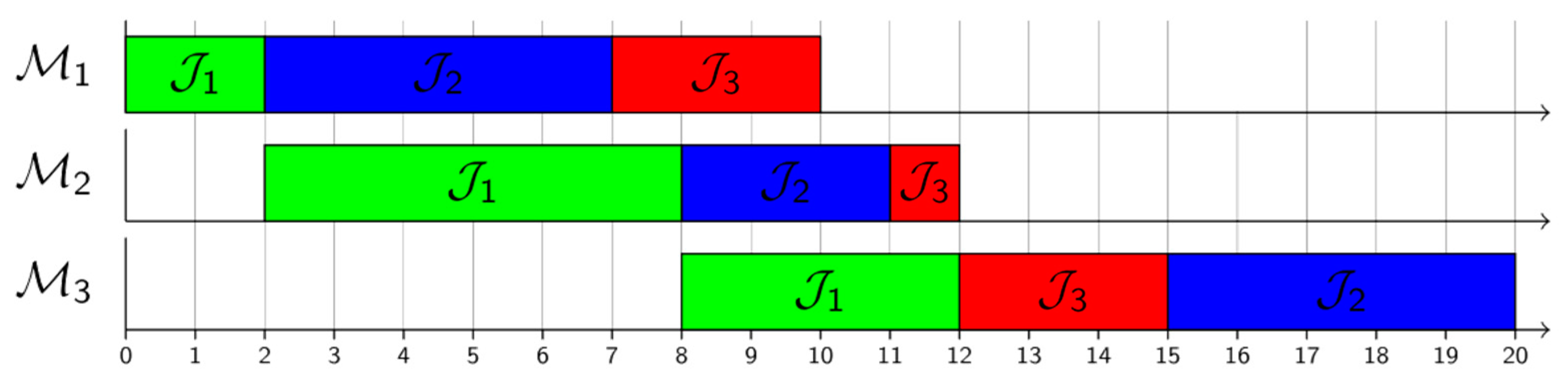
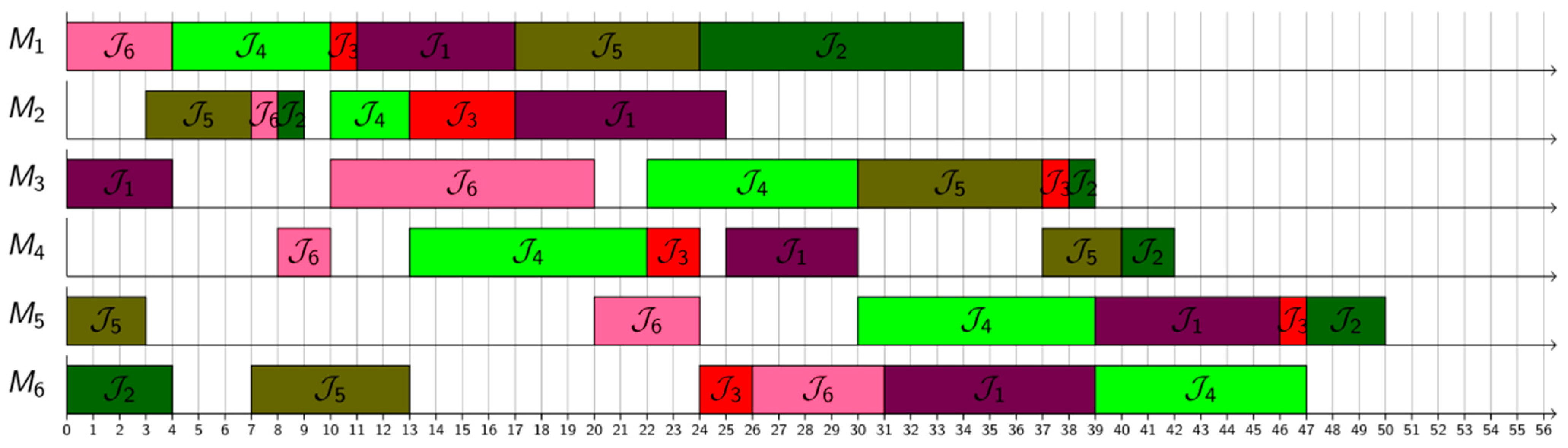
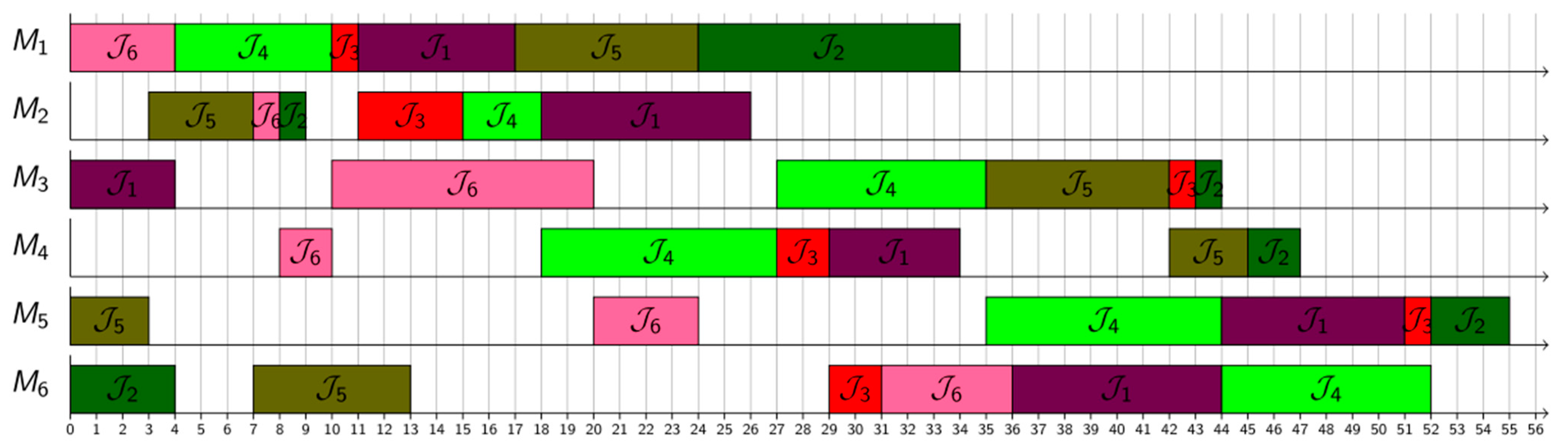
4. Experimental Setup
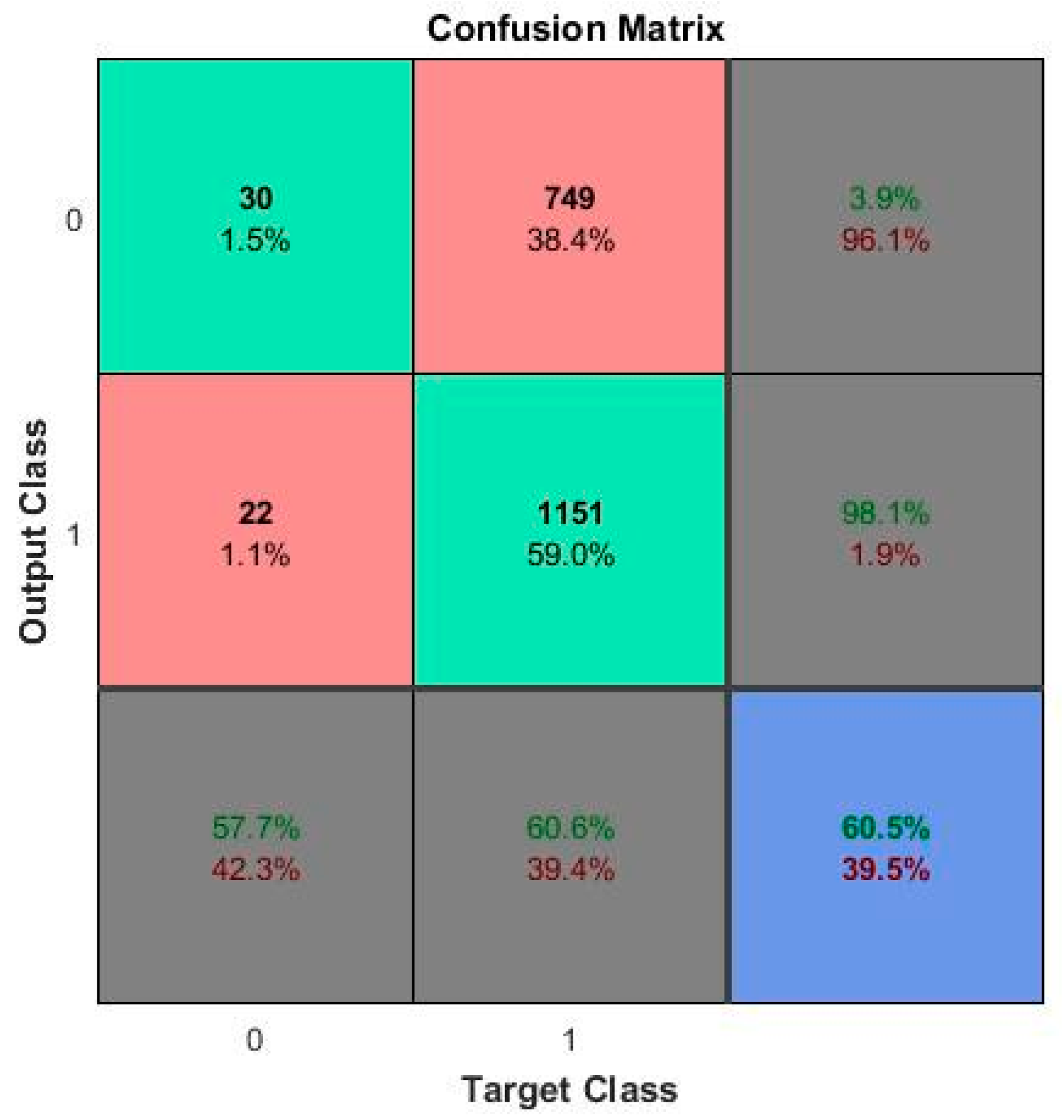
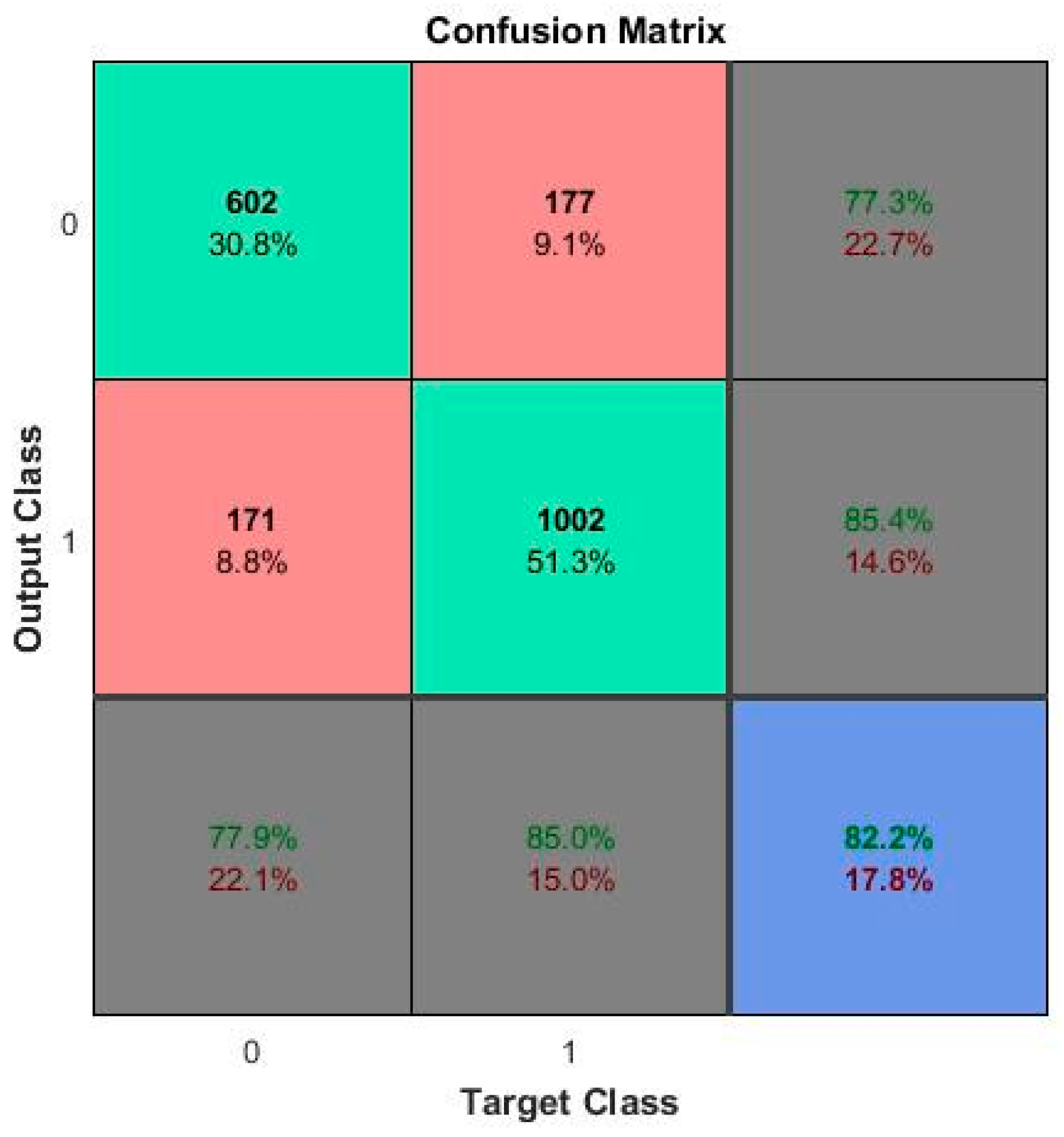
5. Results and Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Shaw, M.J.; Park, S.; Raman, N. Intelligent Scheduling with Machine Learning Capabilities: The Induction of Scheduling Knowledge. IIE Trans. 1992, 24, 156–168. [Google Scholar] [CrossRef]
- Sidney, J.B. Sequencing and scheduling-an introduction to the mathematics of the job-shop, by Simon French, Wiley, 1982, 245 pp. Networks 1983, 13, 310–311. [Google Scholar] [CrossRef]
- Vieira, G.E.; Herrmann, J.W.; Lin, E. Rescheduling manufacturing systems: A Framework of Strategies, Policies, and Methods. J. Sched. 2003, 6, 39–62. [Google Scholar] [CrossRef]
- Montana, D. A comparison of combinatorial optimization and dispatch rules for online scheduling. Mag. West. Hist. 2005, 353–362. [Google Scholar]
- Jain, A.S.; Rangaswamy, B.; Meeran, S. New and “stronger” job-shop neighbourhoods: A Focus on the Method of Nowicki and Smutnicki (1996). J. Heuristics 2000, 6, 457–480. [Google Scholar] [CrossRef]
- Pierreval, H.; Mebarki, N. Dynamic scheduling selection of dispatching rules for manufacturing system. Int. J. Prod. Res. 1997, 35, 1575–1591. [Google Scholar] [CrossRef]
- Geiger, C.D.; Uzsoy, R.; Aytuǧ, H. Rapid modeling and discovery of priority dispatching rules: An Autonomous Learning Approach. J. Sched. 2006, 9, 7–34. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Guan, Z.; Rao, Y. A tabu search algorithm with a new neighborhood structure for the job shop scheduling problem. Comput. Oper. Res. 2007, 34, 3229–3242. [Google Scholar] [CrossRef]
- Jain, A.S.; Meeran, S. A State-of-the-Art Review of Job-Shop Scheduling Techniques; Technical report; Department of Applied Physics, Electronic and Mechanical Engineering, University of Dundee: Dundee, UK, 1998; pp. 1–48. [Google Scholar]
- Choi, H.S.; Kim, J.S.; Lee, D.H. Real-time scheduling for reentrant hybrid flow shops: A Decision Tree Based Mechanism and its Application to a TFT-LCD Line. Expert Syst. Appl. 2011, 38, 3514–3521. [Google Scholar] [CrossRef]
- Wang, W.; Liu, W. A Hybrid Backpropagation Network-based Scheduling Knowledge Acquisition Algorithm. Proceedings of the 2006 International Conference on Computational Intelligence and Security 3-6 November 2006, 1, 151–154. [Google Scholar]
- Shahzad, A.; Mebarki, N. Data mining based job dispatching using hybrid simulation-optimization approach for shop scheduling problem. Eng. Appl. Artif. Intell. 2012, 25, 1173–1181. [Google Scholar] [CrossRef]
- Mouelhi-Chibani, W.; Pierreval, H. Training a neural network to select dispatching rules in real time. Comput. Ind. Eng. 2010, 58, 249–256. [Google Scholar] [CrossRef]
- Priore, P.; de la Fuente, D.; Gomez, A.; Puente, J. A review of machine learning in dynamic scheduling of flexible manufacturing systems. AI EDAM 2001, 15, 251–263. [Google Scholar] [CrossRef]
- Shiue, Y.-R. Data-mining-based dynamic dispatching rule selection mechanism for shop floor control systems using a support vector machine approach. Int. J. Prod. Res. 2009, 47, 3669–3690. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Usher, J.M. Application of reinforcement learning for agent-based production scheduling. Eng. Appl. Artif. Intell. 2005, 18, 73–82. [Google Scholar] [CrossRef]
- Lee, K.K. Fuzzy rule generation for adaptive scheduling in a dynamic manufacturing environment. Appl. Soft Comput. 2008, 8, 1295–1304. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. Learning iterative dispatching rules for job shop scheduling with genetic programming. Int. J. Adv. Manuf. Technol. 2013, 67, 85–100. [Google Scholar] [CrossRef]
- Yazgan, H.R. Selection of dispatching rules with fuzzy ANP approach. Int. J. Adv. Manuf. Technol. 2010, 52, 651–667. [Google Scholar] [CrossRef]
- Coello, C.; Rivera, D.; Cortés, N. Use of an artificial immune system for job shop scheduling. Artif. Immune Syst. 2003, 2787, 1–10. [Google Scholar]
- Muhamad, A.; Deris, S. An artificial immune system for solving production scheduling problems: A Review. Artif. Intell. Rev. 2013, 39, 97–108. [Google Scholar] [CrossRef]
- Aytug, H.; Bhattacharyya, S.; Koehler, G.J.; Snowdon, J.L. Review of machine learning in scheduling. IEEE Trans. Eng. Manag. 1994, 41, 165–171. [Google Scholar] [CrossRef]
- Choudhary, A.K.; Harding, J.A.; Tiwari, M.K. Data mining in manufacturing: A Review Based on the Kind of Knowledge. J. Intell. Manuf. 2009, 20, 501–521. [Google Scholar] [CrossRef]
- Priore, P.; Gómez, A.; Pino, R.; Rosillo, R. Dynamic scheduling of manufacturing systems using machine learning: An Updated Review. Artif. Intell. Eng. Des. Anal. Manuf. AIEDAM 2014, 28, 83–97. [Google Scholar] [CrossRef]
- Pierreval, H.; Ralambondrainy, H. Generation of Knowledge About the Control of a Flow-Shop Using Simulation and a Learning Algorithm; INRIA Research Report No. 897; INRIA: Rocquencourt, France, 1998. [Google Scholar]
- Nakasuka, S.; Yoshida, T. New Framework for Dynamic Scheduling of Production Systems. In International Workshop on Industrial Applications of Machine Intelligence and Vision; IEEE: Tokyo, Japan, 1989; pp. 253–258. [Google Scholar]
- Piramuthu, S.; Raman, N.; Shaw, M.J. Learning-Based Scheduling in a Flexible Manufacturing Flow Line. IEEE Trans. Eng. Manag. 1994, 41, 172–182. [Google Scholar] [CrossRef]
- Priore, P.; de la Fuente, D.; Gomez, A.; Puente, J. Dynamic Scheduling of Manufacturing Systems with Machine Learning. Int. J. Found. Comput. Sci. 2001, 12, 751–762. [Google Scholar] [CrossRef]
- Priore, P.; de la Fuente, D.; Puente, J.; Parreno, J. A comparison of machine-learning algorithms for dynamic scheduling of flexible manufacturing systems. Eng. Appl. Artif. Intell. 2006, 19, 247–255. [Google Scholar] [CrossRef]
- Metan, G.; Sabuncuoglu, I.; Pierreval, H. Real time selection of scheduling rules and knowledge extraction via dynamically controlled data mining. Int. J. Prod. Res. 2010, 48, 6909–6938. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Piramuthu, S.; Tsai, Y.-K. Job shop scheduling with a genetic algorithm and machine learning. Int. J. Prod. Res. 1997, 35, 1171–1191. [Google Scholar] [CrossRef]
- Koonce, D.; Tsa, C.-C. Using data mining to find patterns in genetic algorithm solutions to a job shop schedule. Comput. Ind. Eng. 2000, 38, 361–374. [Google Scholar] [CrossRef]
- Dimopoulos, C.; Zalzala, A.M.S. Investigating the use of genetic programming for a classic one-machine scheduling problem. Adv. Eng. Softw. 2001, 32, 489–498. [Google Scholar] [CrossRef]
- Harrath, Y.; Chebel-Morello, B.; Zerhouni, N. A genetic algorithm and data mining based meta-heuristic for job shop scheduling problem. IEEE Int. Conf. Syst. Man Cybern. 2002, 7, 6. [Google Scholar]
- Kwak, C.; Yih, Y. Data-mining approach to production control in the computer-integrated testing cell. IEEE Trans. Robot. Autom. 2004, 20, 107–116. [Google Scholar] [CrossRef]
- Huyet, A.L.; Paris, J.L. Synergy between evolutionary optimization and induction graphs learning for simulated manufacturing systems. Int. J. Prod. Res. 2004, 42, 4295–4313. [Google Scholar] [CrossRef]
- Li, X.; Olafsson, S. Discovering dispatching rules using data mining. J. Sched. 2005, 8, 515–527. [Google Scholar] [CrossRef]
- Huyet, A.L. Optimization and analysis aid via data-mining for simulated production systems. Eur. J. Oper. Res. 2006, 173, 827–838. [Google Scholar] [CrossRef]
- Shiue, Y.-R.; Guh, R.-S. Learning-based multi-pass adaptive scheduling for a dynamic manufacturing cell environment. Robot. Comput. Manuf. 2006, 22, 203–216. [Google Scholar] [CrossRef]
- Chiu, C.; Yih, Y. A Learning-Based Methodology for Dynamic Scheduling in Distributed Manufacturing Systems. Int. J. Prod. Res. 1995, 33, 3217–3232. [Google Scholar] [CrossRef]
- NhuBinh, H.; Tay, J.C. Evolving Dispatching Rules for solving the Flexible Job-Shop Problem. 2005 IEEE Congr. Evol. Comput. 2005, 3, 2848–2855. [Google Scholar]
- Wang, C.L.; Rong, G.; Weng, W.; Feng, Y.P. Mining scheduling knowledge for job shop scheduling problem. IFAC Pap. OnLine 2015, 48, 835–840. [Google Scholar] [CrossRef]
- Ingimundardottir, H.; Runarsson, T.P. Generating Training Data for Supervised Learning Linear Composite Dispatch Rules for Scheduling. In Learning and Intelligent Optimization 6683; Coello, C.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 263–277. [Google Scholar]
- Roy, B.; Vincke, P. Multicriteria analysis: Survey and New Directions. Eur. J. Oper. Res. 1981, 8, 207–218. [Google Scholar] [CrossRef]
- Rajendran, K.; Kevrekidis, I.G. Analysis of data in the form of graphs. 2013. [Google Scholar]
- Koutra, D.; Parikh, A.; Ramdas, A.; Xiang, J. Algorithms for Graph Similarity and Subgraph Matching; Technical Report of Carnegie-Mellon-University; Carnegie-Mellon-University: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Schuster, C.J. A fast tabu search algorithm for the no-wait job shop problem. Manag. Sci. 2003, 42, 797–813. [Google Scholar]
- Zhang, G.; Gao, L.; Shi, Y. A Genetic Algorithm and Tabu Search for Multi Objective Flexible Job Shop Scheduling Problems. 2010 Int. Conf. Comput. Control Ind. Eng. 2010, 1, 251–254. [Google Scholar]
- Cardin, O.; Trentesaux, D.; Thomas, A.; Castagna, P.; Berger, T.; Bril, H. Coupling predictive scheduling and reactive control in manufacturing: State of the Art and Future Challenges. J. Int. Manuf. 2015. [Google Scholar] [CrossRef]
- Kemppainen, K. Priority Scheduling Revisited—Dominant Rules, Open Protocols, and Integrated Order Management; Helsinki School of Economics: Helsinki, Finland, 2005. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature Selection for Classification: A Review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Shiue, Y.-R.; Guh, R.-S. The optimization of attribute selection in decision tree-based production control systems. Int. J. Adv. Manuf. Technol. 2005, 28, 737–746. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseefi, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Cho, H.; Wysk, R.A. A robust adaptive scheduler for an intelligent workstation controller. Int. J. Prod. Res. 1993, 31, 771–789. [Google Scholar] [CrossRef]
- Chen, C.C.; Yih, Y. Indentifying attributes for knowledge-based development in dynamic scheduling environments. Int. J. Prod. Res. 1996, 34, 1739–1755. [Google Scholar] [CrossRef]
- Siedlecki, W.; Sklansky, J. A note on genetic algorithms for large-scale feature selection. Pattern Recognit. Lett. 1989, 10, 335–347. [Google Scholar] [CrossRef]


| Reference | Approach | Learning | Application |
|---|---|---|---|
| [25] | Simulation/Learning | GENREG | Simplified flow shop |
| [26] | Simulation/Learning | LADS | FMS with transportation |
| [27] | Simulation/Learning | C4.5, PDS | Flow shop with machine failure |
| [28] | Simulation/Learning | Inductive Learning | Flow shop, Job shop |
| [29] | Simulation/Learning | C4.5, BPNN, CBR | FMS with transportation |
| [30] | Simulation/Data Mining | C4.5 | Job shop |
| [31] | GA/Learning | C4.5 | Job shop |
| [32] | GA/Data Mining | Attribute Oriented Induction | Job shop |
| [33] | GP | C4.5 | Single machine |
| [34] | GA/Data Mining | C4.5 | Job shop |
| [35] | Simulation/Data Mining | C4.5 | FMS |
| [36] | GA/Learning | C4.5 | Job shop |
| [37] | Simulation/ Data Mining | C4.5 | Single machine |
| [7] | GP | C4.5 | Single machine, Flow shop |
| [38] | GA/Learning | C4.5 | Job shop |
| [39] | GA/Learning | ANN /C4.5 | FMS |
| [40] | Simulation/GA | Distributed manufacturing system | |
| [41] | GP | Flexible JSSP with recirculation | |
| [42] | Data Mining/ Timed petrinets | C4.5 | Job shop |
| [43] | Data Mining | Preference learning | Job shop |
| [13] | Simulation/ Optimization | Neural networks | Flow shop |
| 1,2 | 2,6 | 3,4 | |
| 1,5 | 2,3 | 3,5 | |
| 1,3 | 2,1 | 3,3 |
| 3,4 | 1,6 | 2,8 | 4,5 | 6,8 | 5,7 | 22 | |
| 6,4 | 2,1 | 1,10 | 3,1 | 4,2 | 5,3 | 26 | |
| 1,1 | 2,4 | 4,2 | 6,2 | 3,1 | 5,1 | 25 | |
| 1,6 | 2,3 | 4,9 | 3,8 | 5,9 | 6,8 | 23 | |
| 5,3 | 2,4 | 6,6 | 1,7 | 3,7 | 4,3 | 18 | |
| 1,4 | 2,1 | 4,2 | 3,10 | 5,4 | 6,5 | 28 | |
| Expression | Description |
|---|---|
| Number of jobs in the system at any instant. | |
| Difference between maximum and average remaining processing times. | |
| Percentage of jobs with relatively longer processing times. | |
| Percentage of jobs with relatively loose due dates. | |
| Average remaining processing time. | |
| Average remaining time until due-dates. | |
| Relative tightness ratio. | |
| Bound on the value of , where . | |
| Quality Index of the best solution among solutions provided by PDRs, . |
| Parameter | Value |
|---|---|
| Datasets | Training Dataset, and Test Dataset, () |
| Problem size | |
| Number of training instances, | |
| Number of test instances, | |
| Release dates, | |
| Operation processing times, | |
| Due-dates, | |
| Objective function, |
| Rule | Definition | Rank | Priority index |
|---|---|---|---|
| FIFO | First in first out | min | |
| SI | Shortest imminent processing time | min | |
| SPT | Shortest processing time | min | |
| EDD | Earliest due-date | min | |
| SLACK | Slack | min | |
| CR | Critical Ratio | min | |
| CRSI | Critical Ratio/Shortest Imminent | min | |
| MOD | Modified operation due date | min | |
| COVERT | Cost over time | max | |
| ATC | Apparent tardiness cost | max | |
| MF | Multi-factor | max | where |
| CEXSPT | Conditionally expediting SPT | - | Partition into three queues, late queue, operationally late queue and ahead-of-schedule queue, with SI as selection criterion within queues. Shifting of job to other queues is not allowed. |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, A.; Mebarki, N. Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation. Computers 2016, 5, 3. https://doi.org/10.3390/computers5010003
Shahzad A, Mebarki N. Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation. Computers. 2016; 5(1):3. https://doi.org/10.3390/computers5010003
Chicago/Turabian StyleShahzad, Atif, and Nasser Mebarki. 2016. "Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation" Computers 5, no. 1: 3. https://doi.org/10.3390/computers5010003
APA StyleShahzad, A., & Mebarki, N. (2016). Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation. Computers, 5(1), 3. https://doi.org/10.3390/computers5010003






