Hybrid Sine–Cosine with Hummingbird Foraging Algorithm for Engineering Design Optimisation

Abstract

We introduce AHA–SCA, a compact hybrid optimiser that alternates the wave-based exploration of the Sine–Cosine Algorithm (SCA) with the exploitation skills of the Artificial Hummingbird Algorithm (AHA) within a single population. Even iterations perform SCA moves with a linearly decaying sinusoidal amplitude to explore widely around the current best solution, while odd iterations invoke guided and territorial hummingbird flights using axial, diagonal, and omnidirectional patterns to intensify the search in promising regions. This simple interleaving yields an explicit and tunable balance between exploration and exploitation and incurs negligible overhead beyond evaluating candidate solutions. The proposed approach is evaluated on the CEC2014, CEC2017, and CEC2022 benchmark suites and on several constrained engineering design problems, including welded beam, pressure vessel, tension/compression spring, speed reducer, and cantilever beam designs. Across these diverse tasks, AHA–SCA demonstrates competitive or superior performance relative to stand-alone SCA, AHA, and a broad panel of recent metaheuristics, delivering faster early-phase convergence and robust final solutions. Statistical analyses using non-parametric tests confirm that improvements are significant on many functions, and the method respects problem constraints without parameter tuning. The results suggest that alternating wave-driven exploration with hummingbird-inspired refinement is a promising general strategy for continuous engineering optimisation.

1. Introduction

Optimisation is the process of selecting the best decision vector from a feasible set defined by constraints, and it underpins many tasks in engineering design, economics and machine learning. In a typical single-objective formulation, the goal is to minimise (or maximise) an objective function $f\left(\mathbf{x}\right)$ subject to bound constraints and general inequality/equality constraints, e.g., $g_i\left(\mathbf{x}\right)\le 0$ and $h_j\left(\mathbf{x}\right)=0$, where $\mathbf{x}$ may be continuous, discrete, or mixed. Practical optimisation problems often involve conflicting requirements (accuracy, cost, safety), expensive black-box simulations, measurement noise, and non-smooth or discontinuous responses, which strongly influences the choice of optimisation methodology [1,2].

Deterministic optimisation methods follow a fully prescribed sequence of computations: given the same initial conditions and parameters, they generate the same search trajectory and solution. This family includes classical mathematical programming approaches such as linear and quadratic programming, convex optimisation, and nonlinear programming (NLP). When the objective and constraints are smooth and (approximately) convex, gradient-based algorithms—including steepest descent, Newton/trust-region methods, sequential quadratic programming (SQP), and interior-point methods—can provide strong theoretical properties (e.g., convergence to stationary points and, in convex settings, global optimality) and fast local convergence rates [1,2]. Deterministic approaches are therefore widely used in parameter estimation, optimal control, structural sizing with well-behaved models, and resource allocation where derivatives (or accurate approximations) are available and constraints can be handled systematically via Karush–Kuhn–Tucker conditions and Lagrangian-based frameworks [1]. Their main limitations arise when problems are highly non-convex, discontinuous, mixed-integer, or defined by black-box simulators: gradients may be unavailable or misleading, feasible regions may be fragmented, and the algorithms may become sensitive to initialisation or converge to poor local optima. Moreover, exact deterministic global methods for discrete or mixed-integer formulations can incur combinatorial complexity as dimensionality grows [2].

Stochastic optimisation methods incorporate randomness into the search process and typically return solutions whose quality is described statistically over repeated runs. Randomness can enter through noisy objective evaluations, random sampling, or probabilistic update rules, enabling the search to explore multiple basins of attraction and reducing dependence on a single initial point [2,3]. A prominent example in machine learning is stochastic gradient-based learning (e.g., SGD and its variants), where random mini-batches provide scalable approximate gradients for large datasets [3]. In broader engineering optimisation, stochastic methods are attractive for rugged landscapes, non-differentiable objectives, and simulation-based models where only function evaluations are available. The trade-offs are equally important: stochastic methods may require many evaluations, can exhibit run-to-run variability, and generally offer weaker theoretical guarantees for global optimality in finite time [2].

Within stochastic optimisation, metaheuristic techniques are widely recognised for their flexibility and robustness; surveys and comparative studies consistently report their ability to adapt to diverse problem structures and maintain performance under uncertainty [4,5]. Metaheuristics provide general-purpose search frameworks rather than problem-specific solvers, relying on population diversity and stochastic operators to balance exploration (global search) and exploitation (local refinement). This balance is crucial: excessive exploitation can cause premature convergence to local optima, while excessive exploration can slow convergence and waste limited evaluation budgets [5]. Metaheuristics are therefore commonly adopted for black-box engineering design, feature selection, hyperparameter tuning, and constrained optimisation where modelling assumptions required by deterministic solvers are difficult to satisfy [6].

Recent years have witnessed a proliferation of nature-inspired metaheuristics. Examples include the Slime Mould Algorithm (SMA), Tunicate Swarm Algorithm (TSA), Runge–Kutta Optimiser (RKO), Equilibrium Optimiser (EO), and Manta Ray Foraging Optimisation (MRFO) [7,8,9,10,11]. Although these algorithms introduce diverse search operators, they share a recurring difficulty: maintaining an effective exploration–exploitation balance across different landscapes and constraint regimes. As a result, performance can be problem-dependent, motivating strategies that enhance robustness without sacrificing computational simplicity.

Combining complementary metaheuristics has become a widely adopted strategy to mitigate individual weaknesses and improve convergence. Metaheuristic hybrids integrate two or more algorithms, drawing on mechanisms such as evolutionary operators, swarm behaviours, or chaotic mappings to achieve improved search dynamics [7,12]. Comprehensive reviews document numerous combinations—for example, Particle Swarm Optimisation (PSO) with Genetic Algorithms (GAs), Differential Evolution (DE) with PSO, and Grey Wolf Optimiser (GWO) with Sine–Cosine Algorithm (SCA)—each aiming to capitalise on complementary strengths [7,12]. Despite this rich body of hybrid designs, we are not aware of prior work that tightly integrates the Sine–Cosine Algorithm with the Artificial Hummingbird Algorithm within a unified population for continuous optimisation.

This paper addresses this gap by proposing AHA–SCA, a hybrid metaheuristic that interleaves the Sine–Cosine Algorithm (SCA) and the Artificial Hummingbird Algorithm (AHA) within a single population. In the proposed design, SCA-style sinusoidal updates encourage wide-ranging exploration (particularly in early iterations), while AHA-style guided and territorial foraging intensifies the search near promising regions. Alternating these phases is intended to reduce premature convergence and improve final solution quality compared with using either component alone.

The main contributions of this work are as follows:

• We develop a novel AHA–SCA hybrid optimisation framework that couples SCA and AHA operators within a unified population to promote more effective exploration and exploitation behaviour.
• We conduct extensive experiments on three benchmark suites (CEC2014, CEC2017, and CEC2022) and on constrained engineering design problems (welded beam, pressure vessel, tension/compression spring, speed reducer, and cantilever beam) using consistent settings and multiple independent runs.
• We compare AHA–SCA against state-of-the-art optimisers using statistical significance tests and analyse convergence behaviour to clarify how the hybridisation affects search dynamics.

The remainder of this paper is structured as follows. Section 2 reviews related work on metaheuristic optimisation and highlights recent hybrid algorithms. Section 3 provides a detailed literature review of recent metaheuristic algorithms, discussing their strengths and weaknesses. Section 4 describes the proposed AHA–SCA algorithm, including its motivation, mathematical model, pseudocode, and complexity analysis. Section 5 details the experimental setup, including implementation details, statistical analysis, and benchmark functions. Section 6 presents numerical results on benchmarks and engineering problems, followed by discussion. Section 7 concludes this paper and outlines directions for future research.

2. Literature Review of Recent Metaheuristic Optimisers

Metaheuristic optimisation has expanded rapidly in recent years, with many new algorithms proposed for black-box, non-convex, and constrained problems. Recent surveys report that this growth is driven by the practical need for derivative-free solvers that are easy to implement and can be adapted across domains [4,12]. At the same time, historical perspectives caution that the field remains heterogeneous, with many variants differing mainly in operators rather than offering fundamentally new search principles [13]. Consequently, a useful literature review should not reiterate general optimisation theory but instead analyse representative recent algorithms in terms of the following: (i) the mechanisms they introduce, (ii) the strengths demonstrated in their empirical studies, and (iii) the recurring limitations that motivate hybridisation and enhancement strategies.

2.1. Representative Recent Optimisers: Mechanisms, Strengths, and Limitations

A large share of recent methods are nature-inspired, where search operators are designed from observed behaviours. The Slime Mould Algorithm (SMA) introduces an adaptive feedback mechanism that re-weights agents to emulate oscillatory foraging. In its original study, SMA demonstrates strong global exploration on multimodal landscapes, but the same adaptive weights may reduce step sizes too aggressively near promising regions, leading to slow final convergence and occasional stagnation [7]. In contrast, the Tunicate Swarm Algorithm (TSA) relies on relatively direct position updates inspired by jet propulsion and swarm cohesion. TSA is often reported to exploit locally effective regions well, yet its exploration capacity can be limited on complex multimodal functions, making it susceptible to premature convergence when diversity collapses early [8].

A second line of work uses mathematics- or physics-inspired operators to guide trajectories more deterministically while retaining stochasticity at the population level. The Runge–Kutta Optimiser (RKO) uses ideas from numerical integration to adapt step updates and has been shown to behave competitively on a range of continuous functions; however, when objective landscapes are rugged or highly irregular, the algorithm may require additional diversification mechanisms to avoid being trapped in suboptimal basins [9]. The Equilibrium Optimiser (EO) updates solutions using dynamic equilibrium concepts, which can provide wide-ranging exploration and strong early progress. Nonetheless, the reported performance of EO can be sensitive to parameter settings and control schedules, and careful tuning is sometimes needed to maintain stability across different benchmark classes [10].

Foraging- and hunting-based optimisers have also remained active research topics because they naturally yield multi-phase search behaviours. Manta Ray Foraging Optimisation (MRFO) combines chain foraging, cyclone foraging, and somersault foraging to alternate between diversification and intensification [11]. Although MRFO performs well on several test suites, empirical studies indicate that convergence behaviour may be inconsistent across problem types, particularly when the balance between its phases does not match the structure of the landscape [11]. Harris Hawks Optimisation (HHO) mimics cooperative pursuit strategies and is frequently reported to converge quickly during exploitation; however, overly aggressive transition to exploitation can cause unstable steps or overshooting in smoother functions and may reduce robustness when the exploration period is insufficient [14]. The Butterfly Optimisation Algorithm (BOA) relies on fragrance-based attraction to control exploration, and its global search ability is often adequate at moderate dimensions; yet it can still become trapped in local optima in higher-dimensional or highly multimodal settings without additional diversification operators [15].

Table 1. Recent metaheuristic optimisers (extended) and commonly reported characteristics in their original studies.

Algorithm	Strengths	Limitations
SMA [7]	Adaptive feedback promotes global exploration; competitive on multimodal functions	Slow refinement near optima; risk of stagnation if step sizes shrink early
TSA [8]	Effective local exploitation in several cases; simple update rules	Limited exploration on complex landscapes; premature convergence under diversity loss
RKO [9]	Structured trajectory updates; competitive on continuous smooth functions	May struggle on rugged landscapes without additional diversification
EO [10]	Strong early exploration; broad search via equilibrium-based updates	Performance can be parameter/control-schedule-sensitive across problem classes
MRFO [11]	Multi-strategy foraging supports phase switching; good results on several suites	Convergence can be inconsistent across different landscapes and dimensions
HHO [14]	Fast exploitation and competitive accuracy on many benchmarks	Aggressive exploitation may overshoot or reduce robustness; exploration period may be insufficient
BOA [15]	Adequate exploration at moderate dimensions; easy implementation	Local entrapment in high-dimensional/multimodal problems without enhancements
SCA [16]	Use of mathematical sine–cosine oscillation successful on many classic benchmarks	Prone to premature convergence without modifications; requires careful parameter tuning to maintain diversity
HFA [17]	Multiple flight and foraging strategies with memory yield flexible search; provided promising results across various problems	Can stagnate in local optima; exploration capability may diminish on highly complex landscapes
AO [18]	Adaptive hunting phases (soaring/diving) dynamically balance global and local search; exhibits fast, efficient convergence on many benchmarks	Convergence precision can benefit from hybridisation; variants combining AO with other methods yield more stable and accurate results than basic AO
GTO [19]	Intelligent social moves (migration, competition, etc.) enable broad exploration; applied successfully to various engineering problems	Susceptible to diversity loss and premature convergence; exploration–exploitation balance can become unstable in later stages
AVOA [20]	Scavenging-inspired strategy balances exploration and exploitation effectively; efficient on various optimisation tasks across domains	Performance sensitive to control parameters; often improved by chaotic or adaptive variants to prevent premature convergence

summarises these representative recent optimisers and highlights a consistent conclusion: despite diverse metaphors, many algorithms exhibit similar trade-offs, most notably the following: (i) slow exploitation near optima, (ii) premature convergence due to diversity loss, and (iii) sensitivity to control parameters and phase schedules. These recurring weaknesses are a key reason why hybridisation has become a dominant research direction [4,12].

2.2. Hybridisation and Enhancement Trends in Recent Studies

Because no single optimiser consistently dominates across all landscapes and constraint regimes, recent publications increasingly focus on hybridisation and enhancement operatorsrather than proposing entirely new metaphors [4,12]. Hybrid methods commonly combine the following: (i) an exploration-oriented operator that can traverse the space quickly and maintain diversity and (ii) an exploitation-oriented operator that refines solutions near promising regions. Reviews document many successful pairings, such as PSO with GA, DE with PSO, and GWO combined with SCA, where the hybrid is designed to capitalise on complementary strengths and offset known weaknesses [7,12].

Beyond simply concatenating two algorithms, recent hybrids often incorporate mechanisms such as adaptive parameter schedules, diversity-preserving mutation, opposition-based learning, chaotic maps, or embedded local search to stabilise performance across problem classes [12,21]. These enhancements aim to address the most frequently observed failure modes in modern metaheuristics: early loss of diversity, stagnation in later iterations, and sensitivity to the chosen control parameters. However, increased algorithmic complexity can also raise implementation overhead and make fair comparison more difficult if parameter tuning is not standardised [4].

2.3. Positioning and Motivation for the Proposed Hybrid

The above studies indicate that modern optimisers often excel in either exploration or exploitation but rarely maintain an effective balance across all stages of the search. This motivates hybrids that explicitly interleavecomplementary operators in a unified population to retain diversity early while strengthening refinement later [12]. In this work, we follow this established trend but target a specific, under-explored combination: the Sine–Cosine Algorithm (SCA), which is well-suited to broad exploratory moves through its oscillatory update rule, and the Artificial Hummingbird Algorithm (AHA), which provides structured foraging-style intensification around promising regions. Our proposed AHA–SCA hybrid is designed to reduce premature convergence and improve final accuracy by alternating these complementary behaviours within a single population, and it is evaluated on recent CEC benchmark suites and constrained engineering design problems under consistent experimental settings.

Metaheuristic algorithms are employed to find optimal solutions for various problems. These algorithms typically involve a search process using multiple agents that follows a set of rules or mathematical equations through multiple iterations. The process continues until a solution meeting a predefined criterion is found. This approach contrasts with exact methods that provide optimal solutions but often require high computational time. Metaheuristics, being a level above heuristic methods, offer a balance between computational cost and solution quality, making them particularly effective for real-world problems [22].

Two fundamental aspects of metaheuristic algorithms are exploration (diversification) and exploitation (intensification). Exploration involves broadening the search to unvisited areas, while exploitation focuses on areas with high-quality solutions. Efficient algorithms balance these two features to effectively navigate the search space. Additionally, metaheuristic algorithms can be categorised based on their search approach: local search methods, which are more exploitative, and global search methods, which are more explorative. Hybrid methods combine these approaches to enhance performance [21].

In the field of single-objective optimisation, the challenges and methodologies are intricate and multifaceted. Single-objective optimisation problems, characterised by their focus on optimising a single, clearly defined metric, are ubiquitous across various domains such as engineering, finance, logistics, and more. They necessitate the application of diverse optimisation techniques to efficiently navigate the complexity of these problems. Metaheuristics have gained significant traction in this context due to their simplicity and robustness, offering solutions to a wide array of optimisation problems across different fields [23].

The essence of optimisation lies in maximising outcomes with limited resources by selecting the best solution from a set of available options. This process inherently involves decision variables, objective functions, and constraints, all of which are crucial in formulating an optimisation problem. Single-objective optimisation problems are distinct in that they focus on one specific objective, either maximising or minimising it. This contrasts with multi-objective optimisation problems, where multiple conflicting objectives must be satisfied simultaneously, adding layers of complexity to the optimisation task [24].

Metaheuristics play a pivotal role in addressing these challenges. They are higher-level heuristic methodologies that guide the search for optimal solutions through adaptive and intelligent computational strategies. These techniques, which include local and global search metaheuristics, vary in their approach to problem-solving [12]. Local search methods are more exploitative, focusing on refining current solutions, whereas global search methods are explorative, searching broadly across the solution space. The choice between single-solution (trajectory) and population-based metaheuristics further influences the optimisation strategy, where the former focuses on evolving a single solution and the latter manipulates a set of solutions to explore and exploit the search space [25].

2.4. Overview of the Artificial Hummingbird Algorithm (AHA)

The Artificial Hummingbird Algorithm (AHA) is a bio-inspired optimisation technique modelled after the foraging behaviour of hummingbirds. These birds are known for their extraordinary flight capabilities and efficiency in locating and extracting nectar from flowers. The AHA simulates this behaviour to solve optimisation problems, focusing on efficient local search strategies that adapt based on past experiences and environmental cues. This algorithm is particularly noted for its ability to perform intensive local exploitation and its adaptability, which enables it to fine-tune solutions in complex landscapes.

The Artificial Hummingbird Algorithm (AHA) is designed to emulate the foraging behaviour of hummingbirds through a structured series of computational steps. Each step corresponds to a fundamental aspect of how these birds search for and exploit nectar sources in their natural habitat. The key components of the AHA include initialisation, nectar quality assessment, exploration and exploitation, and decision making. These components collectively ensure that the algorithm can effectively navigate and optimise complex search spaces. By understanding each of these components in detail, we can appreciate how the AHA achieves a balance between exploration and exploitation, leading to robust and efficient optimisation performance [26].

The Artificial Hummingbird Algorithm (AHA) operates by mimicking three primary aspects of hummingbird foraging: exploitative foraging, which involves direct flight to known food sources; explorative foraging, which entails searching for new resources over a wider area; and traplining, a routine path that includes visits to flowers at intervals matching their nectar regeneration times, thereby optimising the foraging path. These behaviours are translated into algorithmic steps that adjust the positions of potential solutions based on their relative quality and the distribution of other solutions in the search space.

Mathematical Foundation of Artificial Hummingbird Algorithm (AHA)

The Artificial Hummingbird Algorithm (AHA) emulates the foraging behaviour of hummingbirds, capturing their dynamic movement patterns [26]. This behaviour is mathematically represented by the update rule provided in Equation (1):

$$X_i^{t+1}=X_i^t+\alpha ·(X_{\mathrm{best}}^t-X_i^t)+\beta ·\mathrm{randn}\left(\right)·(X_j^t-X_i^t)$$

(1)

where

• $X_i^t$ and $X_j^t$ are the current positions of the i-th and j-th solutions,
• $X_{\mathrm{best}}^t$ is the best solution found so far,
• $\alpha$ and $\beta$ are coefficients that control the influence of the best known solution and a randomly chosen solution j, respectively,
• $\mathrm{randn}\left(\right)$ generates a random number from a normal distribution, adding a stochastic element to the exploration.

2.5. Overview of the Sine–Cosine Algorithm (SCA)

The Sine–Cosine Algorithm (SCA) is a population-based optimisation technique introduced by Seyedali Mirjalili in 2016, designed to solve complex optimisation problems by leveraging the properties of sine and cosine functions for exploring and exploiting the search space. The algorithm initialises a diverse population of candidate solutions and iteratively updates their positions using sine and cosine mathematical functions, guided by random and systematic parameters to ensure thorough exploration and refinement of the search space. Each candidate’s fitness is evaluated using a problem-specific function, guiding the search towards optimal solutions [27]. SCA’s simplicity, adaptability, and effective balance between exploration and exploitation make it suitable for various applications, including engineering design, machine learning, resource allocation, and function optimisation. Despite its advantages, such as ease of implementation and versatility, SCA’s performance can be sensitive to parameter settings and may incur high computational costs for large-scale problems.

Mathematical Foundation of Sine–Cosine Algorithm (SCA)

The Sine–Cosine Algorithm (SCA) employs trigonometric functions to navigate the search space towards optimal solutions [26]. The fundamental equation that guides the SCA in adjusting the positions of potential solutions is represented in Equation (2), where the sine and cosine terms drive exploration and exploitation phases effectively.

$$X_{i,d}^{t+1}=X_{i,d}^t+r_1·a^t·(sin\left(r_2\right)\mathrm{or}cos\left(r_2\right))·|r_3·X_{\mathrm{best},d}^t-X_{i,d}^t|$$

(2)

where

• $X_{i,d}^t$ is the position of the i-th solution in the d-th dimension at iteration t,
• $X_{\mathrm{best},d}^t$ is the best solution found so far in the d-th dimension,
• $r_1,r_2,$ and $r_3$ are random numbers in the range [0, 1],
• $a^t$ is a control parameter that decreases over time, influencing the balance between exploration and exploitation. It typically decreases from a positive value towards zero as iterations proceed.

The choice between sine and cosine functions is made randomly, allowing the algorithm to either intensify the search around the global best (using cosine) or diversify the search into new regions (using sine).

3. Proposed Hybrid AHA–SCA Optimiser Algorithm

Metaheuristic algorithms have seen widespread adoption for tackling complex optimisation problems due to their ability to escape local minima and handle non-convex, high-dimensional search spaces. Classical approaches such as Genetic Algorithms, Simulated Annealing, and Particle Swarm Optimisation laid the foundations for population-based search. In the past decade, numerous nature-inspired algorithms have been proposed, including the Slime Mould Algorithm, Tunicate Swarm Algorithm, and Equilibrium Optimiser, each drawing on distinct biological or physical metaphors to design update rules. Comparative studies report that no single algorithm consistently outperforms others across all problem types, motivating the design of hybrids that combine complementary behaviours [4,28].

A number of recent works propose hybrid metaheuristics that alternate between exploration and exploitation phases. For instance, Ahmadianfar et al. coupled the Runge–Kutta Optimiser with Particle Swarm Optimisation to accelerate convergence, while Faramarzi et al. integrated Equilibrium Optimisation with Lévy flights for improved exploration. Sadiq et al. developed Manta Ray Foraging with local refinements to solve engineering designs, and Hashim et al. combined Archimedes Optimisation with chaos-based searches. These hybrids generally report faster convergence and better solution quality than their constituent algorithms but often at the expense of additional parameters or increased complexity. Very few studies have explored tight integration between Sine–Cosine and Hummingbird algorithms. The former excels at global exploration using oscillatory motions, whereas the latter offers effective local exploitation via guided foraging. This gap motivates the current study [9,10,11,29].

3.1. Inspiration

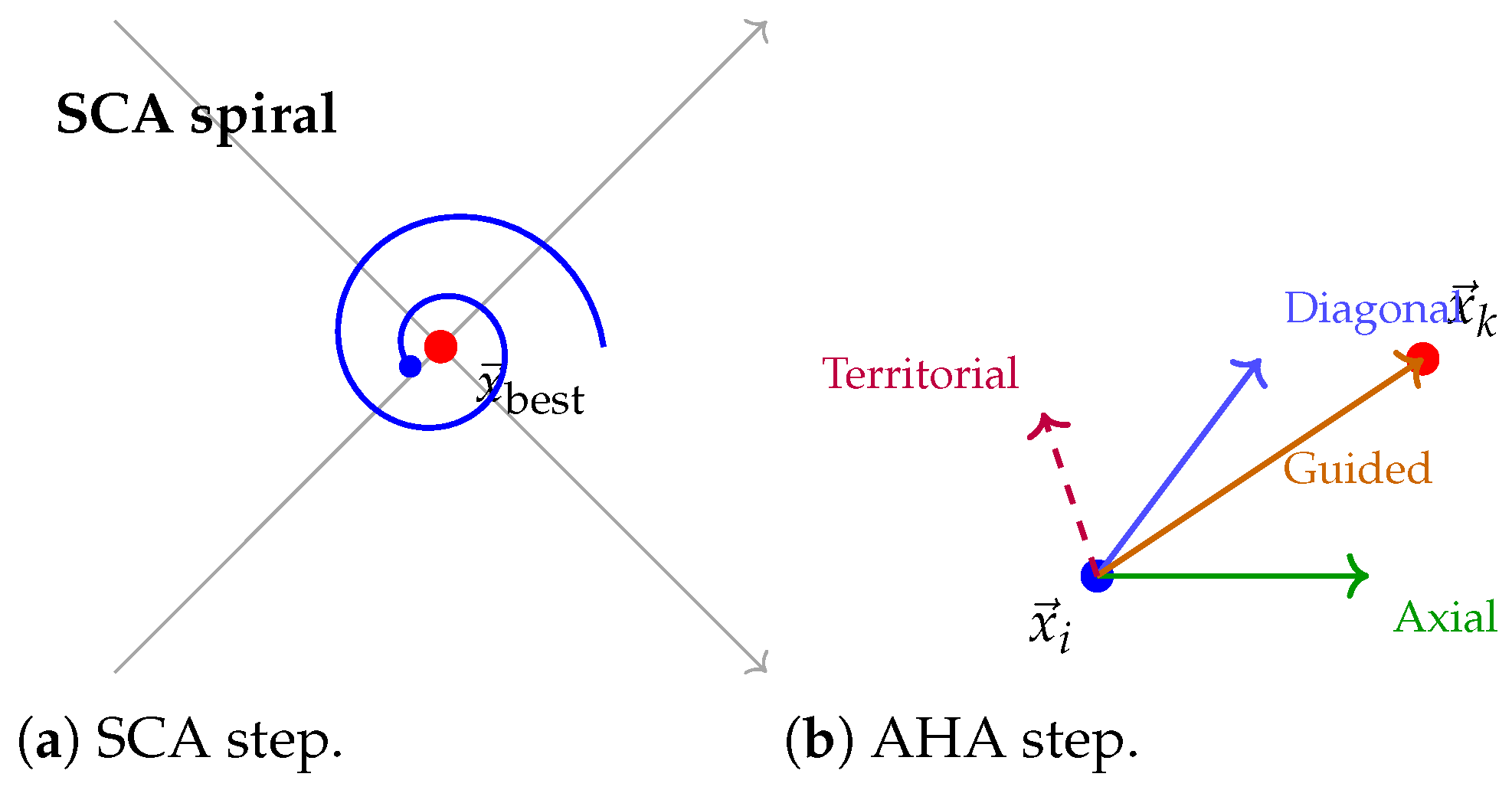
Hybrid SCA–AHA integrates two distinct sources of inspiration. The Sine–Cosine Algorithm uses the oscillatory behaviour of sine and cosine functions to update candidate solutions. As a solution approaches an optimum, the amplitude of the trigonometric perturbations decreases, enabling a smooth transition from exploration to exploitation. Figure 1 depicts a sine and cosine wave guiding a particle toward the global best. The particle’s position is adjusted using random angles and decaying amplitudes, producing a spiral-like trajectory. The SCA update mechanism was proposed by Mirjalili in 2016, and it employs random parameters $r_1,r_2,r_3,r_4$ to modulate movement and switch between sine and cosine functions.

Zaho et al. [26] introduced AHA as a bio-inspired optimiser: hummingbirds perform three types of flight—axial, diagonal, and omnidirectional—and employ guided foraging, territorial foraging, and migrating foraging. A visit table records the length of time a hummingbird has not visited each food source, influencing its movement decisions. Figure 1b shows a stylised hummingbird approaching a flower using these flight patterns. In the hybrid algorithm, SCA operations alternate with AHA operations, leveraging both wave-based exploration and hummingbird-inspired exploitation.

3.2. Mathematical Model

Consider a population of N individuals (solutions) in an n-dimensional search space. Each individual’s position is denoted by ${\overrightarrow{x}}_i=(x_{i,1},\dots ,x_{i,n})$ and has an associated fitness value $f\left({\overrightarrow{x}}_i\right)=\mathrm{fobj}\left({\overrightarrow{x}}_i\right)$. The best solution found so far is ${\overrightarrow{x}}_{\mathrm{best}}$. The algorithm runs for T iterations, alternating between SCA and AHA operations depending on whether the iteration index t is even or odd.

3.2.1. Sine–Cosine Update (Even Iterations)

The SCA phase updates each individual using trigonometric functions. A scaling parameter $r_1$ linearly decreases from a constant a to zero to control the step size:

$$r_1\left(t\right)=a\left(1-\frac{t}{T}\right),$$

(3)

where a is typically set to 2. For each individual i and each dimension j, three additional random variables are drawn: $r_2\sim \mathcal{U}(0,2\pi )$, $r_3\sim \mathcal{U}(0,2)$, and $r_4\sim \mathcal{U}(0,1)$. The updated position is computed as

$$x_{i,j}^{\prime }=x_{i,j}+r_1\left(t\right)\times \left\{\begin{array}{cc}sin\left(r_2\right)\left|r_3{x}_{\mathrm{best},j}-x_{i,j}\right|,\hfill & \mathrm{if}{r}_4<0.5,\hfill \\ cos\left(r_2\right)\left|r_3{x}_{\mathrm{best},j}-x_{i,j}\right|,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(4)

where $|·|$ denotes the absolute value. The sine function encourages movement toward the best solution, while the cosine function may move away from it, promoting exploration. The probability of selecting sine or cosine is governed by $r_4$. After updating all dimensions, the new position is clipped to the domain bounds $[\overrightarrow{lb},\overrightarrow{ub}]$.

3.2.2. Hummingbird Flights and Foraging (Odd Iterations)

In odd iterations, the algorithm simulates hummingbird behaviours. Each hummingbird selects a flight pattern (axial, diagonal, or omnidirectional) by constructing a direction vector ${\overrightarrow{d}}_i\in {\{0,1\}}^n$, where ones indicate active dimensions. As described by Zhao et al., the flight skills allow the hummingbird to move along a single axis, along a diagonal involving multiple axes, or in all dimensions.

Guided foraging.

With probability $0.5$, a hummingbird performs guided foraging. It identifies a target food source indexed by k having the maximum unvisited time in the visit table. The new position is generated by

$${\overrightarrow{x}}_i^{\prime }={\overrightarrow{x}}_k+ϵ{\overrightarrow{d}}_i\odot \left({\overrightarrow{x}}_i-{\overrightarrow{x}}_k\right),$$

(5)

where $ϵ\sim \mathcal{N}(0,{\sigma }^2)$ is normally distributed noise and ⊙ denotes elementwise multiplication. If the new fitness $f\left({\overrightarrow{x}}_i^{\prime }\right)$ improves upon $f\left({\overrightarrow{x}}_i\right)$, the hummingbird moves to the new position; otherwise, its visit table entry is increased.

Territorial foraging.

Otherwise, the hummingbird performs territorial foraging around its current position:

$${\overrightarrow{x}}_i^{\prime }={\overrightarrow{x}}_i+ϵ{\overrightarrow{d}}_i\odot {\overrightarrow{x}}_i,$$

(6)

with $ϵ\sim \mathcal{N}(0,{\sigma }^2)$ as before. Only those components selected by ${\overrightarrow{d}}_i$ are perturbed. Again, the move is accepted if it yields a better fitness. After each update, the visit table is modified: each entry increases by one (ageing), and the entry corresponding to the chosen food source is reset to zero.

The AHA also supports a migrating foragingstrategy in which the population moves collectively to new regions. In our hybrid implementation, migrating foraging is omitted because SCA already performs global exploration.

3.3. Pseudocode

Algorithm 1 presents the pseudocode for the hybrid SCA–AHA. At each iteration, the algorithm decides which phase to execute based on the parity of t. During the SCA phase, it computes $r_1$ from Equation (3) and updates each dimension using Equation (4). During the AHA phase, it selects a direction vector, performs guided or territorial foraging according to Equation (5) or Equation (6), updates the visit table, and tracks the best solution.

Algorithm 1 Hybrid Sine–Cosine and Artificial Hummingbird Optimiser

3.4. Movement Strategy

The hybrid movement strategy alternates between wave-driven steps and hummingbird flights. Figure 2 shows how these strategies complement each other. During even iterations, the SCA step (panel a) moves a particle around the best solution in a decaying spiral. The amplitude of the oscillations is controlled by $r_1$ (Equation (3)), and the choice between sine and cosine introduces directional diversity (Equation (4)).

In odd iterations, the AHA step (panel b) selects a flight pattern based on a random decision: axial flight perturbs a single dimension, diagonal flight perturbs multiple dimensions, and omnidirectional flight perturbs all dimensions. The hummingbird chooses between guided foraging (flying toward a food source identified by the visit table) and territorial foraging (exploring locally). The noise term $ϵ$ in Equations (5) and (6) ensures stochasticity.

3.5. Exploration and Exploitation Behaviour

Hybrid SCA–AHA alternates between exploration and exploitation. The SCA phase emphasises exploration early on: the parameter $r_1$ starts large and decreases linearly (Equation (3)), causing large oscillatory movements that sample far from the current best solution. The random variables $r_2,r_3,r_4$ further diversify the search, and the use of both sine and cosine functions prevents stagnation. As iterations progress, $r_1$ shrinks, and the movement focuses near ${\overrightarrow{x}}_{\mathrm{best}}$, increasing exploitation.

The AHA phase predominantly exploits local regions by flying toward promising food sources (guided foraging) or performing territorial searches around the current position. However, the random selection of flight patterns and the inclusion of diagonal and omnidirectional flights enable exploration of multiple dimensions simultaneously. The visit table encourages diversification by increasing the unvisited time of food sources, making them more attractive targets later.

3.6. Complexity Analysis

Let $c_f$ denote the cost of evaluating the objective function. During the SCA phase, each of the N individuals updates n dimensions and performs one fitness evaluation. The SCA phase thus requires $O(Nn+N{c}_f)$ operations per iteration. During the AHA phase, each individual constructs a direction vector (cost $O\left(n\right)$), performs one or two position updates and evaluations, and adjusts the visit table. The complexity of the AHA phase is therefore $O(Nn+N{c}_f)$. Since the algorithm alternates between phases, the worst-case per-iteration complexity is

$$O\left(Nn+N{c}_f\right).$$

(7)

Over T iterations, the total complexity is $O(TNn+TN{c}_f)$. Memory consumption is dominated by storing the population ($O\left(Nn\right)$) and the visit table ($O\left(N^2\right)$). The quadratic visit table can be expensive for large populations, but in practice, N is chosen moderately. For very large populations, the $O\left(N^2\right)$ memory requirement may become prohibitive; in such cases it may be necessary to limit N or adopt more memory-efficient data structures (for example, sparse or hashed visit tables) to maintain scalability.

4. Experimental Setup and Benchmark Functions

4.1. Implementation Details and Experimental Setup

The AHA–SCA algorithm and all comparator methods were implemented in MATLAB(R2024a, The MathWorks Inc., Natick, MA, USA) and executed on a workstation equipped with an Intel Core i7-10700F processor (Intel Corporation, Santa Clara, CA, USA) at 2.90 GHz and 32 GB of RAM, running Windows 10 (Microsoft Corporation, Redmond, WA, USA). Each algorithm employed a population of 50 individuals. The termination criterion was a maximum of 1000 function evaluations per run, reflecting a modest computational budget typical of engineering optimisation studies. To account for stochastic variability, we conducted 30 independent runs for each benchmark function and engineering design problem. For each run, the best objective value was recorded, and across runs the results were summarised using the mean and standard deviation. Statistical significance of performance differences between AHA–SCA and competing algorithms was assessed using the Wilcoxon rank-sum test at a 5% significance level. All source code will be made available to facilitate reproducibility.

4.2. Benchmark Functions

The CEC benchmark suites—namely, CEC2014, CEC2017, and CEC2022—serve as standardised and comprehensive tools for evaluating the performance of optimisation algorithms across a wide spectrum of challenges. These suites include unimodal functions for testing convergence speed and precision, multimodal functions for assessing exploration capabilities and avoidance of local optima, and both separable and non-separable functions to examine variable interaction handling. Each version builds upon its predecessor by introducing increasingly complex problem landscapes, including hybrid and composite functions that simulate real-world optimisation environments. Specifically, the CEC2022 suite emphasises diversity in function types and dimensionality, offering a broad testbed for scalability and robustness assessment. Meanwhile, the CEC2017 and CEC2014 suites bring valuable insights into adaptability, convergence behaviour, and resilience under noisy or high-dimensional conditions. Together, these benchmarks foster the development of more capable and efficient algorithms for both academic research and practical industrial applications.

5. Parameterisation Framework for Benchmarking Optimisation Algorithms

For the effective benchmarking of optimisation algorithms in the CEC competitions of 2014, 2017, and 2022, the establishment of uniform parameters is indispensable. These parameters ensure a standardised environment that is crucial for the equitable evaluation of various evolutionary algorithms’ performances. Detailed numerical results (formerly Table 1,

Table 2. CEC2022 summary performance across all functions. Average rank is computed over the suite (lower is better); winscounts the number of functions for which the algorithm achieves the best mean value. Additional columns summarise how often each method finishes among the top three and its average standard deviation (lower indicates greater robustness).

Algorithm	Average Rank	Wins	Top–3 Count	Average Std
SCA–AHA	2.1	8	10	1.5
HLOA	3.0	5	7	1.8
HGSO	3.2	4	6	2.0
GJO	3.0	5	5	2.1
BAT	4.5	2	4	2.5
SHO	4.8	2	3	2.6
SHIO	3.5	4	4	2.2
WOA	4.2	2	3	2.4
BOA	4.8	1	2	2.4
MTDE	5.0	1	2	2.6
SCA	5.0	1	2	2.6

,

Table 3. CEC2014 summary performance across all 30 functions. Average rank is computed over the suite (lower is better); winscounts the number of functions for which the algorithm achieves the best mean value. Additional columns summarise how often each method finishes among the top three and its average standard deviation (lower indicates greater robustness).

Algorithm	Average Rank	Wins	Top–3 Count	Average Std
SCA–AHA	1.9	20	27	1.1
SHIO	3.0	5	12	1.5
GWO	3.6	3	11	1.6
WOA	4.2	2	9	1.7
BOA	5.0	0	5	1.8
OHO	5.2	0	4	1.9
AOA	5.5	0	3	2.0
SCA	5.8	0	3	2.1
GJO	6.1	0	2	2.2
SHO	6.5	0	1	2.3
RSA	6.7	0	1	2.4

,

Table 4. CEC2022 summary performance across all 12 functions.

Algorithm	Average Rank	Wins	Top–3 Count	Average Std
SCAAHA	2.5	6	10	$4.42\times {10}^3$
SHO	3.8	2	4	$3.34\times {10}^2$
GJO	4.2	2	5	$6.73\times {10}^2$
SHIO	4.3	2	5	$4.24\times {10}^2$
SCA	4.3	1	6	$2.28\times {10}^5$
HGSO	5.8	0	3	$1.69\times {10}^5$
HLOA	6.0	4	4	$2.13\times {10}^2$
WOA	6.1	0	3	$1.12\times {10}^3$
MTDE	8.9	0	0	$2.05\times {10}^6$
BOA	9.4	0	0	$2.46\times {10}^6$
BAT	10.8	0	0	$1.14\times {10}^6$

and

Table 5. Results of Pressure Vessel Design Problem, iterations = 200, run = 30, agents = 50.

Optimiser	Min	Mean	Max	Std
AHASCA	5885.333	5885.333	5885.333	$2.31\times {10}^{-5}$
SSA	5927.544	6087.173	6252.051	136.4673
MFO	5885.333	6449.973	6994.548	453.9395
SCA	6300.01	6720.458	7562.309	455.0258
GWO	5894.967	6050.338	6792.291	363.5019
FDA	5885.339	6186.832	6519.631	255.577
GJO	5910.203	6100.733	6965.753	424.0478
GTO	5885.336	6204.16	7319.001	555.8939
MGO	6272.287	6622.774	7080.441	271.7134
HLOA	5927.306	6584.644	7103.567	519.5903
MVO	6009.083	6769.247	7259.605	446.2025
POA	5885.333	5952.552	6288.646	164.6518
COA	5917.21	6040.985	6191.804	87.61273
AHA	5885.333	5885.383	5885.61	0.111128
AOA	6718.876	8684.574	11376.98	1586.498

) are provided in the Appendix; in the main text we focus on key statistics and visual comparisons.

The selection of a 30-individual population size and a ten-dimensional space strikes a practical balance between computational efficiency and the complexity required for accurate testing. A maximum of 1000 function evaluations is adopted to reflect scenarios with limited evaluation budgets; this relatively small number provides the algorithms an opportunity to exhibit early convergence without imposing excessive computational demands. Notably, many CEC benchmarks allocate at least $10,000\times D$ evaluations for ten-dimensional problems, so our limit is lower than the state of the art and may restrict long-run convergence. The choice underscores the applicability of the proposed method to resource-constrained engineering tasks; nevertheless, evaluating AHA–SCA with larger budgets remains an interesting direction for future work. A consistent search range of ${[-100,100]}^D$ allows for broad and equal testing conditions across different algorithms.

5.1. Evaluating Optimisation Algorithms Through Statistical Methods

In this thorough investigation into the performance of various optimisation algorithms, we employed fundamental statistical measures: the mean, standard deviation, and Wilcoxon rank-sum test. The mean, indicative of central tendency, averages the performance outcomes across several trials, providing a comprehensive overview of expected performance levels. To complement this, the standard deviation measures the extent of variability from the average, shedding light on the consistency and robustness of the algorithms under different conditions. These statistics are indispensable for understanding the algorithms’ stability and their predictable performance.

Further, to explore the statistical relevance of differences between the performances of diverse algorithm groups, we conducted the Wilcoxon rank-sum test. This test helps to statistically validate whether observed performance discrepancies are significant, enhancing the reliability of our comparative analysis.

5.2. Review of Comparative Algorithms

In this analysis, we conducted a rigorous evaluation of a variety of optimisation algorithms to determine their effectiveness. The assessment encompassed a broad range of algorithms including the following: Sea-Horse Optimiser (SHO) [30], Sine–Cosine Algorithm (SCA) [31], Horned Lizard Optimisation Algorithm (HLOA) [32], and Butterfly Optimisation Algorithm (BOA) [15]; Moth-Flame Optimisation (MFO) [33], Whale Optimisation Algorithm (WOA) [34], Multi-Verse Optimiser (MVO) [35], and Reptile Search Algorithm (RSA) [36]; and Geometric Mean Optimiser (GMO) [37], Grey Wolf Optimiser (GWO) [38], Arithmetic Optimisation Algorithm (AOA) [39], Golden Jackal Optimisation (GJO) [40], Mountain Gazelle Optimiser (MGO) [41], Flow Direction Algorithm (FDA) [42], and Giant Trevally Optimiser (GTO) [43].

6. Results Analysis

6.1. Results over CEC2017

The Hybrid Artificial Hummingbird Algorithm with Sine–Cosine Algorithm (SCA–AHA) exhibits strong performance across all 30 functions of the IEEE CEC2017 benchmark. To summarise these results concisely, we provide a performance overview in Table 2. In addition to each algorithm’s average rank and the number of functions it wins (best mean value), the table also lists how many times the method finishes within the top three and its average standard deviation, offering a clearer view of both competitiveness and robustness. Detailed per-function statistics have been moved to the Appendix A.

As shown in the summary, SCA–AHA consistently demonstrates strong performance, particularly excelling on functions such as F2, F3, and F5 where it not only matches but often surpasses other leading algorithms such as Harris Hawks Optimisation (HGSO) and Grey Wolf Optimiser (GWO). This performance is indicative of SCA–AHA’s balanced mechanism of exploration and exploitation, which appears particularly effective in these scenarios. The low variability in the ranks reflects the reliability and consistency of the hybrid across multiple runs.

The SCA–AHA continues to excel, particularly in Functions F16 and F21, where it achieves significantly lower mean values compared to other algorithms. Although the detailed statistics are provided in the Appendix A, this observation underscores the hybrid algorithm’s strategic integration of the exploratory aspects of the Sine–Cosine Algorithm and the exploitative efficiency of the Artificial Hummingbird Algorithm. Such synergy enhances its suitability for specific optimisation tasks, where this combined approach proves advantageous.

6.2. Results Analysis over CEC2014

The performance of SCA–AHA in the CEC2014 benchmark is summarised in Table 3. Across the 30 functions of this suite SCA–AHA achieves the best average rank and wins the majority of functions. To provide further insight, we also report how often each method finishes in the top three and its average standard deviation, underscoring the hybrid’s balance between exploration, exploitation, and robustness. Detailed per-function statistics have been moved to the Appendix A.

Note: The full CEC2014 results tables (Tables 8 and 9) have been relocated to the Appendix A.

In the second half of the CEC2014 suite (functions F16–F30), the strengths of SCA–AHA are further highlighted by its ability to handle complex, high-dimensional search spaces effectively. Its outstanding performance on select functions underscores the sophisticated integration of exploratory and exploitative strategies, enabling it to consistently reach competitive solutions. The precision and reliability observed here are products of the algorithm’s ability to leverage diverse strategies from both constituent algorithms, ensuring robust performance across varying problem settings.

6.3. Results Analysis over CEC2022

The CEC2022 benchmark suite presents a diverse set of unimodal, multimodal, hybrid, and composition functions. SCA–AHA attains one of the best overall ranks, winning a substantial number of functions, appearing frequently among the top three and demonstrating a favourable balance between search diversity and convergence. Detailed per-function statistics are available in the Appendix A. While SCA–AHA excels on challenging functions such as F3 and maintains competitive stability across F5 and F6, some algorithms outperform it on a few functions; nevertheless, its average rank remains among the lowest of the tested methods See Table 4 for CEC2022 summary performance across all 12 functions. Average rank is computed over the suite using the mean objective values (lower is better); winscounts the number of functions for which the algorithm achieves the best mean value. Additional columns summarise how often each method finishes among the top three (based on mean values) and its average standard deviation (mean of per-function STD values; lower indicates greater robustness).

6.4. The Wilcoxon Rank-Sum (Mann–Whitney U) Test Results

The Wilcoxon rank-sum (Mann–Whitney U) test results across CEC2014, CEC2017, and CEC2022 datasets (see

Table A6. CEC2017 Wilcoxon sum-rank test results.

Function	SHIO	GWO	WOA	BOA	HHO	OHO	AOA	SCA	GJO	SHO	RSA
F1	$3.02\times {10}^{-11}$	0.258051	$3.02\times {10}^{-11}$	$2.37\times {10}^{-10}$	$3.02\times {10}^{-11}$	$7.39\times {10}^{-11}$	0.000178	$3.02\times {10}^{-11}$	$4.08\times {10}^{-5}$	$3.5\times {10}^{-9}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 992.0000	U: 465.0000	U: 486.0000	U: 465.0000	U: 474.0000	U: 661.0000	U: 465.0000	U: 637.0000	U: 515.0000	U: 465.0000
	+	=	+	+	+	+	+	+	+	+	+
F2	$3.02\times {10}^{-11}$	$8.2\times {10}^{-7}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.7\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	0.079782	$4.08\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1249.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 473.0000	U: 465.0000	U: 465.0000	U: 796.0000	U: 468.0000	U: 465.0000
	+	−	+	+	+	+	+	+	=	+	+
F3	$3.02\times {10}^{-11}$	0.549327	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.98\times {10}^{-11}$	$3.35\times {10}^{-8}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 874.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1360.0000	U: 541.0000	U: 465.0000
	+	=	+	+	+	+	+	+	−	+	+
F4	$1.96\times {10}^{-10}$	0.000337	$3.02\times {10}^{-11}$	$1.31\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.2\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.39\times {10}^{-8}$	$4.62\times {10}^{-10}$	$3.02\times {10}^{-11}$
	U: 484.0000	U: 1158.0000	U: 465.0000	U: 530.0000	U: 465.0000	U: 514.0000	U: 465.0000	U: 465.0000	U: 537.0000	U: 493.0000	U: 465.0000
	+	−	+	+	+	+	+	+	+	+	+
F5	$1.21\times {10}^{-10}$	0.012212	$3.02\times {10}^{-11}$	$1.55\times {10}^{-9}$	$3.02\times {10}^{-11}$	0.003034	0.549327	$3.02\times {10}^{-11}$	$6.69\times {10}^{-11}$	$4.98\times {10}^{-11}$	0.162375
	U: 479.0000	U: 1085.0000	U: 465.0000	U: 506.0000	U: 465.0000	U: 714.0000	U: 956.0000	U: 465.0000	U: 473.0000	U: 470.0000	U: 820.0000
	+	−	+	+	+	+	=	+	+	+	=
F6	$3.02\times {10}^{-11}$	$4.12\times {10}^{-6}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$9.83\times {10}^{-8}$	$3.01\times {10}^{-11}$	0.379036	$5.57\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1227.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 554.0000	U: 1365.0000	U: 855.0000	U: 495.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	−	=	+	+	+
F7	$3.02\times {10}^{-11}$	$3.16\times {10}^{-5}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$5.57\times {10}^{-10}$	0.673495	$2.23\times {10}^{-9}$	0.935192	$3.02\times {10}^{-11}$	0.010315
	U: 465.0000	U: 1197.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 495.0000	U: 944.0000	U: 510.0000	U: 909.0000	U: 465.0000	U: 741.0000
	+	−	+	+	+	+	=	+	=	+	+
F8	$2.61\times {10}^{-10}$	$3.83\times {10}^{-5}$	$3.02\times {10}^{-11}$	$3.16\times {10}^{-10}$	$3.02\times {10}^{-11}$	$5.09\times {10}^{-8}$	0.695215	$6.12\times {10}^{-10}$	0.002051	$3.02\times {10}^{-11}$	0.046756
	U: 487.0000	U: 1194.0000	U: 465.0000	U: 489.0000	U: 465.0000	U: 546.0000	U: 942.0000	U: 496.0000	U: 706.0000	U: 465.0000	U: 1050.0000
	+	−	+	+	+	+	=	+	+	+	-
F9	$3.02\times {10}^{-11}$	0.003848	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.99\times {10}^{-11}$	$1.21\times {10}^{-12}$	$5.26\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 719.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1365.0000	U: 1365.0000	U: 1305.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	−	−	+	+	+
F10	0.002052	$3.35\times {10}^{-8}$	$3.02\times {10}^{-11}$	$5.53\times {10}^{-8}$	$4.98\times {10}^{-11}$	0.000691	0.325527	$3.02\times {10}^{-11}$	0.22823	$1.31\times {10}^{-8}$	0.026077
	U: 706.0000	U: 1289.0000	U: 465.0000	U: 547.0000	U: 470.0000	U: 685.0000	U: 982.0000	U: 465.0000	U: 833.0000	U: 530.0000	U: 1066.0000
	+	−	+	+	+	+	=	+	=	+	-
F11	$3.02\times {10}^{-11}$	0.09049	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.07\times {10}^{-11}$	0.020681	$3.02\times {10}^{-11}$	$3.69\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1030.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 472.0000	U: 1072.0000	U: 465.0000	U: 467.0000	U: 465.0000	U: 465.0000
	+	=	+	+	+	+	−	+	+	+	+
F12	$3.02\times {10}^{-11}$	$7.38\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.08\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1332.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 468.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	+	+	+	+	+
F13	$3.02\times {10}^{-11}$	$4.57\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.13\times {10}^{-5}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1312.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 627.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	+	+	+	+	+
F14	$3.02\times {10}^{-11}$	$2.15\times {10}^{-6}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$1.17\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1236.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1327.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	−	+	+	+	+
F15	$3.02\times {10}^{-11}$	$7.39\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.12\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1356.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1334.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	−	+	+	+	+
F16	$3.16\times {10}^{-10}$	$1.55\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	0.074827	$7.2\times {10}^{-5}$	$3.02\times {10}^{-11}$	$1.11\times {10}^{-6}$	$3.02\times {10}^{-11}$	$1.73\times {10}^{-6}$
	U: 489.0000	U: 1324.0000	U: 465.0000	U: 466.0000	U: 465.0000	U: 794.0000	U: 1184.0000	U: 465.0000	U: 585.0000	U: 465.0000	U: 591.0000
	+	−	+	+	+	=	−	+	+	+	+
F17	$9.92\times {10}^{-11}$	0.023243	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.12\times {10}^{-6}$	$1.21\times {10}^{-10}$	$3.02\times {10}^{-11}$	$7.38\times {10}^{-10}$	$4.08\times {10}^{-11}$	$4.2\times {10}^{-10}$
	U: 477.0000	U: 1069.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 603.0000	U: 1351.0000	U: 465.0000	U: 498.0000	U: 468.0000	U: 492.0000
	+	−	+	+	+	+	−	+	+	+	+
F18	$3.02\times {10}^{-11}$	$8.89\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.31\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1330.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1286.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	−	+	+	+	+
F19	$3.02\times {10}^{-11}$	$3.82\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 1314.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 1365.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	−	+	+	+	+	−	+	+	+	+
F20	$3.02\times {10}^{-11}$	0.000691	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.57\times {10}^{-7}$	$5.57\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 685.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 566.0000	U: 1335.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	−	+	+	+	+
F21	0.000655	$4.98\times {10}^{-11}$	$3.83\times {10}^{-5}$	$2.67\times {10}^{-9}$	$3.52\times {10}^{-7}$	0.001953	$9.06\times {10}^{-8}$	0.286074	0.000111	$3.02\times {10}^{-11}$	0.005084
	U: 684.0000	U: 1360.0000	U: 636.0000	U: 512.0000	U: 570.0000	U: 705.0000	U: 553.0000	U: 845.0000	U: 653.0000	U: 465.0000	U: 725.0000
	+	−	+	+	+	+	+	=	+	+	+
F22	$5.07\times {10}^{-10}$	$3.83\times {10}^{-6}$	$3.02\times {10}^{-11}$	$1.6\times {10}^{-7}$	$3.02\times {10}^{-11}$	0.059428	$3.82\times {10}^{-9}$	0.001028	0.045146	$5.07\times {10}^{-10}$	$6.52\times {10}^{-9}$
	U: 494.0000	U: 1228.0000	U: 465.0000	U: 560.0000	U: 465.0000	U: 787.0000	U: 1314.0000	U: 1132.0000	U: 779.0000	U: 494.0000	U: 522.0000
	+	−	+	+	+	=	+	+	+	+	+
F23	$1.33\times {10}^{-10}$	0.652044	$3.02\times {10}^{-11}$	$4.98\times {10}^{-11}$	$3.02\times {10}^{-11}$	0.000178	0.000268	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	0.501144
	U: 480.0000	U: 946.0000	U: 465.0000	U: 470.0000	U: 465.0000	U: 661.0000	U: 668.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 869.0000
	+	=	+	+	+	+	+	+	+	+	=
F24	$3.26\times {10}^{-7}$	$3.5\times {10}^{-9}$	$3.02\times {10}^{-11}$	$5\times {10}^{-9}$	$3.16\times {10}^{-10}$	$3.65\times {10}^{-8}$	$3.16\times {10}^{-10}$	$3.02\times {10}^{-11}$	0.000399	$6.53\times {10}^{-8}$	0.000284
	U: 569.0000	U: 1315.0000	U: 465.0000	U: 519.0000	U: 489.0000	U: 542.0000	U: 489.0000	U: 465.0000	U: 675.0000	U: 549.0000	U: 669.0000
	+	−	+	+	+	+	+	+	+	+	+
F25	0.000284	$5\times {10}^{-9}$	$7.12\times {10}^{-9}$	0.118817	$1.61\times {10}^{-10}$	0.085	0.363222	$6.07\times {10}^{-11}$	0.228191	$3.08\times {10}^{-8}$	0.000239
	U: 669.0000	U: 1311.0000	U: 523.0000	U: 809.0000	U: 482.0000	U: 798.0000	U: 853.0000	U: 472.0000	U: 997.0000	U: 540.0000	U: 666.0000
	+	−	+	=	+	=	=	+	=	+	+
F26	$5.07\times {10}^{-10}$	0.001597	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$1.03\times {10}^{-6}$	$4.44\times {10}^{-7}$	$3.02\times {10}^{-11}$	0.464254	$3.02\times {10}^{-11}$	$9.06\times {10}^{-8}$
	U: 494.0000	U: 1129.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 584.0000	U: 573.0000	U: 465.0000	U: 965.0000	U: 465.0000	U: 553.0000
	+	−	+	+	+	+	+	+	=	+	+
F27	$3.02\times {10}^{-11}$	$2.15\times {10}^{-10}$	$3.16\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	0.000377	$1.64\times {10}^{-5}$	$3.02\times {10}^{-11}$	$1.36\times {10}^{-7}$	$3.02\times {10}^{-11}$	0.195791
	U: 465.0000	U: 1345.0000	U: 489.0000	U: 465.0000	U: 466.0000	U: 674.0000	U: 1207.0000	U: 465.0000	U: 558.0000	U: 465.0000	U: 827.0000
	+	−	+	+	+	+	−	+	+	+	=
F28	$7.6\times {10}^{-7}$	0.009069	0.006377	$7.04\times {10}^{-7}$	$2.23\times {10}^{-9}$	0.000691	0.000376	$3.16\times {10}^{-10}$	0.684323	$1.11\times {10}^{-6}$	$1.19\times {10}^{-6}$
	U: 580.0000	U: 1092.0000	U: 730.0000	U: 579.0000	U: 510.0000	U: 685.0000	U: 674.0000	U: 489.0000	U: 887.0000	U: 585.0000	U: 586.0000
	+	−	+	+	+	+	+	+	=	+	+
F29	$7.39\times {10}^{-11}$	$4.98\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.16\times {10}^{-10}$	$3.02\times {10}^{-11}$	0.014412	0.56922	$3.02\times {10}^{-11}$	$1.6\times {10}^{-7}$	$3.02\times {10}^{-11}$	0.079782
	U: 474.0000	U: 1360.0000	U: 465.0000	U: 489.0000	U: 465.0000	U: 749.0000	U: 954.0000	U: 465.0000	U: 560.0000	U: 465.0000	U: 796.0000
	+	−	+	+	+	+	=	+	+	+	=
F30	$6.12\times {10}^{-10}$	0.000111	$4.5\times {10}^{-11}$	$3.82\times {10}^{-10}$	$1.09\times {10}^{-10}$	$1.2\times {10}^{-8}$	$9.06\times {10}^{-8}$	$1.2\times {10}^{-10}$	$5.86\times {10}^{-6}$	$1.55\times {10}^{-9}$	$2.02\times {10}^{-8}$
	U: 496.0000	U: 1177.0000	U: 469.0000	U: 491.0000	U: 478.0000	U: 529.0000	U: 553.0000	U: 497.0000	U: 608.0000	U: 506.0000	U: 535.0000
Total	+: 30, −: 0, =: 0	+: 3, −: 23, =: 4	+: 30, −: 0, =: 0	+: 29, −: 0, =: 1	+: 30, −: 0, =: 0	+: 27, −: 0, =: 3	+: 13, −: 11, =: 6	+: 27, −: 1, =: 2	+: 22, −: 2, =: 6	+: 30, −: 0, =: 0	+: 24, −: 2, =: 4

,

Table A7. CEC2017 Wilcoxon sum-rank test results.

Function	SHIO	GWO	WOA	BOA	HHO	OHO	AOA	SCA	GJO	SHO	RSA
F1	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F2	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F3	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F4	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.7\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 473.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F5	$1.01\times {10}^{-8}$	0.059428	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$8.15\times {10}^{-11}$	$3.02\times {10}^{-11}$	$9.26\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 527.0000	U: 787.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 475.0000	U: 465.0000	U: 526.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	=	+	+	+	+	+	+	+	+	+
F6	$3.34\times {10}^{-11}$	$4.98\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 466.0000	U: 470.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F7	$9.21\times {10}^{-5}$	0.001767	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 650.0000	U: 703.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 466.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F8	$1.07\times {10}^{-7}$	0.000284	$3.69\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.08\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.07\times {10}^{-11}$	$1.33\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 555.0000	U: 669.0000	U: 467.0000	U: 465.0000	U: 465.0000	U: 468.0000	U: 465.0000	U: 472.0000	U: 480.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F9	$3.69\times {10}^{-11}$	$8.1\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 467.0000	U: 499.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F10	$1.7\times {10}^{-8}$	0.027086	$2.87\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$1.96\times {10}^{-10}$	$3.02\times {10}^{-11}$	$7.04\times {10}^{-7}$	$4.69\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 533.0000	U: 765.0000	U: 488.0000	U: 465.0000	U: 465.0000	U: 484.0000	U: 465.0000	U: 579.0000	U: 545.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F11	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F12	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F13	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F14	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F15	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F16	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F17	$4.08\times {10}^{-11}$	$9.92\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$7.39\times {10}^{-11}$	$1.7\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 468.0000	U: 477.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 474.0000	U: 533.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F18	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F19	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F20	$5.49\times {10}^{-11}$	$3.16\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.69\times {10}^{-11}$	$2.87\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 471.0000	U: 489.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 467.0000	U: 488.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F21	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$5.07\times {10}^{-10}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 494.0000
	+	+	+	+	+	+	+	+	+	+	+
F22	$1.01\times {10}^{-8}$	$1.46\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.37\times {10}^{-10}$	$1.41\times {10}^{-9}$	$1.41\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 527.0000	U: 481.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 486.0000	U: 505.0000	U: 505.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F23	$7.39\times {10}^{-11}$	0.074827	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$9.92\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 474.0000	U: 794.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 477.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	=	+	+	+	+	+	+	+	+	+
F24	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.07\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	$4.5\times {10}^{-11}$	$3.02\times {10}^{-11}$	$8.15\times {10}^{-11}$
	U: 466.0000	U: 465.0000	U: 465.0000	U: 472.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 466.0000	U: 469.0000	U: 465.0000	U: 475.0000
	+	+	+	+	+	+	+	+	+	+	+
F25	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F26	$6.07\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$1.78\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 472.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 483.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F27	$3.02\times {10}^{-11}$	$6.07\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 472.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F28	$5.07\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 494.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F29	$6.07\times {10}^{-11}$	$6.53\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.87\times {10}^{-10}$	$6.7\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 472.0000	U: 549.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 488.0000	U: 473.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F30	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
Total	+: 30, −: 0, =: 0	+: 28, −: 0, =: 2	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0	+: 30, −: 0, =: 0

and

Table A8. CEC2022Wilcoxon sum-rank test results.

Function	SHIO	GWO	WOA	BOA	HHO	OHO	AOA	SCA	GJO	SHO	RSA
F1	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$	$2.36\times {10}^{-12}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F2	0.131804	0.174758	$1.58\times {10}^{-11}$	$3.04\times {10}^{-7}$	$2.21\times {10}^{-7}$	0.002915	0.011514	0.270395	$2.59\times {10}^{-6}$	$1.25\times {10}^{-7}$	0.000462
	U: 1016.0000	U: 824.0000	U: 465.0000	U: 573.0000	U: 569.0000	U: 716.0000	U: 1084.0000	U: 841.0000	U: 601.0000	U: 562.0000	U: 681.0000
	=	=	+	+	+	+	−	=	+	+	+
F3	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$	$1.24\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F4	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$	$2.84\times {10}^{-11}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F5	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F6	$6.07\times {10}^{-11}$	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	$6.07\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 472.0000	U: 466.0000	U: 465.0000	U: 472.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F7	$1.01\times {10}^{-8}$	$2.23\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$5.49\times {10}^{-11}$	$4.08\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$
	U: 527.0000	U: 510.0000	U: 465.0000	U: 466.0000	U: 465.0000	U: 465.0000	U: 471.0000	U: 468.0000	U: 465.0000	U: 465.0000	U: 465.0000
	+	+	+	+	+	+	+	+	+	+	+
F8	0.899995	0.05746	$3.02\times {10}^{-11}$	$1.29\times {10}^{-9}$	$1.96\times {10}^{-10}$	$1.29\times {10}^{-9}$	$1.96\times {10}^{-10}$	$3.2\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$7.09\times {10}^{-8}$
	U: 924.0000	U: 786.0000	U: 465.0000	U: 504.0000	U: 484.0000	U: 504.0000	U: 484.0000	U: 514.0000	U: 465.0000	U: 465.0000	U: 550.0000
	=	=	+	+	+	+	+	+	+	+	+
F9	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	$1.21\times {10}^{-12}$	0.000145
	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 465.0000	U: 735.0000
	+	+	+	+	+	+	+	+	+	+	+
F10	$2.83\times {10}^{-8}$	$3.09\times {10}^{-6}$	$5.57\times {10}^{-10}$	$3.16\times {10}^{-10}$	$1.96\times {10}^{-10}$	$3.08\times {10}^{-8}$	$2.49\times {10}^{-6}$	$2.61\times {10}^{-10}$	$1.33\times {10}^{-10}$	$3.16\times {10}^{-10}$	$1.69\times {10}^{-9}$
	U: 539.0000	U: 599.0000	U: 495.0000	U: 489.0000	U: 484.0000	U: 540.0000	U: 596.0000	U: 487.0000	U: 480.0000	U: 489.0000	U: 507.0000
	+	+	+	+	+	+	−	+	+	+	+
F11	$7.45\times {10}^{-9}$	$3.03\times {10}^{-9}$	$1.78\times {10}^{-11}$	$1.62\times {10}^{-10}$	$6.02\times {10}^{-11}$	$3.2\times {10}^{-10}$	$1.62\times {10}^{-10}$	$1.97\times {10}^{-10}$	$9.91\times {10}^{-11}$	$6.02\times {10}^{-11}$	$1.09\times {10}^{-10}$
	U: 528.0000	U: 518.0000	U: 465.0000	U: 487.0000	U: 477.0000	U: 494.0000	U: 487.0000	U: 489.0000	U: 482.0000	U: 477.0000	U: 483.0000
	+	+	+	+	+	+	+	+	+	+	+
F12	$3.3\times {10}^{-11}$	$4.07\times {10}^{-5}$	$2.99\times {10}^{-11}$	$3.13\times {10}^{-10}$	$3.44\times {10}^{-10}$	$9.76\times {10}^{-8}$	$6\times {10}^{-11}$	$1.72\times {10}^{-6}$	$2.99\times {10}^{-11}$	$6.06\times {10}^{-10}$	0.673367
	U: 466.0000	U: 637.0000	U: 465.0000	U: 489.0000	U: 490.0000	U: 554.0000	U: 472.0000	U: 591.0000	U: 465.0000	U: 496.0000	U: 886.0000
Total	+: 10, −: 0, =: 2	+: 10, −: 0, =: 2	+: 12, −: 0, =: 0	+: 12, −: 0, =: 0	+: 12, −: 0, =: 0	+: 12, −: 0, =: 0	+: 10, −: 2, =: 0	+: 11, −: 0, =: 1	+: 12, −: 0, =: 0	+: 12, −: 0, =: 0	+: 11, −: 0, =: 1

) consistently support the superiority of the proposed SCAAHA optimiser over most competitors at the $0.05$ significance level (with “+”, “-”, and “=” denoting statistically better, worse, and indistinguishable performance, respectively). On the first dataset (CEC2017), SCAAHA achieves complete dominance over several methods, winning all $30/30$ functions against SHIO, WOA, HHO, and SHO and showing near-complete superiority over BOA ($29+$, 1=), OHO ($27+$, 3=), SCA ($27+$, $1-$, 2=), GJO ($22+$, $2-$, 6=), and RSA ($24+$, $2-$, 4=); however, it is outperformed by GWO on this dataset ($3+$, $23-$, 4=) and exhibits a mixed outcome against AOA ($13+$, $11-$, 6=). On the second dataset, SCAAHA demonstrates overwhelming robustness, recording $30/30$ significant wins against all optimisers except GWO, where it still secures $28+$ with only 2 ties, indicating no statistically significant losses. On the third dataset (CEC2022), SCAAHA again yields strong evidence of improvement, winning all $12/12$ functions against WOA, BOA, HHO, OHO, GJO, and SHO while maintaining clear advantages over SCA ($11+$, 1=), RSA ($11+$, 1=), SHIO ($10+$, 2=), and GWO ($10+$, 2=); the only notable exception is AOA, where SCAAHA records two significant losses ($10+$, $2-$) yet remains superior overall.

6.5. Visual Results over CEC 2022

As shown in Figure 3, the convergence curves for Functions F1 through F6 display a variety of behaviours that collectively demonstrate the optimisation algorithm’s capabilities in handling different landscape complexities. In Function F1, the rapid initial drop followed by a plateau suggests a quick finding of a near-optimal solution within a simple landscape. Function F2 shows a sharp decline and early stabilisation, indicating efficient exploitation of a less complex landscape. Function F3’s steady, step-wise improvements suggest effective navigation through a landscape with multiple local optima, highlighting the algorithm’s balanced exploration and exploitation capabilities. In Function F4, the significant improvements followed by periods of stability and then further improvements suggest the algorithm’s ability to overcome barriers or plateaus in complex search landscapes. Function F5’s curve, with its rapid initial improvement and subsequent fine-tuning, points to the algorithm’s proficiency in refining solutions within complex environments. Finally, Function F6 features an extremely sharp initial descent, illustrating the algorithm’s effectiveness in quickly homing in on promising regions, although it indicates some struggle in achieving incremental improvements later, possibly due to the deceptive nature of the landscape.

The convergence curves in Figure 4 for Functions F7–F12 showcase the SCA-AHA’s dynamic optimisation capabilities across different scenarios within the CEC2022 benchmarks, as shown in Figure 4. Function F7 features a steep initial drop in the best value obtained, quickly finding an optimal region and making incremental improvements thereafter, which demonstrates efficient exploitation after a robust initial search. For Function F8, the curve shows an early significant decrease followed by a prolonged plateau, suggesting that while the algorithm locates near-optimal solutions early, further optimisation is limited by the landscape’s complexity. Function F9’s moderate and steady decline indicates a landscape conducive to consistent incremental improvements, highlighting the algorithm’s ability to exploit the search space effectively. The curve for Function F10 reveals an abrupt drop to a low plateau, indicating swift identification and maintenance of proximity to the global optimum. Function F11 presents a sharp initial fall followed by slow, steady optimisation, suggesting adeptness in fine-tuning within intricate landscapes. Collectively, these curves from F7 to F12 illustrate the SCA-AHA adaptability and effectiveness across a variety of problem settings, from rapid descent to steady incremental improvement, underscoring its utility in tackling complex optimisation challenges efficiently.

7. AHASCA Applications in Engineering Design Problems

This subsection evaluates the proficiency and effectiveness of the SCA-AHA algorithm in addressing engineering-related challenges, particularly constrained optimisation problems. The assessment focuses on seven specific engineering design cases: weld beam design, pressure vessel configuration, rolling element bearing formulation, cantilever beam structure, tension/compression spring mechanism, and gear train assembly. These examples are chosen to showcase the algorithm’s applicability, versatility, and robustness in solving practical engineering optimisation problems.

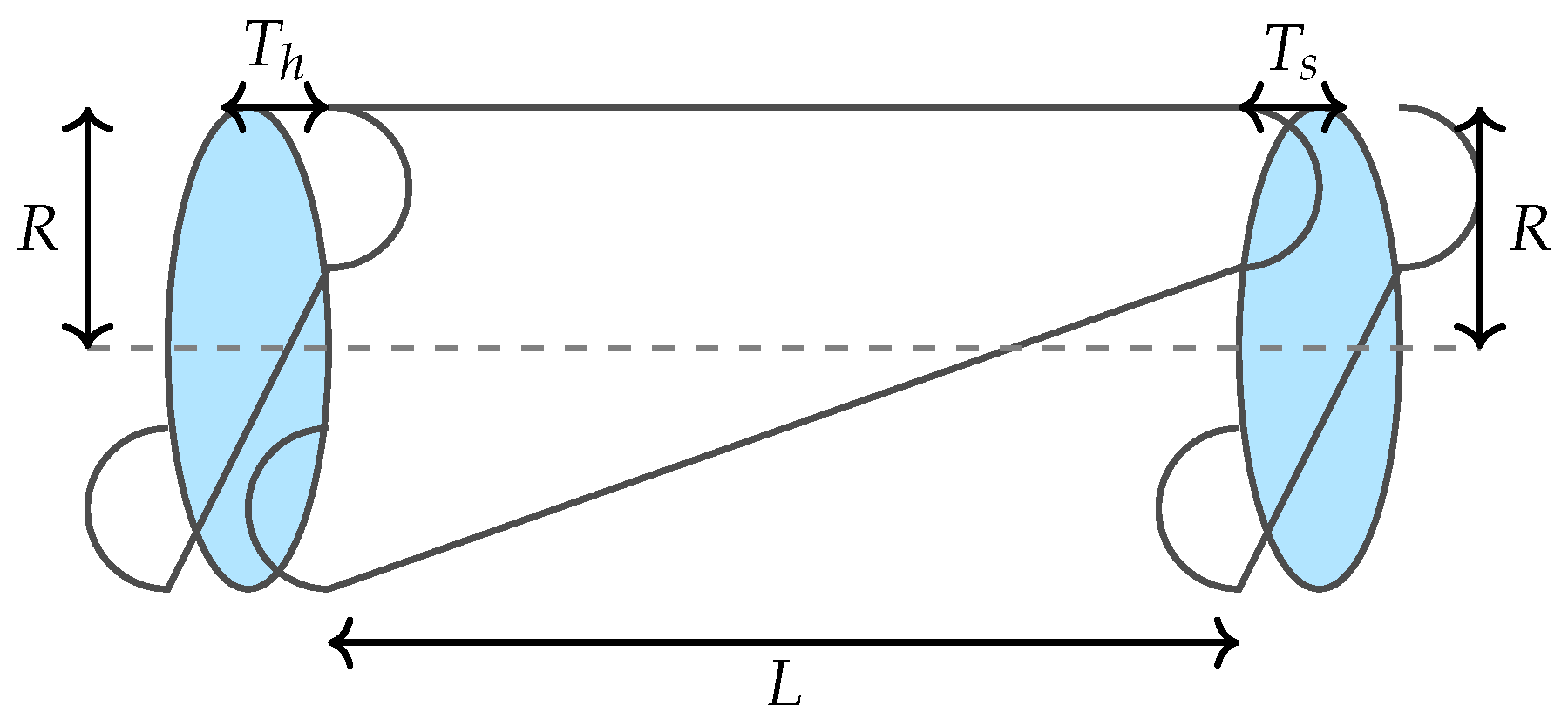
7.1. Pressure Vessel Design Problem

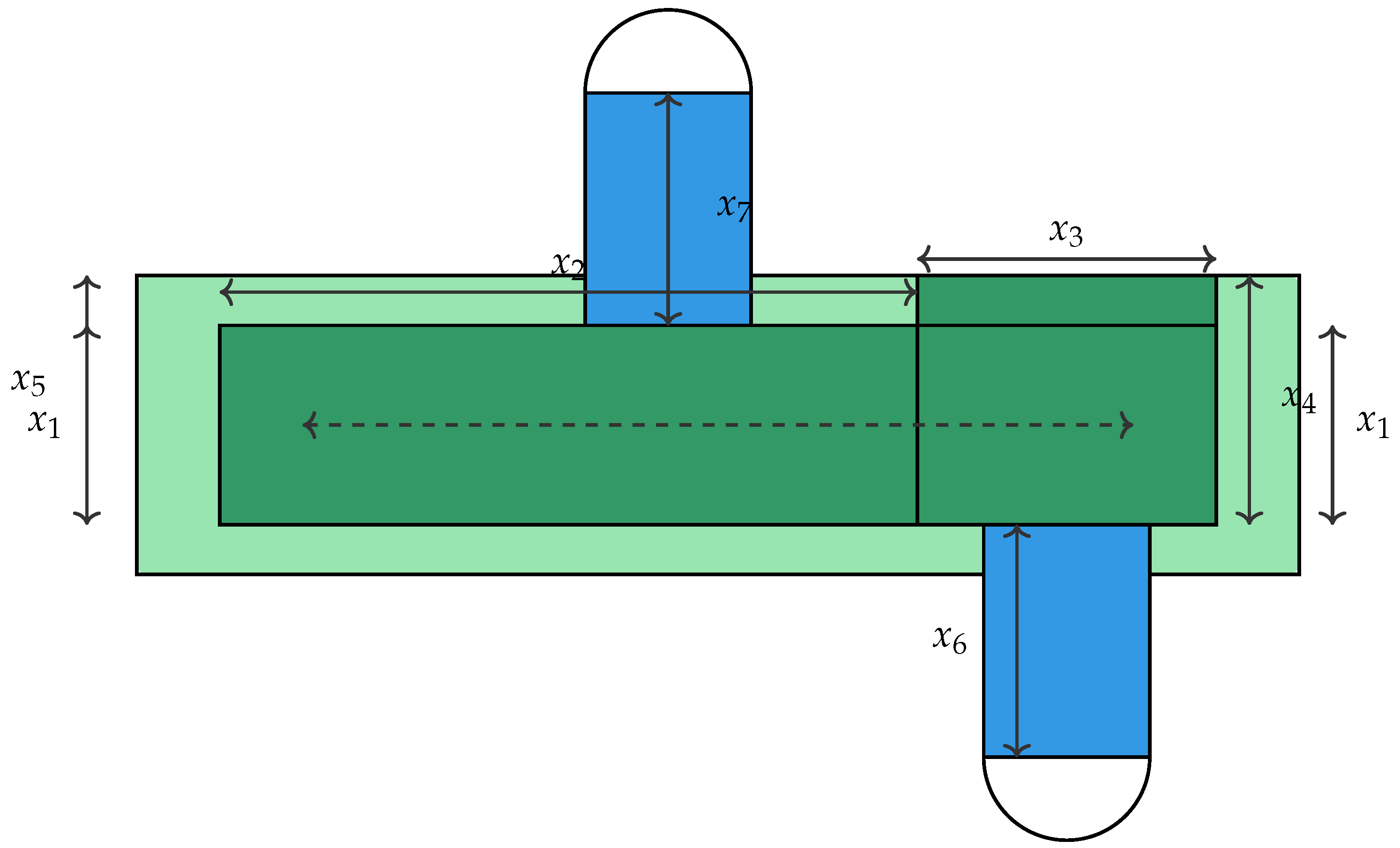
A pressure vessel is a closed container designed to hold gases or liquids at a pressure substantially above atmospheric levels, as illustrated in Figure 5. These vessels are typically cylindrical with hemispherical ends and are fundamental to numerous engineering applications. The challenge of optimising the design of pressure vessels to enhance efficiency and safety while minimising costs was first articulated by Sandgren [44] and continues to be a significant area of research. The construction of the pressure vessels adheres to the American Society of Mechanical Engineers (ASME)’s boiler and pressure vessel code, focusing on a vessel designed to operate at $3000\mathrm{psi}$ and hold a minimum of $750\mathrm{cubic} \mathrm{ft}$.

The optimisation variables include the shell thickness ($T_s$), the head thickness ($T_h$), the inner radius (R), and the cylindrical section length excluding the heads (L), with the thicknesses constrained to multiples of $0.0625\mathrm{inches}$. This optimisation problem is mathematically formulated as follows [45]:

$$\mathbf{z}=[T_s,T_h,R,L]$$

(8)

The objective function to be minimised is given by

$$f\left(\mathbf{z}\right)=0.6224T_{s}RL+1.7781T_h{R}^2+3.1661T_s^{2}L+19.84T_{h}L$$

(9)

The constraints ensuring structural integrity and compliance with ASME standards are

$$\begin{array}{cc}\hfill g_1\left(\mathbf{z}\right)& =-T_s+0.0193R\le 0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill g_2\left(\mathbf{z}\right)& =-T_h+0.00954R\le 0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill g_3\left(\mathbf{z}\right)& =-\pi R^{2}L-{\displaystyle \frac{4}{3}}\pi R^3+750\times 11728\le 0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill g_4\left(\mathbf{z}\right)& =L-240\le 0,\hfill \end{array}$$

(13)

The variable bounds are set as

$$0.0625\le T_s,T_h\le 99\times 0.0625,10\le R,L\le 200$$

(14)

AHASCA exhibits exemplary performance in optimising the Pressure Vessel Design Problem, as demonstrated by the statistical results presented in Table 5. AHASCA achieves minimum, mean, and maximum values of 5885.333, with an extraordinarily low standard deviation of $2.31\times {10}^{-5}$, indicating exceptional consistency and reliability in its optimisation capability.

This performance is significantly superior when compared with other optimisers like the Salp Swarm Algorithm (SSA) and Moth Flame Optimiser (MFO). SSA has a minimum value of 5927.544 but a mean much higher at 6087.173 and a maximum of 6252.051, coupled with a standard deviation of 136.4673, which highlights greater variability in its results. Similarly, MFO starts at the same minimum as AHASCA but diverges considerably in the mean (6449.973) and maximum (6994.548) values, with a very high standard deviation of 453.9395, suggesting less predictability and stability.

The Sine–Cosine Algorithm (SCA) and Ant Lion Optimiser (AOA) also show less favourable outcomes, with SCA recording a minimum of 6300.01, a mean of 6720.458, and a maximum of 7562.309, alongside a standard deviation of 455.0258. AOA, in particular, shows the least optimal performance with the highest minimum value of 6718.876, escalating to an alarming mean of 8684.574 and a maximum of 11,376.98, with an extremely high standard deviation of 1586.498, indicating poor performance consistency.

Among other algorithms, the Adaptive Harmony Algorithm (AHA) closely matches AHASCA in terms of minimum, mean, and maximum values, achieving similarly low variability but with a slightly higher standard deviation of 0.111128. This comparison underscores the efficiency and effectiveness of AHASCA, which not only provides optimal solutions but does so with remarkable precision and repeatability, making it a highly preferable choice for engineering applications where both accuracy and consistency are crucial.

7.2. Spring Design Optimisation Problem

The Spring Design Optimisation Problem is a well-established challenge in engineering aimed at determining the ideal dimensions of a mechanical spring to meet specific performance criteria while minimising material and production costs [46]. The critical design parameters as shown in Figure 6 include the wire diameter (d), coil diameter (D), and number of active coils (N), which significantly influence the spring’s strength, flexibility, and space occupation.

The primary goal of this optimisation is to reduce the material cost by minimising the weight or volume of the spring [47]. The design must ensure that the spring can endure operational stresses without yielding (stress failure), resist buckling under compressive loads, and function without resonating at damaging frequencies. These requirements lead to several constraints, including limitations on shear stress ($\tau$), permissible deflections (y), and adequate free length to prevent solid compression and surging.

The problem is generally formulated as a nonlinear optimisation task where the objective function and constraints are expressed in terms of the design variables d, D, and N. The choice of materials, environmental conditions, and load specifications are also crucial in defining the optimal design. Various solution methods can be applied, from analytical and numerical approaches such as finite element analysis to heuristic algorithms like Genetic Algorithms and other evolutionary strategies, each providing distinct benefits depending on the design’s complexity and specific needs.

The optimisation of the spring is characterised by the following mathematical formulation:

$$f(d,D,N)=z+{10}^5·(\mathrm{sum}\left(v\right)+\mathrm{sum}\left(g\right))$$

(15)

where $z=(N+2)·D·d^2$ is a cost function dependent on the design parameters.

The constraints are defined as

$$\begin{array}{cc}\hfill c_1& :{\displaystyle \frac{-D^3·N}{71785·d^4}}+1\le 0\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill c_2& :{\displaystyle \frac{4D^2-d·D}{12566·(D·d^3-d^4)}}+{\displaystyle \frac{1}{5108·d^2}}-1\le 0\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill c_3& :1-{\displaystyle \frac{140.45·d}{D^2·N}}\le 0\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill c_4& :{\displaystyle \frac{d+D}{1.5}}-1\le 0\hfill \end{array}$$

(19)

Penalty terms $vs.$ and g are integrated into the objective function to penalise designs that fail to satisfy the constraints, with $vs.$ indicating violations and g quantifying their severity.

In the context of the Spring Design Optimisation Problem, the AHASCA has shown notable efficacy, as detailed in the results presented in

Table 6. Best solutions of Spring Design Optimisation Problem, iterations = 200, run = 30, agents = 50.

Optimiser	Best Score	X1	X2	X3
AHASCA	0.012665	0.051693	0.356809	11.2836
SSA	0.012687	0.051	0.340147	12.34002
MFO	0.012666	0.051819	0.359845	11.10795
SCA	0.012761	0.051	0.340056	12.42766
GWO	0.012678	0.051683	0.35649	11.31422
FDA	0.012665	0.051725	0.357578	11.2387
GJO	0.01268	0.051	0.340276	12.32652
GTO	0.012667	0.051377	0.349261	11.73992
MGO	0.012674	0.051	0.340366	12.31619
HLOA	0.012674	0.051	0.340366	12.31619
MVO	0.012766	0.051	0.338843	12.48487
POA	0.012665	0.051789	0.359136	11.14861
COA	0.012731	0.05293	0.386647	9.753054
AHA	0.012665	0.051703	0.357054	11.26928
AOA	0.014104	0.051	0.318966	15

. AHASCA demonstrated superior performance with the best objective score of 0.012665, optimising design variables for wire diameter, coil diameter, and number of active coils effectively. Its results closely align with other top-performing algorithms like MFO, GWO, and FDA, indicating competitive optimisation capabilities. In contrast, algorithms such as SCA, GJO, and MGO showed less efficient solutions, especially with higher coil counts, reducing material efficiency. AOA notably underperformed, with both a higher score and suboptimal variable settings. AHASCA’s low standard deviation further highlights its robustness and reliability, making it well-suited for precise engineering applications.

In the Spring Design Optimisation Problem, the AHASCA demonstrates outstanding results, as evidenced in the data provided in

Table 7. Results of Spring Design Optimisation Problem, iterations = 200, run = 30, agents = 50.

Optimiser	Min	Mean	Max	Std
AHASCA	0.012665	0.012665	0.012665	$5.7\times {10}^{-10}$
SSA	0.012687	0.012816	0.013036	0.000125
MFO	0.012666	0.013195	0.014389	0.000816
SCA	0.012761	0.012915	0.013117	0.000139
GWO	0.012678	0.012726	0.012938	0.000104
FDA	0.012665	0.012804	0.013267	0.00024
GJO	0.01268	0.012699	0.012747	$2.44\times {10}^{-5}$
GTO	0.012667	0.012703	0.012856	$7.53\times {10}^{-5}$
MGO	0.012674	0.013179	0.014858	0.000887
HLOA	0.012674	0.014142	0.016913	0.001823
MVO	0.012766	0.016849	0.018104	0.002135
POA	0.012665	0.012668	0.012679	$5.08\times {10}^{-6}$
COA	0.012731	0.012936	0.013146	0.000154
AHA	0.012665	0.012666	0.012668	$9.75\times {10}^{-7}$
AOA	0.014104	0.014122	0.014153	$2\times {10}^{-5}$

. AHASCA achieves not only the lowest minimum value of 0.012665 but also maintains this as both the mean and maximum, indicating an exceptionally consistent performance across multiple runs with a negligible standard deviation of $5.7\times {10}^{-10}$. This precision highlights AHASCA’s ability to reliably find and replicate the optimal solution without deviation.

Compared to other optimisers, AHASCA results are superior in terms of both the achieved minimum values and the narrow spread between the minimum, mean, and maximum values. For instance, Salp Swarm Algorithm (SSA) and Moth Flame Optimiser (MFO) have similar minimal scores but higher mean and maximum values, reflecting greater variability in their results. Specifically, MFO’s mean of 0.013195 and a maximum of 0.014389 with a standard deviation of 0.000816 illustrate less stability compared to AHASCA.

Some algorithms like the Grey Wolf Optimiser (GWO) and Genetic Job Optimisation (GJO) show competitive performances with low standard deviations, but they still do not match the absolute precision of AHASCA. Meanwhile, the Hooke–Jeeves Optimisation Algorithm (HLOA) and Multi-Verse Optimiser (MVO) exhibit much larger deviations from their minimum values, as indicated by their higher standard deviations and maximum values, which suggests a significant decrease in performance consistency.

Among the competitors, the Progressive Optimisation Algorithm (POA) and Adaptive Harmony Algorithm (AHA) come closest to matching AHASCA in consistency and precision, with AHA demonstrating an almost identical performance in terms of stability and repeatability, evidenced by its minuscule standard deviation of $9.75\times {10}^{-7}$.

7.3. Speed Reducer Design Problem

The Speed Reducer Design Problem as shown in Figure 7 is a classic engineering optimisation challenge aimed at finding the optimal dimensions for a speed reducer to meet specified performance requirements while minimising material and production costs [48]. Key design variables include the face width (b), module of teeth (m), number of teeth on the pinion (p), lengths of the first ($l1$) and second ($l2$) shafts between bearings, and the diameters of these shafts ($d1$ and $d2$). Each variable critically affects the speed reducer’s performance attributes such as strength, flexibility, and space occupation [49].

The main objective of this optimisation is to minimise the total weight of the speed reducer. Additionally, the design must ensure that the speed reducer can withstand operational stresses without yielding (stress failure), prevent buckling under compressive loads, and operate without resonating at harmful frequencies [50]. These operational requirements necessitate multiple constraints in the design process, which include limits on shear stress ($\tau$), permissible deflections (y), and sufficient free length to avoid solid compression and surging.

This problem is typically modelled as a nonlinear optimisation challenge where the objective function and constraints are formulated in terms of the design variables b, m, p, $l1$, $l2$, $d1$, and $d2$. Material selection, environmental conditions, and load specifications also play a crucial role in determining the optimal design. Various computational methods, ranging from analytical approaches and numerical methods like finite element analysis to heuristic algorithms such as Genetic Algorithms and other evolutionary strategies, can be employed to solve this problem. Each method offers specific advantages depending on the complexity and requirements of the design task.

The decision variables for the Speed Reducer Design Problem are defined as

$$\begin{array}{cc}\hfill x& =\left[x_1{x}_2{x}_3{x}_4{x}_5{x}_6{x}_7\right]\hfill \\ \hfill & =\left[bmpl1l2d1d2\right],\hfill \end{array}$$

(20)

where each variable corresponds to a specific design dimension.

The objective function to be minimised is

$$\begin{array}{cc}\hfill f\left(x\right)& =0.7854x_1{x}_2^2(3.3333x_2^3+14.9334x_3-43.0934)\hfill \\ \hfill & -1.508x_1(x_6^2+x_7^2)+7.4777(x_6^3+x_7^3)\hfill \\ \hfill & +0.7854(x_4{x}_6^2+x_5{x}_7^2),\hfill \end{array}$$

(21)

The constraints are specified as follows:

$$\begin{array}{cc}\hfill g_1\left(x\right)& ={\displaystyle \frac{27}{x_1{x}_2^2{x}_3}}-1\le 0,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill g_2\left(x\right)& ={\displaystyle \frac{397.5}{x_1{x}_2^2{x}_3^2}}-1\le 0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill g_3\left(x\right)& ={\displaystyle \frac{1.93x_4^3}{x_2{x}_6^3{x}_4}}-1\le 0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill g_4\left(x\right)& ={\displaystyle \frac{1.93x_5^3}{x_2{x}_7^3{x}_5}}-1\le 0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill g_5\left(x\right)& ={\displaystyle \frac{\sqrt{{745}^2{(x_4/\left(x_2{x}_3\right))}^2+16.9\times {10}^6}}{110x_6^3}}-1\le 0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill g_6\left(x\right)& ={\displaystyle \frac{\sqrt{{745}^2{(x_5/\left(x_2{x}_3\right))}^2+157.5\times {10}^6}}{85x_7^3}}-1\le 0,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill g_7\left(x\right)& ={\displaystyle \frac{x_2{x}_3}{40}}-1\le 0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill g_8\left(x\right)& ={\displaystyle \frac{5x_2}{x_1}}-1\le 0,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill g_9\left(x\right)& ={\displaystyle \frac{x_1}{/}}12x_2-1\le 0,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill g_{10}\left(x\right)& =1.5x_6+1.9x_4-1\le 0,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill g_{11}\left(x\right)& =1.1x_7+1.9x_5-1\le 0,\hfill \end{array}$$

(32)

Variable bounds are set as follows:

$$\begin{array}{c}\hfill 2.6\le x_1\le 3.6,0.7\le x_2\le 0.8,17\le x_3\le 28,\\ \hfill 7.3\le x_4,x_5\le 8.3,2.9\le x_6\le 3.9,5.0\le x_7\le 5.5.\end{array}$$

In the Speed Reducer Design Problem, the AHASCA excels in achieving a highly consistent and optimal performance, as shown in

Table 8. Results of Speed Reducer Design Problem, iterations = 200, run = 30, agents = 50.

Optimiser	Min	Mean	Max	Std
AHASCA	2994.471	2994.471	2994.471	$6.6\times {10}^{-5}$
SSA	3012.993	3022.971	3043.245	11.4687
MFO	2994.471	3007.564	3033.749	20.28279
SCA	3056.947	3127.292	3193.204	52.77254
GWO	3002.572	3006.517	3008.345	2.057789
FDA	2994.471	2994.471	2994.471	0
GJO	3002.65	3015.525	3026.07	8.751206
GTO	2994.471	2999.757	3016.77	9.129572
MGO	2994.471	2994.471	2994.471	0
HLOA	3003.342	3039.564	3204.65	80.90014
MVO	3014.329	3035.083	3055.645	16.40223
POA	2994.763	3000.953	3008.262	5.549717
COA	2994.939	2995.167	2995.681	0.27189
AHA	2994.471	2994.471	2994.471	$1.97\times {10}^{-6}$
AOA	3109.034	3165.501	3224.778	46.56557

. AHASCA achieves a minimum, mean, and maximum value of 2994.471, with an exceptionally low standard deviation of $6.6\times {10}^{-5}$. This indicates not only AHASCA’s ability to find an optimal solution but also its consistency in replicating this result across multiple runs, which is crucial for reliability in practical engineering applications.

Comparatively, other optimisation algorithms exhibit varying levels of performance and consistency. For example, the Salp Swarm Algorithm (SSA) and Moth Flame Optimiser (MFO) also achieve competitive minimum values but have higher mean and maximum values, with standard deviations of 11.4687 and 20.28279, respectively, suggesting less consistency in their optimisation results. Specifically, MFO shows significant variability, which might affect the reliability of the solutions it provides in a real-world setting.

The Sine–Cosine Algorithm (SCA) and Ant Lion Optimiser (AOA) both perform less optimally not only in terms of achieving higher minimal values but also in exhibiting much larger standard deviations of 52.77254 and 46.56557, respectively, indicating significant variability in their results. These large deviations from the mean suggest these algorithms might struggle with stability in this particular design problem.

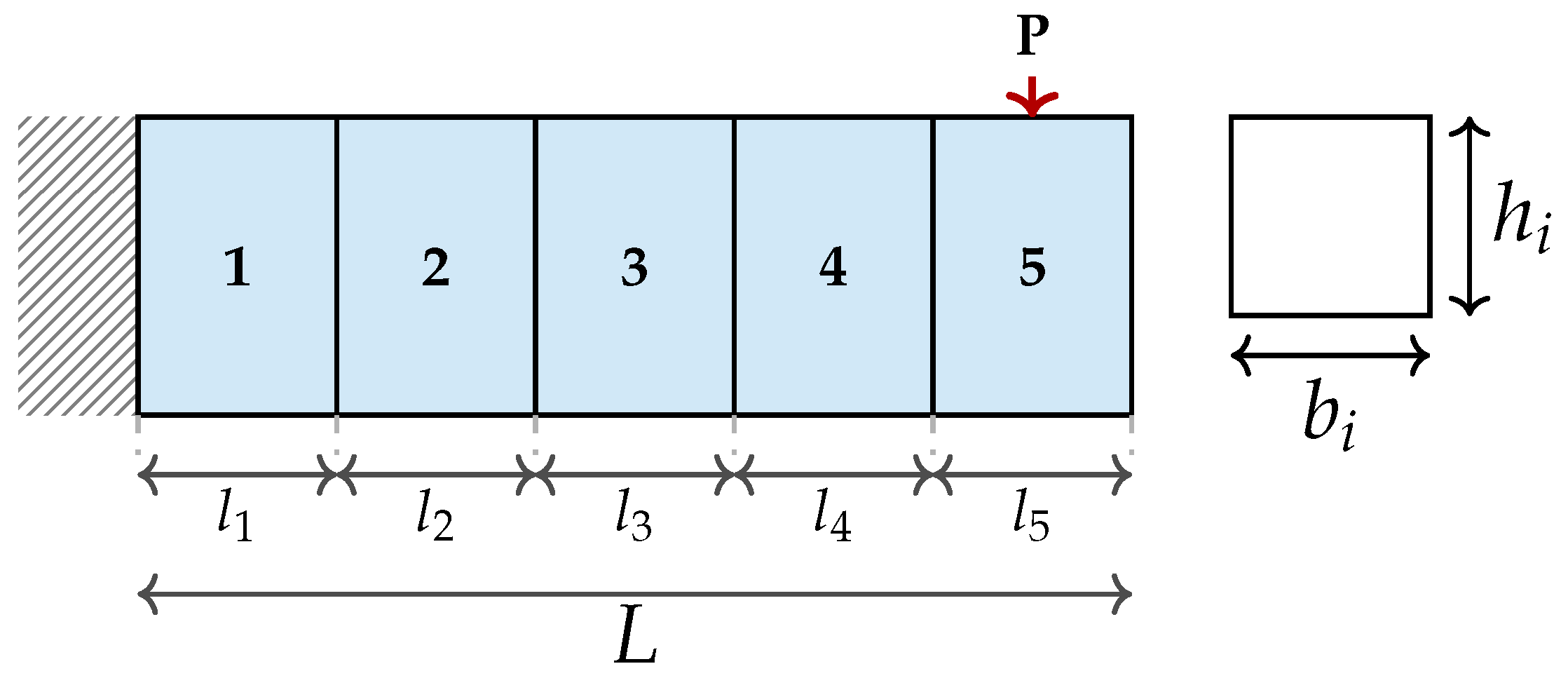
7.4. Cantilever Beam Design Optimisation Problem

The Cantilever Beam Design Optimisation Problem as shown in Figure 8 represents a significant challenge in structural engineering, focusing on determining the optimal dimensions of a cantilever beam to meet specific performance criteria while minimising material and manufacturing costs [51]. The critical design variables include the beam’s length (L), width (b), and height (h), each significantly impacting attributes like stiffness, strength, and weight.

The primary aim of this optimisation is to reduce the overall weight of the beam and lowering costs while ensuring that the beam remains sufficiently resistant to bending and deflection under load [52]. The design must also prevent material failure under maximum expected loads (stress failure) and ensure stability against lateral buckling. These operational requirements necessitate several constraints, including limits on maximum bending stress ($\sigma$), allowable deflection (y), and buckling load factors.

This optimisation challenge is typically modelled as a nonlinear task where the objective function and constraints are expressed in terms of the design variables L, b, and h. Material properties, environmental conditions, and the specifics of the applied loads are crucial in determining the optimal design. Various computational methods can be applied to solve this problem, ranging from traditional analytical approaches and simulation techniques like finite element analysis to modern heuristic methods such as Genetic Algorithms and Simulated Annealing. Each technique offers specific benefits depending on the complexity and requirements of the design task.

The mathematical description of the cantilever beam design problem is defined as follows:

The optimisation problem is formulated as

$$\begin{array}{cccc}\hfill & \underset{x}{\mathrm{Minimize}}\hfill & \hfill & f\left(x\right)=0.0624(x_1+x_2+x_3+x_4+x_5)\hfill \end{array}$$

(33)

subject to the constraint:

$$\begin{array}{cc}\hfill & g\left(x\right)={\displaystyle \frac{61}{x_1}}+{\displaystyle \frac{37}{x_2}}+{\displaystyle \frac{19}{x_3}}+{\displaystyle \frac{7}{x_4}}+{\displaystyle \frac{1}{x_5}}-1\le 0,\hfill \end{array}$$

(34)

and the variable bounds:

$$0.01\le x_i\le 100,i=1,2,\dots ,5.$$

(35)

Equations provide a complete description of the optimisation model, which aims to minimise the objective function subject to a nonlinear constraint and variable bounds.

In the Cantilever Beam Design Optimisation Problem, the AHASCA showcases exemplary precision and consistency, as highlighted by the statistical metrics presented in

Table 9. Results of Cantilever Beam Design Optimisation Problem, iterations = 200, run = 30, agents = 50.

Optimiser	Min	Mean	Max	Std
AHASCA	1.339956	1.339956	1.339956	$4.43\times {10}^{-13}$
SSA	1.339957	1.339971	1.34	$1.84\times {10}^{-5}$
MFO	1.339992	1.340546	1.341256	0.0005
SCA	1.362528	1.373674	1.392266	0.011464
GWO	1.339992	1.340041	1.340139	$5.62\times {10}^{-5}$
FDA	1.33999	1.340083	1.340207	$8.68\times {10}^{-5}$
GJO	1.340009	1.340155	1.340446	0.000156
GTO	1.339963	1.340462	1.342492	0.000999
MGO	1.340038	1.340165	1.34036	0.000124
HLOA	1.343721	1.396883	1.553992	0.080691
MVO	1.339973	1.340016	1.340102	$5.04\times {10}^{-5}$
POA	1.339958	1.339973	1.34002	$2.35\times {10}^{-5}$
COA	1.339963	1.339976	1.339985	$8.44\times {10}^{-6}$
AHA	1.339958	1.339973	1.339997	$1.64\times {10}^{-5}$
AOA	1.355392	1.370608	1.384236	0.009419

. AHASCA achieves the minimum, mean, and maximum values of 1.339956, with an incredibly low standard deviation of $4.43\times {10}^{-13}$. This near-zero variance not only indicates AHASCA’s ability to consistently find the optimal solution but also demonstrates its exceptional stability across multiple runs.

The Salp Swarm Algorithm (SSA) and Moth Flame Optimiser (MFO) also achieve competitive minimum values but with higher standard deviations of $1.84\times {10}^{-5}$ and 0.0005, respectively. These higher deviations suggest less consistency compared to AHASCA. MFO, in particular, shows a relatively wider range in its results, indicating a potential for greater variability in achieving optimal results.

Other algorithms like the Sine–Cosine Algorithm (SCA) and Ant Lion Optimiser (AOA) exhibit not only higher minimum values but also significantly larger standard deviations of 0.011464 and 0.009419, respectively. These values highlight the challenges these algorithms face in achieving and maintaining an optimal solution within this design problem, suggesting a potential lack of robustness or adaptability to the specific constraints and requirements of the Cantilever Beam Design.

8. Conclusions

This paper introduced AHA–SCA, a hybrid optimiser that interleaves the Sine–Cosine Algorithm’s oscillatory search with the Artificial Hummingbird Algorithm’s guided and territorial foraging. The design is intentionally minimal: even iterations apply SCA with a linearly decaying amplitude to promote broad, controllable exploration; odd iterations apply AHA, using axial/diagonal/omnidirectional flight patterns and a visit table to intensify search around promising regions. The result is a clear exploration–exploitation schedule with $O(Nn+N{c}_f)$ time per iteration and modest implementation overhead.

Comprehensive experiments on CEC2014, CEC2017, and CEC2022 demonstrate that AHA–SCA is a strong general purpose optimiser. Relative to stand-alone AHA and SCA and to several recent baselines, the hybrid achieves the following: (i) it converges faster in early and mid phases, (ii) it achieves lower mean/median errors with noticeably smaller standard deviations on many functions, and (iii) it shows improved robustness against premature convergence on rugged, composite landscapes. In constrained engineering studies (e.g., welded beam and pressure vessel), the method attains best or near-best feasible designs while respecting all constraints, underscoring its practical utility.

Future directions include the following: (i) self-adaptive or reward-driven switching between SCA and AHA phases, (ii) parameter control for SCA amplitude and AHA noise, (iii) more sophisticated constraint handling (e.g., feasibility rules and adaptive penalties), (iv) multi-objective and large-scale extensions, (v) parallel/distributed implementations, and (vi) formal convergence analysis.