Perceptual Image Hashing Fusing Zernike Moments and Saliency-Based Local Binary Patterns

Abstract

This paper proposes a novel perceptual image hashing scheme that robustly combines global structural features with local texture information for image authentication. The method starts with image normalization and Gaussian filtering to ensure scale invariance and suppress noise. A saliency map is then generated from a color vector angle matrix using a frequency-tuned model to identify perceptually significant regions. Local Binary Pattern (LBP) features are extracted from this map to represent fine-grained textures, while rotation-invariant Zernike moments are computed to capture global geometric structures. These local and global features are quantized and concatenated into a compact binary hash. Extensive experiments on standard databases show that the proposed method outperforms state-of-the-art algorithms in both robustness against content-preserving manipulations and discriminability across different images. Quantitative evaluations based on ROC curves and AUC values confirm its superior robustness–uniqueness trade-off, demonstrating the effectiveness of the saliency-guided fusion of Zernike moments and LBP for reliable image hashing.

1. Introduction

In the digital era, the proliferation of image-based communication has introduced critical challenges in preserving content authenticity and intellectual property rights. Widespread operations such as resizing, filtering, cropping, and compression, alter low-level visual features while maintaining semantic content. These content-preserving modifications complicate the reliable verification of image origin and integrity, necessitating advanced techniques for tamper detection, source identification, and copyright enforcement. Perceptual image hashing has consequently emerged as a key technological solution, providing a foundation for trustworthy multimedia authentication in environments characterized by large-scale data dissemination [1,2].

Perceptual image hashing generates compact, content-based digital signatures to facilitate efficient similarity comparisons between images. The design of these algorithms must balance two competing requirements: robustness to perceptually irrelevant distortions, and uniqueness to distinguish semantically distinct content [3,4]. Robustness necessitates that hashes remain consistent across content-preserving manipulations, such as brightness adjustment, contrast enhancement, or JPEG compression, while uniqueness requires significant divergence between hashes of visually different images. This inherent trade-off constitutes a fundamental challenge in hashing research, as improvements in one aspect often come at the expense of the other [5]. In response, this paper proposes a novel framework that integrates global and local features using Zernike moments and saliency-aware LBP to simultaneously enhance both robustness and discriminability.

The remainder of this paper is organized as follows. Section 2 surveys classical and recent approaches in perceptual image hashing. Section 3 details the architecture and components of the proposed method. Section 4 offers in-depth analyses of experimental outcomes, focusing on assessing the balance between robustness and discriminative capability. Finally, Section 5 concludes the paper and suggests promising directions for future research.

2. Related Work

Image hashing, as a critical technology for content authentication, similarity retrieval, and copyright protection, has evolved through decades of research. This section reviews key advancements in the field, organizing existing methods into three major categories that reflect both foundational approaches and cutting-edge developments. The field of perceptual image hashing has evolved through various paradigms, each addressing robustness and discriminability from different perspectives. While classical methods provide foundational techniques, they often exhibit specific limitations that motivate the development of more sophisticated fusion approaches. This review critically examines these methods not only to catalog them but to identify the persistent gaps that our proposed method aims to bridge.

2.1. Image Hashing Based on Frequency Domain Transform

Frequency domain transform techniques, including Discrete Wavelet Transform (DWT), Discrete Fourier Transform (DFT), and Discrete Cosine Transform (DCT), have long been at the forefront of image hashing research. These methods leverage the frequency characteristics of images to construct hash sequences, offering distinct advantages in capturing stable visual features.

DWT’s strength in capturing multi-scale frequency features has made it a cornerstone of image hashing. Early work by Venkatesan et al. [6] demonstrated wavelet coefficient statistics for hash construction, though with limited tampering resilience; Mihcak and Venkatesan [7] proved robustness by focusing on low-frequency components but remained vulnerable to contrast adjustments. Monga et al. [5] advanced the field via end-to-end wavelet strategies for salient feature extraction, enhancing discriminability. Recent innovations focus on hybrid frameworks: Tang et al. [8] combined random Gabor filtering with DWT for rotation-resilient compact hashes, Hu et al. [9] introduced dual DWT schemes that enhance perceptual uniformity and localize tampered regions for scalable authentication.

DFT’s powerful frequency-domain feature extraction has driven its wide adoption. Swaminathan et al. [3] laid groundwork using polar-coordinate DFT magnitude spectra, achieving robustness against compression and filtering. Wu et al. [10] combined DWT and DFT on Radon-transformed images to improve print-scan attack resistance. Recent optimizations include: Lei et al. [11] who used Radon-moment invariants to absorb geometric distortions before extracting DFT magnitude features, yielding 128-bit hashes with state-of-the-art robustness and fast retrieval; Qin et al. [12], who applied non-uniform sampling of mid-frequency bands to suppress redundancy and enhance collision resistance; Ouyang et al. [13] who fused quaternion DFT with log-polar mapping for rotation- and JPEG-resistant 256-bit codes, capturing color correlations while equalizing scaling effects.

DCT’s energy concentration in low frequencies enables robust yet discriminative hashing across applications. Tang et al. [14] extracted key coefficients from block rows/columns with column distance quantization, while Tang et al. [15] enhanced this via LLE dimensionality reduction and color vector angle quantization. Tang et al. [16] fused DCT features with NMF decomposition for ordered, discriminative features, and Yu et al. [17] used stable coefficient signs to resist minor transformations (with potential for magnitude feature fusion). In copy detection, Liang et al. [18] captured invariants for duplicate identification, while Shen et al. [19] fused local textures with global DCT features to boost accuracy, Karsh [20] integrated wavelet and DCT features with geometric correction to pinpoint altered regions.

2.2. Image Hashing Based on Dimensionality Reduction Techniques

Multi-view and structural feature integration has emerged as a key direction for improving hash performance. Du et al. [21] leverage multi-view feature fusion combined with dimensionality reduction to capture diverse image characteristics, balancing robustness against transformations and discriminability. Yuan et al. [22] focus on three-dimensional global structural information and energy distribution, strengthening perceptual consistency under content-preserving modifications. Liu et al. [23] integrate texture, shape, and spatial structure to distinguish images with similar global but distinct local details. Zhao et al. [24] fuse color features and intensity gradients, improving resilience to color variations and texture distortions. Strategies to boost efficiency and scalability include: Cao et al. [25] dimension analysis-driven quantizer, optimizing hash codes for large-scale retrieval accuracy. Kozat et al. [26] leverage matrix invariants for features resistant to geometric and intensity changes while preserving perceptual relevance. Liang et al. [27] adopt 2D-2D PCA for compact feature extraction, enabling efficient copy detection via key discriminative information retention. Hashing techniques are increasingly tailored to specific domains and challenges. Zhang et al. [28] develop histopathological image hashing for efficient medical dataset retrieval. Khelaifi et al. [29] use fractal features and ring partitioning to capture stable coding structures, enhancing robustness against scaling and rotation.

2.3. Image Hashing Based on Moment Invariants

Moments, such as Zernike moments, invariant moments, and Hu moments, are extensively employed in image hashing to capture global shape and geometric features. Their inherent invariance to rotation, scaling, and translation makes them ideal for robustness-oriented applications. Current research is evolving from their basic use toward advanced strategies involving feature fusion and integration with deep learning.

Moment-based image hashing leverages the geometric invariance of moments to balance robustness and discrimination, with research evolving from basic moment utilization to advanced feature fusion. First, foundational studies focus on applying invariant moments to core image types. Tang et al. [30] extract invariant moments from normalized color spaces to capture color and shape invariants, outperforming single-domain methods in resisting lighting and compression. Meanwhile, Hosny [31] enhances grayscale image feature accuracy via precise Gaussian–Hermite moment calculations, with encrypted hashes boosting security.

Specialized moments are tailored to specific needs: Zhao et al. [32] use Zernike moments (known for fine-grained shape capture) to localize tampered regions by tracking rotation-invariant in moment characteristics. Ouyang et al. [33] extend this with quaternion Zernike moments, holistically modeling color images to preserve geometric invariance across RGB channels and improve color content authentication. To address single-moment feature sparsity, Li et al. [34] merge diverse orthogonal moments via canonical correlation analysis, reducing redundancy for compact hashes with superior robustness and discrimination.

A key trend is integrating moments with complementary features. Tang et al. [35] combine visual attention mechanisms (e.g., saliency models) with invariant moments, prioritizing perceptually critical regions to balance robustness and discrimination. Ouyang et al. [36] fuse SIFT’s local key points with quaternion Zernike moments’ global invariants, bridging local details and global consistency for comprehensive authentication. Deep learning integration has further advanced performance: Yu et al. [37] pair deep semantic features with moment-based low-level invariants, leveraging deep models’ semantic understanding and moments’ transformation stability to boost accuracy. Yu et al. [38] combine Meixner moments’ shape invariance with deep features’ discriminative power, enhancing copy detection by capturing global structure and local semantics. Practical utility is refined via application-focused designs. Liu et al. [39] use geometric invariant vector distances (rooted in moment properties) to resist rotation, scaling, and translation, enabling efficient copy detection by prioritizing transformation-invariant feature relationships. These advances reflect the field’s progression from fundamental moment utilization to multi-modal fusion, solidifying moment-based hashing as a versatile tool in multimedia security.

2.4. Research Gaps and Motivation

As evidenced in the literature and summarized in Table 1, a recurring challenge is the inherent trade-off between capturing global invariant structures and fine-grained local details. Frequency-domain methods (e.g., DWT, DFT, DCT) offer robustness to common signal processing attacks but are often less effective under significant geometric distortions or in capturing semantically salient local textures [3,8,14]. Dimensionality reduction techniques prioritize compactness but may discard perceptually significant features [21,25]. While moment-based methods excel in geometric invariance, they can be insufficient for distinguishing images with similar global structures but different local content [32,34].

Beyond these hand-crafted feature methods, deep learning has emerged as a powerful alternative for perceptual image hashing [40,41,42]. Deep convolutional networks and transformers can learn highly robust feature representations directly from data, often achieving state-of-the-art performance [41,42]. Some recent work has further explored combining deep features with traditional features to leverage the benefits of both approaches [40]. However, these data-driven methods typically require large-scale training datasets and substantial computational resources, while also suffering from limited interpretability [41,43]. These limitations restrict their practical deployment in resource-constrained or explanation-critical scenarios.

This work does not seek to directly compete with these deep learning benchmarks but rather to explore a potent and explainable fusion strategy within the hand-crafted feature paradigm. The proposed method is motivated by the observation that no single feature family is sufficient. We posit that a judicious fusion of the geometric invariance of Zernike Moments and the texture detail capture of LBP, guided by a perceptually aware saliency map, can achieve a superior balance. Specifically, our approach advances existing Zernike Moments or LBP-based works by: (1) employing a color vector angle-based saliency model to focus feature extraction on perceptually critical regions, thereby enhancing discriminability without sacrificing robustness; (2) integrating global Zernike Moments features and saliency-guided LBP features in a more complementary manner than simple early or late fusion strategies found in prior works like [35,36].

Table 1. Summary of image hashing methods and their characteristics.

Category	Representative Methods	Feature Type	Key Contributions	Limitations
Frequency Domain	DWT [6,7,8,9], DFT [3,10,11,12,13], DCT [14,16,17,18,19,20]	Global spectral features	Multi-scale analysis, compression robustness	Sensitive to geometric distortions; weak local detail capture
Dimensionality Reduction	PCA [27], LLE [15], NMF [16]	Compact global features	Efficient retrieval, reduced redundancy	May lose perceptual saliency and texture information
Moment-Based	Zernike [32,33,34], Hu [30], Quaternion [33]	Global geometric features	Rotation/scale invariance; robust shape representation	Limited local texture description; color handling often weak
Hybrid/Fusion	SIFT + Zernike [36], SVD-CSLBP [19], GF-LVQ [44],	Global + local features	Improved robustness and discrimination	Computational cost; fusion strategy may be suboptimal
Deep Learning	Deep + Texture [40], CNN Constraints [41], Transformer [42], Contrastive SSL [43]	Data-driven deep features	State-of-the-art performance; powerful automatic feature learning; strong generalization	High computational cost; reliance on large-scale training data; lack of model interpretability (black-box nature)
Proposed Method	Zernike + Saliency LBP	Global + local saliency-aware	Color vector angle; saliency-guided LBP; fusion of structure and texture	Slightly higher computation; rotation robustness limited

Table 1. Summary of image hashing methods and their characteristics.

Category	Representative Methods	Feature Type	Key Contributions	Limitations
Frequency Domain	DWT [6,7,8,9], DFT [3,10,11,12,13], DCT [14,16,17,18,19,20]	Global spectral features	Multi-scale analysis, compression robustness	Sensitive to geometric distortions; weak local detail capture
Dimensionality Reduction	PCA [27], LLE [15], NMF [16]	Compact global features	Efficient retrieval, reduced redundancy	May lose perceptual saliency and texture information
Moment-Based	Zernike [32,33,34], Hu [30], Quaternion [33]	Global geometric features	Rotation/scale invariance; robust shape representation	Limited local texture description; color handling often weak
Hybrid/Fusion	SIFT + Zernike [36], SVD-CSLBP [19], GF-LVQ [44],	Global + local features	Improved robustness and discrimination	Computational cost; fusion strategy may be suboptimal
Deep Learning	Deep + Texture [40], CNN Constraints [41], Transformer [42], Contrastive SSL [43]	Data-driven deep features	State-of-the-art performance; powerful automatic feature learning; strong generalization	High computational cost; reliance on large-scale training data; lack of model interpretability (black-box nature)
Proposed Method	Zernike + Saliency LBP	Global + local saliency-aware	Color vector angle; saliency-guided LBP; fusion of structure and texture	Slightly higher computation; rotation robustness limited

3. Proposed Image Hashing

The proposed image hashing framework, illustrated in Figure 1, integrates global structural features and local texture information through a four-stage process: preprocessing, saliency extraction, feature extraction, and hash generation. The selection of Zernike moments is motivated by their well-established rotation invariance and ability to capture global geometric structures [45,46,47], which are crucial for resisting rotational attacks and representing image-wide patterns. Meanwhile, Local Binary Patterns (LBP) are chosen for their effectiveness in encoding fine-grained texture details and computational efficiency [19]. By deriving LBP features from saliency maps, we ensure that local features are extracted from perceptually significant regions, enhancing the hash’s discriminative power without compromising robustness.

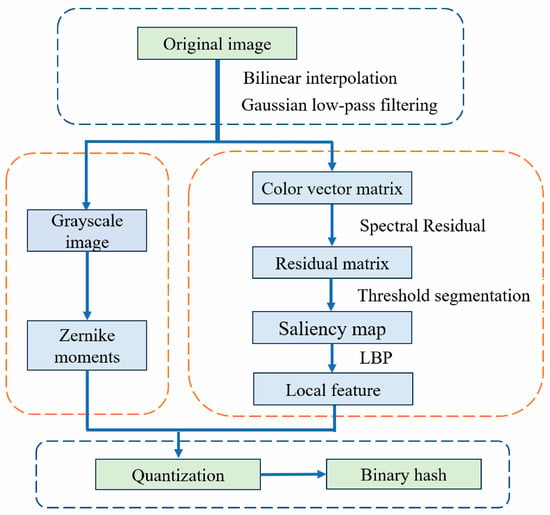
Figure 1. The architecture of the proposed image hashing scheme, which consists of four main stages: (1) Preprocessing for scale normalization and noise reduction; (2) Saliency-based local feature extraction via color vector angle and LBP; (3) Global feature extraction using rotation-invariant Zernike moments; (4) Feature quantization and fusion to generate the final binary hash. This pipeline is designed to integrate complementary global and local features in a perceptually aware manner.

Figure 1 illustrates the overall architecture, which consists of the following main steps:

• Preprocessing: Image normalization and noise reduction.
• Saliency Detection: Using color vector angles to highlight perceptually important regions.
• Feature Extraction: Zernike moments for global structure and LBP for local texture.
• Hash Generation: Feature quantization and concatenation into a binary sequence. The four steps are explained in Section 3.1, Section 3.2, Section 3.3 and Section 3.4, respectively. The parameter selection rationale is discussed in Section 3.5. Subsequently, Section 3.6 illustrates the pseudo-code of the proposed hashing algorithm, and Section 3.7 introduces the similarity evaluation metric.

To establish a consistent basis for comparison, each input image is resized to an $M\times M$ resolution through bilinear interpolation. This geometric normalization guarantees scale invariance and produces a fixed-length descriptor. Subsequently, a Gaussian kernel is convolved with the image to attenuate high-frequency components that predominantly correspond to noise and JPEG compression distortions. This pre-processing step results in a refined secondary image that is more robust to minor input variations.

3.1. Zernike Moments

To represent the global geometric structure of the preprocessed image, we employ Zernike moments as the feature descriptor, leveraging their well-known properties of orthogonality and rotation invariance [45]. The complex Zernike moments of order n with repetition m for a digital image are computed as a discrete summation over the unit disk:

$$Z_{nm}={\displaystyle \frac{n+1}{{\lambda }_N}}{\displaystyle \sum _{(x,y)\in unitdisk}f(x,y)R_{nm}(r_{xy})}\exp (-jm{\theta }_{xy})$$

(1)

where $f(x,y)$ is the grayscale intensity of the preprocessed image at pixel coordinates $(x,y)$, after mapping the image to the unit disk $(x^2+y^2\le 1)$. $r_{xy}=\sqrt{x^2+y^2}$ and ${\theta }_{xy}=\arctan (y/x)$ are the corresponding polar coordinates. $R_{nm}(r)$ is the Zernike radial polynomial (see Equation (2) in [45] for its definitive form). ${\lambda }_N$ is a normalization constant, typically related to the number of pixels inside the unit disk. The constraints $n\ge 0$, $\left|m\right|\le n$, and $n-\left|m\right|$ is even, hold.

In our framework, we employ the magnitude of these moments, $\left|Z_{nm}\right|$, which provides inherent rotation invariance. The radial polynomials $R_{nm}(r)$ are efficiently calculated via stable recurrence relations to avoid computational complexities [45]. Zernike moments from order zero to eight are listed in Table 2. The “Cumulative number” in Table 1 represents the total number of Zernike moments available up to and including the current order n. For example, calculating moments from order n = 0 to n = 8 yields a feature vector of 25 elements. This low-to-medium order range effectively captures the dominant shape and structural information of the image while demonstrating robustness to high-frequency noise [46,47]. Therefore, we computed moments up to a maximum order of eight ($\mathrm{n}=8$) from the luminance channel. The resulting set of magnitude coefficients forms a robust global feature vector, which is subsequently quantized and incorporated into the final hash sequence.

Table 2. List of Zernike moments from order zero to eight.

Order n	Zernike Moments	Number of the Moments	Cumulative Number
0	$Z_{0,0}$	1	1
1	$Z_{1,1}$	1	2
2	$Z_{2,0}$  $Z_{2,2}$	2	4
3	$Z_{3,1}$  $Z_{3,3}$	2	6
4	$Z_{4,0}$  $Z_{4,2}$  $Z_{4,4}$	3	9
5	$Z_{5,1}$  $Z_{5,3}$  $Z_{5,5}$	3	12
6	$Z_{6,0}$  $Z_{6,2}$  $Z_{6,4}$  $Z_{6,6}$	4	16
7	$Z_{7,1}$  $Z_{7,3}$  $Z_{7,5}$  $Z_{7,7}$	4	20
8	$Z_{8,0}$  $Z_{8,2}$  $Z_{8,4}$  $Z_{8,6}$  $Z_{8,8}$	5	25

3.2. Color Vector Angle

For color images, relying solely on the intensity component for hash extraction limits the method’s uniqueness, as it is insensitive to chromatic changes. Consequently, it is essential to select a component that exhibits low sensitivity to intensity variations but high sensitivity to changes in hue and saturation. To this end, we adopt the color vector angle [30,48], a proven metric that possesses these attributes and effectively addresses this limitation.

The color vector angle is particularly well-suited for saliency detection, which is a key step in our framework. Its principal advantage over intensity-based measures is its inherent invariance to changes in illumination intensity and shadows, as it depends on the chromaticity direction in RGB space rather than its magnitude [48]. This property makes it highly sensitive to genuine changes in color content (e.g., hue and saturation), which are strong cues for visual attention, while being robust to common photometric distortions. This makes it an ideal basis for generating a stable saliency map under content-preserving manipulations. Consider two pixels represented by their RGB vectors $P_1={[R_1,G_1,B_1]}^T$ and $P_2={[R_2,G_2,B_2]}^T$, where $R_1$, $R_2$; $G_1$, $G_2$; and $B_1$, $B_2$ denote their respective red, green, and blue components. The color vector angle is defined as the angle $\theta$ between vectors $P_1$ and $P_2$. To reduce computational complexity, the sine of the angle $\theta$ is used in place of the angle value itself [43], as calculated in Equation (2):

$$sin\theta ={\displaystyle \frac{‖P_1\times P_2‖}{‖P_1‖\cdot ‖P_2‖}}$$

(2)

To apply this concept across the entire image, a reference color vector m is first computed, where $P_{ref}={[R_{ref},G_{ref},B_{ref}]}^T$ represents the mean values of the red, green, and blue components over all pixels in the normalized image. Subsequently, by calculating the $sin{\theta }_{i,j}$ values between $P_{ref}$ and $P_{i,j}$ (the color vector at the $i$-th row and $j$-th column, with $1\le i,j\le L$), the color direction angle matrix can be obtained as follows:

$$A=\left[\begin{array}{ccc}\sin {\theta }_{1,1}& \dots & \sin {\theta }_{1,N}\\ ⋮& \ddots & ⋮\\ \sin {\theta }_{N,1}& \dots & \sin {\theta }_{N,N}\end{array}\right]$$

(3)

This matrix $A$ serves as the input for the subsequent saliency detection stage.

3.3. Saliency Map Extraction

Among various saliency detection models, the Frequency-Tuned (FT) method [49] is chosen for its computational efficiency and effectiveness in highlighting entire salient objects with well-defined boundaries. Compared to more complex deep learning-based saliency models, the FT method is lightweight and does not require training, making it well-suited for integration into an efficient hashing pipeline. It operates on the principle that salient regions lie in the residual spectral domain after suppressing the average global spectrum, effectively capturing the “unusual” parts of an image that attract human attention. The process begins by computing the 2D Fourier transform of the color vector angle matrix A:

$$\mathcal{F}\left(u,v\right)={\displaystyle \sum _{x=0}^{M-1}{\displaystyle \sum _{y=0}^{M-1}A(x,y)}}\cdot \exp \left[-j2\pi ({\displaystyle \frac{ux}{M}}+{\displaystyle \frac{vy}{M}})\right]$$

(4)

The log amplitude spectrum $L(u,v)$ is then derived from the magnitude spectrum $\left|\mathcal{F}(u,v)\right|$:

$$L(u,v)=\log (\left|\mathcal{F}(u,v)\right|+1)$$

(5)

The spectral residual $R(u,v)$, which captures the novel and salient information, is obtained by subtracting the averaged log spectrum $\overline{L}$ (computed by applying a local averaging filter to $L(u,v)$):

$$R(u,v)=L(u,v)-\overline{L}(u,v)$$

(6)

The saliency map $S$ is subsequently reconstructed via the inverse Fourier transform, combining the spectral residual $R(u,v)$ with the original phase spectrum:

$$S={\left|{\mathcal{F}}^{-1}[\exp (R(u,v)+j\cdot \varphi (u,v))]\right|}^2$$

(7)

where $\varphi (u,v)$ is the phase component of $\mathcal{F}\left(u,v\right)$.

To binarize the saliency map and identify the most salient regions, a threshold $T_{opt}$ is automatically calculated using Otsu’s method [50]. The binary salient region matrix $B$ is then defined as:

$$B(x,y)=\left\{\begin{array}{cc}1& ifS(x,y)\ge T_{opt}\\ 0& otherwise\end{array}\right.$$

(8)

Finally, to extract robust local texture features, the binary salient region matrix $B$ is divided into non-overlapping blocks of size $r\times r$. The LBP operator is applied to each block, generating a local feature matrix that encodes the texture patterns within the salient regions. The LBP operator is a powerful texture descriptor. For a given center pixel within a block of B, the LBP operator thresholds its P neighboring pixels (evenly spaced on a circle of radius R) with the center pixel’s value and converts the resulting sequence into an LBP code. The mathematical formulation for the basic LBP operator at a pixel location $(x_c,y_c)$ is given by:

$$L_{P,R}(x_c,y_c)={\displaystyle \sum _{p=0}^{P-1}s(g_p-g_c)}\cdot 2^p$$

(9)

where $g_c$ is the intensity value of the center pixel in the block of the binary matrix B, $g_p$ is the intensity of the p-th neighboring pixel, and the function $s(x)$ is defined as $s(x)=1$ if $x\ge 0$, and $s(x)=0$ otherwise. This process is repeated for all pixels in each block of B to form the comprehensive local texture feature matrix L.

3.4. Hash Generation

The final hash sequence is generated by quantizing the extracted local and global features into a compact binary representation. This process involves two independent binarization steps followed by concatenation. The fusion strategy employs mean-based binarization and concatenation for its simplicity and effectiveness, as demonstrated by the results. While more complex fusion strategies, such as feature weighting or learning-based fusion [37], could be explored, they would increase computational complexity. The chosen approach provides a strong baseline that effectively combines the complementary strengths of the global and local features, as evidenced by the high AUC achieved.

The local texture features, encoded in the matrix $L$ derived from the LBP operation on the saliency map (Section 3.3), are converted into a binary sequence. Each element in $L$ is compared to the mean value of the entire matrix:

$$H_{local}(i)=\left\{\begin{array}{cc}1& ifL(i)>mean(L)\\ 0& otherwise\end{array}\right.$$

(10)

where $L(i)$ and $H_{local}(i)$ denote the $i$-th elements of $L$ and $H_{local}$, respectively, and “$mean(L)$” is the average value of all elements in $L$.

Similarly, the global structural features, represented by the magnitude vector $\left|Z\right|$ of the Zernike moments (Section 3.1), are binarized by comparing each moment value to the mean of the vector:

$$H_{global}(j)=\left\{\begin{array}{cc}1& if\left|Z\right|\left(j)>\mathrm{mean}(\left|Z\right|\right)\\ 0& otherwise\end{array}\right.$$

(11)

where $H_{global}(j)$ and $\left|Z\right|(j)$ represent the $j$-th elements of the binary global hash sequence and the Zernike moments magnitude vector, respectively.

The final, compact image hash $H$ is produced by concatenating the local and global binary sequences:

$$H=\left[H_{local}\parallel H_{global}\right]$$

(12)

This unified representation integrates both texture details from salient regions and global geometric invariants, achieving a balanced trade-off between robustness and discriminability.

3.5. Parameter Selection Rationale

The selection of key parameters in the proposed framework is based on established practices in the literature, computational constraints, and empirical observations from prior work, ensuring a balance between feature discriminability, robustness, and algorithmic efficiency.

Zernike Moment Order (n = 8): The maximum order of Zernike moments was set to 8. Lower-order moments (n < 5) primarily capture gross image shape but lack sufficient discriminative detail, while higher-order moments (n > 10) are increasingly sensitive to high-frequency noise and fine details that are unstable under common image manipulations [45,47]. Orders in the range of 6–10 have been widely demonstrated to offer an optimal trade-off for image representation tasks, effectively capturing the dominant global structure without introducing excessive fragility [32,34]. Thus, an order of 8 was chosen to align with this common practice.

LBP Parameters (P = 8, R = 1): The LBP operator was configured with 8 sampling points (P = 8) and a radius of 1 (R = 1). This is the fundamental and most common LBP configuration, proven effective for capturing micro-texture patterns [19,51]. A larger radius would capture more macro-texture information but would also increase sensitivity to deformations and noise. The choice of (8, 1) prioritizes stability and computational simplicity.

Saliency Block Size (64 × 64 pixels): The non-overlapping block size for partitioning the saliency map was set to 64 × 64 pixels. This choice is a deliberate trade-off between texture granularity and feature stability, guided by established practices in image processing [19,30]. Smaller blocks (e.g., 16 × 16) capture finer local details but produce longer hashes that are more susceptible to noise and misalignment. Larger blocks (e.g., 256 × 256) yield more stable but coarser features, potentially losing discriminative power. An intermediate size of 64 × 64 was therefore selected to balance these competing demands, hypothesizing that it would provide an optimal compromise for generating a discriminative yet robust hash.

Final Hash Length (89 bits): The final hash length is a direct consequence of the chosen feature dimensions: 25 coefficients from Zernike moments and 64 features from the LBP extraction over an 8 × 8 grid of saliency blocks. This design yields a compact 89-bit hash, which is intentionally concise to ensure efficiency in storage and comparison, making it suitable for large-scale image retrieval and authentication applications.

3.6. Pseudo-Code Description

The proposed image-hashing framework integrates three core procedures: (i) saliency-guided texture encoding via LBP, (ii) global structure modeling with rotation-invariant Zernike moments, and (iii) joint feature quantization to yield a compact binary hash. For clarity, the complete algorithmic flow is summarized in Algorithm 1.

3.7. Similarity Analysis

Since the proposed scheme generates binary hashes, the Hamming distance is naturally adopted as the similarity metric between two hash vectors. Given two image hashes $H_1=[h_1(1),h_1(2),\cdots ,h_1(N)]$ and $H_2=[h_2(1),h_2(2),\cdots ,h_2(N)]$, the distance is defined as

$$D_H(H_1,H_2)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=0}^N\left|h_1(i)-h_2(i)\right|}$$

(13)

where $h_1(i)$ and $h_2(i)$ denote the $i$-th bits of the two hashes. A smaller $D_H$ indicates stronger visual correspondence. With a pre-defined threshold T, two images are declared perceptually identical when $D_H\le T$ and distinct otherwise.

Algorithm 1: Proposed Image Hashing

Input: An input image $I$, parameters: image size $M\times M$, block size for saliency map segmentation $r\times r$, Zernike moments order $n$.

Output: A hash $H$.

1: Resize the input image I to $M\times M$ dimensions using bilinear interpolation, apply Gaussian low-pass filtering to suppress high-frequency noise.

2: Compute the mean RGB vector of the filtered image, then calculate the color vector angle matrix $A$ using Equation (3).

3: Generate the saliency map $S$ from $A$ via frequency-tuned method (Equations (4)–(7)). Partition the saliency map $S$ into non-overlapping blocks of size $r\times r$. Compute the mean value of each block to form a mean matrix $M$.

4: Apply LBP operator to $M$, to obtain texture feature matrix $L$ by Equation (9).

5: Convert the filtered image to grayscale, then Compute Zernike moments up to order $n$ to form global feature vector $Z$.

6: Quantize $L$ to binary sequence $H_{local}$ using Equation (9). Quantize $Z$ to binary sequence $H_{global}$ using Equation (10).

7: Concatenate $H_{local}$ and $H_{global}$ to form the final hash sequence $H$.

4. Experimental Results

In this experiment, we implemented the proposed algorithm using Python 3.10.5 on a workstation equipped with an Intel Core i5-11400F desktop processor (4.1 GHz) and 16 GB of RAM. Section 4.1 details the parameter configurations and databases employed. Section 4.2 and Section 4.3 evaluate the robustness and discriminative capability of our image hashing scheme, respectively. We further investigate the impact of block size selection. In the following experiments, the parameters we used are set as follows. For saliency map processing, the image is divided into non-overlapping blocks of size $64\times 64$ for subsequent feature averaging. The key parameters for feature extraction are set to capture both local texture and global structure: the LBP operator uses 8 sampling points ($P=8$) with a radius of 1 ($R=1$), while the Zernike moments are computed up to a degree of 8 ($\mathrm{n}=8$) with a radius of 5 ($\rho =5$). This configuration results in a final hash length of 89 bits. The experiments are tested on three open image databases, i.e., Kodak standard image database [52], USC-SIPI Image Database [53] and UCID database [54].

The Hamming distance is adopted as the similarity metric due to its suitability for comparing binary hash sequences [3,5]. It efficiently measures the number of differing bits, providing a direct indication of perceptual similarity. The Receiver Operating Characteristic (ROC) curve and Area Under the Curve (AUC) are used to evaluate the trade-off between robustness and discriminability [55]. These metrics are widely accepted in image hashing literature for their ability to visualize classification performance under varying thresholds.

4.1. Robustness Evaluation

To verify the robustness of the proposed algorithm, the Kodak standard image database was selected for testing. This database contains 24 color images, with representative samples presented in Figure 2. To construct variant samples that are highly similar to the original images in terms of visual features, a series of robustness test attacks were conducted using MATLAB (R2024b, MathWorks, Inc., Natick, MA, USA), Adobe Photoshop (v25.12.0, Adobe Inc., San Jose, CA, USA), and the StirMark4.0 image tool [56]. The tested operations include brightness adjustment, contrast correction, gamma correction, Gaussian low-pass filtering, salt-and-pepper noise contamination, speckle noise interference, JPEG compression, watermark embedding, image scaling, and the combined rotation-cropping-rescaling attack. It is worth noting that the rotation-cropping-rescaling attack is a composite operation, which follows a specific process: first rotating the image, cropping out the padded pixels generated during rotation, and then rescaling the cropped image to the original size.

Figure 2. Representative sample images from the Kodak standard image database used for robustness evaluation. The dataset contains a variety of scenes, textures, and color distributions, which helps to comprehensively assess the generalization capability of the hashing algorithm.

For each attack operation, different parameter combinations were set in the experiment (specific parameter ranges are listed in Table 3), and a total of 74 distinct operation schemes were determined. This means that each original image in the database corresponds to 74 visually similar variant samples, resulting in 24 × 74 = 1776 pairs of visually similar image pairs. By extracting hash features from each pair of similar images, the Hamming distance was used to quantify feature similarity. The mean Hamming distances for each operation under different parameter settings were calculated, and the results are shown in Figure 3. Analysis reveals that the mean values of all operations, except for the rotation-cropping-rescaling operation, are far below 15; The maximum mean value of the composite operation is approximately 20, directly due to composite operations introducing greater cumulative distortion than single operations, as they involve superposition of multiple distortion factors, leading to more significant feature deviations. Additionally, the block-based approach used for local feature extraction fails to resist rotation operations.

Table 3. Digital operations and their parameter settings.

Operation	Parameter Value	Number
Brightness adjustment	parameter: ±10, ±20	4
Contrast adjustment	parameter: ±10, ±20	4
Gamma correction	Angle (degree): ±1, ±2, ±3, ±4, ±5	10
Gaussian low-pass filtering	filter size: 3 × 3, standard deviation: 0.3–1.0	8
Image scaling	γ: 0.75, 0.9, 1.1, 1.25	4
JPEG compression	ratio: 0.5, 0.75, 0.9, 1.1, 1.5, 2	6
Rotation, cropping and rescaling	compression fact: 30–100, step: 10	8
Salt and Pepper noise	density: 0.001–0.01, step: 0.001	10
Speckle noise	density: 0.001–0.01, step: 0.001	10
Watermark embedding	strength: 10–100, step: 10	10

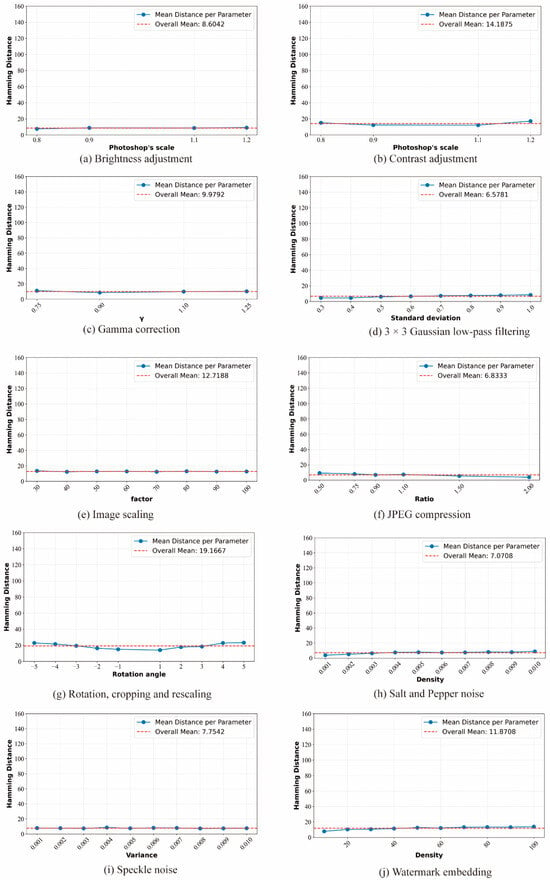
Figure 3. Mean Hamming distances under ten types of content-preserving manipulations. Error bars represent one standard deviation. The results demonstrate strong robustness to a wide range of distortions: photometric attacks (a–c,h–j), filtering operations (d), geometric transformations (e), and JPEG compression (f), with all mean distances consistently remaining below 15. Notably, the composite rotation-cropping-rescaling operation (g) introduces the highest distortion, leading to a larger mean Hamming distance (~19.2). This is analyzed in Section 4.4, attributed to the spatial misalignment of block-based LBP features under severe geometric attacks.

Further statistical analysis of the maximum, minimum, mean, and standard deviation of Hamming distances across different operations (as presented in Table 4) reveals that the mean Hamming distance for the rotation-cropping-rescaling operation stands at 19.7, whereas the mean values for all other operations are below 15. This significant discrepancy can be attributed to a recognized limitation of the block-based LBP feature extraction process. While Zernike moments themselves are rotation-invariant, the division of the saliency map into fixed, non-overlapping blocks means that the spatial layout of the extracted LBP features is not preserved under rotation. This spatial misalignment leads to the observed significant changes in the resulting binary sequence. Additionally, the standard deviations of all digital operations are small, indicating that a threshold T = 37 can be selected to mitigate interference from most of the tested operations. With this threshold, the correct detection rate reaches 76.5% when excluding rotated variant images and increases to 86.23% when rotated variant images are included. This insight suggests a direction for future work: incorporating a rotation-invariant LBP variant or employing a block alignment correction step prior to feature extraction could markedly improve performance under such geometric attacks.

Table 4. Performance comparisons among different operations.

Operation	Min	Max	Mean	Deviation
Brightness adjustment	0	19	8.6	13.8
Contrast adjustment	2	32	14.1	30.1
Gamma correction	4	32	10.0	19.4
Gaussian low-pass filtering	0	14	6.58	9.8
Image scaling	0	18	6.83	15.0
JPEG compression	6	21	12.72	12.0
Rotation, cropping and rescaling	6	36	19.17	35.7
Salt and Pepper noise	0	18	7.1	14.6
Speckle noise	0	16	7.75	12.7
Watermark embedding	1	28	11.9	18.3

4.2. Discrimination Analysis

The discriminative capability of the proposed hashing method was evaluated using the UCID database and USC-SIPI Image Database. A total of 1000 color images were selected for comprehensive assessment. To evaluate discrimination performance, Hamming distances were computed between the hash codes of all possible unique image pairs. Therefore, a representative subset of 1000 images were randomly selected for this analysis, resulting in a total of 499,500 pairwise distances calculated (equivalent to the number of unique pairs among 1000 images). The distribution of these distances is presented in Figure 4.

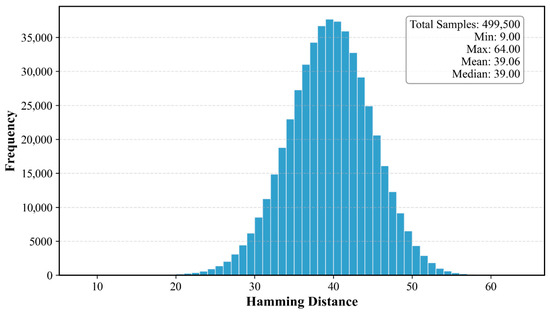
Figure 4. The distribution of Hamming distances between hashes of 499,500 unique image pairs from the UCID and USC-SIPI databases. The distribution is centered at a high mean value (~39.1) with a widespread, indicating that the hashes of distinct images are vastly different. This clear separation from the robustness-based distances (c.f., Figure 3) confirms the strong discriminative capability (uniqueness) of the proposed method.

Statistical analysis indicates that the Hamming distance spans from 9 to 64, with an average value of 39.06 and a standard deviation of 5.36. Notably, this average distance between distinct images is significantly higher than the maximum average distance found among similar images (19.74, derived from the robustness test). This considerable disparity effectively showcases the strong discriminative ability of the proposed hashing approach.

The balance between discrimination (false detection rate) and robustness (correct detection rate) depends inherently on the threshold. The total error rate, which balances false positives and negatives, is minimized at a threshold of 18, making this the optimal choice for balancing discriminative power and robustness. However, the threshold can be adjusted based on application needs, prioritizing either criterion.

4.3. Block Size Selection

To view our performances under different dimension selections, the Receiver Operating Characteristics (ROC) graph [55] is used to carry out experimental analysis. In ROC curve analysis, the following key metric definitions need to be clarified: Let $N_{sim}$ represent the total number of similar image pairs (i.e., pairs belonging to the same underlying image), among which $TP$ (True Positives) denotes the number of pairs correctly identified as similar. Let $N_{dissim}$ denote the total number of dissimilar image pairs (i.e., pairs belonging to different images), with $FP$ (false positives) represents dissimilar pairs incorrectly classified as similar. Two core evaluation metrics are derived from these:

• Correct Detection Rate (CDR), calculated as: $CDR={\displaystyle \frac{TP}{N_{sim}}}$.
• False Detection Rate (FDR), defined as: $FDR={\displaystyle \frac{FP}{N_{dissim}}}$.

In the ROC graph, the position of the curve directly reflects the algorithm’s performance: the closer the curve is to the upper-left corner, the stronger the algorithm’s ability to correctly identify similar images and effectively distinguish dissimilar ones, indicating superior overall discrimination performance.

To validate the parameter selection rationale outlined in Section 3.5, we evaluated the performance under different saliency block sizes. The used datasets are consistent with the image libraries of Section 3. Different block size selections in feature learning are discussed, i.e., different d values. Specifically, the block size is chosen from {16, 64, 256, 1024}, and other parameter settings remain the same. As demonstrated in Figure 5 and Table 5, a block size of 64 × 64 achieved a superior balance, yielding the highest AUC (0.9987) among the tested sizes while maintaining a compact hash length (89 bits) and minimal computational overhead. These results empirically confirm that our pre-defined choice, based on a theoretical trade-off, was indeed optimal. The results demonstrate that the AUC values of the block sizes of 16, 64, 256, 1024 are 0.9508, 0.9987, 0.9854, and 0.9931, respectively. Obviously, the AUC value of block size 64 is larger than those of other dimension values, while there is slight difference in running time. Performances under different block sizes are listed in Table 5. Therefore, our proposed robust hashing reaches preferable performance when block sizes are 64.

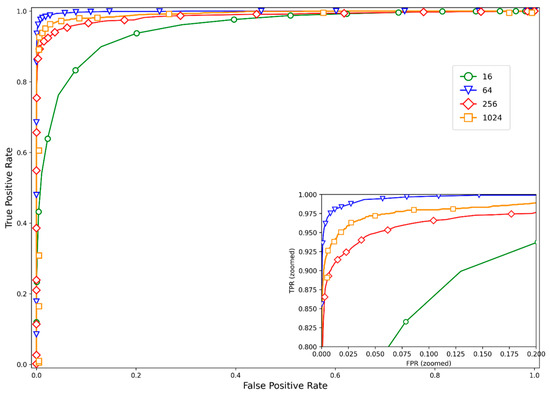
Figure 5. Receiver Operating Characteristic (ROC) curves under different block sizes (d) for saliency map partitioning. The block size of d = 64 yields the highest Area Under the Curve (AUC = 0.9987), indicating it provides the optimal granularity for balancing the capture of local texture details and feature stability. Smaller blocks (d = 16) are more sensitive to noise, while larger blocks (d = 256, 1024) oversmooth local details, with both cases resulting in a degradation in performance.

Table 5. Performance comparisons under different block sizes.

$\mathit{r}\times \mathit{r}$	Hash Length (bit)	Computational Time (s)	AUC
$4\times 4$	41	0.0932	0.9508
$8\times 8$	89	0.0916	0.9987
$16\times 16$	281	0.0915	0.9854
$32\times 32$	1049	0.0935	0.9931

4.4. Performance Comparisons

To demonstrate advantages, some popular robust hashing methods are employed for comparison, including the SVD-CSLBP method [19], GF-LVQ [44], and the HCVA-DCT method [30]. The compared schemes have been recently published in reputable journals or conferences. Moreover, the SVD-CSLBP method also uses LBP as a local feature while HCVA-DCT selects color vector angle as prepressing, enabling a meaningful evaluation of our feature design. To ensure a fair comparison, all parameter settings and similarity metrics were adopted directly from the original publications, and all images were resized to 512 × 512 before they were input to these methods.

The image databases described in Section 4.1 and Section 4.2 were employed to evaluate the classification performance of our scheme, utilizing 1776 images for robustness assessment and 499,500 image pairs for discrimination analysis. Receiver Operating Characteristic (ROC) curves were again used for visual comparison, with all evaluated schemes plotted together in Figure 6 to facilitate direct juxtaposition. To enhance clarity, local details of these curves are enlarged in an inset within the same figure. Evidently, our scheme’s curve lies closer to the upper-left corner than those of the comparative methods, confirming through visual analysis that our approach achieves superior classification performance. In addition, we calculated the Area Under the Curve (AUC) to quantitatively evaluate the trade-off performance, where a larger AUC value indicates a better balance. The results show that the AUC values of HCVT-DCT hashing, GF-LVQ hashing, and SVD-CSLBP hashing are 0.9747, 0.9902, and 0.9964, respectively. In contrast, our proposed method achieves an AUC of 0.9987, which outperforms all compared algorithms. Both the ROC curves and AUC values confirm that our method exhibits superior trade-off performance between robustness and discrimination compared to the competing approaches. This advantage originates from our novel integration of features: Zernike moments effectively capture global structural characteristics, while color vector matrices highlight region-of-interest information, and LBP further refines local textural details from the saliency maps. Notably, the color vector angle was adopted due to its superior properties over intensity-based measures. Unlike luminance, it is inherently invariant to changes in illumination intensity and shadows, as it depends on the direction of chromaticity in RGB space rather than its magnitude [43]. This makes it highly sensitive to genuine changes in color content while being robust to common photometric distortions.

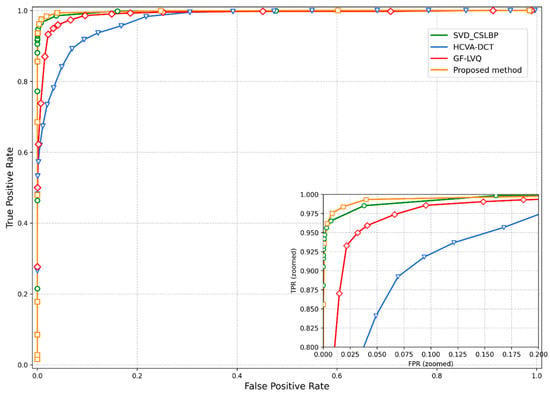
Figure 6. Performance comparison of different hashing algorithms using ROC curves. The proposed method’s curve lies closest to the top-left corner and achieves the highest AUC value (0.9987), demonstrating its superior overall trade-off between robustness and discriminability compared to state-of-the-art methods. This advantage stems from the effective fusion of saliency-guided texture features and global invariant moments.

Despite its overall strong performance, the proposed method has certain limitations. It remains sensitive to severe geometric attacks causing spatial misalignment, such as large-angle rotation with cropping. Furthermore, while robust to mild noise, LBP performance can degrade under strong noise or blurring. Zernike features also lack inherent scale invariance beyond the initial normalization step. Notwithstanding these limitations, our method offers distinct advantages over existing competitors. Unlike SVD-CSLBP which uses DCT global features, our use of Zernike moments provides better inherent rotation invariance. Compared to GF-LVQ, our saliency-guided LBP extraction focuses computation on relevant regions, improving discriminability. Compared to HCVA-DCT, our fusion of Zernike moments and LBP captures a more diverse set of features (geometry + texture) than color angles alone.

These theoretical advantages are further substantiated by comparing practical performance metrics. As summarized in Table 6, our method achieves a favorable balance between performance and economy. Although the hashing generation time (0.0923 s) is slightly higher than some alternatives, the difference is marginal for practical applications. More significantly, our algorithm requires only 89 bits of storage—substantially lower than the floating-point representations needed by HCVA-DCT (20 floats) and SVD-CSLBP (64 floats), and also lower than the 120 bits required by GF-LVQ.

Table 6. Performance comparisons among different hashing algorithms.

Algorithm	Time (s)	Storage	AUC
HCVA-DCT	0.0693	20 floats	0.9747
SVD-CSLBP	0.0611	64 floats	0.9967
GF-LVQ	0.1725	120 bits	0.9702
Proposed method	0.0923	89 bits	0.9987

In conclusion, the proposed global-local fusion hashing method achieves balanced discriminability, robustness, and compact storage (89 bits). To address the identified limitations, future work will focus on enhancing LBP’s noise resistance and optimizing the computational efficiency of Zernike moment calculation.

5. Conclusions

This paper presented a perceptual image hashing scheme that fuses Zernike moments and saliency-based LBP. The method demonstrates excellent robustness against common content-preserving manipulations and high discriminability between different images, achieving a superior trade-off compared to several state-of-the-art algorithms, as confirmed by ROC and AUC analysis.

However, the study also reveals important limitations. The method’s performance is susceptible to compound geometric attacks like rotation-cropping, and computational efficiency, while acceptable, may require further optimization for real-time, high-throughput applications. The implications of this work extend to practical applications in image authentication, copyright protection, and tamper detection for digital assets, where explainable and efficient hashing is required. Ethically, like any hashing technology, it could be used for both content protection and potential privacy-invasive tracking, underscoring the need for responsible use.

Future work will directly address the identified limitations. We will investigate the following: (1) integrating rotation-invariant LBP descriptors or employing geometric correction techniques to improve resilience against spatial transformations; (2) exploring deep learning-based feature extractors to replace hand-crafted ones for enhanced robustness to complex distortions like severe noise and blur; (3) optimizing the computational pipeline, particularly the Zernike moments calculation, through approximate algorithms or hardware acceleration to reduce the hashing time for large-scale deployment.