Abstract
Determining how to balance data utilities and data privacy when datasets are released to be utilized outside the scope of data-collecting organizations constitutes a major challenge. To achieve this aim in data collection (datasets), several privacy preservation models have been proposed, such as k-Anonymity and l-Diversity. Unfortunately, these privacy preservation models may be insufficient to address privacy violation issues in datasets that have high-dimensional attributes. For this reason, the privacy preservation models, km-Anonymity and LKC-Privacy, for addressing privacy violation issues in high-dimensional datasets are proposed. However, these privacy preservation models still exhibit privacy violation issues from using data comparison attacks, and they further have data utility issues that must be addressed. Therefore, a privacy preservation model can address privacy violation issues in high-dimensional datasets to be proposed in this work, such that there are no concerns about privacy violations in released datasets from data comparison attacks, and it is highly efficient and effective in data maintenance. Furthermore, we show that the proposed model is efficient and effective through extensive experiments.
1. Introduction
User privacy violation is a serious issue that data holders must consider when collected data are released to be utilized outside the scope of data-collecting organizations [1,2,3,4,5,6,7,8,9]. Therefore, in this paper, k-Anonymity [10] is proposed to address this issue before datasets are released. All explicit user identifier values are available in the datasets to be removed. Moreover, users’ unique quasi-identifier values are suppressed or generalized by their less-specific values to be at least k indistinguishable tuples.
Here, we provide an example of privacy preservation based on k-Anonymity constraints in conjunction with data generalization [10,11]. With k-Anonymity, the parameter k represents the privacy preservation consultant such that it is represented by a positive integer that is equal to or greater than 2, i.e., and . Suppose that k is set to 2, i.e., . Let Table 1 be the raw dataset. In Table 1, there are two explicit identifier attributes ( and ), three quasi-identifier attributes (, , and ), and a sensitive attribute (). For privacy preservation, the and data are removed in the first step. Finally, all unique quasi-identifier values are generalized by their less-specific values to be at least two indistinguishable tuples. The resulting released version of the data from Table 1 is shown in Table 2.

Table 1.
An example of a raw dataset.

Table 2.
The released version of the data in Table 1, which satisfies 2-Anonymity constraints.
Table 2 shows that all possible data utilization conditions, owing to their quasi-identifier attributes, always have at least two tuples that are satisfied. In this situation, privacy violation in Table 2 seems impossible. Unfortunately, in [12], the authors demonstrate that Table 2 still has privacy violation issues that must be addressed. For example, let be the target user such that ’s disease is the target data of the adversary. We assume that the adversary believes the user profile tuple in Table 2 to be ’s. Moreover, the adversary knows that is a 48-year-old male. Thus, the adversary can be confident based on Table 2 that has . Although two user profile tuples match the adversary’s knowledge about , the adversary can see that only is shown in the attribute of these tuples. From this example, we can conclude that although the released datasets guarantee that all possible data utilization conditions, owing to their quasi-identifier attributes, always have at least k satisfied tuples, they still have privacy violation issues that must be addressed. To address this vulnerability of k-Anonymity, l-Diversity [12] is proposed. For privacy preservation with l-Diversity, in addition to removing the explicit identifier values and distorting (suppressing or generalizing) all unique quasi-identifier values, the number of distinct sensitive values available in each sensitive attribute is also considered, i.e., every group of indistinguishable quasi-identifier values must relate to at least l different sensitive values, where and , in every sensitive attribute.
Here, an example of privacy preservation is given based on l-Diversity, where Table 1 is the raw dataset. For privacy preservation, let the value of l be set to 2. The released version of the data from Table 1 satisfying the 2-Diversity constraints is shown in Table 3. In Table 3, it is guaranteed that all possible data utilization conditions, owing to the quasi-identifier attributes, always have at least l different sensitive values to be satisfied. Therefore, we can conclude that l-Diversity is more secure in terms of privacy preservation than k-Anonymity.

Table 3.
The released version of the data from Table 1, which satisfies 2-Diversity constraints.
Unfortunately, to the best of our knowledge about l-Diversity, it is generally insufficient to address privacy violation issues in datasets that have high-dimensional attributes and are independently released when new data becomes available [13,14,15,16,17]. To eliminate these vulnerabilities in l-Diversity in high-dimensional datasets, -Anonymity [18] and -Privacy [19,20,21] are proposed. These privacy preservation models assume that the adversary has limited background knowledge about the target user. That is, in terms of the adversary’s background knowledge about the target user, the m and L values are limited by -Anonymity and -Privacy, respectively, so m or L sizes of the unique quasi-identifier values are suppressed or generalized to be k or K indistinguishable tuples. However, the effectiveness of these privacy preservation models is questioned because they are based on an estimation of the adversary’s level of background knowledge about the target user, and they are inadequate for addressing privacy violation issues in datasets that do not allow the quasi-identifier attributes to determine or the empty value. Moreover, these privacy preservation models can also be inadequate for addressing privacy violation issues in datasets that are independently released and have multiple sensitive attributes [22,23,24,25,26,27,28].
To address privacy violation issues in datasets that have multiple sensitive attributes, two well-known privacy preservation models have been proposed, i.e., aggregate query frameworks [29,30] and data anonymization models for multiple sensitive attributes [31,32,33]. For privacy preservation with aggregate query frameworks, the data analyst is not allowed to utilize the data available in datasets directly, i.e., they can only utilize the data via aggregate query frameworks. Another well-known privacy preservation solution is distorting users’ unique quasi-identifier values in datasets to make them indistinguishable. Moreover, the number of distinct sensitive values and re-identifiable sensitive values in every sensitive attribute of each group of indistinguishable quasi-identifier values are also considered when establishing privacy preservation constraints.
For preserving data privacy in independently released datasets, in [26,34], the authors recommend that, in addition to releasing datasets that satisfy privacy preservation constraints, all results that could be compared between the released and original datasets must also satisfy the privacy preservation constraints.
In addition, to the best of our knowledge about the above-mentioned privacy preservation models, they have serious vulnerabilities that must be improved. That is, they are inadequate for addressing privacy violation issues in datasets that have high-dimensional quasi-identifier attributes, multiple sensitive attributes, and independent data releases. These vulnerabilities in these privacy preservation models will be explained in Section 2.
This paper is organized as follows. The motivation for this work is explained in Section 2. Then, our privacy preservation model for high-dimensional datasets is proposed in Section 3. Subsequently, the experimental results are discussed in Section 4. Finally, our conclusion and directions for future work in this field are discussed in Section 5 and Section 6, respectively.
2. Motivation
Before we explain the motivation for this work, we present the necessary definitions.
Definition 1
(High-dimensional datasets). Let = be the set of quasi-identifier attributes. Let = be the data domain of ∈, where 1 ≤r≤p. Let be the set of sensitive attributes. Let = be the data domain of , where . Let be the high-dimensional dataset. Every of D, where , represents the profile tuple of the user such that it is in the form , i.e., =, where , , , , , and . Let be a sub-data version of D such that it is constructed from , where and , i.e., ⊆ and ⊆S. Thus, every of , where , is in the form . The data projection on Γ and Δ of is and , respectively. The data projection on and of is and , respectively.
Definition 2
(Data generalization hierarchy). Let be the generalized function of from the level ζ to such that all values of the level ζ are more specific than their related values at the level . Therefore, we can write the data generalization sequence of , , from the level 0 to L, as …. That is, all values at the level 0 are more specific than at other levels, and the values at level L are less specific than at other levels.
Definition 3
(Data generalization). Let Λ be the set of specified quasi-identifier values in of D. The meaning of data generalization is that Λ is distorted by an appropriately less-specific value that is presented by as indistinguishable.
Definition 4
(Data suppression). Let be an arbitrary tuple of D. The meaning of data suppression is that is not available in the released version of the data in D.
Definition 5
(Adversary’s background knowledge about the target user). Let = be the information about the user . If is the adversary’s background knowledge about the user in D, must satisfy both limitations as follows: and .
Definition 6
(Privacy violation concerns). Let l be a positive integer such that it is equal to or greater than two, i.e., and . Let be a specific sensitive attribute. If the number of distinct sensitive values available in is at most , has privacy violation concerns that must be addressed.
Definition 7
(l-Diversity). Let l be the privacy preservation constraint. Let D be the function for transforming D into . That is, all unique quasi-identifier values are available in of , and they are suppressed or generalized by their less-specific values in to be indistinguishable. Moreover, every group of indistinguishable quasi-identifier tuples must be related to at least l distinct sensitive values of every sensitive attribute . In addition, every group of indistinguishable quasi-identifier tuples satisfies l-Diversity constraints, and they are referred to as equivalence classes of . Hence, can be presented by the set of its equivalence classes, i.e., .
Here, we give an example of privacy preservation based on l-Diversity constraints in datasets that have multiple sensitive attributes. Let Table 4 be the raw dataset D. Let the value of l be set to 2. With these instances, the released version of the data in Table 4 satisfies the 2-Diversity constraints, as shown in Table 5. In Table 5, there are three equivalence classes, i.e., , , and . Moreover, Table 5 guarantees that all possible data utilization conditions, owing to the quasi-identifier attributes, always have at least l distinctly satisfied sensitive values in every sensitive attribute. However, Table 5 has data utility issues that must be addressed, i.e., the meaning of the data in Table 5 is much less clear than in Table 4.

Table 4.
An example of raw datasets that have high-dimensional quasi-identifiers and sensitive attributes.

Table 5.
The released version of the data in Table 4, which satisfies 2-Diversity constraints.
2.1. Data Utility Issues
2.1.1. Data Utility Issues Based on the Number of Attributes
Let the value of l be set to 2, and let Table 4 without be the raw dataset D. For these instances, the released version of the data in Table 4 satisfies the 2-Diversity constraints, as shown in Table 6. In another situation, let Table 4 without , , , and be the raw dataset D. For these instances, the released version of the data in Table 4 satisfies the 2-Diversity constraints, as shown in Table 7. In Table 6 and Table 7, we can see that Table 7 utilizes more data than Table 6. Therefore, we can conclude that the number of quasi-identifier attributes directly influences the data utility of .

Table 6.
The released version of the data in Table 4 without , which satisfies 2-Diversity constraints.

Table 7.
The released version of the data in Table 4 without , , , and , which satisfies 2-Diversity constraints.
2.1.2. Data Utility Issues Based on the Number of S Attributes
Let the value of l be set to 2, and let Table 4 without , , and be the raw dataset D. For these instances, the released version of the data in Table 4 satisfies the 2-Diversity constraints, as shown in Table 8. In Table 7 and Table 8, we can see that Table 7 utilizes more data than Table 8. Therefore, we can conclude that the number of sensitive attributes also influences the data utility of .

Table 8.
The released version of the data in Table 4 without , , and , which satisfies 2-Diversity constraints.
Based on Section 2.1.1 and Section 2.1.2, it is clear that the number of and S attributes influences the data utility of . For this reason, only the utilized and S attributes of D should be available in in D. For example, let Table 4 be the raw dataset D. Suppose that if the data holder only needs to show a statistical report of employee salaries based on gender and position, only , , and are available in the released version of the data in Table 4. Although this privacy preservation solution addresses the data utility issues of , it often leads to privacy violation from data comparison attacks when the adversary has background knowledge about the target user and has received enough released versions of the data in D.
2.2. Privacy Violation from Data Comparison Attacks
In this section, a data privacy attack (violation) on independently released datasets D using data comparison is demonstrated. It is based on the assumption that datasets can be changed when new data becomes available. Moreover, we assume that the adversary has received the corresponding released version of the data in D. The adversary believes that the tuple of the received datasets is the profile tuple of the target user. In addition, we assume that the adversary has enough background knowledge about the target user and that the sensitive attribute targeted by the adversary is available in all received datasets. Privacy violation is considered to have occurred when the comparison result of the targeted sensitive attribute in the received datasets does not satisfy the given value of l.
Let be a sub-data version of D such that it is constructed from and . Let be a sub-data version of D such that it is constructed from and , where , ∣∪∣<∣+∣, and ∩≠∅. For privacy preservation, let :, where ∈ is the function for transforming into . Let :, where ∈ is the function for transforming into . That is, and are satisfied by Definition 7. Let ∈∩ be the sensitive attribute targeted by the adversary such that it is available in and . Let be the target user of the adversary. Let be the adversary’s background knowledge about the target user . Let the values in ∪…∪ and ∪…∪ match those in . Moreover, and without data generalities satisfy the limitations ∪…∪⊂∪…∪ and ∣∪…∪−∪…∪∣<. Therefore, the targeted value of the target user is available in in and , and it can be revealed by ∪ … ∪ − ∪ … ∪ .
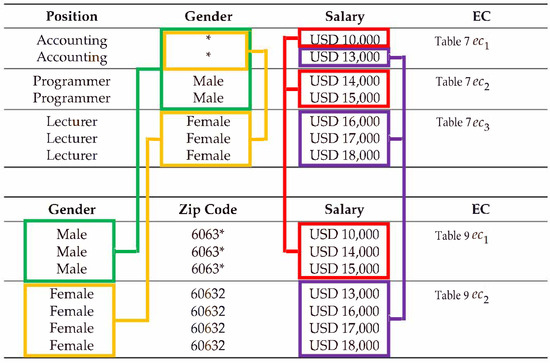
Here, we provide an example of privacy violation issues in an independently released dataset D from data comparison attacks. Let Table 4 be the raw dataset. Let the value of l be set to 2. Let Table 7 be the released version of the data in a sub-table of Table 4 such that it is constructed from , , and , and it further satisfies the 2-Diversity constraints. Moreover, let Table 9 be the released version of the data in a sub-table of Table 4 such that it is constructed from , , and . In addition, Table 9 satisfies the 2-Diversity constraints. Suppose that the adversary has received Table 7 and Table 9. Let John be the target user of the adversary such that they strongly believe that the tuple in Table 7 and Table 9 is ’s profile tuple. Moreover, the adversary knows that Johnis a male accountant. Furthermore, we assume that the adversary needs to reveal John’s salary, which is given in Table 7 and Table 9. In this situation, the adversary can be confident that the tuple of Table 7- and Table 9- must be ’s profile tuple because only the quasi-identifier values of these equivalence classes match the adversary’s background knowledge about . Moreover, the adversary can see that Table 9- relates to Table 7- and Table 7-, and they also see that the Table 9- relates to Table 7- and Table 7-. Therefore, the adversary can infer from Table 7 and Table 9 that USD 10,000 is John’s salary. The data relationships between Table 7 and Table 9 are shown in Figure 1.

Table 9.
The released version of the data in Table 4 without , , , and , which satisfies 2-Diversity constraints.
Based on Section 2.1 and Section 2.2, it is clear that although the datasets satisfy l-Diversity constraints, they still have two serious issues that must be addressed, i.e., data utility and privacy violation. To eliminate these vulnerabilities in l-Diversity, we propose a new extended privacy preservation model of l-Diversity. It will be presented in Section 3.
3. The Proposed Model
In this section, we describe a new privacy preservation model that can address privacy violation issues in high-dimensional datasets that are allowed to change and independently release data when new data becomes available such that released datasets are not susceptible to privacy violation from data comparison attacks.
3.1. Privacy Preservation in High-Dimensional Datasets
Let l be a privacy preservation constraint represented by a positive integer that is equal to or greater than two. Let be the specific raw dataset that is released at the timestamp j. Let be the released versions of the data D such that they relate to and are released from the timestamp 1 to . For privacy preservation, let be the function for transforming into . That is, all unique quasi-identifier values are suppressed or generalized by their less-specific values in to be indistinguishable. Moreover, every group of indistinguishable quasi-identifier tuples must relate at least l distinct sensitive values in every . In addition, every group of tuples in is then satisfied by the given value of l to call an equivalence class of . Thus, we can say that is the set of its equivalence classes, i.e., . In addition to suppressing or generalizing all unique quasi-identifiers and considering the number of distinct sensitive values, the comparison result between the sensitive values in and every related in , where , must also be satisfied by the given value of l, i.e., ∣−∣≥l.
In addition, after datasets satisfy the proposed privacy preservation constraint, they are often more secure in terms of privacy preservation than their corresponding raw datasets, but they lose some data utility. Moreover, a given privacy preservation constraint for each dataset generally has various released versions of the data that can be satisfied. For example, let Table 4 without , , , and be the raw dataset for public use. Suppose that only Table 7 is the previously released version of the data that relates to the specific raw dataset. Let the value of l be set to 2. For these instances, Table 10 and Table 11 are both released versions of the data that are not susceptible to privacy violation from data comparison attacks. However, Table 10 and Table 11 are different, so they could be different in terms of data utilization. Only the released version of the data has the desired high data utility. Therefore, the data utility metric is a necessity in the proposed model; this will be discussed in Section 3.2.

Table 10.
The released version of the data in Table 4 without , , , and , which satisfies the proposed privacy preservation constraint, where .

Table 11.
The released version of the data in Table 4 without , , , and , which also satisfies the proposed privacy preservation constraint, where .
3.2. Data Utility Metric
Although satisfies the proposed privacy preservation constraint, it is generally higher in terms of privacy preservation than . However, often loses some data utility. For this reason, only has sufficiently high data utility. Thus, the data utility metric is a necessity in the proposed privacy preservation model. Since privacy preservation based on data suppression and generalization was established, several data utility metrics have been proposed, e.g., the precision metric () for data suppression in conjunction with data generalization [35], the discernibility metric () [36], and relative error [37,38]. These metrics will be explained in Section 3.2.1, Section 3.2.2, and Section 3.2.3, respectively.
3.2.1. Precision Metric (PREC) for Data Suppression in Conjunction with Data Generalization [35]
With the proposed privacy preservation model, can satisfy the privacy preservation constraints using data suppression in conjunction with data generalization. For this reason, has two data penalty costs that must be considered, i.e., the penalty costs of data suppression and data generalization. With data generalization, the penalty cost of depends on the level and the number of generalized values such that a high level and a larger number of generalized values lead to a higher penalty cost of . Therefore, the penalty cost of data generalization for can be defined by Equation (1), i.e., the penalty cost of data generalization for is between 0 and ∣∣ · ∣∣. A higher penalty cost of means that is more generalized.
where
- ∣∣ is the number of quasi-identifier attributes that are available in ;
- is the generalized level of the quasi-identifier value that is available in of ;
- ∣∣ is the height of the data generalization hierarchy for ;
- ∣∣ is the number of tuples that are available in .
Another penalty cost for is data suppression, which depends on the number of suppressed tuples and the size of . Thus, the penalty cost of data suppression for can be defined by Equation (2). That is, the penalty cost of is between 0 and ∣. A higher penalty cost of means that is more suppressed.
Therefore, the total penalty cost of can be defined based on the penalty cost of and , as shown in Equation (3). In addition, a higher penalty cost of means that has lower data utility.
3.2.2. Discernibility Metric (DM) [36]
The metric is a data utility metric that can also be used to define the penalty cost or the data utility of . With the metric, the penalty cost of depends on the size of its equivalence classes. That is, it can be defined by Equation (4). The penalty cost of is between 0 and ∣. A higher penalty cost means that has lower data utility.
3.2.3. Relative Error [37,38]
The relative error is the metric that is used to define the penalty cost of . With this metric, the data utility of depends on the difference in the queried results between and its original dataset . A higher relative error means that has lower data utility. For query results that are represented by numerical data, their relative errors can be defined by Equation (5).
where
- is the result that is queried from ;
- is the relative result of such that it is queried from .
With query results that are not represented by numerical data, their relative errors can be defined by Equation (6).
where
- is the number of values that are queried from ;
- is the number of relative values of such that they are queried from .
3.3. The Proposed Algorithm
In this section, a new privacy preservation algorithm, -, ), is presented that can address privacy violation issues in high-dimensional datasets that are allowed to change and independently release data when new data become available. With the proposed algorithm, in addition to privacy preservation, the data utility and exclusion time are also maintained where possible. To achieve the aims of the proposed algorithm, greedy [39,40,41,42] and data clustering [43,44,45] are applied. Moreover, the proposed algorithm is based on the assumption that all corresponding released versions of the data are released from the timestamp 1 to , i.e., , and they always satisfy the proposed privacy preservation model. Thus, only is considered to construct of . The proposed algorithm (Algorithm 1) is shown below.
The inputs of the proposed privacy preservation algorithm are a positive integer l, the sub-data version of D, the corresponding released version of the data in , and the data generalization hierarchies and . The output of the proposed privacy preservation algorithm is the released version of the data in such that it satisfies the proposed privacy preservation constraints that are presented in Section 3.1.
| Algorithm 1-, ) |
|
For privacy preservation, is first investigated to answer the question “can be transformed to satisfy the given value of l?”. If cannot be transformed to satisfy the given value of l, the algorithm returns . If it can be transformed, the second or third part of the algorithm is enabled. In the second part, the algorithm investigates the question “is there a corresponding released version of the data in ?”. That is, if is , it means that does not have a corresponding released version of the data. Thus, can be transformed to satisfy the given value of l, without considering privacy violation from data comparison attacks, using the following steps:
- In the first step, an arbitrary tuple is chosen to be the initialized tuple for constructing the first equivalence class of . Moreover, is removed from and kept by .
- In the second step, the maximum penalty cost for constructing the first equivalence class of is determined such that it is kept by , i.e., .
- In the third step, all tuples of are iterated until they cannot satisfy the given value of l. In each iteration, a tuple of is assigned to its appropriate equivalence class of and removed from . In addition, to construct each new equivalence class of , an arbitrary tuple is chosen to be the initialized tuple, and the maximum penalty cost, , for constructing the equivalence class is set to be maximized.
- In the fourth step, the unique quasi-identifier values are made available in and are generalized by their less-specific values, which are represented by and , respectively.
- Finally, is returned.
In addition, the tuples of cannot be transformed to satisfy the given value of l; they are suppressed.
Another part of the algorithm is enabled when can be satisfied by the given value of l and when the corresponding released version of the data in is available. In this part of the algorithm, in addition to generalizing the unique quasi-identifier values and considering the number of unique sensitive values, all compared results between each equivalence class of and its comparable equivalence class in are also considered to satisfy the given value of l. Moreover, the tuples of cannot be transformed to satisfy the given value of l; they are also suppressed. Finally, is returned.
The Complexity of the Proposed Algorithm
In this section, we discuss the complexity of the proposed algorithm. With the proposed algorithm, we can see that before every equivalence class of is constructed, its most similar tuples are first determined such that they are as minimized as possible, and each of their sensitive attributes must collect at least l distinct sensitive values. In addition, the most similar tuples are determined and removed from in each iteration of the proposed algorithm. For this reason, the tuples of are reduced by one in every iteration. Therefore, the cost of determining the most similar tuples in the proposed algorithm can be defined by Equation (7).
For example, suppose that six tuples are available in . An infographic illustrating the cost of determining the most similar tuples in the proposed algorithm is shown in Figure 2, where the blue square is the number of tuples that are considered by each iteration of the proposed algorithm.
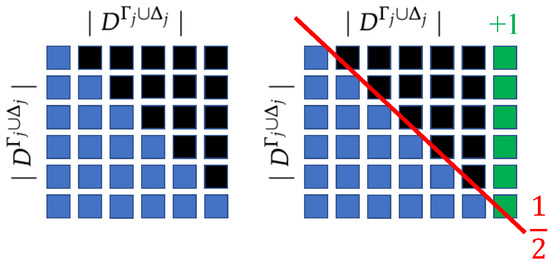
Figure 2.
An infographic illustrating the cost of determining the most similar tuples to construct equivalence classes of .
In addition to the cost of determining the most similar tuples, the proposed algorithm has two further costs that must be considered, i.e., the cost of data generalization and the cost of comparing the results between each constructed equivalence class of and its comparable equivalence classes in .
The cost of data generalization depends on the number of quasi-identifier attributes, the height of the data generalization hierarchy of each quasi-identifier attribute, and the number of equivalence classes of . Therefore, the cost of generalizing the unique quasi-identifier values of the proposed algorithm can be defined by Equation (8).
Another cost of the proposed algorithm is that of comparing the results between each constructed equivalence class of and its comparable equivalence classes in . This cost depends on the number of sensitive attributes, the number of equivalence classes of , and the number of equivalence classes of . Therefore, the cost of comparing the results between each constructed equivalence class of and its comparable equivalence class in can be defined by Equation (9).
Thus, the total cost (the complexity) for the proposed algorithm of constructing the released version of the dataset in can be defined by Equation (10).
4. Experiment
This section is focused on evaluating the effectiveness and efficiency of the proposed privacy preservation model by comparing it with l-Diversity [12] and -Privacy [19].
4.1. Experimental Setup
All experiments were performed to evaluate the effectiveness and efficiency of the proposed privacy preservation model; they were conducted on both Intel(R) Xeon(R) Gold 5218 @2.30 GHz CPUs with 64 GB memory and six 900 GB HDDs with RAID-5. Furthermore, all implementations were built and executed using Microsoft Windows Server 2019 in connection with Microsoft Visual Studio 2019 Community Edition and Microsoft SQL Server 2019.
Moreover, all of the experimental results discussed were obtained from the dataset, which is available at the Machine Learning Repository [46]. This dataset is constructed from 32561 user profile tuples. Each user profile tuple consists of 14 attributes, i.e., , , , , -, -, , , , , -, -, --, and -. To effectively conduct the experiments, only the attributes , , , -, , , , -, --, and - were made available in the experimental datasets. The attributes , , -, , , and - were set as the quasi-identifier attributes. Other attributes (i.e., , -, --, and ) were set as the sensitive attributes. Moreover, in this dataset, all user profile tuples include the values “?” and “0”; for the purposes of this study, they were removed. Therefore, the experimental dataset only included 1428 user profile tuples. We assumed that all experimental datasets had been released twice. Histograms and the cumulative percentages of each quasi-identifier attribute and each sensitive attribute are shown in Figure 3 and Figure 4, respectively.
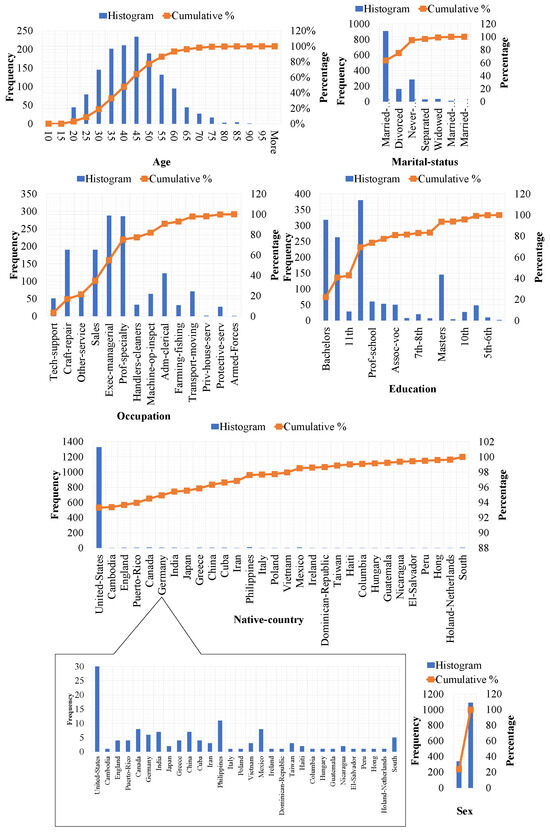
Figure 3.
Histograms and the cumulative percentages of each quasi-identifier attribute of the experimental dataset.
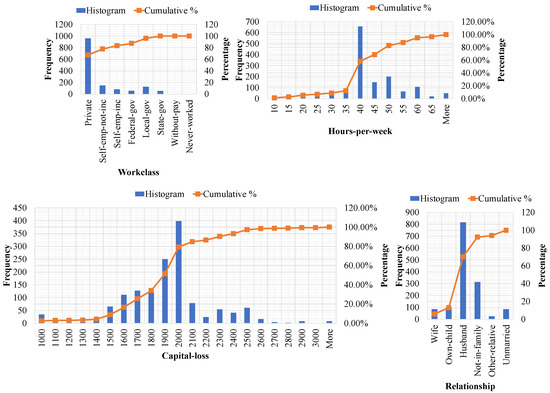
Figure 4.
Histograms and the cumulative percentages of each sensitive attribute of the experimental dataset.
4.2. Experimental Results and Discussion
4.2.1. Effectiveness of the Model
In the first experiment, we evaluate the effect of the number of quasi-identifier attributes on the data utility of the datasets constructed by the proposed model and the compared models such that they are based on and penalty costs. For the experiment, the value of l is fixed at 2 for the proposed model and l-Diversity. For -Privacy, the values of L, K, and C are set to the number of quasi-identifier attributes, l, and , respectively. Furthermore, all sensitive values available in the experimental datasets are protected sensitive values. Only - is set as a sensitive attribute. The number of quasi-identifier attributes varies from 1 to 6. The process of varying the number of quasi-identifier attributes is as follows.
- Initially, only - is a quasi-identifier attribute.
- In the second experiment, the experimental dataset only contains - and as quasi-identifier attributes.
- -, , and - are the quasi-identifier attributes in the third experiment.
- The fourth experiment has the quasi-identifier attributes -, , -, and .
- The quasi-identifier attributes in the fifth experimental dataset are -, , -, , and .
- In the final experimental dataset, , , -, , , and - are all set as quasi-identifier attributes.
As shown in Figure 5 and Figure 6, when the number of quasi-identifier attributes is increased, the and penalty costs of all experimental datasets also increase. Moreover, l-Diversity and -Privacy are equally effective and exhibit higher performance than the proposed model. However, they are slightly different. The higher and penalty costs in the experimental datasets with an increasing number of quasi-identifier attributes are due to the increase in the number of quasi-identifier attributes, and the size of the equivalence classes also increases. In addition, larger equivalence classes generally lead to more suppressed or generalized values. Moreover, larger equivalence classes often lead to a large number of generalized values in datasets. The reason l-Diversity and -Privacy are equally effective in terms of maintaining the data utility of the experimental datasets with every experiment is that when the experimental datasets do not allow for the retrieval of missing values and all sensitive values are protected sensitive values, the released version of the data from the datasets based on l-Diversity is not different from that based on -Privacy. The reason for the reduced effectiveness of the proposed model compared to the other models is that, in addition to datasets needing to satisfy the privacy preservation constraints, the compared results between datasets and their corresponding released versions must also satisfy the privacy preservation constraints. For this reason, the datasets satisfy the privacy preservation constraint of the proposed model; they are not susceptible to privacy violation from data comparison attacks. However, datasets constructed from l-Diversity and -Privacy are still susceptible to such attacks.
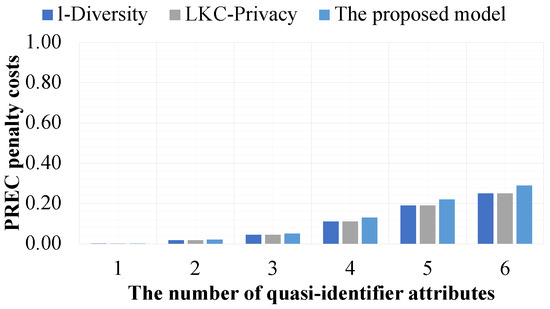
Figure 5.
The effectiveness of the models based on the number of quasi-identifier attributes and .
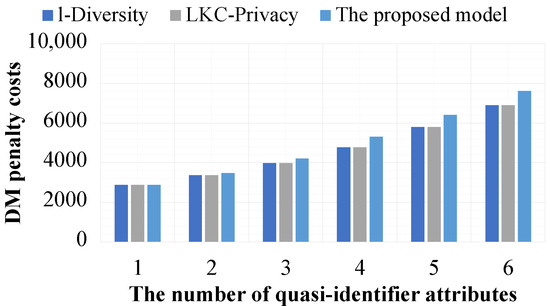
Figure 6.
The effectiveness of the models based on the number of quasi-identifier attributes and .
In the second experiment, we evaluate the effect of the number of sensitive attributes on the data utility of datasets constructed by the proposed model and the compared models such that they are based on and . In this experiment, the proposed model is only evaluated by comparison with l-Diversity because -Privacy cannot address privacy violation issues in datasets with multiple sensitive attributes. In this experiment, the value of l is fixed at 2; all quasi-identifier attributes are available in the experimental datasets; and the number of sensitive attributes varies from 1 to 4. The process of varying the number of sensitive attributes is as follows.
- The first experimental dataset only has - as a sensitive attribute.
- The second experimental dataset only contains - and as sensitive attributes.
- -, , and are the sensitive attributes in the third experimental dataset.
- In the final experimental dataset, -, , , and -- are all set as sensitive attributes.
Figure 7 and Figure 8 show that when the number of sensitive attributes is increased, the and penalty costs of all experimental datasets are also increased. The reason for the higher and penalty costs in the experimental datasets with an increasing number of sensitive attributes is that when the number of sensitive attributes is increased, the size of the equivalence classes also increases. Moreover, l-Diversity is more effective than the proposed model. However, they are slightly different. The reason for the reduced effectiveness of the proposed model compared to l-Diversity is that, in addition to datasets needing to satisfy the privacy preservation constraints, the compared results between datasets and their corresponding released versions must also satisfy the privacy preservation constraints, but this privacy preservation constraint is not considered by l-Diversity. For this reason, although the proposed model is less effective than l-Diversity, it is more secure in terms of privacy preservation.
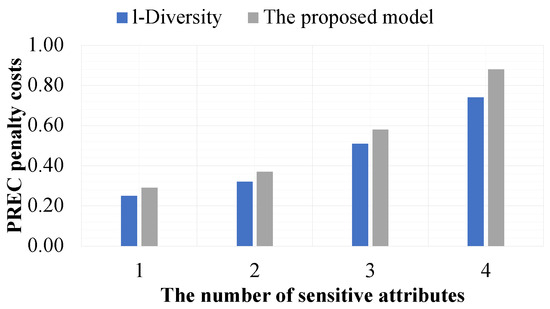
Figure 7.
The effectiveness of the models based on the number of sensitive attributes and .
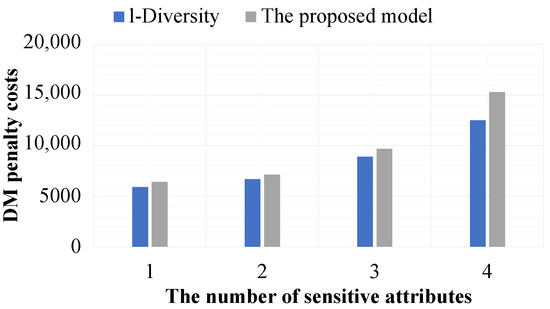
Figure 8.
The effectiveness of the models based on the number of sensitive attributes and .
In the third experiment, we evaluate the effect of the value of l on the data utility of datasets constructed by the proposed model and the other models such that they are based on and . In this experiment, only - is set as a sensitive attribute, and all quasi-identifier attributes are available in the experimental datasets. The value of l is varied from 2 to 10 for the proposed model and l-Diversity. In -Privacy, the values of L, K, and C are set to the number of quasi-identifier attributes, l, and , respectively. Furthermore, all sensitive values available in the experimental datasets are protected sensitive values.
Figure 9 and Figure 10 show that when the value of l is increased, the and penalty costs of all experimental datasets are also increased. This is because when the value of l is increased, the size of the equivalence classes is also increased. Moreover, the compared models are more effective than the proposed model. However, they are slightly different. The reason that the proposed model is less effective than the compared models is that in addition to datasets needing to satisfy the privacy preservation constraints, the compared results between the datasets and their corresponding released versions must also satisfy the privacy preservation constraints, but this privacy preservation constraint is not considered by the compared models.

Figure 9.
The effectiveness of the models based on the value of l and .
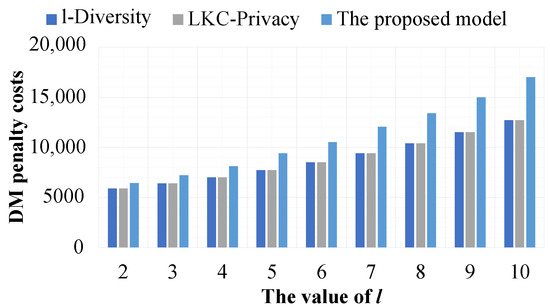
Figure 10.
The effectiveness of the models based on the value of l and .
Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show that the number of sensitive attributes and the value of l have a greater effect on the data utility in the datasets than the number of quasi-identifier attributes; this is because the privacy preservation constraint of the proposed model and of the compared models is based on the number of distinct sensitive values.
In the fourth experiment, we evaluate the effect of a limited number of quasi-identifier attributes on the data utility of datasets constructed by the proposed model and the compared models such that they are based on and . In this experiment, we assume that the data holder needs to limit the number of quasi-identifier attributes for data release from one to six attributes. In this experiment, the value of l is fixed at 2 for the proposed model and l-Diversity. In -Privacy, the values of L, K, and C are set to the number of quasi-identifier attributes, l, and , respectively. Furthermore, all sensitive values available in the experimental datasets are protected sensitive values. Only - is set as a sensitive attribute. All quasi-identifier attributes are available in the experimental datasets.
Figure 11 and Figure 12 show that the proposed model is more effective than the compared models in all experiments constructed from experimental datasets with five quasi-identifier attributes at most. The reason for this is that it supports separation of the quasi-identifier attributes to preserve the privacy of data in datasets, while the compared models do not consider this property in their privacy preservation constraints. For this reason, the compared models must consider all quasi-identifier attributes in every experiment. However, when the experimental dataset has six quasi-identifier attributes, the proposed model is less effective than the compared models. This is because the experimental datasets are the same size, and in addition to datasets needing to satisfy the privacy preservation constraints, the compared results between datasets and their corresponding released versions must also satisfy the privacy preservation constraint of the proposed model.
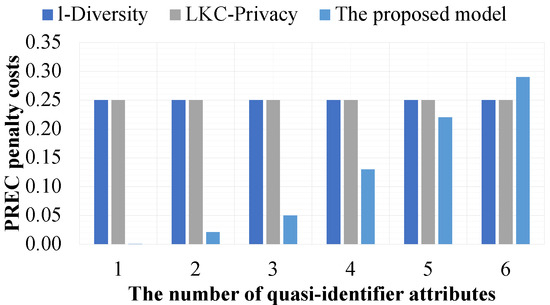
Figure 11.
The effectiveness of the model based on the limited number of quasi-identifier attributes and .
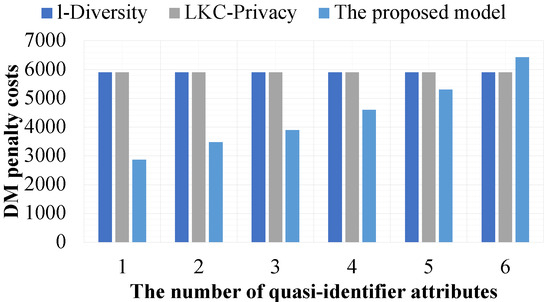
Figure 12.
The effectiveness of the models based on a limited number of quasi-identifier attributes and .
In the fifth experiment, we evaluate the effect of a limited number of sensitive attributes on the data utility of datasets constructed by the proposed model and the compared models such that they are based on and . In this experiment, the proposed model is only evaluated by comparison with l-Diversity because -Privacy cannot address privacy violation issues in datasets that have multiple sensitive attributes, and we assume that the data holder needs to limit the number of sensitive attributes for data release from one to four attributes. For this experiment, the value of l is fixed at 2. All quasi-identifiers and sensitive attributes are available in the experimental datasets.
Figure 13 and Figure 14 show that the proposed model is more effective than the compared models in all experiments constructed from the experimental datasets with three sensitive attributes at most. The reason for this is that it supports separation of the sensitive attributes to preserve the privacy of data in datasets, while the compared models do not consider this property in their privacy preservation constraints. For this reason, the compared models must consider all sensitive attributes in every experiment. However, when the experimental dataset has four sensitive attributes, the proposed model is less effective than the compared models. The reason for this is that the experimental datasets are the same size, and in addition to datasets needing to satisfy the privacy preservation constraints, the compared results between datasets and their corresponding released versions must also satisfy the privacy preservation constraint of the proposed model.
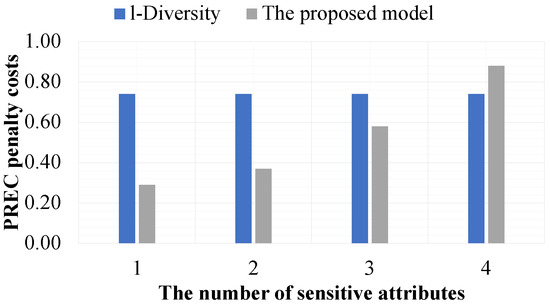
Figure 13.
The effectiveness of the models based on a limited number of sensitive attributes and .
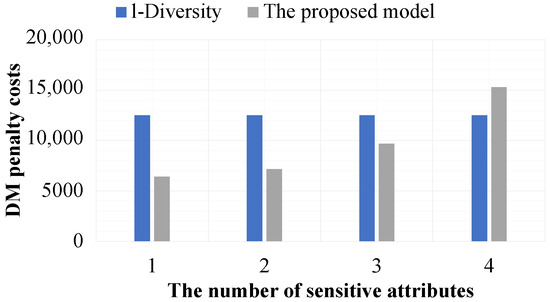
Figure 14.
The effectiveness of the models based on a limited number of sensitive attributes and .
Figure 11, Figure 12, Figure 13 and Figure 14 clearly indicate that the proposed model is more secure in terms of privacy preservation and better in terms of maintaining the data utility of datasets compared to the other models.
In the sixth experiment, we evaluate the data utility of datasets that satisfy the privacy preservation constraint of the proposed model, l-Diversity, and -Privacy such that they are based on the query function in conjunction with the or query operator and the range of queries and they are evaluated by the relative error metric presented in Section 3.2.3. In this experiment, the value of l is fixed at 2 for the proposed model and l-Diversity. With -Privacy, the values of L, K, and C are set to the number of quasi-identifier attributes, l, and , respectively. Furthermore, all sensitive values available in the experiment datasets are protected sensitive values. Only - is a sensitive attribute, and all quasi-identifier attributes are available in the experimental datasets. Moreover, all of the experimental results are shown in Figure 15 and Figure 16 and are presented as the mean of the average of the results of 15 randomized queries in the form of Query 1. The experimental results are shown in Figure 17 and are presented as the mean of the average results of 15 randomized queries in the form of Query 2.
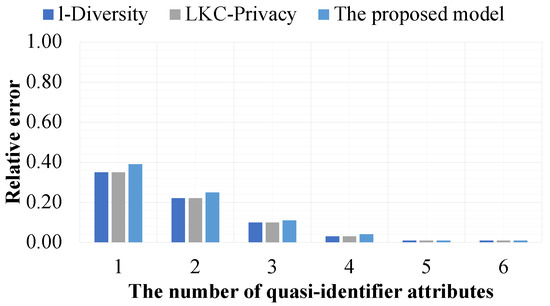
Figure 15.
The effectiveness of the models based on the query operation.
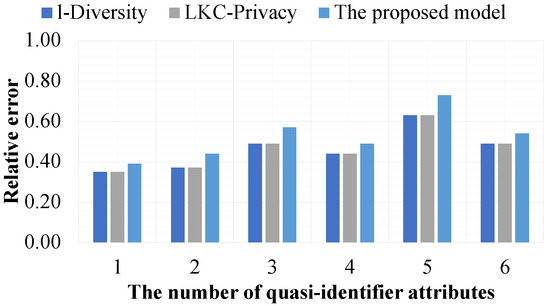
Figure 16.
The effectiveness of the models based on the query operation.
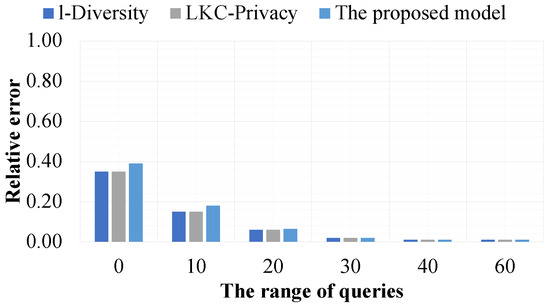
Figure 17.
The effectiveness of the models based on the range of queries.
- Query 1: SELECT AVERAGE (Capital-loss) WHERE = [AND/OR] … [AND/OR] = ;
- Query 2: SELECT AVERAGE (Capital-loss) WHERE Age BETWEEN LB AND UB.
The elements of these queries are defined as follows:
- are the specified quasi-identifier attributes , , -, , , and -.
- are the specified values for querying the data from the datasets.
- is the lower bound for querying the data from the datasets.
- is the upper bound for querying the data from the datasets.
In Figure 15, we show the data utility of query results affected by the query operation. The experimental results show that the number of query-condition attributes inversely influences the data utility of query results; i.e., a larger number of query-condition attributes leads to higher data utility of the query results. This is because a larger number of query-condition attributes gives all experimental models more options for generalizing the data in datasets, thus resulting in fewer errors.
Figure 16 shows the effect of using the query operation on the query results. Obviously, when the number of query-condition attributes is increased, the relative errors of the query results are also increased. This is because all experimental models have limitations regarding the values satisfied in data queries.
Figure 17 shows the effect of using the range of queries on the query results. Note that when the query range condition is set to 0, it means that the exact same value is applied. The trend of the experimental results in Figure 17 is similar to that of the experimental results shown in Figure 15 for the same reason, i.e., a wide range of query conditions often leads to more options for generalizing the data in datasets, thus resulting in fewer errors.
4.2.2. Efficiency
In the seventh experiment, we evaluate the efficiency of the proposed model, which is based on the number of quasi-identifier attributes. In this experiment, the value of l is fixed at 2 for the proposed model and l-Diversity. With -Privacy, the values of L, K, and C are set to the number of quasi-identifier attributes, l, and , respectively. Furthermore, all sensitive values available in the experimental datasets are set as protected sensitive values. Only - is a sensitive attribute, and the number of quasi-identifier attributes varies from 1 to 6.
Figure 18, Figure 19 and Figure 20 show that the proposed model is less efficient than l-Diversity, but it is more efficient than -Privacy. The reason l-Diversity is more efficient than all other experimental models is that its privacy preservation constraints are simpler than those of the other models. That is, with the proposed model, in addition to the datasets needing to satisfy the privacy preservation constraints, the compared results must also satisfy the model’s privacy preservation constraints. Thus, in addition to the cost of considering the data from datasets to satisfy privacy preservation constraints, the model incurs the cost of data comparison between it and its corresponding datasets. The reason -Privacy is less efficient than the other experimental models is that it must consider sub-datasets with a size of L at most.
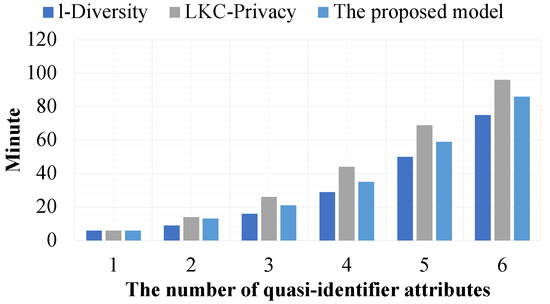
Figure 18.
The efficiency of the models based on the number of quasi-identifier attributes.
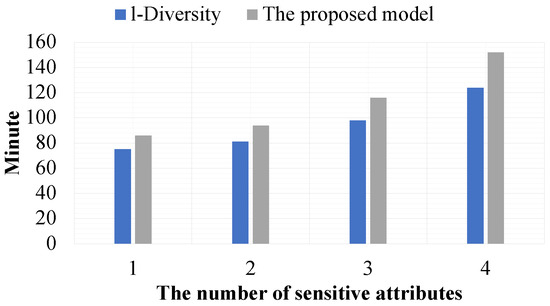
Figure 19.
The efficiency of the models based on the number of sensitive attributes.
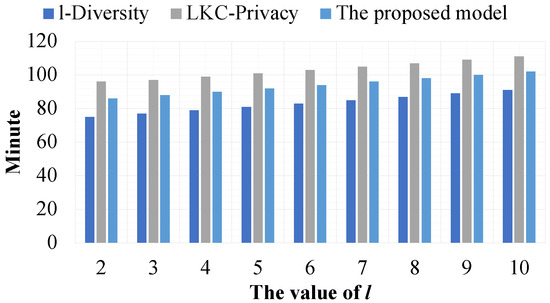
Figure 20.
The efficiency of the models based on the value of l.
5. Conclusions
This work enumerates and explains the vulnerabilities of privacy preservation models to data comparison attacks when datasets are independently released. To address the vulnerabilities of privacy preservation models, we propose a new model that can address privacy violations caused by data comparison attacks on datasets. Moreover, our experimental results indicate that released datasets are satisfied by the proposed model, which is found to be more secure in terms of privacy preservation and better in terms of maintaining the data utility of datasets compared to the other models.
6. Future Work
Although the proposed model can address privacy violation issues resulting from data comparison attacks on independently released datasets, adversaries will discover new approaches to compromising the privacy of data. Thus, an appropriate privacy preservation model that can address newly discovered privacy violation issues should be proposed.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All data can be found online in the dataset, which is available at the Machine Learning Repository.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Alferidah, D.K.; Jhanjhi, N. A review on security and privacy issues and challenges in internet of things. Int. J. Comput. Sci. Netw. Secur. IJCSNS 2020, 20, 263–286. [Google Scholar]
- Alwarafy, A.; Al-Thelaya, K.A.; Abdallah, M.; Schneider, J.; Hamdi, M. A survey on security and privacy issues in edge-computing-assisted internet of things. IEEE Internet Things J. 2020, 8, 4004–4022. [Google Scholar] [CrossRef]
- Deep, S.; Zheng, X.; Jolfaei, A.; Yu, D.; Ostovari, P.; Kashif Bashir, A. A survey of security and privacy issues in the Internet of Things from the layered context. Trans. Emerg. Telecommun. Technol. 2022, 33, e3935. [Google Scholar] [CrossRef]
- Hathaliya, J.J.; Tanwar, S. An exhaustive survey on security and privacy issues in Healthcare 4.0. Comput. Commun. 2020, 153, 311–335. [Google Scholar] [CrossRef]
- Edemacu, K.; Wu, X. Privacy preserving prompt engineering: A survey. ACM Comput. Surv. 2025, 57, 1–36. [Google Scholar] [CrossRef]
- Newaz, A.I.; Sikder, A.K.; Rahman, M.A.; Uluagac, A.S. A survey on security and privacy issues in modern healthcare systems: Attacks and defenses. ACM Trans. Comput. Healthc. 2021, 2, 1–44. [Google Scholar] [CrossRef]
- Zhi, Y.; Fu, Z.; Sun, X.; Yu, J. Security and privacy issues of UAV: A survey. Mob. Netw. Appl. 2020, 25, 95–101. [Google Scholar] [CrossRef]
- Riyana, S.; Sasujit, K.; Homdoung, N.; Chaichana, T.; Punsaensri, T. Effective Privacy Preservation Models for Rating Datasets. ECTI Trans. Comput. Inf. Technol. (ECTI-CIT) 2023, 17, 1–13. [Google Scholar]
- Riyana, S. Achieving Anatomization Constraints in Dynamic Datasets. ECTI Trans. Comput. Inf. Technol. (ECTI-CIT) 2023, 17, 27–45. [Google Scholar]
- Sweeney, L. K-Anonymity: A Model for Protecting Privacy. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Riyana, S.; Nanthachumphu, S.; Riyana, N. Achieving privacy preservation constraints in missing-value datasets. SN Comput. Sci. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Gehrke, J.; Kifer, D.; Venkitasubramaniam, M. L-diversity: Privacy beyond k-anonymity. In Proceedings of the 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 24. [Google Scholar] [CrossRef]
- Yin, X.; Zhu, Y.; Hu, J. A Comprehensive Survey of Privacy-Preserving Federated Learning: A Taxonomy, Review, and Future Directions; ACM: New York, NY, USA, 2021; Volume 54, pp. 1–36. [Google Scholar]
- Liang, W.; Ji, N. Privacy Challenges of IoT-Based Blockchain: A Systematic Review; Springer: Berlin/Heidelberg, Germany, 2022; Volume 25, pp. 2203–2221. [Google Scholar]
- Peng, C.; Luo, M.; Wang, H.; Khan, M.K.; He, D. An efficient privacy-preserving aggregation scheme for multidimensional data in IoT. IEEE Internet Things J. 2021, 9, 589–600. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, Y.; Chang, C.C.; Peng, Q. Privacy-preserving high-dimensional data publishing for classification. Comput. Secur. 2020, 93, 101785. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L.; Zhang, Q. Outsourcing high-dimensional healthcare data to cloud with personalized privacy preservation. Comput. Netw. 2015, 88, 136–148. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, J.; Yang, W.; Fan, J.; Lam, K.Y.; Zhao, J. Privacy-preserving aggregation in federated learning: A survey. IEEE Trans. Big Data 2022. early access. [Google Scholar] [CrossRef]
- Fung, B.C.M.; Cao, M.; Desai, B.C.; Xu, H. Privacy Protection for RFID Data. In Proceedings of the 2009 ACM Symposium on Applied Computing, SAC ’09, Honolulu, HI, USA, 12 March 2008–8 March 2009; pp. 1528–1535. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N. A Privacy Preservation Model for RFID Data-Collections is Highly Secure and More Efficient than LKC-Privacy. In Proceedings of the The 12th International Conference on Advances in Information Technology, IAIT2021, New York, NY, USA, 29 June–1 July 2021. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N. Achieving Anonymization Constraints in High-Dimensional Data Publishing Based on Local and Global Data Suppressions. SN Comput. Sci. 2022, 3, 3. [Google Scholar] [CrossRef]
- Gangarde, R.; Sharma, A.; Pawar, A.; Joshi, R.; Gonge, S. Privacy preservation in online social networks using multiple-graph-properties-based clustering to ensure k-anonymity, l-diversity, and t-closeness. Electronics 2021, 10, 2877. [Google Scholar] [CrossRef]
- Cassa, C.A.; Miller, R.A.; Mandl, K.D. A novel, privacy-preserving cryptographic approach for sharing sequencing data. J. Am. Med. Inform. Assoc. 2013, 20, 69–76. [Google Scholar] [CrossRef][Green Version]
- Jayapradha, J.; Prakash, M.; Alotaibi, Y.; Khalaf, O.I.; Alghamdi, S.A. Heap bucketization anonymity—An efficient privacy-preserving data publishing model for multiple sensitive attributes. IEEE Access 2022, 10, 28773–28791. [Google Scholar] [CrossRef]
- Lu, D.; Zhang, Y.; Zhang, L.; Wang, H.; Weng, W.; Li, L.; Cai, H. Methods of privacy-preserving genomic sequencing data alignments. Briefings Bioinform. 2021, 22, bbab151. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N.; Nanthachumphu, S. Privacy Preservation Techniques for Sequential Data Releasing. In Proceedings of the The 12th International Conference on Advances in Information Technology, Bangkok, Thailand, 29 June–1 July 2021; pp. 1–9. [Google Scholar]
- Wang, M.; Guo, Y.; Zhang, C.; Wang, C.; Huang, H.; Jia, X. MedShare: A privacy-preserving medical data sharing system by using blockchain. IEEE Trans. Serv. Comput. 2021, 16, 438–451. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, J.; Fan, J.; Vijayakumar, P.; Chang, V. Achieving privacy-preserving DSSE for intelligent IoT healthcare system. IEEE 2021, 18, 2010–2020. [Google Scholar] [CrossRef]
- Riyana, S. (lp1, …, lpn)-Privacy: Privacy preservation models for numerical quasi-identifiers and multiple sensitive attributes. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 9713–9729. [Google Scholar] [CrossRef]
- Liu, H.; Gu, T.; Shojafar, M.; Alazab, M.; Liu, Y. OPERA: Optional dimensional privacy-preserving data aggregation for smart healthcare systems. IEEE Trans. Ind. Inform. 2022, 19, 857–866. [Google Scholar] [CrossRef]
- Khan, R.; Tao, X.; Anjum, A.; Sajjad, H.; Khan, A.; Amiri, F. Privacy preserving for multiple sensitive attributes against fingerprint correlation attack satisfying c-diversity. Wirel. Commun. Mob. Comput. 2020, 2020, 8416823. [Google Scholar] [CrossRef]
- Riyana, S.; Ito, N.; Chaiya, T.; Sriwichai, U.; Dussadee, N.; Chaichana, T.; Assawarachan, R.; Maneechukate, T.; Tantikul, S.; Riyana, N. Privacy Threats and Privacy Preservation Techniques for Farmer Data Collections Based on Data Shuffling. ECTI Trans. Comput. Inf. Technol. (ECTI-CIT) 2022, 16, 289–301. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N.; Sujinda, W. An Anatomization Model for Farmer Data Collections. SN Comput. Sci. 2021, 2, 353. [Google Scholar] [CrossRef]
- Bourahla, S.; Laurent, M.; Challal, Y. Privacy preservation for social networks sequential publishing. Comput. Netw. 2020, 170, 107106. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N.; Nanthachumphu, S. An effective and efficient heuristic privacy preservation algorithm for decremental anonymization datasets. Adv. Intell. Syst. Comput. 2021, 1200 AISC, 244–257. [Google Scholar]
- Bayardo, R.J.; Agrawal, R. Data privacy through optimal k-anonymization. In Proceedings of the 21st International Conference on Data Engineering (ICDE’05), Tokyo, Japan, 5–8 April 2005; pp. 217–228. [Google Scholar] [CrossRef]
- Riyana, S.; Riyana, N.; Nanthachumphu, S. Enhanced (k,e)-Anonymous for categorical data. In Proceedings of the ICSCA 2017: 2017 6th International Conference on Software and Computer Applications, Bangkok, Thailand, 26–28 April 2017; pp. 62–67. [Google Scholar]
- Zhang, Q.; Koudas, N.; Srivastava, D.; Yu, T. Aggregate Query Answering on Anonymized Tables. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15 April 2006–20 April 2007; pp. 116–125. [Google Scholar] [CrossRef]
- Chekuri, C.; Pal, M. A recursive greedy algorithm for walks in directed graphs. In Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS’05), Pittsburgh, PA, USA, 23–25 October 2005; pp. 245–253. [Google Scholar]
- Feldman, M.; Naor, J.; Schwartz, R. A unified continuous greedy algorithm for submodular maximization. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; pp. 570–579. [Google Scholar]
- Korte, B.; Lovász, L. Mathematical structures underlying greedy algorithms. In Fundamentals of Computation Theory; Gécseg, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 205–209. [Google Scholar]
- Koutsoupias, E.; Papadimitriou, C.H. On the greedy algorithm for satisfiability. Inf. Process. Lett. 1992, 43, 53–55. [Google Scholar] [CrossRef]
- Hammouda, K.; Karray, F. A Comparative Study of Data Clustering Techniques; University of Waterloo: Waterloo, ON, Canada, 2000; Volume 1. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Yong, W.; Hodges, J. Yong Wang.; Hodges, J. Document Clustering with Semantic Analysis. In Proceedings of the 39th Annual Hawaii International Conference on System Sciences (HICSS’06), Kauai, HI, USA, 4–7 January 2006; Volume 3, p. 54c. [Google Scholar] [CrossRef]
- Kohavi, R. Scaling up the Accuracy of Naive-Bayes Classifiers: A Decision-Tree Hybrid. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96, Portland, OR, USA, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996; pp. 202–207. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).