A Method for Few-Shot Modulation Recognition Based on Reinforcement Metric Meta-Learning

Abstract

In response to the problem where neural network models fail to fully learn signal sample features due to an insufficient number of signal samples, leading to a decrease in the model’s ability to recognize signal modulation methods, a few-shot signal modulation mode recognition method based on reinforcement metric meta-learning (RMML) is proposed. This approach, grounded in meta-learning techniques, employs transfer learning to building a feature extraction network that effectively extracts the data features under few-shot conditions. Building on this, by integrating the measurement of features of similar samples and the differences between features of different classes of samples, the metric network’s target loss function is optimized, thereby improving the network’s ability to distinguish between features of different modulation methods. The experimental results demonstrate that this method exhibits a good performance in processing new class signals that have not been previously trained. Under the condition of 5-way 5-shot, when the signal-to-noise ratio (SNR) is 0 dB, this method can achieve an average recognition accuracy of 91.8%, which is 2.8% higher than that of the best-performing baseline method, whereas when the SNR is 18 dB, the model’s average recognition accuracy significantly improves to 98.5%.

1. Introduction

With the rapid development of modern radio communication technology, automatic modulation recognition has become an indispensable component in both military and civil fields [1]. In the military field, modulation recognition is a key means to formulating effective military strategies and jamming enemy communications in modern warfare. In civil communications, modulation identification has a wide range of applications in spectrum management and resource allocation. Modulation identification can optimize the efficiency of the communication system and improve the spectrum utilization, allowing the communication network to operate efficiently and reliably [2]. The traditional modulation identification methods are mainly divided into two categories: those based on the likelihood ratio and those based on signal feature extraction. The likelihood ratio method is theoretically comprehensive but requires extensive a priori knowledge [3]. On the other hand, the signal feature extraction method is applicable to a variety of signal-to-noise ratios but relies on experience, and its identification stability and the range of recognizable modulation modes are limited [4].

In recent years, with the rapid development of deep learning, the use of neural networks for modulation identification has become a new trend [5,6,7,8,9,10,11,12]. Deep-learning-based methods have strong automatic learning capabilities and can extract deeper features. Compared with traditional methods, these methods offer a higher recognition accuracy. However, they require a large number of labeled signals for support. Acquiring these signals may be time-consuming. This requirement limits their application in real-world environments to a certain extent, especially in military confrontations. Therefore, accurately identifying the modulation of signals with few-shot learning has become a new research trend.

In order to address the aforementioned issues, many scholars have conducted in-depth research and proposed various solutions, which can be categorized into three main groups: generative adversarial network (GAN)-based methods, transfer learning, and meta-learning. For example, Mansi et al. proposed a new data augmentation method based on conditional generative adversarial networks (CGANs) which uses a small amount of sample data to generate labeled data, thereby significantly improving the recognition accuracy of CNN-based modulation classification networks in few-shot learning [13]. Zhidong Xie et al. enhanced the recognition performance of Support Vector Machines (SVMs) by constructing a deep convolutional generative adversarial network (LDCGAN) that included layer normalization [14]. To address the issue of confusing signals such as QPSK, BPSK, and QAM, Tang et al. used preprocessed constellation diagrams as the inputs and employed an Auxiliary Classifier Generative Adversarial Network (ACGAN) to identify the signal modulation modes, successfully improving the recognition accuracy for these confusing signals [15].

The above GAN-based methods significantly improve the modulation recognition accuracy in few-shot learning through data augmentation. However, their training process is complex, and the demand for computational resources is high, which poses limitations for practical applications. Transfer learning and meta-learning methods can effectively address this issue.

The training process of transfer learning is simple and can effectively utilize the knowledge from the source domain to enhance the feature extraction capability of the target domain. Bu et al. proposed an adversarial transfer learning architecture (ATLA) which aimed to reduce the difference in sampling rates, significantly improving the recognition accuracy of the target model while utilizing merely half of the training data [16]. Hu et al. employed a Domain Adaptation Network (DAN) for transfer learning, which maintained the recognition accuracy of the algorithm even with a significantly reduced number of samples in the target dataset [17]. Jing et al. proposed an adaptive focal loss function combined with transfer learning for radar signal intra-pulse modulation classification with small samples. By training a CNN in the source domain and transferring it to the target domain, the method significantly improves the recognition performance. The adaptive focal loss function focuses on difficult samples, achieving an average recognition rate of over 90% [18]. Xu et al. proposed a CNN-based transfer learning model for modulation format recognition [19]. The model uses the Hough transform of constellation diagrams to improve the recognition performance. This method effectively transfers knowledge from general tasks to specialized tasks, enhancing the overall recognition accuracy.

In the field of meta-learning, meta-learning can be classified into three main categories according to the different learning strategies employed: optimization-based meta-learning [20,21,22,23], model-based meta-learning [24,25,26,27], and metric-based meta-learning [28,29,30,31,32]. The metric-based meta-learning method has the ability to quickly adapt to new tasks compared with other methods. This method only requires a few labeled signals to achieve modulation mode recognition when facing new classes of signals, effectively solving the problem of recognizing modulation modes with few-shot learning. Therefore, many scholars have adopted metric-based meta-learning methods to address the few-shot modulation mode recognition problem. Pang Yi-Qiong et al. used a multi-task training strategy based on meta-learning to train the network through a large number of different tasks, enabling it to have cross-task signal recognition capabilities. This approach allows the network to quickly adapt with only a small number of samples when encountering new signal categories, achieving a recognition accuracy of up to 88.43% under the condition of only five labeled signal samples per category during the testing stage [33]. Zhang et al. proposed a novel attentional relational network model that fuses channel attention mechanisms with spatial attention mechanisms, aiming to learn and represent the features more efficiently [34]. Liu et al. introduced a scalable AMC scheme using the Meta-Transformer with few-shot learning and main-subtransformer-based encoders, enabling efficient and flexible modulation classification [35]. Hao et al. proposed a new meta-learning method, M-MFOR, for improving the efficiency and generalization of AMCs in the IoT. By combining multi-frequency ResNet and meta-task optimization, this method showed a better performance in environments with distributional bias [36].

The method of transfer learning has a better feature extraction ability when facing the target task, but it cannot directly cope with recognition problems when there are only a few shots [37]. Metric-based meta-learning effectively solves the recognition problem with only a few labeled samples, but its insufficient sample size leads to inadequate feature extraction by the network, which in turn affects the recognition accuracy [38]. Additionally, the existing metric functions do not sufficiently consider the relationships between inter- and intra-classes of different modulation methods. To address the above problems, this paper proposes a few-shot modulation mode recognition method based on reinforcement metric meta-learning (RMML). This method skillfully integrates the advantages of transfer learning and metric learning, effectively improving the extraction of the signal features by combining the strategies of transfer learning with the techniques of metric learning. Furthermore, innovative optimization of the metric loss function significantly enhances the model’s ability to recognize different modulation modes, effectively solving the problem of a poor modulation mode recognition performance under few-shot conditions.

2. Metric-Based Meta-Learning

In the radio environment, the signal $r\left(t\right)$ that we collect is influenced by the transmission characteristics $C\left(t\right)$ of the radio channel and the additive Gaussian white noise $n\left(t\right)$. Therefore, $r\left(t\right)$ can be expressed as Equation (1):

$$r\left(t\right)=C\left(t\right)\ast x\left(t\right)+n\left(t\right).$$

(1)

In this formula, $x\left(t\right)$ denotes the transmitted modulated signal, $C\left(t\right)$ denotes the transfer function of the radio channel, and $n\left(t\right)$ denotes the additive Gaussian white noise. In few-shot modulation recognition, only a limited number of received signal samples are available for identifying the modulation type.

2.1. The Theoretical Basis of Metric Meta-Learning

The metric-based meta-learner is composed of two main components: the encoder and the metric function. The encoder typically consists of Convolutional Neural Networks (CNNs), which are utilized to extract the signal features from the support set and the query set. The metric function is employed to assess the similarity between the encoded query and support, thereby further optimizing the meta-learner.

In the meta-training phase, a model suitable for specific tasks is developed by training on the meta-training set $D_{tr}$ using an N-way K-shot strategy. Consequently, during the meta-testing phase, only a minimal number of labeled signals are required to rapidly adapt to new tasks, demonstrating strong generalization capabilities. It is important to note that the modulation methods used in the meta-training set do not overlap with those in the meta-test set, and the categories present in the meta-test set have never appeared in the meta-training set.

The N-way K-shot strategy: In the meta-training process, we employ an episode-based training strategy. In each episode, N categories of modulations are randomly selected from the meta-training set, and K labeled signals are chosen from each category. The collected N × K signals form the support set, denoted as $D^S$. Additionally, Q unlabeled signals are selected from the remaining signals of each category to compose the query set $D^Q$. The metric loss function is optimized by measuring the distance, d, between the signals of the query set and the support set to determine the category from the support set to which the query set signals belong. The N-way K-shot training process is detailed in Algorithm 1.

Algorithm 1 The training procedure for N-way K-shot.

Input:  $D_{tr}={\left\{(x_i,y_i)\right\}}_{i=1}^n$      $D_{tr}$ denotes the data of the training set; $x_i$ denotes the signal sample; $y_i$ denotes the sample label; Output:  $\theta$      $\theta$ denotes the weight of the model. 1: formed by randomly selecting N-class samples from $D_{tr}$ to construct $D^S$ and $D^Q$; 2:  for $\mathit{iter}=0$ to Iterations do 3:     Select N categories in the training data and K in each category to form $D^S$; $D^S\leftarrow D_{tr}$; 4:     Select Q of the remaining samples from N categories to form $D^Q$; $D^Q\leftarrow D_{tr}$; 5:     $C_k\leftarrow \frac{1}{K}{\sum }_{(x_i,y_i)\in D^S}{f}_{\phi }\left(x_i\right)$; 6:  end for 7:  $J\left(\phi \right)\leftarrow 0$; 8:  for $k\in \{0,\dots ,N-1\}$ do 9:     for $(x,y)\in D^Q$ do 10:        $J\left(\phi \right)\leftarrow J\left(\phi \right)+softmax\left(d\left(f_{\phi }\left(x\right),C_k\right)\right)$; 11:     end for 12:  end for

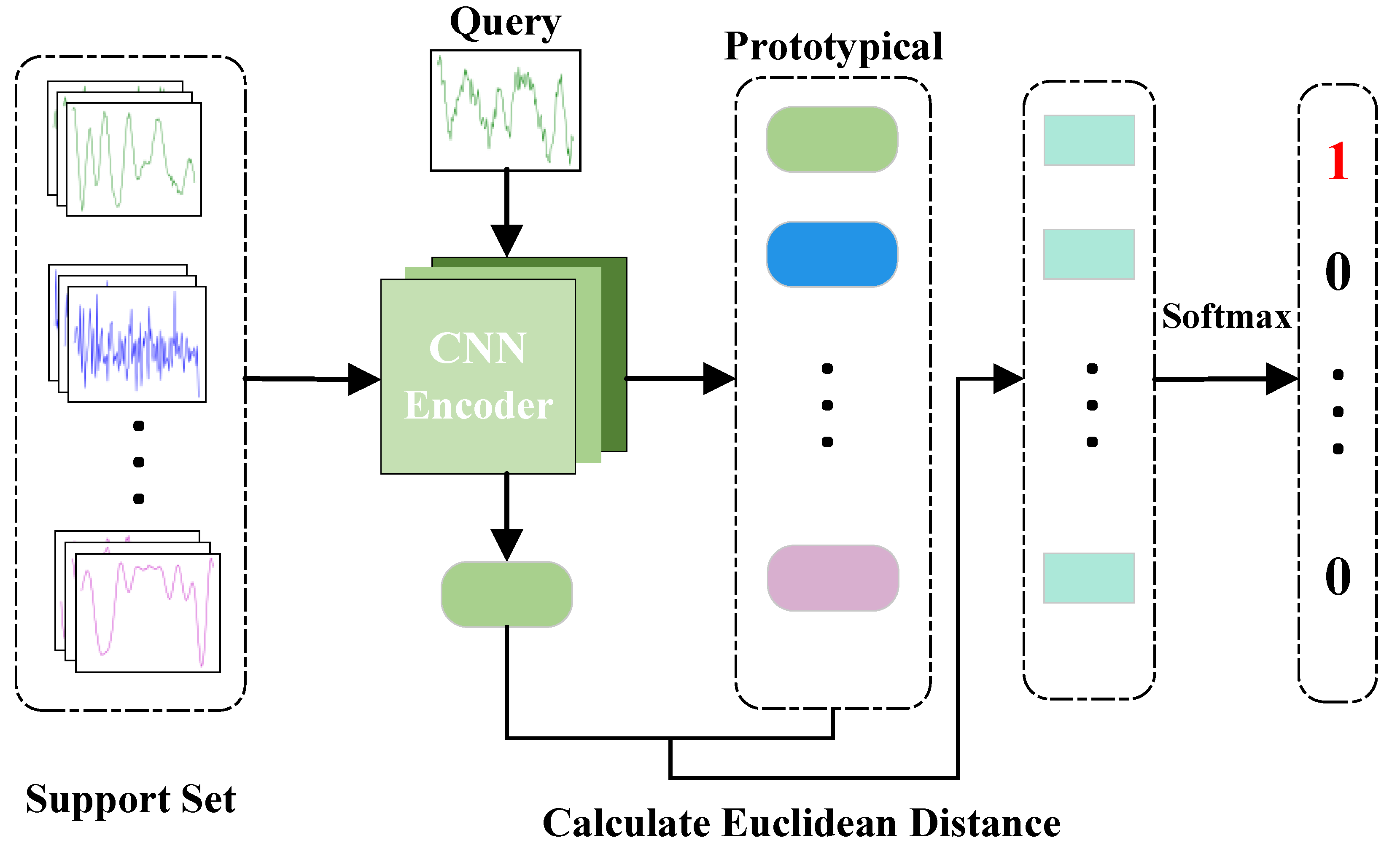
2.2. The Prototype Network

The prototype network is an efficient classification network within metric learning. This network achieves fast and accurate few-shot recognition through prototype representation of categories. Compared to other metric learning methods, it offers superior generalization capabilities and reduced computational costs.

In this paper, we will optimize the meta-learner using a modified prototype network. The workflow of the prototype network is illustrated in Figure 1, and its training adheres to the N-way K-shot strategy previously mentioned. Initially, an encoder $f_{\phi }$ is utilized to extract features from the signals in the support and query sets, producing embedding $f_{\phi }\left(x\right)$. Subsequently, the mean of K embeddings for each class in the support set is calculated to obtain the prototype representation of that class $c_k$, as demonstrated in Equation (2).

$$c_k={\displaystyle \frac{1}{K}}\sum _i{f}_{\varphi }\left(X_i^k\right).$$

(2)

Thus, the essence of a class prototype is the average embedding of all samples for each class in the support set. When a new query point is introduced, the same embedding function used to create the class prototypes is employed to generate an embedding for this query point. The class to which the query point belongs is determined by comparing the distances between the query point’s embedding and each class prototype. The Euclidean distance can be utilized to measure these distances. After calculating the distances between all class prototypes and the query point embedding, a softmax function is applied to these distances to derive the probability of the query point belonging to each class, as illustrated in Equation (3).

$$P(Y^{\prime }=k\mid X)={\displaystyle \frac{exp(-d(f_{\varphi }\left(X\right),c_k))}{{\sum }_{k}exp(-d(f_{\varphi }\left(X\right),c_k))}}.$$

(3)

The method, however, exhibits some shortcomings when applied to the field of modulation mode recognition. With very few labeled signal samples available, the feature extraction network may fail to adequately extract features. Furthermore, the metric function only considers the geometric distances between the query set samples and the support set, neglecting the intra-class and inter-class relationships. This oversight results in lower accuracy in modulation recognition. We have made improvements to this approach, which will be detailed in Section 3.

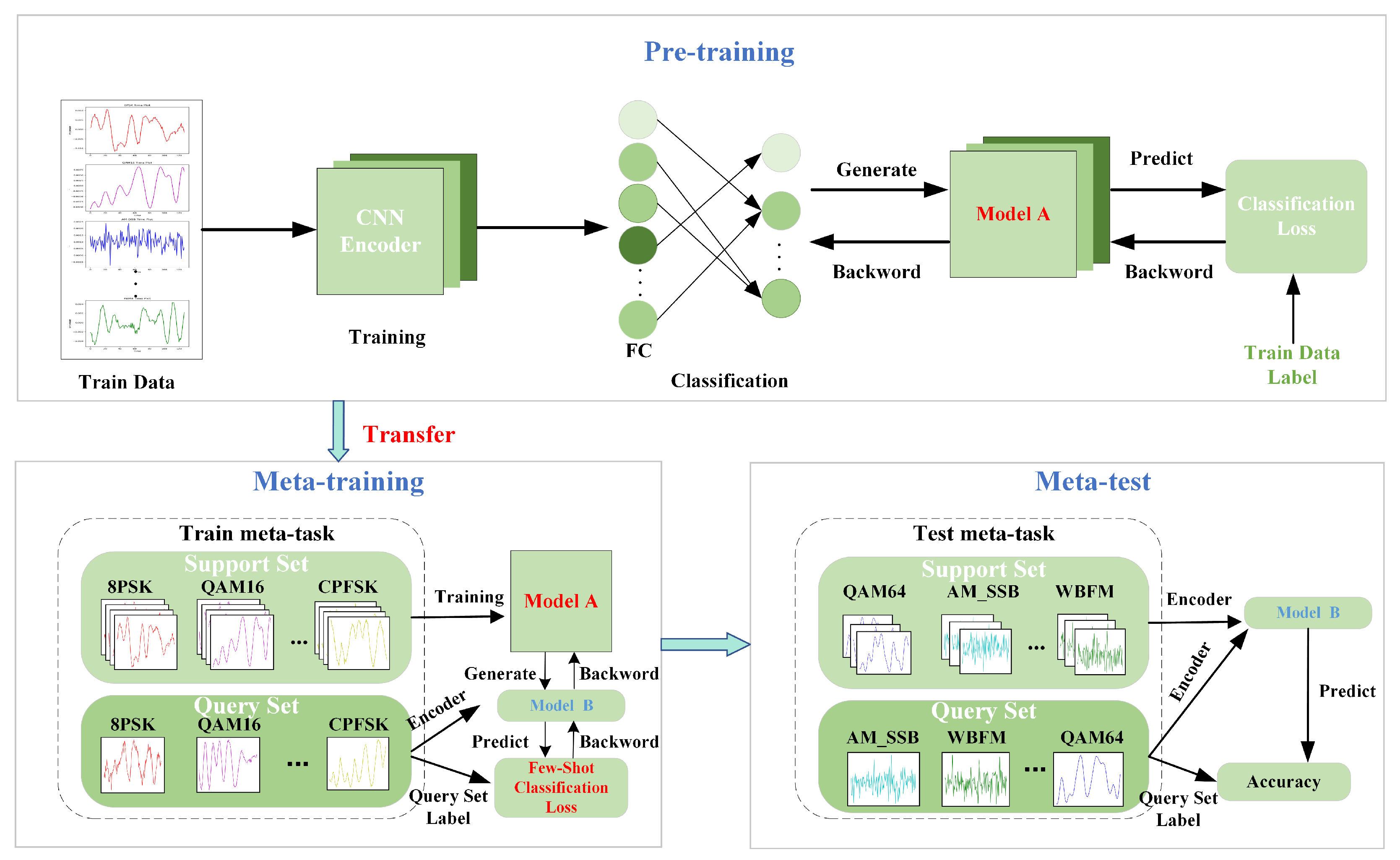
3. Method

In order to address the aforementioned issues, we propose a few-shot modulation recognition method based on reinforcement metric meta-learning (RMML). This method is structured into three phases—the pre-training phase, the meta-learning phase, and the meta-testing phase—as illustrated in Figure 2.

In the pre-training phase, the encoder, which is the MAFNet feature extraction network, is trained using traditional deep learning methods with a large number of sample signals from the training set. This process results in an initial network model, referred to as Model A.

In the meta-training phase, pre-trained Model A undergoes further optimization and training using the N-way K-shot strategy and a prototype network. Simultaneously, the metric loss function within the prototype network is enhanced to better accommodate the few-shot modulation mode recognition task. At this stage, we have successfully refined and optimized the existing network model, now referred to as Model B.

In the meta-testing phase, we use Model B to predict new signal classes in the meta-test set that never appeared in the pre-training and meta-training phases. We input the support set containing a small number of labeled signals from the meta-testing task and the unlabeled query set into Model B for feature extraction and then determine the modulation type of the signals in the query set via a metric function. We will detail the exact implementation in the following.

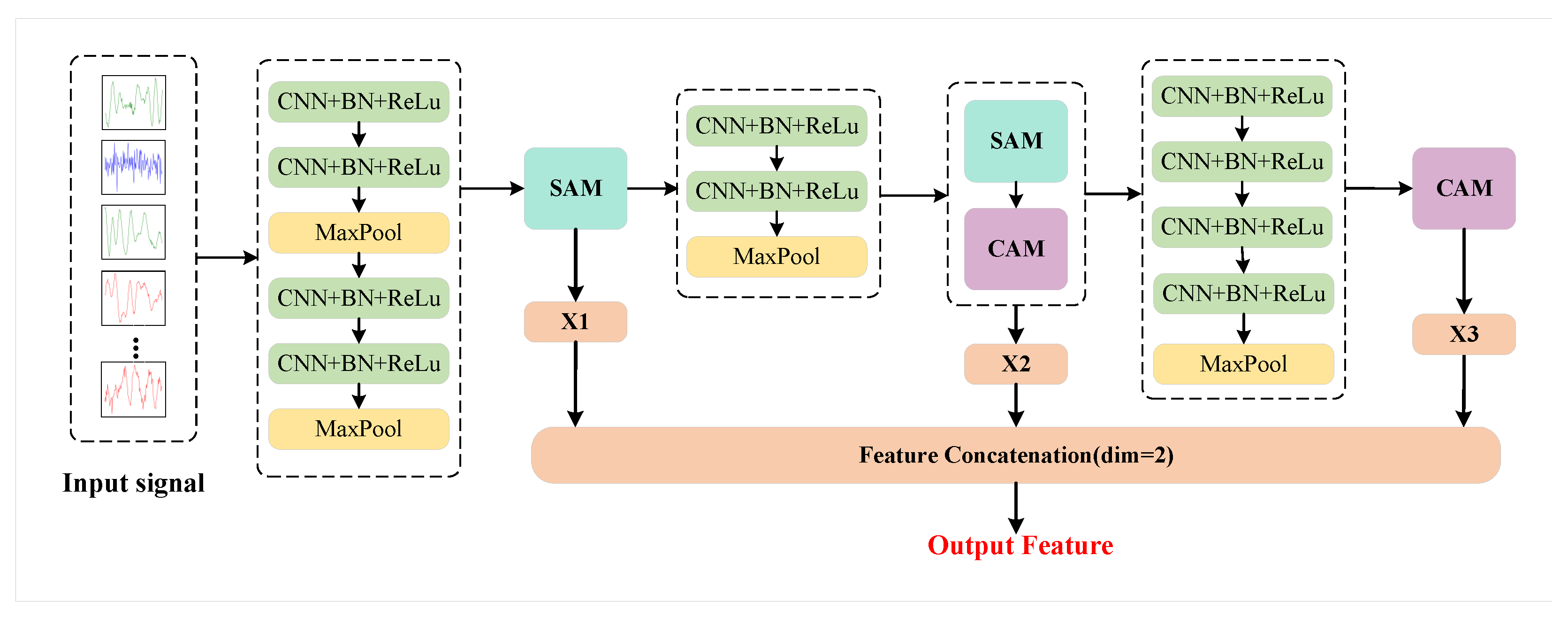
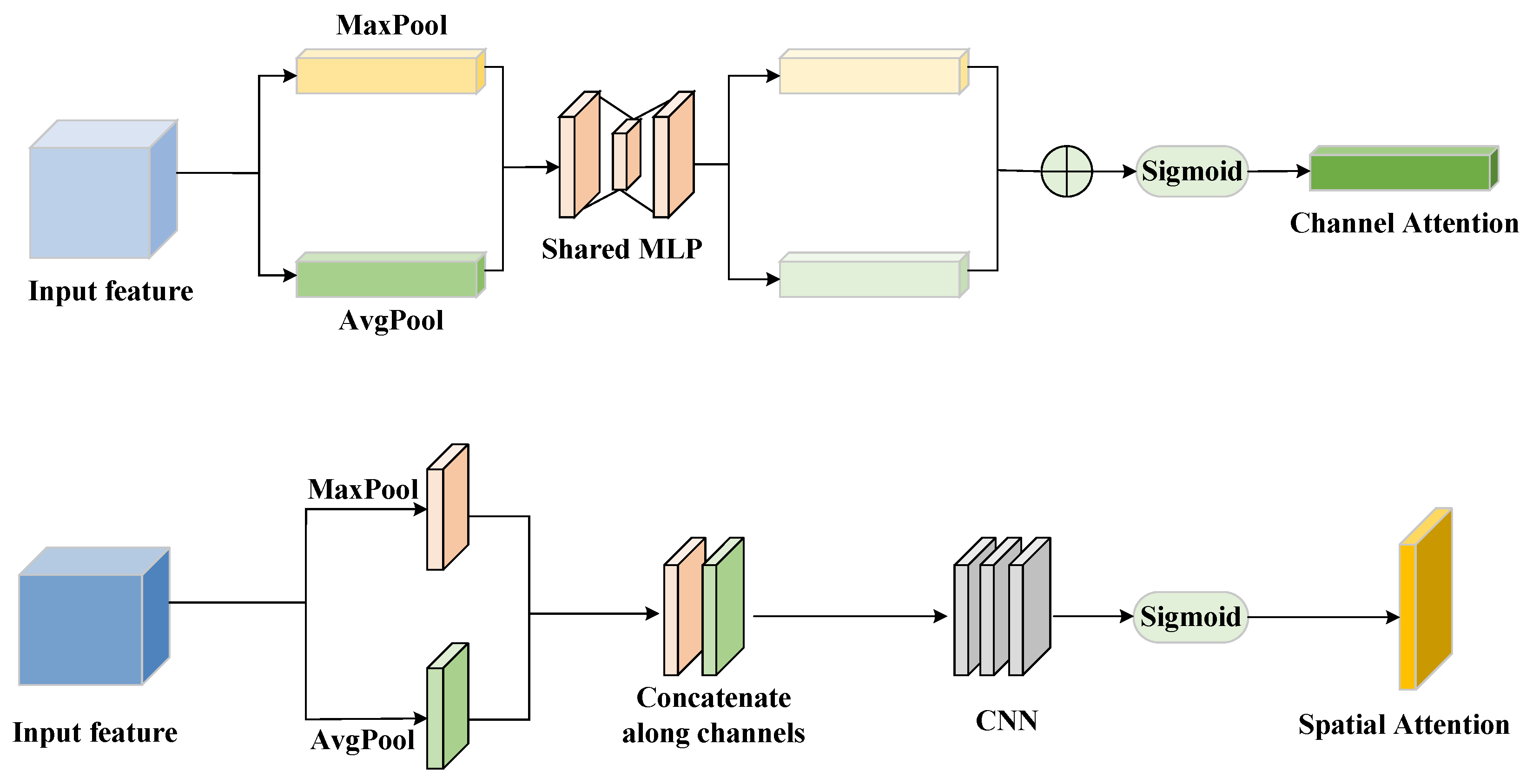
3.1. The MAFNet Feature Extraction Network

To fully extract features at different levels, our method employs the Multi-Style Attention Fusion Network (MAFNet) [39] as the encoder. As shown in Figure 3, this network structure comprises three main components: a deep convolutional module, a Spatial Attention Module (SAM), and a Channel Attention Module (CAM). The structures of the SAM and the CAM are shown in the Figure 4. To ensure that the network can effectively extract signal features from various dimensions, it fuses low-, middle-, and high-level features through feature concatenation.

In the first feature fusion module, the SAM is applied to extracting the low-level features, which mainly come from the shallow convolutional layers and focus on capturing the local spatial structures of the signal. For middle-level features, a dual attention mechanism that combines the SAM and CAM is used to jointly enhance and integrate both spatial and channel information from intermediate convolutional layers. High-level features are obtained from the deep convolutional layers through the CAM, emphasizing the interdependencies between channels at a higher abstraction level. These low-, middle-, and high-level features, extracted from different network modules, are subsequently fused through a learnable convolutional fusion operation. Finally, the features from these three levels are aggregated. It is noteworthy that this approach does not merely add or stack multi-level features; instead, it uses a convolutional network for feature fusion. This feature fusion module is learnable, enabling it to better capture and integrate multi-level features. The specific parameters and details of the network are presented in

Table 1. The details of each layer in MAFNet.

Model	Input Channels	Output Channels	Kernal Size	Stride	Padding	Additional Notes
Custom_cnn	2	64	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	64	64	3	1	1	Conv1d + BatchNorm1d + ReLU
MaxPool1d	64	64	3	2	1	–
Custom_cnn	64	128	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	128	128	3	1	1	Conv1d + BatchNorm1d + ReLU
MaxPool1d	128	128	3	2	1	–
SAM	128	128	7	1	3	–
Custom_cnn	128	256	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	256	256	3	1	1	Conv1d + BatchNorm1d + ReLU
MaxPool1d	256	256	3	2	1	–
SAM	256	256	7	1	3	–
CAM	256	256	1	1	0	AdaptiveAvgPool1d + AdaptiveMaxPool1d
Custom_cnn	256	512	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	512	512	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	512	512	3	1	1	Conv1d + BatchNorm1d + ReLU
Custom_cnn	512	512	3	1	1	Conv1d + BatchNorm1d + ReLU
MaxPool1d	512	512	3	2	1	–
CAM	512	512	1	1	0	AdaptiveAvgPool1d + AdaptiveMaxPool1d
Custom_cnn (X1)	128	32	1	1	0	Conv1d + BatchNorm1d + ReLU
Custom_cnn (X2)	256	32	1	1	0	Conv1d + BatchNorm1d + ReLU
Custom_cnn (X3)	512	32	1	1	0	Conv1d + BatchNorm1d + ReLU
Concatenation	–	–	–	–	–	Concatenate outputs of X1, X2, X3

. The authors of [40] pointed out that replacing large convolutional kernels with multiple smaller ones can effectively reduce the number of parameters and computational cost without sacrificing accuracy. Therefore, this paper employs multiple convolutional kernels with a size of 3.

3.2. The Optimization of Feature Extraction Networks

In metric-based meta-learning frameworks, the main problem in the feature extraction phase is that the scarcity of training samples makes it difficult for the network to achieve effective convergence, which hinders the comprehensive extraction of the signal features. To address this issue effectively, this study integrates the concepts of transfer learning and metric learning.

Transfer learning leverages pre-training on large-scale datasets to enable the models to learn common feature representations, which are then transferred to the target task. This transfer of knowledge helps the model learn and adapt more quickly to new tasks, especially when there is limited data available.

In this method, we can initially pre-train the MAFNet feature extraction network using 70% of the sample signals from the meta-training set to extract a generalized feature representation. This pre-trained network, already equipped with extensive feature extraction capabilities, can more accurately capture and extract information from the data, thereby quickly adapting to new tasks.

During the meta-learning process, a pre-trained MAFNet feature extraction network is used as the initial network. It is fine-tuned using an N-way K-shot training strategy, along with an improved prototype network, to adapt to specific meta-learning tasks better. This strategy effectively leverages the benefits of transfer learning, both accelerating the model convergence and significantly enhancing the model’s learning capabilities and generalization performance in few-shot scenarios.

3.3. Optimization of the Metric Function

The metric function in prototype networks typically utilizes the Euclidean distance. However, the Euclidean distance only accounts for the geometric distances between data points and overlooks the distribution characteristics of the samples, potentially affecting the accuracy of the metric results. Furthermore, when optimizing the loss function, the focus is solely on the distances between query points and the class prototypes in the support set. This approach neglects the relationships both among different classes within the support set and among similar samples within the same class, resulting in a reduced discriminative ability between different modulations, which adversely affects the recognition accuracy.

To address these issues, this paper introduces a novel joint loss function that comprehensively accounts for the relationships both between the query set and the support set and within the support set itself. This approach significantly enhances the discriminative ability between different modulations and the overall prediction accuracy of the model. Not only does this method consider the geometric distances between sample points but it also takes into account the distribution among the samples, effectively addressing the shortcomings of using the Euclidean distance as the metric function.

We propose a joint metric function which is composed of two components: the support set loss and query set loss. First, we use an encoder to encode the signal, obtaining an embedding. We then represent the signal using the mean and variance for this embedding. Subsequently, for each class of signal, we calculate the mean and variance. The mean is denoted as $mea{n}_i$ for the prototype of class i, and the variance is denoted as $intr{a}_{va{r}_i}$, representing the dispersion among all signals within class i. Furthermore, we calculate the variance across all classes in the support set, termed the inter-class variance, which reflects the relationships between different classes within the support set. Further, the variance is calculated again for all classes within the support set to obtain the inter-class variance $inte{r}_{var}$, which reflects the relationships between different classes in the support set.

First, we normalize $intr{a}_{va{r}_i}$ for each class in the support set and transform it using the Sigmoid function. Subsequently, we compute the mean of the normalized variances, sum these means, and divide by the total number of classes to obtain the intra-class loss of the whole support set. For the inter-class loss, we performed the same Sigmoid normalization of the $inte{r}_{var}$ and calculated its mean as the inter-class loss for the entire support set. Finally, in order to make the modulated signals of the same class closer to each other and those of different classes farther away, we obtain the support set loss by calculating the ratio of the intra-class loss to the inter-class loss as shown in Equation (4).

$$los{s}_S={\displaystyle \frac{\frac{1}{N}{\sum }_N^{i=1}mean\left(Sigmoid\left(intr{a}_{va{r}_i}\right)\right)}{mean\left(Sigmoid\left(inte{r}_{var}\right)\right)}}.$$

(4)

For the query set loss, we utilize the Mean Squared Error (MSE) to measure the distance between a query point and its corresponding class prototype in the support set, aiming to increase the similarity between the query point and the class prototype. Specifically, as depicted in Equation (5), y represents the vector of query points derived from the encoder-processed query set, $\mu$ is the class prototype corresponding to that query point, and M is the total number of samples in the query set.

$$los{s}_Q={\displaystyle \frac{{\sum }_{j=1}^M\left(\frac{1}{n}{\sum }_{i=1}^n{(y_{ji}-\mu )}^2\right)}{M}}.$$

(5)

We define the joint loss as the weighted sum of the support set loss and the query set loss, as denoted in Equation (6). Extensive experimental validation has shown that the best results are achieved when the ratio factor for the support set loss is set to 10.

$$loss=10\times los{s}_S+los{s}_Q.$$

(6)

3.4. Meta-Testing

In the meta-testing phase, we randomly draw a large number of N-way K-shot test tasks from the meta-test set. Unlike in the meta-training phase, the query set is no longer used to tune the model parameters at this stage; it is solely for evaluating the model’s performance. For each test task, the trained model is utilized to extract features from both the support and query sets. We then predict the modulation mode of the signals in the query set by calculating the Mean Squared Error (MSE) distance between the query points and the support set prototypes.

4. Experiments and Analysis

4.1. The Dataset and Experimental Details

In order to validate the effectiveness of RMML, we have selected the RadioML 2016.10a dataset [41] for simulation validation. This dataset contains 11 different modulation modes, with detailed information as shown in

Table 2. Experimental dataset.

Parameter	Assignment
Modulation types	8PSK, AM-DSB, AM-SSB, BPSK, CPFSK, GFSK, PAM4, 16QAM, 64QAM, QPSK, WBFM (11 classes)
Train set	Randomly select 6 types of modulation from all modulation types (6 classes)
Test set	5 types remaining besides the train set (5 classes)
SNR	−18∼18 dB
Support set	N-way K-shot (N = 3, 5; K = 1, 5, 10, 15)
Query set	100 samples

. The signal-to-noise ratio ranges from −20 to 18 dB, with intervals of 2 dB, and each modulation method includes 1000 samples. We divided all of the modulation modes into a meta-training set and a meta-test set, randomly selecting 6 modulations to form the meta-training set and the remaining 5 modulations to form the meta-test set. It is important to note that the modulation modes in the meta-training set and the meta-test set do not overlap.

In the pre-training phase, we optimized the MAFNet network parameters using Adam, with an initial learning rate set to 0.01, over 30 epochs of training. During the meta-training phase, we conducted training across 1000 episodes. In each episode, we randomly selected N-way K-shot recognition tasks from the meta-training set for training, with the specific settings of N and K detailed in Table 1 and Table 2. We used the pre-trained model as the initial model and continued optimization using the Adam optimizer, maintaining the initial learning rate at 0.01 and dynamically adjusting it based on the loss function. In the meta-testing phase, to eliminate the randomness of a single test experiment and ensure the reliability and stability of the evaluation results, we randomly selected 200 test tasks and calculated their average recognition accuracy and standard deviation (95% confidence) as the final evaluation metric for this method. Similar to the meta-training phase, in each test experiment, we also randomly selected N-way K-shot tasks from the meta-test set for testing.

All experiments were performed on a workstation equipped with an NVIDIA RTX 3090 GPU (24 GB memory), an Intel Xeon W-2245 CPU, and 128 GB of RAM. The pre-training phase took approximately 1.5 h for 30 epochs, while in the 5-way 5-shot setting, meta-training over 1000 episodes required about 0.5 h. Meta-testing under each configuration was completed in less than 1 min.

4.2. Analyzing the Performance of RMML Across Various Sample Sizes

In order to assess the impact of varying sample sizes on the recognition performance of RMML under consistent conditions, we conducted experiments focusing on recognition tasks for 3- and 5-class modulated signals, namely 3/5-way K-shot tasks. We analyzed various aspects of the recognition performance when the number of samples (K) in each support set class was set to 1, 5, 10, and 15, respectively. Figure 5 and Figure 6 illustrate how the recognition accuracy varies with changes in the signal-to-noise ratio. At a signal-to-noise ratio of 10 dB, a 3-way 1-shot test task achieved a recognition accuracy of 83.2%, further demonstrating the viability of RMML in few-shot scenarios.

When the value of K is small, increasing the sample size significantly enhances the recognition accuracy. However, when $\mathrm{K}⩾5$, further increases in the sample size do not significantly improve the recognition accuracy. This result suggests that RMML is more suitable for solving the problem of modulation recognition in extreme cases where only a small number of labeled signal samples are available.

4.3. The Ablation Experiment

4.3.1. The Improvement Ablation Experiment

To enhance the modulation recognition accuracy of the few-shot recognition model further when dealing with only a few labeled samples, this paper optimizes the metric function of the prototype network and introduces a migration pre-training module. To validate the effectiveness of these improvements, an ablation experiment was conducted using the dataset in Table 2, with the average of 200 test recognition accuracies chosen as the measure of the performance. The experimental results, presented in Figure 7, demonstrate that each modification made to the prototype network significantly boosts the model’s recognition capabilities.

4.3.2. Comparative Ablation Experiments

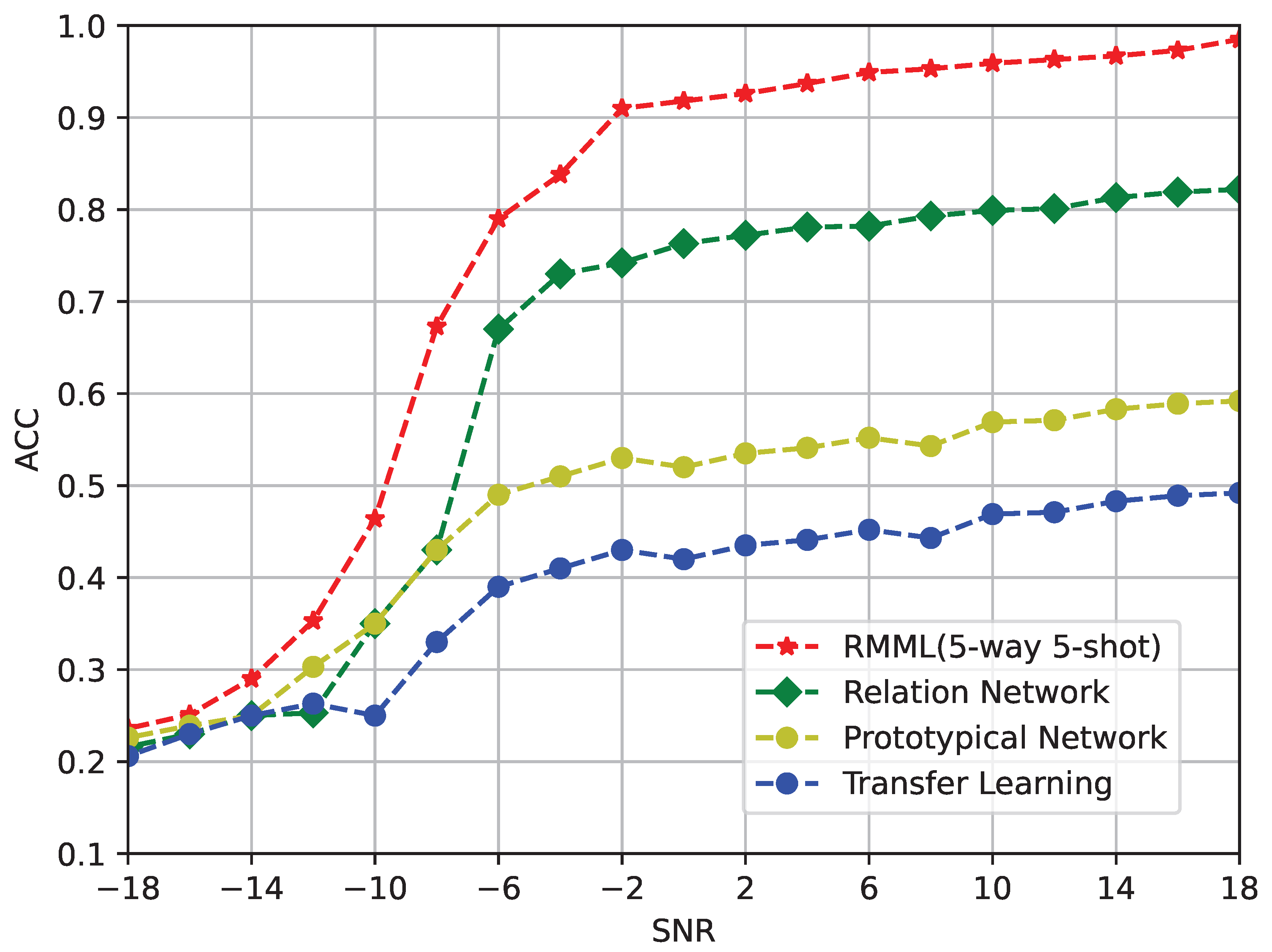
To demonstrate the performance advantage of RMML over other small-sample modulation recognition methods, this section includes comparative experiments with three approaches: a prototypical network, relation network, and transfer learning. To ensure fairness in these comparisons, all experiments employed the experimental data and the MAFNet feature extraction network structure, as shown in Table 2. The variation in the average recognition accuracy of the modulation methods with the signal-to-noise ratio for a 5-way 5-shot test task is depicted in Figure 8.

As shown in the figure, the method used in this study achieved the highest recognition accuracy. The recognition performance of the relational network is superior compared to that of the other two methods. This method also employs a metric-based meta-learning strategy that utilizes a neural network instead of the traditional metric function. However, this modification leads to an increase in the number of parameters and the complexity of neural network training.

The approach based on transfer learning exhibits the lowest recognition accuracy, primarily because when there are only a very small number of samples in the target domain, the model’s insufficient generalization capability can lead to severe overfitting during the testing phase, significantly impairing the recognition performance. This observation further corroborates the point made in the introduction that transfer learning methods are unable to effectively address recognition challenges with only a few labeled samples. The recognition accuracy of the prototypical network is also relatively low due to two main factors, the shortcomings of its metric function and the limited number of samples, which results in insufficient feature extraction by the network, thereby reducing its recognition accuracy.

4.4. A Comparative Analysis of Different Few-Shot Modulation Recognition Methods

To further validate the performance advantages of RMML, this experiment compares it with four state-of-the-art small-sample modulation recognition methods. The selected methods for comparison include an Attention-Based Modulation Classification Relational Network (AMCRN) [42], Feature-Transformation-Based Few-Shot Modulation Recognition (FTFMR) [43], a Hybrid Prototypical Network (HPN) [17], and Model-Agnostic Meta-Learning (MAML) [25]. All of the methods utilized the dataset shown in Table 2 to ensure consistency in the experimental conditions. The experiments were conducted under 5-way 5-shot conditions, and the results on the average accuracy of modulation mode recognition with various the signal-to-noise ratio are depicted in Figure 9. The shaded region in the figure denotes the error obtained by repeatedly partitioning the training and test sets, with the upper and lower bounds corresponding to the maximum and minimum accuracies, respectively. The simulation results demonstrate that RMML achieves a higher recognition accuracy than the other comparative methods.

The AMCRN is a method that achieves efficient modulation mode classification by constructing a relational network, maintaining a high classification accuracy even at low signal-to-noise ratios. FTFMR combines transfer learning and MAML, achieving efficient modulation mode recognition under small-sample conditions by leveraging the existing knowledge of large-scale datasets. The HPN combines the advantages of prototype networks and other machine learning models, also achieving efficient modulation mode recognition under small-sample conditions. MAML is a model-independent meta-learning approach that enables quick adaptation to new tasks by sharing the model parameters across different tasks, making it suitable for small-sample learning scenarios.

The experimental results show that the average accuracy of modulation mode recognition with RMML is higher than that with the AMCRN, FTFMR, HPN, and MAML under various signal-to-noise ratio conditions. This further validates the performance advantage of RMML in small-sample modulation mode recognition and proves its feasibility for practical applications.

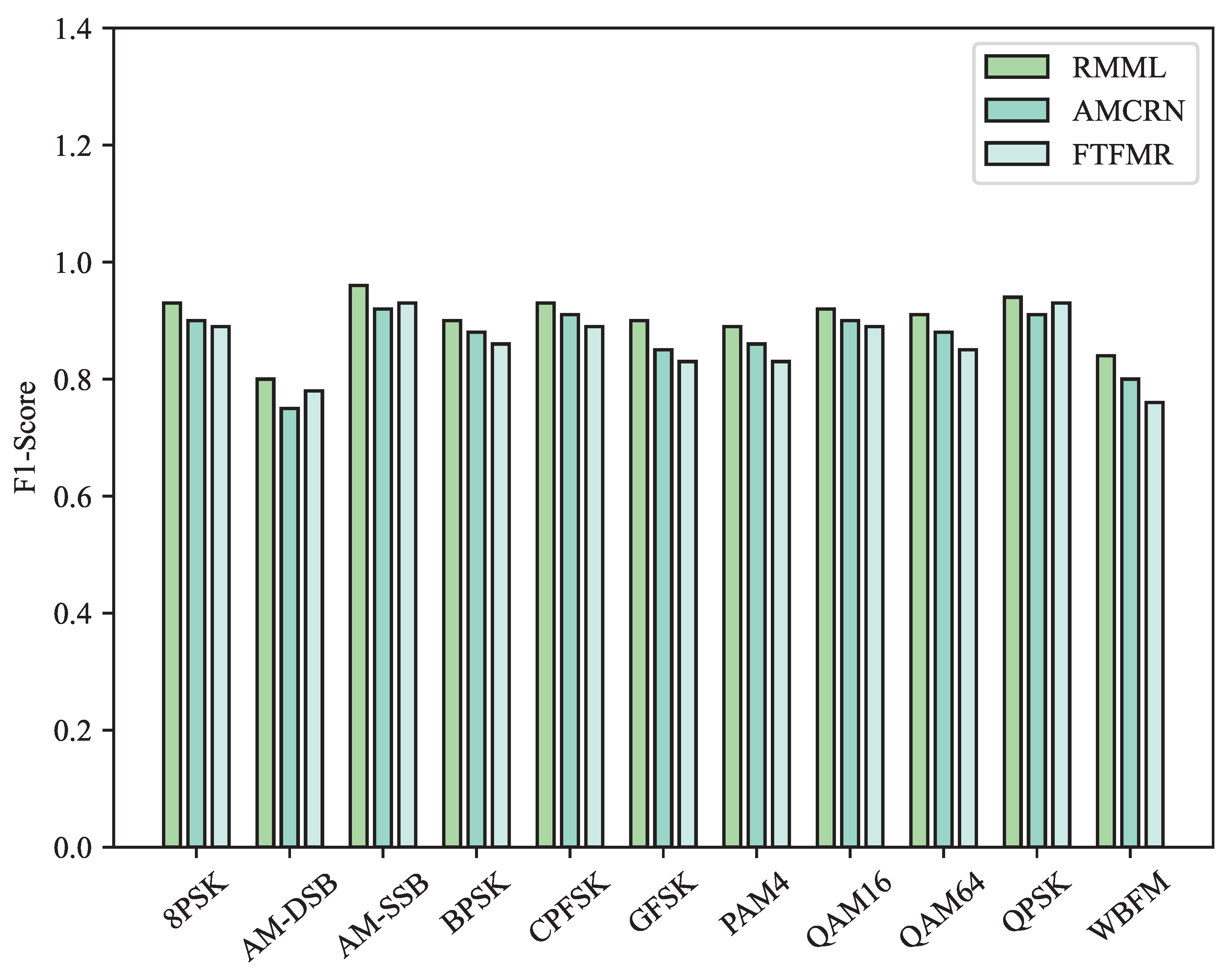
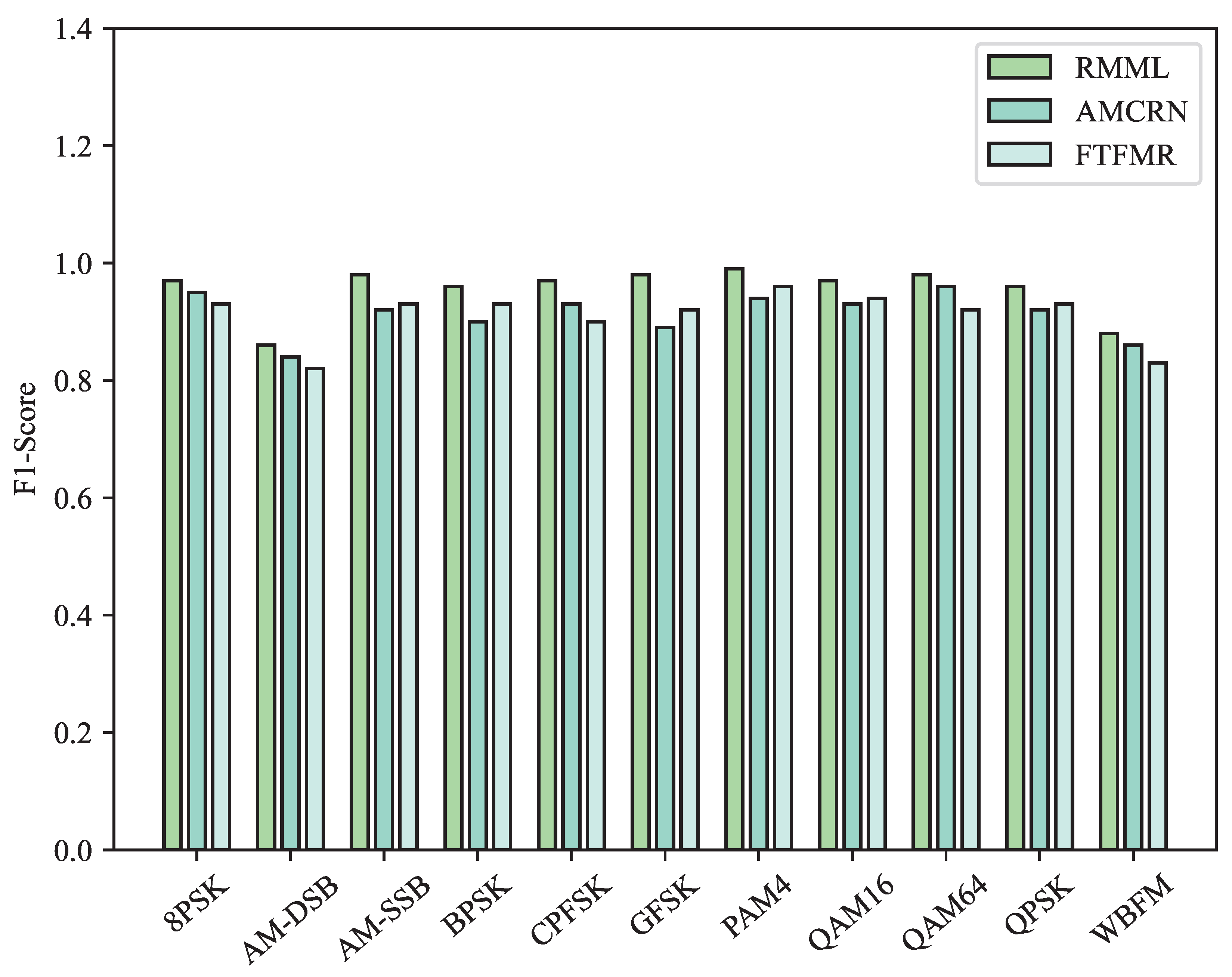
Figure 10 and Figure 11 display the F1-scores of the RMML, AMCRN, and FTFMR methods for 11 types of modulated signals in the meta-test set under SNR conditions of 0 dB and 10 dB, respectively. The figures clearly show that the RMML method proposed in this study achieves superior F1-scores in recognizing the 11 modulated signals compared to those of the other two methods under both 0 dB and 10 dB SNR conditions.

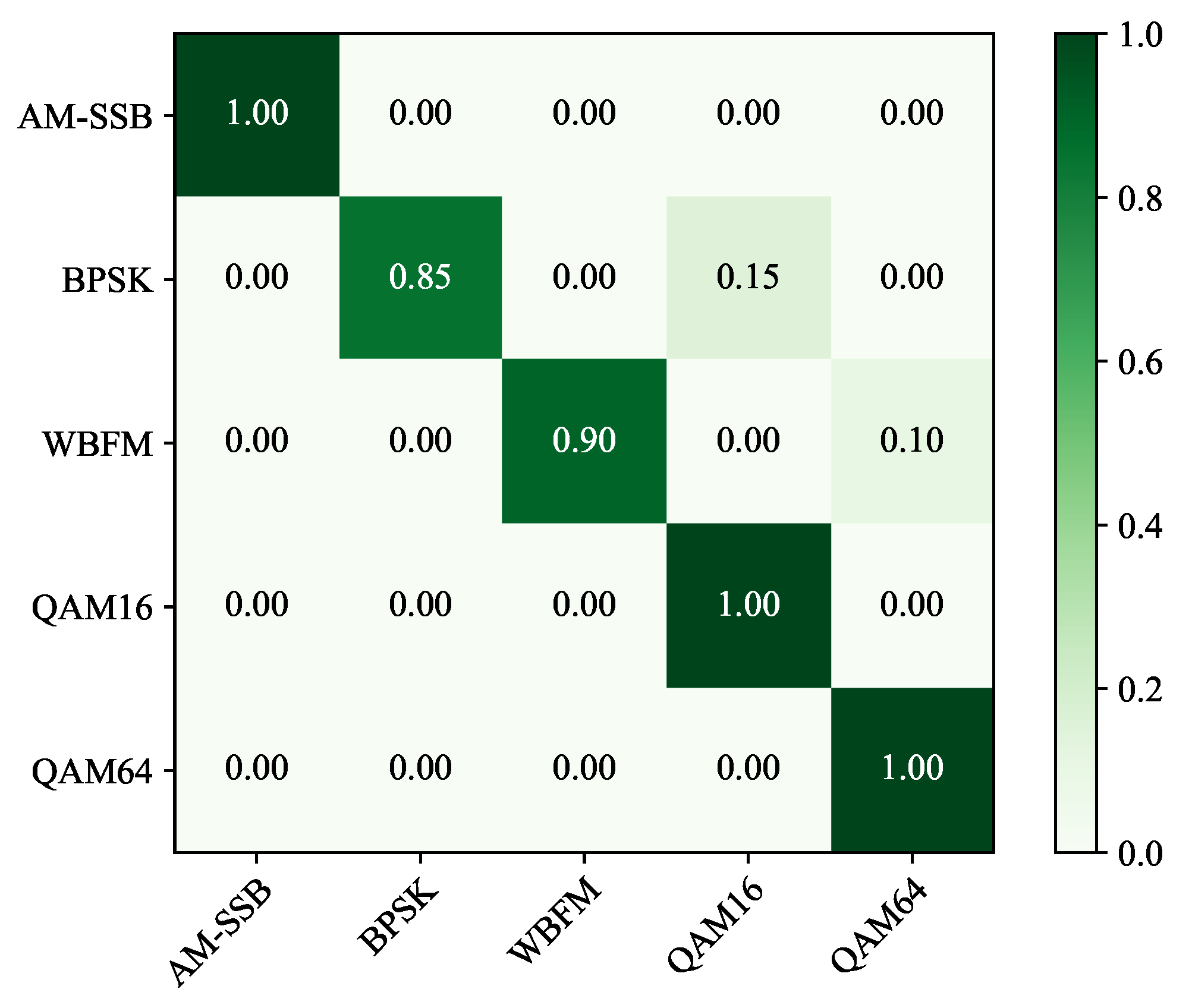
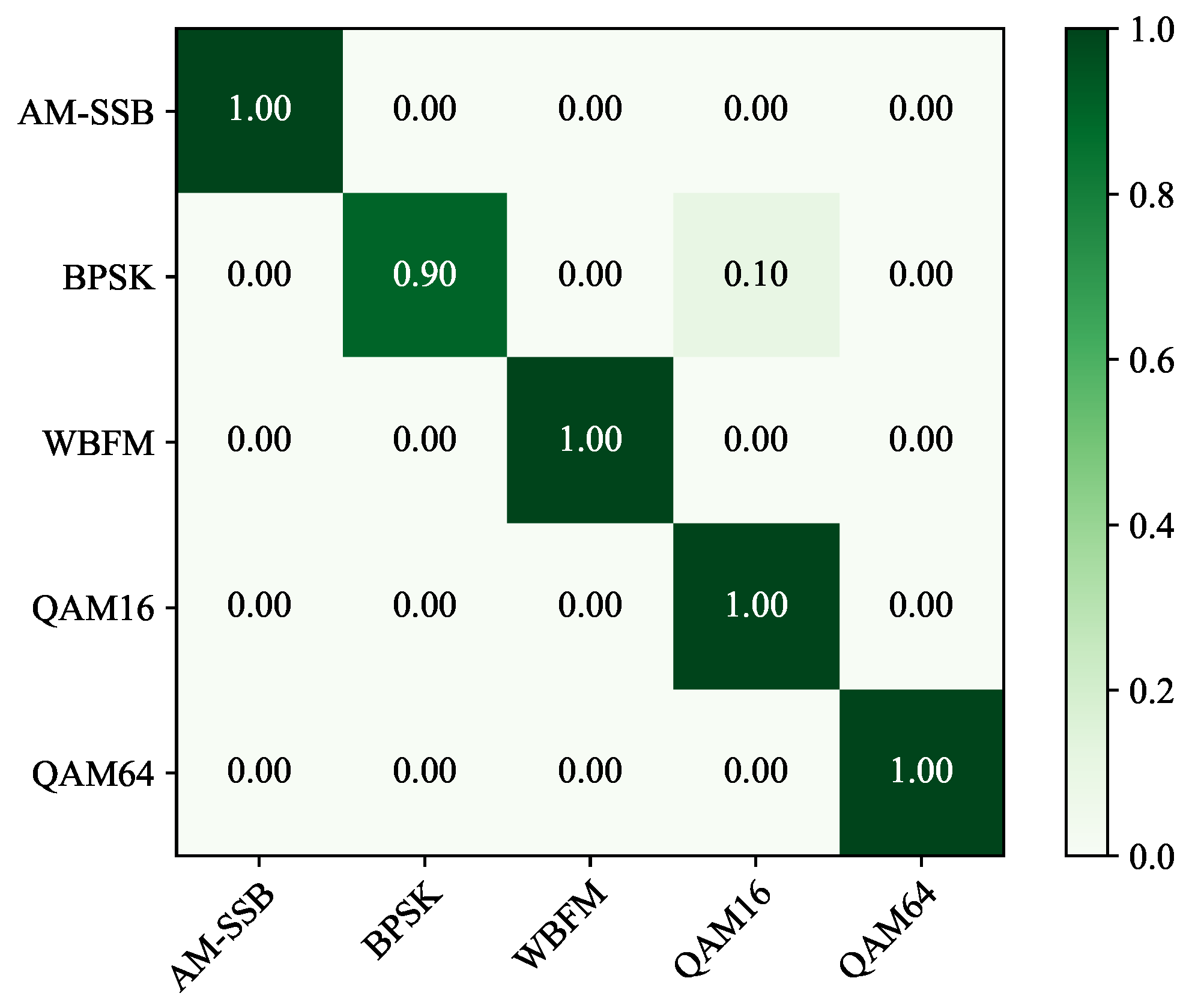
In the field of modulation mode identification, distinguishing between high-order modulated signals (e.g., 64QAM) and low-order signals (e.g., 16QAM) has been a continual challenge [8]. To investigate RMML’s discernment, these two types of modulations, AM-SSB, BPSK, WBFM, 16QAM, and 64QAM, were selected as the meta-test set, while the remaining six modulation types were used as the meta-training set. The experiment was conducted under two different SNR levels (0 dB and 10 dB) in a 5-way 5-shot scenario. The experimental results are depicted in the confusion matrix shown in Figure 12 and Figure 13.

From the experimental results depicted in Figure 12 and Figure 13, it is evident that the method described in this paper demonstrates a superior performance in distinguishing between high-order and low-order modulated signals, without the anticipated significant signal confusion. This suggests that our method possesses notable advantages over the conventional modulation mode identification methods in addressing the challenge of differentiating between high-order and low-order modulated signals.

In order to validate the generalization capability of RMML further, we intentionally configured the meta-training set to include only digital modulation (digital modulation is a modulation method that transmits information through discrete changes in amplitude, phase, or frequency) methods, specifically including 8PSK, BPSK, CPFSK, GFSK, 16QAM, and QPSK. The meta-testing set, on the other hand, comprised a combination of analog (analog modulation refers to continuous-wave modulation schemes such as wide-band frequency modulation and amplitude modulation variants) and digital modulations, specifically for WBFM, 64QAM, AM-DSB, PAM4, and AM-SSB. As clearly demonstrated by the confusion matrices shown in Figure 14 and Figure 15, this particular setup did not adversely affect the recognition performance of RMML.

5. Conclusions

This paper proposes RMML, a few-shot modulation recognition framework that integrates transfer learning with metric-based meta-learning, and explicitly characterizes intra-class compactness and inter-class separability through a joint loss function. The MAFNet encoder is first pre-trained via transfer learning and then fine-tuned with the proposed metric extension, which effectively alleviates the problem of insufficient feature extraction under few-shot conditions. On the RadioML2016.10a dataset within the SNR range of −18 dB to 18 dB, RMML achieves consistent advantages over the representative baseline methods. The simulation results show that under the 5-way 5-shot setting with an SNR = 10 dB, RMML attains an average accuracy of approximately 96.5%, surpassing the best comparative model by 5.13% and outperforming the existing baselines, thereby effectively addressing the challenges of signal modulation recognition in few-shot scenarios. In addition, the method demonstrates a strong capability to distinguish high-order from low-order modulations and also exhibits advantages in terms of its generalization performance.

The main contribution of RMML lies in effectively coupling transfer learning with a variance-sensitive metric that accounts for the intra-class and inter-class relationships while explicitly separating the corresponding loss terms. This design brings substantial improvements under few-shot constraints. Furthermore, during inference, RMML only requires prototype construction and distance computation, resulting in a low overhead. Although pre-training and episode-based meta-learning incur additional training costs, compared with more parameter-intensive metric models (such as relation networks), RMML offers a more favorable accuracy–efficiency trade-off. This makes it well suited to scenarios with scarce labeled data that require rapid adaptation and deployment.

As the present study is based on a single public dataset and simulated channels, future work will focus on validating the robustness of RMML against domain shifts using real over-the-air data and broader datasets. Extensions to more diverse datasets and real-world communication channels, as well as the exploration of adaptive weighting or alternative metrics, will optimize the accuracy–efficiency balance further. Overall, RMML provides a novel and practically valuable solution for few-shot modulation recognition while also pointing to future directions for enhancing the methodological rigor and engineering applicability.