Swallow Search Algorithm (SWSO): A Swarm Intelligence Optimization Approach Inspired by Swallow Bird Behavior
Abstract
1. Introduction
1.1. Metaheuristic Algorithms Classifications
- Based on search strategy: Metaheuristic can be classified into single-solution, which focuses on iteratively improving a single candidate solution. For example, Simulated Annealing (SA) [7], Tabu Search (TS) [5], or population-based [8] methods work with a group of solutions simultaneously, promoting diversity and exploration. For example, Genetic Algorithms (GAs) [9], Particle Swarm Optimization (PSO) [10], Ant Colony Optimization (ACO) [11], and Differential Evolution (DE) [2].
- Based on the nature of inspiration: Metaheuristics can be classified into three types: bio-inspired algorithms, physics-based algorithms [12], and social and cultural algorithms. The first type mimics the way living organisms solve their problems in their environments, such as how birds flock, ants find food, or how evolution drives survival through natural selection. By imitating these behaviors, bio-inspired algorithms can solve complex optimization problems where traditional algorithms might struggle. There are several examples of this type of optimization, such as evolutionary-based [13] GA, swarm-based PSO [14], ACO, artificial bee colony (ABC) [15], and behavioral-based Cuckoo Search [16] and Firefly Algorithm [17]. The second type is inspired by physical laws and phenomena. For example, Simulated Annealing (thermodynamics) [18] and the gravitational search algorithm (Newtonian gravity) [19,20]. The third one is based on social behaviors or human-inspired processes, such as Harmony Search [21] (musical improvisation) and Teaching–Learning-Based Optimization (classroom dynamics) [22].
- Based on trajectory control: Metaheuristics can be classified as deterministic, stochastic, or a mixture or hybrid of both. Deterministic algorithms follow a rigorous procedure with repeatable design variables and functions. For example, hill-climbing. On the other hand, stochastic algorithms always have some randomness to explore the search space and avoid local optima (most metaheuristics fall into this category) [3].
- Based on single or multiple solutions: Metaheuristics can be classified as trajectory-based or population-based [22]. Trajectory-based metaheuristics focus on finding a single solution and use iterative improvement to refine that solution. For example, simulated annealing [23]. Population-based metaheuristics focus on finding multiple solutions and use a population of solutions to explore the search space. For example, the genetic algorithms (GAs), Ant Colony Optimization (ACO), and particle swarm optimization (PSO) [24].
1.2. Optimization Problems Classification
1.3. Challenges
1.4. Contribution
- The new Swallow Search optimization algorithm (SWSO) serves as a novel metaheuristic that finds inspiration from swallow migration patterns.
- The proposed algorithm has been evaluated using a range of benchmark functions, including unimodal, multimodal, and fixed-dimension functions, as well as the functions of the CEC2019 benchmark.
- A comparison of the (SWSO) algorithm’s performance has been made with different algorithms, such as MFO, PSO, GSA, BA, FPA, SMS, FA, GA, DA, WOA, BOA, COA, FDO, FOX, and AFO.
- The SWSO algorithm has been applied to two constrained engineering design problems, and its performance has been compared to the more recent outcomes found in the literature.
2. Literature Review
2.1. Swarm Intelligence and Optimization Algorithms
2.2. Metaheuristic and Hybrid Algorithms
2.3. Bio-Inspired and Hybrid Optimization Models
3. Swallow Search Optimization Algorithm (SWSO)
3.1. Inspiration
3.2. Biological Behavior of Swallows
- Foraging: Swallows forage in groups, dynamically adjusting their flight patterns to locate and capture prey efficiently.
- Migration: Swallows undertake long migratory journeys, navigating complex environments and adapting to changing conditions.
- Social Interaction: Swallows communicate and coordinate within flocks, sharing information about food sources and dangers.
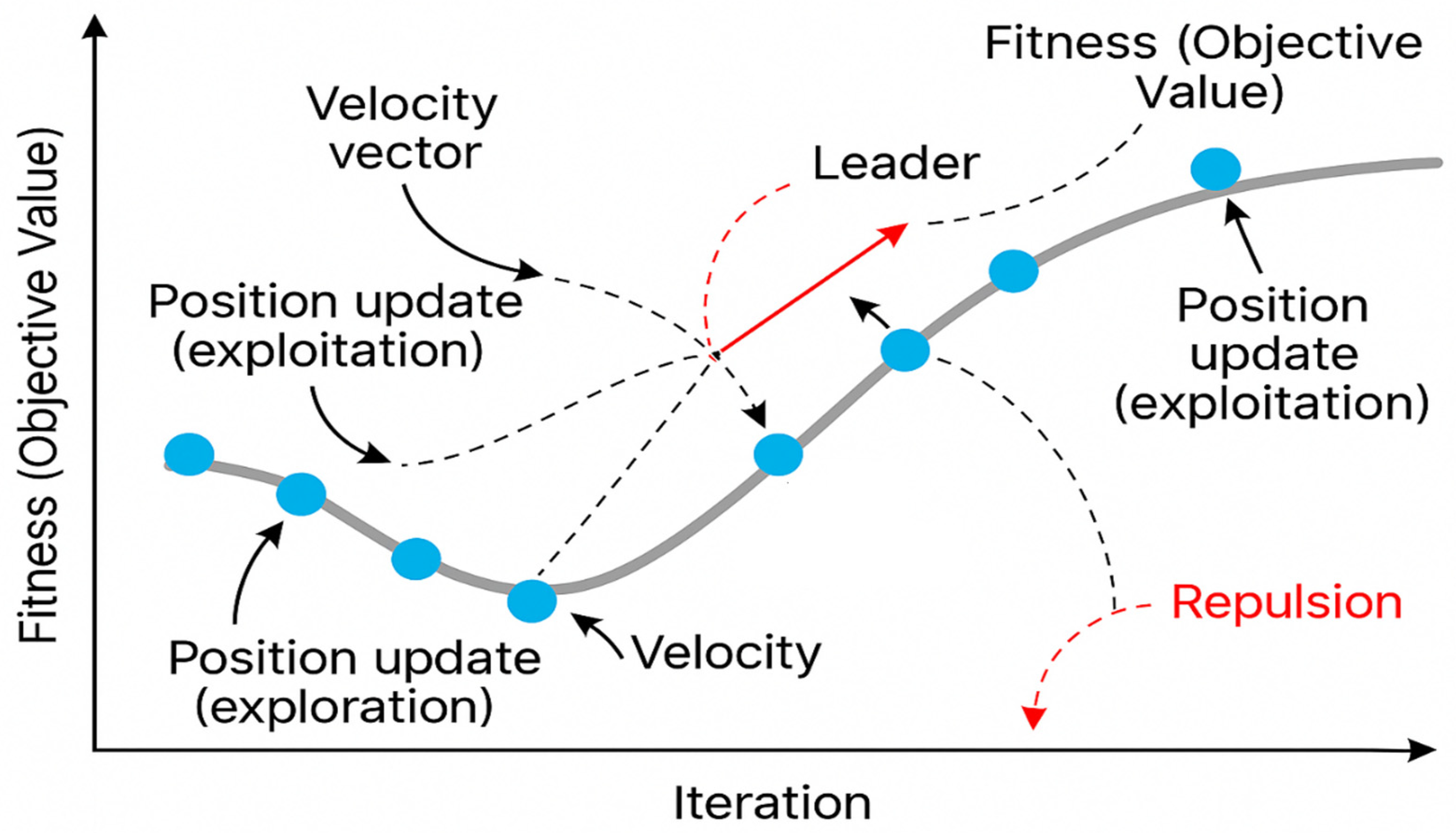
- Fly in a V-shape flock: This method allows swallows to cover the greatest possible distance by taking advantage of the total air flow formed by the entire flock, thus reducing the effort expended during flight. Figure 3 shows the V-shaped formation during flight. This means that when each bird flaps its wings in the air, it generates energy that helps it fly and also helps the bird following it, which enables all the birds in the flock to cooperate in the flight process.
- Power saving: Studies have shown that the V-shape formation in flight enables the entire flock to cover a distance of 71% more than if the bird flew alone. Not only that, but researchers have found that the birds alternate their places in the flock in a strange way. When one of the birds feels tired, it returns back so that it can take advantage of the air current resulting from the flock as a whole, thus saving power by reducing the effort expended to the maximum degree, then after resting a while, it returns to its place again, making way for another bird to rest.
4. Methodology and Mathematical Model
4.1. Swallow Foraging Behavior
- Initialization
- Exploration (with probability 1 − α)
- is a decaying exploration factor, encouraging convergence over time.
- is a random vector.
4.2. Swallow Migration Behavior
- Fitness Evaluation
- Position Update Formula
- is the position of the leader.
- is a small Gaussian perturbation (for local search).
- Velocity Update Formula
- The term retains a portion of the previous velocity, which controls the momentum, allows for smoother motion in the search space, and helps the agent to keep exploring in a similar direction. The typical range for the parameter w falls between 0 and 1, while its common use value amounts to 0.7.
- The term is the cognitive component which reflects the personal experience of the agent and pulls the agent toward its own historically best position. is the cognitive learning coefficient, and is a random value in [0, 1], which adds stochasticity. In this case, is the personal best position found by particle iii on its search history and it augments the particle in exploiting parts of the search space that gave good fitness values previously.
- The term is the social component that encourages social learning by attracting the agent to the current leader’s position. is the social learning coefficient, and is another random value in [0, 1].
4.3. Social Interaction and Information Sharing
- Leader Selection
- Energy Dynamics
| Algorithm 1. Pseudo code of the SWSO algorithm. |
|
5. Validation and Comparison
5.1. Benchmark Functions
- Unimodal functions: The single global optimum of unimodal functions, as shown in Figure 5, provides an excellent platform for testing both convergence efficiency and exploitation capabilities of algorithms.
- Multimodal functions: Multimodal functions serve as crucial evaluation tools to test Swallow Search Optimization Algorithm’s (SWSO) ability to prevent premature convergence while escaping local minima during evaluations. The search space complexity is measured through these functions which contain multiple local optima to test SWSO’s exploration capabilities.
- Fixed-dimension multimodal functions: Multimodal functions with fixed dimensions differ from those that provide scalable dimensional capabilities. The test functions with fixed dimensions present predetermined dimensions that limit their ability to evaluate problems of different sizes. Although using the multimodal functions provides adjustable design variable counts, their landscape structures still differ from those provided by the multimodal with fixed dimensions [74].
- The composite functions: The complexity of composite test functions increases because they use transformations including random shifts of the global optimum along with search space rotations and boundary-based placement of optima. Composite functions provide excellent benchmarking capabilities for SWSO under dynamic and deceptive conditions because they include features which enhance robustness and adaptability across various optimization scenarios [30,73]. Table 3, Table 4 and Table 5 describe the unimodal, multimodal, and fixed-dimension multimodal, respectively. These tables give a detailed overview of the equations, problem dimensions , upper and lower bands in the boundaries, and minimum goal values of each function ( [75].
| Function Name | Function | Range | ||
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | 0 | |
| Schwefel 2.22 | 30 | [−10, 10] | 0 | |
| Schwefel 1.2 | 30 | [−100, 100] | 0 | |
| Schwefel 2.21 | 30 | [−100, 100] | 0 | |
| Rosenbrock | 30 | [−30, 30] | 0 | |
| Step | 30 | [−100, 100] | 0 | |
| Quartic | 30 | [−1.28, 1.28] | 0 |
| Function Name | Function | Range | ||
|---|---|---|---|---|
| Schwefel 2.26 | 30 | [−500, 500] | −418.9829 | |
| Shifted Rastrigin | 30 | [−5.12, 5.12] | 0 | |
| Ackley | 30 | [−32, 32] | 0 | |
| Griewangk | 30 | [−600, 600] | 0 | |
| Penalized function one | 30 | [−50, 50] | 0 | |
| Penalized function two | 30 | [−50, 50] | 0 |
| Function Name | Function | Range | ||
|---|---|---|---|---|
| De Jong Function | 2 | [−65, 65] | 1 | |
| Kowalik’s Function | 4 | [−5, 5] | 0.00030 | |
| Six-Hump Camel | 2 | [−5, 5] | −1.0316 | |
| Branin Function | 2 | [−5, 5] | 0.397887 | |
| Goldstein-Price Function | 2 | [−2, 2] | 3 | |
| Hartmann 3-Dimensional Function | 3 | [0, 1] | −3.86278 | |
| Hartmann 6-Dimensional Function | 6 | [0, 1] | −3.32237 | |
| Shekel Function | 4 | [0, 10] | −10.1532 | |
| Shekel Function | 4 | [0, 10] | −10.4028 | |
| Shekel Function | 4 | [0, 10] | −10.5364 |
5.2. Comparison with Other Algorithms
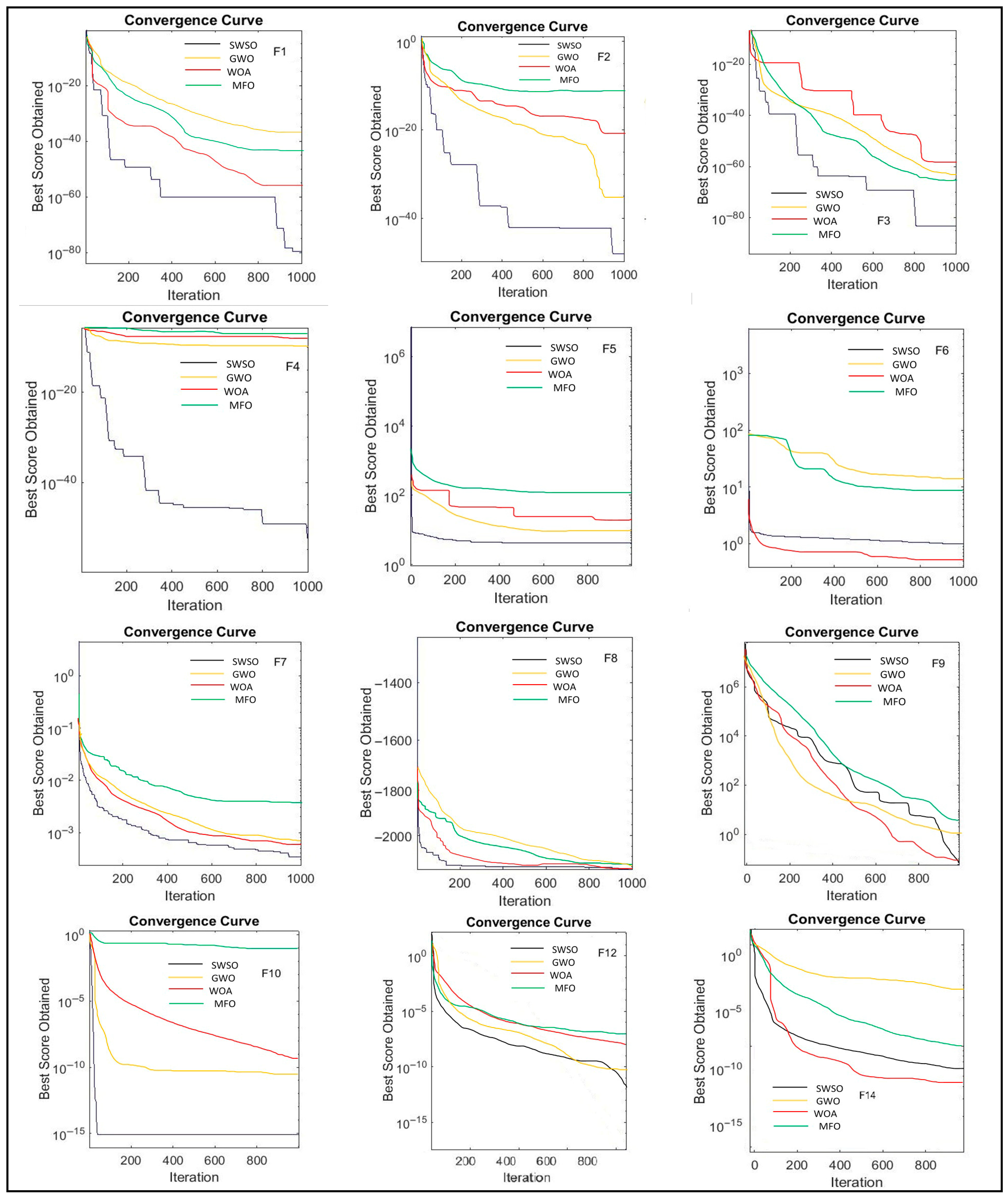
5.2.1. The Unimodal Benchmark Test Functions (F1–F7): Exploitation Capability
5.2.2. The Multimodal Benchmark Test Functions (F8–F13): Exploration Capability
5.2.3. The Fixed-Dimension Benchmark Test Functions (F14–F19): Balanced Optimization
5.2.4. CEC2019 Benchmark Test Functions (CEC01–CEC10): Surrogate Optimization in the Real World [25]
5.3. Result Analysis and Discussion
5.3.1. Unimodal Functions (F1–F7)
5.3.2. Multimodal Functions (F8–F13)
5.3.3. Fixed Dimension (F14–F19)
5.3.4. The CEC2019 Benchmark Test Functions (CEC01–CEC10)
6. Case Studies (Engineering Optimization Problems)
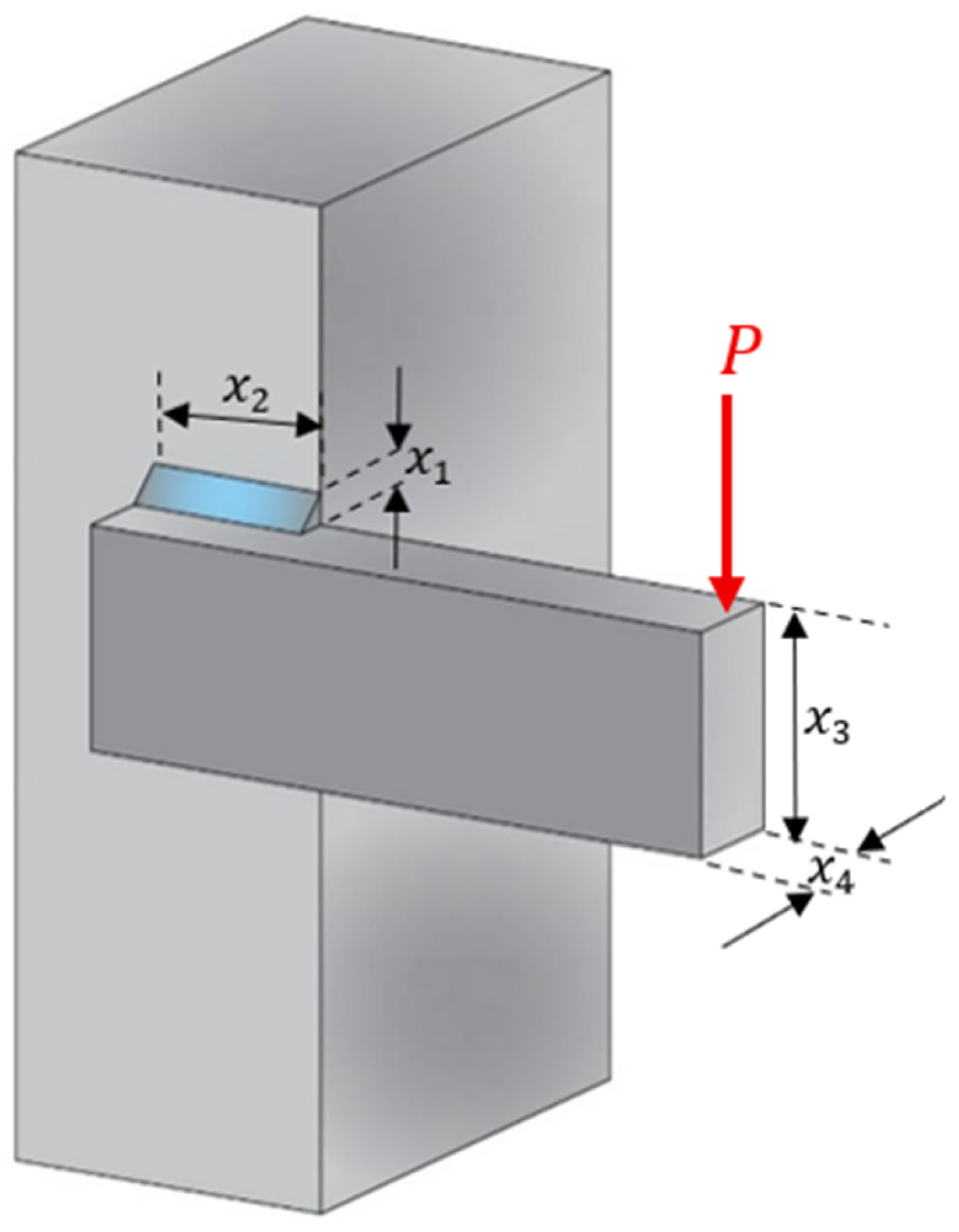
6.1. The Welded Beam Design Problem
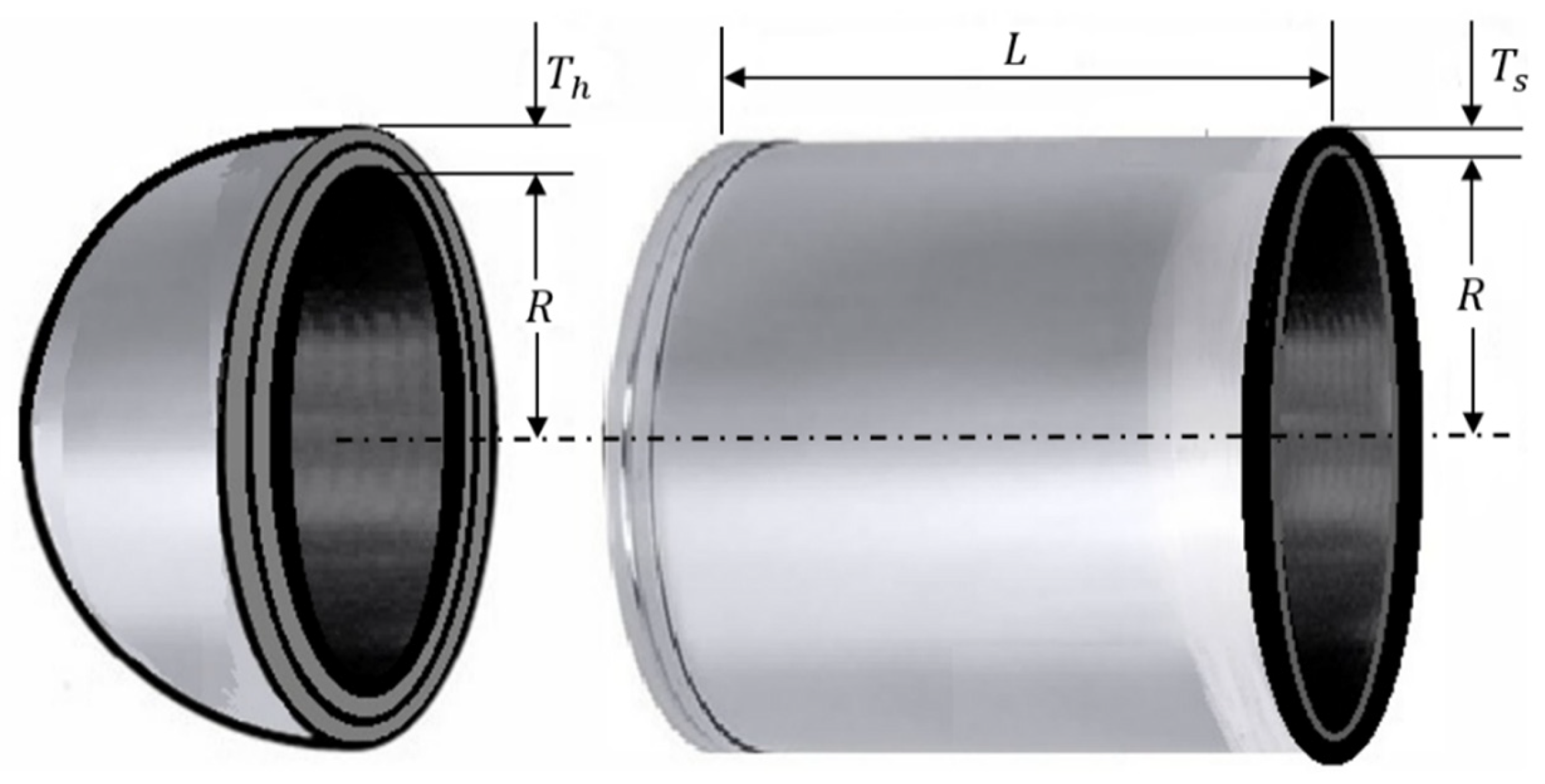
6.2. Pressure Vessel Design Problem
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Result Analysis and Discussion
Appendix A.1.1. Unimodal Functions (F1–F7)
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | WOA | FEP | ACO | VGWO | INFO | SCA | GWO | RIME |
| F1 | 1 | 3 | 5 | 7 | 7 | 2 | 8 | 4 | 6 |
| F2 | 1 | 3 | 6 | 5 | 7 | 2 | 8 | 4 | 9 |
| F3 | 1 | 3 | 7 | 6 | 5 | 2 | 9 | 4 | 8 |
| F4 | 1 | 4 | 5 | 8 | 9 | 2 | 7 | 3 | 6 |
| F5 | 1 | 5 | 2 | 7 | 3 | 4 | 9 | 6 | 8 |
| F6 | 5 | 7 | 1 | 3 | 4 | 2 | 9 | 6 | 8 |
| F7 | 1 | 2 | 8 | 6 | 5 | 3 | 9 | 4 | 7 |
| Average Rank | 1.57 | 3.85 | 4.85 | 6.00 | 5.71 | 2.42 | 8.42 | 4.42 | 6.28 |
| (b) | |||||||||
| Test Function | SWSO | WOA | FEP | ACO | VGWO | INFO | SCA | GWO | RIME |
| F1 | 1 | 3 | 5 | 7 | 6 | 2 | 9 | 4 | 8 |
| F2 | 1 | 3 | 5 | 7 | 6 | 2 | 8 | 4 | 9 |
| F3 | 1 | 3 | 5 | 7 | 6 | 2 | 9 | 4 | 8 |
| F4 | 1 | 4 | 5 | 8 | 9 | 2 | 7 | 3 | 6 |
| F5 | 4 | 2 | 5 | 7 | 6 | 1 | 9 | 3 | 8 |
| F6 | 3 | 4 | 1 | 5 | 7 | 2 | 8 | 3 | 6 |
| F7 | 1 | 3 | 8 | 7 | 6 | 2 | 9 | 4 | 5 |
| Average Rank | 1.71 | 3.14 | 4.85 | 6.85 | 6.57 | 1.85 | 8.42 | 3.57 | 7.14 |
| (c) | |||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | ||
| Average Ranks | 11 | ||||||||
| F1 | SWSO | INFO | WOA | GWO | FEP | 1 | |||
| F2 | SWSO | INFO | WOA | GWO | IACO | 1 | |||
| F3 | SWSO | INFO | WOA | GWO | VGWO | 1 | |||
| F4 | SWSO | INFO | GWO | WOA | FEP | 1 | |||
| F5 | SWSO | FEP | VGWO | INFO | WOA | 1 | |||
| F6 | FEP | INFO | IACO | VGWO | SWSO | 5 | |||
| F7 | SWSO | WOA | INFO | GWO | VGWO | 1 | |||
| Standard Deviation Ranks | 12 | ||||||||
| F1 | SWSO | INFO | WOA | GWO | FEP | 1 | |||
| F2 | SWSO | INFO | WOA | GWO | FEP | 1 | |||
| F3 | SWSO | INFO | WOA | GWO | FEP | 1 | |||
| F4 | SWSO | INFO | GWO | WOA | FEP | 1 | |||
| F5 | INFO | WOA | GWO | SWSO | FEP | 4 | |||
| F6 | FEP | INFO | SWSO | WOA | IACO | 3 | |||
| F7 | SWSO | INFO | WOA | GWO | RIME | 1 | |||
| |||||||||
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | IFOX |
| F1 | 1 | 3 | 4 | 2 | 9 | 7 | 6 | 8 | 5 |
| F2 | 1 | 2 | 5 | 9 | 7 | 8 | 3 | 7 | 4 |
| F3 | 1 | 5 | 3 | 6 | 9 | 4 | 8 | 7 | 2 |
| F4 | 1 | 8 | 2 | 3 | 8 | 5 | 6 | 4 | 9 |
| F5 | 1 | 5 | 4 | 3 | 7 | 6 | 9 | 8 | 5 |
| F6 | 5 | 3 | 2 | 1 | 9 | 6 | 8 | 7 | 4 |
| F7 | 1 | 5 | 6 | 4 | 9 | 7 | 3 | 8 | 2 |
| Average Rank | 1.57 | 4.42 | 3.71 | 3.57 | 8.14 | 5.85 | 6.28 | 7.28 | 4.14 |
| (b) | |||||||||
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | IFOX |
| F1 | 1 | 3 | 4 | 2 | 9 | 7 | 6 | 8 | 5 |
| F2 | 1 | 2 | 5 | 6 | 9 | 8 | 3 | 7 | 4 |
| F3 | 2 | 6 | 4 | 7 | 9 | 5 | 1 | 8 | 3 |
| F4 | 1 | 7 | 2 | 3 | 8 | 5 | 6 | 4 | 9 |
| F5 | 1 | 4 | 2 | 3 | 9 | 6 | 7 | 8 | 5 |
| F6 | 4 | 3 | 2 | 1 | 9 | 6 | 8 | 7 | 5 |
| F7 | 1 | 5 | 4 | 3 | 9 | 7 | 2 | 8 | 6 |
| Average Rank | 1.57 | 4.28 | 3.28 | 3.57 | 8.85 | 6.28 | 4.71 | 7.14 | 5.28 |
| (c) | |||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | ||
| Average Ranks | 11 | ||||||||
| F1 | SWSO | GSA | MFO | PSO | SMS | 1 | |||
| F2 | SWSO | MFO | SMS | IFOX | PSO | 1 | |||
| F3 | SWSO | IFOX | PSO | FPA | MFO | 1 | |||
| F4 | SWSO | PSO | GSA | FPA | FA | 1 | |||
| F5 | SWSO | IFOX | GSA | PSO | MFO | 1 | |||
| F6 | GSA | PSO | MFO | IFOX | SWSO | 5 | |||
| F7 | SWSO | IFOX | SMS | GSA | MFO | 1 | |||
| Standard Deviation Ranks | 11 | ||||||||
| F1 | SWSO | GSA | MFO | PSO | IFOX | 1 | |||
| F2 | SWSO | MFO | SMS | IFOX | PSO | 1 | |||
| F3 | SMS | SWSO | IFOX | PSO | FPA | 2 | |||
| F4 | SWSO | PSO | GSA | FA | FPA | 1 | |||
| F5 | SWSO | PSO | GSA | MFO | IFOX | 1 | |||
| F6 | GSA | PSO | MFO | SWSO | IFOX | 4 | |||
| F7 | SWSO | SMS | GSA | PSO | MFO | 1 | |||
| |||||||||
Appendix A.1.2. Multimodal Functions (F8–F13)
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA |
| F8 | 1 | 9 | 6 | 4 | 10 | 2 | 8 | 3 | 7 | 5 |
| F9 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F10 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F11 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F12 | 4 | 2 | 5 | 7 | 1 | 10 | 3 | 6 | 9 | 8 |
| F13 | 3 | 4 | 5 | 9 | 1 | 10 | 2 | 7 | 6 | 8 |
| Average Rank | 1.83 | 3.00 | 3.16 | 3.83 | 2.50 | 5.66 | 2.66 | 3.66 | 5.16 | 4.00 |
| (b) | ||||||||||
| Test Function | SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA |
| F8 | 2 | 1 | 9 | 10 | 7 | 3 | 4 | 8 | 5 | 6 |
| F9 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F10 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F11 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 2 | 3 | 1 |
| F12 | 4 | 2 | 5 | 7 | 1 | 10 | 3 | 6 | 9 | 8 |
| F13 | 3 | 5 | 4 | 8 | 1 | 10 | 2 | 7 | 6 | 9 |
| Average Rank | 2.00 | 1.83 | 3.50 | 4.66 | 2.00 | 5.83 | 2.00 | 4.50 | 4.83 | 4.33 |
| (c) | ||||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | |||
| Average Ranks | 11 | |||||||||
| F8 | SWSO | SCA | GWO | SCSO | ZOA | 1 | ||||
| F9 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F10 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F11 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F12 | AVOA | MINFO | HHO | SWSO | INFO | 4 | ||||
| F13 | AVOA | HHO | SWSO | MINFO | INFO | 3 | ||||
| Standard Deviation Ranks | 12 | |||||||||
| F8 | MINFO | SWSO | SCA | HHO | RIME | 2 | ||||
| F9 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F10 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F11 | SWSO | GWO | RIME | SCA | - | 1 | ||||
| F12 | AVOA | MINFO | HHO | SWSO | INFO | 4 | ||||
| F13 | AVOA | HHO | SWSO | INFO | MINFO | 3 | ||||
| ||||||||||
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA |
| F8 | 1 | 8 | 3 | 2 | 9 | 7 | 5 | 4 | 6 |
| F9 | 1 | 3 | 6 | 2 | 5 | 4 | 7 | 8 | 9 |
| F10 | 1 | 2 | 5 | 3 | 7 | 4 | 9 | 6 | 8 |
| F11 | 1 | 2 | 5 | 3 | 8 | 4 | 9 | 6 | 7 |
| F12 | 1 | 3 | 5 | 2 | 8 | 4 | 7 | 6 | 9 |
| F13 | 2 | 1 | 5 | 3 | 9 | 4 | 7 | 6 | 8 |
| Average Rank | 1.16 | 3.16 | 4.83 | 2.5 | 7.66 | 4.5 | 7.33 | 6.0 | 7.83 |
| (b) | |||||||||
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA |
| F8 | 4 | 9 | 8 | 6 | 1 | 2 | 7 | 3 | 5 |
| F9 | 1 | 5 | 4 | 2 | 9 | 3 | 7 | 6 | 8 |
| F10 | 1 | 6 | 9 | 2 | 7 | 8 | 3 | 4 | 5 |
| F11 | 1 | 2 | 5 | 3 | 9 | 4 | 7 | 6 | 8 |
| F12 | 1 | 3 | 5 | 2 | 9 | 4 | 7 | 6 | 8 |
| F13 | 2 | 3 | 6 | 4 | 9 | 5 | 1 | 7 | 8 |
| Average Rank | 1.66 | 4.66 | 6.16 | 3.16 | 7.33 | 4.33 | 5.33 | 5.33 | 7.00 |
| (c) | |||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | ||
| Average Ranks | 7 | ||||||||
| F8 | SWSO | GSA | PSO | FA | SMS | 1 | |||
| F9 | SWSO | GSA | MFO | FPA | BA | 1 | |||
| F10 | SWSO | MFO | GSA | FPA | PSO | 1 | |||
| F11 | SWSO | MFO | GSA | FPA | PSO | 1 | |||
| F12 | SWSO | GSA | MFO | FPA | PSO | 1 | |||
| F13 | MFO | SWSO | GSA | FPA | PSO | 2 | |||
| Standard Deviation Ranks | 10 | ||||||||
| F8 | BA | FPA | FA | SWSO | GA | 4 | |||
| F9 | SWSO | GSA | FPA | PSO | MFO | 1 | |||
| F10 | SWSO | GSA | SMS | FA | GA | 1 | |||
| F11 | SWSO | MFO | GSA | FPA | PSO | 1 | |||
| F12 | SWSO | GSA | MFO | FPA | PSO | 1 | |||
| F13 | SMS | SWSO | MFO | GSA | FPA | 2 | |||
| |||||||||
Appendix A.1.3. Fixed Dimension (F14–F19)
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA |
| F14 | 3 | 1 | 8 | 2 | 7 | 4 | 6 | 9 | 5 |
| F15 | 1 | 4 | 7 | 3 | 9 | 2 | 6 | 8 | 5 |
| F16 | 1 | 2 | 7 | 4 | 9 | 3 | 8 | 5 | 6 |
| F17 | 1 | 3 | 6 | 2 | 9 | 4 | 7 | 8 | 5 |
| F18 | 1 | 2 | 8 | 4 | 9 | 3 | 6 | 7 | 5 |
| F19 | 1 | 5 | 6 | 8 | 9 | 3 | 4 | 7 | 2 |
| Average Rank | 1.33 | 2.83 | 7.00 | 3.83 | 8.66 | 3.16 | 6.16 | 7.33 | 4.66 |
| (b) | |||||||||
| Test Function | SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA |
| F14 | 3 | 1 | 8 | 2 | 9 | 6 | 4 | 7 | 5 |
| F15 | 1 | 4 | 7 | 3 | 9 | 2 | 6 | 8 | 5 |
| F16 | 1 | 2 | 8 | 6 | 9 | 4 | 7 | 3 | 5 |
| F17 | 1 | 5 | 6 | 7 | 8 | 2 | 4 | 9 | 3 |
| F18 | 1 | 2 | 9 | 4 | 8 | 3 | 7 | 6 | 5 |
| F19 | 1 | 9 | 8 | 3 | 4 | 5 | 6 | 7 | 2 |
| Average Rank | 1.33 | 3.83 | 7.66 | 4.16 | 7.83 | 3.66 | 5.66 | 6.66 | 4.16 |
| (c) | |||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | ||
| Average Ranks | 8 | ||||||||
| F14 | MFO | GSA | SWSO | FPA | GA | 3 | |||
| F15 | SWSO | FPA | GSA | MFO | GA | 1 | |||
| F16 | SWSO | MFO | FPA | GSA | FA | 1 | |||
| F17 | SWSO | GSA | MFO | FPA | GA | 1 | |||
| F18 | SWSO | MFO | FPA | GSA | GA | 1 | |||
| F19 | SWSO | GA | FPA | SMS | MFO | 1 | |||
| Standard Deviation Ranks | 8 | ||||||||
| F14 | MFO | GSA | SWSO | SMS | GA | 3 | |||
| F15 | SWSO | FPA | GSA | MFO | GA | 1 | |||
| F16 | SWSO | MFO | FA | FPA | GA | 1 | |||
| F17 | SWSO | FPA | GA | SMS | MFO | 1 | |||
| F18 | SWSO | MFO | FPA | GSA | GA | 1 | |||
| F19 | SWSO | GA | GSA | BA | FPA | 1 | |||
| |||||||||
Appendix A.1.4. The CEC2019 Benchmark Test Functions (CEC01–CEC10)
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA |
| Cec01 | 8 | 1 | 5 | 3 | 4 | 10 | 2 | 7 | 9 | 6 |
| Cec02 | 2 | 1 | 1 | 3 | 1 | 4 | 2 | 3 | 5 | 4 |
| Cec03 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Cec04 | 1 | 4 | 5 | 6 | 7 | 9 | 10 | 3 | 2 | 8 |
| Cec05 | 1 | 2 | 3 | 7 | 6 | 8 | 10 | 5 | 4 | 9 |
| Cec06 | 2 | 1 | 6 | 6 | 3 | 8 | 7 | 9 | 5 | 4 |
| Cec07 | 1 | 3 | 5 | 9 | 8 | 10 | 6 | 7 | 4 | 2 |
| Cec08 | 1 | 3 | 5 | 6 | 8 | 7 | 10 | 9 | 4 | 2 |
| Cec09 | 1 | 3 | 4 | 8 | 5 | 10 | 6 | 7 | 2 | 9 |
| Cec10 | 1 | 2 | 4 | 4 | 2 | 5 | 5 | 5 | 2 | 3 |
| Average Rank | 1.9 | 2.1 | 3.9 | 5.3 | 4.5 | 7.2 | 5.9 | 5.6 | 3.8 | 4.8 |
| (b) | ||||||||||
| Test Function | SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA |
| Cec01 | 8 | 1 | 6 | 3 | 2 | 10 | 5 | 7 | 9 | 4 |
| Cec02 | 4 | 1 | 2 | 6 | 3 | 8 | 5 | 7 | 10 | 9 |
| Cec03 | 4 | 1 | 2 | 6 | 3 | 10 | 7 | 8 | 5 | 9 |
| Cec04 | 1 | 4 | 5 | 10 | 8 | 9 | 7 | 3 | 2 | 6 |
| Cec05 | 1 | 9 | 10 | 5 | 6 | 3 | 8 | 4 | 2 | 7 |
| Cec06 | 1 | 8 | 10 | 7 | 9 | 3 | 5 | 2 | 6 | 4 |
| Cec07 | 6 | 2 | 8 | 1 | 10 | 9 | 4 | 7 | 5 | 3 |
| Cec08 | 7 | 9 | 8 | 4 | 6 | 2 | 3 | 10 | 5 | 1 |
| Cec09 | 1 | 3 | 4 | 8 | 6 | 9 | 5 | 7 | 2 | 10 |
| Cec10 | 10 | 9 | 2 | 1 | 4 | 6 | 3 | 8 | 5 | 7 |
| Average Rank | 4.3 | 4.7 | 5.7 | 5.1 | 5.9 | 6.9 | 5.2 | 6.3 | 5.1 | 6.0 |
| (c) | ||||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | |||
| Average Ranks | 19 | |||||||||
| Cec01 | MINFO | HHO | SCSO | AVOA | INFO | 8 | ||||
| Cec02 | MINFO, INFO, AVOA | SWSO, HHO | SCSO, GWO | SCA, ZOA | RIME | 2 | ||||
| Cec03 | SWSO, MINFO, INFO, SCSO, AVOA, SCA, HHO, GWO, RIME, ZOA | - | - | - | - | 1 | ||||
| Cec04 | SWSO | RIME | GWO | MINFO | INFO | 1 | ||||
| Cec05 | SWSO | MINFO | INFO | RIME | GWO | 1 | ||||
| Cec06 | MINFO | SWSO | AVOA | ZOA | RIME | 2 | ||||
| Cec07 | SWSO | ZOA | MINFO | RIME | INFO | 1 | ||||
| Cec08 | SWSO | ZOA | MINFO | RIME | INFO | 1 | ||||
| Cec09 | SWSO | RIME | MINFO | INFO | AVOA | 1 | ||||
| Cec10 | SWSO | MINFO, AVOA, RIME | ZOA | INFO, SCSO | SCA, HHO, GWO | 1 | ||||
| Standard Deviation Ranks | 43 | |||||||||
| Cec01 | MINFO | AVOA | SCSO | ZOA | HHO | 8 | ||||
| Cec02 | MINFO | INFO | AVOA | SWSO | HHO | 4 | ||||
| Cec03 | MINFO | INFO | AVOA | SWSO | RIME | 4 | ||||
| Cec04 | SWSO | RIME | GWO | MINFO | INFO | 1 | ||||
| Cec05 | SWSO | RIME | SCA | GWO | SCSO | 1 | ||||
| Cec06 | SWSO | GWO | SCA | ZOA | HHO | 1 | ||||
| Cec07 | SCSO | MINFO | ZOA | HHO | RIME | 6 | ||||
| Cec08 | ZOA | SCA | HHO | SCSO | RIME | 7 | ||||
| Cec09 | SWSO | RIME | MINFO | INFO | HHO | 1 | ||||
| Cec10 | SCSO | INFO | HHO | AVOA | RIME | 10 | ||||
| ||||||||||
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | IWOA | NRO | BDA | CEBA | IPSO | IAGA | BBOA | FOX | IFOX |
| Cec01 | 9 | 8 | 3 | 7 | 10 | 5 | 6 | 4 | 1 | 2 |
| Cec02 | 3 | 10 | 5 | 7 | 9 | 6 | 8 | 4 | 1 | 2 |
| Cec03 | 8 | 3 | 4 | 6 | 7 | 2 | 3 | 1 | 7 | 5 |
| Cec04 | 1 | 7 | 4 | 6 | 9 | 3 | 5 | 8 | 10 | 2 |
| Cec05 | 4 | 6 | 1 | 5 | 9 | 2 | 3 | 7 | 8 | 3 |
| Cec06 | 1 | 2 | 2 | 3 | 4 | 2 | 5 | 2 | 3 | 2 |
| Cec07 | 5 | 7 | 1 | 6 | 9 | 3 | 2 | 8 | 9 | 4 |
| Cec08 | 6 | 2 | 1 | 2 | 5 | 1 | 1 | 3 | 4 | 1 |
| Cec09 | 1 | 5 | 3 | 6 | 9 | 3 | 4 | 7 | 8 | 2 |
| Cec10 | 1 | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 3 | 3 |
| Average Rank | 3.9 | 5.2 | 2.6 | 5.2 | 7.4 | 3.0 | 3.9 | 4.6 | 5.4 | 2.6 |
| (b) | ||||||||||
| Test Function | SWSO | IWOA | NRO | BDA | CEBA | IPSO | IAGA | BBOA | FOX | IFOX |
| Cec01 | 9 | 7 | 3 | 8 | 4 | 5 | 6 | 6 | 1 | 2 |
| Cec02 | 1 | 6 | 5 | 9 | 4 | 8 | 7 | 6 | 2 | 3 |
| Cec03 | 1 | 6 | 8 | 7 | 3 | 8 | 6 | 5 | 2 | 4 |
| Cec04 | 1 | 8 | 6 | 9 | 7 | 4 | 5 | 5 | 2 | 3 |
| Cec05 | 1 | 6 | 8 | 9 | 3 | 6 | 7 | 4 | 2 | 5 |
| Cec06 | 4 | 9 | 8 | 2 | 1 | 7 | 10 | 6 | 3 | 5 |
| Cec07 | 7 | 6 | 5 | 8 | 2 | 5 | 4 | 4 | 1 | 3 |
| Cec08 | 8 | 6 | 3 | 7 | 5 | 2 | 4 | 1 | 1 | 1 |
| Cec09 | 1 | 9 | 5 | 10 | 3 | 6 | 7 | 8 | 2 | 4 |
| Cec10 | 10 | 7 | 9 | 4 | 1 | 5 | 6 | 8 | 2 | 3 |
| Average Rank | 4.3 | 7.0 | 6.0 | 7.3 | 3.3 | 5.6 | 6.2 | 5.3 | 1.8 | 3.3 |
| (c) | ||||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | |||
| Average Ranks | 39 | |||||||||
| Cec01 | FOX | IFOX | NRO | BBOA | IPSO | 9 | ||||
| Cec02 | FOX | IFOX | SWSO | BBOA | NRO | 3 | ||||
| Cec03 | BBOA | IPSO | IWOA, IAGA | NRO | IFOX | 8 | ||||
| Cec04 | SWSO | IFOX | IPSO | NRO | IAGA | 1 | ||||
| Cec05 | NRO | IPSO | IAGA, IFOX | SWSO | BDA | 4 | ||||
| Cec06 | SWSO | IWOA, NRO, IPSO, BBOA, IFOX | BDA, FOX | CEBA | IAGA | 1 | ||||
| Cec07 | NRO | IAGA | IPSO | IFOX | SWSO | 5 | ||||
| Cec08 | NRO, IPSO, IAGA, IFOX | IWOA, BDA | BBOA | FOX | CEBA | 6 | ||||
| Cec09 | SWSO | IFOX | NRO, IPSO | IAGA | IWOA | 1 | ||||
| Cec10 | SWSO | IWOA, NRO, IAGA, BBOA | BDA, CEBA, IPSO, FOX, IFOX | - | - | 1 | ||||
| Standard Deviation Ranks | 43 | |||||||||
| Cec01 | FOX | IFOX | NRO | CEBA | IPSO | 9 | ||||
| Cec02 | SWSO | FOX | IFOX | CEBA | NRO | 1 | ||||
| Cec03 | SWSO | FOX | CEBA | IFOX | BBOA | 1 | ||||
| Cec04 | SWSO | FOX | IFOX | IPSO | IAGA, BBOA | 1 | ||||
| Cec05 | SWSO | FOX | CEBA | BBOA | IFOX | 1 | ||||
| Cec06 | CEBA | BDA | FOX | SWSO | IFOX | 4 | ||||
| Cec07 | FOX | CEBA | IFOX | IAGA, BBOA | NRO, IPSO | 7 | ||||
| Cec08 | BBOA, FOX, IFOX | IPSO | NRO | IAGA | CEBA | 8 | ||||
| Cec09 | SWSO | FOX | CEBA | IFOX | NRO | 1 | ||||
| Cec10 | CEBA | FOX | IFOX | BDA | IPSO | 10 | ||||
| ||||||||||
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Test Function | SWSO | Hybrid | FOX | TSA | PSO | GWO | MRSO | RSO |
| Cec01 | 8 | 1 | 5 | 3 | 2 | 4 | 7 | 6 |
| Cec02 | 5 | 1 | 4 | 3 | 2 | 2 | 4 | 5 |
| Cec03 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 2 |
| Cec04 | 4 | 6 | 1 | 3 | 5 | 2 | 9 | 8 |
| Cec05 | 5 | 4 | 8 | 3 | 1 | 2 | 6 | 7 |
| Cec06 | 4 | 3 | 1 | 5 | 2 | 6 | 7 | 8 |
| Cec07 | 2 | 4 | 6 | 3 | 1 | 5 | 7 | 8 |
| Cec08 | 1 | 4 | 5 | 6 | 3 | 2 | 7 | 8 |
| Cec09 | 4 | 1 | 5 | 2 | 3 | 6 | 7 | 8 |
| Cec10 | 1 | 2 | 6 | 4 | 5 | 3 | 7 | 8 |
| Average Rank | 3.6 | 2.7 | 4.3 | 3.3 | 2.5 | 3.3 | 6.3 | 6.8 |
| (b) | ||||||||
| Test Function | SWSO | Hybrid | FOX | TSA | PSO | GWO | MRSO | RSO |
| Cec01 | 8 | 1 | 6 | 2 | 3 | 4 | 7 | 5 |
| Cec02 | 6 | 7 | 3 | 5 | 1 | 2 | 4 | 8 |
| Cec03 | 2 | 1 | 6 | 8 | 5 | 7 | 3 | 4 |
| Cec04 | 3 | 6 | 1 | 2 | 5 | 4 | 8 | 7 |
| Cec05 | 1 | 3 | 8 | 5 | 2 | 4 | 6 | 7 |
| Cec06 | 3 | 4 | 8 | 1 | 7 | 2 | 6 | 5 |
| Cec07 | 4 | 2 | 5 | 3 | 1 | 8 | 7 | 6 |
| Cec08 | 7 | 1 | 2 | 6 | 5 | 8 | 3 | 4 |
| Cec09 | 3 | 8 | 1 | 2 | 4 | 5 | 7 | 6 |
| Cec10 | 8 | 3 | 1 | 2 | 7 | 6 | 5 | 4 |
| Average Rank | 4.5 | 3.6 | 4.1 | 3.6 | 4.0 | 5.0 | 5.6 | 5.6 |
| (c) | ||||||||
| Test Function | 1st | 2nd | 3rd | 4th | 5th | SWSO Rank | Subtotal | |
| Average Ranks | 36 | |||||||
| Cec01 | Hybrid | PSO | TSA | GWO | FOX | 8 | ||
| Cec02 | Hybrid | PSO, GWO | TSA | FOX, MRSO | SWSO, RSO | 5 | ||
| Cec03 | Hybrid, TSA, PSO, GWO | SWSO, FOX, MRSO, RSO | - | - | - | 2 | ||
| Cec04 | FOX | GWO | TSA | SWSO | PSO | 4 | ||
| Cec05 | PSO | GWO | TSA | Hybrid | SWSO | 5 | ||
| Cec06 | FOX | PSO | Hybrid | SWSO | TSA | 4 | ||
| Cec07 | PSO | SWSO | TSA | Hybrid | GWO | 2 | ||
| Cec08 | SWSO | GWO | PSO | Hybrid | FOX | 1 | ||
| Cec09 | Hybrid | TSA | PSO | SWSO | FOX | 4 | ||
| Cec10 | SWSO | Hybrid | GWO | TSA | PSO | 1 | ||
| Standard Deviation Ranks | 45 | |||||||
| Cec01 | Hybrid | TSA | PSO | GWO | RSO | 8 | ||
| Cec02 | PSO | GWO | FOX | MRSO | TSA | 6 | ||
| Cec03 | Hybrid | SWSO | MRSO | RSO | PSO | 2 | ||
| Cec04 | FOX | TSA | SWSO | GWO | PSO | 3 | ||
| Cec05 | SWSO | PSO | Hybrid | GWO | TSA | 1 | ||
| Cec06 | TSA | GWO | SWSO | Hybrid | RSO | 3 | ||
| Cec07 | PSO | Hybrid | TSA | SWSO | FOX | 4 | ||
| Cec08 | Hybrid | FOX | MRSO | RSO | PSO | 7 | ||
| Cec09 | FOX | TSA | SWSO | PSO | GWO | 3 | ||
| Cec10 | FOX | TSA | Hybrid | RSO | MRSO | 8 | ||
| ||||||||
| Category | Compared Group(s) | Average Rank (Avg) | Average Rank (SD) | SWSO Rank |
|---|---|---|---|---|
| Unimodal | Group A and B | 1.57 | 1.64 | 1st |
| Multimodal | Group C and D | 1.49 | 1.83 | 1st |
| Fixed-Dimension Modal | Group D | 1.33 | 1.33 | 1st |
| CEC2019 | Group C, Group E, and Group F | 3.1 | 4.36 | 1st, 3rd, 4th |
References
- Arora, J.S. Introduction to Optimum Design, 3rd ed.; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; Available online: https://www.researchgate.net/publication/263171713 (accessed on 19 August 2024).
- Arcos-García, Á.; Álvarez-García, J.A.; Soria-Morillo, L.M. Deep neural network for traffic sign recognition systems: An analysis of spatial transformers and stochastic optimisation methods. Neural Netw. 2018, 99, 158–165. [Google Scholar] [CrossRef]
- Hjeij, M.; Vilks, A. A brief history of heuristics: How did research on heuristics evolve? Humanit. Soc. Sci. Commun. 2023, 10, 64. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Correia, A.; Worrall, D.E.; Bondesan, R. Neural Simulated Annealing. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 25–29 April 2022. [Google Scholar]
- Samsuddin, S.; Othman, M.S.; Yusuf, L.M. A review of single and population-based metaheuristic algorithms solving multi depot vehicle routing problem. Int. J. Comput. Syst. Softw. Eng. 2018, 4, 80–93. [Google Scholar] [CrossRef]
- Du, X.; Zhang, Y.; Wang, J.; Li, C. GA-OMTL: Genetic algorithm optimization for multi-task learning. Expert Syst. Appl. 2025, 232, 122973. [Google Scholar] [CrossRef]
- Refaat, A.; Elbaz, A.; Khalifa, A.-E.; Elsakka, M.M.; Kalas, A.; Elfar, M.H. Performance evaluation of a novel self-tuning particle swarm optimization algorithm-based maximum power point tracker for porton exchange membrane fuel cells under different operating conditions. Energy Convers. Manag. 2024, 301, 118014. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Thammachantuek, I.; Ketcham, M.; Mirjalili, S. Path planning for autonomous mobile robots using multi-objective evolutionary particle swarm optimization. PLoS ONE 2022, 17, e0271924. [Google Scholar] [CrossRef]
- Wang, G.; Wang, F.; Wang, J.; Li, M.; Gai, L.; Xu, D. Collaborative target assignment problem for large-scale UAV swarm based on two-stage greedy auction algorithm. Aerosp. Sci. Technol. 2024, 149, 109146. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Pathak, V.K.; Srivastava, A.K. A novel upgraded bat algorithm based on cuckoo search and Sugeno inertia weight for large scale and constrained engineering design optimization problems. Eng. Comput. 2022, 38, 1731–1758. [Google Scholar] [CrossRef]
- Wang, C.; Liu, K. A Randomly Guided Firefly Algorithm Based on Elitist Strategy and Its Applications. IEEE Access 2019, 7, 141343–141355. [Google Scholar] [CrossRef]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Yang, Z.; Cai, Y.; Li, G. Improved Gravitational Search Algorithm Based on Adaptive Strategies. Entropy 2022, 24, 1826. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, R.M.C.; Torres, D.F.M.; Herdeiro, C.A.R.; Santos, M.P. Universe-inspired algorithms for Control Engineering: A review. arXiv 2024, 10, e31771. [Google Scholar] [CrossRef] [PubMed]
- Dubey, S.R.; Kumar, V.; Kaur, M.; Dao, T.-P. A Systematic Review on Harmony Search Algorithm: Theory, Literature, and Applications. Math. Probl. Eng. 2021, 2021, 5594267. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, V. A review of Teaching–Learning-Based Optimization and its applications. Swarm Evol. Comput. 2020, 55, 100–135. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. 2007, 20, 89–99. [Google Scholar] [CrossRef]
- Bacanin, N.; Budimirovic, N.; Venkatachalam, K.; Strumberger, I.; Alrasheedi, A.F.; Abouhawwash, M. Novel Chaotic Opposi-tional Fruit Fly Optimization Algorithm for Feature Selection Applied on COVID-19 Patients’ Health Prediction. PLoS ONE 2022, 17, e0275727. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, H.; Wu, Y.; Shi, X.; Song, M.; Zhang, W.; Wang, Z. A review on multi-objective optimization of building performance—Insights from bibliometric analysis. Heliyon 2025, 11, e42480. [Google Scholar] [CrossRef] [PubMed]
- Khodadadi, N.; Khodadadi, E.; Abdollahzadeh, B.; Ei-Kenawy, E.-S.M.; Mardanpour, P.; Zhao, W.; Gharehchopogh, F.S.; Mirjalili, S. Multi-objective generalized normal distribution optimization: A novel algorithm for multi-objective problems. Clust. Comput. 2024, 27, 10589–10631. [Google Scholar] [CrossRef]
- Kang, S.; Li, K.; Wang, R. A survey on pareto front learning for multi-objective optimization. J. Membr. Comput. 2024, 7, 128–134. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Science and Business Media: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optim; Cambridge University Press: Cambridge, UK, 2004; Available online: https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf (accessed on 19 August 2024).
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Clay Mathematics Institute. P vs. NP Problem. 2000. Available online: https://www.claymath.org/wp-content/uploads/2022/06/pvsnp.pdf (accessed on 19 August 2024).
- Datta, S.; Roy, S.; Davim, J.P. Optimization Techniques: An Overview. In Optimization in Industry; Datta, S., Davim, J., Eds.; Management and Industrial Engineering; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Almufti, S. Using Swarm Intelligence for solving NP Hard Problems. Acad. J. Nawroz Univ. 2017, 6, 46–50. [Google Scholar] [CrossRef]
- Wolchover, N. The Questions That Computers Can Never Answer. Wired. (2014, February 6). Available online: https://www.wired.com/2014/02/halting-problem (accessed on 19 August 2024).
- Sivakumar, R.; Angayarkanni, S.A.; Ramana, R.Y.V.; Sadiq, A.S. Traffic flow forecasting using natural selection based hybrid bald eagle search-grey wolf optimization algorithm. PLoS ONE 2022, 17, e0275104. [Google Scholar] [CrossRef]
- Peres, F.; Castelli, M. Combinatorial Optimization Problems and Metaheuristics: Review, Challenges, Design, and Development. Appl. Sci. 2021, 11, 6449. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-billed blue magpie optimizer: A novel metaheuristic algorithm for 2D/3D UAV path planning and engineering design problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- Al-Sharqi, M.A.; Al-Obaidi, A.T.S.; Al-Mamory, S.O. Apiary Organizational-Based Optimization Algorithm: A new nature-inspired metaheuristic algorithm. Int. J. Intell. Eng. Syst. 2024, 17, 482–494. [Google Scholar]
- Zhang, Z.; Zhu, H.; Xie, M. Differential privacy may have a potential optimization effect on some swarm intelligence algorithms besides privacy-preserving. Inf. Sci. 2024, 654, 119870. [Google Scholar] [CrossRef]
- Wu, S.; He, B.; Zhang, J.; Chen, C.; Yang, J. PSAO: An enhanced Aquila Optimizer with particle swarm mechanism for engineering design and UAV path planning problems. Alex. Eng. J. 2024, 106, 474–504. [Google Scholar] [CrossRef]
- Wang, H.; Shi, L. A multi-direction guided mutation-driven stable swarm intelligence algorithm with translation and rotation invariance for global optimization. Appl. Soft Comput. 2024, 159, 111614. [Google Scholar] [CrossRef]
- Jain, S.; Saha, A. Improving and comparing performance of machine learning classifiers optimized by swarm intelligent algorithms for code smell detection. Sci. Comput. Program. 2024, 237, 103140. [Google Scholar] [CrossRef]
- Gülmez, E.; Koruca, H.I.; Aydin, M.E.; Urganci, K.B. Heuristic and swarm intelligence algorithms for work-life balance problem. Comput. Ind. Eng. 2024, 187, 109857. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Wang, D.; Xu, Y.; Hua, G. WOAD3QN-RP: An intelligent routing protocol in wireless sensor networks—A swarm intelligence and deep reinforcement learning based approach. Expert Syst. Appl. 2024, 246, 123089. [Google Scholar] [CrossRef]
- Fountas, N.A.; Kechagias, J.D.; Vaxevanidis, N.M. Swarm intelligence algorithms for optimising sliding wear of nanocomposites. Tribol. Mater. 2024, 3, 44–50. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M. Swallow swarm optimization algorithm: A new method to optimization. Neural Comput. Appl. 2013, 23, 429–454. [Google Scholar] [CrossRef]
- Kareem, S.W.; Mohammed, A.S.; Khoshaba, F.S. Novel nature-inspired meta-heuristic optimization algorithm based on hybrid dolphin and sparrow optimization. Int. J. Nonlinear Anal. Appl. 2023, 14, 355–373. [Google Scholar] [CrossRef]
- Yao, Z.; Shangguan, H.; Xie, W.; Liu, J.; He, S.; Huang, H.; Li, F.; Chen, J.; Zhan, Y.; Wu, X.; et al. SIPSC-Kac: Integrating swarm intelligence and protein spatial characteristics for enhanced lysine acetylation site identification. Int. J. Biol. Macromol. 2024, 282, 137237. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Di Nardo, M.; Yin, S. Improved Swarm Intelligence-Based Logistics Distribution Optimizer: Decision Support for Multimodal Transportation of Cross-Border E-Commerce. Mathematics 2024, 12, 763. [Google Scholar] [CrossRef]
- Ma, R.; Kareem, S.W.; Kumar, P.; Kalra, A.; Miah, S.; Doewes, R.I. Optimization of electric automation control model based on artificial intelligence algorithm. Wirel. Commun. Mob. Comput. 2022, 2022, 7762493. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, H.; Chen, J.; Zhang, Z.; Huang, X. Novel intelligent grazing strategy based on remote sensing, herd perception and UAVs monitoring. Comput. Electron. Agric. 2024, 219, 108807. [Google Scholar] [CrossRef]
- Shamsaldin, A.S.; Rashid, T.A.; Al-Rashid Agha, R.A.; Al-Salihi, N.K.; Mohammadi, M. Donkey and smuggler optimization algorithm: A collaborative working approach to path finding. J. Comput. Des. Eng. 2019, 6, 562–583. [Google Scholar] [CrossRef]
- Alrahhal, H.; Jamous, R. AFOX: A new adaptive nature-inspired optimization algorithm. Artif. Intell. Rev. 2023, 56, 15523–15566. [Google Scholar] [CrossRef]
- Huang, H.; Zheng, B.; Wei, X.; Zhou, Y.; Zhang, Y. NSCSO: A novel multi-objective non-dominated sorting chicken swarm optimization algorithm. Sci. Rep. 2024, 14, 4310. [Google Scholar] [CrossRef]
- Mardiastuti, A.; Hartono, T.T.; Firmansyah, F.S.; Manurung, R.; Refiandy, M. Barn swallow roosting at an oil gathering station. IOP Conf. Ser. Earth Environ. Sci. 2023, 1271, 012021. [Google Scholar] [CrossRef]
- Hobson, K.A.; Kardynal, K.J.; Van Wilgenburg, S.L.; Albrecht, G.; Salvadori, A.; Fox, J.W.; Brigham, R.M. A Continent-Wide Migratory Divide in North American Breeding Barn Swallows (Hirundo rustica). PLoS ONE 2015, 10, e0129340. [Google Scholar] [CrossRef]
- Encyclopædia Britannica. Swallow. In Britannica.com. 17 June 2025. Available online: https://www.britannica.com/animal/swallow-bird (accessed on 19 August 2024).
- Brown, C.R.; Brown, M.B. Barn Swallow (Hirundo rustica) (Version 2.0). In The Birds of North America; Rodewald, P.G., Ed.; Cornell Lab of Ornithology: New York, NY, USA, 1999; Available online: https://www.allaboutbirds.org/guide/Barn_Swallow/id (accessed on 19 August 2024).
- Barn Swallow|Audubon Field Guide. Available online: https://www.audubon.org (accessed on 13 March 2024).
- Vogel, S. Life in Moving Fluids. The Physical Biology of Flow, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Pennycuick, C.J. Power Requirements for Horizontal Flight in the Pigeon Columba Livia. J. Exp. Biol. 1968, 49, 527–555. [Google Scholar] [CrossRef]
- Kareem, S.W. A nature-inspired metaheuristic optimization algorithm based on crocodiles hunting search (CHS). Int. J. Swarm Intell. Res. 2022, 13, 1–23. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Stützle, T. Parameter control in metaheuristics. J. Heuristics 2012, 18, 769–793. [Google Scholar] [CrossRef]
- Tokic, M. Adaptive ε-greedy exploration in reinforcement learning based on value differences. In KI 2010: Advances in Artificial Intelligence; Dillmann, R., Beyerer, J., Hanebeck, U.D., Schultz, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6359, pp. 203–210. [Google Scholar] [CrossRef]
- Barros-Everett, T.; Montero, E.; Rojas-Morales, N. Parameter Prediction for Metaheuristic Algorithms Solving Routing Problem Instances Using Machine Learning. Appl. Sci. 2025, 15, 2946. [Google Scholar] [CrossRef]
- Hsieh, F.-S. A self-adaptive meta-heuristic algorithm based on success rate and differential evolution for improving the performance of ridesharing systems with a discount guarantee. Algorithms 2024, 17, 9. [Google Scholar] [CrossRef]
- Kareem, S.W.; Okur, M.C. Bayesian network structure learning using hybrid Bee optimization and greedy search. In Proceedings of the 3rd International Mediterranean Science and Engineering Congress (IMSEC 2018), Çukurova University, Adana, Turkey, 24–26 October 2018; pp. 1–7. Available online: https://www.researchgate.net/publication/333320417 (accessed on 13 March 2024).
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Russo, D.; Van Roy, B.; Kazerouni, A.; Osband, I.; Wen, Z. A tutorial on Thompson sampling. Found. Trends Mach. Learn. 2018, 11, 1–96. [Google Scholar] [CrossRef]
- Awla, H.Q.; Kareem, S.W.; Mohammed, A.S. A comparative evaluation of Bayesian networks structure learning using Falcon Optimization Algorithm. Int. J. Interact. Multimed. Artif. Intell. 2023; in press. [Google Scholar] [CrossRef]
- Martínez-Ríos, F.; Murillo-Suárez, A. A new swarm algorithm for global optimization of multimodal functions over multi-threading architecture hybridized with simulating annealing. Procedia Comput. Sci. 2018, 135, 449–456. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Naseem, R. Common benchmark functions for metaheuristic evaluation: A review. JOIV Int. J. Inform. Vis. 2017, 1, 218–223. [Google Scholar] [CrossRef]
- Tang, K.; Chen, Y.; Suganthan, P.N.; Liang, J.J. Benchmark Functions for the CEC’2010 Special Session and Competition on Large-Scale Global Optimization; Technical Report; Nature Inspired Computation and Applications Laboratory, USTC: Hefei, China, 2009. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report 201212; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China, Technical Report; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, S.; Liang, L.; Wei, Y.; Wu, Y. A flower pollination optimization algorithm based on cosine cross-generation differential evolution. Sensors 2023, 23, 606. [Google Scholar] [CrossRef]
- Cuevas, E.; Echavarría, A.; Ramírez-Ortegón, M.A. An optimization algorithm inspired by the States of Matter that improves the balance between exploration and exploitation. Appl. Intell. 2014, 40, 256–272. [Google Scholar] [CrossRef]
- Khan, W.A.; Hamadneh, N.N.; Tilahun, S.L.; Ngnotchouye, J.M.T. A Review and Comparative Study of Firefly Algorithm and Its Modified Version; InTech: Toulon, France, 2016. [Google Scholar] [CrossRef]
- Jumaah, M.A.; Ali, Y.H.; Rashid, T.A. Improved FOX Optimization Algorithm. arXiv 2025, arXiv:2504.09574. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Calis, G.; Yuksel, O. An improved ant colony optimization algorithm for construction site layout problems. J. Build. Constr. Plan. Res. 2015, 3, 221–232. [Google Scholar] [CrossRef][Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ebeed, M.; Hassan, S.; Kamel, S.; Nasrat, L.; Mohamed, A.W.; Youssef, A.-R. Smart building energy management with renewables and storage systems using a modified weighted mean of vectors algorithm. Sci. Rep. 2025, 15, 4733. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Aula, S.A.; Rashid, T.A. FOX-TSA: Navigating complex search spaces and superior performance in benchmark and real-world optimization problems. Ain Shams Eng. J. 2024, 16, 103185. [Google Scholar] [CrossRef]
- Abdulla, H.S.; Ameen, A.A.; Saeed, S.I.; Mohammed, I.A.; Rashid, T.A. MRSO: Balancing exploration and exploitation through modified rat swarm optimization for global optimization. Algorithms 2024, 17, 423. [Google Scholar] [CrossRef]
- Gim, G.H.H. Optimal Design of a Class of Welded Beam Structures Based on Design for Latitude. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 1984. [Google Scholar]
- Ragsdell, K.M.; Phillips, D.T. Optimal design of a class of welded structures using geometric programming. J. Eng. Ind. 1976, 98, 1021–1025. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gafar, M.H.A.; Fawzy, N.; Sayed, A.Y. Recent metaheuristic algorithms for solving some civil engineering optimization problems. Sci. Rep. 2025, 15, 7929. [Google Scholar] [CrossRef]
- Ren, J.; Wei, H.; Yuan, Y.; Li, X.; Luo, F.; Wu, Z. Boosting sparrow search algorithm for multi-strategy-assist engineering optimization problems. AIP Adv. 2022, 12, 095201. [Google Scholar] [CrossRef]
- Sakthivel, R.; Selvadurai, K. Slime Mould Reproduction: A new optimization algorithm for constrained engineering problems. J. Comput. Sci. 2024, 20, 96–105. [Google Scholar] [CrossRef]
- Karami, H.; Anaraki, M.V.; Farzin, S.; Mirjalili, S. Flow Direction Algorithm (FDA): A novel optimization approach for solving optimization problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, N.; Wang, P.; Chen, H.; Li, C. Chaos-enhanced synchronized bat optimizer. Appl. Math. Model. 2020, 77, 1201–1215. [Google Scholar] [CrossRef]
- Mohapatra, S.; Mohapatra, P. American zebra optimization algorithm for global optimization problems. Sci. Rep. 2023, 13, 31876. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. An efficient hybrid algorithm based on water cycle and moth-flame optimization algorithms for solving numerical and constrained engineering optimization problems. Soft. Comput. 2019, 23, 1699–1722. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Cuevas, E.; Cienfuegos, M. A new algorithm inspired in the behavior of the social-spider for constrained optimization. Expert Syst. Appl. 2014, 41, 412–425. [Google Scholar] [CrossRef]
- A Hashim, F.; Mostafa, R.R.; Abu Khurma, R.; Qaddoura, R.; A Castillo, P. A new approach for solving global optimization and engineering problems based on modified sea horse optimizer. J. Comput. Des. Eng. 2024, 11, 73–98. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Ong, P.; Ho, C.S.; Chin, D.D.V.S. An improved cuckoo search algorithm for design optimization of structural engineering problems. Commun. Comput. Appl. Math. 2020, 2, 31–44. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Sun, P.; Liu, H.; Zhang, Y.; Tu, L.; Meng, Q. An intensify atom search optimization for engineering design problems. Appl. Math. Model. 2021, 89, 837–859. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. Water evaporation optimization: A novel physically inspired optimization algorithm. Comput. Struct. 2016, 167, 69–85. [Google Scholar] [CrossRef]
- Shang, C.; Zhou, T.-T.; Liu, S. Optimization of complex engineering problems using modified sine cosine algorithm. Sci. Rep. 2022, 12, 20528. [Google Scholar] [CrossRef]
- Chang, C.; Zhang, T.; Chen, S. Solving the problem of pressure vessel with constraint conditions through marine predators algorithm. Mod. Econ. Manag. Forum 2025, 6, 127–139. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 245–265. [Google Scholar] [CrossRef]
- Beausoleil, R.P. Solving engineering optimization problems with Tabu/Scatter Search (Resolviendo problemas de optimización en ingeniería con búsqueda Tabú/Dispersa). Rev. Matemática: Teoría Apl. 2017, 24, 157–188. [Google Scholar]
- Frimpong, S.A.; Darkwah, K.F. Implementation of the Sine–Cosine Algorithm to the Pressure Vessel Design Problem. Int. J. Innov. Sci. Res. Technol. IJISRT 2022, 7, 1069–1073. Available online: https://www.ijisrt.com/assets/upload/files/IJISRT22DEC721.pdf (accessed on 19 August 2024).
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Li, M.; Hussien, A.G.; Abbas, M. Multi-strategy enhanced jellyfish search algorithm for engineering applications. Eng. Comput. 2023, 11, 851. [Google Scholar] [CrossRef]
- Li, L.D.; Li, X.; Yu, X. A multi-objective constraint-handling method with PSO algorithm for constrained engineering optimization problems. In Proceedings of the IEEE World Congress on Computational Intelligence (CEC 2008), Hong Kong, China, 1–6 June 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello, C.A.C.; Velázquez-Reyes, J.; Muñoz-Dávila, L. Multiple trial vectors in differential evolution for engineering design. Eng. Optim. 2007, 39, 567–589. [Google Scholar] [CrossRef]
- Belkourchia, Y.; Azrar, L.; Zeriab, E.M. A hybrid optimization algorithm for solving constrained engineering design problems. In Proceedings of the 2019 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sandgren, E. Nonlinear integer and discrete programming in mechanical design. In Proceedings of the ASME Design Technology Conference, Kissimmee, FL, USA, 25–28 September 1988; pp. 95–105. [Google Scholar]



| Abbreviation | Term |
|---|---|
| SI | Swarm Intelligence |
| SWSO | Swallow Search Optimization |
| P | Polynomial Time |
| NP | Nondeterministic Polynomial Time |
| NP-Complete | Nondeterministic Polynomial-time Complete |
| NP-Hard | Nondeterministic Polynomial-time Hard |
| TSP | Traveling Salesman Problem |
| MOPSO | Multiobjective Particle Swarm Optimization |
| MOCH-PSO | Multiobjective Constraint-Handling-PSO |
| AOOA | Apiary Organizational-Based Optimization Algorithm |
| DP | Differential Privacy |
| AO | Aquila Optimizer |
| PSAO | An enhanced Aquila Optimizer with Particle Swarm |
| WSNs | Wireless Sensor Networks |
| D3QN | Dueling Double Deep Q-Network |
| RP | Routing Protocol |
| WOAD3QN-RP | Whale Optimization Algorithm uses D3QN |
| SSO | Swallow Swarm Optimization |
| Kac | lysine acetylation |
| SIPSC-Kac | Swarm Intelligence and Protein Spatial Characteristics-Kac |
| B2C e-commerce | Business-to-Consumer electronic commerce |
| PSO | Particle Swarm Optimization |
| IPSO | Improved Particle Swarm Optimization |
| GA-PSO-SQP | Genetic Algorithm- Particle Swarm Optimization- Sequential Quadratic Programming |
| CPSO | Co-Evolutionary Particle Swarm Optimization |
| MPPT | Maximum Power Point Tracking |
| PEM | Proton Exchange Membrane |
| DSO | Donkey and Smuggler Optimization |
| AFOX | Adaptive Fox Optimization |
| FOX | Fox Optimization |
| IFOX | Improved FOX |
| NSCSO | Non-Dominated Sorting Chicken Swarm Optimization |
| GWO | Grey Wolf Optimizer |
| VGWO | Variant Grey Wolf Optimizer |
| GA | Genetic Algorithm |
| IAGA | Improved Adaptive Genetic Algorithm |
| DA | Dragon-Fly Algorithm |
| BDA | Binary Dragonfly Algorithm |
| WOA | Whale Optimization Algorithm |
| IWOA | Improved Whale Optimization Algorithm |
| BOA | Butterfly Optimization Algorithm |
| COA | Chimp Optimization Algorithm |
| FDO | Fitness Dependent Optimizer |
| MFO | Moth–Flame Optimization |
| GSA | Gravitational Search Algorithm |
| BA | Bat Algorithm |
| CEBA | Chaos-Enhanced Bat Algorithm |
| FPA | Flower Pollination Algorithm |
| SMS | State of Mater Search |
| FA | Firefly Algorithm |
| DE | Dolphin Echolocation |
| FEP | Fast Evolutionary Programing |
| ACO | Ant Colony Optimization |
| IACO | Improved Ant Colony Optimization |
| INFO | Weighted Mean of Vectors Algorithm |
| MINFO | Modified Weighted Mean of Vectors Algorithm |
| SCSO | Sand Cat Search Optimizer |
| AVOA | African Vultures Optimization Algorithm |
| SCA | Sine Cosine Algorithm |
| MSCA | Modified Sine Cosine Algorithm |
| HHO | Harris Hawks Optimization |
| RIME | A RIME-Ice physical phenomenon-based optimization. |
| ZOA | Zebra Optimization Algorithm |
| NRO | Nuclear Reaction Optimization |
| BBOA | Brown-Bear Optimization Algorithm |
| TSA | Tree-Seed Algorithm |
| FOX-TSA | Hybrid FOX- Tree-Seed Algorithm |
| RSO | Rat Swarm Optimization |
| MRSO | Modified Rat Swarm Optimization |
| SMR | Slime Mould Reproduction |
| MSSSA | Multistrategy-Sparrow Search Algorithm |
| ASO | Atom Search Optimization |
| SO | Snake Optimizer |
| MVO | Multiverse Optimizer |
| ABC | Artificial Bee Colony |
| MSHO | Modified Sea Horse Optimizer |
| AZOA | American Zebra Optimization Algorithm |
| FDA | Flow Direction Algorithm |
| CBO | Colliding Bodies Optimization |
| CS | Cuckoo Search |
| SSO-C | Social Spider Optimization |
| ACSA | An Improved Cuckoo Search Algorithm |
| WEOA | Water Evaporation Optimization Algorithm. |
| WCMFO | Water Cycle and Moth-Flame Optimization |
| EJS | Enhanced Jellyfish Search |
| CSS | Charged System Search |
| MDE | Multiple Differential Evolution |
| Symbols | Definition |
|---|---|
| Probability of following the leader | |
| Energy threshold for leader switching | |
| Adaptive inertia weight | |
| Exploration decay factor | |
| Local random Gaussian noise |
| No. | Functions | Range | ||
|---|---|---|---|---|
| Cec01 | Storn’s Chebyshev Polynomial Fitting Problem | 9 | [−8192, 8192] | 1 |
| Cec02 | Inverse Hilbert Matrix Problem | 16 | [−16,384, 16,384] | 1 |
| Cec03 | Lennard–Jones Minimum Energy Cluster | 18 | [−4, 4] | 1 |
| Cec04 | Rastrigin’s Function | 10 | [−100, 100] | 1 |
| Cec05 | Griewank’s Function | 10 | [−100, 100] | 1 |
| Cec06 | Weierstrass Function | 10 | [−100, 100] | 1 |
| Cec07 | Modified Schwefel’s Function | 10 | [−100, 100] | 1 |
| Cec08 | Expanded Schaffer’s F6 Function | 10 | [−100, 100] | 1 |
| Cec09 | Happy Cat Function | 10 | [−100, 100] | 1 |
| Cec10 | Ackley Function | 10 | [−100, 100] | 1 |
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | IFOX | |
| F | Ave | ||||||||
| F1 | 1.2466 × 10−84 | 1.1700 × 10−4 | 1.36 × 10−4 | 2.53 × 10−16 | 2.0792 × 10+4 | 2.0364 × 10+2 | 1.2000 × 10+2 | 7.4807 × 10+3 | −2.0 × 10+2 |
| F2 | 1.5366 × 10−48 | 6.3900 × 10−4 | 4.21 × 10−2 | 5.57 × 10−2 | 8.9786 × 10+1 | 1.1169 × 10+1 | 2.0531 × 10−2 | 3.9325 × 10+1 | 3.6 × 10−2 |
| F3 | 3.5466 × 10−86 | 6.9673 × 10+2 | 7.01 × 10+1 | 8.96 × 10+2 | 6.2481 × 10+4 | 2.3757 × 10+2 | 3.7820 × 10+4 | 1.7357 × 10+4 | 3.5 × 10−3 |
| F4 | 9.2386 × 10−53 | 7.0686 × 10+1 | 1.09 × 10+0 | 7.35 × 10+0 | 4.9743 × 10+1 | 1.2573 × 10+1 | 6.9170 × 10+1 | 3.3954 × 10+1 | −9.6 × 10+2 |
| F5 | 4.214 × 10+0 | 1.3915 × 10+2 | 9.67 × 10+1 | 6.75 × 10+1 | 1.9951 × 10+6 | 1.0975 × 10+4 | 6.3822 × 10+6 | 3.7950 × 10+6 | 7.4 × 10+0 |
| F6 | 1.039 × 10+0 | 1.1300 × 10−4 | 1.02 × 10−4 | 2.5 × 10−16 | 1.7053 × 10+4 | 1.7538 × 10+2 | 4.1439 × 10+4 | 7.8287 × 10+3 | 2.2 × 10−2 |
| F7 | 3.027 × 10−4 | 9.1155 × 10−2 | 1.23 × 10−1 | 8.94 × 10−2 | 6.0451 × 10+0 | 1.3594 × 10−1 | 4.9520 × 10−2 | 1.9063 × 10+0 | 3.7 × 10−3 |
| F | SD | ||||||||
| F1 | 6.326 × 10−84 | 1.5000 × 10−4 | 2.02 × 10−4 | 9.67 × 10−17 | 5.8924 × 10+3 | 7.8398 × 10+1 | 0.0000 × 10+0 | 8.9485 × 10+2 | 2.2 × 10−1 |
| F2 | 6.4714 × 10−48 | 8.7700 × 10−4 | 4.54 × 10−2 | 1.94 × 10−1 | 4.1958 × 10+1 | 2.9196 × 10+0 | 4.7180 × 10−3 | 2.4659 × 10+0 | 3.3 × 10−2 |
| F3 | 2.4891 × 10−85 | 1.8853 × 10+2 | 2.21 × 10+1 | 3.18 × 10+2 | 2.9769 × 10+4 | 1.3665 × 10+2 | 0.0000 × 10+0 | 1.7401 × 10+3 | 4.8 × 10−2 |
| F4 | 6.5246 × 10−52 | 5.2751 × 10+0 | 3.17 × 10−1 | 1.74 × 10+0 | 1.0144 × 10+1 | 2.2900 × 10+0 | 3.8767 × 10+0 | 1.8697 × 10+0 | 1.1 × 10+2 |
| F5 | 1.360 × 10+0 | 1.2026 × 10+2 | 6.01 × 10+1 | 6.22 × 10+1 | 1.2524 × 10+6 | 1.2057 × 10+4 | 7.2997 × 10+5 | 7.5903 × 10+5 | 1.6 × 10+2 |
| F6 | 2.990 × 10−1 | 9.8700 × 10−5 | 8.28 × 10−5 | 1.74 × 10−16 | 4.9176 × 10+3 | 6.3453 × 10+1 | 3.2952 × 10+3 | 9.7521 × 10+2 | 3.4 × 10−1 |
| F7 | 1.993 × 10−4 | 4.6420 × 10−2 | 4.50 × 10−2 | 4.34 × 10−2 | 3.0453 × 10+0 | 6.1212 × 10−2 | 2.4015 × 10−2 | 4.6006 × 10−1 | 5.3 × 10−2 |
| (b) | |||||||||
| SWSO | WOA | FEP | IACO | VGWO | INFO | SCA | GWO | RIME | |
| F | Ave | ||||||||
| F1 | 1.2466 × 10−84 | 1.41 × 10−30 | 5.70 × 10−4 | −2.0 × 10+2 | −2.0 × 10+2 | 5.453 × 10−53 | 2.125 × 10+2 | 7.667 × 10−22 | 6.491 × 10+0 |
| F2 | 1.5366 × 10−48 | 1.06 × 10−21 | 8.10 × 10−3 | 3.3 × 10−3 | 5.4 × 10−2 | 3.880 × 10−26 | 4.671 × 10−1 | 1.344 × 10−13 | 4.601 × 10+0 |
| F3 | 3.5466 × 10−86 | 5.39 × 10−7 | 1.60 × 10−2 | 1.4 × 10−2 | 8.0 × 10−3 | 6.698 × 10−50 | 2.290 × 10+4 | 2.249 × 10−3 | 3.317 × 10+3 |
| F4 | 9.2386 × 10−53 | 7.26 × 10−2 | 3.00 × 10−1 | −1.6 × 10+2 | −3.3 × 10+2 | 6.986 × 10−27 | 5.866 × 10+1 | 5.559 × 10−5 | 1.952 × 10+1 |
| F5 | 4.214 × 10+0 | 2.79 × 10+1 | 5.06 × 10+0 | 3.2 × 10+1 | 1.3 × 10+1 | 2.542 × 10+1 | 2.570 × 10+6 | 2.877 × 10+1 | 2.489 × 10+3 |
| F6 | 1.039 × 10+0 | 3.12 × 10+0 | 0 | 7.4 × 10−2 | 1.5 × 10−1 | 6.157 × 10−6 | 3.62 × 10+2 | 1.764 × 10+0 | 6.476 × 10+0 |
| F7 | 3.027 × 10−4 | 1.43 × 10−3 | 1.42 × 10−1 | 1.5 × 10−2 | 8.1 × 10−3 | 4.792 × 10−3 | 1.944 × 10+0 | 5.162 × 10−3 | 9.443 × 10−2 |
| F | SD | ||||||||
| F1 | 6.326 × 10−84 | 4.91 × 10−30 | 1.30 × 10−4 | 5.8 × 10−1 | 4.1 × 10−1 | 1.48 × 10−53 | 5.474 × 10+1 | 1.84 × 10−22 | 1.285 × 10+0 |
| F2 | 6.4714 × 10−48 | 2.39 × 10−21 | 7.70 × 10−4 | 3.8 × 10−2 | 3.7 × 10−2 | 7.744 × 10−27 | 1.78 × 10−1 | 3.639 × 10−14 | 9.219 × 10−1 |
| F3 | 2.4891 × 10−85 | 2.93 × 10−6 | 1.40 × 10−2 | 1.8 × 10−1 | 1.1 × 10−1 | 1.956 × 10−50 | 6.724 × 10+3 | 6.62 × 10−4 | 6.295 × 10+2 |
| F4 | 6.5246 × 10−52 | 3.97 × 10−1 | 5.00 × 10−1 | 7.8 × 10+1 | 2.2 × 10+2 | 1.587 × 10−27 | 1.170 × 10+1 | 1.372 × 10−5 | 4.246 × 10+0 |
| F5 | 1.360 × 10+0 | 7.64 × 10−1 | 5.87 × 10+0 | 5.5 × 10+2 | 2.8 × 10+2 | 5.659 × 10−1 | 5.99 × 10+5 | 9.021 × 10−1 | 5.231 × 10+2 |
| F6 | 2.990 × 10−1 | 5.32 × 10−1 | 0 | 9.2 × 10−1 | 2.7 × 10+0 | 1.370 × 10−6 | 8.40 × 10+1 | 4.020 × 10−1 | 1.130 × 10+0 |
| F7 | 1.993 × 10−4 | 1.15 × 10−3 | 3.52 × 10−1 | 2.5 × 10−1 | 1.4 × 10−1 | 1.133 × 10−3 | 4.345 × 10−1 | 1.355 × 10−3 | 1.997 × 10−2 |
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA | ||
| F | Ave | |||||||||
| F8 | −2.1935 × 10+3 | −8.505 × 10+3 | −3.575 × 10+3 | −2.355 × 10+3 | 6.555 × 10+4 | −8.095 × 10+3 | −3.945 × 10+3 | −3.665 × 10+3 | −6.335 × 10+3 | |
| F9 | 0 | 8.465 × 10+1 | 1.245 × 10+2 | 3.105 × 10+1 | 9.625 × 10+1 | 9.275 × 10+1 | 1.535 × 10+2 | 2.155 × 10+2 | 2.375 × 10+2 | |
| F10 | 8.8825 × 10−16 | 1.265 × 10+0 | 9.175 × 10+0 | 3.745 × 10+0 | 1.595 × 10+1 | 6.845 × 10+0 | 1.915 × 10+1 | 1.465 × 10+1 | 1.785 × 10+1 | |
| F11 | 0 | 1.915 × 10−2 | 1.245 × 10+1 | 4.875 × 10−1 | 2.205 × 10+2 | 2.725 × 10+0 | 4.215 × 10+2 | 6.975 × 10+1 | 1.805 × 10+2 | |
| F12 | 5.0135 × 10−2 | 8.945 × 10−1 | 1.395 × 10+1 | 4.635 × 10−1 | 2.895 × 10+7 | 4.115 × 10+0 | 8.745 × 10+6 | 3.685 × 10+5 | 3.415 × 10+7 | |
| F13 | 1.715 × 10−1 | 1.165 × 10−1 | 1.185 × 10+4 | 7.625 × 10+0 | 1.095 × 10+8 | 6.245 × 10+1 | 1.005 × 10+8 | 5.565 × 10+6 | 1.085 × 10+8 | |
| F | SD | |||||||||
| F8 | 2.3185 × 10+2 | 7.265 × 10+2 | 4.315 × 10+2 | 3.825 × 10+2 | 0 | 1.555 × 10+2 | 4.045 × 10+2 | 2.145 × 10+2 | 3.335 × 10+2 | |
| F9 | 0 | 1.625 × 10+1 | 1.435 × 10+1 | 1.375 × 10+1 | 1.965 × 10+1 | 1.425 × 10+1 | 1.865 × 10+1 | 1.725 × 10+1 | 1.905 × 10+1 | |
| F10 | 0 | 7.305 × 10−1 | 1.575 × 10+0 | 1.715 × 10−1 | 7.755 × 10−1 | 1.255 × 10+0 | 2.395 × 10−1 | 4.685 × 10−1 | 5.315 × 10−1 | |
| F11 | 0 | 2.175 × 10−2 | 4.175 × 10+0 | 4.985 × 10−2 | 5.475 × 10+1 | 7.285 × 10−1 | 2.535 × 10+1 | 1.215 × 10+1 | 3.245 × 10+1 | |
| F12 | 1.2485 × 10−2 | 8.815 × 10−1 | 5.855 × 10+0 | 1.385 × 10−1 | 2.185 × 10+6 | 1.045 × 10+0 | 1.415 × 10+6 | 1.725 × 10+5 | 1.895 × 10+6 | |
| F13 | 3.035 × 10−2 | 1.935 × 10−1 | 3.075 × 10+4 | 1.235 × 10+0 | 1.055 × 10+8 | 9.485 × 10+1 | 0 | 1.695 × 10+6 | 3.855 × 10+6 | |
| (b) | ||||||||||
| SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA | |
| F | Ave | |||||||||
| F8 | −2.1935 × 10+3 | −1.2575 × 10+4 | −6.9225 × 10+3 | −4.8135 × 10+3 | −1.525 × 10+4 | −3.3845 × 10+3 | −1.2565 × 10+4 | −4.5665 × 10+3 | −8.7595 × 10+3 | −5.425 × 10+3 |
| F9 | 0 | 0 | 0 | 0 | 0 | 1.2665 × 10+2 | 0 | 1.4675 × 10+1 | 9.3545 × 10+1 | 0 |
| F10 | 8.8825 × 10−16 | 8.8825 × 10−16 | 8.8825 × 10−16 | 8.8825 × 10−16 | 8.8825 × 10−16 | 2.345 × 10+ 01 | 8.8825 × 10−16 | 4.3005 × 10−12 | 3.925 × 10+0 | 8.8825 × 10−16 |
| F11 | 0 | 0 | 0 | 0 | 0 | 5.6205 × 10+0 | 0 | 1.9015 × 10−2 | 1.4605 × 10+0 | 0 |
| F12 | 5.0135 × 10−2 | 2.4215 × 10−5 | 1.375 × 10−1 | 2.3375 × 10−1 | 9.175 × 10−7 | 1.785 × 10+7 | 4.9735 × 10−5 | 1.465 × 10−1 | 1.3565 × 10+1 | 4.2465 × 10−1 |
| F13 | 1.715 × 10−1 | 4.175 × 10−1 | 4.655 × 10−1 | 2.895 × 10+0 | 1.145 × 10−7 | 4.245 × 10+6 | 2.085 × 10−4 | 1.195 × 10+0 | 8.905 × 10−1 | 2.885 × 10+0 |
| F | SD | |||||||||
| F8 | 2.3185 × 10+2 | 5.2525 × 10−4 | 9.2505 × 10+2 | 9.7165 × 10+2 | 7.295 × 10+2 | 2.6695 × 10+2 | 2.8885 × 10+0 | 8.1675 × 10+2 | 5.5385 × 10+2 | 6.7835 × 10+2 |
| F9 | 0 | 0 | 0 | 0 | 0 | 3.8275 × 10+1 | 0 | 3.6605 × 10+0 | 1.4315 × 10+1 | 0 |
| F10 | 0 | 0 | 0 | 0 | 0 | 7.895 × 10+0 | 0 | 8.9845 × 10−13 | 5.365 × 10−1 | 0 |
| F11 | 0 | 0 | 0 | 0 | 0 | 9.2435 × 10−1 | 0 | 5.5835 × 10−3 | 3.2275 × 10−2 | 0 |
| F12 | 1.2485 × 10−2 | 5.4135 × 10−6 | 2.3185 × 10−2 | 5.9155 × 10−2 | 1.9025 × 10−7 | 2.5155 × 10+6 | 1.6985 × 10−5 | 4.0165 × 10−2 | 3.4205 × 10+0 | 9.1455 × 10−2 |
| F13 | 3.035 × 10−2 | 1.165 × 10−1 | 1.075 × 10−1 | 2.755 × 10−1 | 3.945 × 10−8 | 1.3405 × 10+6 | 5.535 × 10−5 | 2.465 × 10−1 | 1.645 × 10−1 | 3.475 × 10−1 |
| SWSO | MFO | PSO | GSA | BA | FPA | SMS | FA | GA | |
|---|---|---|---|---|---|---|---|---|---|
| F | Ave | ||||||||
| F14 | 9.980 × 10−1 | 8.25 × 10−31 | 1.38 × 10+2 | 5.43 × 10−19 | 1.30 × 10+2 | 1.01 × 10+1 | 1.06 × 10+2 | 1.76 × 10+2 | 9.21 × 10+1 |
| F15 | 4.661 × 10−4 | 6.67 × 10+1 | 1.67 × 10+2 | 2.04 × 10+1 | 5.44 × 10+2 | 1.14 × 10+1 | 1.56 × 10+2 | 3.54 × 10+2 | 9.67 × 10+1 |
| F16 | −1.03+0 | 1.19 × 10+2 | 3.95 × 10+2 | 2.45 × 10+2 | 6.97 × 10+2 | 2.35 × 10+2 | 4.07 × 10+2 | 3.08 × 10+2 | 3.69 × 10+2 |
| F17 | 4.286 × 10−1 | 3.45 × 10+2 | 4.86 × 10+2 | 3.15 × 10+2 | 7.45 × 10+2 | 3.55 × 10+2 | 5.19 × 10+2 | 5.49 × 10+2 | 4.51 × 10+2 |
| F18 | 3.0908+0 | 1.04 × 10+1 | 2.57 × 10+2 | 7.00 × 10+1 | 5.44 × 10+2 | 5.48 × 10+1 | 1.54 × 10+2 | 1.75 × 10+2 | 9.59 × 10+1 |
| F19 | −3.8617+0 | 7.07 × 10+2 | 7.90 × 10+2 | 8.82 × 10+2 | 8.96 × 10+2 | 5.73 × 10+2 | 6.12 × 10+2 | 8.30 × 10+2 | 5.24 × 10+2 |
| F | SD | ||||||||
| F14 | 1.235 × 10−4 | 1.08 × 10−30 | 1.16 × 10+2 | 1.35 × 10−19 | 1.19 × 10+2 | 3.16 × 10+1 | 2.69 × 10+1 | 8.69 × 10+1 | 2.79 × 10+1 |
| F15 | 7.774 × 10−5 | 5.32 × 10+1 | 1.64 × 10+2 | 6.31 × 10+1 | 1.49 × 10+2 | 3.38 × 10+0 | 6.82 × 10+1 | 1.03 × 10+2 | 9.70 × 10+0 |
| F16 | 8.761 × 10−4 | 2.83 × 10+1 | 1.22 × 10+2 | 4.91 × 10+1 | 1.91 × 10+2 | 3.96 × 10+1 | 6.54 × 10+1 | 3.74 × 10+1 | 4.28 × 10+1 |
| F17 | 2.721 × 10−2 | 4.31 × 10+1 | 6.73 × 10+1 | 1.01 × 10+2 | 1.43 × 10+2 | 2.06 × 10+1 | 4.27 × 10+1 | 1.63 × 10+2 | 3.15 × 10+1 |
| F18 | 9.449 × 10−2 | 3.75 × 10+0 | 2.00 × 10+2 | 4.83 × 10+1 | 1.99 × 10+2 | 4.21 × 10+1 | 9.69 × 10+1 | 8.32 × 10+1 | 5.38 × 10+1 |
| F19 | 3.57 × 10−4 | 1.95 × 10+2 | 1.89 × 10+2 | 4.52 × 10+1 | 8.63 × 10+1 | 1.49 × 10+2 | 1.55 × 10+2 | 1.57 × 10+2 | 2.29 × 10+1 |
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SWSO | MINFO | INFO | SCSO | AVOA | SCA | HHO | GWO | RIME | ZOA | |
| F | Ave | |||||||||
| Cec01 | 9.55 × 10+8 | 3.84 × 10+3 | 5.50 × 10+4 | 5.37 × 10+4 | 5.46 × 10+4 | 5.45 × 10+10 | 8.73 × 10+3 | 3.47 × 10+8 | 1.45 × 10+10 | 5.53 × 10+4 |
| Cec02 | 1.84 × 10+1 | 1.83 × 10+1 | 1.83 × 10+1 | 1.87 × 10+1 | 1.83 × 10+1 | 1.92 × 10+1 | 1.84 × 10+1 | 1.87 × 10+1 | 2.03 × 10+1 | 1.92 × 10+1 |
| Cec03 | 1.370 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 |
| Cec04 | 4.84 × 10+1 | 1.18 × 10+2 | 2.47 × 10+2 | 2.63 × 10+3 | 3.39 × 10+2 | 3.89 × 10+2 | 9.17 × 10+2 | 1.14 × 10+2 | 6.33 × 10+1 | 3.59 × 10+2 |
| Cec05 | 2.09 × 10+0 | 2.29 × 10+0 | 2.35 × 10+0 | 3.28 × 10+0 | 3.24 × 10+0 | 3.84 × 10+0 | 4.65 × 10+0 | 2.85 × 10+0 | 2.49 × 10+0 | 4.24 × 10+0 |
| Cec06 | 1.07 × 10+1 | 1.02 × 10+1 | 1.16 × 10+1 | 1.16 × 10+1 | 1.08 × 10+1 | 1.30 × 10+1 | 1.26 × 10+1 | 1.32 × 10+1 | 1.11 × 10+1 | 1.09 × 10+1 |
| Cec07 | 2.82 × 10+2 | 3.21 × 10+2 | 5.97 × 10+2 | 9.64 × 10+2 | 9.37 × 10+2 | 1.21 × 10+3 | 7.51 × 10+2 | 8.76 × 10+2 | 4.10 × 10+2 | 3.02 × 10+2 |
| Cec08 | 2.88 × 10+0 | 5.65 × 10+0 | 6.33 × 10+0 | 6.57 × 10+0 | 7.16 × 10+0 | 6.73 × 10+0 | 7.27 × 10+0 | 7.25 × 10+0 | 5.82 × 10+0 | 5.60 × 10+0 |
| Cec09 | 3.47 × 10+0 | 3.99 × 10+0 | 4.54 × 10+0 | 3.58 × 10+2 | 5.58 × 10+0 | 4.03 × 10+2 | 6.62 × 10+0 | 7.98 × 10+0 | 3.81 × 10+0 | 3.88 × 10+2 |
| Cec10 | 1.97 × 10+1 | 2.12 × 10+1 | 2.14 × 10+1 | 2.14 × 10+1 | 2.12 × 10+1 | 2.16 × 10+1 | 2.16 × 10+1 | 2.16 × 10+1 | 2.12 × 10+1 | 2.13 × 10+1 |
| F | SD | |||||||||
| Cec01 | 8.48 × 10+8 | 1.19 × 10+3 | 1.33 × 10+4 | 3.52 × 10+3 | 3.49 × 10+3 | 1.38 × 10+10 | 8.79 × 10+3 | 1.11 × 10+8 | 3.49 × 10+9 | 4.27 × 10+3 |
| Cec02 | 5.75 × 10−2 | 3.65 × 10−15 | 3.46 × 10−15 | 1.27 × 10−1 | 1.31 × 10−4 | 1.75 × 10−1 | 9.78 × 10−2 | 1.39 × 10−1 | 4.37 × 10−1 | 3.00 × 10−1 |
| Cec03 | 1.11 × 10−9 | 1.82 × 10−15 | 2.80 × 10−15 | 2.82 × 10−6 | 1.50 × 10−10 | 8.37 × 10−5 | 8.70 × 10−6 | 9.36 × 10−6 | 3.80 × 10−9 | 2.40 × 10−5 |
| Cec04 | 1.06 × 10+1 | 3.27 × 10+1 | 5.28 × 10+1 | 7.55 × 10+2 | 6.74 × 10+1 | 6.88 × 10+2 | 1.98 × 10+2 | 1.72 × 10+1 | 1.15 × 10+1 | 1.79 × 10+2 |
| Cec05 | 5.83 × 10−2 | 6.23 × 10−1 | 7.29 × 10−1 | 2.83 × 10−1 | 3.76 × 10−1 | 1.86 × 10−1 | 5.93 × 10−1 | 2.43 × 10−1 | 1.18 × 10−1 | 5.63 × 10−1 |
| Cec06 | 6.00 × 10−1 | 1.86 × 10+0 | 2.26 × 10+0 | 1.60 × 10+0 | 2.20 × 10+0 | 7.68 × 10−1 | 1.25 × 10+0 | 6.62 × 10−1 | 1.37 × 10+0 | 8.72 × 10−1 |
| Cec07 | 1.72 × 10+2 | 1.19 × 10+2 | 2.39 × 10+2 | 2.88 × 10+1 | 2.58 × 10+2 | 2.52 × 10+2 | 1.52 × 10+2 | 2.38 × 10+2 | 1.67 × 10+2 | 1.22 × 10+2 |
| Cec08 | 7.45 × 10−1 | 8.95 × 10−1 | 7.54 × 10−1 | 6.25 × 10−1 | 6.94 × 10−1 | 3.44 × 10−1 | 5.76 × 10−1 | 9.34 × 10−1 | 6.48 × 10−1 | 3.40 × 10−1 |
| Cec09 | 5.39 × 10−2 | 1.38 × 10−1 | 2.78 × 10−1 | 9.89 × 10+1 | 6.42 × 10−1 | 1.01 × 10+2 | 6.14 × 10−1 | 1.06 × 10+0 | 1.00 × 10−1 | 1.20 × 10+2 |
| Cec10 | 5.10 × 10+0 | 3.58 × 10+0 | 1.46 × 10−1 | 1.15 × 10−1 | 5.66 × 10−1 | 9.52 × 10−1 | 1.60 × 10−1 | 2.96 × 10+0 | 5.73 × 10−1 | 1.44 × 10+0 |
| (b) | ||||||||||
| SWSO | IWOA | NRO | BDA | CEBA | IPSO | IAGA | BBOA | FOX | IFOX | |
| F | Ave | |||||||||
| Cec01 | 9.55 × 10+8 | 1.1 × 10+8 | 4.5 × 10+6 | 6.6 × 10+7 | 9.8 × 10+8 | 1.1 × 10+7 | 5.5 × 10+7 | 7.2 × 10+6 | 6.2 × 10+2 | 7.0 × 10+5 |
| Cec02 | 1.84 × 10+1 | 5.0 × 10+3 | 1.3 × 10+2 | 8.2 × 10+2 | 4.7 × 10+3 | 5.9 × 10+2 | 1.4 × 10+3 | 8.9 × 10+1 | 5.3 × 10+0 | 1.5 × 10+1 |
| Cec03 | 1.370 × 10+1 | 5.8 × 10+0 | 6.1 × 10+0 | 8.0 × 10+0 | 1.2 × 10+1 | 5.4 × 10+0 | 5.8 × 10+0 | 4.8 × 10+0 | 1.2 × 10+1 | 7.5 × 10+0 |
| Cec04 | 4.84 × 10+1 | 3.7 × 10+3 | 2.9 × 10+2 | 3.4 × 10+3 | 1.8 × 10+4 | 2.7 × 10+2 | 3.7 × 10+2 | 9.9 × 10+3 | 2.4 × 10+4 | 2.3 × 10+2 |
| Cec05 | 2.09 × 10+0 | 2.6 × 10+0 | 1.3 × 10+0 | 2.5 × 10+0 | 6.4 × 10+0 | 1.4 × 10+0 | 1.7 × 10+0 | 3.4 × 10+0 | 5.2 × 10+0 | 1.7 × 10+0 |
| Cec06 | 1.07 × 10+1 | 1.1 × 10+1 | 1.1 × 10+1 | 1.2 × 10+1 | 1.4 × 10+1 | 1.1 × 10+1 | 8.1 × 10+0 | 1.1 × 10+1 | 1.2 × 10+1 | 1.1 × 10+1 |
| Cec07 | 2.82 × 10+2 | 4.4 × 10+2 | 2.8 × 10+1 | 3.2 × 10+2 | 1.3 × 10+3 | 9.9 × 10+1 | 5.3 × 10+1 | 6.0 × 10+2 | 1.3 × 10+3 | 1.6 × 10+2 |
| Cec08 | 2.88 × 10+0 | 1.1 × 10+0 | 1.0 × 10+0 | 1.1 × 10+0 | 1.8 × 10+0 | 1.0 × 10+0 | 1.0 × 10+0 | 1.3 × 10+0 | 1.6 × 10+0 | 1.0 × 10+0 |
| Cec09 | 3.47 × 10+0 | 5.6 × 10+1 | 9.3 × 10+0 | 1.1 × 10+2 | 8.8 × 10+2 | 9.3 × 10+0 | 1.4 × 10+1 | 2.2 × 10+2 | 8.7 × 10+2 | 6.3 × 10+0 |
| Cec10 | 1.97 × 10+1 | 2.1 × 10+1 | 2.1 × 10+1 | 2.2 × 10+1 | 2.2 × 10+1 | 2.2 × 10+1 | 2.1 × 10+1 | 2.1 × 10+1 | 2.2 × 10+1 | 2.2 × 10+1 |
| F | SD | |||||||||
| Cec01 | 8.48 × 10+8 | 1.5 × 10+8 | 3.5 × 10+7 | 2.5 × 10+8 | 4.2 × 10+7 | 5.8 × 10+7 | 5.9 × 10+7 | 5.9 × 10+7 | 1.4 × 10+4 | 1.3 × 10+7 |
| Cec02 | 5.75 × 10−2 | 4.2 × 10+2 | 3.9 × 10+2 | 2.0 × 10+3 | 2.0 × 10+2 | 4.5 × 10+2 | 4.3 × 10+2 | 4.2 × 10+2 | 5.6 × 10+0 | 1.6 × 10+2 |
| Cec03 | 1.11 × 10−9 | 1.5 × 10+0 | 2.2 × 10+0 | 1.6 × 10+0 | 9.8 × 10−2 | 2.2 × 10+0 | 1.5 × 10+0 | 1.1 × 10+0 | 5.0 × 10−2 | 9.2 × 10−1 |
| Cec04 | 1.06 × 10+1 | 2.1 × 10+3 | 1.5 × 10+3 | 6.0 × 10+3 | 2.0 × 10+3 | 1.3 × 10+3 | 1.4 × 10+3 | 1.4 × 10+3 | 3.4 × 10+2 | 1.2 × 10+3 |
| Cec05 | 5.83 × 10−2 | 3.8 × 10−1 | 4.8 × 10−1 | 1.1 × 10+0 | 2.8 × 10−1 | 3.8 × 10−1 | 4.1 × 10−1 | 2.9 × 10−1 | 1.4 × 10−1 | 3.7 × 10−1 |
| Cec06 | 6.00 × 10−1 | 8.4 × 10−1 | 8.0 × 10−1 | 3.9 × 10−1 | 7.3 × 10−2 | 7.6 × 10−1 | 1.2 × 10+0 | 7.0 × 10−1 | 5.8 × 10−1 | 6.2 × 10−1 |
| Cec07 | 1.72 × 10+2 | 1.6 × 10+2 | 1.2 × 10+2 | 4.1 × 10+2 | 5.3 × 10+1 | 1.2 × 10+2 | 1.1 × 10+2 | 1.1 × 10+2 | 3.2 × 10+1 | 9.5 × 10+1 |
| Cec08 | 7.45 × 10−1 | 1.0 × 10−1 | 5.4 × 10−2 | 2.6 × 10−1 | 6.1 × 10−2 | 5.1 × 10−2 | 6.0 × 10−2 | 4.9 × 10−2 | 4.9 × 10−2 | 4.9 × 10−2 |
| Cec09 | 5.39 × 10−2 | 8.9 × 10+1 | 4.7 × 10+1 | 2.2 × 10+2 | 1.7 × 10+1 | 5.0 × 10+1 | 5.4 × 10+1 | 5.6 × 10+1 | 4.9 × 10+0 | 3.7 × 10+1 |
| Cec10 | 5.10 × 10+0 | 1.7 × 10−1 | 6.2 × 10−1 | 8.6 × 10−2 | 1.0 × 10−2 | 1.1 × 10−1 | 1.3 × 10−1 | 3.3 × 10−1 | 7.4 × 10−2 | 8.0 × 10−2 |
| (c) | ||||||||||
| SWSO | Hybrid FOX−TSA | FOX | TSA | PSO | GWO | MRSO | RSO | |||
| F | Ave | |||||||||
| Cec01 | 9.55 × 10+8 | 2.33 × 10−6 | 6.51 × 10+3 | 1.60 × 10+3 | 1.33 × 10+3 | 3.05 × 10+3 | 1.588 × 10+5 | 6.263 × 10+4 | ||
| Cec02 | 1.84 × 10+1 | 1.71 × 10+1 | 1.83 × 10+1 | 1.74 × 10+1 | 1.73 × 10+1 | 1.73 × 10+1 | 1.83 × 10+1 | 1.84 × 10+1 | ||
| Cec03 | 1.37 × 10+1 | 1.27 × 10+1 | 1.370 × 10+1 | 1.27 × 10+1 | 1.27 × 10+1 | 1.27 × 10+1 | 1.37 × 10+1 | 1.37 × 10+1 | ||
| Cec04 | 4.84 × 10+1 | 1.37 × 10+3 | 1.80 × 10+1 | 4.76 × 10+1 | 6.37 × 10+1 | 4.13 × 10+1 | 9.20 × 10+3 | 8.86 × 10+3 | ||
| Cec05 | 2.09 × 10+0 | 1.92 × 10+0 | 6.30 × 10+0 | 1.55 × 10+0 | 1.26 × 10+0 | 1.35 × 10+0 | 4.57 × 10+0 | 4.631 × 10+0 | ||
| Cec06 | 1.07 × 10+1 | 8.39 × 10+0 | 5.68 × 10+0 | 1.03 × 10+1 | 6.51 × 10+0 | 1.06 × 10+1 | 1.09 × 10+1 | 1.16 × 10+1 | ||
| Cec07 | 2.82 × 10+2 | 3.12 × 10+2 | 4.56 × 10+2 | 2.96 × 10+2 | 1.65 × 10+2 | 3.85 × 10+2 | 6.11 × 10+2 | 7.89 × 10+2 | ||
| Cec08 | 2.88 × 10+0 | 5.28 × 10+0 | 5.68 × 10+0 | 5.71 × 10+0 | 5.19 × 10+0 | 4.60 × 10+0 | 6.31 × 10+0 | 6.32 × 10+0 | ||
| Cec09 | 3.47 × 10+0 | 1.35 × 10+0 | 3.80 × 10+0 | 2.43 × 10+0 | 2.79 × 10+0 | 3.99 × 10+0 | 4.96 × 10+2 | 5.86 × 10+2 | ||
| Cec10 | 1.97 × 10+1 | 2.01 × 10+1 | 2.10 × 10+1 | 2.04 × 10+1 | 2.08 × 10+1 | 2.03 × 10+1 | 2.13 × 10+1 | 2.14 × 10+1 | ||
| F | SD | |||||||||
| Cec01 | 8.48 × 10+8 | 2.65 × 10−3 | 2.73 × 10+4 | 2.68 × 10+2 | 8.21 × 10+2 | 1.93 × 10+3 | 3.199 × 10+5 | 1.392 × 10+4 | ||
| Cec02 | 5.75 × 10−2 | 7.52 × 10−2 | 4.60 × 10−4 | 1.35 × 10−2 | 6.63 × 10−15 | 1.13 × 10−4 | 7.231 × 10−3 | 1.981 × 10−1 | ||
| Cec03 | 1.11 × 10−9 | 1.02 × 10−9 | 8.42 × 10−4 | 1.13 × 10−3 | 6.78 × 10−4 | 1.04 × 10−3 | 1.337 × 10−6 | 1.828 × 10−4 | ||
| Cec04 | 1.06 × 10+0 | 8.77 × 10+2 | 6.98 × 10+0 | 8.78 × 10+0 | 3.38 × 10+1 | 1.53 × 10+1 | 3.203 × 10+3 | 2.152 × 10+3 | ||
| Cec05 | 5.83 × 10−2 | 1.15 × 10−1 | 7.49 × 10−1 | 2.39 × 10−1 | 9.23 × 10−2 | 2.00 × 10−1 | 4.133 × 10−1 | 4.290 × 10−1 | ||
| Cec06 | 6.00 × 10−1 | 6.39 × 10−1 | 1.59 × 10+0 | 4.19 × 10−1 | 1.44 × 10+0 | 4.90 × 10−1 | 1.011 × 10+0 | 8.597 × 10−1 | ||
| Cec07 | 1.72 × 10+2 | 1.45 × 10+2 | 1.97 × 10+2 | 1.62 × 10+2 | 1.05 × 10+2 | 3.33 × 10+2 | 2.291 × 10+2 | 2.154 × 10+2 | ||
| Cec08 | 7.45 × 10−1 | 3.46 × 10−1 | 3.62 × 10−1 | 6.05 × 10−1 | 4.87 × 10−1 | 1.00 × 10+0 | 4.138 × 10−1 | 4.334 × 10−1 | ||
| Cec09 | 5.39 × 10−2 | 9.61 × 10+0 | 6.09 × 10−3 | 2.97 × 10−2 | 3.61 × 10−1 | 9.07 × 10−1 | 1.493 × 10+2 | 1.362 × 10+2 | ||
| Cec10 | 5.10 × 10+0 | 8.16 × 10−2 | 8.72 × 10−3 | 8.11 × 10−2 | 4.76 × 10+0 | 4.89 × 10−1 | 1.490 × 10−1 | 1.116 × 10−1 | ||
| References | Algorithm | Minimum Cost | h | l | t | b |
|---|---|---|---|---|---|---|
| Proposed model | SWSO | 1.5878 | 0.1677 | 4.0646 | 9.9985 | 0.1682 |
| [97] | SMR | 1.6570 | 0.2016 | 3.2324 | 9.0461 | 0.2057 |
| [96] | MSSSA | 1.6952 | 0.2041 | 3.2830 | 9.0366 | 0.2057 |
| [98] | FDA | 1.6954 | 0.2055 | 3.2578 | 9.0366 | 0.2057 |
| [99] | CEBA | 1.6977 | 0.2047 | 3.2734 | 9.0390 | 0.2058 |
| [100] | AZOA | 1.7200 | 0.4690 | 1.9400 | 5.7200 | 0.5140 |
| [12] | RIME | 1.722821 | 0.2080 | 3.2500 | 9.0537 | 0.2086 |
| [101] | WCMFO | 1.7235 | 0.2067 | 3.4495 | 9.0367 | 0.2057 |
| [77] | MFO | 1.72452 | 0.2057 | 3.4703 | 9.0364 | 0.2057 |
| [102] | CBO | 1.7246 | 0.2057 | 3.4704 | 9.0372 | 0.2057 |
| [103] | SSO-C | 1.7248 | 0.2057 | 3.4704 | 9.0366 | 0.2057 |
| [15] | ABC | 1.7248 | 0.2057 | 3.4704 | 9.0366 | 0.2057 |
| [104] | MSHO | 1.7248 | 0.2057 | 3.4704 | 9.0366 | 0.2057 |
| [105] | SO | 1.7248 | 0.2057 | 3.4705 | 9.0366 | 0.2057 |
| [106] | ACSA | 1.7249 | 0.2057 | 3.4705 | 9.0366 | 0.2057 |
| [107] | MVO | 1.7254 | 0.2056 | 3.4721 | 9.0409 | 0.2057 |
| [90] | SCA | 1.7591 | 0.2046 | 3.5362 | 9.0042 | 0.2100 |
| [80] | BA | 1.7851 | 0.2026 | 3.5271 | 9.0075 | 0.2105 |
| [108] | GA | 1.8739 | 0.1641 | 4.0325 | 10.000 | 0.2236 |
| [109] | ASO | 2.0868 | 0.1753 | 7.9569 | 9.8477 | 0.1732 |
| [79] | GSA | 2.1728 | 0.1470 | 5.4907 | 10.000 | 0.2177 |
| [110] | WEOA | 2.2182 | 0.2057 | 7.0923 | 9.0366 | 0.2057 |
| [111] | MSCA | 2.3832 | 0.2442 | 6.2063 | 8.3121 | 0.2443 |
| Parameters | Parameter’s Title | Type of Variable |
|---|---|---|
| = | shell thickness | Discrete |
| = | head thickness | Discrete |
| = | inner radius | Continuous |
| = | length of the vessel cylindrical section | Continuous |
| References | Algorithm | Minimum Cost | R | L | ||
|---|---|---|---|---|---|---|
| Case-A | ||||||
| This paper | SWSO | 5754.7738 | 0.7448 | 0.3792 | 40.6413 | 195.6608 |
| [118] | EJS | 5870.1250 | 0.7770 | 0.3848 | 40.4253 | 198.5706 |
| [88] | GWO | 5870.3903 | 0.7741 | 0.3833 | 40.3196 | 200.0000 |
| [119] | MOCH-PSO | 5971.4003 | 0.7964 | 0.3994 | 41.0039 | 190.8011 |
| [120] | CSS | 6059.0888 | 0.8125 | 0.4375 | 42.1036 | 176.5726 |
| [121] | MDE | 6059.7016 | 0.8125 | 0.4375 | 42.0984 | 176.6360 |
| [77] | MFO | 6059.7143 | 0.8125 | 0.4375 | 42.0984 | 176.6365 |
| [85] | WOA | 6059.7410 | 0.8125 | 0.4375 | 42.0983 | 176.6390 |
| [12] | RIME | 6055.5868 | 0.8750 | 0.4375 | 45.9482 | 135.3594 |
| Case-B | ||||||
| This paper | SWSO | 5770.3503 | 0.7650 | 0.3761 | 41.1353 | 188.9529 |
| [122] | GA-PSO-SQP | 5798.7989 | 0.8809 | 0.4337 | 45.6342 | 137.2499 |
| [115] | CSA | 5888.5213 | 0.8259 | 0.3814 | 42.7444 | 168.7212 |
| [120] | ACO | 6059.0888 | 0.8125 | 0.4375 | 42.1036 | 176.5727 |
| [113] | CS | 6059.7143 | 0.8125 | 0.4375 | 42.0984 | 176.6365 |
| [80] | BA | 6059.7143 | 0.8125 | 0.4375 | 42.0984 | 176.6365 |
| [28] | IPSO | 6059.7143 | 0.8125 | 0.4375 | 42.0984 | 176.6366 |
| [24] | CPSO | 6061.0777 | 0.8125 | 0.4375 | 42.0912 | 176.7465 |
| [123] | Branch-bound | 8129.1036 | 1.1250 | 0.6250 | 47.7000 | 117.7010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoshaba, F.S.; Kareem, S.W.; Hawezi, R.S. Swallow Search Algorithm (SWSO): A Swarm Intelligence Optimization Approach Inspired by Swallow Bird Behavior. Computers 2025, 14, 345. https://doi.org/10.3390/computers14090345
Khoshaba FS, Kareem SW, Hawezi RS. Swallow Search Algorithm (SWSO): A Swarm Intelligence Optimization Approach Inspired by Swallow Bird Behavior. Computers. 2025; 14(9):345. https://doi.org/10.3390/computers14090345
Chicago/Turabian StyleKhoshaba, Farah Sami, Shahab Wahhab Kareem, and Roojwan Sc Hawezi. 2025. "Swallow Search Algorithm (SWSO): A Swarm Intelligence Optimization Approach Inspired by Swallow Bird Behavior" Computers 14, no. 9: 345. https://doi.org/10.3390/computers14090345
APA StyleKhoshaba, F. S., Kareem, S. W., & Hawezi, R. S. (2025). Swallow Search Algorithm (SWSO): A Swarm Intelligence Optimization Approach Inspired by Swallow Bird Behavior. Computers, 14(9), 345. https://doi.org/10.3390/computers14090345









