A Decision Support System for Classifying Suppliers Based on Machine Learning Techniques: A Case Study in the Aeronautics Industry
Abstract
1. Introduction
2. Theoretical Framework
2.1. Machine Learning Techniques for Clustering
2.1.1. K-Means
An Elbow Method Algorithm
The Gap Statistic Algorithm
The Silhouette Coefficient Algorithm
The Canopy Algorithm
2.1.2. Hierarchical K-Means
- Agglomerative hierarchical clustering (from bottom to top), which operates as follows: It starts with n clusters, where each object is in its own cluster. The most similar objects are merged. Repeat step 2 until all objects are in the same cluster.
- Divisive hierarchical clustering (top to bottom), which operates as follows: Starts with a cluster where all objects are together. The most dissimilar objects are divided. Repeat step 2 until all objects are in their own clusters.
2.1.3. AGNES
- Calculate the similarity matrix;
- Allocate each example of the data into a group, creating leaf nodes of tree D;
- As long as there is the possibility of merging groups, the algorithm will calculate;
- The algorithm checks the distance between all pairs of groups, using the similarity matrix;
- The algorithm finds the most similar pair of groups and transforms them into a single group, creating an entire node in the d-tree hierarchy.
2.1.4. Fuzzy
2.2. Indices
2.2.1. Average Proportion of Non-Overlap (APN)
2.2.2. Average Distance
2.2.3. Average Distance Between Means
2.2.4. Figure Of Merit
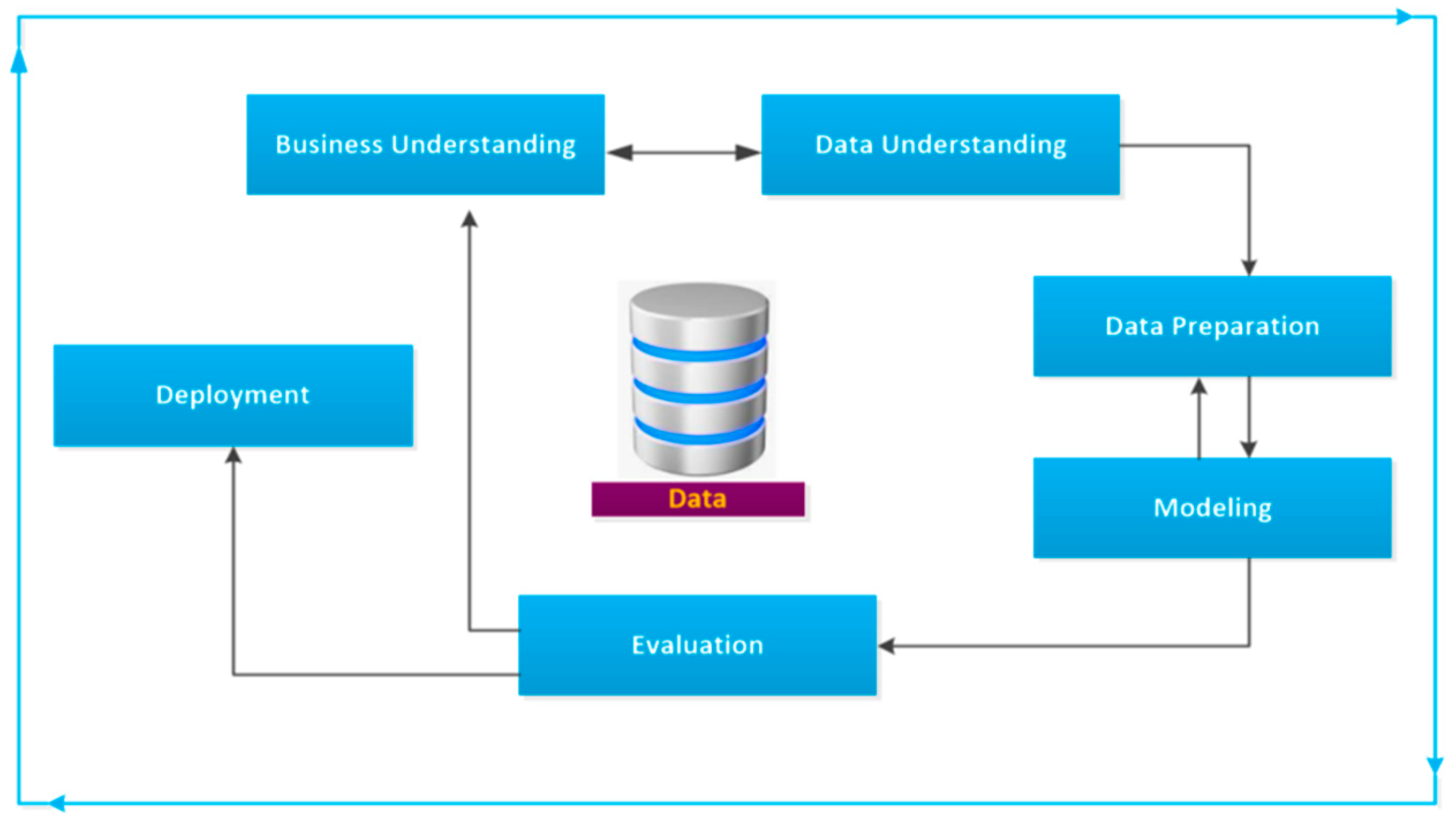
3. Materials and Methods
3.1. Business Understanding
- Determine business objectives: The objective was understood, and expectations were aligned with the project. The objective of this work is to reduce costs related to supplier management and improve the decision-making process, since the supplier base is extensive and heterogeneous, and the process of managing these partners has proved to be costly in terms of time and financial resources. In the end, we hope to have a tool to support the clustering of suppliers for any company.
- Assess the project start situation: The project requirements were determined, the risks were assessed, and a cost–benefit analysis related to the present work was carried out. The project requirements were based on mapping the current situation of suppliers, defining criteria for clustering suppliers, and defining the integration of information systems for data analysis (ERP, Excel, and R-Studio Software—version 2022.12.0+353). The risks raised were as follows: obtaining clusters with high-risk suppliers, excessive standardization of processes after clustering, changes in the business environment throughout the project, and results that lead to inflexible decisions since the sector studied is characterized as dynamic. Finally, the cost–benefit proved to be valid, as it would represent low costs for the company compared to the expected benefits.
- Determine the objectives of the data science project: It was determined that the objective of the project would be to build a computational program that would obtain an accuracy of 80% in the results shown. The objective can be defined jointly with the managers involved, based on their experience in other similar projects.
3.2. Data Understanding
- Reevaluate data collection: The data was initially checked and found to be sufficient for the planned analyses.
- Describe the data: Subsequently, the data were superficially examined. Formats were standardized, cells were formatted, and outliers and empty cells were detected. At this stage, any columns of duplicate and/or unnecessary information were also evaluated, such as anticipated requalification forecast, type of purchasing document, brief text, item, group of buyers, center, warehouse, quantity in stock, and tracking number. Adjustments were made so that we could move on to the next phase.
- Explore the data: At this stage, the data was examined more deeply. A “flat table” was generated with the available data and graphs. Through this flat table, an assessment of the relationship between the data and a descriptive analysis of them were made.
- Check the quality of the data: Finally, after the above phases, it was seen that there are no adjustments to be made and that the quality of the data meets the needs of the project. For confirmation, there was also interaction with experts to ensure an accurate interpretation of the data and the identification of significant variables.
3.3. Data Preparation
- Select data: The dataset used was selected, which consisted of around 560 suppliers.
- Clean data: Cleaning was carried out, and, in the end, 64 suppliers were maintained for the application of the model. The cleaning excluded suppliers classified as blocked and those that did not have some information considered mandatory for this research, such as the location of the supplier base. In addition, the information (columns) to be worked on are as follows: supplier code, name, base city, country, group according to the company’s internal classification, evaluation tool, status (approved or blocked), qualification date, expiration date of certifications, periodicity, final validity of qualification, number of product non-conformities, number of non-conformities in audit, classification of non-conformities, material, purchasing document reference, document date, order quantity to be supplied, currency, expected quantity, and net order value. The other columns were not considered for this research, as they do not contain relevant information.
- Build data: The need to build new data was not identified.
- Integrate data: A “flat table” was generated with the data to integrate all databases, originating from the ERP system and Excel spreadsheets.
- Formatting data: Finally, the data was formatted again, with the standardization completed, which includes converting text to numbers.
3.4. Modeling
- Model selection: Four algorithms (K-Means, Hierarchical K-Means, AGNES (Agglomerative Nesting), and Fuzzy Clustering) were selected to compose the model. Ref. [61] also used the K-Means and Hierarchical K-Means algorithms to support the demand management system and concluded that, with the proposed grouping method, different types of household appliances can be classified, selecting the appropriate characteristics for the proposed purpose. Ref. [62] used the combination of the AGNES algorithm with another and observed that a good performance was obtained for segmenting customers. It can then be seen that the work, when applying the algorithms chosen here, had good results.
- Generate the test plan: The data was separated for training, testing, and validation. For training, 20% of the data were considered, and 100% of the available data were tested. The four algorithms were run with this division.
- Build the model: The clustering model has been built. This phase involved choosing, implementing, and adjusting the algorithm to meet the specific objectives of the project. It followed the flowchart in Figure 6:
- The execution of each of the phases is detailed below:
- Algorithm Selection: Based on the nature of the data and the objectives of the project, as already mentioned, four algorithms were chosen: K-Means, Hierarchical K-Means, AGNES (Agglomerative Nesting), and Fuzzy Clustering.
- Model Implementation: The following libraries were used to implement the model:
- –
- K-Means algorithm: R-Studio base library, using the kmeans() function directly;
- –
- Hierarchical K-Means algorithm: The hclust() and cutree() functions were used, included in the R-Studio standard library;
- –
- AGNES: The cluster library was used;
- –
- Fuzzy Clustering: The fclust library was used.
- Data Normalization/Standardization: Data was normalized to ensure that all variables contribute equally to the formation of clusters.
- Parameter Adjustment: The parameters related to the number of clusters were adjusted when the K-Means algorithm was tested.
- Model Validation: The model was evaluated using specific metrics for clustering: Silhouette, Connectivity, and Dunn indices, in addition to the stability of the algorithms using the Average Proportion of Non-overlap (APN), Average Distance (AD), Average Distance Between Means (ADM), and Figure Of Merit (FOM).
- Interpretation of Results: Finally, the generated clusters were analyzed, and the results were interpreted. Details will be discussed later.
- 4.
- Evaluate the model: The next step involved analyzing the results of the four models using the algorithms. In this analysis, the stability of the algorithms was validated, using the indicators Average Proportion of Non-overlap (APN), Average Distance (AD), Average Distance Between Means (ADM), and Figure Of Merit (FOM). The comparison between the algorithms was carried out by evaluating the values of such indicators, in addition to additional evaluations by experts so that it was possible to arrive at the model that would best meet the objective of the work: developing a model capable of evaluating and segregating suppliers based on the algorithm clustering system developed with a view to supporting the decision-making process, reducing costs and associated risks, and optimizing resources.
3.5. Evaluation
3.6. Implementation
3.7. Numerical Results and Discussion
- Hierarchical K-Means: The hierarchical K-Means approach produced satisfactory results, especially with regard to the APN and ADM indices, which are similar to the best indices returned by the software (value 0). According to the literature, for both indices, the value must be between 0 and 1, and the lower it is, the more consistent the generated cluster is. Furthermore, when comparing these two indices, generated by the Hierarchical K-Means method for the four cluster sizes, it is seen that the value for four clusters is the best.
- 2.
- K-Means: This algorithm also showed promising results, with good supplier segmentation. Unlike Hierarchical K-Means, the AD and FOM indices were those that had results equal to the best indices shown by the software used, 215,488.81 and 35,971.72, respectively. Furthermore, according to the literature, for both indices, the value must be between 0 and infinity, and the lower it is, the more consistent the generated cluster is. Furthermore, when comparing these two indices, generated by the K-Means method for the four cluster sizes, it is seen that the value for seven clusters is the best.
- Fuzzy Clustering: Although it showed acceptable results, Fuzzy Clustering was unable to outperform K-Means in our experiments, when evaluating the APN, AD, ADM, and FOM indices.
- AGNES (Agglomerative Nesting): Like Fuzzy Clustering, the AGNES algorithm was unable to outperform K-Means in our experiments, when evaluating the APN, AD, ADM, and FOM indices, despite its simplicity of use.
4. Conclusions
- The results obtained in this research reveal significant improvements related to costs when implementing the supplier clustering strategy. A reduction of around 7% in the costs involved with initial qualifications and requalification was estimated, especially those involving international suppliers. Furthermore, qualifications and requalification considered not relevant could be canceled, positively impacting the saving of financial resources. The detailed analysis demonstrates a substantial reduction in operational expenses, resulting in an efficient optimization of financial resources. Furthermore, the consolidation of suppliers also showed positive impacts on purchasing, as it provided better price negotiations and contractual conditions. Additionally, the simplification of the supply chain resulted in logistical efficiencies, reducing costs associated with transportation and storage. These results suggest that supplier clustering not only promotes tangible savings but also represents an effective strategic approach for efficient cost management in the business context.
- In terms of time, the implementation of supplier clustering revealed significant improvements in operational efficiency. The consolidation resulted in simplified processes, reducing the time involved in external missions for audits, face-to-face meetings, and activity setup in preparation for travel. This temporal optimization not only increased the company’s responsiveness but also allowed for better allocation of human resources in the supplier management process.
- With regard to risk management, supplier clustering stood out as an effective approach in mitigating potential threats to the supply chain. Consolidation allowed greater visibility and control over risks, identifying areas of vulnerability and implementing preventive measures. Supplier diversification was replaced by a more focused and strategic approach, reducing exposure to risks. Ultimately, this approach has proven to be a solid foundation for operational sustainability in the face of challenges and uncertainty.
- Regarding supplier performance, the results indicate substantial gains in the overall performance of the supply chain. Clustering allowed for better quality management, with suppliers more aligned with established standards. This resulted in more reliable products and services, meeting customer expectations. Performance analysis shows a notable increase in customer satisfaction, demonstrating the positive impact of this strategy on operational excellence.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Villegas-Ch, W.; Navarro, A.M.; Sanchez-Viteri, S. Optimization of inventory management through computer vision and machine learning technologies. Intell. Syst. Appl. 2024, 24, 200438. [Google Scholar] [CrossRef]
- Gámez-Albán, H.M.; Guisson, R.; De Meyer, A. Optimizing the organization of the first mile in agri-food supply chains with a heterogeneous fleet using a mixed-integer linear model. Intell. Syst. Appl. 2024, 23, 200426. [Google Scholar] [CrossRef]
- Brandenburg, M.; Gruchmann, T.; Oelze, N. Sustainable Supply Chain Management—A Conceptual Framework and Future Research Perspectives. Sustainability 2019, 11, 7239. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Lee, P.T.-W.; Yuan, C.; Long, S.; Cheng, Y. Effects of supply chain innovation and application policy on firm performance: Evidence from China. Prod. Plan. Control. 2024, 1–13. [Google Scholar] [CrossRef]
- Deepu, T.S.; Ravi, V. A conceptual framework for supply chain digitalization using integrated systems model approach and DIKW hierarchy. Intell. Syst. Appl. 2021, 10–11, 200048. [Google Scholar] [CrossRef]
- Cui, L.; Wu, H.; Dai, J. Modelling flexible decisions about sustainable supplier selection in multitier sustainable supply chain management. Int. J. Prod. Res. 2021, 61, 4603–4624. [Google Scholar] [CrossRef]
- Ali, N.; Ghazal, T.M.; Ahmed, A.; Abbas, S.; Alzoubi, H.M.; Farooq, U.; Ahmad, M.; Khan, M.A. Fusion-Based Supply Chain Collaboration Using Machine Learning Techniques. Intell. Autom. Soft Comput. 2022, 31, 1671–1687. [Google Scholar] [CrossRef]
- Goodarzian, F.; Ghasemi, P.; Appolloni, A.; Ali, I.; Cárdenas-Barrón, L.E. Supply chain network design based on Big Data Analytics: Heuristic-simulation method in a pharmaceutical case study. Prod. Plan. Control 2024, 1–21. [Google Scholar] [CrossRef]
- Toorajipour, R.; Sohrabpour, V.; Nazarpour, A.; Oghazi, P.; Fischl, M. Artificial intelligence in supply chain management: A systematic literature review. J. Bus. Res. 2021, 122, 502–517. [Google Scholar] [CrossRef]
- Helo, P.; Hao, Y. Artificial intelligence in operations management and supply chain management: An exploratory case study. Prod. Plan. Control 2021, 33, 1573–1590. [Google Scholar] [CrossRef]
- Richey, R.G.; Chowdhury, S.; Davis-Sramek, B.; Giannakis, M.; Dwivedi, Y.K. Artificial intelligence in logistics and supply chain management: A primer and roadmap for research. J. Bus. Logist. 2023, 44, 532–549. [Google Scholar] [CrossRef]
- Suraraksa, J.; Shin, K.S. Comparative Analysis of Factors for Supplier Selection and Monitoring: The Case of the Automotive Industry in Thailand. Sustainability 2019, 11, 981. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Mohammed, M.A.; Majumdar, A.; Thinnukool, O. Supplier Selection through Multicriteria Decision-Making Algorithmic Approach Based on Rough Approximation of Fuzzy Hypersoft Sets for Construction Project. Buildings 2022, 12, 940. [Google Scholar] [CrossRef]
- Cavalcante, I.M.; Frazzon, E.M.; Forcellini, F.A.; Ivanov, D. A supervised machine learning approach to data-driven simulation of resilient supplier selection in digital manufacturing. Int. J. Inf. Manag. 2019, 49, 86–97. [Google Scholar] [CrossRef]
- Amiri, M.; Hashemi-Tabatabaei, M.; Ghahremanloo, M.; Keshavarz-Ghorabaee, M.; Zavadskas, E.K.; Banaitis, A. A new fuzzy BWM approach for evaluating and selecting a sustainable supplier in supply chain management. Int. J. Sustain. Dev. World Ecol. 2020, 28, 125–142. [Google Scholar] [CrossRef]
- Schmitt, M. Automated machine learning: AI-driven decision making in business analytics. Intell. Syst. Appl. 2023, 18, 200188. [Google Scholar] [CrossRef]
- Barrera, F.; Segura, M.; Maroto, C. Multicriteria sorting method based on global and local search for supplier segmentation. Int. Trans. Oper. Res. 2023, 31, 3108–3134. [Google Scholar] [CrossRef]
- Luan, J.; Yao, Z.; Zhao, F.; Song, X. A novel method to solve supplier selection problem: Hybrid algorithm of genetic algorithm and ant colony optimization. Math. Comput. Simul. 2019, 156, 294–309. [Google Scholar] [CrossRef]
- Bahadori, M.; Hosseini, S.M.; Teymourzadeh, E.; Ravangard, R.; Raadabadi, M.; Alimohammadzadeh, K. A supplier selection model for hospitals using a combination of artificial neural network and fuzzy VIKOR. Int. J. Heal. Manag. 2017, 13, 286–294. [Google Scholar] [CrossRef]
- Islam, S.; Amin, S.H.; Wardley, L.J. Machine learning and optimization models for supplier selection and order allocation planning. Int. J. Prod. Econ. 2021, 242, 108315. [Google Scholar] [CrossRef]
- Resende, C.H.; Geraldes, C.A.; Lima, F.R. Decision Models for Supplier Selection in Industry 4.0 Era: A Systematic Literature Review. Procedia Manuf. 2021, 55, 492–499. [Google Scholar] [CrossRef]
- Alavi, B.; Tavana, M.; Mina, H. A Dynamic Decision Support System for Sustainable Supplier Selection in Circular Economy. Sustain. Prod. Consum. 2021, 27, 905–920. [Google Scholar] [CrossRef]
- Lin, H.; Lin, J.; Wang, F. An innovative machine learning model for supply chain management. J. Innov. Knowl. 2022, 7, 100276. [Google Scholar] [CrossRef]
- Krieger, F.; Drews, P.; Funk, B. Automated invoice processing: Machine learning-based information extraction for long tail suppliers. Intell. Syst. Appl. 2023, 20, 200285. [Google Scholar] [CrossRef]
- Awaliyah, D.A.; Prasetyio, B.; Muzayanah, R.; Lestari, A.D. Optimizing Customer Segmentation in Online Retail Transactions through the Implementation of the K-Means Clustering Algorithm. Sci. J. Inform. 2024, 11, 539–548. [Google Scholar] [CrossRef]
- Yu, M.; Principato, L.; Formentini, M.; Mattia, G.; Cicatiello, C.; Capoccia, L.; Secondi, L. Unlocking the potential of surplus food: A blockchain approach to enhance equitable distribution and address food insecurity in Italy. Socio-Econ. Plan. Sci. 2024, 93, 101868. [Google Scholar] [CrossRef]
- Husna, A.U.; Ghasempoor, A.; Amin, S.H. A proposed framework for supplier selection and order allocation using machine learning clustering and optimization techniques. J. Data Inf. Manag. 2024, 6, 235–254. [Google Scholar] [CrossRef]
- Trianasari, N.; Permadi, T.A. Analysis of Product Recommendation Models at Each Fixed Broadband Sales Location Using K-Means, DBSCAN, Hierarchical Clustering, SVM, RF, and ANN. J. Appl. Data Sci. 2024, 5, 636–652. [Google Scholar] [CrossRef]
- Nhu, N.V.Q.; Van Hop, N. New fuzzy subtractive clustering approach: An application of order allocation in e-supply chain system. Int. J. Logist. Syst. Manag. 2024, 48, 279–295. [Google Scholar] [CrossRef]
- Rahiminia, M.; Razmi, J.; Farahani, S.S.; Sabbaghnia, A. Cluster-based supplier segmentation: A sustainable data-driven approach. Mod. Supply Chain Res. Appl. 2023, 5, 209–228. [Google Scholar] [CrossRef]
- Kamran, M.A.; Kia, R.; Goodarzian, F.; Ghasemi, P. A new vaccine supply chain network under COVID-19 conditions considering system dynamic: Artificial intelligence algorithms. Socio-Econ. Plan. Sci. 2022, 85, 101378. [Google Scholar] [CrossRef] [PubMed]
- Anand, M.C.J.; Kalaiarasi, K.; Martin, N.; Ranjitha, B.; Priyadharshini, S.S.; Tiwari, M. Fuzzy C-Means Clustering with MAIRCA -MCDM Method in Classifying Feasible Logistic Suppliers of Electrical Products. In Proceedings of the 2023 First International Conference on Cyber Physical Systems, Power Electronics and Electric Vehicles (ICPEEV), Hyderabad, India, 28–30 September 2023. [Google Scholar]
- Guan, Y.; Huang, Y.; Qin, H. Inventory Management Optimization of Green Supply Chain Using IPSO-BPNN Algorithm under the Artificial Intelligence. Wirel. Commun. Mob. Comput. 2022, 2022, 8428964. [Google Scholar] [CrossRef]
- Huang, W.; Ding, C.; Wang, S.; Hu, S. An efficient cluster mining algorithm for the internal motion target path based on the enhanced AGNES. In Proceedings of the 2015 Trustcom/BigDataSE/ISPA, Helsinki, Finland, 20–22 August 2015. [Google Scholar]
- Xu, B.; Choo, K.K.R.; Wang, J. Clustering and classification for graph data: A survey. ACM Comput. Surv. (CSUR) 2019, 52. [Google Scholar]
- Yuan, C.; Yang, H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J. Multidiscip. Sci. J. 2019, 2, 226–235. [Google Scholar] [CrossRef]
- Ravindra, R.; Rathod, R.D.G. Design of electricity tariff plans using gap statistic for K-Means clustering based on consumers monthly electricity consumption data. Int. J. Energy Sect. Manag. 2017, 2, 295–310. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Xiao, Y.; Yu, J. Gap statistic and K-Means algorithm. J. Comput. Res. Dev. 2007, 44, 176–180. [Google Scholar]
- Kaufman, I.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Waggoner, P.D. Unsupervised Machine Learning for Clustering in Political and Social Research; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly: Sebastopol, CA, USA, 2019. [Google Scholar]
- Hu, H.; Liu, J.; Zhang, X.; Fang, M. An Effective and Adaptable K-means Algorithm for Big Data Cluster Analysis. Pattern Recognit. 2023, 139, 109404. [Google Scholar] [CrossRef]
- Nwanganga, F.; Chapple, M. Practical Machine Learning in R; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A review of moving object trajectory clustering algorithms. Artif. Intell. Rev. 2016, 47, 123–144. [Google Scholar] [CrossRef]
- Ramadan, H.S.; El Bahnasy, K. A Review of Clustering Algorithms for Determination of Cancer Signatures. Int. J. Intell. Comput. Inf. Sci. 2022, 22, 138–151. [Google Scholar] [CrossRef]
- Sano, A.V.D.; Imanuel, T.D.; Calista, M.I.; Nindito, H.; Condrobimo, A.R. The Application of AGNES Algorithm to Optimize Knowledge Base for Tourism Chatbot. In Proceedings of the 2018 International Conference on Information Management and Technology (ICIMTech), Jakarta, Indonesia, 3–5 September 2018. [Google Scholar]
- Chen, Y.-T.; Jhang, Y.-C.; Liang, R.-H. A fuzzy-logic based auto-scaling variable step-size MPPT method for PV systems. Sol. Energy 2016, 126, 53–63. [Google Scholar] [CrossRef]
- Danandeh, M.A. A new architecture of INC-fuzzy hybrid method for tracking maximum power point in PV cells. Sol. Energy 2018, 171, 692–703. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Adaptive Neuro-Fuzzy Inference System modelling for performance prediction of solar thermal energy system. Renew. Energy 2016, 86, 302–315. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Wang, H.-Y.; Wang, J.-S.; Wang, G. A survey of fuzzy clustering validity evaluation methods. Inf. Sci. 2022, 618, 270–297. [Google Scholar] [CrossRef]
- Li, X.; Wen, H.; Hu, Y.; Jiang, L. A novel beta parameter based fuzzy-logic controller for photovoltaic MPPT application. Renew. Energy 2019, 130, 416–427. [Google Scholar] [CrossRef]
- Gupta, A.; Chauhan, Y.K.; Pachauri, R.K. A comparative investigation of maximum power point tracking methods for solar PV system. Sol. Energy 2016, 136, 236–253. [Google Scholar] [CrossRef]
- Askari, S. Fuzzy C-Means clustering algorithm for data with unequal cluster sizes and contaminated with noise and outliers: Review and development. Expert Syst. Appl. 2021, 165, 113856. [Google Scholar] [CrossRef]
- Küçükdeniz, T.; Erkal Sönmez, Ö. Integrated Warehouse Layout Planning with Fuzzy C-Means Clustering. In International Conference on Intelligent and Fuzzy Systems; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Brock, G.; Pihur, V.; Datta, S.; Datta, S. clValid: An R package for cluster validation. J. Stat. Softw. 2008, 25, 1–22. [Google Scholar] [CrossRef]
- Schröer, C.; Kruse, F.; Gómez, J.M. A Systematic Literature Review on Applying CRISP-DM Process Model. Procedia Comput. Sci. 2021, 181, 526–534. [Google Scholar] [CrossRef]
- Matshabaphala, N.S. Implementation of Clustering Techniques for Segmentation of Mozambican Cassava Suppliers. Ph.D. Dissertation, Stellenbosch University, Stellenbosch, South Africa, 2021. [Google Scholar]
- Purnamasari, D.I.; Permadi, V.A.; Saepudin, A.; Agusdin, R.P. Demand Forecasting for Improved Inventory Management in Small and Medium-Sized Businesses. J. Nas. Pendidik. Tek. Inform. 2023, 12, 56–66. [Google Scholar] [CrossRef]
- Simsar, S.; Alborzi, M.; Ghatari, A.R.; Varjani, A. Residential Appliance Clustering Based on Their Inherent Characteristics for Optimal Use Based K-Means and Hierarchical Clustering Method. J. Optim. Ind. Eng. 2023, 16, 119–127. [Google Scholar]
- Sun, Z.-H.; Zuo, T.-Y.; Liang, D.; Ming, X.; Chen, Z.; Qiu, S. GPHC: A heuristic clustering method to customer segmentation. Appl. Soft Comput. 2021, 111, 107677. [Google Scholar] [CrossRef]





| Authors | Clustering Algorithm | Paper Objective |
|---|---|---|
| [25] | K-Means | The main objective of this research is to optimize the use of customer segmentation using the Recency, Frequency, and Monetary (RFM) approach. |
| [26] | AGNES | To identify factors that determine the volume and economic value of surplus food redistribution. |
| [27] | K-Means Clustering, Gaussian Mixture Model, and Balance Iterative Reducing and Clustering using Hierarchies | This research proposes a new framework to address the challenges of supplier selection and order allocation (SS&OA) by introducing a two-phase combined approach. |
| [28] | K-Means, DBSCAN, Hierarchical Clustering, SVM, RF, AND, and ANN | This research aims to develop an optimal product recommendation model for each sales location, using machine learning with a mixed method approach, with a combination method of clustering and classification, where the clustering method is used for the geographic segmentation stage. |
| [29] | K-Means | This study proposes a so-called new Fuzzy subtractive clustering (NFSC) algorithm to allocate orders to the appropriate hub with three criteria, namely, traveling distance, delivery time, and order quantity. |
| [30] | K-Means | This study aims to develop a clustering-based approach to sustainable supplier segmentation. |
| [31] | Variable Neighborhood Search (VNS) and Whale Optimization Algorithm (WOA) | A new stochastic multi-objective, multi-period, and multi-commodity simulation-optimization model has been developed for the COVID-19 vaccine’s production, distribution, location, allocation, and inventory control decisions. |
| [32] | Fuzzy C-Means Clustering (FCM) | The model uses a machine learning algorithm to classify the logistics suppliers of electrical products based on their feasibility in the first phase. |
| [33,34] | Particle Swarm Optimization (PSO) | The objective is to reduce the waste of resources in supply chain inventory management and provide better services for green supply chain management. |
| [4] | Artificial Neural Network, Genetic Algorithm, and Particle Swarm Algorithm | This article used three artificial intelligence (AI) algorithms to analyze the risk of financial services in the international trade supply chain of the energy industry. |
| Clustering Methods | Validation Measures | Cluster Size | |||
|---|---|---|---|---|---|
| 4 | 5 | 6 | 7 | ||
| Hierarchical K-Means | APN | 0.0000 | 0.0002 | 0.0009 | 0.0021 |
| AD | 315,138.3323 | 285,425.0805 | 263,134.6146 | 238,478.4101 | |
| ADM | 0.0000 | 1309.5945 | 3500.6336 | 9981.5808 | |
| FOM | 48,853.5990 | 45,858.7935 | 44,964.8962 | 44,249.6444 | |
| K-Means | APN | 0.0007 | 0.0014 | 0.0006 | 0.0019 |
| AD | 270,055.9391 | 248,376.7107 | 225,484.0109 | 215,488.8132 | |
| ADM | 3268.6880 | 6109.7056 | 3805.2117 | 7294.7871 | |
| FOM | 47,206.3387 | 44,874.7968 | 38,584.4582 | 35,971.7238 | |
| Fuzzy | APN | 0.0447 | 0.0562 | N/A | 0.0974 |
| AD | 537,393.0755 | 522,189.0211 | N/A | 444,587.5577 | |
| ADM | 24,766.7075 | 35,004.1902 | N/A | 33,169.3428 | |
| FOM | 213,731.6898 | 213,223.0471 | N/A | 201,439.7572 | |
| AGNES | APN | 0.0000 | 0.0002 | 0.0009 | 0.0021 |
| AD | 315,138.3323 | 285,425.0805 | 263,134.6146 | 238,478.4101 | |
| ADM | 0.0000 | 1309.5945 | 3500.6336 | 9981.5808 | |
| FOM | 48,853.5990 | 45,858.7935 | 44,964.8962 | 44,249.6444 | |
| Optimal Scores | |||
|---|---|---|---|
| Validation Measures | Score | Method | Cluster |
| APN | 0 | Hierarchical K-Means | 4 |
| AD | 214,588.81 | K-Means | 7 |
| ADM | 0 | Hierarchical K-Means | 4 |
| FOM | 35,971.72 | K-Means | 7 |
| Cluster | Supplier Code | Analysis |
|---|---|---|
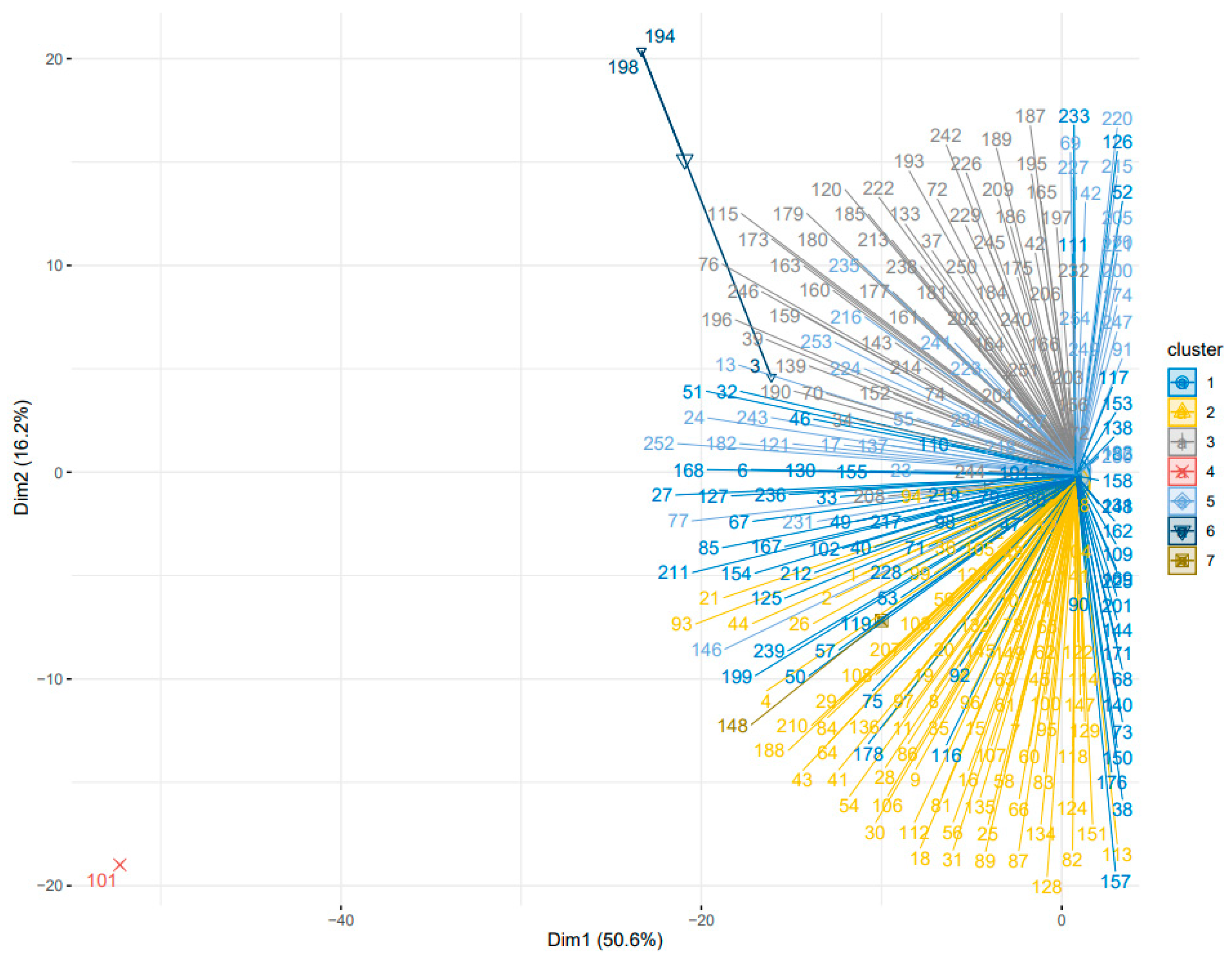
| 5 | 220 | Suppliers may require auditing, are located in American countries, have a low rate of product non-conformities, have a low associated purchase value, are classified as medium risk for the company |
| 69 | ||
| 227 | ||
| 215 | ||
| 142 | ||
| 1 | 168 | Suppliers that do not require auditing, are located in countries in America and Europe, have a low rate of product non-conformities, have a high associated purchasing value, are classified as medium/high risk for the company |
| 6 | ||
| 130 | ||
| 155 | ||
| 211 | ||
| 2 | 93 | Suppliers that do not require auditing, are located in countries in America and Europe, have a high rate of product non-conformities, have an average associated purchase value, are classified as low risk for the company |
| 21 | ||
| 44 | ||
| 26 | ||
| 2 | ||
| 3 | 242 | Suppliers may require auditing, are located in American countries, have a high rate of product non-conformities, have a high associated purchasing value, are classified as medium risk for the company |
| 193 | ||
| 222 | ||
| 139 | ||
| 76 |
| Supplier | Previous Cluster | Current Cluster |
|---|---|---|
| 3 | 6 | 3 |
| 101 | 4 | 3 |
| 148 | 7 | 3 |
| 194 | 6 | 1 |
| 198 | 6 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade Ferreira, A.C.; de Pinho, A.F.; Francisco, M.B.; de Siqueira, L.A., Jr.; Vasconcelos, G.A.V.B. A Decision Support System for Classifying Suppliers Based on Machine Learning Techniques: A Case Study in the Aeronautics Industry. Computers 2025, 14, 271. https://doi.org/10.3390/computers14070271
Andrade Ferreira AC, de Pinho AF, Francisco MB, de Siqueira LA Jr., Vasconcelos GAVB. A Decision Support System for Classifying Suppliers Based on Machine Learning Techniques: A Case Study in the Aeronautics Industry. Computers. 2025; 14(7):271. https://doi.org/10.3390/computers14070271
Chicago/Turabian StyleAndrade Ferreira, Ana Claudia, Alexandre Ferreira de Pinho, Matheus Brendon Francisco, Laercio Almeida de Siqueira, Jr., and Guilherme Augusto Vilas Boas Vasconcelos. 2025. "A Decision Support System for Classifying Suppliers Based on Machine Learning Techniques: A Case Study in the Aeronautics Industry" Computers 14, no. 7: 271. https://doi.org/10.3390/computers14070271
APA StyleAndrade Ferreira, A. C., de Pinho, A. F., Francisco, M. B., de Siqueira, L. A., Jr., & Vasconcelos, G. A. V. B. (2025). A Decision Support System for Classifying Suppliers Based on Machine Learning Techniques: A Case Study in the Aeronautics Industry. Computers, 14(7), 271. https://doi.org/10.3390/computers14070271







