3.1. Odd–Even Sort Algorithms (Closely Related to Bubble Sort)
Bubble sort is one of the first sort algorithms taught to programmers due to its simplicity. The name is an analogy for the sorting behavior that occurs in a column of intermixed heavy liquid and light gas when exposed to some kind of uniform force (for example, gravity on Earth or apparent centrifugal forces in a centrifuge). When the force acts upon the mixture, the lighter gas will clump together in bubbles and move towards the “top” of the column (i.e., the opposite direction of the force), while the heavier liquid will move towards the “bottom” of the column (i.e., in the direction of the force). The bubbling process appears to stop when the gas and liquid have been completely separated (sorted) at the “top” and “bottom” of the column, respectively. The bubble sort algorithm works in a very similar way on a list by iteratively bubbling smaller values towards one end of a list and larger values toward the other end. Given enough iterations of the algorithm (no more than the number of elements minus one), the list will be sorted in order.
The traditional bubble sort algorithm is expressed algorithmically in
Figure 4 [
18]. It is composed of an outer loop that iterates over the entire list multiple times and an inner loop that iterates across contiguous element pairs in the list. Essentially, the inner loop implements a sliding window that encompasses two contiguous elements at a time. When the two elements are out-of-order with respect to on another, the elements are swapped. The type of list ordering (i.e., ascending in value, descending in value, etc.) is selected in the “if” condition inside the loops by specifying how one value is greater than another. Overall, the two loops sweep the swap window over the list multiple times. The smaller values appear to “bubble” to one end of the list, while the larger values settle to the other side of the list.
The number of potential swap operations in traditional bubble sort algorithm is
The outer loop of the algorithm is represented in the equation by the summation operation. The
j within the summation represents the number of potential swaps in each inner loop. The
N represents the number of items in the list. Notice that the equivalent form of the equation says that the number of potential swaps increases by the square of the number of elements in the list.
Figure 5 shows an example of a list of numbers in descending order that is bubble sorted into ascending order [
18]. The “bubbles” are shown as circles and the swap window is shown as brackets. The term “pass” refers to the iteration number of single single sweep of the swap window through the entire list (i.e., the index of the outer loop in
Figure 4). The term “pair” refers to the index of the left value in the swap window (i.e., the index of the inner loop in
Figure 4). Notice that the largest value in a pass of the swap window across the list always ends up in its final sorted list position. In successive passes of the swap window, there is no need to include values that are in their final sorted position, so the algorithm skips these values in successive passes of the swap window.
Unfortunately, the bubble sort algorithm shown in
Figure 4 is not parallelizable. Each iteration is dependent on the results of the previous iteration because the swap windows overlap between iterations.
However, the traditional bubble sort algorithm can be rearranged so that a set of swap windows can be executed in parallel at any one time (i.e., they have no dependencies with one another). This rearrangement is called an odd–even sort [
27,
28,
29,
30,
31,
32].
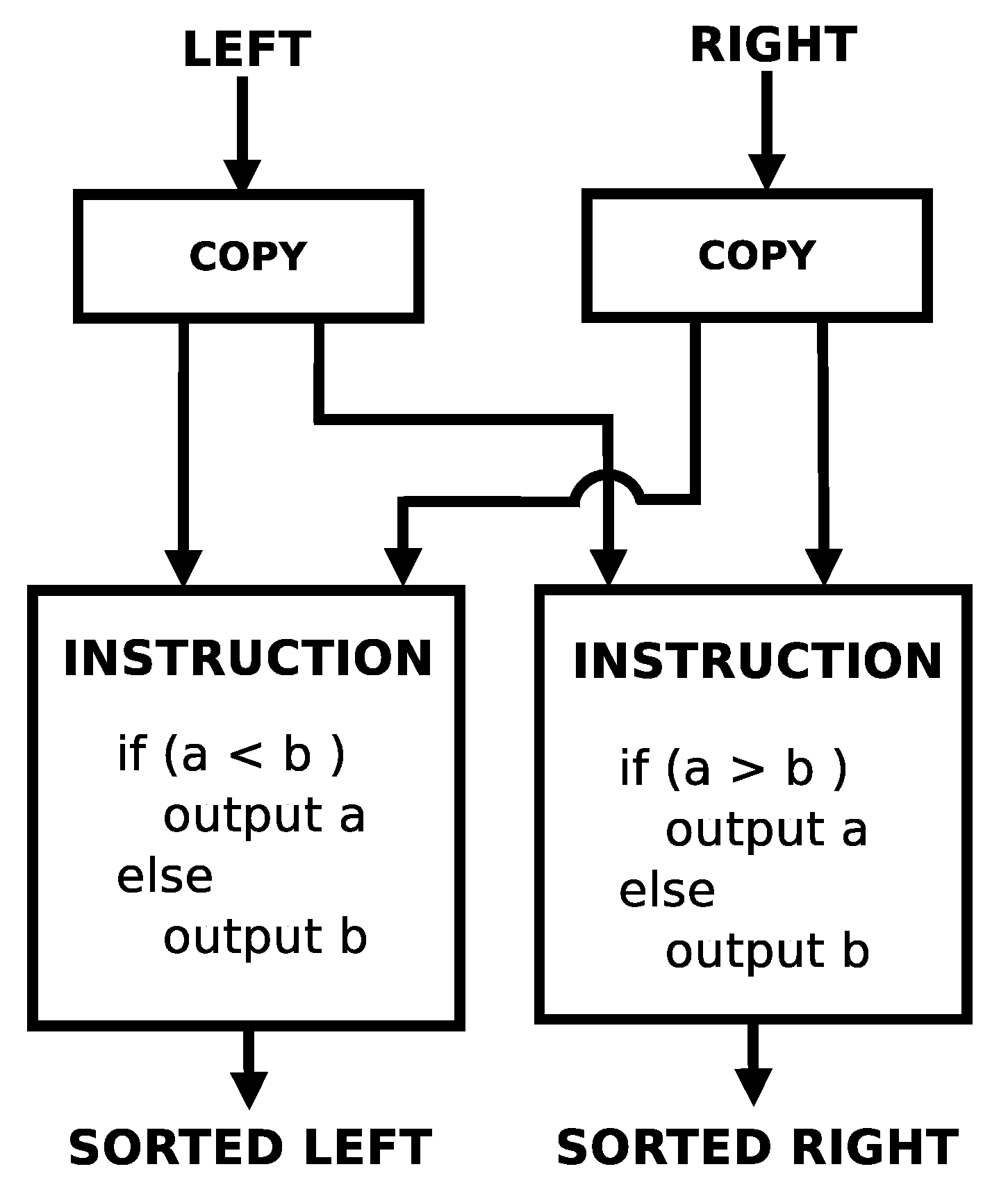
Figure 6 shows a rearranged version of the bubble sort algorithm (i.e., an odd–even sort algorithm) where the iterations of the inner loops can be executed in parallel (i.e., the loops can be “unrolled”).
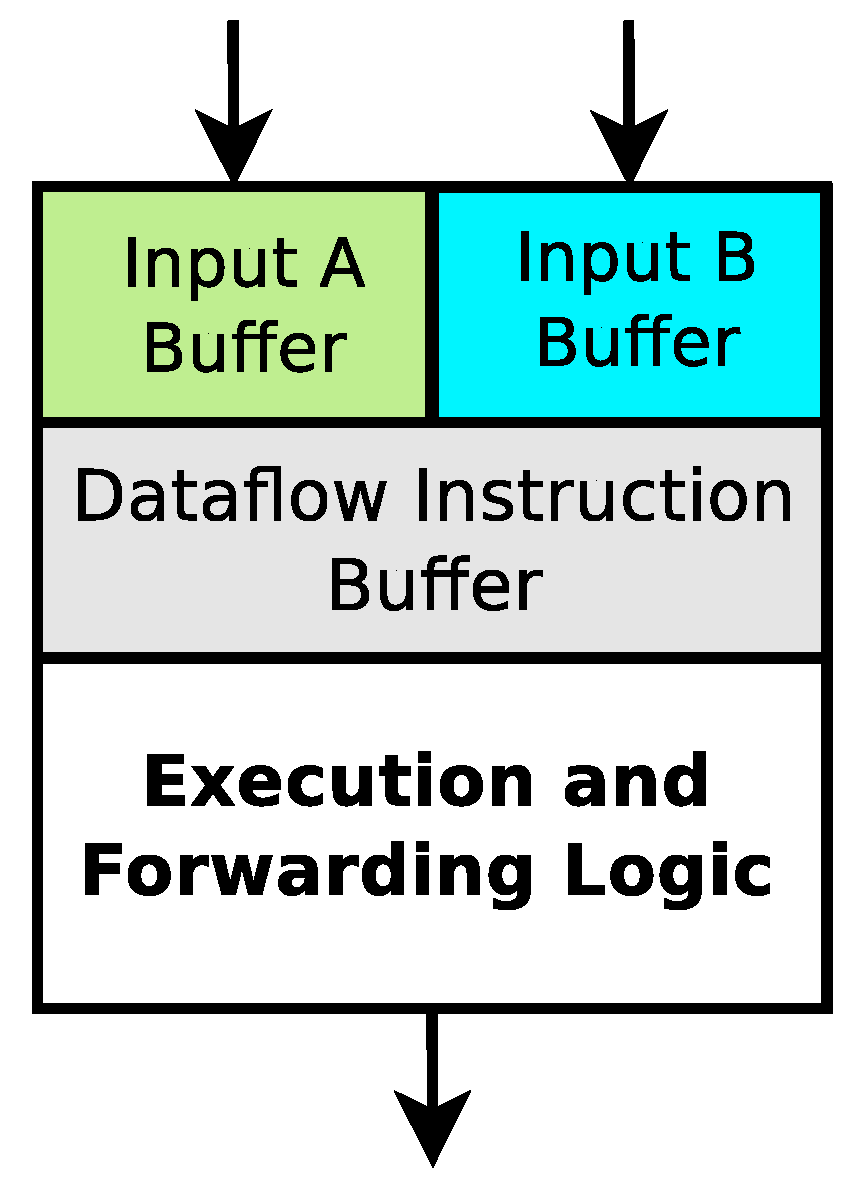
Figure 7 shows the implementation of a single swap in this dataflow processor. It takes 4 instructions to implement. Notice that there are potential parallel execution opportunities within this swap. The left and right branches can potentially execute in parallel. Assuming that both inputs into the swap are available simultaneously, both copy instructions could potentially execute simultaneously in 1 clock cycle, and then both propagate instructions could potentially execute simultaneously in 1 clock cycle. So, in theory, a single swap could complete in 2 clock cycles.
The rearranged algorithm can be
fully unrolled into the underlying swap pairs.
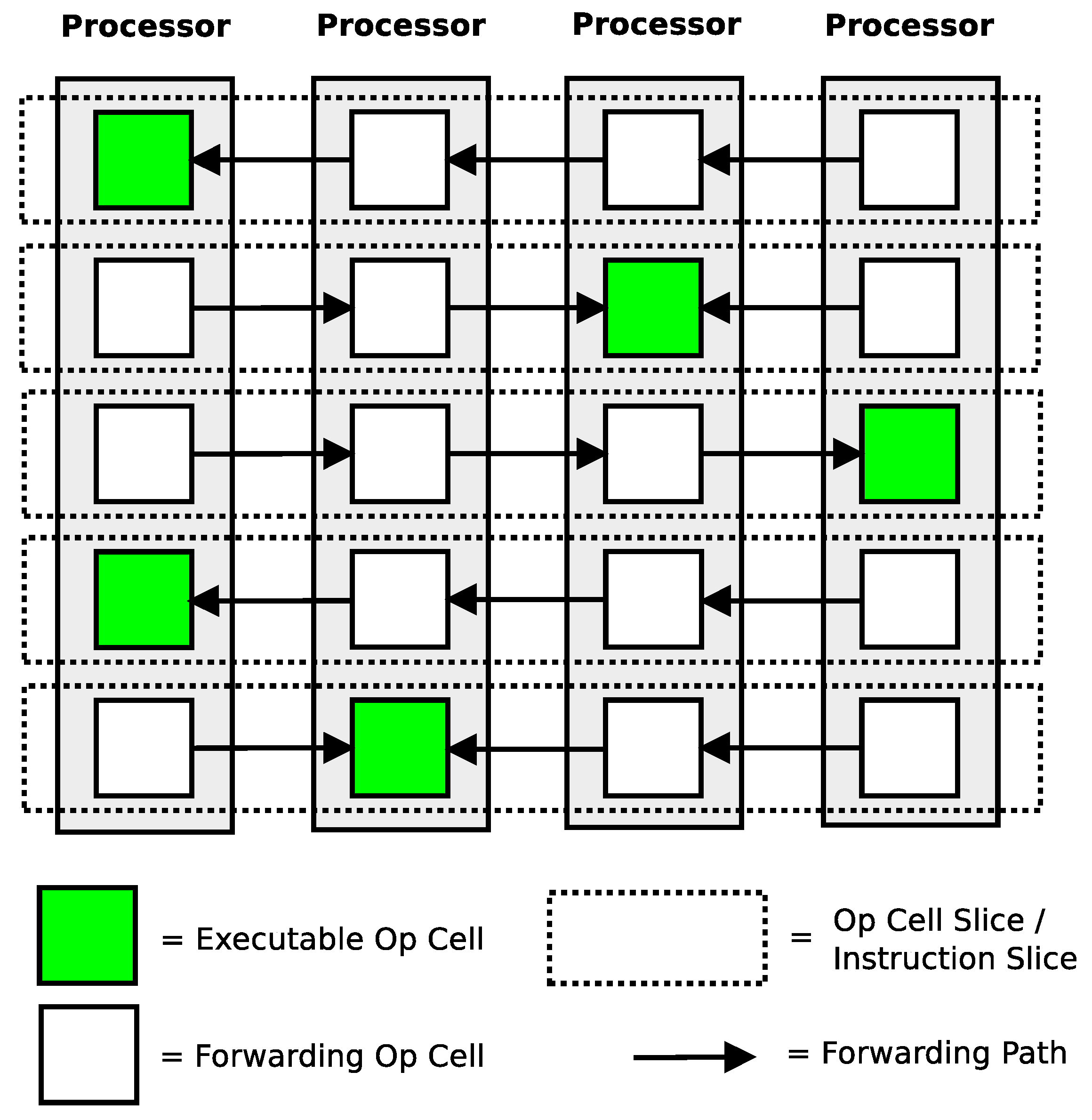
Figure 8 and
Figure 9 show the algorithm fully unrolled along with examples of a worst case list as it progresses along the lattice. Each swap in a row can be executed in parallel with any of the other swaps in a row. Each row corresponds to one of the inner loops in
Figure 6. There are two different patterns that emerge in this rearrangement: one when the number of inputs is even and one when the number of inputs is odd.
The even number of inputs pattern of the rearranged algorithm is characterized by
N (number of inputs) rows. The even-numbered rows have
potential swaps. There are
of these rows. The odd-numbered rows have
potential swaps. There are
of these rows as well. The number of potential swaps in the rearranged algorithm is given by
Notice that this is the same number of potential swaps as the traditional algorithm.
The odd number of inputs pattern of the rearranged algorithm is characterized by
N (number of inputs) rows, and each row has
potential swaps. In this case, the number of potential swaps is given by
Notice that the number of swaps in the traditional case (Equation (
1)), the rearranged even case (Equation (
2)), and the rearranged odd case case (Equation (
3)) are identical.
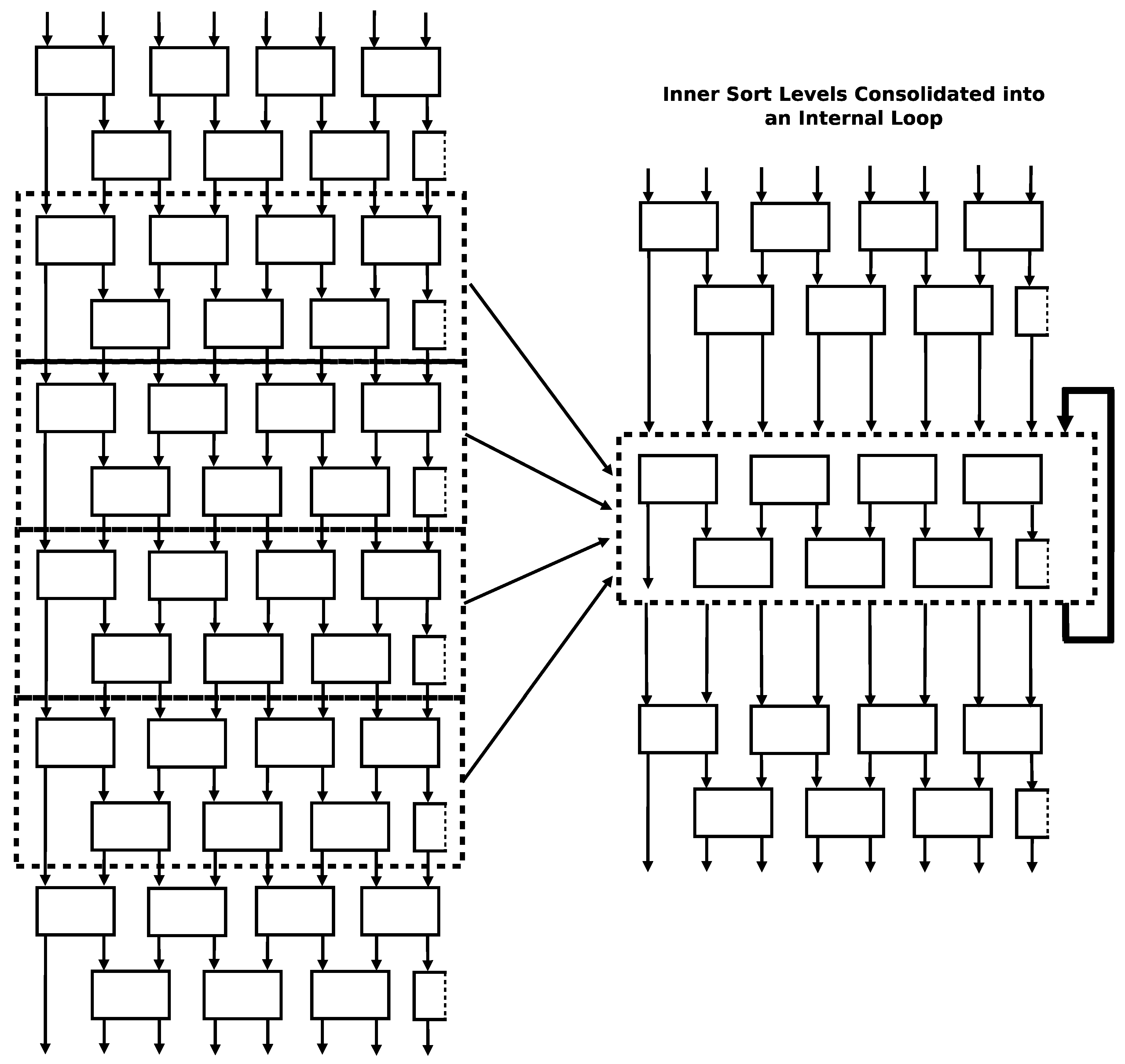
Since the number of swaps in the algorithm rises as a function of the square of the number of inputs, the number of instructions in a fully unrolled version of the rearranged algorithm rises by the square of the number of inputs too. This explosion of instructions can be mitigated by recognizing that every even row/odd row pair in the unrolled structure is identical. These rows can represented as a single entity and placed inside of a loop to reduce the number of actual instructions while still maintaining the ability to execute swaps in parallel. This compaction strategy is visually shown in
Figure 10.
Figure 11 shows a diagram of the
compact odd–even sort program that is suitable to be implemented in the dataflow processor instruction set of this work [
16,
18]. It is the odd–even sort algorithm where the inner swap pair rows are nested inside of a loop. The loop mechanism introduces some overall overhead but does not interfere with the amount of simultaneous parallel execution opportunities within the swap pairs in each row. The program implements the first one or two rows independently (one if there is an odd number of inputs and two if there is an even number of inputs), then implements the loop over the inner rows pairs, then implements the last two rows independently. In the figure, the implementation of the first swap row is shown in “Level 0 Sort Level”. The second swap row is shown in “Level 1 Sort Level” (however, this sort row is only implemented in sorts with an even number of inputs). The inner sort rows are shown in “Double Sort Levels Iterator”. The last two sort rows are shown in “Final Double Sort Levels”. The rest of the figure boxes show algorithm flow control. The minimum number of inputs that this program can handle is five. This is the case because there are the same number of swap rows and inputs in the rearranged algorithm. Since this program executes a minimum of five rows (i.e., a minimum of one independently at the beginning, two in a single loop iteration, and two at the end), this means that it can handle a minimum of five inputs. There is no theoretical upper bound on the number of inputs it can handle though. The first and last rows are implemented independently outside of the loop to act as buffers for different execution instances of the sort. The first rows can accept inputs for the next run of the sort while the current run is still being processed in the loop. These support the necessary serialization of multiple runs of the sort. The last row of sorts acts as buffers for the final result of the previous sort and allows the next run of the sort to progress inside of the loop. This allows a new run of the sort to execute concurrently even when the old run has not fully completed yet. (This may happen when the client of the previous sort has not collected all of its results yet).
As an aside: in this work, the odd–even sort is used as a test kernel to evaluate the performance of the polymorphic computing architecture. However, the odd–even sort implementations above can be readily adapted for independent use in FPGAs (Field Programmable Gate Arrays) and ASICs (Application-Specific Integrated Circuits). For instance, Korat, Yadav, and Shah have already independently implemented odd–even sort in an FPGA [
31].
3.2. Evaluation Methods
To evaluate the odd–even sort algorithm in this polymorphic computing architecture, five different algorithm variations were each assessed in different geometric configurations of the polymorphic computing architecture. Each assessment was composed of three evaluations performed in a custom clock-accurate computer architecture simulator:
Evaluation of ideal performance;
Evaluation of performance of best-found geometric placement from a genetic algorithm;
Evaluation of performance of best-found geometric placement from a deterministic algorithm.
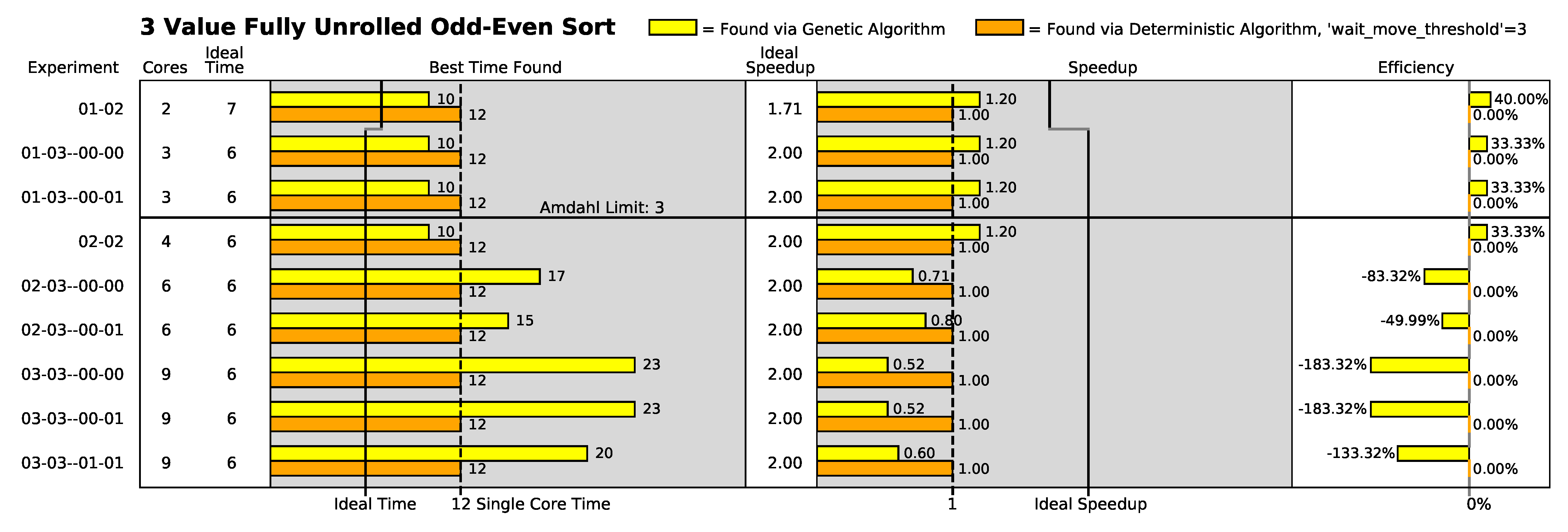
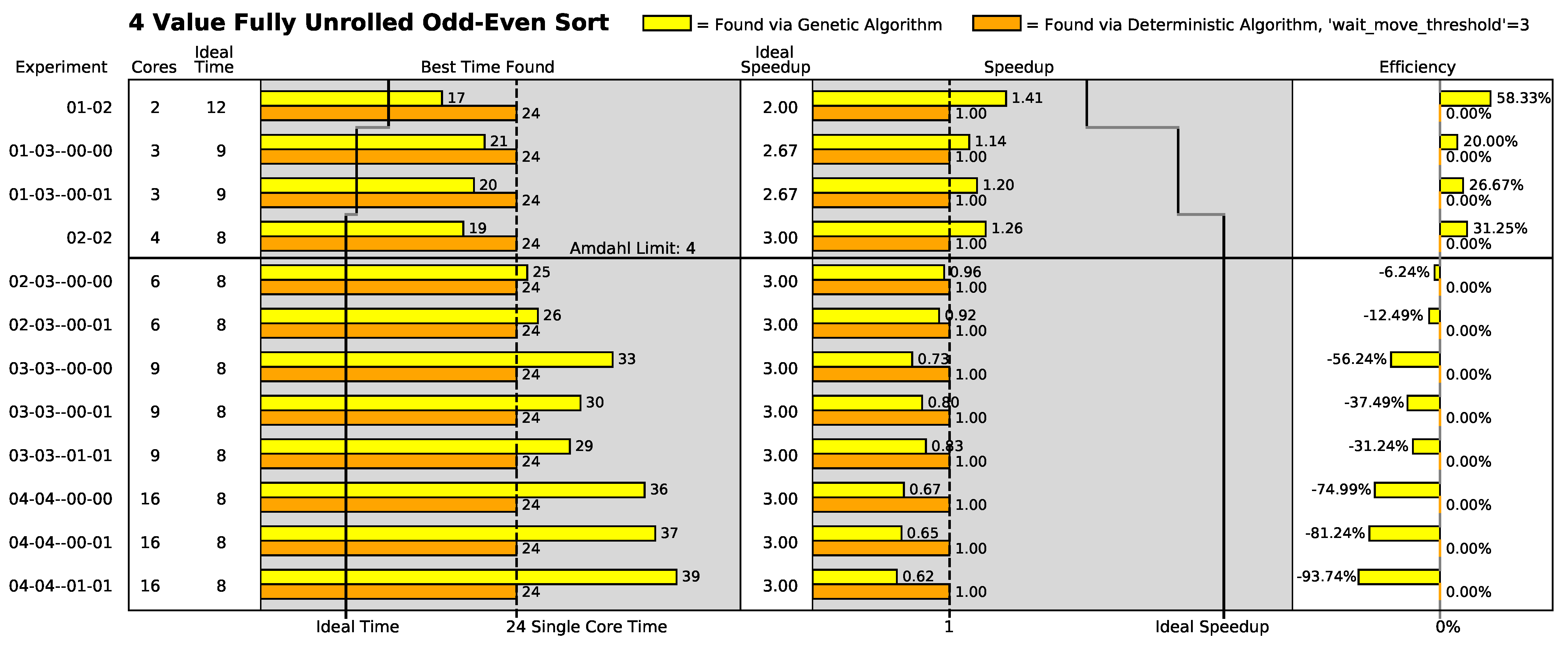
The five different algorithm variations are shown in
Table 1. The first two variations are the fully unrolled versions of the algorithm. Each swap operation in the fully unrolled form of the algorithm is given its own unique instructions. The fully unrolled form of the algorithm is potentially the most performance-efficient form of the algorithm because it does not have any instruction control flow overhead outside of the swapping actions themselves. Unfortunately, the number of swaps increases by the square of the number of elements (as indicated by Equations (
2) and (
3)). As a result, all algorithms that handle lists of size five or larger use the compact form of the algorithm to keep the size of the implementation down. The last variant of the algorithm was chosen to be very large to explore algorithm behavior at a very different scale from the first four variants.
Twelve 2-dimensional geometric configurations of the polymorphic computing architecture were chosen for this study and are shown in
Table 2. Notice that the configuration name in the table encodes the specific geometric configuration of the polymorphic architecture. The first two numbers of a configuration name encode the number of rows and columns in the configuration. If present, the third and fourth numbers of the configuration name indicate which core served as the sole I/O (input/output) core (i.e., the core where the inputs were injected and the results were gathered). For example, the configuration name “02-03–00-01” means that the polymorphic architecture was a 2-row by 3-column configuration where the core at row 0, column 1 served as the I/O core. When the third and fourth numbers are not present in the configuration name, this means that the location of the I/O core, while physically present, is not a relevant differentiator from other configurations.
All odd–even sort algorithm variations with the exception of the 3-value variation were evaluated in all geometric configurations shown in
Table 2. The 3-value algorithm variation was limited to a nine-configuration subset of the twelve configurations. The configurations that were omitted provided more processor cores than there are instructions in the algorithm (i.e., these additional cores would provide no utility to the 3-value algorithm variation).
Ideal performance was measured for each algorithm variant in a clock-cycle-accurate processor simulator. The simulator was configured as a single-core processor with a fixed number of instruction processing units (also called arithmetic logic units or ALUs) that had enough resources to execute all ready-to-execute instructions simultaneously up to the number of available ALUs. Each instruction and transaction was configured to have a latency of one clock cycle. Essentially, the simulator was configured to create a situation where the sole performance bottleneck was the number of instruction execution units (i.e., the effects of array geometry, interprocessor communication latency, and number of separate processors are completely eliminated). Each algorithm was then executed/timed in each processor configuration. Note that the architecture configurations in
Table 2 with the same number of cores have the same ideal performance for a given algorithm variant since configuration geometry is ignored by this evaluation.
The genetic search algorithm evaluation and the deterministic search algorithm evaluation were the two methods that were used to evaluate algorithm performance in actual geometric configurations. These search (optimization) techniques were used to find “good” instruction placements of the algorithm in a particular configuration since actual “ideal” instruction placements are not known. For performance evaluations, the choice of “good” instruction placements is extremely important since performance is highly dependent on how the instructions are placed (i.e., “draped”) in a particular array geometry. For instance, best performance will generally occur when the instruction placement mechanism simultaneously minimizes the bottleneck (serial) execution paths to a single core to avoid inter-core communication latencies and maximizes the simultaneous parallelism (time overlap) of inter-core communication and instruction executions to “hide” the time penalties of inter-core communication. Additionally, using two diverse techniques provides a comparative assessment of the quality of the search techniques themselves. (It should be noted that the genetic search algorithm and the deterministic search algorithm currently represent the complete list of instruction placement methods in existence for this polymorphic computing architecture. More instruction placement methods are expected to be developed in the future.)
The genetic search algorithm used to find “good” placements has the parameters found in
Table 3,
Table 4 and
Table 5. It is essentially a multi-population evolutionary algorithm based on random changes, where the best-performing individuals are preserved intact from one generation to the next (i.e., an elitist selection policy). The population segments are defined by the types of parents. The different population segments are intended to maintain genetic diversity while still rewarding elitism. A union of two parents produces a single offspring string where each 32-bit value maps an instruction in the algorithm to a processor core in the geometric array. Each bit in an offspring string is randomly selected (at a 50% rate) from the bits in the same position in the parent strings (i.e., one possible bit from each parent). Mutations occur on only 50% of the new offspring in 8-bit “bursts”. The lack of mutations in 50% of the new offspring is intended to encourage the exploration of different combinations of traits in the current population without mutation noise. The “burst” mutations are intended to encourage large changes in individual instruction locations. Fitness is determined first and foremost by the number of cores utilized by the placement. A core utilization is defined as having one or more instructions located in a particular core. For placements utilizing the same number of cores, faster execution speed (i.e., fewer clocks) is rewarded over slower execution speed (i.e., more clocks).
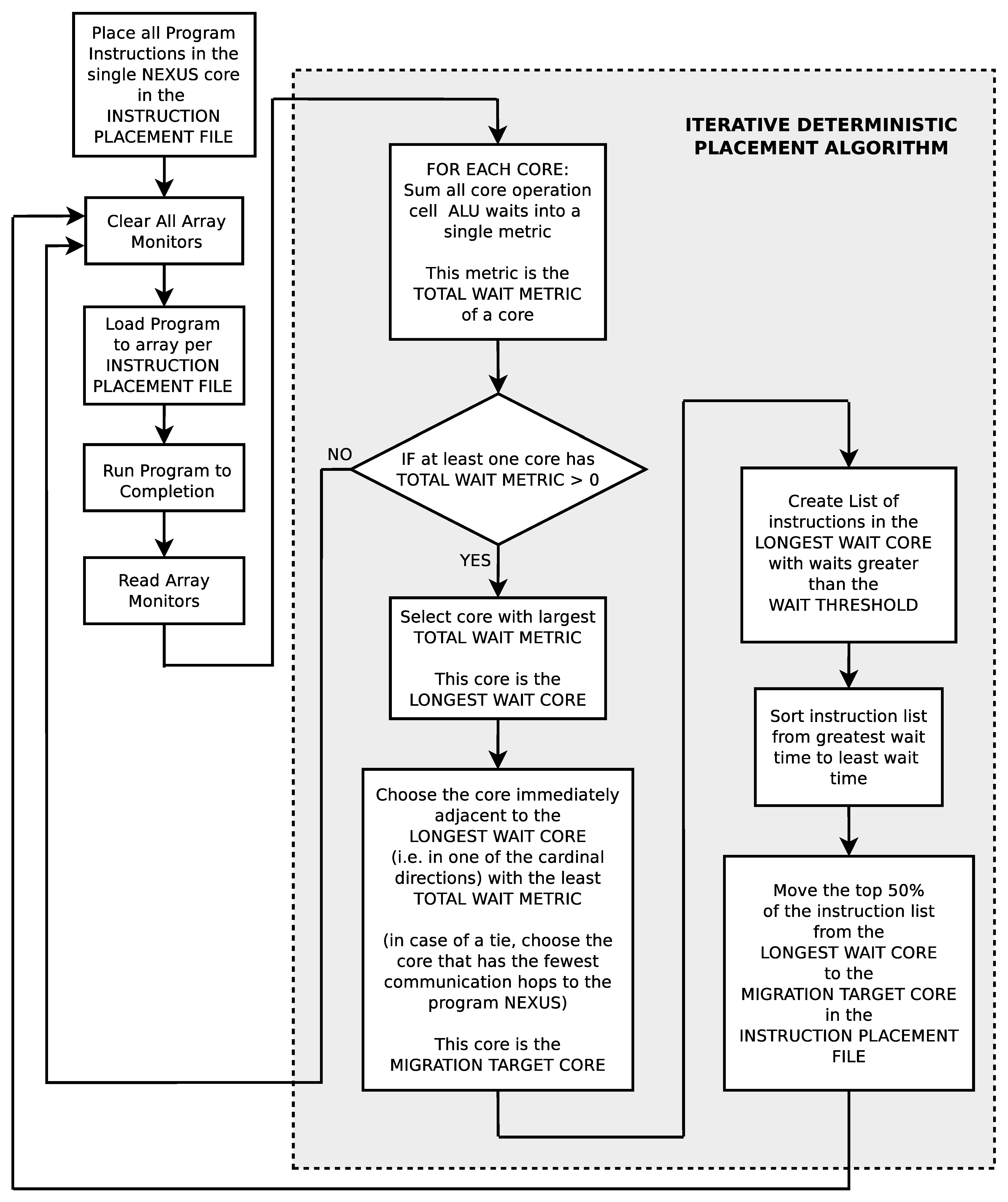
The deterministic search algorithm to find good instruction placements (see
Figure 12) is a very different technique than the genetic search algorithm. In this iterative technique, the wait times of each instruction (i.e., the time in clocks between when an instruction became ready to execute and the time it actually was executed) are individually measured on each processor core in the simulator. Essentially, these wait times indicate missed opportunities for instruction execution parallelism. Each iteration of the search essentially runs the current instruction placement in the simulated geometry, measures the individual instruction wait times, selects the processor core with the most cumulative instruction wait times, and moves the selected processor core’s individual instructions that are above a specified wait threshold to the immediately adjacent processor with the least cumulative wait times. The search starts with all instructions located in an individual core and iteratively moves instructions from the most heavily loaded core (as defined by cumulative instruction waiting time) to the least loaded immediately adjacent core. Unlike the genetic algorithm, the deterministic search algorithm does not have a bias to necessarily use all of the processor cores in an array.