Abstract
Quantum machine learning (QML) integrates quantum computing with classical machine learning. Within this domain, QML-CQ classification tasks, where classical data is processed by quantum circuits, have attracted particular interest for their potential to exploit high-dimensional feature maps, entanglement-enabled correlations, and non-classical priors. Yet, practical realizations remain constrained by the Noisy Intermediate-Scale Quantum (NISQ) era, where limited qubit counts, gate errors, and coherence losses necessitate frugal, noise-aware strategies. The Data Re-Uploading (DRU) algorithm has emerged as a strong NISQ-compatible candidate, offering universal classification capabilities with minimal qubit requirements. While DRU has been experimentally demonstrated on ion-trap, photonic, and superconducting platforms, no implementations exist for spin-based quantum processing units (QPU-SBs), despite their scalability potential via CMOS-compatible fabrication and recent demonstrations of multi-qubit processors. Here, we present a pulse-level, noise-aware DRU framework for spin-based QPUs, designed to bridge the gap between gate-level models and realistic spin-qubit execution. Our approach includes (i) compiling DRU circuits into hardware-proximate, time-domain controls derived from the Loss–DiVincenzo Hamiltonian, (ii) explicitly incorporating coherent and incoherent noise sources through pulse perturbations and Lindblad channels, (iii) enabling systematic noise-sensitivity studies across one-, two-, and four-spin configurations via continuous-time simulation, and (iv) developing a noise-aware training pipeline that benchmarks gate-level baselines against spin-level dynamics using information-theoretic loss functions. Numerical experiments show that our simulations reproduce gate-level dynamics with fidelities near unity while providing a richer error characterization under realistic noise. Moreover, divergence-based losses significantly enhance classification accuracy and robustness compared to fidelity-based metrics. Together, these results establish the proposed framework as a practical route for advancing DRU on spin-based platforms and motivate future work on error-attentive training and spin–quantum-dot noise modeling.
1. Introduction
Quantum computing (QC) leverages the principles of quantum mechanics, such as superposition and entanglement, to solve computational problems more efficiently and with reduced energy consumption [1]. Building on this foundation, quantum machine learning (QML) seeks to integrate QC with classical machine learning (ML) to tackle problems that may be intractable for classical methods alone [2]. Overall, QML has found applications across diverse domains, including cancer detection [3], economic forecasting and high-energy physics [4], quantum computing fault detection [5], quantum chemistry [6], and materials science [7]. Two complementary strands now shape QML: quantum circuits as trainable ML models and quantum acceleration for ML subroutines. The former employs a parameterized quantum circuit (PQC)—also called a variational quantum circuit or quantum neural network—to fit data by optimizing gate parameters exactly as one would train a classical model. This circuit-as-model view underpins quantum circuit learning and variational classifiers, with theory and practice showing expressive non-linear function approximation and successful small-scale experiments [8]. Further, the second QML line treats ML as the beneficiary of quantum algorithmic speedups in core primitives—kernels, linear algebra, and search/sampling—thereby enhancing otherwise classical pipelines. A central example is quantum feature maps and kernels, where a quantum device estimates inner products in large Hilbert spaces to power kernel methods, e.g., support vector machines (SVMs), and yield tasks with plausible or provable separations [9].
QML tasks are commonly categorized as CC, CQ, QC, and QQ depending on whether both the algorithm and data are classical (C) or quantum (Q) [10]. Within this taxonomy, QML-CQ classification tasks stand out, as they involve classical input data processed through quantum models. Namely, parameterized or variational quantum circuits act as expressive learners, exploiting entanglement to capture high-order correlations that are otherwise costly to model. Compact amplitude- and state-based encodings enable efficient representation of structured data, while quantum preprocessing routines such as quantum principal component analysis (qPCA) enhance dimensionality reduction and feature extraction. Prominent examples include quantum kernels and quantum support vector machines (QSVMs), which leverage quantum devices to estimate large Hilbert-space inner products [11]. Furthermore, probabilistic quantum generative models introduce non-classical priors that enrich hypothesis spaces, and query/sampling advantages grounded in amplitude estimation or Grover-type subroutines offer algorithmic speedups. Together, these elements provide both representational and computational pathways that are difficult to emulate with classical resources, establishing QML-CQ as a fertile ground for demonstrating tangible quantum advantages in supervised learning [12].
While QML algorithmic advances are promising, current quantum processing units (QPUs) remain firmly in the Noisy Intermediate-Scale Quantum (NISQ) era. In this regime, limited qubit counts, short coherence times, and significant gate and readout errors sharply constrain both circuit depth and the scalability of quantum models [13]. As a result, QML approaches designed for near-term deployment must be explicitly engineered for noise resilience and quantum-resource efficiency, carefully minimizing the number of qubits, gate operations, and measurement shots. Such frugality is not merely a hardware necessity but also a methodological imperative, ensuring that algorithmic performance in ML tasks can be meaningfully assessed under realistic noise models rather than idealized assumptions [14].
In this context, the QML Data Re-Uploading (DRU) algorithm emerges as a particularly well-suited candidate for the NISQ era [15]. By repeatedly re-encoding classical features into the same quantum register, DRU achieves expressive data representations while keeping qubit requirements and circuit depth remarkably low. This economy of quantum resources makes it highly compatible with current hardware limitations. Beyond its practical appeal, DRU enjoys rigorous theoretical guarantees: it has been formally established that even with almost a single qubit, the method can serve as a universal classifier, with its formulation naturally extending to multi-qubit architectures for enhanced representational power [16]. Conceptually, DRU resembles a single-layer neural network, yet it sidesteps fundamental quantum restrictions such as the no-cloning theorem, leveraging quantum interference and re-uploaded rotations to build expressive decision boundaries unattainable by purely classical linear models [17].
Experimental realizations of DRU have been successfully reported across diverse QPU platforms—most prominently on ion-trap processors [18], bosonic and photonic circuits [19], and superconducting quantum simulators [20]—underscoring both the adaptability of the algorithm and the strong experimental interest in probing its performance under noisy conditions [21]. Also, spin-based qubits remain an active research frontier with extensive progress on electronic-spin platforms, particularly nitrogen-vacancy (NV) center implementations [22]. Still, no experimental realization of DRU has been reported on spin-based QPUs, marking a significant gap in experimental validation and motivating targeted efforts to extend DRU to spin-based frameworks [16]. Indeed, spin-qubit quantum processing units (QPU-SBs) have emerged as one of the most promising platforms for scalable quantum information processing. Unlike atomic-spin realizations such as NMR, which face intrinsic scalability constraints [23], or NV centers in diamond, where reproducibility is limited by the stochastic placement of lattice defects, QPU-SB architectures leverage compatibility with standard CMOS/MOS fabrication processes [24]. This industrial alignment enables the direct transfer of decades of semiconductor expertise into the quantum domain, providing a credible pathway toward large-scale integration and manufacturable processors [25]. In particular, the quantum dot spin qubit [26], realized by controlling the spin of a confined electron with external magnetic fields, supports high-fidelity single- and two-qubit gate operations [27], with initialization and readout fidelities exceeding 99% [28] and coherence times approaching ∼120 μs [29]. Moreover, recent demonstrations of a six-qubit programmable processor further underscore the viability of this platform [30].
Despite the advantages of the DRU method and the QPU-SB technology, their practical realization demands an architecture-aware, pulse-level workflow. Such a workflow must (i) translate high-level algorithmic gates into hardware-native pulse schedules with optimized control waveforms [31], (ii) explicitly incorporate noise models that capture both quantum noise (QN) arising from decoherence and depolarization, as well as coherent control noise (CN) stemming from instrumental instabilities and pulse-shape fluctuations [10], and (iii) establish noise-aware training and benchmarking protocols to ensure that DRU-based learning remains robust under the realistic dynamics of spin-based devices [32].
Recent gate-to-pulse efforts have shown that DRU can be instantiated across multiple physical platforms, with successful implementations relying critically on platform-specific pulse calibration, detailed noise characterization, and fine-grained control tuning [20]. Notwithstanding impressive full-stack demonstrations reaching down to microwave/RF control of NV centers [33], most existing gate-to-pulse toolchains remain technology or architecture-specific, and thus do not seamlessly extend to QPU-SB built on quantum-dot architectures [26]. Attempts to bridge the gate- and pulse-level gap using spin-oriented frameworks, such as QuTiP-based modules or other pulse programming toolkits [34,35], highlight practical shortcomings, including rigid parameterizations, limited scalability to multi-qubit regimes, and embedded interaction models that restrict flexibility. These constraints hinder the direct realization of DRU-tailored pulse programming for electronic quantum-dot spin processors, underscoring the need for more adaptable and noise-aware spin-specific techniques.
In turn, available simulation infrastructures further accentuate this gap. Gate-level platforms such as PyQuil, Qiskit, Cirq, ProjectQ, and PennyLane incorporate noise through Kraus operators, stochastic Pauli channels, or simplified relaxation models [36]. While useful for benchmarking logical circuits, these discrete-time abstractions cannot faithfully reproduce continuous-time decoherence processes or distortions induced by time-dependent control waveforms. Pulse-level environments, by contrast, enable the explicit modeling of coherent noise sources and full time-domain dynamics [34,37]. However, such frameworks are largely optimized for superconducting architectures and often lack the flexible spin-Hamiltonian parametrization and efficient parameter-sweep capabilities needed to realistically capture spin-based device behavior [38]. Publicly accessible spin-based QPUs remain scarce. QuTech has released limited access to its Spin-2 and upgraded Spin-2+ demonstrators through the Quantum Inspire platform [39], providing one of the few cloud interfaces to spin-qubit hardware. By contrast, broader semiconductor initiatives such as the QLSI and QLSI2 projects target large-scale silicon-spin processors, with demonstrators envisioned at the tens-to-hundreds of qubits level. However, these efforts remain primarily in the development stage and do not yet offer wide public accessibility, see https://qt.eu/projects/computing/qlsi (accessed on 1 July 2025). Consequently, quantitative noise investigations for quantum-dot spin models must currently rely on simulation toolchains and gate-to-pulse adaptations specifically tailored to spin Hamiltonians. Performance assessments of DRU under noise reflect these methodological constraints: existing evaluations—whether gate-level analyses [40] or hardware/simulator-based demonstrations [41]—remain confined to one or two qubits, preferentially model superconducting architectures, and often emphasize narrow classification benchmarks [42]. These restrictions, compounded by the absence of controlled studies of coherent noise in QPU-SB, underscore the pressing need for the electronic-spin and pulse-level DRU.
In this paper, we introduce an end-to-end framework that bridges the gap between gate-level DRU models and QPU-SB execution by integrating pulse-level compilation, explicit noise modeling, and noise-aware training. The proposed approach is organized around the following key contributions:
- –
- Pulse-level compilation of DRU circuits: We translate gate-level DRU operations into hardware-proximate, time-domain controls consistent with the Loss–DiVincenzo (LD) Hamiltonian [26], employing the flexible parametrization of exchange interactions and external fields to enable pulse shaping, amplitude/phase modulation, and alignment with experimentally constrained spin-qubit controls.
- –
- Explicit modeling of device imperfections: CN is incorporated through stochastic and systematic perturbations on control amplitudes, while incoherent QN is captured using Lindblad-type dissipation channels [43], permitting continuous-time simulation that better reflect realistic device dynamics.
- –
- Spin-specific simulation environment: The framework supports systematic parameter sweeps over control variables and Hamiltonian parameters, enabling quantitative studies of noise sensitivity across one-, two-, and four-spin configurations. Our simulations demonstrate fidelities near unity with gate-level dynamics while providing richer insight into error propagation at the pulse level.
- –
- Noise-aware training and benchmarking: We implement a training pipeline that benchmarks gate-level baselines [44] against spin-QPU pulse-level simulations under varying noise regimes. Information-theoretic loss functions, including von Neumann and Rényi divergences, are shown to enhance classification robustness compared to standard fidelity-based objectives. Classifier evaluation with AUC [42] confirms improved performance in noisy environments.
Attained results reveal that (i) pulse-level simulations faithfully reproduce gate-level dynamics with high fidelity, (ii) divergence-based loss functions substantially improve classifier accuracy and robustness under noise, and (iii) the proposed framework establishes, to our knowledge, the first pulse-level, noise-aware spin-based QML classifier, paving the way for error-attentive training strategies and more realistic modeling of spin–quantum-dot noise processes.
2. Related Work
2.1. Gate-to-Pulse Level Approaches in DRU Compilation
Compiling quantum algorithms into pulse-level implementations has become a crucial step toward realistic QML, particularly in the context of noise-aware execution. The DRU algorithm has been experimentally realized on diverse hardware platforms, including bosonic systems [45], superconducting devices [20], ion traps [18], qudit systems [41], and NV centers in diamond [33]. These studies consistently highlight the importance of platform-specific pulse calibration, noise characterization, and fine-grained control optimization in determining classification fidelity and robustness. The NV-center experiment in [33] is particularly notable for compiling DRU into microwave and RF pulse sequences, achieving a full-stack realization of QML down to hardware-level control at room temperature. Yet, most of these implementations are technology specific and do not directly extend to spin-based quantum-dot platforms governed by the LD Hamiltonian [26]. Attempts to generalize compilation frameworks have been reported. For instance, QuTiP-based modules [34] provide customizable Hamiltonian modeling but remain constrained by rigid parameterizations and reliance on the rotating wave approximation (RWA). Similarly, pulse programming toolkits such as [35] offer structures closer to the LD model but remain limited to single-qubit setups and embed interaction terms that restrict flexibility. Remarkably, while prior work has demonstrated the feasibility of DRU compilation at the pulse level, no existing study has implemented DRU within a spin-based QPU governed by the LD Hamiltonian, nor has any explored its robustness under coherent control noise.
2.2. Simulation Frameworks for Noisy Pulse-Level Compilation
Simulation frameworks represent a central tool for assessing the performance of QML algorithms under noise. These efforts can be broadly divided into static (gate-level) and dynamic (pulse-level) approaches. At the gate level, simulators incorporate QN and sometimes CN using probabilistic channel models. Examples include PyQuil [46], Qiskit [47], Cirq [47], ProjectQ [48], and PennyLane [36]. These platforms simulate noise via Kraus operators, stochastic Pauli channels, or simplified relaxation models. While effective for algorithmic prototyping, their discrete-time abstractions cannot capture continuous decoherence processes or time-dependent distortions induced by pulse control. Dynamic (pulse-level) frameworks provide a closer match to hardware by modeling time-domain evolution under explicit control fields. OpenPulse [49] enables pulse compilation with customizable Hamiltonians, while [37] integrates Lindblad operators for simulating Markovian noise. QuTiP-based approaches [34] extend this by perturbing control amplitudes for CN and modeling QN via Lindblad terms associated with .
Despite these advances, key limitations persist. Gate-level simulators lack the ability to model continuous-time dynamics, preventing insight into weakly coupled environments. Pulse-level frameworks, although more expressive, are largely optimized for superconducting architectures, offering limited adaptability to spin Hamiltonians and lacking efficient parameter-sweep capabilities. Among the reviewed works, only [34] employs spin Hamiltonians, but its default model diverges from the LD Hamiltonian, precluding its direct application to quantum-dot spin qubits.
2.3. Performance Studies of DRU Under Noisy Conditions
Evaluating the robustness of the DRU algorithm under noise has been the subject of several investigations spanning three contexts:
- –
- Gate-level simulations. Works such as [40,50] analyze how Kraus-modeled noise channels (amplitude damping, depolarization, and bit-flip) and circuit depth influence DRU cost functions and classification accuracy.
- –
- Pulse-level and hardware demonstrations. Studies like [41,51] benchmark DRU performance under noisy superconducting backends, focusing on depth-dependent accuracy and dataset size but remain tied to superconducting simulators (e.g., IBM devices).
- –
- Noisy dataset evaluations. Other approaches introduce noise directly into the data used for training and testing, focusing on classifier robustness to data corruption rather than quantum or control noise channels [52,53].
Across these contexts, several limitations consistently emerge. Most studies remain confined to restricted system sizes, typically exploring only one or two qubits or, in some cases, single qudits. Performance evaluation is often reduced to narrow accuracy-based metrics, overlooking more informative measures such as F1-score or AUC that better capture classifier behavior under imbalance and noise [42]. In addition, error models are generally static, relying on fixed Kraus channels that fail to account for time-dependent dynamics or the impact of coherent control noise. A strong platform bias is also evident, as the majority of evaluations focus on superconducting hardware, leaving the influence of coherent noise in spin-based QPUs largely unexplored. Finally, some studies employ non-comparable information units, such as qudits rather than qubits, which complicates benchmarking across different architectures.
Of note, no performance study has addressed DRU under coherent noise within spin-based QPUs governed by the LD Hamiltonian, underscoring a critical research gap. This gap frames the central motivation for our pulse-level, noise-aware DRU framework for spin-based architectures.
3. Materials and Methods
3.1. Data Re-Uploading for Quantum Classification
Data Re-Uploading (DRU) is a quantum embedding and classification strategy in which each classical feature vector , corresponding to the n-th sample in a dataset of size N, is repeatedly encoded into the parameters of a parameterized quantum circuit (PQC) [16]. The central idea is to alternate layers of trainable unitaries with multiple re-introductions of the same classical data, thereby enriching the expressive capacity of the quantum model while maintaining a compact circuit depth [15]. Formally, each DRU layer applies a single-qubit unitary whose rotation angles depend jointly on trainable parameters and on the components of the classical data vector. Specifically, the i-th layer in the DRU scheme is defined as
where denotes a single-qubit unitary parameterized by the vector of rotation angles , typically expressed through a Euler decomposition such as . The vector contains trainable parameters that define baseline rotations for the i-th layer, while is a trainable weight structure that modulates the influence of the classical input. Moreover, ⊙ represents the Hadamard (element-wise) product, ensuring that each feature component is scaled before being re-uploaded.
Thus, the effective angles combine learnable parameters with reintroduced classical information. Of note, this construction allows the PQC to repeatedly embed classical data across layers, overcoming the representational limitations of shallow circuits and enabling universal function approximation with single-qubit architectures when combined with suitable measurement schemes. When the input dimension satisfies , the feature vector is partitioned into k subvectors with . A single DRU layer is then realized as a product of sub-encodings [54]:
allowing high-dimensional features to be efficiently re-uploaded through multiple three-angle encodings per layer.
By stacking layers, the full single-qubit DRU circuit is obtained, parameterized by the trainable weights :
The resulting quantum state is then
This repeated re-uploading of across layers induces non-linear dependence on the input, thereby enhancing the expressive power of the model for classification tasks [55].
3.2. Fundamentals of the Quantum Processing Unit-Spin-Based (QPU-SB)
The spin-based quantum processing unit (QPU-SB) provides a natural physical platform for pulse-level compilation, where external control fields directly modulate the Hamiltonian dynamics of electronic spins. We begin with the single-spin model under the rotating-wave approximation (RWA), which captures the essential features of coherent control [56]. Consider a single electronic spin subjected to a magnetic field of the form
The spin energy eigenstates are defined as
In the rotating frame at frequency , the detuning is defined as , where as the Larmor frequency, and the Rabi frequency . Under the RWA, the Hamiltonian yields [57]
which makes explicit that a resonant drive () generates coherent rotations about the x-axis with rotation angle , where specifies the time-dependent pulse envelope. The latter can be extended to a register of electronic spins by adding both static and time-dependent contributions. The resulting Hamiltonian is written as [58]
Here, denotes the frequency of the x-component of a square pulse applied to the i-th spin, remaining constant during the pulse, while represents a transverse drive. Both controls can be compactly expressed using analytic forms such as rectangular windows . In explicit tensor-product notation, the Pauli operator acting on qubit i is expressed as
In simulation environments such as QuTiP [59], the static part is typically specified once, while the time-dependent coefficients for and are provided as callables encoding the chosen pulse envelopes.
Beyond single-qubit dynamics, entangling interactions are realized through the isotropic Heisenberg exchange coupling [60]. Then, for a pair of spins with tunable exchange strength , the Hamiltonian takes the form
If the pulse area is defined as , the corresponding two-qubit propagator can be written as
Special cases include , which up to single-qubit phases implements a SWAP gate, and , which yields a , a universal entangling operation when combined with local rotations [61,62].
Together, these Hamiltonians describe the fundamental building blocks of spin-based quantum processors. They not only capture the essential physics of single- and two-qubit operations but also provide the foundation for noise-aware pulse-level compilation, where realistic pulse shapes and control imperfections can be systematically integrated into quantum algorithm design.
3.3. Quantum and Coherence Noise Modeling
In modeling realistic spin-based quantum processors, two principal noise mechanisms must be considered: fluctuations in the control amplitudes, commonly referred to as coherent noise (CN), and dissipative processes that arise from coupling to the environment, collectively captured under quantum noise (QN). We first formalize the treatment of amplitude noise in the driven single-spin Hamiltonian and then extend the discussion to open-system dynamics through Lindblad master equations and their corresponding collapse operators [63].
In this work, amplitude fluctuations in the transverse driving field are introduced through an additive stochastic process. For the i-th qubit, the noisy control field can be written as
where denotes a Gaussian random variable with zero mean and variance . In practical simulations, however, the transverse field is represented by a rectangular pulse. This motivates the use of a scaled-noise formulation in which the stochastic term perturbs the ideal rectangular envelope, yielding
Here, the relative variance emerges naturally from the scaling property of Gaussian variables [64]: if , then for any constant c, the rescaled variable follows . This connection makes explicit the relation between absolute noise variance and its normalized counterpart when expressed with respect to the drive amplitude. The inclusion of scaled amplitude noise leads to a decomposition of the driven Hamiltonian into deterministic and stochastic parts. For a transverse drive on qubit i,
This decomposition highlights the role of the control pulse as the intended coherent operation, while simultaneously isolating the stochastic perturbation introduced by amplitude noise. Such a formulation is advantageous because it enables both the analytical evaluation of error rates and efficient sampling-based numerical simulations.
In addition to coherent fluctuations, spin qubits are subject to incoherent noise processes originating from their interaction with the surrounding environment. These processes are modeled using the Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) master equation in the Schrödinger picture, given by [65]
where denotes the system’s density matrix and the set contains collapse or jump operators associated with specific decoherence channels.
For longitudinal relaxation, which describes the irreversible decay of an excited state with characteristic time , the corresponding jump operator is [66]
where . Pure dephasing, in contrast, captures the loss of phase coherence without population transfer. It is represented by a Hermitian operator proportional to [67]:
The relation between relaxation and dephasing processes is usually expressed in terms of the transverse coherence time :
In experiments, the inhomogeneous dephasing time is often reported, which accounts for ensemble broadening effects. A commonly used approximation is [68]
although the precise relation depends on the noise spectrum and should be applied cautiously. An alternative dephasing ansatz sometimes adopted in simulations replaces with the population-projection operator , yielding [69]
Since and , both choices are equivalent in their physical action, although the -based form is algebraically simpler and more widely employed.
When extending these noise models to registers of multiple qubits, the collapse operators must be embedded into the full Hilbert space so that dissipation acts selectively on specific qubits. For a register of size with a designated target qubit , the single-qubit operators are mapped into the global system by tensoring with identity operators on all non-target sites:
The resulting full-system collapse operators are then
In numerical implementations with QuTiP [70], these operators are passed as entries of the collapse-operator list supplied to the master-equation solver so that the solver automatically includes both relaxation and dephasing channels in accordance with the Lindblad equation. Through this combined treatment of coherent amplitude fluctuations and Lindblad-type incoherent processes, our simulation framework is equipped to capture the dominant noise sources present in spin-based quantum processors. This dual-layer noise modeling provides the foundation for systematically evaluating the robustness of pulse-driven DRU classifiers under realistic device conditions.
3.4. Spin-Based Data Re-Uploading Framework
The proposed spin-based DRU framework builds upon the circuit architectures introduced in [16] as shown in Figure 1. The baseline configurations include one-, two-, and four-qubit circuits—denoted as DRU1Q, DRU2Q, and DRU4Q—and their entangled extensions, DRU2QE and DRU4QE. Each model is trained at the gate level (GL), where intermediate quantum states are represented by red dashed lines and expressed as , with i indexing the circuit layer and denoting the embedded data point .
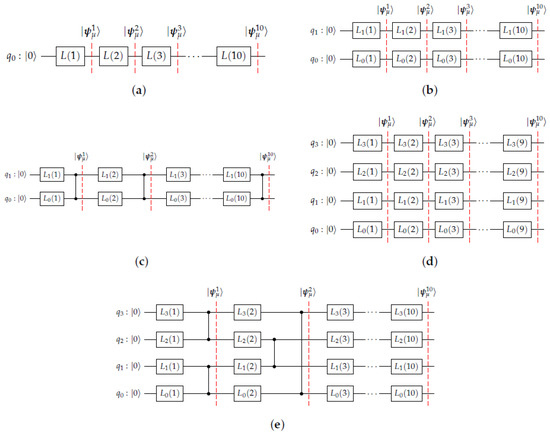
Figure 1.
Baseline DRU circuits employed in this study. Circuits incorporating entanglement are denoted by the suffix “E”. Intermediate intra-layer states are indicated by red dashed lines. (a) DRU1Q, (b) DRU2Q, (c) DRU2QE, (d) DRU4Q, and (e) DRU4QE.
Each DRU ansatz is composed of three fundamental building blocks: the single-qubit DRU layer , the two-qubit controlled-Z gate (), and the four-qubit controlled-Z constructed via SWAP networks (). Here, and denote the control and target qubits, respectively. The pulse-level compilation of these models on the spin-based quantum processing unit (QPU-SB) follows the single-spin Hamiltonian in Equation (7) and the exchange-coupling model in Equation (10), assuming a linear array of electron spins with nearest-neighbor coupling.
3.4.1. Single Layer Model
Each DRU layer is parameterized as a unitary operator whose rotation angles depend linearly on trainable parameters and classical inputs [16] as defined in Equation (1). This formulation separates trainable variables from the input-dependent modulation , enabling efficient gradient-based optimization. The single-qubit operation is expressed through a three-angle Euler decomposition:
where . Since the QPU-SB supports control only along the x and z axes, rotations are synthesized using the standard conjugation identity [71]:
Thus, all layer unitaries can be expressed in terms of native and rotations, fully compatible with pulse-level synthesis via transverse-field and detuning controls. The rotation angle for an gate is determined by the pulse area (), where denotes the pulse duration, while rotations correspond to detuning-induced or virtual-frame operations. These mappings translate the DRU parameters into physically realizable control envelopes within the Hamiltonian models of Equations (7) and (10).
3.4.2. Two-Qubit CZ Gate
The controlled-Z primitive (CZ-2), shown in Figure 2, is implemented through two operations interleaved with single-qubit phase gates:
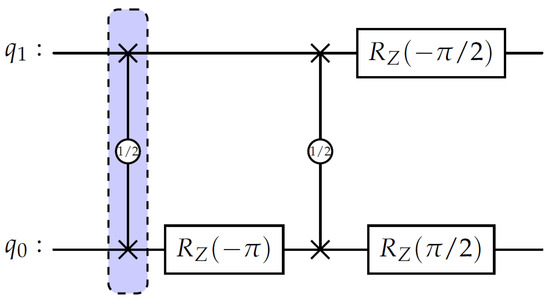
Figure 2.
CZ-2 decomposition into primitives and single-qubit rotations.
This decomposition reproduces the canonical CZ operation (up to a global phase) and naturally maps to exchange-pulse sequences and local phase adjustments in the QPU-SB.
3.4.3. Four-Qubit CZ4 Gate
The non-adjacent controlled-Z operation (CZ4), illustrated in Figure 3, is realized using SWAP networks that bring distant qubits into adjacency. The construction employs Hadamard gates to toggle between CZ and CNOT forms, with SWAP layers restoring the original qubit ordering. The Hadamard gate is decomposed as
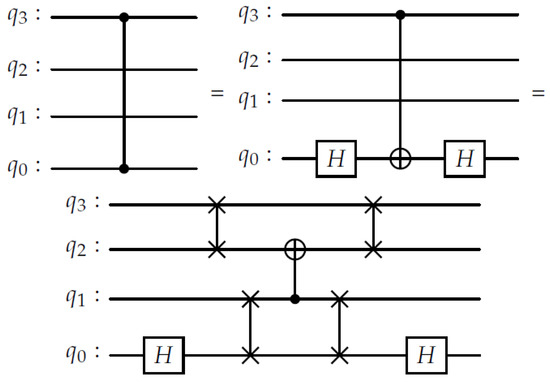
Figure 3.
SWAP-network implementation of a non-adjacent controlled gate (CZ-4/CNOT-4). Blue dashed areas denote primitives.
3.4.4. CNOT Decomposition and Hardware Mapping
Figure 4 shows the decomposition of an adjacent CNOT gate into native spin-QPU primitives. The entangling operation is achieved through gates, while local rotations are implemented using the – synthesis rules established above. This mapping provides a consistent bridge between gate-level and pulse-level abstractions, forming the foundation for benchmarking DRU compilation on spin-based architectures.
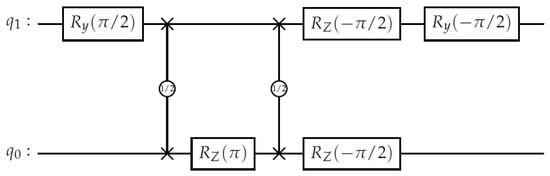
Figure 4.
Adjacent CNOT decomposition using native spin-QPU primitives ( and single-qubit rotations).
4. Experimental Set-Up
We evaluate our proposed Spin-based Quantum Classifier (SQC) framework through comprehensive simulations conducted at both the pulse and gate levels. This dual-level evaluation enables a direct comparison between abstract circuit-based performance and the underlying continuous-time spin dynamics governed by the Loss–DiVincenzo Hamiltonian. To demonstrate the classification capabilities of the SQC under realistic noise and control constraints, we employ a benchmark dataset widely used in quantum and classical machine learning studies, allowing the systematic assessment of accuracy, robustness, and noise sensitivity across different spin configurations.
4.1. Tested Dataset
For empirical validation, we employ the Iris dataset, a canonical benchmark in both classical and quantum machine learning studies [64]. The dataset consists of 150 labeled samples evenly distributed across three species: setosa, versicolor, and virginica. Each sample is characterized by four continuous features—sepal length, sepal width, petal length, and petal width—normalized within the range for quantum encoding. The Iris dataset provides an ideal testbed for evaluating quantum classifiers due to its mixed separability properties: while setosa is linearly separable from the remaining species, versicolor and virginica exhibit substantial overlap, introducing a non-linear decision boundary that challenges low-dimensional quantum representations. Despite its simplicity, this dataset enables the controlled analysis of embedding expressivity, decision boundary complexity, and noise robustness within constrained spin-based architectures [72].
Although the dataset employed is the Iris dataset, which originally consists of four features and three classes embedded, in this work we adopt the notation , where n denotes the dimensionality of features (with Principal Component Analysis, PCA, applied when to reduce dimensionality) and m specifies the number of selected classes from the dataset, namely, Iris-Setosa, Iris-Versicolour, and Iris-Virginica.
4.2. Training Details and Baselines
Gate-level training was carried out using the PennyLane Python library with the Adam optimizer configured as and [73]. For each circuit, the labeled quantum states are defined as , where denotes the number of classes. These states were prepared as pure states under the maximum orthogonality labeling criterion proposed in [16]. Representative labeling configurations are shown in Figure 5.
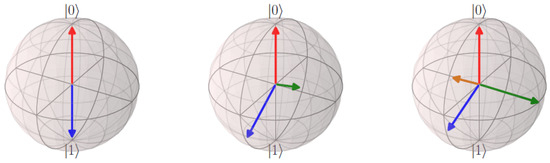
Figure 5.
Gate-level class-label encoding. Visualization of single-qubit states used to represent class labels for , , and , shown from left to right (two, three, and four class-configurations). Color assignments correspond to label 0 (red), label 1 (blue), label 2 (green), and label 3 (yellow).
Representative quantum states are defined for each tested qubit–class configuration as follows:
- –
- For a single qubit and two classes, we use and .
- –
- When extending to three classes, the states are defined as , , and .
- –
- For four classes, we adopt , , , and .
- –
- For two-qubit circuits, the states corresponding to two classes are and ,
- –
- While for three classes we use , , and .
- –
- Finally, for four-qubit encodings, we select and for two classes, and extend to for three-class configurations.
Further, quantum fidelity provides a fundamental measure of similarity between quantum states and serves a dual purpose in this study: (i) as an evaluation metric to quantify the accuracy of pulse-to-gate compilation, and (ii) as a supervised cost function for classification. For two quantum states and represented by density matrices, fidelity is defined as [74]
with , where denotes identical states and indicates orthogonality. Within spin-based QPU simulations, fidelity is computed between an ideal layer state and its compiled counterpart , thereby capturing deviations arising from QN and CN. Also, the average fidelity over all samples after the final layer, and , quantifies the accuracy of the compiled dynamics.
For classification, fidelity acts as a quantum scoring function that maps the predicted quantum state to the most similar label state , given by
This procedure yields a classical label for each predicted quantum state, which is subsequently evaluated using the classical Area Under the ROC Curve (AUC) measure [44]
where TPR and FPR denote the true and false positive rates, respectively.
In addition, the DRU algorithm’s performance is benchmarked under non-ideal conditions, analyzing how circuit configuration (number of qubits ), depth (), and cost function choice affect classification outcomes across varying levels of coherent noise () and quantum decoherence (). All evaluations are performed under a one-vs-rest AUC scheme to identify optimal training strategies for noise-aware DRU models on spin-based quantum processors [75]. A 5-fold cross-validation scheme is fixed for classification training and testing. Each model was trained for 10 epochs with a batch size of 32. To assess robustness, the coherent control noise amplitude was varied within [T], while decoherence times ranged from [s] [76].
For each circuit architecture, depths of were tested. The training objective minimized one of four loss functions, each quantifying the dissimilarity between the true and predicted quantum states density matrices and , respectively. Specifically [77,78]: (i) the Trace Distance measures the distinguishability between two quantum states; (ii) the Quantum Relative Entropy quantifies their information divergence (i.e., von Neumann divergence); (iii) the Rényi Divergence generalizes entropy-based distances for tunable , commonly fixed as or 2; and (iv) the Fidelity Complement Loss penalizes dissimilarity in terms of state fidelity. Their analytical forms are given as follows:
After training, the optimized parameters were deployed to the QPU for pulse-level simulation under noisy conditions. Each test input produced a corresponding quantum state, from which the predicted class label was inferred via fidelity-based comparison. The classification performance was then quantified using the AUC metric, providing a robust measure of separability under realistic noise. The complete end-to-end workflow is illustrated in Figure 6.
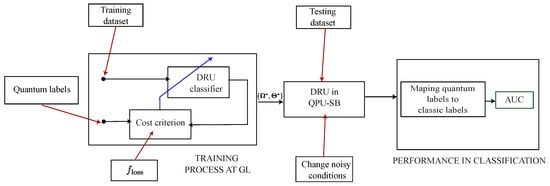
Figure 6.
General experimental framework for benchmarking DRU on spin-based quantum processes under varying hyperparameters and noise conditions.
5. Results and Discussion
5.1. Pulse and Fidelity Compilation
This subsection presents the simulation outcomes for the implementation and compilation of DRU circuits on the spin-based QPU under ideal (noise-free) conditions. We first analyze the impact of detuning, caused by variations in the resonance frequency, using a single-qubit DRU circuit with (see Figure 7). Consistent with experimental observations in spin-based quantum hardware [79], we evaluate the frequency response of an rotation. The transition probability peaks when the driving frequency matches the qubit resonance, i.e., MHz. This probability is computed by projecting the time-evolved state onto the measurement basis and evaluating or . The resulting Rabi-like oscillations show reduced amplitudes under off-resonance conditions, a behavior also observed in the DRU1Q circuit, where detuning significantly modifies the population transfer between basis states.
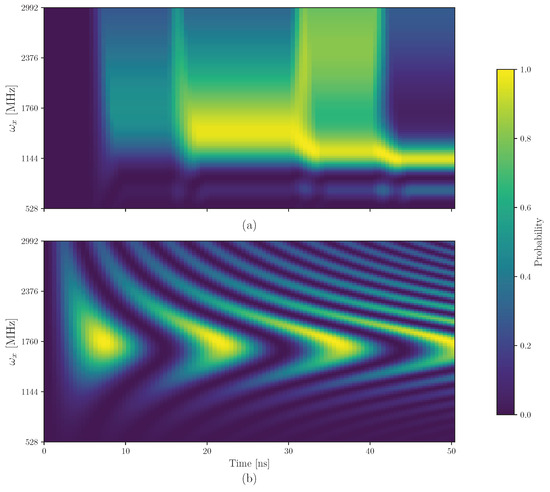
Figure 7.
Frequency-dependent transition probability of the spin-based QPU. (a) DRU1Q circuit with showing Rabi-like oscillations and detuning effects. (b) Reference rotation highlighting maximum transition probability at resonance ().
Next, we validate the time evolution of gates for two- and four-qubit systems. These operations, combined with Hadamard gates, enable the construction of the gates required in DRU architectures (see Figure 8). In the two-qubit case, with as the control and as the target, the simulation reproduces the expected transition from to . Similarly, in the four-qubit configuration, where controls , the state of flips from to , consistent with theoretical predictions [80].
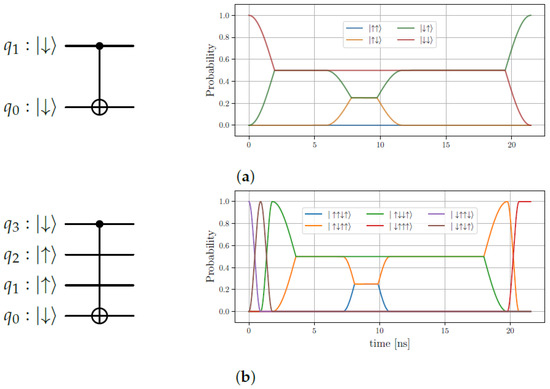
Figure 8.
Time response of a gate implementations for two and four qubits in the spin-based QIPU simulation. The left side shows the corresponding quantum circuits, and the right side presents their respective time evolutions. (a) Implementation of for tow qubits. (b) Implementation of for four qubits.
Figure 9 further demonstrates the tomography of the Bell state , confirming the simulator’s ability to reproduce entangled states [28]. The close agreement between the simulated and ideal density matrices validates the capability of our spin-based QPU framework to generate and preserve non-classical correlations with high fidelity.
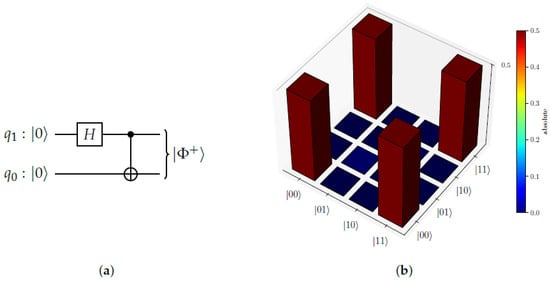
Figure 9.
Tomography of a Bell state generated using our spin-based QIPU simulation framework. (a) Quantum circuit for generating a Bell state. (b) Quantum tomography of a Bell state .
Also, we assess the compilation accuracy of the DRU algorithm through fidelity evaluations between trained gate-level models and their corresponding spin-based pulse implementations. Table 1 reports the average fidelities and standard deviations for the DRU1Q circuit trained on the Iris dataset using . All results exhibit fidelities near unity, confirming an accurate mapping of the DRU layers into the spin-based QPU under ideal conditions.

Table 1.
Average training fidelities for one-qubit DRU circuits with increasing layer depth . All models exhibit near-unity fidelity under ideal (noise-free) conditions.
Of note, the optimized parameters define the control amplitudes that generate the pulse sequences for QPU execution. Each input corresponds to a distinct pulse configuration. Next, Figure 10 shows an example pulse schedule for a DRU2QE circuit, where transverse (), longitudinal (), and exchange () pulses orchestrate spin rotations and entangling interactions. Virtual I gates (red) synchronize layer durations when . Although these idle intervals are not yet modeled with real Z fields, their inclusion in future implementations would improve physical realism. The simulation employs an exchange interaction strength of Hz, resulting in and SWAP gate durations of 15 ps and 30 ps, respectively—significantly shorter than single-qubit rotation pulses. Consequently, subsystem states remain effectively stable during entangling operations.
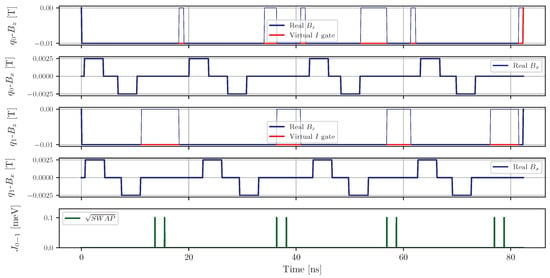
Figure 10.
Pulse schedule for the compilation of DRU2QE using an arbitrary test data point after training.
Overall, these findings demonstrate that the proposed DRU-based architectures can be reliably compiled into the spin-based QPU simulation, achieving near-unity fidelities and physically interpretable pulse-level control across all tested configurations.
5.2. Noise Modeling Results
Next, a comprehensive experiment is conducted to evaluate the effect of CN and QN on the fidelity of quantum states produced by trained DRU circuits. Five DRU ansatzes (see Figure 1) are tested using the Iris dataset. For CN, we introduce random fluctuations in the transverse field amplitude across a logarithmic range of [T]. For QN, we simulate dephasing processes over the interval [s]. Afterward, fidelity is computed between the simulated QPU output states and the noise-free baseline states for all test samples.
As shown in Figure 11, fidelity consistently decreases with increasing , reflecting stronger field amplitude perturbations under CN, and with decreasing , due to faster decoherence under QN—trends that align with theoretical expectations [81]. These results demonstrate that our spin-based QPU simulation successfully captures both noise mechanisms and their impact on quantum state degradation. Importantly, the inclusion of CN and QN within our simulation framework highlights its capability to model realistic spin-based quantum processors. Since near-term quantum devices operate in the NISQ regime, the ability to incorporate both error sources is essential for evaluating algorithmic robustness and reliability.
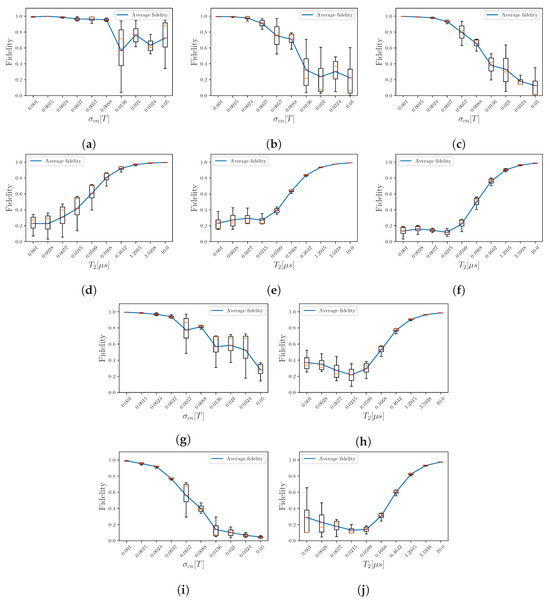
Figure 11.
Average fidelity degradation for spin-based DRU architectures under CN and QN noise. (a–c) CN for 1-, 2-, and 4-qubit without entanglement. (d–f) QN for 1-, 2-, and 4-qubit without entanglement. (g,h) CN and QN for 2-qubit entangled. (i,j) CN and QN for 4-qubit entangled.
5.3. Quantum Classification Results
As an illustrative example, Figure 12 shows the underlying structure of the Iris dataset through a 2D Principal Component Analysis (PCA) projection and its corresponding Bloch sphere representations obtained from the one-qubit DRU circuit. The visualization highlights how the data evolves from randomly initialized embeddings to optimized quantum feature representations after training. This transformation demonstrates how the trained spin-based DRU parameters reshape the input manifold, enhancing inter-class separability and geometric clustering in the Bloch space. So, the circuit effectively encodes non-linear decision boundaries in a physically interpretable quantum state space.
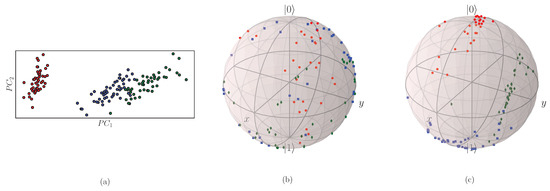
Figure 12.
Iris visualization results: (a) 2D PCA projection (red: setosa, blue: versicolor, green: virginica). (b) Bloch sphere representation using a DRU1Q model with random weights (). (c) Bloch sphere embedding obtained after training the DRU1Q with optimized parameters, showing improved class separability.
Figure 13 presents the benchmarking results for our spin-based DRU quantum classifier. Specifically, the plots correspond to the one-qubit DRU ansatz across different layer configurations (), where the AUC is reported. Each cell represents the average AUC from a 5-fold cross-validation across multiple loss functions. The best performance is achieved for , which exhibits greater robustness against both CN and QN. This finding is consistent with theoretical expectations, as lower values and longer coherence times preserve state fidelity and enhance classification performance.
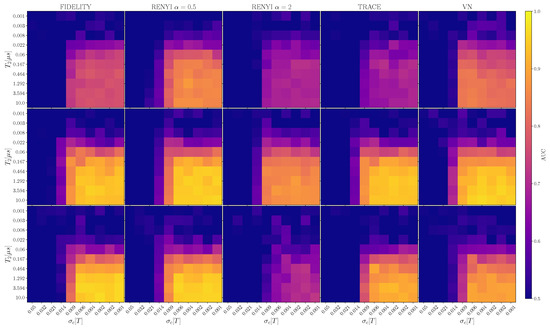
Figure 13.
AUC classification results for a one-qubit DRU ansatz with layers under varying classical noise () and quantum noise () conditions using different loss functions.
To assess the statistical significance of these findings, the Friedman test [82] was applied across all ansatzes and layer configurations. Table 2 summarizes the average ranking for each loss function. The test confirms significant differences among the evaluated losses ( in all cases except for DRU4QE with ), indicating that the observed performance rankings are statistically reliable. Overall, the VN divergence and Rényi divergence with consistently achieved the best results across most configurations, suggesting that these entropy-based criteria are particularly well-suited for training gate-level DRU models under realistic spin-based QPU conditions.

Table 2.
Average ranking (Friedman test) of loss criteria across DRU ansatzes on a spin-based QPU. For each configuration, the best and second-best criteria are shown with mean ranks (in parentheses), along with the Friedman statistic and p-value.
Importantly, this study adopts the AUC metric instead of accuracy. The latter can be misleading in imbalanced datasets, where a model biased toward the majority class may yield artificially high accuracy—a phenomenon known as the accuracy paradox. In the context of quantum classification, this issue is exacerbated by the system’s intrinsic relaxation dynamics. Although the depolarization time is longer than the coherence time , it still introduces bias, as the quantum state tends to relax toward the ground state . This can inflate accuracy scores and obscure the model’s actual discriminative power. The AUC measure, by contrast, provides a more balanced and noise-resilient assessment of classifier performance.
6. Conclusions
We introduced a pulse-driven quantum machine learning paradigm that bridges algorithmic modeling and physical realization on spin-based quantum processing units (QPU-SB). Built upon the Data Re-Uploading (DRU) algorithm, the framework translates gate-level operations into time-domain pulse controls governed by the Loss–DiVincenzo Hamiltonian. By explicitly incorporating both coherent and quantum noise sources—modeled through stochastic control perturbations and Lindblad dynamics, our proposal establishes a comprehensive route to simulate and train quantum classifiers under realistic device conditions. Remarkably, our framework extends beyond abstract gate-based learning, providing a physically interpretable and experimentally aligned methodology to explore the interplay between quantum information encoding, spin-qubit control, and noise resilience in the NISQ regime.
The experimental results demonstrate that the proposed pulse-level DRU compilation preserves the functional integrity of gate-level quantum circuits, achieving near-unity fidelities across all tested spin configurations. Also, continuous-time simulations reveal that our approach accurately captures both oscillations and exchange-coupling dynamics, validating its consistency with spin-qubit control physics. In fact, when noise is introduced, the model exhibits predictable fidelity degradation with increasing amplitude fluctuations and reduced coherence times, confirming the realism of the noise-aware simulation. Moreover, classification benchmarks on the Iris dataset show that the trained spin-based DRU models effectively capture decision boundaries, improving class separability through physically interpretable embeddings. Also, divergence-based loss functions—particularly the von Neumann and Rényi divergences—yielded superior robustness and AUC performance compared to fidelity-based criteria, reinforcing their suitability for quantum classification under noisy environments.
Future work includes the experimental deployment of the proposed framework on real spin-qubit hardware, leveraging programmable exchange interactions and CMOS-compatible control lines to validate the pulse-level simulation and its correspondence with physical spin dynamics. Extending the model to multi-qubit DRU architectures and hybrid quantum–classical optimization routines will enhance scalability and expressivity [41]. Further, advanced noise characterization—particularly for non-Markovian environments and correlated dephasing—will allow the design of adaptive, error-attentive training protocols [83]. Moreover, integrating pulse-level learning with quantum control theory may enable self-calibrating classifiers capable of compensating for device imperfections in situ [84]. Lastly, we will also integrate a realistic measurement model by simulating quantum state tomography to reconstruct the final output states of the QPU-SB. This approach will allow for the analysis of statistical errors arising from finite-shot measurements, effectively introducing shot noise into the evaluation of expectation values. Such an extension will offer a more accurate assessment of the algorithm’s performance under experimental conditions [85,86].
Author Contributions
Conceptualization, C.R.-M., A.M.Á.-M. and G.C.-D.; data curation, C.R.-M.; methodology, C.R.-M. and A.M.Á.-M.; project administration, A.M.Á.-M.; supervision, A.M.Á.-M. and G.C.-D.; resources, C.R.-M. All authors have read and agreed to the published version of the manuscript.
Funding
Under grants provided by the project: “Aprendizaje de máquina cuántico utilizando espines electrónicos”, Hermes-62836, funded by Universidad Nacional de Colombia and Universidad de Caldas. Also, G. Castellanos-Dominguez thanks to the project: “Sistema de visión artificial para el monitoreo y seguimiento de efectos analgésicos y anestésicos administrados vía neuroaxial epidural en población obstétrica durante labores de parto para el fortalecimiento de servicios de salud materna del Hospital Universitario de Caldas-SES HUC”, Hermes 57661, funded by Universidad Nacional de Colombia.
Data Availability Statement
The publicly available dataset analyzed in this study and our Python codes can be found at https://github.com/6arlos6/QML_with_spins_using_DRU_algorithm (accessed on 30 July 2025).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Elsayed, N.; Maida, A.S.; Bayoumi, M. A review of quantum computer energy efficiency. In Proceedings of the 2019 IEEE Green Technologies Conference (GreenTech), Lafayette, LA, USA, 3–6 April 2019; pp. 1–3. [Google Scholar]
- Schmidhuber, A.; O’Donnell, R.; Kothari, R.; Babbush, R. Quartic Quantum Speedups for Planted Inference. Phys. Rev. X 2025, 15, 021077. [Google Scholar] [CrossRef]
- Jain, S.; Ziauddin, J.; Leonchyk, P.; Yenkanchi, S.; Geraci, J. Quantum and classical machine learning for the classification of non-small-cell lung cancer patients. SN Appl. Sci. 2020, 2, 1088. [Google Scholar] [CrossRef]
- Alaminos, D.; Salas, M.B.; Fernández-Gámez, M.A. Quantum computing and deep learning methods for GDP growth forecasting. Comput. Econ. 2022, 59, 803–829. [Google Scholar] [CrossRef]
- Kookani, A.; Mafi, Y.; Kazemikhah, P.; Aghababa, H.; Fouladi, K.; Barati, M. SpookyNet: Advancement in Quantum System Analysis through Convolutional Neural Networks for Detection of Entanglement. arXiv 2023, arXiv:2309.03890. [Google Scholar]
- Sajjan, M.; Li, J.; Selvarajan, R.; Sureshbabu, S.H.; Kale, S.S.; Gupta, R.; Singh, V.; Kais, S. Quantum machine learning for chemistry and physics. Chem. Soc. Rev. 2022, 51, 6475–6573. [Google Scholar] [CrossRef]
- Huang, B.; Symonds, N.O.; von Lilienfeld, O.A. Quantum machine learning in chemistry and materials. In Handbook of Materials Modeling: Methods: Theory and Modeling; Springer International Publishing: Cham, Switzerland, 2020; pp. 1883–1909. [Google Scholar]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum circuit learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, M.; Verdon, G.; Huang, H.Y.; Cincio, Ł.; Coles, P.J. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci. 2022, 2, 567–576. [Google Scholar] [CrossRef] [PubMed]
- Muser, T.; Zapusek, E.; Belis, V.; Reiter, F. Provable advantages of kernel-based quantum learners and quantum preprocessing based on Grover’s algorithm. arXiv 2023, arXiv:2309.14406. [Google Scholar] [CrossRef]
- Xiao, T.; Zhai, X.; Huang, J.; Fan, J.; Zeng, G. Quantum deep generative prior with programmable quantum circuits. Commun. Phys. 2024, 7, 276. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Jerbi, S.; Fiderer, L.J.; Poulsen Nautrup, H.; Kübler, J.M.; Briegel, H.J.; Dunjko, V. Quantum machine learning beyond kernel methods. Nat. Commun. 2023, 14, 517. [Google Scholar] [CrossRef]
- Pérez-Salinas, A.; Cervera-Lierta, A.; Gil-Fuster, E.; Latorre, J.I. Data re-uploading for a universal quantum classifier. Quantum 2020, 4, 226. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Dutta, T.; Pérez-Salinas, A.; Phua Sing Cheng, J.; Latorre, J.I.; Mukherjee, M. Single-qubit universal classifier implemented on an ion-trap quantum device. Phys. Rev. A 2022, 106, 012411. [Google Scholar] [CrossRef]
- Mauser, M.F.; Four, S.; Predl, L.M.; Albiero, R.; Ceccarelli, F.; Osellame, R.; Petersen, P.; Dakić, B.; Agresti, I.; Walther, P. Experimental data re-uploading with provable enhanced learning capabilities. arXiv 2025, arXiv:2507.05120. [Google Scholar] [CrossRef]
- Tolstobrov, A.; Fedorov, G.; Sanduleanu, S.; Kadyrmetov, S.; Vasenin, A.; Bolgar, A.; Kalacheva, D.; Lubsanov, V.; Dorogov, A.; Zotova, J.; et al. Hybrid quantum learning with data reuploading on a small-scale superconducting quantum simulator. Phys. Rev. A 2024, 109, 012411. [Google Scholar] [CrossRef]
- Periyasamy, M.; Meyer, N.; Ufrecht, C.; Scherer, D.D.; Plinge, A.; Mutschler, C. Incremental data-uploading for full-quantum classification. In Proceedings of the 2022 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 18–23 September 2022; pp. 31–37. [Google Scholar]
- Stone, D.G.; Bradac, C. Machine and quantum learning for diamond-based quantum applications. Mater. Quantum Technol. 2023, 3, 012001. [Google Scholar] [CrossRef]
- Boykin, P.O.; Mor, T.; Roychowdhury, V.; Vatan, F.; Vrijen, R. Algorithmic cooling and scalable NMR quantum computers. Proc. Natl. Acad. Sci. USA 2002, 99, 3388–3393. [Google Scholar] [CrossRef]
- Sangtawesin, S.; Brundage, T.O.; Atkins, Z.J.; Petta, J.R. Highly tunable formation of nitrogen-vacancy centers via ion implantation. Appl. Phys. Lett. 2014, 105, 063107. [Google Scholar] [CrossRef]
- De Michielis, M.; Ferraro, E.; Prati, E.; Hutin, L.; Bertrand, B.; Charbon, E.; Ibberson, D.J.; Gonzalez-Zalba, M.F. Silicon spin qubits from laboratory to industry. J. Phys. D: Appl. Phys. 2023, 56, 363001. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
- Mills, A.R.; Guinn, C.R.; Gullans, M.J.; Sigillito, A.J.; Feldman, M.M.; Nielsen, E.; Petta, J.R. Two-qubit silicon quantum processor with operation fidelity exceeding 99%. Sci. Adv. 2022, 8, eabn5130. [Google Scholar] [CrossRef]
- Watson, T.; Philips, S.; Kawakami, E.; Ward, D.; Scarlino, P.; Veldhorst, M.; Savage, D.; Lagally, M.; Friesen, M.; Coppersmith, S.; et al. A programmable two-qubit quantum processor in silicon. Nature 2018, 555, 633–637. [Google Scholar] [CrossRef]
- Chan, K.W.; Sahasrabudhe, H.; Huang, W.; Wang, Y.; Yang, H.C.; Veldhorst, M.; Hwang, J.C.; Mohiyaddin, F.A.; Hudson, F.E.; Itoh, K.M.; et al. Exchange coupling in a linear chain of three quantum-dot spin qubits in silicon. Nano Lett. 2021, 21, 1517–1522. [Google Scholar] [CrossRef]
- Philips, S.G.; Mądzik, M.T.; Amitonov, S.V.; de Snoo, S.L.; Russ, M.; Kalhor, N.; Volk, C.; Lawrie, W.I.; Brousse, D.; Tryputen, L.; et al. Universal control of a six-qubit quantum processor in silicon. Nature 2022, 609, 919–924. [Google Scholar] [CrossRef]
- Cho, Y.; Beck, K.M.; Castelli, A.R.; Wendt, K.A.; Evert, B.; Reagor, M.J.; DuBois, J.L. Direct pulse-level compilation of arbitrary quantum logic gates on superconducting qutrits. arXiv 2023, arXiv:2303.04261. [Google Scholar] [CrossRef]
- Berberich, J.; Fink, D.; Holm, C. Robustness of quantum algorithms against coherent control errors. arXiv 2023, arXiv:2303.00618. [Google Scholar] [CrossRef]
- Herrmann, N.; Akhtar, M.; Arya, D.; Doherty, M.W.; Macha, P.; Preis, F.; Prestel, S.; Walker, M.L. First quantum machine learning applications on an on-site room-temperature quantum computer. arXiv 2023, arXiv:quant-ph/2312.11673. [Google Scholar] [CrossRef]
- Li, B.; Ahmed, S.; Saraogi, S.; Lambert, N.; Nori, F.; Pitchford, A.; Shammah, N. Pulse-level noisy quantum circuits with QuTiP. Quantum 2022, 6, 630. [Google Scholar] [CrossRef]
- Lasek, A.; Lepage, H.V.; Zhang, K.; Ferrus, T.; Barnes, C.H. Pulse-controlled qubit in semiconductor double quantum dots. arXiv 2023, arXiv:2303.04823. [Google Scholar] [CrossRef] [PubMed]
- Bergholm, V.; Izaac, J.; Schuld, M.; Gogolin, C.; Ahmed, S.; Ajith, V.; Alam, M.S.; Alonso-Linaje, G.; AkashNarayanan, B.; Asadi, A.; et al. Pennylane: Automatic differentiation of hybrid quantum-classical computations. arXiv 2018, arXiv:1811.04968. [Google Scholar]
- Alexander, T.; Kanazawa, N.; Egger, D.J.; Capelluto, L.; Wood, C.J.; Javadi-Abhari, A.; McKay, D.C. Qiskit pulse: Programming quantum computers through the cloud with pulses. Quantum Sci. Technol. 2020, 5, 044006. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Paraoanu, G.S. Simulating spin chains using a superconducting circuit: Gauge invariance, superadiabatic transport, and broken time-reversal symmetry. Adv. Quantum Technol. 2020, 3, 1900121. [Google Scholar] [CrossRef]
- Last, T.; Samkharadze, N.; Eendebak, P.; Versluis, R.; Xue, X.; Sammak, A.; Brousse, D.; Loh, K.; Polinder, H.; Scappucci, G.; et al. Quantum Inspire: QuTech’s platform for co-development and collaboration in quantum computing. In Proceedings of the Novel Patterning Technologies for Semiconductors, MEMS/NEMS and MOEMS 2020, SPIE, San Jose, CA, USA, 24–27 February 2020; Volume 11324, pp. 49–59. [Google Scholar]
- Molina, D.E.; Hamilton, K. Noise Robustness of Data Re-Uploading Quantum Classifiers. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 2–6 October 2023; Volume 2, pp. 395–396. [Google Scholar]
- Wach, N.L.; Rudolph, M.S.; Jendrzejewski, F.; Schmitt, S. Data re-uploading with a single qudit. arXiv 2023, arXiv:2302.13932. [Google Scholar] [CrossRef]
- Valverde-Albacete, F.J.; Peláez-Moreno, C. 100% classification accuracy considered harmful: The normalized information transfer factor explains the accuracy paradox. PLoS ONE 2014, 9, e84217. [Google Scholar] [CrossRef]
- Linden, O.; May, V. Quantum master equation, Lindblad-type of dissipation and temperature dependent Monte Carlo wave-function propagation. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2000, 12, 473–485. [Google Scholar] [CrossRef]
- Schetakis, N.; Aghamalyan, D.; Griffin, P.; Boguslavsky, M. Review of some existing QML frameworks and novel hybrid classical–quantum neural networks realising binary classification for the noisy datasets. Sci. Rep. 2022, 12, 11927. [Google Scholar] [CrossRef]
- Ono, T.; Roga, W.; Wakui, K.; Fujiwara, M.; Miki, S.; Terai, H.; Takeoka, M. Demonstration of a Bosonic Quantum Classifier with Data Reuploading. Phys. Rev. Lett. 2023, 131, 13601. [Google Scholar] [CrossRef]
- Smith, R.S.; Curtis, M.J.; Zeng, W.J. A practical quantum instruction set architecture. arXiv 2016, arXiv:1608.03355. [Google Scholar]
- Fingerhuth, M.; Babej, T.; Wittek, P. Open source software in quantum computing. PLoS ONE 2018, 13, e0208561. [Google Scholar] [CrossRef] [PubMed]
- Steiger, D.S.; Häner, T.; Troyer, M. ProjectQ: An open source software framework for quantum computing. Quantum 2018, 2, 49. [Google Scholar] [CrossRef]
- Gokhale, P.; Javadi-Abhari, A.; Earnest, N.; Shi, Y.; Chong, F.T. Optimized quantum compilation for near-term algorithms with openpulse. In Proceedings of the 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Virtual, 17–21 October 2020; pp. 186–200. [Google Scholar]
- Easom-Mccaldin, P.; Bouridane, A.; Belatreche, A.; Jiang, R. On depth, robustness and performance using the data re-uploading single-qubit classifier. IEEE Access 2021, 9, 65127–65139. [Google Scholar] [CrossRef]
- Alam, M.; Ghosh, S. QNet: A scalable and noise-resilient quantum neural network architecture for noisy intermediate-scale quantum computers. Front. Phys. 2022, 9, 702. [Google Scholar] [CrossRef]
- Berberich, J.; Fink, D.; Pranjić, D.; Tutschku, C.; Holm, C. Training robust and generalizable quantum models. arXiv 2023, arXiv:2311.11871. [Google Scholar] [CrossRef]
- Schetakis, N.; Aghamalyan, D.; Boguslavsky, M.; Griffin, P. Binary classifiers for noisy datasets: A comparative study of existing quantum machine learning frameworks and some new approaches. arXiv 2021, arXiv:2111.03372. [Google Scholar] [CrossRef]
- Pérez-Salinas, A.; López-Núñez, D.; García-Sáez, A.; Forn-Díaz, P.; Latorre, J.I. One qubit as a Universal Approximant. Phys. Rev. A 2021, 104, 012405. [Google Scholar] [CrossRef]
- Yu, Z.; Yao, H.; Li, M.; Wang, X. Power and limitations of single-qubit native quantum neural networks. arXiv 2022, arXiv:2205.07848. [Google Scholar] [CrossRef]
- Burkard, G.; Ladd, T.D.; Pan, A.; Nichol, J.M.; Petta, J.R. Semiconductor spin qubits. Rev. Mod. Phys. 2023, 95, 025003. [Google Scholar] [CrossRef]
- Zeuch, D.; Hassler, F.; Slim, J.J.; DiVincenzo, D.P. Exact rotating wave approximation. Ann. Phys. 2020, 423, 168327. [Google Scholar] [CrossRef]
- Naus, H.W.L.; Versluis, R. Semi-analytical RWA formalism to solve Schrödinger equations for multi-qubit systems with resonator couplings. arXiv 2017, arXiv:1707.02862. [Google Scholar]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]
- Fan, H.; Roychowdhury, V.; Szkopek, T. Optimal two-qubit quantum circuits using exchange interactions. Phys. Rev. A 2005, 72, 052323. [Google Scholar] [CrossRef]
- DiVincenzo, D.P.; Bacon, D.; Kempe, J.; Burkard, G.; Whaley, K.B. Universal Quantum Computation with the Exchange Interaction. Phys. Rev. A 2000, 61, 062301. [Google Scholar] [CrossRef] [PubMed]
- Fanchini, F.F.; de Jesus Napolitano, R.; Çakmak, B.; Caldeira, A.O. Protecting the √SWAP operation from general and residual errors by continuous dynamical decoupling. arXiv 2015, arXiv:1504.00592. [Google Scholar] [CrossRef]
- Schwartzman-Nowik, Z.; Shirizly, L.; Landa, H. Modeling error correction with Lindblad dynamics and approximate channels. arXiv 2025, arXiv:2402.16727. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Manzano, D. A short introduction to the Lindblad master equation. AIP Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
- Boulant, N.; Havel, T.F.; Pravia, M.A.; Cory, D.G. A robust method for estimating the Lindblad operators of a dissipative quantum process from measurements of the density operator at multiple time points. arXiv 2002, arXiv:quant-ph/0211046. [Google Scholar] [CrossRef]
- Marquardt, F. Introduction to dissipation and decoherence in quantum systems. arXiv 2008, arXiv:0809.4403. [Google Scholar] [CrossRef]
- Ithier, G.; Collin, E.; Joyez, P.; Meeson, P.J.; Vion, D.; Esteve, D.; Chiarello, F.; Shnirman, A.; Makhlin, Y.; Schön, G.; et al. Decoherence in a superconducting quantum bit circuit. Phys. Rev. B 2005, 72, 134519. [Google Scholar] [CrossRef]
- Gambetta, J.; Motzoi, F.; Merkel, S.T.; Wilhelm, F.K. Building logical qubits in a superconducting quantum computing system. Phys. Rev. Lett. 2017, 119, 180501. [Google Scholar] [CrossRef]
- Lambert, N.; Giguère, E.; Menczel, P.; Li, B.; Hopf, P.; Suárez, G.; Gali, M.; Lishman, J.; Gadhvi, R.; Agarwal, R.; et al. QuTiP 5: The Quantum Toolbox in Python. arXiv 2024, arXiv:2412.04705. [Google Scholar]
- Möttönen, M.; Vartiainen, J.J. Decompositions of general quantum gates. In Trends in Quantum Computing Research; Amazon: Seattle, WA, USA, 2006; p. 149. [Google Scholar]
- Tomal, S.; Shafin, A.A.; Afaf, A.; Bhattacharjee, D. Quantum Convolutional Neural Network: A Hybrid Quantum-Classical Approach for Iris Dataset Classification. arXiv 2024, arXiv:2410.16344. [Google Scholar] [CrossRef]
- PennyLane. PennyLane Documentation. 2024. Available online: https://docs.pennylane.ai/en/stable/code/api/pennylane.AdamOptimizer.html (accessed on 1 July 2025).
- Liang, Y.C.; Yeh, Y.H.; Mendonça, P.E.; Teh, R.Y.; Reid, M.D.; Drummond, P.D. Quantum fidelity measures for mixed states. Rep. Prog. Phys. 2019, 82, 076001. [Google Scholar] [CrossRef]
- Aminpour, S.; Banad, M.; Sharif, S. Strategic Data Re-Uploads: A Pathway to Improved Quantum Classification Data Re-Uploading Strategies for Improved Quantum Classifier Performance. Available online: https://arxiv.org/abs/2405.09377 (accessed on 15 May 2024).
- Vahapoglu, E.; Slack-Smith, J.; Leon, R.C.; Lim, W.H.; Hudson, F.; Day, T.; Cifuentes, J.; Tanttu, T.; Yang, C.H.; Saraiva, A.; et al. Coherent control of electron spin qubits in silicon using a global field. Npj Quantum Inf. 2022, 8, 126. [Google Scholar] [CrossRef]
- Berta, M.; Fawzi, O.; Tomamichel, M. On variational expressions for quantum relative entropies. Lett. Math. Phys. 2017, 107, 2239–2265. [Google Scholar] [CrossRef]
- Perrier, E.; Youssry, A.; Ferrie, C. QDataSet, quantum datasets for machine learning. Sci. Data 2022, 9, 582. [Google Scholar] [CrossRef]
- Veldhorst, M.; Hwang, J.; Yang, C.; Leenstra, A.; de Ronde, B.; Dehollain, J.; Muhonen, J.; Hudson, F.; Itoh, K.M.; Morello, A.T.; et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 2014, 9, 981–985. [Google Scholar] [CrossRef]
- Mastriani, M. Quantum splitting of multi-qubit gates. Opt. Quantum Electron. 2024, 56, 336. [Google Scholar] [CrossRef]
- Bartkiewicz, K.; Gneiting, C.; Černoch, A.; Jiráková, K.; Lemr, K.; Nori, F. Experimental kernel-based quantum machine learning in finite feature space. Sci. Rep. 2020, 10, 12356. [Google Scholar] [CrossRef] [PubMed]
- Japkowicz, N.; Shah, M. Performance evaluation in machine learning. In Machine Learning in Radiation Oncology: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 41–56. [Google Scholar]
- Pernice, A.; Helm, J.; Strunz, W.T. System–environment correlations and non-Markovian dynamics. J. Phys. B: At. Mol. Opt. Phys. 2012, 45, 154005. [Google Scholar] [CrossRef]
- Levi, N.; Feldman, O.; Rosenzweig, Y.; Groswasser, D.; Elgarat, A.; Gal-Katizri, M.; Folman, R. Quantum control of Nitrogen-Vacancy spin in Diamonds: Towards matter-wave interferometry with massive objects. arXiv 2025, arXiv:2508.15504. [Google Scholar]
- Wang, Z.J.; Dechant, D.; Patel, Y.J.; Tura, J. Mitigating shot noise in local overlapping quantum tomography with semidefinite programming. Phys. Rev. A 2025, 111, 052444. [Google Scholar] [CrossRef]
- Scriva, G.; Astrakhantsev, N.; Pilati, S.; Mazzola, G. Challenges of variational quantum optimization with measurement shot noise. arXiv 2024, arXiv:2308.00044v2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).