Abstract
This paper investigates whether ChatGPT, a large language model, can assist in the implementation of lattice-based cryptography and fully homomorphic encryption algorithms, specifically the Ring Learning-with-Errors encryption scheme and the Brakerski–Fan–Vercauteren FHE scheme. To the best of our knowledge, this study represents the first systematic exploration of ChatGPT’s ability to implement these cryptographic algorithms. Fully homomorphic encryption, despite its theoretical and practical significance, poses significant challenges due to its computational complexity and efficiency requirements. This study evaluates ChatGPT’s capability as a development tool from both algorithmic and implementation perspectives. At the algorithmic level, ChatGPT demonstrates a solid understanding of the Rring Learning-with-Errors lattice encryption scheme but faces limitations in comprehending the intricate structure of the Brakerski–Fan–Vercauteren FHE scheme. At the code level, ChatGPT can generate functional C++ implementations of both encryption schemes, significantly reducing manual coding effort. However, debugging and corrections remain necessary, particularly for the more complex Brakerski–Fan–Vercauteren scheme, where additional effort is required to ensure correctness. The findings highlight ChatGPT’s potential and limitations in supporting cryptographic algorithm development, offering insights into its application for advancing implementations of complex cryptographic systems.
1. Introduction
Fully homomorphic encryption (FHE) represents a pivotal innovation in cryptography, enabling computations on encrypted data without requiring decryption. This capability preserves data privacy while allowing meaningful operations on the data, opening new avenues in cloud computing, privacy-preserving machine learning, and secure data sharing. Despite its theoretical and practical significance, FHE had long been an open problem in the field of cryptography. The breakthrough came in 2009, when Craig Gentry proposed the first FHE scheme, marking a milestone in both cryptography and computer science [1]. Since then, several FHE schemes have emerged, including Brakerski–Fan–Vercauteren (BFV), BGV, TFHE, and CKKS, each addressing specific challenges like noise management and performance optimization [2,3,4,5,6,7]. However, FHE algorithms remain computationally intensive.
To bridge the gap between theory and practice, researchers have developed FHE libraries such as SEAL, HElib, and Palisade [8,9,10]. These libraries aim to make FHE more accessible for real-world applications. Despite these advancements, FHE implementations continue to face performance bottlenecks, particularly in terms of computational efficiency and usability. For example, selecting optimal parameter sets and implementing homomorphic operations demand substantial expertise and resources. Addressing these challenges is crucial for further adoption of FHE technologies.
Parallel to advancements in cryptography, artificial intelligence (AI) has shown remarkable potential in supporting software development. ChatGPT, a state-of-the-art natural language processing (NLP) model developed by OpenAI, has emerged as a versatile tool for generating text and code based on user prompts. Since its launch in November 2022, ChatGPT has gained widespread attention for its ability to assist in academic writing, coding, and technical problem-solving [11]. Beyond generating coherent text, ChatGPT has demonstrated the ability to implement algorithms [12], even in domains with significant mathematical complexity.
Recent studies have explored ChatGPT’s capacity to implement cryptographic algorithms. For instance, researchers have successfully used ChatGPT to generate correct and functional implementations of symmetric encryption algorithms like AES and CHAM [13]. Similarly, ChatGPT has been applied to develop the ASCON lightweight encryption algorithm, recently adopted as a NIST lightweight cryptography standard [14]. These examples illustrate that ChatGPT can handle cryptographic algorithms with rigorous mathematical foundations and generate efficient code. However, symmetric encryption algorithms are relatively straightforward compared to public-key cryptographic schemes, which involve more complex mathematical operations and structural intricacies.
This raises a central question: Can ChatGPT assist in the implementation of public-key cryptography, particularly lattice-based encryption and fully homomorphic encryption (FHE)? Public-key cryptographic algorithms like Ring Learning-with-Errors (Ring-LWE) encryption and FHE pose unique challenges due to their intricate mathematical structures. Implementing these algorithms requires a deep understanding of cryptographic principles, meticulous parameter tuning, and significant coding effort, especially for FHE schemes.
This paper addresses this question by systematically evaluating ChatGPT’s ability to implement lattice-based cryptography and FHE. Specifically, we focus on the Ring-LWE encryption scheme and the BFV FHE scheme. These two algorithms represent distinct levels of complexity: Ring-LWE is a foundational lattice-based encryption scheme, while BFV extends lattice encryption to enable fully homomorphic operations. By examining both algorithms, we assess ChatGPT’s proficiency in handling varying levels of cryptographic complexity.
Our evaluation is conducted from two perspectives:
Algorithmic comprehension: We assess ChatGPT’s understanding of the theoretical constructs underlying the Ring-LWE encryption and BFV FHE schemes. While ChatGPT demonstrates a strong grasp of the Ring-LWE encryption mechanism, its understanding of BFV’s intricate bootstrapping process is limited.
Code implementation: We analyze ChatGPT’s ability to generate functional C++ code for both schemes. ChatGPT effectively produces complete code for both algorithms, significantly reducing manual effort. However, debugging and corrections are required, particularly for the BFV scheme, where complexity results in more frequent errors.
This study evaluates the performance of ChatGPT in assisting the implementation of cryptographic algorithms, specifically Ring-LWE lattice cryptography and BFV fully homomorphic encryption. Through comparative experiments between manual implementation and ChatGPT-assisted implementation, significant improvements in coding efficiency were observed. For Ring-LWE cryptography, ChatGPT reduced the overall development time by 65%, while for the more complex BFV encryption, the reduction was 57%. ChatGPT demonstrated remarkable proficiency in generating the initial code and addressing syntax-related errors but required human intervention for higher-level logical and algorithmic issues.
These findings highlight ChatGPT’s potential to simplify cryptographic implementation processes, even for industry-recognized complex algorithms, providing a foundation for further exploration in cryptographic engineering. However, its limitations highlight the need for user expertise to validate and refine the generated code. In the case of the BFV scheme, ChatGPT requires substantial guidance to address issues in homomorphic operations and noise management.
This study makes the following contributions:
First evaluation of ChatGPT in public-key cryptography: To the best of our knowledge, this is the first systematic exploration of ChatGPT’s capabilities in implementing lattice-based cryptography and FHE.
Insights into ChatGPT’s potential and limitations: The study identifies areas where ChatGPT excels, such as generating initial code, and areas where it struggles, such as handling intricate mathematical structures.
Guidance for AI-assisted cryptographic development: By analyzing ChatGPT’s performance, we provide recommendations for leveraging AI tools in implementing complex cryptographic algorithms.
In summary, this paper demonstrates that, while ChatGPT can simplify certain aspects of cryptographic development, its application to highly complex algorithms like FHE requires complementary expertise. These findings lay the groundwork for future research on AI-assisted cryptographic implementation, bridging the gap between advanced cryptographic techniques and practical software development.
2. Preliminaries
2.1. Ring-LWE Encryption
Lattice-based cryptography is currently one of the most promising candidates for resisting quantum computing attacks. It leverages the mathematical properties of lattices, which make its encryption schemes highly secure in both classical and quantum computing environments. A lattice is a discrete set of points in an n-dimensional Euclidean space, which can be understood as a set of points formed by the integer linear combinations of vectors. By using mathematical problems related to lattices, such as the approximate Shortest Vector Problem (SVP) and the approximate Closest Vector Problem (CVP), it is possible to design encryption algorithms that are extremely difficult to break. Common lattice-based encryption algorithms include the following: LWE encryption algorithm, Ring-LWE encryption algorithm, and NTRU encryption algorithm.
Ring-LWE is an important variant of lattice-based cryptography, originating from the Learning-with-Errors (LWE) problem introduced by Regev [15]. The LWE problem essentially involves solving a system of noisy linear equations and attempting to recover the original solution despite the noise. Due to its close connection to lattice problems, the LWE problem is considered computationally difficult and therefore provides strong cryptographic security.
Ring-LWE extends the LWE problem to a ring structure, significantly improving the algorithm’s efficiency. The core idea of Ring-LWE is to use polynomial representations over rings, which drastically reduces the dimension and computational complexity of the lattice, thereby enhancing performance in practical applications. Similar to traditional encryption schemes, Ring-LWE includes key generation, encryption, and decryption algorithms, maintaining the necessary operations for secure communication while improving efficiency.
When implementing the Ring-LWE encryption algorithm, it is important to note that it uses a centered modulus. In traditional modulus q, the range is [0, q), while for centered modulus, the range is [−q/2, q/2). The centered modulus q is defined as a mod q = a − a/q · q, where a is an integer, and a/q represents rounding the result of a/q to the nearest integer. If a < 0, it is defined as—(|a| mod q), where |a| represents the absolute value of a.
On the other hand, the traditional modulus q is defined as a mod q = a − ⌊a/q⌋·q, where ⌊a/q⌋ is the floor function, meaning it rounds down to the nearest integer. This difference in modulus handling between the traditional and centered modulusmoduli affects how numbers are represented in the encryption and decryption processes.
In addition, in the decryption process of the Ring-LWE algorithm, decryption is performed as v←(c2−s·c1) mod q and m←(2/q)·v, where (c1, c2) is the ciphertext, s is the key, m is the plaintext, and q is the modulus. It is important to note that, after computing (c2 − s·c1), you need to apply modulo q. Additionally, after computing (2/q)·v, rounding to the nearest integer is required. These details are often overlooked by ChatGPT.
2.2. BFV FHE Scheme
In 2012, Brakerski proposed a fully homomorphic encryption (FHE) scheme where the modulus reduction scaling factor remains constant throughout operations [4]. This scaling factor is constant, implicit in the homomorphic multiplication operation. Later, Fan and Vercauteren built upon Brakerski’s work, adapting the algorithm to the Ring-LWE problem [16]. This fully homomorphic encryption scheme is now known as the BFV (Brakerski-Fan-Vercauteren) homomorphic encryption algorithm. The BFV scheme includes key generation, encryption, decryption, homomorphic addition, homomorphic multiplication, and key switching operations.
When implementing the BFV homomorphic encryption algorithm, special attention needs to be given to the homomorphic multiplication process. The process is as follows: given two ciphertexts, ct1 = (c11, c21) and ct2 = (c12, c22), where ct1 is the ciphertext of the encrypted message m1, and ct2 is the ciphertext of the encrypted message m2, with the corresponding secret key (−s, 1). After performing homomorphic multiplication on these two ciphertexts, the output is ctmult = (cm1, cm2, cm3), where cm1 = (t/q)·(c11·c12) mod q, cm2 = (t/q)·((c21·c12) + (c11·c22)) mod q, and cm3= (t/q)·(c21·c22) mod q, with the corresponding new secret key (s2, −s, 1).
It is important to emphasize that, during the calculation of (c11·c12), (c21·c12) + (c11·c22), and (c21·c22), no modulus reduction by q is needed. This is a common source of errors in implementation.
When implementing lattice-based cryptography and the BFV homomorphic encryption algorithm in C++, it is essential to use the NTL (Number Theory Library) for handling large integers. NTL is an open source C++ library specifically designed to provide mathematical functions related to number theory, with a focus on high-performance computations in algebraic and arithmetic problems. It is widely used in fields such as cryptography, computational algebra, and computer science, making it suitable for operations involving polynomial arithmetic, linear algebra, and lattice-based problems.
2.3. Security Parameters
In Ring-LWE encryption, the larger the dimension n, the higher the security of the system, but the computational cost also increases. The modulus q is a large prime or integer used to define the modulus operation for the polynomial coefficients. The standard deviation σ of the Gaussian distribution is used to generate the random noise introduced during the encryption process. Table 1 presents the recommended parameters for Ring-LWE encryption.

Table 1.
Recommended parameters for Ring-LWE encryption.
The parameter settings for BFV fully homomorphic encryption mainly depend on the application scenario (such as target security level, computational efficiency, depth of homomorphic operations, etc.). Below Table 2 are the recommended parameters.

Table 2.
Recommended parameters for BFV fully homomorphic encryption.
3. Overall Design
The overall design of this paper aims to assess ChatGPT’s understanding of lattice-based encryption and fully homomorphic encryption from both the algorithmic and coding levels, as shown in Figure 1. One of the significant features of ChatGPT is its ability to provide accurate outputs on familiar topics. Therefore, the first step is to inquire about ChatGPT’s understanding of the concepts. Subsequently, we will delve deeper, questioning ChatGPT’s grasp of the algorithms, measuring its ability to accurately produce the algorithms at a conceptual level. For instance, ChatGPT can accurately output the lattice-based encryption algorithm based on Ring-LWE, but it struggles to accurately reproduce the BFV fully homomorphic encryption algorithm. One possible reason for this discrepancy is that lattice-based encryption algorithms are more mature, whereas the BFV fully homomorphic encryption algorithm is relatively newer.
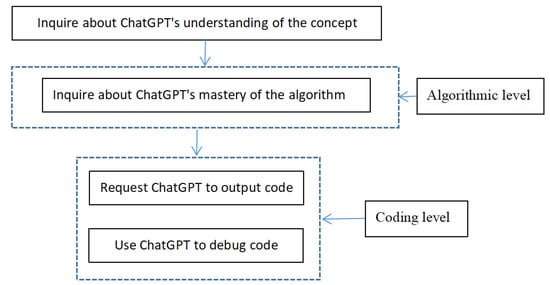
Figure 1.
Overall design approach.
If ChatGPT cannot accurately output the algorithms, we have two options. One is to “feed” the correct algorithm to ChatGPT, allowing it to grasp the correct implementation. The other approach is to directly work at the code level, prompting ChatGPT to output the code, and then correcting any errors in the code to achieve the goal of obtaining the correct implementation. Of course, during the process of debugging the code, we will rely on ChatGPT to identify and rectify the issues. It is important to note that when compilation errors occur, if they are syntax errors, ChatGPT can provide effective solutions. However, if the errors are at the algorithmic level, ChatGPT may struggle to identify the problems, necessitating manual review of the code to detect issues. Once the problems are identified, resolving them with ChatGPT is very efficient.
4. Implementation of Ring-LWE Lattice Cryptography Based on ChatGPT
4.1. Lattice Cryptography Algorithm and Code
To enable ChatGPT to implement the Ring-LWE lattice encryption, we first need to understand how well ChatGPT has grasped the Ring-LWE lattice encryption algorithm, so we ask ChatGPT.
Question: Are you familiar with the lattice encryption algorithm based on Ring-LWE? If so, please describe the algorithm and provide its parameters.
ChatGPT provided a very detailed response, covering the background of the Ring-LWE problem, the Ring-LWE encryption algorithm, the selection of algorithm parameters, and the advantages of the Ring-LWE encryption scheme. More importantly, the description of the Ring-LWE encryption algorithm given by ChatGPT was completely correct, detailing the processes from key generation to encryption and decryption. This confirmed that ChatGPT has a solid understanding of the Ring-LWE lattice encryption algorithm at the algorithmic level, allowing me to proceed with generating the corresponding code.
Question: Great. Now we would like to implement the above Ring-LWE encryption algorithm using C++. Please provide the complete code.
ChatGPT provided a very complete C++ code implementation of the Ring-LWE encryption algorithm, which is based on the NTL large integer library. It also included detailed explanations of the code. We were pleasantly surprised that it could generate such comprehensive code.
The code includes the following main functions:
- (1)
- Ring Definition: The InitRing function implements the polynomial ring , where q is the modulus, n is the polynomial degree, and the ring’s characteristic is realized through the modulus polynomial . Later, we will discuss that defining this function makes the code redundant and has no practical significance.
- (2)
- Random Polynomial Generation: The RandomPolynomial function generates a random polynomial with coefficients in the range [−q/2, q/2).
- (3)
- Center Modulus: The CenterMod function converts polynomial coefficients modulo q to the center modulus range [−q/2, q/2).
- (4)
- Key Generation: The KeyGen function generates the private key s and the public key (a,b).
- (5)
- Encryption Process: The Encrypt function encrypts the plaintext polynomial mmm using the public key (a,b) to obtain the ciphertext (c1, c2).
- (6)
- Decryption Process: The Decrypt function decrypts the ciphertext (c1, c2) using the private key s to recover the plaintext m.
4.2. Debugging the Code
Based on the Ring-LWE lattice encryption code provided by ChatGPT, we will next copy the code into the compiler and compile it. Our approach is to first compile and run the code, then provide any compilation error messages back to ChatGPT to obtain solutions. After that, we will modify and debug the code according to ChatGPT’s suggestions to see if the issues can be resolved. If the problems persist, we will continue to inform ChatGPT of the feedback. This process will be repeated, primarily to assess ChatGPT’s problem-solving capabilities.
4.2.1. Parameter Mismatch Issue of the MulMod Function
The first error message encountered while compiling the code is as follows:
No matching function for call to ‘MulMod(NTL::ZZX&, NTL::ZZX&, NTL::ZZX&, const NTL::ZZ_pXModulus&)’.
Note that the MulMod function is a built-in function in NTL, with the prototype ‘void MulMod(ZZX& x, const ZZX& a, const ZZX& b, const ZZX& f)’, which performs the operation x = a·b mod f. However, in the code provided by ChatGPT, one of the parameters for MulMod is of type ‘ZZ_pXModulus’ instead of ‘ZZX’, resulting in a compilation error. So, we inquired with ChatGPT.
Question: When compiling the code, the error message displayed is “no matching function for call to ‘MulMod(NTL::ZZX&, NTL::ZZX&, NTL::ZZX&, const NTL::ZZ_pXModulus&)’.”
ChatGPT’s response indicated that the MulMod function’s parameters were not correctly matched during the call. It suggested that this might be because the MulMod function was either not defined or its definition did not conform to the types of the parameters being passed. ChatGPT then redefined the MulMod function, changing its fourth parameter type to ZZ_pXModulus, and provided the modified code.
Although this solution resolves the issue, the root cause actually lies within the InitRing() function.
Additionally, in the modified code returned by ChatGPT, the main function (‘main()’) is missing key algorithm modules for key generation, encryption, and decryption. Therefore, we informed ChatGPT that we preferred the original code and requested it to modify only the definition of the ‘MulMod’ function based on that initial version. This highlights the variability in ChatGPT’s responses; the same question can yield different answers. Hence, the way we frame our questions becomes crucial—the more precise and detailed the questions, the better the responses. Everyone can refer to prompt engineering techniques to enhance the quality of their inquiries.
4.2.2. Remove the InitRing() Function
The purpose of the ‘InitRing()’ function is to define a polynomial ring with the modulus f(x) = xn + 1. However, it does not serve any real function and instead complicates the program. We can directly define the polynomial modulus f as a ‘ZZX’ type and assign it the value xn + 1.
Additionally, the use of the ‘ZZ_pXModulus’ type in the code adds complexity without serving a significant purpose. Therefore, it is advisable to remove the ‘InitRing()’ function and eliminate all instances of the ‘ZZ_pXModulus’ type from the program. Instead, we can directly use f as the polynomial modulus. So, we asked ChatGPT about this.
Question: The following areas in the above code need to be modified:
(1) Remove the InitRing() function, as it does not serve any purpose and adds complexity. Instead, directly define f as a ZZX type and assign it the value xn + 1.
(2) Eliminate the ZZX_pXModulus type from the program and directly call f.
ChatGPT’s response acknowledged our suggestions as reasonable and promptly modified the program. It maintained the program’s integrity by directly replacing instances of the ZZX_pXModulus type with calls to f. The revised code became more streamlined, eliminating unnecessary functions and types. This showcases ChatGPT’s strength in code optimization and simplification.
4.2.3. The Issue of Direct Indexing Without Initializing the Polynomial
When compiling the code again, another error message appeared related to the statement ‘m = RandomPolynomial(2)’. So, we inquired with ChatGPT.
Question: When compiling this line of code m = RandomPolynomial(2), an error is displayed: invalid initialization of reference of type ‘const NTL::ZZ&’ from expression of type ‘int’.
ChatGPT believes that the reason for this error is that the RandomPolynomial() function expects a parameter of type const NTL::ZZ&, but you are passing an integer 2. In the NTL library, ZZ is a large integer type, so you need to convert 2 to the ZZ type.
It seems that ChatGPT does not notice some detail errors when programming itself. The good thing is that when you send the compilation error messages to ChatGPT, it will provide solutions and modified code, allowing for continuous modification, error discovery, and subsequent adjustments. After compiling the corrected code, there were no compilation errors, but there was no output. So, we inquired with ChatGPT.
Question: There are no compilation errors, but there is no output at all.
ChatGPT provided possible reasons for the lack of output, suggesting that the generated polynomial m, the ciphertexts c1 and c2, or the decrypted polynomial recovered_m might be empty or have all coefficients equal to 0. It also offered relevant solutions and modified code to address the issue.
After compiling the modified code provided by ChatGPT, there was still no output. When we asked ChatGPT about it, it suggested possible reasons and corresponding solutions, but the problem remained unresolved. Finally, ChatGPT recommended gradually debugging the program and checking the output at each step. So, we added output statements at each critical point and eventually discovered that the line ‘poly[i] = RandomBnd(2);’ was not being executed, so we asked ChatGPT about this.
Question: There is still no output. After testing, we found that the statement ‘poly[i] = RandomBnd(2);’ was not executed. Could there be an issue with this assignment?
ChatGPT still did not provide a proper solution. In the end, we discovered that it seems we cannot directly assign values to poly[i]. We should use SetCoeff to assign coefficients to the polynomial. So, we asked ChatGPT about this.
Question: The reason for the lack of output in the above code is that in RandomBinaryPolynomial(), we cannot directly assign a value to poly[i] using the statement poly[i] = RandomBnd(2). We should use SetCoeff to assign coefficients to the polynomial, for example, int r = RandomBnd(2); SetCoeff(poly, i, r);. We would like to know if it is not possible to directly manipulate polynomial coefficients using indexing in NTL, such as poly[i]?
ChatGPT’s response was that in the NTL library, using poly[i] to directly index coefficients is indeed possible, but its usage is slightly different from standard std::vector or std::array. You can directly access and modify the coefficients of the polynomial using poly[i], provided that the polynomial poly is initialized and the index i does not exceed its current degree.
Since manual modifications are cumbersome, we asked ChatGPT to incorporate the changes into the entire code. ChatGPT provided the modified complete code based on the request, which included using the SetCoeff function to generate binary polynomials and corrected the initialization and setting of polynomial coefficients. It is important to note that, when ChatGPT codes, it may overlook some detailed errors, and human intervention is necessary in such cases.
4.2.4. Encoding and Decoding of Message Integers
At this point, the code is functioning correctly. The next step is to improve some details of the code. For example, the message in the code is currently a randomly assigned binary coefficient polynomial. In practical applications, the message is an integer, and during testing, we need to verify that the encrypted message is the same as the decrypted message. If the message is a polynomial, it can be cumbersome to validate due to its lengthy display. Therefore, we will ask ChatGPT to implement the message as an integer, converting it into a binary polynomial during encryption, and converting the binary polynomial back into an integer during decryption.
Question: Generally, the encrypted message is an integer. After the user inputs an integer, it needs to be represented as a binary polynomial, where the coefficients are the binary digits of the integer. Similarly, after decryption, this binary polynomial needs to be converted back into an integer.
Please add two functions to the program: one function to convert the input integer into a binary polynomial for use in the encryption function and another function to convert the binary polynomial back into an integer after decryption. Please modify the program accordingly.
ChatGPT modified the program as requested, adding two functions: ‘IntToBinaryPolynomial’ and ‘BinaryPolynomialToInt’. The ‘IntToBinaryPolynomial’ function converts an integer into a binary coefficient polynomial, while the ‘BinaryPolynomialToInt’ function restores the binary polynomial back into an integer.
4.2.5. Improvements to the Decryption Function Code
In reviewing the program code, we found that in the Decrypt() function, ChatGPT restores the plaintext by comparing the coefficients’ intervals, which follows Regev’s description of the decryption algorithm in the lattice-based cryptography paper. This implementation is somewhat complicated. In fact, it can be directly obtained using the following mathematical formula: (2/q)·v mod 2, where v = c2 − s·c1 mod q and the ciphertext is (c1, c2). Therefore, we would like to inquire with ChatGPT.
Question: In the Decrypt() function, the implementation to restore the plaintext at the end is somewhat complicated. It can be directly obtained using the following mathematical formula: (2/q)·v mod 2. Please implement the above formula in code and add it to the Decrypt() function.
ChatGPT modified the program as requested, calculating the plaintext coefficients in the ‘Decrypt()’ function using (2/q)·v[i], and taking the integer part followed by modulo 2. This simplified the rounding process.
The modified program was compiled successfully, but the execution stopped at the decryption function. So, we inquired with ChatGPT.
Question: The compilation was successful, but the execution stops at the decryption function.
ChatGPT provided methods to add debugging code to identify the issue, but none were effective. Eventually, we discovered that it was the same old problem: the polynomial was not initialized, so its coefficients could not be referenced directly. Therefore, we could not assign values using m[i] = conv<int>(temp_coeff) % 2. Instead, we needed to use SetCoeff to assign values to the coefficients of m. We were a bit surprised that ChatGPT did not catch this issue that had appeared previously. We then asked ChatGPT to update the code, which is something it excels at.
The program can now run, but the encrypted message and the decrypted message do not match. Upon checking the code, we suspect that the CenterMod function may have issues, so we asked ChatGPT.
Question: In the code above, there seems to be an issue with the implementation of the CenterMod function. Please check it.
In ChatGPT’s response, it stated that the range for the center modulus is [−q/2, q/2]. Therefore, we provided feedback to ChatGPT, pointing out that the range for the center modulus q should be [−q/2, q/2). Based on this requirement, ChatGPT adjusted the code for the CenterMod function.
At this point, the code still cannot produce the correct output, meaning that the encrypted message and the decrypted message do not match. Inquiring ChatGPT did not yield the correct reason for the issue. After careful examination, we found that the statement ZZ temp_coeff = (two * v[i])/q in the decryption function cannot perform the rounding for the calculation of (2/q) · v[i]. Therefore, we asked ChatGPT how to modify it, and ChatGPT provided a solution by replacing the code with ZZ temp_coeff = RoundToZZ(to_RR(two * v[i])/to_RR(q)) to produce the correct results.
We found that as long as the problem is identified, ChatGPT can provide effective solutions. However, if the issue is not clear, it is generally challenging to have ChatGPT identify the root cause of the problem, indicating that ChatGPT is better suited for problem-solving.
Following this, we improved the code by changing the error term from a randomly selected binary polynomial to one chosen from a discrete Gaussian distribution. We also inquired about the parameter settings for the Ring-LWE encryption algorithm, and ChatGPT provided a comprehensive and excellent response.
4.2.6. Explanation
At this point, we have implemented the Ring-LWE encryption algorithm based on ChatGPT, summarized as follows:
- (1)
- From an algorithmic level, ChatGPT is familiar with the Ring-LWE encryption algorithm and can accurately describe it in a professional manner.
- (2)
- From a coding level, ChatGPT can generate complete the Ring-LWE encryption program code, but there may be compilation issues that require debugging. If you inform ChatGPT of the compilation error messages, it will provide possible solutions, although these may not always resolve the issue, indicating that ChatGPT has a certain level of code debugging ability.
- (3)
- When the problem is identified, ChatGPT consistently provides effective solutions and modified code, which is an area in which it excels.
5. Implementation of BFV Fully Homomorphic Encryption Based on ChatGPT
5.1. BFV Fully Homomorphic Encryption Algorithm and Code
Before asking ChatGPT to implement the code for the BFV fully homomorphic encryption algorithm, we first inquired whether it has a solid understanding of the BFV fully homomorphic encryption algorithm at the algorithmic level. Only with a correct understanding of the BFV fully homomorphic encryption algorithm can it output correct code. So, we asked ChatGPT.
Question: Do you know the BFV fully homomorphic encryption algorithm? If so, please explain the algorithm.
There are several issues with the BFV fully homomorphic encryption algorithm generated by ChatGPT:
- (1)
- In the key generation algorithm, there is no detailed arithmetic representation provided for calculating the public key used for key exchange; it only describes in words that a computation key needs to be generated and applied in the key switching process after the homomorphic multiplication operation.
- (2)
- The description of homomorphic multiplication is incorrect. In homomorphic multiplication, obtaining the triple ciphertext first requires multiplying by (t/q) and then rounding the result. These operations are missing in the homomorphic multiplication operation provided by ChatGPT.
- (3)
- There is a lack of description of the key exchange process.
- (4)
- In the description of noise management techniques, ChatGPT mentions using modulus switching to manage noise, which is clearly incorrect. The BFV algorithm does not use modulus switching; this technique is employed in the BGV fully homomorphic encryption scheme.
Therefore, we provided feedback to ChatGPT, asking it to give a new description of the BFV algorithm. However, in its revised description, the key generation part still did not provide an arithmetic representation for calculating the public key. Additionally, the issues in the homomorphic multiplication section were not corrected. Although a description of the key exchange process was added in the homomorphic multiplication section, this description was incomplete and did not conform to standard key exchange algorithms.
We then provided feedback to ChatGPT again, but it still could not give a correct description of the BFV algorithm. At this point, we had two options: one was to provide the correct description of the BFV algorithm to let ChatGPT learn and then generate code; the other was to have ChatGPT generate the code directly and then ask it to modify the code. We chose the latter. Since it was more efficient to have ChatGPT focus on code debugging and modifications, which is where it excels, we asked it to generate the code for the BFV algorithm.
Question: Now we want to implement the BFV fully homomorphic encryption algorithm using C++. Please provide the complete code.
After reviewing the BFV code provided by ChatGPT, we found the following issues:
- (1)
- The center modulus function is incorrect.
- (2)
- There is a lack of functions to convert a message integer into a t-base polynomial and to convert a t-base polynomial back into an integer after decryption. This can refer to the lattice-based cryptography part in Ring LWE.
- (3)
- The key generation part is missing the generation of the public key (used for key switching).
- (4)
- After performing homomorphic addition, the center modulus reduction is not applied.
- (5)
- In the homomorphic multiplication process, there is no multiplication of the ternary ciphertext by (t/q), followed by rounding.
- (6)
- The process in the key switching function is incomplete and does not consider noise control.
- (7)
- The main function is missing calls to the homomorphic addition and multiplication functions.
- (8)
- The main function lacks output for validating the results of homomorphic addition and multiplication.
It should be noted that the first issue was naturally resolved during the interaction with ChatGPT. In the returned modified code for other issues, ChatGPT provided the correct implementation of the center modulus function. This suggests that ChatGPT may have a self-optimization capability. The fourth issue was also resolved in a similar manner. Next, we will address the other issues.
5.2. Figures, Tables, and Schemes
5.2.1. Conversion Between Message Integers and t-Base Coefficient Polynomials
In the BFV fully homomorphic encryption algorithm, the message integer is encoded as a t-base coefficient polynomial before encryption and converted back to an integer after decryption, where t is known as the plaintext modulus. The coefficient range of the t-base coefficient polynomial is [−t/2, t/2). However, in the code generated by ChatGPT, the message integer is simply converted to a constant term polynomial. Therefore, we asked ChatGPT to modify the code.
Question: Now we need to modify the code to convert the message integer into a t-base coefficient polynomial and then convert this t-base coefficient polynomial back to an integer after decryption. Here, t is the plaintext modulus.
ChatGPT generated two functions: one function, ‘IntToTaryPolynomial’, converts an integer into a t-base coefficient polynomial, and the other function, ‘TaryPolynomialToInt’, converts the t-base coefficient polynomial back into an integer. However, there are three problematic statements in the ‘IntToTaryPolynomial’ function. For instance, the statement ‘ZZ half_t = t/2’ should round the value of ‘t/2’ correctly, but here, it produces a truncated value. After informing ChatGPT, it suggested changing it to ‘ZZ half_t = (t + 1)/2’. Additionally, the statement ‘coeff > half_t’ should have the symbol ‘>’ changed to ‘≥’. Furthermore, the statement ‘temp/ = t’ should also be rounded to be correct. ChatGPT recommended changing it to ‘temp = (temp + (t/2))/t’.
5.2.2. Generation of the Relinearization Key
In the code generated by ChatGPT, the KeyGen() function is missing the generation of the relinearization key (used for key switching). So, we asked ChatGPT about it.
Question: In the code above, the KeyGen() function is missing the generation of the relinearization_key. Please modify it.
In the modified code provided by ChatGPT, although it added the generation of the relinearization_key in the key generation function, the representation of the relinearization_key is incorrect. For example, it states ‘relinearization_key = a * s^2 + e mod q’, whereas the correct representation should be ‘relinearization_key = p2(s^2) + a1 · s + e mod q’. Additionally, when generating the relinearization_key, a random polynomial vector ‘a1’ is also required. Both ‘a1’ and ‘relinearization_key’ are made public as part of the evaluation key for the subsequent key switching function (KeySwitch()). To generate the correct evaluation key, we informed ChatGPT of the process for generating the relinearization key and then asked it the following question.
Question: The process of generating the relinearization_key in KeyGen() is incorrect. To generate the relinearization_key, a random polynomial vector ‘a1’ is also needed. Both ‘a1’ and ‘relinearization_key’ are made public as part of the evaluation key for the subsequent KeySwitch() function.
The process of generating ‘a1’ and ‘relinearization_key’ in KeyGen() is as follows:
- Let l = int(logw(q)) + 1, and p2(s^2) = (s^2 mod q, t·s^2 mod q, …, t^(l−1)·s^2 mod q). Note that the ‘mod q’ here refers to the center modulus.
- Randomly and uniformly select a polynomial vector ‘a1’ of length ‘l’ and select a noise polynomial vector ‘e_rlk’ of length ‘l’ from a Gaussian distribution. Again, the ‘mod q’ here refers to the center modulus.
- Compute relinearization_key = p2(s^2)+ a1·s + e_rlk mod q, with the ‘mod q’ here referring to the center modulus.
Please write code to implement the above process for generating ‘a1’ and ‘relinearization_key’ and add the code to the KeyGen() function.
ChatGPT generated the evaluation key as requested. After reviewing the code, we found that there was an issue with the definition range of the ‘a1’ vector, so we asked ChatGPT.
Question: There is a problem in the code above; the ‘a1’ vector used to generate the ‘relinearization_key’ is not defined in the ‘main()’ function, which makes it impossible to call ‘a1’ in the subsequent ‘KeySwitch()’ function. Therefore, ‘a1’ should be defined in the ‘main()’ function at the same time as the ‘relinearization_key’.
ChatGPT modified the code to complete the adjustments to the relinearization key.
5.2.3. Correction of the Homomorphic Multiplication Code
We are now addressing the issues in homomorphic multiplication. In the homomorphic multiplication code provided by ChatGPT, the step of multiplying the ternary ciphertext by (t/q) and then performing rounding is missing. We will inform ChatGPT of the specific process for homomorphic multiplication so that it can implement the code.
Question: The implementation of the homomorphic multiplication function ‘HomomorphicMul()’ has issues. During homomorphic multiplication, the step of multiplying the ternary ciphertext by (t/q) and then rounding is missing. The specific process for homomorphic multiplication is as follows:
Input two ciphertexts (c1_1, c2_1) and (c1_2, c2_2):
- Calculate result_c1 = round ((t/q)·(c1_1 · c1_2)) mod q.
- Calculate result_c2 = round ((t/q)·(c1_1 · c2_2 + c1_2 · c2_1)) mod q.
- Calculate result_c3 = round ((t/q)·(c2_1 · c2_2)) mod q.
Note that ‘mod q’ is the center modulus.
In ChatGPT’s response, it correctly provided the modified code. Providing the specific algorithm process for ChatGPT to implement the code is something it excels at.
5.2.4. Implementation of the Key Switching Process
In the description of the BFV algorithm provided by ChatGPT, the specific process of key switching was not mentioned. Consequently, the implementation of the key switching function ‘KeySwitch()’ given by ChatGPT is also incorrect. To address this, we informed ChatGPT of the specific key switching process so that it could implement the code.
Question: The implementation of the ‘KeySwitch()’ function is incorrect. The specific process of ‘KeySwitch()’ is as follows:
Input ciphertexts (ca1, ca2, and ca3):
- Let D2(ca3) = (ca3 mod w, int(ca3/w) mod w,…, int(ca3/w^(l − 1))) mod w). Here, “mod w” refers to the center modulus.
- Calculate cb1 = [ca2 + <D2(ca1),a1>] mod q, cb2 = [ca3 + <D2(ca1), relinearization_key>] mod q. Here, “mod q” refers to the center modulus.
- Output (cb1, cb2).
Please write code to implement the above process and add it to the complete code.
Based on the specific process of key switching we provided, ChatGPT accurately generated the implementation code.
5.2.5. Code Optimization and Improvement
The next task is to improve the main() function with the following steps:
- (1)
- Input two integer messages, then encrypt these two integers separately, and output the two ciphertexts.
- (2)
- Next, test the homomorphic addition. Perform homomorphic addition on these two ciphertexts and output the result of the homomorphic addition.
- (3)
- Then, decrypt the result of the homomorphic addition.
- (4)
- Test homomorphic multiplication. Perform homomorphic multiplication on these two ciphertexts and output the result of the homomorphic multiplication.
- (5)
- Perform relinearization on the result of the homomorphic multiplication and output the result.
- (6)
- Decrypt and output the result.
Based on the above question, ChatGPT provided the corresponding code. Occasionally, in ChatGPT’s code, the modular reduction by polynomial f is missing after multiplying polynomials, where f is the polynomial modulus. For example, in the code that generates the relinearization key, after executing the ‘mul(s_squared, s, s)’ code, the modular reduction by f was not applied. Upon discovery, this line of code was manually corrected to ‘PolyMulMod(s_squared, s, s, f)’.
Additionally, if an error occurs during compilation, ChatGPT can often provide good solutions if the error is related to syntax usage. For example, when compiling the code ‘result_c1 = RoundToZZ(to_RR(t)/to_RR(q) * to_RR(temp_c1))’, the compiler returned the error message: “no matching function for call to ‘to_RR(NTL::ZZX&)’. After informing ChatGPT, it correctly pointed out that the problem arose when trying to convert a polynomial of type ‘ZZX’ to a floating-point type (‘RR’). The function ‘to_RR()’ only applies to the type ‘ZZ’ (i.e., integers) and not to polynomials (‘ZZX’). It explained that you cannot directly convert a polynomial to ‘RR’ because polynomials have multiple coefficients, and each coefficient needs to be handled separately. It then provided the corrected code.
However, if the error is on the algorithmic level, ChatGPT may struggle to identify the problem. For instance, an error occurred when decrypting the result of homomorphic multiplication. After asking ChatGPT for help, it could not resolve the issue. So, we proceeded to decrypt the result of the homomorphic multiplication, specifically decrypting the three-term ciphertext, and found that the decryption was also incorrect. This led us to conclude that the issue occurred within the homomorphic multiplication function. By continuously inserting output statements, we eventually discovered that the issue was caused by the use of the ‘PolyMulMod()’ function. In homomorphic multiplication, operations are performed over R, so modulus q is not needed, but ‘PolyMulMod()’ was performing a modulus q operation. Replacing ‘PolyMulMod()’ with ‘MulMod()’ solved the problem.
Since noise should be sampled from a discrete Gaussian distribution, although the code provided by ChatGPT used the ‘SampleGaussian()’ function, it lacked the definition for this function. After informing ChatGPT, it provided detailed code for it.
6. Time Cost Analysis
To evaluate the effectiveness of ChatGPT-assisted programming, we divided the time required for code implementation into two parts: coding time and debugging time. Coding time refers to the time spent generating the code, while debugging time is the time developers spend identifying and fixing code errors. Debugging may involve the following types of errors:
- Logical errors: Business logic errors in the code that do not meet expectations or align with the algorithm’s intended logic.
- Runtime errors: Errors that cause the program to crash or behave abnormally during execution.
- Compilation errors: Errors that prevent the code from compiling successfully.
There are two comparison groups: ChatGPT-assisted implementation and manual implementation. The experimental design is as follows:
- (1)
- Manual Implementation
- Select three experienced developers to manually write and debug the code.
- Record the total time required for the developers to write, debug, and pass all tests.
- Document the total time taken.
- (2)
- ChatGPT-Assisted Implementation
- Use ChatGPT to generate the same algorithm code (providing specific prompts and requiring ChatGPT to generate the implementation code).
- Record the total time taken from generating the code to fixing errors and passing all tests.
The experimental data is shown in Table 3. Table 3 presents a comparison of the time costs for the Ring-LWE lattice cryptography and BFV fully homomorphic encryption algorithms under manual implementation and ChatGPT-assisted implementation. The time statistics are divided into coding, debugging, testing, and total time. Through data analysis, it becomes clear that ChatGPT demonstrates significant advantages in coding efficiency but has limitations during the debugging phase.

Table 3.
Comparison between manual implementation and ChatGPT-assisted implementation.
For Ring-LWE lattice cryptography, during the coding phase, manual implementation took 6 h, while ChatGPT-assisted implementation required only 1 h, reducing the time by 83%. This demonstrates ChatGPT’s ability to quickly generate initial code, significantly reducing the manual coding time. During the debugging phase, manual implementation took 10 h, while ChatGPT-assisted implementation required 4 h, reducing the time by 60%. Although ChatGPT-generated code reduced some errors, debugging still required developers to locate and correct issues. The need for manual review reflects that ChatGPT-generated code has a relatively high initial correctness. It is worth noting that, when compilation errors occur, ChatGPT effectively resolves syntax-related issues. However, for algorithm-level errors, ChatGPT struggles to identify problems, requiring manual code review to detect issues. Once the issue is identified, ChatGPT quickly provides solutions.
In the testing phase, the time was further reduced: manual implementation took 4 h, while ChatGPT-assisted implementation took 2 h, cutting the time by 50%. This indicates that the overall code structure is relatively standardized, reducing the difficulty of testing and validation.
Overall, the total time for the manual implementation of Ring-LWE lattice cryptography was 20 h, while ChatGPT-assisted implementation required only 7 h, reducing the total time by approximately 65%. This proves that ChatGPT can significantly enhance the development efficiency in standardized and relatively simple cryptographic algorithm implementations.
For BFV fully homomorphic encryption, during the coding phase, manual implementation took 20 h, while ChatGPT-assisted implementation required only 3 h, reducing the time by approximately 85%. This further validates ChatGPT’s efficiency in generating initial code, particularly for constructing large-scale code frameworks. The debugging phase accounted for the largest time cost in BFV algorithm implementation: manual implementation took 25 h, while ChatGPT-assisted implementation required 15 h, reducing the time by 40%. Although ChatGPT significantly reduced the coding time, the high complexity of the BFV algorithm (such as homomorphic operations and noise management) still required substantial manual intervention during debugging. In the testing phase, manual implementation took 11 h, while ChatGPT-assisted implementation took 6 h, reducing the time by 45%.
The total time for the manual implementation of BFV fully homomorphic encryption was 56 h, while ChatGPT-assisted implementation required 24 h, reducing the total time by 57%. This indicates that, even for highly complex encryption algorithms, ChatGPT can significantly improve development efficiency, although the debugging phase remains the main time-consuming stage.
Table 4 below reflects the handling of different types of errors during the compilation process and ChatGPT’s performance in addressing these issues.

Table 4.
Handling of different types of errors.
ChatGPT’s Performance on Syntax Errors: ChatGPT can quickly identify syntax errors (such as missing semicolons, bracket mismatches, etc.) and provide effective solutions. These issues can usually be resolved directly by ChatGPT without manual intervention.
Algorithm Logic Errors and Mathematical Formula Issues: For algorithm-level logic errors or issues in mathematical formula implementations, ChatGPT can partially detect the problems. In some cases, a manual code review and problem description are required. Once the issue is clearly described, ChatGPT is highly efficient in generating the corrective code.
Dependence on Manual Effort for Complex Problems: For highly complex issues (such as unreasonable data structure design or performance optimization bottlenecks), ChatGPT has some ability to identify problems. However, it can quickly generate partial optimization solutions based on manual guidance.
ChatGPT’s Efficiency in Fixing Issues: ChatGPT’s primary strength lies in its efficiency in fixing issues. Even if the problem needs to be identified manually, once the issue is clearly articulated, ChatGPT can quickly generate solutions.
7. Conclusions
This paper demonstrates the implementation of lattice cryptography based on Ring Learning-with-Errors and Brakerski–Fan–Vercauteren fully homomorphic encryption using ChatGPT. To the best of our knowledge, this is the first time these two encryption algorithms have been implemented with ChatGPT. Implementing cryptographic algorithms is a challenging task, but the method outlined in this paper shows that ChatGPT can significantly enhance the efficiency of cryptographic algorithm implementation.
Although ChatGPT made errors in certain cases, it was able to correct its source code and accurately produce revised versions after the errors were pointed out. Overall, ChatGPT greatly simplifies the process of implementing cryptographic algorithms. The fact that even complex algorithms like fully homomorphic encryption, which are widely recognized as challenging, can be implemented using ChatGPT demonstrates its immense potential in the field of cryptography. This paper serves as a guide for utilizing ChatGPT in the implementation of cryptographic algorithms. As an initial, in-depth, foundational study, we deliberately focus on a single widely accessible LLM (ChatGPT); future work will extend this analysis to a comparative evaluation across multiple contemporary models (e.g., Gemini, Claude, and Copilot).
With the rapid development of artificial intelligence technology, ChatGPT holds broad prospects for application in the field of cryptographic engineering. Not only can it play a significant role in the algorithm implementation phase, but it may also have a profound impact on other aspects of cryptography in the future. Furthermore, future research must address the interpretability of these AI models, as their “black-box” nature poses a significant challenge to validating the security of the generated cryptographic code, which is a crucial direction for ensuring their reliable application in security-critical fields. For responsible use, we disclose that ChatGPT served only as an assistive tool, and all cryptographic designs and code were reviewed and verified by the authors.
Author Contributions
Conceptualization, Z.C.; methodology, Z.C.; software, X.S.; validation, L.C.; formal analysis, H.L.; methodology, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Natural Science Foundation of China under Grants U24A20240 and 62002081.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Efficient Fully Homomorphic Encryption from (Standard) LWE. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; Ostrovsky, R., Ed.; Annual IEEE Symposium on Foundations of Computer Science. IEEE Computer Society: Los Alamitos, CA, USA, 2011; pp. 97–106. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 309–325. [Google Scholar]
- Brakerski, Z. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. In Advances in Cryptology—CRYPTO 2012; Safavi-Naini, R., Canetti, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7417, pp. 868–886. [Google Scholar]
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic Encryption from Learning with Errors: Conceptually Simpler, Asymptotically Faster, Attribute-Based. In Advances in Cryptology—CRYPTO 2013; Canetti, R., Garay, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8042, pp. 75–92. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. In Advances in Cryptology—ASIACRYPT 2017; Takagi, T., Peyrin, T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 409–437. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast Fully Homomorphic Encryption Over the Torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar] [CrossRef]
- Halevi, S.; Shoup, V. Algorithms in HElib. In Advances in Cryptology—CRYPTO 2014, Proceedings of the 34th Annual Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2014; Proceedings, Part I; Garay, J.A., Gennaro, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 554–571. [Google Scholar]
- Microsoft SEAL. 2020. Available online: https://github.com/Microsoft/SEAL (accessed on 1 July 2024).
- Polyakov, Y.; Rohloff, K.; Ryan, G.W.; Cousins, D. Palisade Lattice Cryptography Library User Manual; Cybersecurity Research Center, New Jersey Institute of Technology (NJIT): Newark, NJ, USA, 2017; Technical Report No. 15. [Google Scholar]
- Shahriar, S.; Hayawi, K. Let’s have a chat! A Conversation with ChatGPT: Technology, Applications, and Limitations. In Proceedings of the Artificial Intelligence and Applications, 2024, Corfu, Greece, 27–30 June 2024; pp. 11–20. [Google Scholar]
- Dong, Y.; Jiang, X.; Jin, Z.; Li, G. Self-Collaboration Code Generation via ChatGPT. ACM Trans. Softw. Eng. Methodol. 2024, 33, 1–38. [Google Scholar] [CrossRef]
- Kwon, H.; Sim, M.; Song, G.; Lee, M.; Seo, H. Novel Approach to Cryptography Implementation Using ChatGPT. Cryptol. ePrint Arch. 2023, 606. [Google Scholar]
- Cintas-Canto, A.; Kaur, J.; Mozaffari-Kermani, M.; Azarderakhsh, R. ChatGPT vs. Lightweight Security: First Work Implementing the NIST Cryptographic Standard ASCON. arXiv 2023, arXiv:2306.08178. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. In Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; pp. 84–93. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptol. ePrint Arch. 2012, 144. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).