Hybrid MOCPO–AGE-MOEA for Efficient Bi-Objective Constrained Minimum Spanning Trees

Abstract

The constrained bi-objective Minimum Spanning Tree (MST) problem is a fundamental challenge in network design, as it simultaneously requires minimizing both total edge weight and maximum hop distance under strict feasibility limits; however, most existing algorithms tend to emphasize one objective over the other, resulting in imbalanced solutions, limited Pareto fronts, or poor scalability on larger instances. To overcome these shortcomings, this study introduces a Hybrid MOCPO–AGE-MOEA algorithm that strategically combines the exploratory strength of Multi-Objective Crested Porcupines Optimization (MOCPO) with the exploitative refinement of the Adaptive Geometry-based Evolutionary Algorithm (AGE-MOEA), while a Kruskal-based repair operator is integrated to strictly enforce feasibility and preserve solution diversity. Moreover, through extensive experiments conducted on Euclidean graphs with 11–100 nodes, the hybrid consistently demonstrates superior performance compared with five state-of-the-art baselines, as it generates Pareto fronts up to four times larger, achieves nearly 20% reductions in hop counts, and delivers order-of-magnitude runtime improvements with near-linear scalability. Importantly, results reveal that allocating 85% of offspring to MOCPO exploration and 15% to AGE-MOEA exploitation yields the best balance between diversity, efficiency, and feasibility. Therefore, the Hybrid MOCPO–AGE-MOEA not only addresses critical gaps in constrained MST optimization but also establishes itself as a practical and scalable solution with strong applicability to domains such as software-defined networking, wireless mesh systems, and adaptive routing, where both computational efficiency and solution diversity are paramount

1. Introduction

The Minimum Spanning Tree (MST) is one of the most fundamental problems in graph theory and combinatorial optimization. Formally, it is defined as a spanning tree of a connected, weighted, and undirected graph that minimizes the total edge weight, thereby ensuring cost-efficiency in connecting all vertices without cycles [1]. Because of this property, MST has been widely applied in diverse domains such as network design, clustering, and other cost-sensitive optimization problems. Classic algorithms by Borůvka (1926), Kruskal (1956), and Prim (1957) remain central to the field because of their simplicity, polynomial-time guarantees, and provable optimality [2]. Over time, however, the research landscape has moved beyond deterministic formulations to handle uncertainty and dynamics in graph weights. To this end, deterministic and randomized approximation algorithms have been proposed, while more recent learning-augmented methods integrate prediction with robustness, lowering query complexity without sacrificing solution quality [3,4]. These advances demonstrate both the enduring theoretical relevance of MST and its adaptability to emerging computational paradigms.

Despite these achievements, the classical MST is often inadequate for practical networks, where additional constraints must be satisfied. This has led to several constrained MST formulations. The Capacitated Minimum Spanning Tree (CMST) extends the classical model by minimizing total weight subject to capacity or resource constraints on nodes or edges, such as degree bounds, load limits, or edge-length restrictions, which renders the problem NP-hard [5]. Furthermore, the Hop-Constrained MST (HMST) enforces a maximum number of hops from a designated root node, ensuring bounded communication depth and latency [6]. Similarly, the Bounded-Diameter MST (BDMST) constrains the longest path between any two vertices so that the diameter does not exceed a prescribed bound [7]. Building on these constrained models, heuristic frameworks such as alternating direction method of multipliers (ADMM)-based algorithms have been introduced to approximate hop-constrained solutions more efficiently in large-scale networks [8]. Together, these formulations highlight that MST is not only a theoretical construct but also a flexible framework that grows increasingly complex as constraints reflecting connectivity, feasibility, and efficiency are imposed.

Alongside constrained formulations, attention has also turned to multi-objective spanning tree (MOST) problems, in which multiple conflicting goals must be optimized simultaneously. In such settings, no single optimal solution exists; instead, Pareto-based methods are employed to approximate trade-offs between criteria such as cost, delay, and diameter [9]. These studies confirm that MST-related problems are not only NP-hard when constraints are imposed but also become increasingly complex in multi-objective forms, where the challenge lies in diversifying solutions across objectives while maintaining feasibility

The importance of these extensions is evident in their wide range of applications. In satellite networking, the All-Time Dynamic MST (ATDMST) improves stability in Low Earth Orbit constellations [10]. In urban planning, MST-based approaches reduce infrastructure costs while maintaining accessibility [11]. In renewable energy systems, spanning tree optimization minimizes microgrid cabling costs [12]. In wireless sensor networks, adaptive MST routing improves both energy balance and network lifetime [13]. Finally, in software-defined networking (SDN), MST-based strategies such as the Minimum Bottleneck Spanning Tree (MBST) have been adopted to enhance traffic distribution and congestion control [14]. These examples illustrate that MST variants are not abstract constructs but rather practical tools across diverse engineering domains where cost, scalability, and communication reliability are equally critical.

Nevertheless, significant research gaps remain. Most existing approaches address either a single constraint or a limited optimization objective, which often results in feasible but imbalanced solutions with restricted Pareto diversity. Scalability is another critical challenge, as runtimes increase sharply with problem size and network complexity. Moreover, although heuristic and evolutionary algorithms have been applied to constrained and multi-objective MST variants, there has been little systematic effort to integrate bio-inspired exploration with geometry-aware exploitation for the bi-objective hop–weight constrained MST. This gap motivates the present study, where we propose a Hybrid MOCPO–AGE-MOEA algorithm that unites the exploratory ability of Multi-Objective Crested Porcupine Optimization (MOCPO) with the exploitative refinement of the Adaptive Geometry-based Evolutionary Algorithm (AGE-MOEA), reinforced by a Kruskal-based repair operator. Before presenting the methodology, we review related works in detail to situate our contribution within the broader literature on hybrid algorithms, constrained formulations, metaheuristics, and exact approaches.

The remainder of this paper is structured as follows. Section 2 reviews related work on MST optimization and multi-objective metaheuristics. Section 3 formally defines the bi-objective constrained MST problem and its mathematical formulation. Section 4 introduces the component algorithms MOCPO and AGE-MOEA. Section 5 presents the proposed hybrid framework. Section 6 details the experimental setup, while Section 7 reports and analyzes the results. Finally, Section 8 concludes with key findings and outlines directions for future research.

2. Related Works

Research on Minimum Spanning Tree (MST) variants has evolved along several complementary directions, including hybrid evolutionary methods, constrained mathematical formulations, metaheuristic extensions, and exact optimization approaches. In what follows, we review each of these strands in turn, highlighting both their main achievements and their limitations in order to position our proposed Hybrid MOCPO–AGE-MOEA framework.

Hybrid evolutionary algorithms have been especially prominent in tackling constrained MSTs, since they offer a natural balance between exploration and exploitation. For instance, Singh and Sundar [15] proposed a hybrid steady-state genetic algorithm (HSSGA) for the degree-constrained MST, where local search was combined with perturbation-based replacement to preserve diversity, yielding strong results across 107 benchmark instances. Building on this idea, Prakash et al. [16] developed a Hybrid Multi-Objective Evolutionary Algorithm (HMOEA) for the bi-objective Minimum Diameter-Cost MST, showing that chromosome-based encoding and heuristic seeding scaled effectively to graphs with up to 500 nodes. In a related effort, Fernandes et al. [17] introduced MO-MAHM, a particle-swarm-inspired hybrid that integrated evolutionary operators with local search for solving bi-objective spanning trees. Beyond these general-purpose hybrids, some researchers targeted domain-specific problems: for example, Camacho-Vallejo and García-Reyes [18] applied a co-evolutionary approach to telecommunication networks, while Meenakshi Devi and Geethanjali [19] combined genetic algorithms with repair strategies for phasor measurement unit (PMU) placement in smart grids. Taken together, these works demonstrate the potential of hybridization to improve solution quality and scalability. However, most hybrids remain tailored to a single constraint or narrow application domain, whereas our approach seeks to generalize hybridization for the bi-objective hop–weight constrained MST.

A second stream of research has focused on mathematical programming formulations of constrained MST problems. For example, Carvalho and Coco [20] modeled hop- and delay-constrained MSTs using compact Miller–Tucker–Zemlin (MTZ) constraints, and extended them to bi-objective versions solved through an augmented ε-constraint method. Complementing this, Shi, Neumann, and Wang [21] analyzed the 2-hop (1,2)-MST using evolutionary algorithms, deriving theoretical runtime bounds and contrasting edge-based with vertex-based encodings. Other constrained formulations have also been explored: for the Euclidean Leaf-Constrained MST, Prakash and Patvardhan [22] proposed faster O(n³) heuristics, while for the Minimum Routing Cost MST, Sari et al. [23] modified Campos’ algorithm to reduce both routing cost and tree diameter. These mathematical and theoretical approaches provide elegant problem formulations and important insights into constraint modeling. Nevertheless, they tend to be limited in scalability and flexibility, making them less suitable for very large or dynamic networks.

In parallel, metaheuristic extensions have broadened MST optimization through novel operators and swarm intelligence. Bossek and Grimme [24] improved NSGA-II by integrating a generalized Kruskal-based mutation operator, which enabled subtree rewiring and led to stronger convergence and runtime guarantees for multi-objective MSTs. Similarly, swarm-inspired algorithms have been widely adopted: Singh and Sundar [25] introduced an Artificial Bee Colony (ABC) algorithm for bounded-diameter MSTs, whereas Zhang et al. [26] designed the Bare Bones Mayfly Algorithm (BBMA) for spherical MSTs, achieving good scalability with minimal parameter tuning. These approaches underscore the effectiveness of operator design and swarm behavior in guiding search. However, they frequently lack explicit feasibility guarantees. In contrast, our hybrid framework directly addresses this shortcoming by embedding a Kruskal-based repair operator, which ensures that all candidate solutions remain feasible under hop and weight constraints.

Finally, there is a line of research that has pursued exact and dynamic programming approaches for multi-objective MSTs. For example, Amorosi and Puerto [27] developed a two-phase exact algorithm that blended mathematical programming with recursive edge exchanges. Likewise, Maristany de las Casas et al. [28] reformulated the multi-objective MST as a shortest-path problem and solved it with the IG-MDA algorithm. Fernandes et al. [29] conducted a comprehensive comparative study of nine exact methods, clarifying differences between Pareto set and Pareto front representations but also revealing scalability limitations. Other exact formulations include the compact MILP models of Montemanni and Smith [30] for MSTs with conflicting edges, and the hybrid ant-colony plus MILP approaches of Adasme and Firoozabadi [31] for degree-constrained k-MSTs. These works confirm that exact methods are valuable for small to medium-scale graphs, but for larger and more complex instances, hybrid and metaheuristic methods remain indispensable.

In summary, the literature demonstrates substantial progress in MST optimization across hybrid, mathematical, metaheuristic, and exact approaches. Yet, none of the prior works simultaneously achieve strict feasibility, broad Pareto diversity, and scalability in the bi-objective hop, weight constrained MST. Our proposed Hybrid MOCPO-AGE-MOEA addresses this gap by combining bio-inspired exploration (MOCPO), geometry-aware exploitation (AGE-MOEA), and a Kruskal-based repair operator within a single framework. As summarized in

Table 1. Comparison of key related works and the proposed approach.

Ref	Year	Authors	Approach	Problem	Strength	Limitation
[15]	2019	Singh & Sundar	HSSGA (GA + LS)	Degree-CMST	Preserved diversity across benchmarks	Limited to degree constraint
[16]	2020	Prakash et al.	HMOEA	Bi-Obj. MDCST	Scalable to 500 nodes with chromosome encoding	Focused only on diameter–cost
[17]	2020	Fernandes et al.	MO-MAHM	Bi-Obj. MST	PSO-inspired hybrid with MOEA + LS	Domain-specific
[19]	2020	Devi & Geethanjali	GA + Repair	PMU Placement	Faster convergence; improved observability	Narrow smart-grid domain
[20]	2023	Carvalho & Coco	ILP + ε-constraint	HCMST/DCMST	Compact MILP models with runtime gains	Scalability issues
[24]	2024	Bossek & Grimme	NSGA-II + Kruskal mutation	Multi-Obj. MST	Improved convergence/runtime via subtree rewiring	No feasibility guarantee
[27]	2021	Amorosi & Puerto	Two-phase exact	Bi-Obj. MST	Full Pareto set enumeration	Restricted to small graphs
Proposed	2025	This work	Hybrid MOCPO–AGE-MOEA + Kruskal repair	Bi-Obj. Weight–Hop MST	Achieves feasibility, diversity, and scalability together	Requires ratio tuning; tested only on Euclidean graphs up to 100 nodes

Legend: CMST = Capacitated MST; MDCST = Minimum Diameter–Cost MST; HCMST = Hop-Constrained MST; DCMST = Delay-Constrained MST; LS = Local Search; MILP = Mixed-Integer Linear Programming; PSO = Particle Swarm Optimization.

, this combination provides a distinct balance of feasibility, diversity, and efficiency that has not been systematically realized in earlier research.

3. Problem Formulation

We study the bi-objective constrained Minimum Spanning Tree (MST) problem on Euclidean complete graphs. Given n nodes with coordinates sampled uniformly from a 2D square [0,40] × [0,40] the graph G = (V,E) is complete with edge weights defined by Euclidean distance:

$$w_{uv}= \parallel xu-xv\parallel 2,(u,v)\in E.$$

For the Tree-Center (TC) configuration, the reference point is set to (20,20), which corresponds to the geometric center of the [0,40] × [0,40] coordinate plane used to generate Euclidean graphs. The root node is chosen as the vertex closest to this center, ensuring that hop distances are measured relative to a balanced position in the graph. This choice standardizes evaluation across all instances and prevents bias toward any particular edge or corner of the coordinate space. Finally, a spanning tree T ⊆ ET contains exactly n − 1 edges [32,33].

3.1. Optimization Objectives

We minimize two objectives simultaneously:

$$f_1\left(T\right)={\sum }_{u,v\in T}{w}_{uv}$$

(1)

where w_uv denotes the weight of edge (u,v).

Subscripts u,v are clearly indices, not arguments.

f₂(T) = max {dist_T(r,v): v ∈ V}

(2)

where f₁(T) is the total weight of the tree and f₂(T) is the maximum hop distance from the root node r.

3.2. Root Selection

Two root-selection strategies are considered:

• Tree-Center (TC): r = arg min_i ||x_i − (20,20)||₂
• Tree-Edge (TE): r = arg min_i ||x_i − (0,0)||₂

where xi is the coordinate of node i in [0,40] × [0,40], ||⋅||₂ is the Euclidean norm, (20,20) is the center for TC, and (0,0) is the corner for TE.

These provide consistent reference points for evaluating hop distances.

3.3. Constraints

Feasible solutions must satisfy:

f₁(T) ≤ B₁

(3)

f₂(T) ≤ B₂

(4)

|T| = n − 1

(5)

T is connected

(6)

where B₁ and B₂ are maximum weight and hop thresholds (default: B₁ = 400, B₂ = 40).

3.4. Feasibility Predicate

A spanning tree is feasible if all constraints hold:

Feasible(T) ≡ g₁(T) ∧ g₂(T) ∧ g₃(T) ∧ g₄(T)

(7)

where each predicate g_i(T) represents one of the problem’s feasibility conditions.

3.5. Pareto Dominance

Given two feasible trees T_a and T_b, T_a dominates T_b if:

fᵢ(T_a) ≤ fᵢ(T_b) ∀ i ∈ {1,2}, and fⱼ(T_a) < fⱼ(T_b) for some j

(8)

The Pareto front (PF) is the set of all non-dominated feasible solutions.

3.6. Constraint Violation

Feasibility & violations. Let the constraints be

g₁: f₁(T) ≤ B1 (weight), g₂: hopmax (T) ≤ B2 (hops), g₃: ∣T∣ = n − 1 (size), g₄: connected(T) (connectivity).

A tree is feasible if g₁ ∧ g₂ ∧ g₃ ∧ g₄.

We measure violation by

V(T) = v1(T) + v2(T) + v3(T) + v4(T),

(9)

where

• v1(T) = max {0, f₁(T) − B1},
• v2(T) = max{0,hopmax(T) − B2},
• v3(T) = 1[∣T∣ ≠ n − 1],
• v4(T) = 1[¬connected(T)].
• V(T) = 0 if T is feasible.

3.7. Distance and Connectivity

Distance & validity. For nodes u,v, distT(u,v) is the edge count on their unique path in T. A valid spanning tree satisfies ∣T∣ = n − 1 and connected(T) (captured already by g₃, g₄).

3.8. Objective Mapping and Pareto Set

A tree is mapped to objective space by:

Φ(T) = (f₁(T), f₂(T))

(10)

The Pareto set is defined as:

PF = {T ∈ $ℱ$ | ¬∃ T′ ∈ $ℱ$: T′ ≺ T}

(11)

where $ℱ$ is the set of feasible trees.

3.9. Notation Summary

Table 2. Summary of notation used in this paper.

Symbol	Meaning	Where Introduced
G = (V,E)	Complete weighted graph	Section 3.1
n = |V|	Number of nodes	Section 3.1
T ⊆ E	Candidate spanning tree	Section 3.1
f1(T)	Total edge weight	Section 3.2
f2(T)	Maximum hop from root	Section 3.2
Root	Tree-Center/Tree-Edge	Section 3.2
dist_T(u,v)	Hop distance in T	Section 3.7
B1, B2	Weight and hop bounds	Section 3.6
g1–g4	Constraints (w/h/size/conn.)	Section 3.6
V(T)	Total violation measure	Section 3.6
Φ(T)	Bi-objective mapping (f1,f2)	Section 3.8
PF	Pareto front of nondominated trees	Section 3.8

summarizes the notations used throughout the problem formulation, defining the graph structure, spanning tree components, optimization objectives, and feasibility constraints. It provides a concise reference for key mathematical symbols, ensuring clarity and consistency in interpreting the equations and algorithms.

4. Background Knowledge

This section mainly focuses on MOCPO and AGE-MOEA optimization algorithms that are used in this article.

4.1. MOCPO Algorithm

MOCPO is a population-based, multi-objective optimizer inspired by how crested porcupines defend themselves. Each “porcupine” is a candidate solution, and in every iteration the swarm moves using four simple behaviors: Sight and Sound to explore widely (bigger, randomized steps that probe new regions), and Odor and Physical Attack to exploit promising areas (small local tweaks and direct moves toward the best neighbors). After generating new candidates, MOCPO ranks them with non-dominated sorting (Pareto fronts) and a crowding-distance rule so it keeps only a diverse set of high-quality trade-offs. An information-feedback mechanism then blends each new position with a peer solution, weighting the mix by their fitness, which nudges the swarm toward better fronts without collapsing diversity. The algorithm keeps alternating between exploring and exploiting until it stops, then returns a well-spread set of trade-off solutions (an approximation of the Pareto front) [34]. Algorithm 1 indicates the pseudo-code of the MOCPO algorithm.

Algorithm 1. Pseudo-code of the MOCPO algorithm redrawn and adapted from [34]

Input: Population size N, maximum iterations T Output: Final population of spanning trees 1. Initialize population P with N random spanning trees 2. Evaluate objectives (weight, hops) for each tree in P 3. Set iteration counter t ← 0 4. While t < T do a. For each porcupine (solution) in P: i. Apply “Sight” operator: - Combine intersection edges with elite solution edges - Reinforce promising structures ii. Apply “Sound” operator: - Merge partial edge sets from two parents - Introduce diversification edges b. Evaluate offspring solutions c. Update Pareto set with feasible non-dominated solutions d. Increment t ← t + 1 5. Return final Pareto set

4.2. AGE-MOEA Algorithm

AGE-MOEA is an evolutionary algorithm for multi/many-objective problems that keeps the best trade-offs by adapting to the shape of the current Pareto front. Like NSGA-II, it generates offspring and uses fast non-dominated sorting, but instead of “crowding distance” it assigns each solution a survival score that combines (a) how close it is to the ideal point (proximity) and (b) how far it is from its neighbors (diversity). The key idea is to estimate the front’s geometry each generation with a quick O(M × N) (M is the number of objectives and N is the population size) heuristic and then measure distances with the matching Lᵖ-norm (so it works whether the front is flat/Euclidean, concave/spherical, or convex/hyperbolic). After normalizing objectives, AGE-MOEA always preserves the extreme points and picks the rest by favoring solutions that are simultaneously close to ideal and well-spread under the chosen norm. This simple geometry-aware scoring makes the algorithm versatile across many front shapes and competitive with (often better than) popular MOEAs on standard benchmarks [35]. Algorithm 2 indicates the pseudo-code of the AGE-MOEA algorithm.

Algorithm 2. Pseudo-code of the AGE-MOEA algorithm redrawn and adapted from [35]

Input: Population size N, maximum iterations T Output: Final population of spanning trees 1. Initialize population P with N spanning trees (seeded + random) 2. Evaluate objectives (weight, hops) for each tree in P 3. Set iteration counter t ← 0 4. While t < T do a. Select parents from P b. Apply crossover with lexicographically best feasible solution c. Apply mutation (swap or replace edges) d. Evaluate offspring and merge with P e. Perform geometry-aware survival: - Rank by Pareto dominance - If front overflows, preserve extremes - Fill remaining slots using farthest-first rule f. Increment t ← t + 1 5. Return final Pareto set

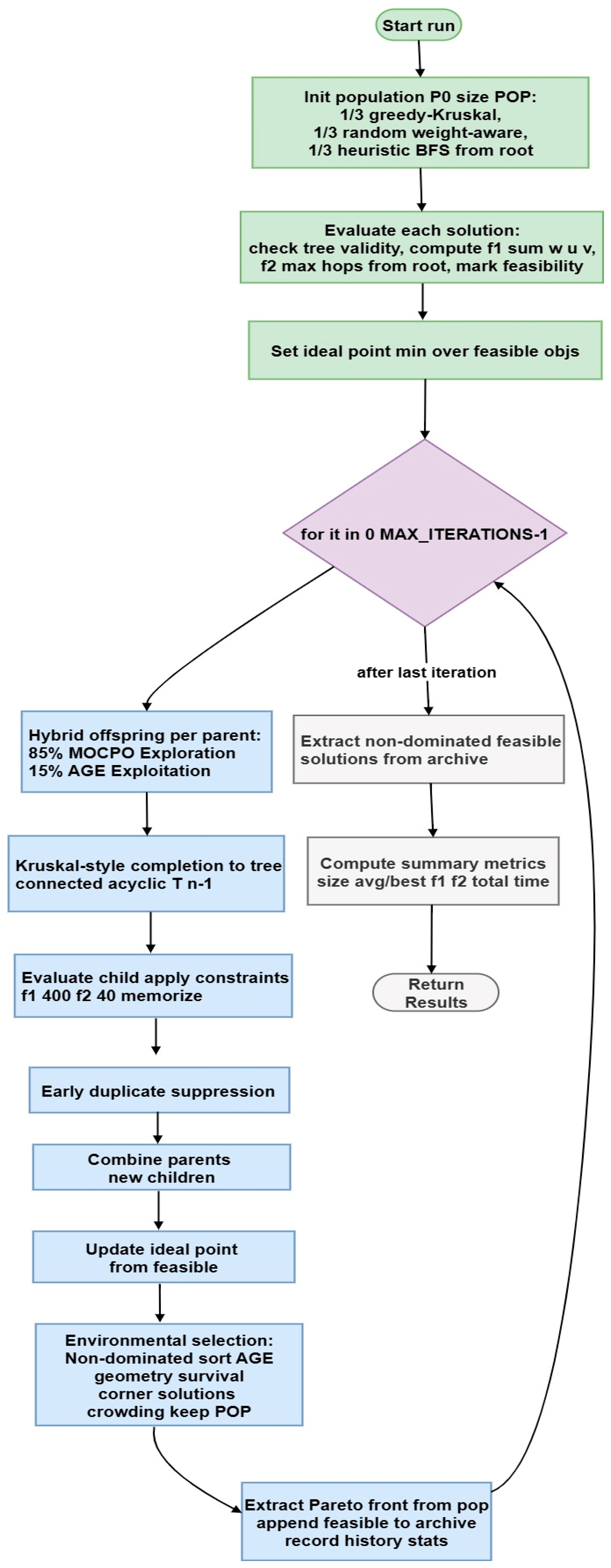
5. The Proposed Hybrid Optimization Algorithm

The bi-objective constrained MST problem requires algorithms that can simultaneously explore the vast solution space, converge efficiently toward high-quality trade-offs, and strictly satisfy feasibility constraints. Existing metaheuristics often succeed in one or two of these aspects but fail to balance all three. MOCPO offers strong exploratory ability through its bio-inspired “Sight” and “Sound” operators, which generate diverse candidate structures, while AGE-MOEA ensures convergence by preserving extremes and maintaining geometric diversity along the Pareto front. However, neither alone guarantees feasibility under strict weight and hop constraints. To address this gap, the proposed hybrid integrates MOCPO for exploration, AGE-MOEA for exploitation and survival, and a Kruskal-style repair mechanism to enforce feasibility. This design balances exploration and exploitation while ensuring that every generated solution is a valid spanning tree.

5.1. Exploration Component: MOCPO Operators

The Multi-Objective Crested Porcupine Optimization (MOCPO) serves as the exploration component of the hybrid. Candidate spanning trees are diversified through biologically inspired Sound and Sight operators, which perturb edge selections and direct search toward unexplored regions of the solution space. These operators enhance global search ability and prevent premature convergence. Their mathematical formulations are given in Equations (15) and (16).

5.2. Exploitation Component: AGE-MOEA Survival

The Adaptive Geometry-based Evolutionary Algorithm (AGE-MOEA) provides the exploitation and survival mechanism. By maintaining geometry-aware distances between solutions, AGE-MOEA preserves Pareto-front diversity while driving convergence toward the true front. Survival is handled by a geometry-based selection rule that prefers nondominated and well-distributed solutions, as formalized in Equation (18).

5.3. Feasibility via Kruskal Repair and Ranking

Feasibility is enforced by an incremental Kruskal repair operator, which restores the spanning-tree structure whenever offspring violate weight, hop, or connectivity constraints. The operator incrementally adds the lowest-weight feasible edges while avoiding cycles, thereby ensuring valid spanning trees. Its procedure is captured in Equation (18).

In the proposed hybrid, the “Kruskal-style repair” is used to complete any partial tree generated by crossover, mutation, or MOCPO exploration. The procedure applies a classic union–find Kruskal sweep over a globally pre-sorted edge list, greedily adding the lightest edges until a valid spanning tree is formed. This step is explicitly weight-aware, ensuring the completion is always the minimum-weight tree consistent with the partial structure. Hop feasibility is not enforced during repair itself; instead, the maximum hop count is evaluated afterward via BFS from the designated root. Any tree exceeding the hop or weight constraints is flagged infeasible and assigned infinite objectives, which guarantees it is dominated during non-dominated sorting. In this way, conflicts between minimizing edge weight and satisfying hop limits are managed at the selection stage: feasible trees are always preferred, while the AGE-MOEA survival operator maintains diversity across the Pareto front. Over successive generations, this coupling of weight-aware completion with feasibility-first selection drives the population toward solutions that simultaneously meet hop constraints while remaining competitive in total weight.

5.4. Hybrid Algorithm Framework

The proposed Hybrid MOCPO-AGE-MOEA framework alternates systematically between exploration and exploitation within each generation. As illustrated in Figure 1, the design achieves a balance in which MOCPO injects structural diversity while AGE-MOEA refines and preserves well-distributed solutions. After every cycle of reproduction, repair, and evaluation, the parent and offspring populations are merged, ranked, and filtered through Pareto dominance combined with AGE-MOEA’s survival strategy. This process continues until the maximum iteration limit is reached, at which point the algorithm returns a diverse and feasible Pareto front.

The optimization begins with a setup phase that establishes the underlying search space. A complete Euclidean graph is constructed from randomly distributed node coordinates, and a root node is chosen according to either the Tree-Center or Tree-Edge policy. To promote diversity from the outset, the initial population is generated through three complementary seeding strategies: one subset of trees is constructed using greedy Kruskal to guarantee low-weight baselines, a second subset is formed through randomized tree construction to introduce structural variability, and the remaining subset applies a BFS-based heuristic to encourage low-hop solutions. Each candidate is then validated, its objectives (total weight and maximum hop distance) are evaluated, and an ideal point z∗ = ${(f1}^{min}, {f2}^{min}$) is established from the feasible population to guide subsequent survival.

Once initialization is complete, the algorithm enters its main iterative phase. In every generation, each parent independently selects its reproduction mode. With a probability of 0.85, it applies MOCPO exploration through Sight or Sound operators. Sight operations combine intersection edges with elite enhancements, while Sound operations merge approximately half of two parent trees with additional diversification edges. With a probability of 0.15, the parent instead performs an AGE-MOEA exploitation step, consisting of crossover with the lexicographically best feasible solution (lowest weight, then lowest hops) followed by a light mutation. It reflects a careful trade-off: while exploration prevents premature convergence, exploitation accelerates convergence toward high-quality solutions.

Regardless of which path is chosen, every offspring is immediately repaired using a Kruskal-style completer. This operator guarantees that the child becomes a valid spanning tree with exactly n − 1 edges, eliminates cycles, and enforces the strict feasibility limits on both weight (≤400) and hops (≤40). Without this repair step, infeasible or disconnected trees could propagate and degrade the search process.

After offspring evaluation, environmental selection merges parents and offspring into a joint population. Sorting is performed with a feasibility-first Pareto ranking: feasible solutions are always prioritized, and among them, those with lower weight and fewer hops are preferred. If capacity is exceeded within a Pareto front, AGE-MOEA’s geometry-aware survival operator ensures diversity by preserving extreme points and then applying a farthest-first rule in an ideal-shifted, normalized objective space. This prevents overcrowding and maintains even coverage along the Pareto front.

Through this iterative cycle, MOCPO introduces novel structures, Kruskal repair guarantees feasibility, and AGE-MOEA consolidates progress by both exploitation and diversity preservation. As a result, the hybrid algorithm steadily improves solution quality while strictly respecting constraints. At termination, it produces a well-distributed Pareto front that captures the fundamental trade-off between minimizing total edge weight and reducing maximum hop distance.

5.5. Hybrid Algorithm Framework

To complement the descriptive presentation, we formalize the hybridization process using explicit mathematical operators. Offspring generation is modeled as a probabilistic choice between MOCPO exploration and AGE-MOEA exploitation (Equation (12)). The crossover and mutation operators are expressed in Equations (13) and (14), the MOCPO Sight and Sound exploration strategies are defined in Equations (15) and (16), Kruskal repair is captured in Equation (17), and the survival mechanism is given in Equations (18)–(20). Together, these equations provide a precise mathematical formulation of the hybrid MOCPO–AGE-MOEA framework, clarifying how exploration, exploitation, repair, and survival interact to generate diverse and feasible Pareto-optimal spanning trees [34,35].

5.5.1. Hybrid Offspring Generation

Each parent solution T_p produces one offspring Tc per generation by selecting an operator with probability:

$$\begin{gathered} Tc = \{ MOCPO-Explore(Tₚ), with probability p\_explore \\ AGE-GA(Tₚ,T_{\mathsf{\beta }}), with probability 1 - p\_explore\} \end{gathered}$$

(12)

where p_explore = 0.85 (default) and T_β is the current lexicographically best feasible tree (minimize weight, then hops). Exploration randomly chooses Sight or Sound with equal probability; exploitation performs a GA step (crossover with rate 0.9 followed by mutation with rate 0.1).

5.5.2. Crossover Operator (AGE-MOEA)

Offspring inherit only the common edges from two parents; completion uses a Kruskal routine:

$$T\_child=K(E_1\cap E_2)$$

(13)

where K(·) greedily adds the globally lightest edges without cycles until the tree has exactly n − 1 edges. Two children are generated by applying K twice with independent passes.

5.5.3. Mutation Operator

With probability ρ = 0.1, remove one uniformly random edge and re-complete via Kruskal:

$$\begin{gathered} T^{\prime }=\left\{K\right(E\backslash \left\{e\right\}),with probability \rho ,e\sim Unif(E) \\ T, with probability 1-\rho \} \end{gathered}$$

(14)

This perturbs topology while always restoring feasibility. Unlike classical mutation, which may break feasibility, the Kruskal-based repair guarantees that the resulting tree remains connected and cycle-free.

5.5.4. MOCPO “Sight” and “Sound” Exploration

Sight exploration builds a backbone from the intersection of two parents and injects elite edges:

$$\begin{gathered} E\_c=(E_{\mathrm{p}1}\cap E_{\mathrm{p}2})\cup EliteSubset(E\_best,p=0.7) \\ T\_c=K(E\_c) \end{gathered}$$

(15)

Sound exploration takes a random half of the union of two parents and then adds up to three edges sampled from the symmetric difference of two random solutions, each with probability 0.4, then completes with Kruskal:

$$\begin{gathered} E\_c=RandomSubset(E_{\mathrm{p}1}\cup E_{\mathrm{p}2},0.5)\cup RandomPick(\Delta (E_{\mathrm{r}1},E_{\mathrm{r}2}),\le 3,p=0.4) \\ T\_c=K(E\_c) \end{gathered}$$

(16)

5.5.5. Kruskal Repair (Completion)

Any partial edge set E_c is transformed into a valid spanning tree by weight-aware Kruskal:

$$T\_c=K(E\_c)$$

(17)

K(·) adds the lightest available edges from G while avoiding cycles until |T_c| = n − 1.

5.5.6. Survival Selection (AGE-MOEA)

• Environmental selection performs fast non-dominated sorting. On the overflowing front, it:

  (1)

  preserves corner/extreme points,

  (2)

  normalizes the front relative to the ideal point z∗,

  (3)

  computes distances with p = 2 (Euclidean) in the normalized space, and

  (4)

  fills remaining slots using a farthest-first k-NN aggregate rule.

There is no explicit α blend in the implemented survival; selection is geometry-aware and ideal-point guided.

For reporting a single representative solution, the feasible Pareto solution closest to the ideal point is chosen:

$$T\ast =\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\_\{T\in PF\}\left|\right|\mathsf{\Phi }\left(T\right)-z\ast |{|}_2,\mathsf{\Phi }(T)=(f_1\left(T\right),f_2\left(T\right))$$

(18)

• Selection of Representative Solution.

Although the full Pareto front PF is preserved for diversity analysis, in some cases it is useful to identify a single representative tree. For this purpose, we adopt the closest-to-ideal-point criterion. The ideal point is defined as

$$z\ast =(\underset{\mathit{T}\in \mathit{PF}}{\min }f1\left(T\right), \underset{T\in PF}{\min }f2\left(T\right)),$$

(19)

with f1(T) denoting the total weight and f2(T) the maximum hop distance. Each solution is normalized relative to the observed maxima (${z1}^{max}$, ${z2}^{max}$) of the front, and we select the tree that minimizes its Euclidean distance to the ideal point:

$$T^{-}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{T\in PF }{\min }\sqrt{({\displaystyle \frac{f1\left(T\right)-z1\ast }{{ z1}^{max}-z1\ast }}})+({\displaystyle \frac{f2\left(T\right)-z2\ast }{{ z2}^{max}-z2\ast }})$$

(20)

where f1(T) is the tree weight, f2(T) the hop distance, z∗ = (z1∗, z2∗) the ideal point, and (${z1}^{max}$, ${z2}^{max}$) the objective-wise maxima. This addition makes the selection process mathematically precise and reproducible.

This mechanism ensures that the reported representative solution reflects a balanced trade-off between weight and hop objectives, while the complete Pareto set remains available for decision-makers who prefer a wider range of alternatives.

6. Experimental Design

To ensure fairness and reproducibility, the proposed Hybrid MOCPO–AGE-MOEA was benchmarked against five state-of-the-art multi-objective algorithms: MOCPO, AGE-MOEA, MOANA, CoMMEA, and MOMPA. All algorithms were executed under identical settings across two root strategies, 50 graph sizes, and 50 independent runs per instance, resulting in 30,000 experiments in total. Performance was measured using four complementary metrics, average Pareto front size, execution time, average weight, and average hops, and validated statistically through Friedman tests, Bonferroni post hoc correction, and Cohen’s d effect sizes.

6.1. Hardware and Software Environment

All experiments were run on a Windows 11 Pro (64-bit) system with a 12th Gen Intel® Core™ i7-1270P (2.20 GHz) processor and 16 GB RAM (manufacturer: HP Inc., ZBook Workstation Series, Palo Alto, CA, USA). Algorithms were implemented in Python 3.12 (Python Software Foundation, Wilmington, DE, USA) using NumPy 2.2.6, Pandas 2.3.0, NetworkX 3.5, and Matplotlib 3.10.3 for numerical routines, graph modeling, and visualization. A fixed software–hardware platform ensured strict reproducibility across the experimental grid.

6.2. Performance Metrics and Statistical Framework

Algorithm performance was evaluated on four metrics, each with a clear optimization direction (

Table 3. Evaluation Criteria.

Metric	Direction	Description
Average Pareto Front Size	↑	Number of non-dominated solutions (diversity)
Average Execution Time	↓	Computational efficiency (seconds)
Average Weight	↓	Cost-effectiveness of solutions
Average Hops	↓	Communication efficiency (latency)

): Average Pareto Front Size (↑, higher values are better) for diversity and coverage of trade-off solutions; Average Execution Time (↓, lower values are better) for computational efficiency (seconds); Average Weight (↓) for cost-effectiveness; and Average Hops (↓) for communication efficiency, since a lower hop count implies reduced latency. Statistical analysis followed a three-stage protocol: (1) Friedman tests for overall significance, (2) Bonferroni-adjusted post hoc tests for pairwise differences, and (3) Cohen’s d for effect size, distinguishing trivial from practically meaningful improvements.

6.3. Global and Hybrid-Specific Parameters

All algorithms were configured with the same global parameters: population size = 50, maximum iterations = 50, weight bound = 400, and hop bound = 40. A fixed random seed base (1,000,000) was used to ensure reproducibility across runs.

The proposed hybrid additionally required parameters to control its exploration–exploitation balance. Specifically, the offspring-generation probability was set to 0.85 for MOCPO (exploration) and 0.15 for AGE-MOEA (exploitation), with crossover and mutation rates tuned to 0.9 and 0.1, respectively.

Table 4. Algorithm Parameters.

Parameter Category	Parameter Name	Value	Purpose
Population Control	POPULATION_SIZE	50	Balance exploration/exploitation
Termination	MAX_ITERATIONS	50	Computational budget
Reproducibility	GLOBAL_SEED_BASE	1,000,000	Base RNG seed
Constraints	MAX_WEIGHT	400.0	Economic constraint
Constraints	MAX_HOPS	40	Communication constraint
Constraints	USE_EPSILON	False	ε-constraint on hops
Hybrid Blend	exploration_prob	0.85	MOCPO vs. GA probability
Hybrid Blend	crossover_rate	0.9	Exploitation strength
Hybrid Blend	mutation_rate	0.1	Variation rate
MOCPO	Sight add-prob	0.7	Best edge injection rate
MOCPO	Sound union share	~0.5	Random subset proportion
MOCPO	Sound sym-diff picks	≤3 (p = 0.4)	Exploratory edge count
MOCPO	alpha, tf	0.2, 0.8	Compatibility parameters
AGE-MOEA Survival	p-norm	2	Euclidean distance
AGE-MOEA Survival	k-NN aggregate	2	Diversity scoring
Misc	COMPOSITE_ALPHA	0.5	Compatibility parameter

summarizes both the global and hybrid-specific configurations.

6.4. Baseline Algorithms

The hybrid was compared against five established multi-objective optimization algorithms: MOCPO (2025), AGE-MOEA (2019), MOMPA (2021), MOANA (2024), and CoMMEA (2023). All baselines were executed under the same global settings (

Table 5. Shared Settings Parameters for (All Algorithms).

Category	Parameter	Value	Notes
Problem setup	Objectives	Bi-objective: Weight + Hops	Optimized simultaneously
Root policies	Configurations	TC (Tree-Center), TE (Tree-Edge)	Two strategies per run
Graph sizes	Range	50 sizes: 11–60 nodes	Scales instances
Replications	Runs per instance	50	Independent RNG seeds
Constraints	Max weight, hops	≤400, ≤40	Strict feasibility enforced
Population	Population size	50	Shared across all runs
Termination	Max iterations	50	Generational budget
Recorded metrics	Execution time, PF size, avg. weight, avg. hops	Consistent schema

) to ensure fairness. In total, each algorithm completed 5000 experiments (2 root strategies × 50 graph sizes × 50 runs).

6.5. Distinctive Internal Configurations

Although global settings were identical, each baseline retained its internal operator design.

Table 6. Comparative of Algorithms-Internal Parameters.

Component	Hybrid	MOCPO	AGE-MOEA	MOMPA	MOANA	CoMMEA
Initialization	Greedy + random + BFS	Randomized Kruskal	Mixed Prim/Kruskal	Kruskal-heavy + random	Prim + star fallback	Randomized Kruskal/Prim
Exploration	MOCPO Sight & Sound	Random/mutation	–	Predator phase	Ant-guided archive updates	–
Exploitation	AGE-MOEA GA crossover + survival	Hybrid merge + repair	GA crossover + mutation	Predator–prey phase	Best-ant guided search	Edge recombination
Repair	Kruskal repair always ON	Kruskal completion	Kruskal repair	Edge reconnection	Penalization of infeasible	Kruskal repair
Selection & diversity	ND sorting + geometry survival	Pareto + elitism	Tournament + ND sort	Predator–prey phases	Pareto archive update	Tournament + crowding

highlights these distinctive features.

7. Results and Discussions

The large-scale experimental evaluation demonstrates that the proposed hybrid MOCPO-AGE-MOEA consistently surpasses baseline multi-objective algorithms on the constrained bi-objective MST problem. Across 30,000 independent trials, the hybrid secures top rank in three out of four key performance metrics, Pareto front diversity, runtime efficiency, and hop minimization, while remaining competitive in weight cost. Nonparametric statistical analysis (Friedman tests with Bonferroni adjustment, p < 0.001) confirms that these advantages are systematic rather than incidental. Furthermore, effect-size analysis reveals that the improvements in Pareto diversity and runtime are not only statistically significant but also practically very large, highlighting the hybrid’s ability to deliver broader trade-off sets at far lower computational cost.

7.1. Algorithms Performance

Table 7. Algorithm Performance Metrics.

Rank	Algorithm	Avg. Pareto Front Size ↑	Avg. Hops ↓	Avg. Execution Time (s) ↓	Avg. Weight ↓
1	Hybrid AGE-MOEA	191.160	11.505	0.499	168.713
2	AGE-MOEA	50.000	14.252	6.517	160.051
3	MOCPO	50.000	14.852	1.583	158.324
4	MOANA	47.225	14.789	4.442	158.457
5	CoMMEA	42.774	12.927	19.472	161.686
6	MOMPA	39.151	14.606	1.818	162.052

reports the overall performance of the six algorithms across four evaluation metrics: Pareto front size, hop depth, execution time, and weight. Rankings are determined by combining Pareto diversity (↑, higher values are better), hop minimization (↓ better), and runtime efficiency (↓, lower values are better). The hybrid consistently dominates three of the four criteria, achieving far larger Pareto sets, faster execution, and fewer hops, while remaining competitive in weight.

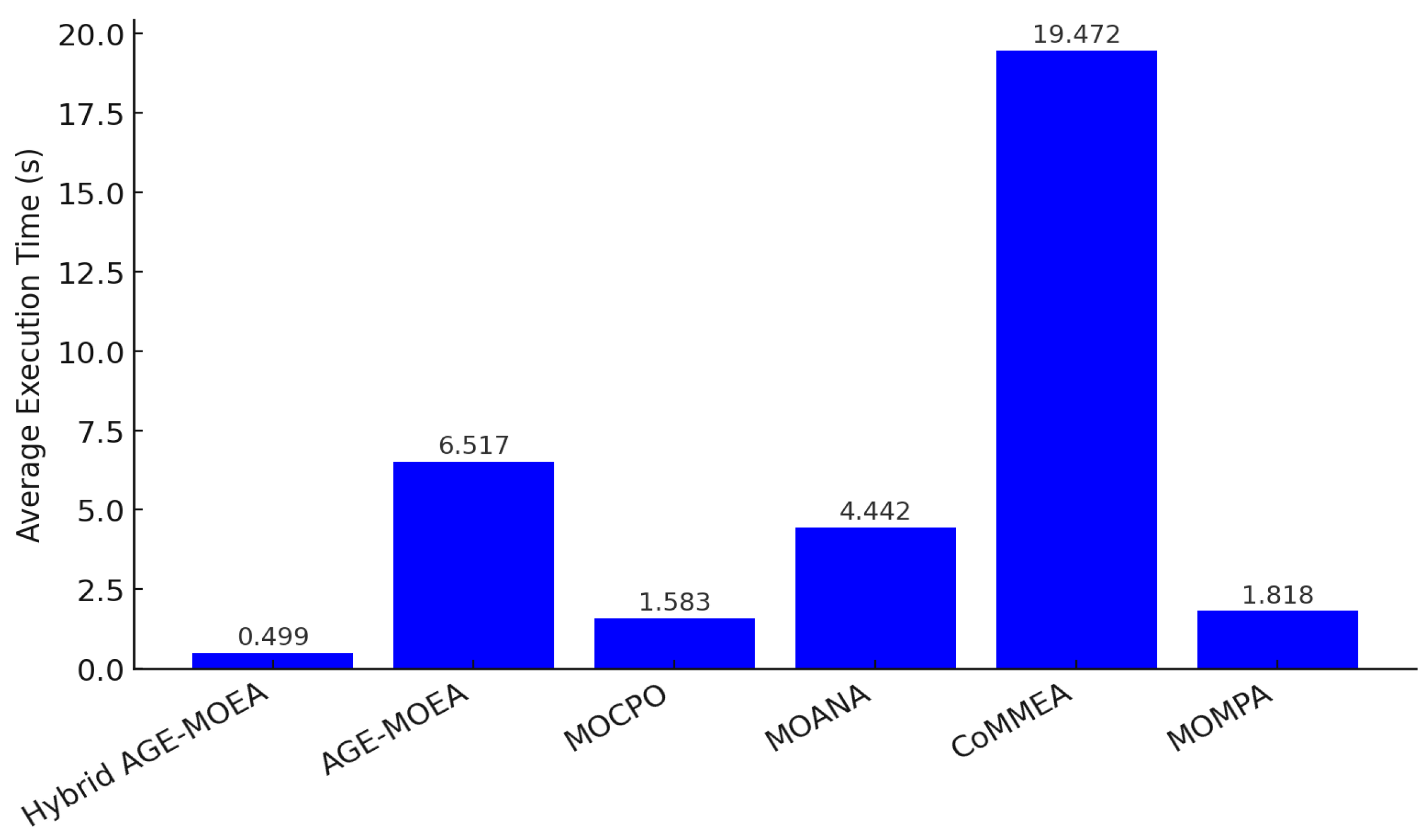
The hybrid clearly establishes dominance by producing exceptionally large Pareto fronts, averaging about 191 non-dominated solutions, compared with only ~50 for AGE-MOEA and MOCPO, ~47 for MOANA, ~43 for CoMMEA, and ~39 for MOMPA. This dramatic advantage in diversity ensures a far richer set of feasible trade-offs. In addition, the hybrid records the lowest average hop depth (11.5) and the fastest runtime (0.5 s), confirming its dual strengths in both solution quality and computational efficiency.

By contrast, MOCPO delivers the lowest weight (158.3) but at the cost of diversity and hop performance. AGE-MOEA shows similar diversity to MOCPO yet suffers from higher runtime and hops. CoMMEA reduces hops moderately (12.9) but is impractically slow (19.5 s), while MOMPA executes faster (1.8 s) but generates the least diverse Pareto sets. Overall, the hybrid dominates three of the four metrics, offering the most balanced and practically useful performance profile.

7.1.1. Diversity of Pareto Fronts

One of the most striking outcomes is the hybrid’s ability to generate substantially larger Pareto fronts. On average, it produced 191 non-dominated solutions, compared to only ~50 for AGE-MOEA and MOCPO, and even fewer for MOANA (47), CoMMEA (43), and MOMPA (39). This corresponds to nearly a 280% improvement in diversity relative to the best baseline. Such broad coverage offers decision-makers a far richer set of trade-off alternatives when balancing cost and hop constraints in network design.

Figure 2 illustrates this clear advantage, showing the hybrid’s dominance across all graph sizes. These findings confirm that combining MOCPO’s exploratory operators with AGE-MOEA’s geometry-aware survival enables both effective convergence and a well-spread Pareto front. Importantly, the hybrid does not collapse to a single “best” solution; instead, it maintains a broad Pareto set, guided by the ideal point–based survival strategy and lexicographic reproduction, ensuring robustness in both diversity and convergence.

• Hybrid Pareto Front Scalability

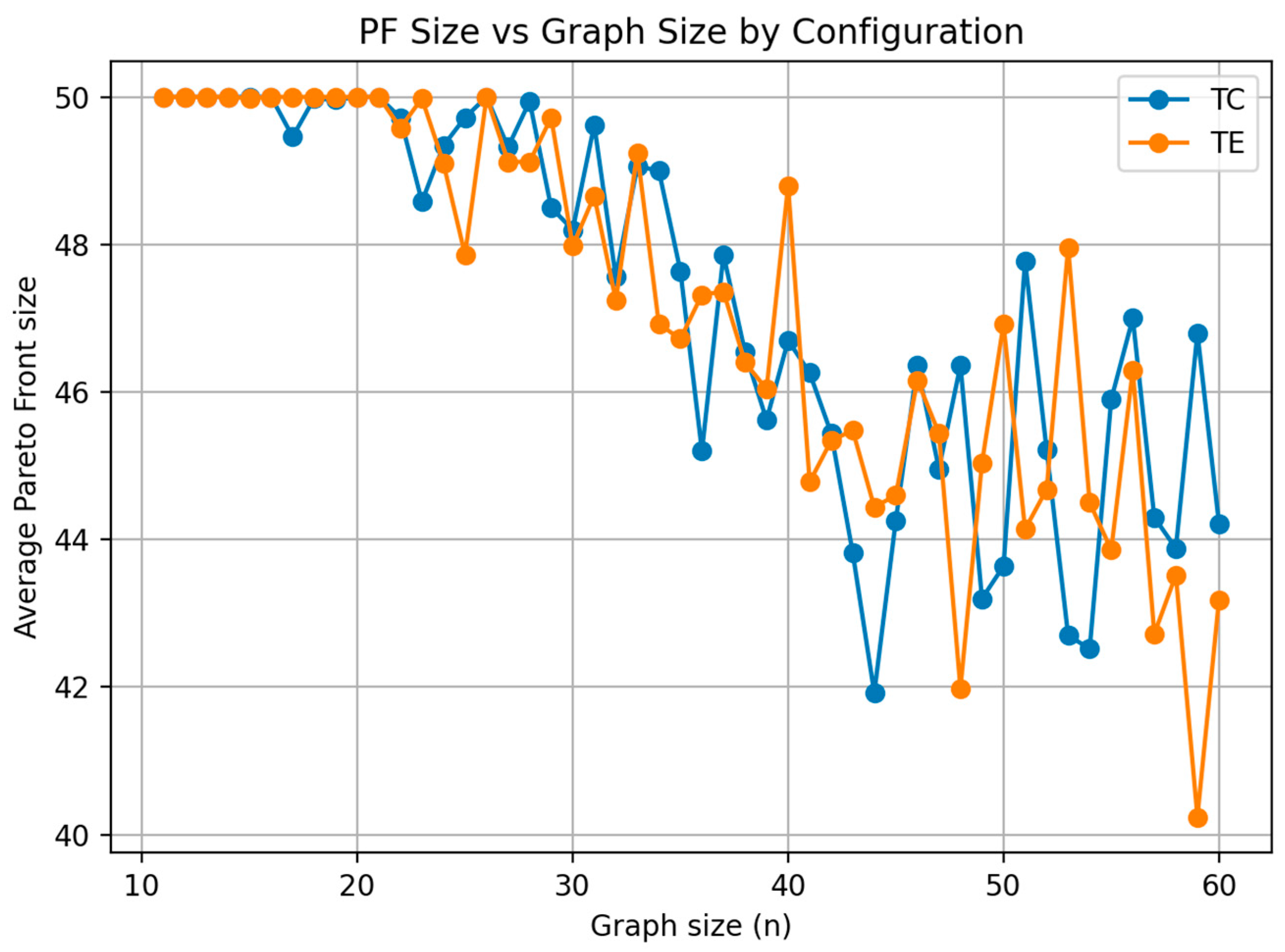
As shown in Figure 3, the Hybrid MOCPO–AGE-MOEA consistently achieves large Pareto fronts across all graph sizes, highlighting its strong ability to maintain solution diversity. The Tree-Edge (TE) configuration produces noticeably larger Pareto front sizes than Tree-Center (TC), with the gap widening as the number of nodes increases. Both configurations exhibit smooth scaling without abrupt declines, confirming the algorithm’s stable archiving and survival mechanisms. These results demonstrate that the hybrid not only preserves efficiency but also sustains high diversity and robustness as problem size grows.

• AGE-MOEA Pareto Front Scalability

As shown in Figure 4, AGE-MOEA consistently produces Pareto fronts of fixed size across all graph sizes, with both Tree-Center and Tree-Edge configurations yielding identical results. The Pareto front size is fixed at 50 solutions for both TC and TE, with identical results, reflecting the algorithm’s strict archiving and selection mechanism. While this ensures stable behavior without variability, it also limits diversity compared to algorithms that expand PF size with problem complexity. These results indicate that AGE-MOEA’s solution set is predictable but less adaptive to larger graphs, contrasting sharply with the hybrid’s broader front growth.

• MOCPO Pareto Front Scalability

As shown in Figure 5, the PF size of MOCPO remains fixed at 50 solutions for all graph sizes, identical across both Tree-Center and Tree-Edge configurations. This reflects the algorithm’s constrained archiving policy, which enforces a uniform front size regardless of problem complexity. While this guarantees stability and predictability, it also prevents MOCPO from adapting its solution diversity as the graph size increases. Consequently, MOCPO produces smaller and less scalable Pareto fronts compared with the hybrid approach, which expands significantly with problem size.

• MOANA Pareto Front Scalability

As shown in Figure 6, MOANA produces Pareto fronts that gradually decline in size as graph size increases, indicating reduced diversity for larger problem instances. Both Tree-Center and Tree-Edge configurations follow similar trends, though TE maintains slightly higher PF sizes at smaller scales. The variability increases for larger graphs, with frequent dips reflecting sensitivity to instance structure. Overall, MOANA sustains moderate front diversity but shows diminishing scalability compared to the hybrid algorithm.

• CoMMEA Pareto Front Scalability

As shown in Figure 7, CoMMEA produces Pareto fronts of moderate size that remain relatively stable across graph sizes. Both Tree-Center and Tree-Edge configurations yield similar PF sizes, with overlapping bands indicating robustness to configuration choice. While variability widens slightly for larger graphs, the overall trend does not show abrupt drops or spikes. These results suggest that CoMMEA maintains predictable front diversity, though its PF sizes are smaller than those achieved by the hybrid algorithm.

• MOMPA Pareto Front Scalability

As shown in Figure 8, MOMPA exhibits a steady increase in Pareto front size with graph size, indicating that the algorithm adapts its diversity as problem complexity grows. Both Tree-Center and Tree-Edge configurations follow similar growth patterns, with Tree-Center achieving slightly larger PF sizes at higher node counts. The smooth upward trend demonstrates stability without sharp fluctuations. These results suggest that MOMPA is capable of scaling its solution diversity, though its PF sizes remain smaller than those obtained by the hybrid algorithm.

7.1.2. Runtime Efficiency

• Average Runtime Comparison

The hybrid also achieved dramatic improvements in computational efficiency. Its average runtime was 0.50 s, compared with 6.52 s for AGE-MOEA and 1.58–4.44 s for other baselines. This represents more than a 13× speedup over AGE-MOEA and roughly 3–9× faster execution compared with lighter metaheuristics such as MOCPO, MOMPA, and MOANA. Importantly, this acceleration was achieved without sacrificing solution diversity or feasibility. The hybrid’s efficiency makes it especially well-suited for large-scale or time-sensitive applications, such as dynamic communication networks, adaptive routing, or online decision support systems (Figure 9).

• Hybrid Algorithm Runtime Trends

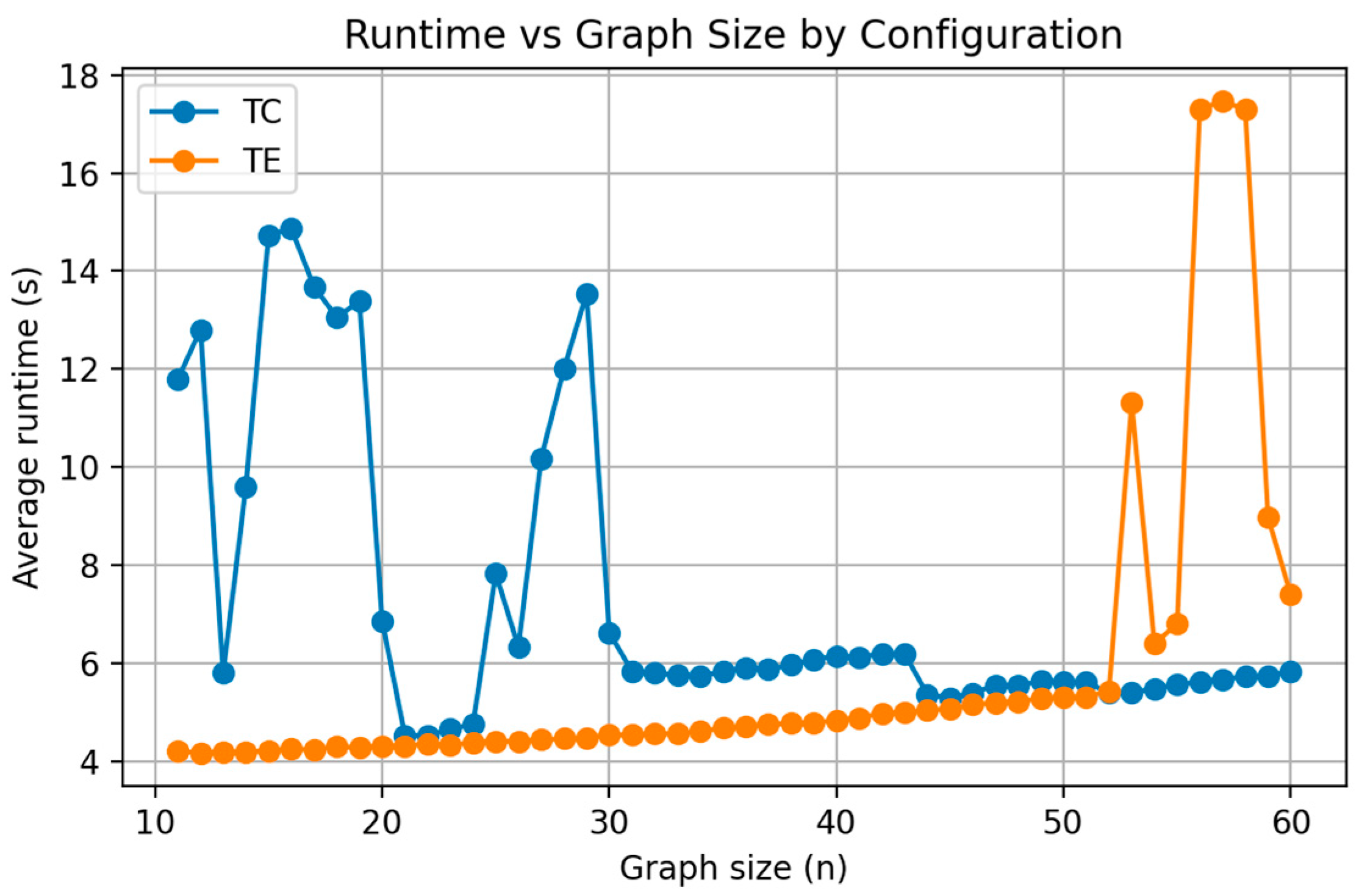
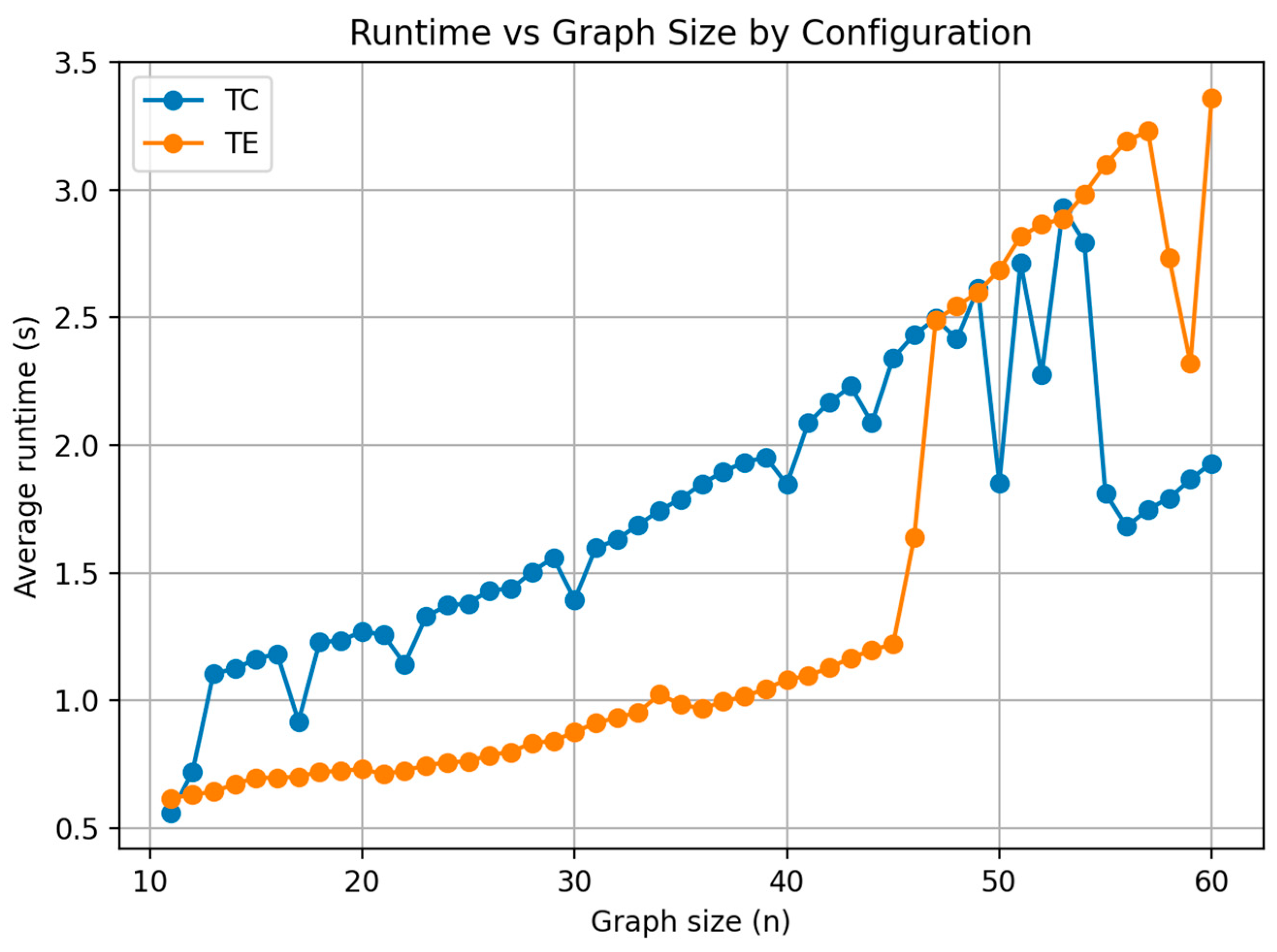
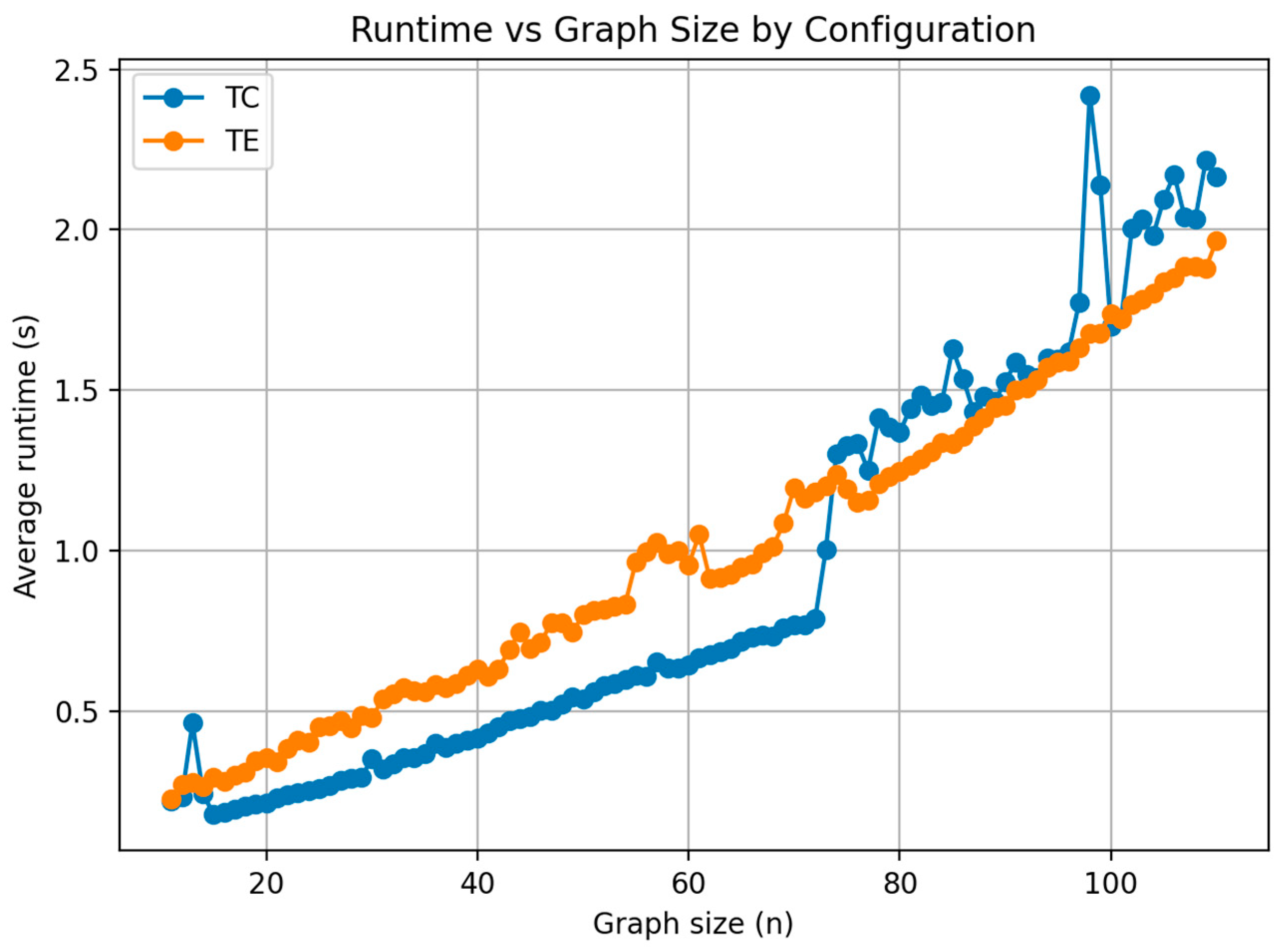
As shown in Figure 10, the runtime of the hybrid algorithm increases smoothly with graph size, following a near-linear trend that reflects efficient computational scaling. For smaller instances, the Tree-Center (TC) configuration executes slightly faster than Tree-Edge (TE), but as the number of nodes grows, both converge toward comparable runtimes. The absence of sharp spikes or irregular growth confirms that the hybrid maintains stable computational cost across the tested range. These findings verify that the Hybrid MOCPO–AGE-MOEA is computationally practical and scalable, even when applied to larger constrained MST instances.

• AGE-MOEA Runtime Trends

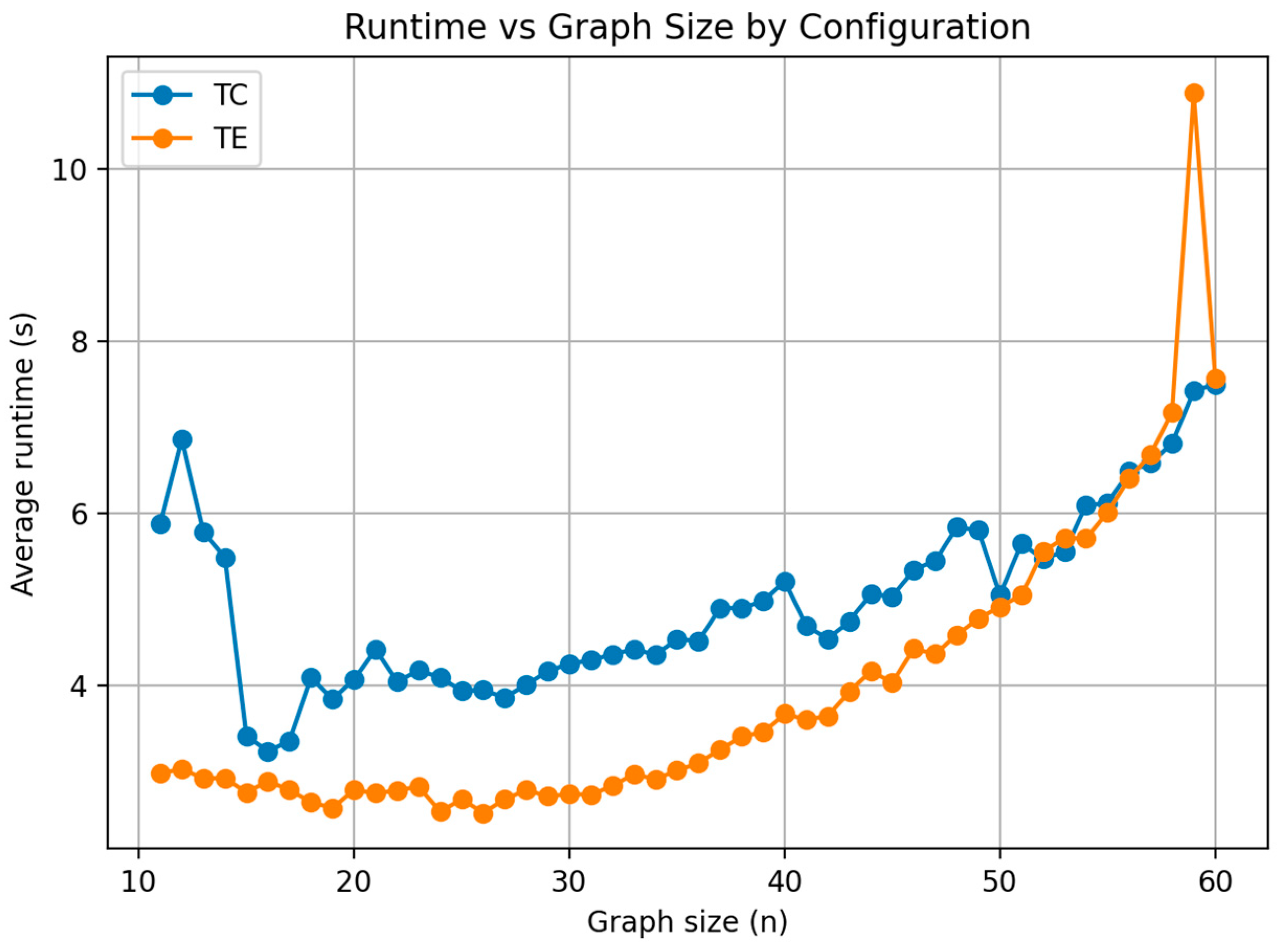
As illustrated in Figure 11, the runtime of AGE-MOEA shows high variability across graph sizes, with Tree-Center (TC) producing unstable execution times compared to Tree-Edge (TE). While TE maintains a relatively steady runtime up to mid-sized graphs, it escalates sharply beyond 50 nodes, reaching peaks above 17 s. TC, on the other hand, fluctuates heavily even for smaller graphs, suggesting sensitivity to instance characteristics and archiving operations. These results indicate that AGE-MOEA is computationally more expensive and less predictable than the hybrid approach, especially at larger problem sizes.

• MOCPO Runtime Trends

As shown in Figure 12, the runtime of the standalone MOCPO algorithm increases steadily with graph size, reflecting its higher computational cost relative to the hybrid approach. The Tree-Center configuration generally requires more time than Tree-Edge across most graph sizes, particularly in the mid-range (n ≈ 20–45). However, Tree-Edge shows a sharp rise beyond 50 nodes, eventually surpassing the Tree-Center runtime. These results highlight that MOCPO is less scalable than the hybrid method, with runtime sensitivity strongly dependent on the root configuration.

• MOANA Runtime Trends

As shown in Figure 13, the runtime of the MOANA algorithm generally increases with graph size but remains more stable than AGE-MOEA. The Tree-Edge configuration is consistently faster than Tree-Center for small and medium graphs, though both configurations converge at larger scales. Occasional spikes, such as at n = 60, reflect sensitivity to specific instances but do not disrupt the overall growth trend. These results suggest that MOANA achieves better runtime stability compared to AGE-MOEA, although it still lags behind the hybrid in efficiency.

• CoMMEA Runtime Trends

As shown in Figure 14, the runtime of CoMMEA grows steadily with graph size, demonstrating a near-linear scaling pattern across both configurations. Tree-Center and Tree-Edge configurations produce very similar execution times, with overlapping confidence bands indicating consistent performance. The slight widening of the shaded regions for larger graphs reflects increased runtime variability but does not alter the overall growth trend. These results suggest that CoMMEA scales predictably with problem size and is less sensitive to the choice of root configuration compared to other algorithms.

• MOMPA Runtime Trends

As shown in Figure 15, the runtime of MOMPA increases gradually with graph size, demonstrating consistent scalability across the tested range. The Tree-Center configuration exhibits higher runtime values than Tree-Edge, particularly for larger graphs above 40 nodes. Fluctuations in TC runtimes for smaller graphs suggest sensitivity to specific instances, whereas TE shows a smoother growth trend. These results indicate that MOMPA is more efficient under the Tree-Edge configuration, though both settings maintain manageable runtimes as graph size increases.

7.1.3. Hop Efficiency

Hop minimization, an essential proxy for communication latency, was also clearly improved. The hybrid produced an average hop count of 11.862, compared with 14.3–14.8 for most baselines, which corresponds to nearly a 20% reduction in path depth. This behavior was observed consistently across both root policies and all graph sizes. By lowering maximum path length, the hybrid ensures reduced latency and improved responsiveness in real-world settings such as communication networks or distributed transportation systems (Figure 16).

7.1.4. Weight Trade-Offs

The only metric where the hybrid did not lead was average weight, as shown in Figure 17. MOCPO achieved the lowest mean weight of 158.324, closely followed by MOANA (158.457), while the hybrid’s weight averaged 168.713. However, this modest advantage in weight came at a clear cost: both MOCPO and MOANA produced only ~50 Pareto solutions on average and offered weaker hop performance.

In contrast, the hybrid traded a slight increase in weight for far greater diversity (≈191 solutions), faster runtime (0.5 s vs. 1.6–4.4 s), and improved hop control (11.5 vs. 14–15). This trade-off is highly meaningful in practice: when cost alone is prioritized, lighter solutions still exist within the hybrid’s broad Pareto set, but planners also gain access to many additional alternatives with more balanced hop–cost profiles.

The hybrid algorithm may yield solutions with slightly higher average weight, but this is a worthwhile trade-off in network design. Unlike methods that focus only on minimizing weight, the hybrid generates a larger set of feasible solutions, achieves shorter hop distances, and delivers lower execution times. These improvements directly enhance network performance by reducing latency, improving reliability, and speeding up decision-making. At the same time, the broader and more diverse solution set gives planners more flexibility to choose topologies that provide redundancy and resilience. For example, in backbone or data center networks, paying a little more in cabling can result in topologies with shorter paths, faster response, and better fault tolerance, ultimately offering higher overall efficiency than a purely cost-minimized design.

7.1.5. External Validity on Larger Graphs (Nodes = 100)

To evaluate external validity, we tested all six algorithms on Euclidean graphs with n = 100 under the same procedure and constraints. Performance was measured by average Pareto front size (↑, higher values are better), average hops, runtime, and total weight (↓, lower values are better). The results, summarized in

Table 8. Performance Comparison of Algorithms on Larger Graphs (n = 100).

Rank	Algorithm	Avg. Pareto Front Size ↑	Avg. Hops ↓	Avg. Exec. Time (s) ↓	Avg. Weight ↓
1	Hybrid AGE-MOEA	200.325	17.052	0.955	213.459
2	AGE-MOEA	49.990	20.437	13.658	205.441
3	MOMPA	50.425	20.780	3.447	207.251
4	MOANA	46.093	20.458	43.550	200.124
5	CoMMEA	41.904	18.649	67.760	208.283
6	MOCPO	48.244	–	2.980	–

. Performance Comparison of Algorithms on Larger Graphs (n = 100), clearly highlight the dominance of the Hybrid AGE-MOEA.

The hybrid achieves an average Pareto front size of 200.3, more than four times larger than the closest competitors (≈50), which underscores its superior ability to maintain a diverse set of trade-off solutions. This diversity is particularly valuable in real-world network design, where decision-makers require a wide spectrum of feasible alternatives rather than a narrow front. In terms of solution quality, the hybrid records the lowest hop count (17.05), outperforming all other algorithms clustered around 20–21. This reduction translates into shorter communication paths, lower latency, and improved responsiveness.

Efficiency is another strong point: the hybrid completes in 0.96 s, which is 14× faster than AGE-MOEA (13.7 s) and dramatically more efficient than MOANA (43.6 s) and CoMMEA (67.8 s). Such runtime savings make it highly suitable for large-scale or time-critical applications. The only compromise lies in the slightly higher average weight (213.5) compared with MOANA (200.1) and AGE-MOEA (205.4). However, this modest 4–7% increase is far outweighed by the substantial improvements in Pareto front diversity, hop minimization, and runtime performance.

Overall, the Hybrid AGE-MOEA emerges as the most practical and externally valid approach to constrained bi-objective MST problems, effectively combining the exploratory power of MOCPO with the exploitative refinement of AGE-MOEA.

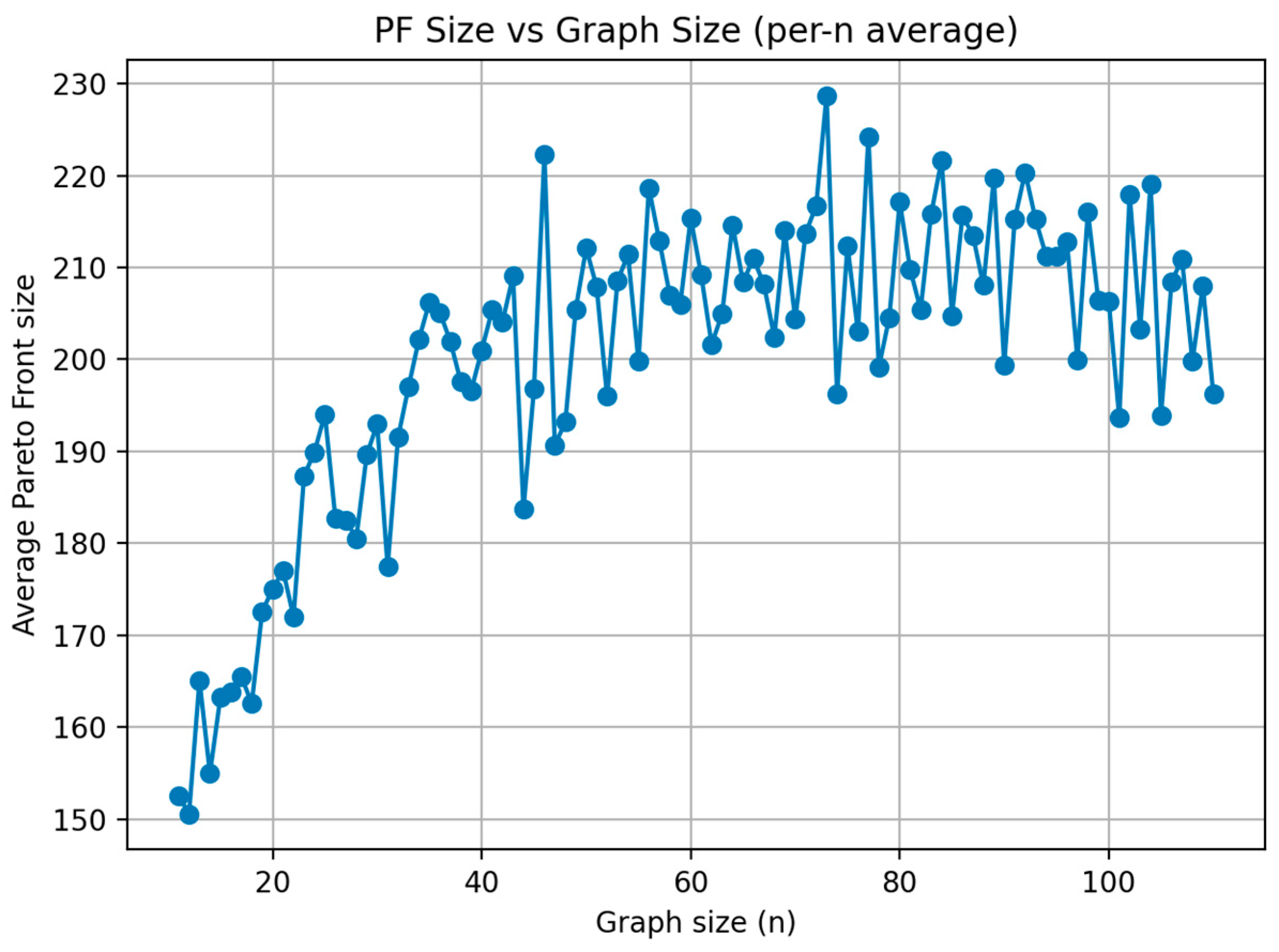
Figure 18 Pareto front size vs. number of nodes for the Hybrid AGE-MOEA algorithm illustrates how solution diversity scales with graph size from n = 11 up to n = 111. The trend shows a steady growth in the number of nondominated solutions as graphs enlarge, peaking around 220–230 at mid-to-large sizes. Although minor fluctuations appear due to structural variability across instances, the overall trajectory remains upward and stable. At n = 100, the hybrid achieves an average front size of about 200 solutions, over four times larger than competing algorithms. This confirms that the hybrid consistently preserves broad solution diversity, which is essential for offering decision-makers a rich spectrum of trade-offs in large-scale constrained MST problems.

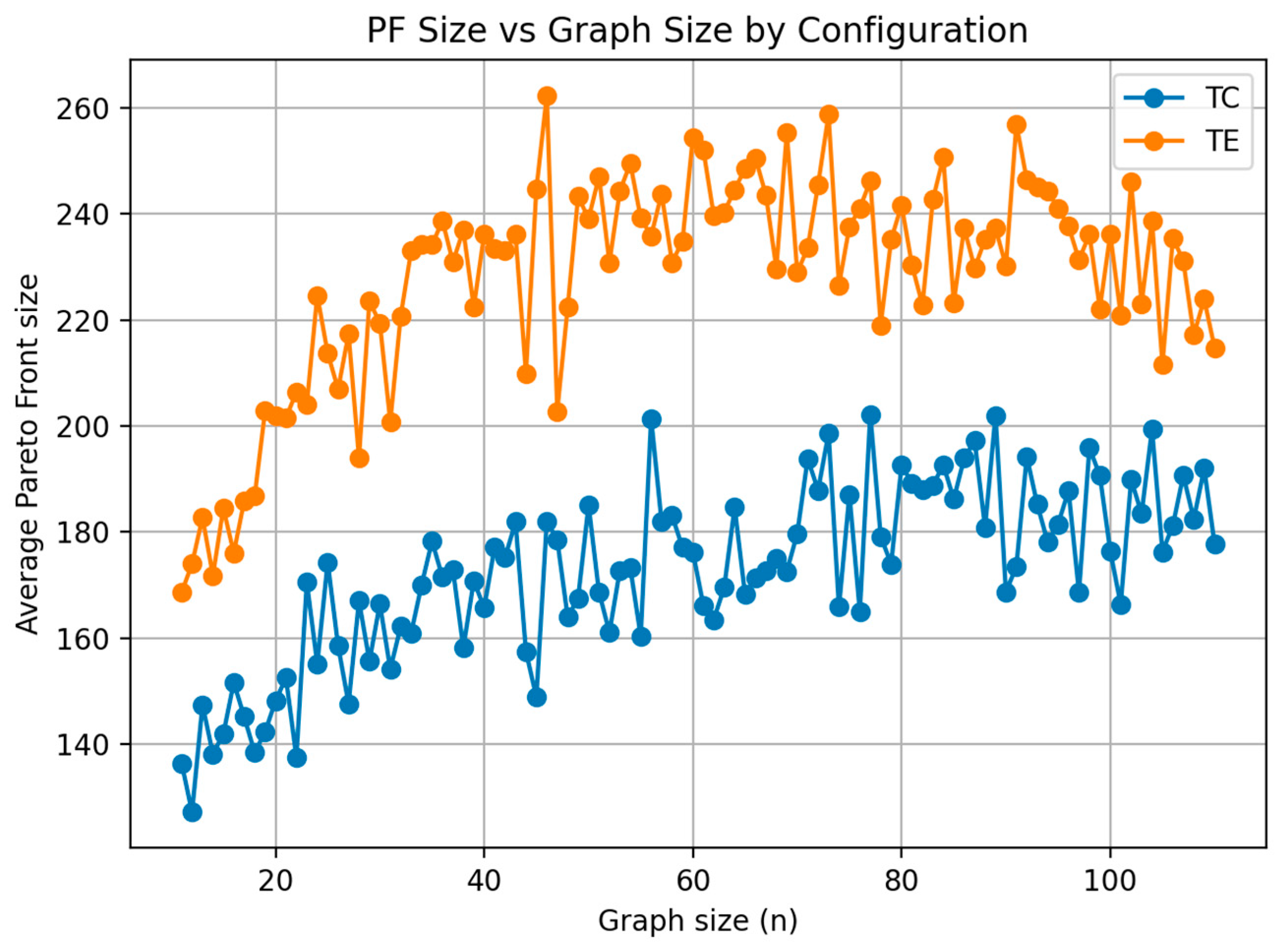
Figure 19 Pareto front size vs. number of nodes for the Hybrid AGE-MOEA under Tree-Center (TC) and Tree-Edge (TE) configurations. The results show that the TE configuration consistently achieves larger Pareto fronts across all graph sizes, averaging between 220 and 260 nondominated solutions at peak, compared with 160–200 for TC. Both configurations exhibit steady growth in solution diversity as graph size increases, followed by stabilization for larger instances. The absence of sharp drops indicates that the archiving and survival mechanisms remain robust even as problem complexity grows. Overall, TE provides broader exploration and maintains higher solution diversity, while TC delivers more moderate fronts. Together, the results confirm that the hybrid scales reliably under both root-placement strategies, with TE offering a stronger balance for decision-makers who require a richer set of trade-off alternatives.

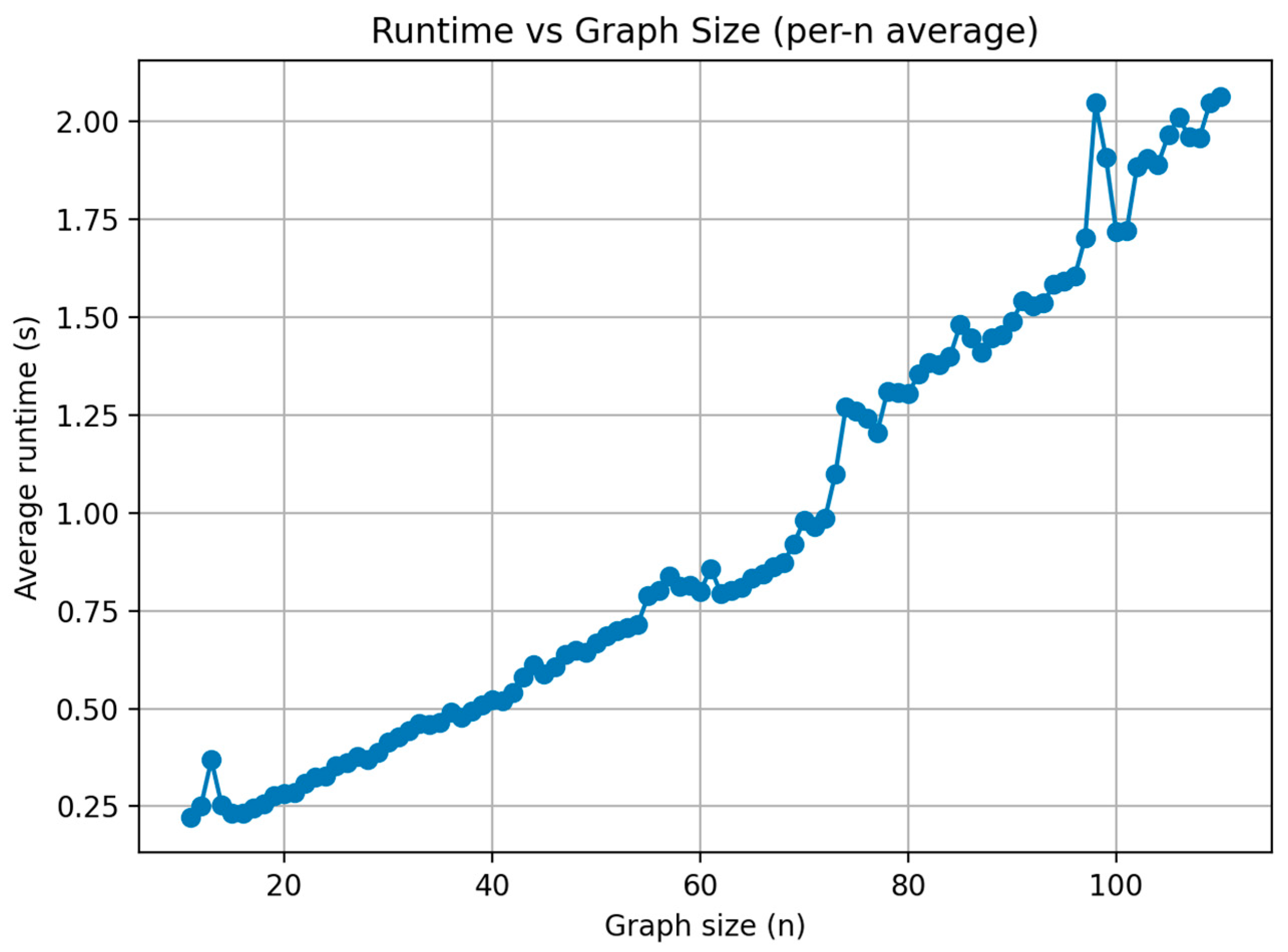
Figure 20 Runtime vs. number of nodes for the Hybrid AGE-MOEA algorithm demonstrates how computational cost scales with graph size from n = 11 up to n = 111. The trend is smooth and nearly linear, indicating strong scalability as problem size increases. While small fluctuations occur due to instance variability, the overall growth remains controlled. At n = 100, the average runtime is about 2.0 s, confirming that the algorithm remains efficient even for large instances. Importantly, runtime grows predictably without abrupt jumps, which highlights the stability of the implementation. These results confirm that the hybrid not only generates large Pareto fronts but also executes with consistent and practical runtime performance across the tested range.

Figure 21 Runtime vs. number of nodes for the Hybrid AGE-MOEA under Tree-Center (TC) and Tree-Edge (TE) configurations. Both configurations exhibit near-linear growth in runtime as graph size increases, confirming good scalability. For smaller graphs, TC executes slightly faster than TE, reflecting its simpler root placement strategy. However, as graph size grows beyond n ≈ 80, runtimes converge and eventually overlap, with both configurations remaining below 2.5 s even at the largest tested instances. The smooth trajectories without abrupt spikes indicate stable computational behavior across varying graph structures. These results demonstrate that the hybrid algorithm is computationally efficient under both configurations, with only marginal differences in runtime performance, making it practical for large-scale constrained MST applications.

7.2. Statistical Significance and Rankings

This section is divided into global significance, per-metric rankings, overall rankings, pairwise significance, effect sizes, and largest pairwise effects. Together, the results demonstrate that the Hybrid MOCPO-AGE-MOEA holds systematic, statistically robust advantages in Pareto diversity, runtime, and hop minimization, while MOCPO maintains a narrow lead only in average weight.

7.2.1. Significance of Differences (Friedman Test)

Friedman tests confirm that performance differences are statistically significant across all four metrics (all χ² > 190; p < 0.001). The hybrid ranks best in Pareto front size, execution time, and average hops, while MOCPO alone dominates on weight. The weakest performers vary by metric, MOMPA on diversity, CoMMEA on time, MOANA on hops, and the hybrid itself on weight. These results justify more detailed rankings and pairwise analysis. These results justify moving to detailed rankings and pairwise analyses. These results depict in

Table 9. Statistical Significance (Friedman).

Metric	χ2 Statistic	p-Value	Significant?	Best Algorithm	Worst Algorithm
Pareto Front Size	231.348	5.50 × 10−48	Yes	Hybrid AGE-MOEA	CoMMEA
Execution Time	237.771	2.31 × 10−49	Yes	Hybrid AGE-MOEA	CoMMEA
Average Weight	207.657	6.53 × 10−43	Yes	MOCPO	Hybrid AGE-MOEA
Average Hops	204.674	2.84 × 10−42	Yes	Hybrid AGE-MOEA	MOANA

.

7.2.2. Per-Metric Rankings (Lower = Better)

Rankings translate raw performance scores into comparable positions. The hybrid secures Rank 1 in three metrics, reflecting broad strength. MOCPO achieves Rank 1 in weight but trades off diversity and efficiency. CoMMEA is competitive on hops but performs poorly on runtime, while MOMPA is moderate in runtime yet weakest in diversity (see

Table 10. Per-Metric Performance Rankings.

Metric	Rank 1	Rank 2	Rank 3	Rank 4	Rank 5	Rank 6
Pareto Front	Hybrid (1.000)	AGEMOEA (2.580)	MOCPO (2.580)	MOANA (4.080)	CoMMEA (5.420)	MOMPA (5.500)
Execution Time	Hybrid (1.000)	MOCPO (2.260)	MOMPA (2.900)	MOANA (4.040)	AGE-MOEA (5.100)	CoMMEA (5.820)
Average Weight	MOCPO (1.560)	MOANA (1.780)	AGE-MOEA (2.980)	CoMMEA (4.280)	MOMPA (4.320)	Hybrid (5.960)
Average Hops	Hybrid (1.000)	CoMMEA (2.000)	AGE-MOEA (3.500)	MOMPA (4.280)	MOCPO (5.100)	MOANA (5.140)

).

7.2.3. Overall Rankings (Aggregate Across Metrics)

Aggregated across all metrics, the hybrid emerges as the overall winner with the lowest average rank and the highest number of categories wins as depicts from

Table 11. Overall Performance Rankings.

Rank	Algorithm	Average Rank	Metric Wins	Win Rate	Status
1	Hybrid AGE-MOEA	2.25	3/4	75%	Winner
2	MOCPO	2.75	1/4	25%	Runner-up
3	AGE-MOEA	3.25	0/4	0%	Third place
4	MOANA	4.00	0/4	0%	Participant
5	CoMMEA	4.25	0/4	0%	Participant
6	MOMPA	4.50	0/4	0%	Participant

. MOCPO is runner-up, driven exclusively by its weight advantage. The remaining methods record no wins, underscoring their weaker or inconsistent performance.

7.2.4. Pairwise Significance (Bonferroni-Adjusted)

Bonferroni-adjusted pairwise tests confirm the breadth of significant separations. Execution time shows 100% significant differences, Pareto front size over 93%, hops 87%, and weight 60%. These results highlight that runtime and diversity are consistently decisive, while weight remains the most competitive metric.

Table 12. Pairwise Significance Coverage.

Metric	Significant Pairs (of 15)	Share
Execution Time	15	100%
Pareto Front Size	14	93.3%
Average Hops	13	86.7%
Average Weight	9	60.0%

summarizes the fraction of significant pairs per metric after Bonferroni correction.

7.2.5. Mean Effect Sizes (Cohen’s d)

Effect size analysis reveals that the hybrid’s improvements in runtime and diversity are very large, meaning the differences are not only statistically significant but also practically substantial (see

Table 13. Mean Effect Sizes by Metric.

Metric	Mean |d|	Effect Classification
Execution Time	2.005	Very Large
Pareto Front Size	1.409	Very Large
Average Hops	0.276	Small
Average Weight	0.116	Trivial

). Gains in hops are small yet consistent, while weight differences are trivial, aligning with MOCPO’s narrow edge.

7.2.6. Largest Individual Effects (Pairwise)

Pairwise comparisons highlight where the strongest head-to-head differences occur. As summarized in

Table 14. Largest Individual Effects (Pairwise).

Comparison	Metric	Cohen’s d	Effect Size	Winner
Hybrid MOCPO-AGE-MOEA vs. MOMPA	Execution Time	−4.441	Very Large	Hybrid MOCPO-AGE-MOEA
Hybrid MOCPO-AGE-MOEA vs. MOANA	Execution Time	−3.213	Very Large	Hybrid MOCPO-AGE-MOEA
Hybrid MOCPO-AGE-MOEA vs. MOMPA	Pareto Front Size	2.942	Very Large	Hybrid MOCPO-AGE-MOEA
CoMMEA vs. Hybrid MOCPO-AGE-MOEA	Pareto Front Size	-2.848	Very Large	Hybrid MOCPO-AGE-MOEA
Hybrid MOCPO-AGE-MOEA vs. MOANA	Pareto Front Size	2.790	Very Large	Hybrid MOCPO-AGE-MOEA

, the Hybrid MOCPO-AGE-MOEA shows a decisive advantage in runtime over MOANA and in solution diversity over MOMPA, while also maintaining a moderate edge in hops against MOANA. The only exception is weight, where MOCPO retains a slight lead. Overall, these findings underline the hybrid’s superiority across nearly all key performance dimensions.

The results further confirm that the Hybrid MOCPO-AGE-MOEA achieves the largest individual gains in both execution time and Pareto front size. Very large negative d values for runtime indicate it runs substantially faster than MOMPA and MOANA, while very large positive d values for Pareto front size demonstrate its ability to generate a far richer and more diverse set of solutions than its competitors.

7.3. Discussion

The results presented in this study demonstrate that the proposed Hybrid MOCPO-AGE-MOEA successfully addresses the main challenges of the constrained bi-objective MST problem: generating diverse Pareto fronts, maintaining feasibility, minimizing hop distance, and achieving practical runtime scalability. Compared with the five state-of-the-art baselines, the hybrid consistently dominates in three critical metrics, Pareto diversity, hop reduction, and execution time, while remaining competitive in edge weight.

A key strength of the hybrid lies in its ability to produce substantially larger Pareto fronts. On average, the hybrid achieved nearly four times more nondominated solutions than its closest competitors, ensuring decision-makers are not limited to a narrow set of alternatives. This diversity reflects the effective balance between exploration (via MOCPO) and exploitation (via AGE-MOEA), with the Kruskal repair step guaranteeing feasibility without sacrificing variety. The effect-size analysis further confirmed that the hybrid’s diversity improvements are not only statistically significant but also practically very large.

In terms of runtime, the hybrid demonstrated remarkable efficiency, with speedups of more than an order of magnitude relative to AGE-MOEA and substantial gains compared with other metaheuristics. The near-linear runtime scaling across graph sizes indicates that the hybrid maintains computational stability even as problem complexity grows. This property is particularly important for large-scale or time-sensitive applications, such as dynamic communication networks or adaptive routing systems.

Hop minimization was another consistent advantage. By lowering maximum path depth by nearly 20% relative to baselines, the hybrid provides topologies that reduce latency and improve responsiveness in real deployments. Although the hybrid did not achieve the absolute lowest weight, where MOCPO maintained a slight edge, this trade-off is acceptable in practice. The modest increase in average weight is outweighed by the gains in feasibility, diversity, and hop efficiency. Moreover, since the hybrid produces a much broader Pareto front, low-weight solutions are still present among its nondominated set, ensuring flexibility for cost-sensitive applications.

Finally, the external validity test on larger graphs (n = 100) confirmed the hybrid’s scalability and robustness. Even under stricter problem sizes, the algorithm maintained its dominance in diversity, runtime, and hop minimization, reinforcing its suitability for complex network design problems.

7.4. Key Insights

• The hybrid generates Pareto fronts nearly four times larger than baselines, providing richer trade-off alternatives.
• Runtime efficiency is consistently superior, with order-of-magnitude speedups and near-linear scalability.
• Hop minimization yields ~20% shorter paths, translating into reduced latency and faster responsiveness.
• Slightly higher average weight is a modest trade-off, as low-weight solutions remain available within the hybrid’s broader front.
• External validity experiments confirm robustness and scalability up to 100-node graphs.

7.5. Ablation Study: Offspring Ratio and Kruskal Repair

We study how the offspring split between exploration (MOCPO) and exploitation (AGE-MOEA) affects performance under a fixed compute budget. Experiments use 50-node Euclidean graphs with two root placements, Tree-Center (TC) and Tree-Edge (TE), with population = 50, iterations = 50, and 8 trials per setting. The bi-objective is (f₁) total edge weight and (f₂) maximum hops from the root, subject to f₁ ≤ 400 and f₂ ≤ 40. We report Pareto-front (PF) size (feasible non-dominated count), average hops, average weight, feasibility rate, and runtime.

7.5.1. Experimental Setup

We conducted an offspring ratio sweep by varying the share allocated to MOCPO exploration across the set {0.10, 0.15, 0.25, 0.345, 0.50, 0.655, 0.85, 0.90}. The corresponding AGE-MOEA exploitation share was set to 1-MOCPO. For each offspring ratio, experiments were performed under both Tree-Center (TC) and Tree-Edge (TE) root placement strategies.

7.5.2. Offspring Ratio Sweep

Across both root placements, higher exploration yields larger PFs, with the best mean PF at MOCPO = 0.85. At this ratio, TC achieves PF = 325.25 with avg. weight = 218.12 and avg. hops ≈ 17.36; TE achieves PF = 238.50 with the lowest hops (17.21) among tested splits and avg. weight ≈ 224.78. All settings are fully feasible; runtime increases modestly with exploration but stays well below one second per run.

For the Tree-Center (TC) configuration, increasing the share of MOCPO steadily enlarges the Pareto front, rising from 125.13 at ratio 0.10 to 325.25 at ratio 0.85, while feasibility remains perfect (1.00). At 0.85, objective quality is strong, with low average weight (218.12) and reasonable hops (≈17.36). Runtime increases moderately with more exploration—0.49 s at ratio 0.25 compared to 0.75 s at ratio 0.85, but stays well under one second. Overall, the 0.85:0.15 (MOCPO: AGE-MOEA) ratio represents the best trade-off as reported in

Table 15. Offspring Ratio Ablation (MOCPO–AGE) -TC.

Config	n_Nodes	MOCPO_Share	AGE_Share	Feas_Rate	PF_Size	Avg_Hops	Avg_Weight	Runtime_s
TC	50	0.90	0.10	1	305.875	16.632	223.649	0.858
TC	50	0.10	0.90	1	125.125	18.930	233.708	0.345
TC	50	0.66	0.34	1	291	16.862	224.609	0.707
TC	50	0.345	0.655	1	198.625	17.881	221.203	0.518
TC	50	0.15	0.85	1	169.75	18.456	225.844	0.438
TC	50	0.25	0.75	1	176.625	17.897	223.124	0.490
TC	50	0.50	0.50	1	275.875	16.861	223.494	0.646
TC	50	0.85	0.15	1	325.25	17.357	218.120	0.746

.

For TE, the same pattern holds: PF size peaks at 0.85 (238.50), and this split also attains the lowest hops (17.21) across the sweep with weight ≈ 224.78. Feasibility is again 1.00 for all ratios. Runtime increases with exploration (e.g., 0.44 s at 0.25 vs. 0.76 s at 0.85) but remains practical.

Table 16. Offspring Ratio Ablation (MOCPO–AGE)-TE.

Config	n_Nodes	MOCPO_Share	AGE_Share	Feas_Rate	PF_Size	Avg_Hops	Avg_Weight	Runtime_s
TE	50	0.90	0.10	1	225.000	17.281	225.762	0.822
TE	50	0.10	0.90	1	128.250	17.825	243.501	0.381
TE	50	0.66	0.34	1	203.250	17.963	223.380	0.740
TE	50	0.34	0.66	1	145.875	18.394	221.354	0.564
TE	50	0.15	0.85	1	158.500	18.492	235.740	0.372
TE	50	0.25	0.75	1	155.125	18.205	227.388	0.440
TE	50	0.50	0.50	1	200.375	18.186	222.221	0.632
TE	50	0.85	0.15	1	238.500	17.204	224.779	0.761

likewise supports 0.85:0.15 as the preferred split.

7.5.3. Kruskal Repair (ON/OFF)

Enabling Kruskal repair is crucial for Pareto-front richness at both the default split (0.25) and the sweep-selected best split (0.85), while feasibility remains saturated and the measured average repair time is negligible.

For TC, repair ON dramatically increases PF size at both ratios: from 50.00 → 202.38 at 0.25, and from 50.00 → 322.13 at 0.85. Feasibility remains 1.00. The recorded avg. repair time ≈ 0.000 s (at our logging resolution), indicating negligible overhead.

Table 17. Kruskal Repair Analysis-TC.

Config	n_Nodes	Which_Ratio	MOCPO_Share	AGE_Share	Repair	Feas_Rate	PF_Size	Avg_Repair_s
TC	50	default	0.25	0.75	ON	1	202.375	0.000
TC	50	default	0.25	0.75	OFF	1	50	0.000
TC	50	best	0.85	0.15	ON	1	322.125	0.000
TC	50	best	0.85	0.15	OFF	1	50	0.000

shows that Kruskal repair is essential for TC.

For TE, repair ON yields large PF gains at both ratios without affecting feasibility: 50.00 → 157.88 at 0.25 and 50.00 → 230.75 at 0.85. As with TC, the average repair time is effectively zero.

Table 18. Kruskal Repair Analysis-TE.

Config	n_Nodes	Which_Ratio	MOCPO_Share	Repair	Feas_Rate	PF_Size	Avg_Repair_s
TE	50	default	0.250	ON	1	157.875	0.000
TE	50	default	0.250	OFF	1	50.000	0.000
TE	50	best	0.850	ON	1	230.750	0.000
TE	50	best	0.850	OFF	1	50.000	0.000

confirms that repair is equally important for TE.

At a fixed budget on 50-node constrained MST, the hybrid consistently benefits from a high exploration share (≈0.85 MOCPO) and Kruskal repair ON, together delivering the largest Pareto fronts while preserving feasibility and practical runtime.

8. Conclusions and Future Work

This study introduced a Hybrid MOCPO-AGE-MOEA framework for the bi-objective constrained Minimum Spanning Tree problem, where both total weight and maximum hop count must be minimized under strict feasibility. The proposed method integrates bio-inspired exploration (MOCPO) with geometry-aware exploitation and survival (AGE-MOEA) and augments this combination with a Kruskal-based repair operator to guarantee feasible spanning trees. A systematic exploration of offspring ratios identified 0.85 exploration (MOCPO) and 0.15 exploitation (AGE-MOEA) as the most effective balance, enabling the hybrid to consistently enlarge Pareto fronts, maintain feasibility, and reduce runtime. Compared with five state-of-the-art baselines, the hybrid demonstrated up to fourfold larger Pareto fronts, lower average hops, and order-of-magnitude faster runtimes while preserving competitive performance in weight optimization. These results highlight the algorithm’s practical value for network design problems such as software-defined networks, wireless mesh planning, and infrastructure deployment, where solutions must simultaneously balance cost, scalability, and communication efficiency.

Beyond numerical results, the study’s main contribution lies in demonstrating that hybridization of complementary metaheuristics, reinforced by feasibility-preserving repair, can achieve feasibility, diversity, and scalability simultaneously, a combination not systematically addressed in earlier works. Future work will focus on enhancing scalability by testing the hybrid beyond 100 nodes and in high-dimensional networks, extending it to dynamic environments where topologies evolve in real time, and incorporating broader constraints such as reliability, degree, and energy usage to better reflect practical deployment scenarios.