A Regularized Physics-Informed Neural Network to Support Data-Driven Nonlinear Constrained Optimization
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Nonlinear Optimization Fundamentals (NOPT)
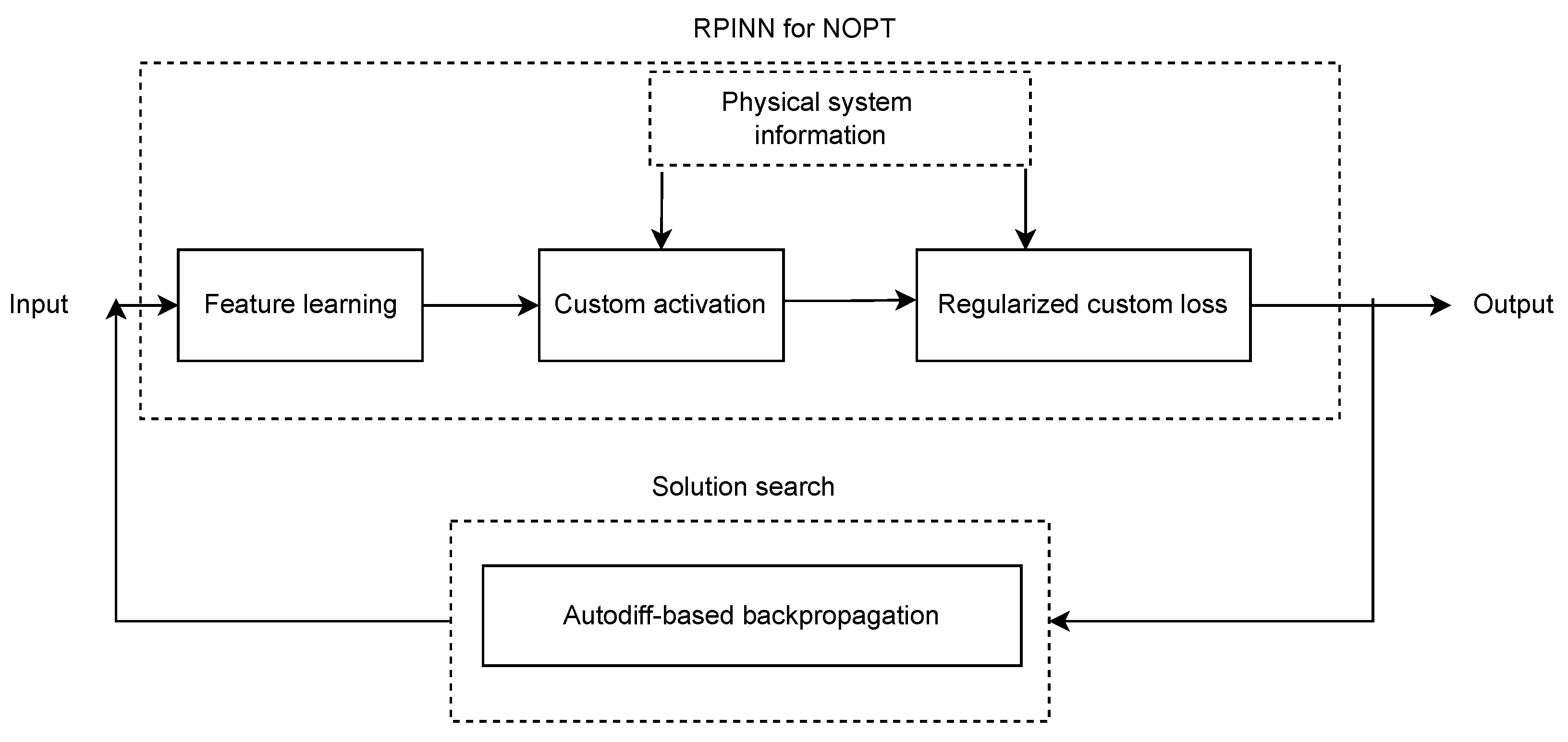
3.2. Regularized Physics-Informed Neural Network (RPINN)
4. Tested Scenarios for NOPT Using RPINN
4.1. Supervised Constrained Optimization: Uniform Mixture Model
4.2. Unsupervised Constrained Optimization: Gas-Powered System
5. Experimental Set-Up
5.1. Deep Learning Architectures
5.2. Training Details and Method Comparison
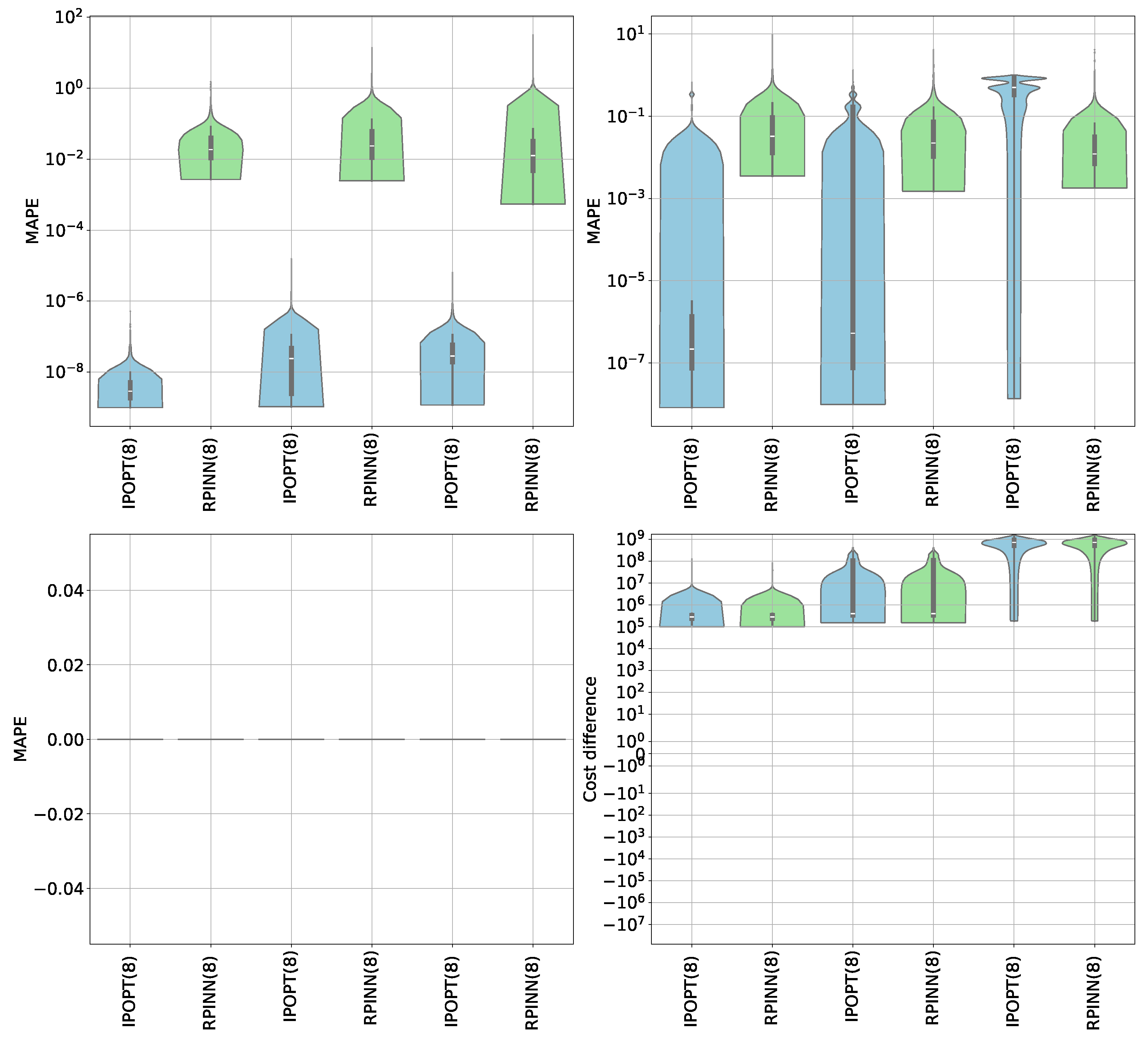
6. Results and Discussion
6.1. Supervised Constrained Optimization Results
6.2. Unsupervised Constrained Optimization Results
6.3. Computational Cost Results
6.4. Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stanimirović, P.S.; Ivanov, B.; Ma, H.; Mosić, D. A survey of gradient methods for solving nonlinear optimization. Electron. Res. Arch. 2020, 28, 1573–1624. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of optimization algorithms in modern neural networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Chen, Q.; Zuo, L.; Wu, C.; Bu, Y.; Lu, Y.; Huang, Y.; Chen, F. Short-term supply reliability assessment of a gas pipeline system under demand variations. Reliab. Eng. Syst. Saf. 2020, 202, 107004. [Google Scholar] [CrossRef]
- Yu, W.; Huang, W.; Wen, Y.; Li, Y.; Liu, H.; Wen, K.; Gong, J.; Lu, Y. An integrated gas supply reliability evaluation method of the large-scale and complex natural gas pipeline network based on demand-side analysis. Reliab. Eng. Syst. Saf. 2021, 212, 107651. [Google Scholar] [CrossRef]
- Kohjitani, H.; Koda, S.; Himeno, Y.; Makiyama, T.; Yamamoto, Y.; Yoshinaga, D.; Wuriyanghai, Y.; Kashiwa, A.; Toyoda, F.; Zhang, Y.; et al. Gradient-based parameter optimization method to determine membrane ionic current composition in human induced pluripotent stem cell-derived cardiomyocytes. Sci. Rep. 2022, 12, 19110. [Google Scholar] [CrossRef] [PubMed]
- Shcherbakova, G.; Krylov, V.; Qianqi, W.; Rusyn, B.; Sachenko, A.; Bykovyy, P.; Zahorodnia, D.; Kopania, L. Optimization methods on the wavelet transformation base for technical diagnostic information systems. In Proceedings of the 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Cracow, Poland, 22–25 September 2021; Volume 2, pp. 767–773. [Google Scholar]
- Weiner, A.; Semaan, R. Backpropagation and gradient descent for an optimized dynamic mode decomposition. arXiv 2023, arXiv:2312.12928. [Google Scholar]
- Han, M.; Du, Z.; Yuen, K.F.; Zhu, H.; Li, Y.; Yuan, Q. Walrus optimizer: A novel nature-inspired metaheuristic algorithm. Expert Syst. Appl. 2024, 239, 122413. [Google Scholar] [CrossRef]
- Mhanna, S.; Mancarella, P. An exact sequential linear programming algorithm for the optimal power flow problem. IEEE Trans. Power Syst. 2021, 37, 666–679. [Google Scholar] [CrossRef]
- Chang, H.; Chen, Q.; Lin, R.; Shi, Y.; Xie, L.; Su, H. Controlling Pressure of Gas Pipeline Network Based on Mixed Proximal Policy Optimization. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 4642–4647. [Google Scholar]
- Wang, G.; Zhao, W.; Qiu, R.; Liao, Q.; Lin, Z.; Wang, C.; Zhang, H. Operational optimization of large-scale thermal constrained natural gas pipeline networks: A novel iterative decomposition approach. Energy 2023, 282, 128856. [Google Scholar] [CrossRef]
- Montoya, O.; Gil-González, W.; Hernández, J.C.; Giral-Ramírez, D.A.; Medina-Quesada, A. A mixed-integer nonlinear programming model for optimal reconfiguration of DC distribution feeders. Energies 2020, 13, 4440. [Google Scholar] [CrossRef]
- Robuschi, N.; Zeile, C.; Sager, S.; Braghin, F. Multiphase mixed-integer nonlinear optimal control of hybrid electric vehicles. Automatica 2021, 123, 109325. [Google Scholar] [CrossRef]
- Arya, A.K.; Jain, R.; Yadav, S.; Bisht, S.; Gautam, S. Recent trends in gas pipeline optimization. Mater. Today Proc. 2022, 57, 1455–1461. [Google Scholar] [CrossRef]
- Sadat, S.A.; Sahraei-Ardakani, M. Customized sequential quadratic programming for solving large-scale ac optimal power flow. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar]
- Awwal, A.M.; Kumam, P.; Abubakar, A.B. A modified conjugate gradient method for monotone nonlinear equations with convex constraints. Appl. Numer. Math. 2019, 145, 507–520. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z. A benders decomposition based algorithm for steady-state dispatch problem in an integrated electricity-gas system. IEEE Trans. Power Syst. 2021, 36, 3817–3820. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Zhou, M.; Yu, Y. A multi-layered gravitational search algorithm for function optimization and real-world problems. IEEE/CAA J. Autom. Sin. 2020, 8, 94–109. [Google Scholar] [CrossRef]
- Pillutla, K.; Roulet, V.; Kakade, S.M.; Harchaoui, Z. Modified Gauss-Newton Algorithms under Noise. In Proceedings of the 2023 IEEE Statistical Signal Processing Workshop (SSP), Hanoi, Vietnam, 2–5 July 2023; pp. 51–55. [Google Scholar] [CrossRef]
- Jamii, J.; Trabelsi, M.; Mansouri, M.; Mimouni, M.F.; Shatanawi, W. Non-Linear Programming-Based Energy Management for a Wind Farm Coupled with Pumped Hydro Storage System. Sustainability 2022, 14, 11287. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A Feasibility-Optimized Deep Neural Network Approach for AC Optimal Power Flow Problems. IEEE Syst. J. 2023, 17, 673–683. [Google Scholar] [CrossRef]
- Nellikkath, R.; Chatzivasileiadis, S. Physics-informed neural networks for ac optimal power flow. Electr. Power Syst. Res. 2022, 212, 108412. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of Physics-Informed Neural Networks in Power Systems—A Review. IEEE Trans. Power Syst. 2023, 38, 572–588. [Google Scholar] [CrossRef]
- Stiasny, J.; Chevalier, S.; Chatzivasileiadis, S. Learning without data: Physics-informed neural networks for fast time-domain simulation. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; pp. 438–443. [Google Scholar]
- Strelow, E.L.; Gerisch, A.; Lang, J.; Pfetsch, M.E. Physics informed neural networks: A case study for gas transport problems. J. Comput. Phys. 2023, 481, 112041. [Google Scholar] [CrossRef]
- Applegate, D.; Diaz, M.; Hinder, O.; Lu, H.; Lubin, M.; O’Donoghue, B.; Schudy, W. Practical Large-Scale Linear Programming using Primal-Dual Hybrid Gradient. In Proceedings of the Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 20243–20257. [Google Scholar]
- Zhao, Z.; Liu, S.; Zhou, M.; Abusorrah, A. Dual-objective mixed integer linear program and memetic algorithm for an industrial group scheduling problem. IEEE/CAA J. Autom. Sin. 2020, 8, 1199–1209. [Google Scholar] [CrossRef]
- Vo, T.Q.T.; Baiou, M.; Nguyen, V.H.; Weng, P. Improving Subtour Elimination Constraint Generation in Branch-and-Cut Algorithms for the TSP with Machine Learning. In Proceedings of the Learning and Intelligent Optimization; Sellmann, M., Tierney, K., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 537–551. [Google Scholar]
- Sun, Y.; Zhang, B.; Ge, L.; Sidorov, D.; Wang, J.; Xu, Z. Day-ahead optimization schedule for gas-electric integrated energy system based on second-order cone programming. CSEE J. Power Energy Syst. 2020, 6, 142–151. [Google Scholar]
- Lin, Y.; Zhang, X.; Wang, J.; Shi, D.; Bian, D. Voltage Stability Constrained Optimal Power Flow for Unbalanced Distribution System Based on Semidefinite Programming. J. Mod. Power Syst. Clean Energy 2022, 10, 1614–1624. [Google Scholar] [CrossRef]
- Chowdhury, M.M.U.T.; Kamalasadan, S. A new second-order cone programming model for voltage control of power distribution system with inverter-based distributed generation. IEEE Trans. Ind. Appl. 2021, 57, 6559–6567. [Google Scholar] [CrossRef]
- Asgharieh Ahari, S.; Kocuk, B. A mixed-integer exponential cone programming formulation for feature subset selection in logistic regression. EURO J. Comput. Optim. 2023, 11, 100069. [Google Scholar] [CrossRef]
- Kumar, J.; Rahaman, O. Lower bound limit analysis using power cone programming for solving stability problems in rock mechanics for generalized Hoek–Brown criterion. Rock Mech. Rock Eng. 2020, 53, 3237–3252. [Google Scholar] [CrossRef]
- Abubakar, A.B.; Kumam, P. A descent Dai-Liao conjugate gradient method for nonlinear equations. Numer. Algorithms 2019, 81, 197–210. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Wang, C.; Yao, B.; Tian, Y.; Wu, Y.S. Automatic fracture optimization for shale gas reservoirs based on gradient descent method and reservoir simulation. Adv. Geo-Energy Res. 2021, 5, 191–201. [Google Scholar] [CrossRef]
- Mahapatra, D.; Rajan, V. Multi-task learning with user preferences: Gradient descent with controlled ascent in pareto optimization. In Proceedings of the International Conference on Machine Learning, PMLR, Online conference, 13–18 July 2020; pp. 6597–6607. [Google Scholar]
- Karimi, M.; Shahriari, A.; Aghamohammadi, M.; Marzooghi, H.; Terzija, V. Application of Newton-based load flow methods for determining steady-state condition of well and ill-conditioned power systems: A review. Int. J. Electr. Power Energy Syst. 2019, 113, 298–309. [Google Scholar] [CrossRef]
- Mannel, F.; Rund, A. A hybrid semismooth quasi-Newton method for nonsmooth optimal control with PDEs. Optim. Eng. 2021, 22, 2087–2125. [Google Scholar] [CrossRef]
- Pinheiro, R.B.; Balbo, A.R.; Cabana, T.G.; Nepomuceno, L. Solving Nonsmooth and Discontinuous Optimal Power Flow problems via interior-point lp-penalty approach. Comput. Oper. Res. 2022, 138, 105607. [Google Scholar] [CrossRef]
- Delgado, J.A.; Baptista, E.C.; Balbo, A.R.; Soler, E.M.; Silva, D.N.; Martins, A.C.; Nepomuceno, L. A primal–dual penalty-interior-point method for solving the reactive optimal power flow problem with discrete control variables. Int. J. Electr. Power Energy Syst. 2022, 138, 107917. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Q.; Zhang, H.; Wu, H. An interior-point solver for AC optimal power flow considering variable impedance-based FACTS devices. IEEE Access 2021, 9, 154460–154470. [Google Scholar] [CrossRef]
- Haji, S.H.; Abdulazeez, A.M. Comparison of optimization techniques based on gradient descent algorithm: A review. PalArch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Ibrahim, I.A.; Hossain, M.J. Low voltage distribution networks modeling and unbalanced (optimal) power flow: A comprehensive review. IEEE Access 2021, 9, 143026–143084. [Google Scholar] [CrossRef]
- Goulart, P.; Chen, Y. Clarabel Documentation. 2024. Available online: https://oxfordcontrol.github.io/ClarabelDocs/stable/ (accessed on 12 June 2024).
- Gurobi Optimization. 2024. Available online: https://www.gurobi.com/ (accessed on 12 June 2024).
- MOSEK. 2024. Available online: https://www.mosek.com/ (accessed on 12 June 2024).
- Xpress Optimization. 2024. Available online: https://www.fico.com/en/products/fico-xpress-optimization (accessed on 12 June 2024).
- O’Donoghue, B. Operator Splitting for a Homogeneous Embedding of the Linear Complementarity Problem. SIAM J. Optim. 2021, 31, 1999–2023. [Google Scholar] [CrossRef]
- Ipopt Deprecated Features. 2024. Available online: https://coin-or.github.io/Ipopt/deprecated.html (accessed on 12 June 2024).
- Zimmerman, R.D.; Murillo-Sánchez, C.E. MATPOWER User’s Manual; Zenodo: Tempe, AZ, USA, 2020. [Google Scholar] [CrossRef]
- Wang, H.; Murillo-Sanchez, C.E.; Zimmerman, R.D.; Thomas, R.J. On Computational Issues of Market-Based Optimal Power Flow. IEEE Trans. Power Syst. 2007, 22, 1185–1193. [Google Scholar] [CrossRef]
- García-Marín, S.; González-Vanegas, W.; Murillo-Sánchez, C. MPNG: A MATPOWER-Based Tool for Optimal Power and Natural Gas Flow Analyses. IEEE Trans. Power Syst. 2022, 39, 5455–5464. [Google Scholar] [CrossRef]
- Beal, L.; Hill, D.; Martin, R.; Hedengren, J. GEKKO Optimization Suite. Processes 2018, 6, 106. [Google Scholar] [CrossRef]
- Mugel, S.; Kuchkovsky, C.; Sanchez, E.; Fernandez-Lorenzo, S.; Luis-Hita, J.; Lizaso, E.; Orus, R. Dynamic portfolio optimization with real datasets using quantum processors and quantum-inspired tensor networks. Phys. Rev. Res. 2022, 4, 013006. [Google Scholar] [CrossRef]
- Diamond, S.; Boyd, S. CVXPY: A Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Agrawal, A.; Boyd, S. Disciplined quasiconvex programming. arXiv 2020, arXiv:1905.00562. [Google Scholar] [CrossRef]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. J. Optim. Theory Appl. 2016, 169, 1042–1068. [Google Scholar] [CrossRef]
- Pan, X.; Zhao, T.; Chen, M.; Zhang, S. DeepOPF: A Deep Neural Network Approach for Security-Constrained DC Optimal Power Flow. IEEE Trans. Power Syst. 2021, 36, 1725–1735. [Google Scholar] [CrossRef]
- Baker, K. A learning-boosted quasi-newton method for ac optimal power flow. arXiv 2020, arXiv:2007.06074. [Google Scholar]
- Zhou, M.; Chen, M.; Low, S.H. DeepOPF-FT: One Deep Neural Network for Multiple AC-OPF Problems With Flexible Topology. IEEE Trans. Power Syst. 2023, 38, 964–967. [Google Scholar] [CrossRef]
- Liang, H.; Zhao, C. DeepOPF-U: A Unified Deep Neural Network to Solve AC Optimal Power Flow in Multiple Networks. arXiv 2023, arXiv:2309.12849. [Google Scholar]
- Falconer, T.; Mones, L. Leveraging Power Grid Topology in Machine Learning Assisted Optimal Power Flow. IEEE Trans. Power Syst. 2023, 38, 2234–2246. [Google Scholar] [CrossRef]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-informed neural networks for power systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Misyris, G.S.; Stiasny, J.; Chatzivasileiadis, S. Capturing power system dynamics by physics-informed neural networks and optimization. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; pp. 4418–4423. [Google Scholar]
- Habib, A.; Yildirim, U. Developing a physics-informed and physics-penalized neural network model for preliminary design of multi-stage friction pendulum bearings. Eng. Appl. Artif. Intell. 2022, 113, 104953. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Schiassi, E.; De Florio, M.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Physics-informed neural networks and functional interpolation for data-driven parameters discovery of epidemiological compartmental models. Mathematics 2021, 9, 2069. [Google Scholar] [CrossRef]
- Raynaud, G.; Houde, S.; Gosselin, F.P. ModalPINN: An extension of physics-informed Neural Networks with enforced truncated Fourier decomposition for periodic flow reconstruction using a limited number of imperfect sensors. J. Comput. Phys. 2022, 464, 111271. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- González-Vanegas, W.; Álvarez Meza, A.; Hernández-Muriel, J.; Orozco-Gutiérrez, Á. AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning. Entropy 2019, 21, 932. [Google Scholar] [CrossRef]
- García-Marín, S.; González-Vanegas, W.; Murillo-Sánchez, C. MPNG: MATPOWER-Natural Gas. 2019. Available online: https://github.com/MATPOWER/mpng (accessed on 12 June 2024).
- Owerko, D.; Gama, F.; Ribeiro, A. Unsupervised optimal power flow using graph neural networks. arXiv 2022, arXiv:2210.09277. [Google Scholar]
- Mustajab, A.H.; Lyu, H.; Rizvi, Z.; Wuttke, F. Physics-Informed Neural Networks for High-Frequency and Multi-Scale Problems Using Transfer Learning. Appl. Sci. 2024, 14, 3204. [Google Scholar] [CrossRef]
- Eleftheriadis, P.; Leva, S.; Ogliari, E. Bayesian hyperparameter optimization of stacked bidirectional long short-term memory neural network for the state of charge estimation. Sustain. Energy Grids Netw. 2023, 36, 101160. [Google Scholar] [CrossRef]
- Ma, X.; Huang, H.; Wang, Y.; Romano, S.; Erfani, S.; Bailey, J. Normalized loss functions for deep learning with noisy labels. In Proceedings of the International Conference on Machine Learning, PMLR, Online Meeting, 13–18 July 2020; pp. 6543–6553. [Google Scholar]
- Jeon, H.J.; Van Roy, B. An Information-Theoretic Framework for Deep Learning. Adv. Neural Inf. Process. Syst. 2022, 35, 3279–3291. [Google Scholar]
- Thangamuthu, A.; Kumar, G.; Bishnoi, S.; Bhattoo, R.; Krishnan, N.; Ranu, S. Unravelling the performance of physics-informed graph neural networks for dynamical systems. Adv. Neural Inf. Process. Syst. 2022, 35, 3691–3702. [Google Scholar]










| Solver | LP | QP | SOCP | SDP | EXP | PCP | MIP | NLP | Strategy | Open Source | Software |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Clarabel [45] | ✓ | ✓ | ✓ | ✓ | ✓ | x | x | x | IP | ✓ | CVXPY 1.5 |
| Gurobi [46] | ✓ | ✓ | ✓ | x | x | x | ✓ | x | IP, Simplex, BC | x | MATPOWER 8.0, CVXPY 1.5 |
| Mosek [47] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ * | x | IP | x | MATPOWER 8.0, CVXPY 1.5 |
| Xpress [48] | ✓ | ✓ | ✓ | x | x | x | ✓ | ✓ ** | IP, Simplex, BC | x | CVXPY 1.5 |
| SCS [49,58] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | x | x | IP | ✓ | CVXPY 1.5 |
| IPOPT [50] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | IP | ✓ | MATPOWER 8.0, GEKKO 1.0.3 |
| Layer Name | Type | Output Shape | Param. # | Memory Size |
|---|---|---|---|---|
| Input | InputLayer | (, 5) | 0 | 0 KB |
| Dense_1 | Dense (SELU) | (, 5) | 25 | 0.1 KB |
| Dense_2 | Dense (SELU, l1-max-constraint) | (, 1) | 5 | 0.02 KB |
| Layer Name | Type | Output Shape | Param. # | Memory Size |
|---|---|---|---|---|
| Input | InputLayer | (, 8) | 0 | 0 KB |
| Dense_1 | Dense (SELU) | (, 236) | 2124 | 8.3 KB |
| Dense_2 | Dense (SELU) | (, 8) | 1896 | 7.41 KB |
| Source switching | CustomDense | (, 1) | 1 | 4 B |
| BatchNormalization_1 | BatchNormalization | (, 236) | 944 | 3.69 KB |
| BatchNormalization_2 | BatchNormalization | (, 8) | 32 | 0.12 KB |
| Partial flows | BoundedDense | (, 50) | 2274 | 8.88 KB |
| Unsupply gas switching | CustomDense | (, 8) | 0 | 0 KB |
| Flow prediction | Concatenate | (, 59) | 0 | 0KB |
| Dense_3 | Dense (SELU) | (, 236) | 2124 | 8.3 KB |
| BatchNormalization_3 | BatchNormalization | (, 236) | 944 | 3.69 KB |
| Pressure prediction | BoundedDense | (, 8) | 1896 | 7.41 KB |
| Node balance | CustomDense | (, 8) | 472 | 1.84 KB |
| Weymouth | CustomDense | (, 14) | 0 | 0 KB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Rosero, D.A.; Álvarez-Meza, A.M.; Castellanos-Dominguez, C.G. A Regularized Physics-Informed Neural Network to Support Data-Driven Nonlinear Constrained Optimization. Computers 2024, 13, 176. https://doi.org/10.3390/computers13070176
Perez-Rosero DA, Álvarez-Meza AM, Castellanos-Dominguez CG. A Regularized Physics-Informed Neural Network to Support Data-Driven Nonlinear Constrained Optimization. Computers. 2024; 13(7):176. https://doi.org/10.3390/computers13070176
Chicago/Turabian StylePerez-Rosero, Diego Armando, Andrés Marino Álvarez-Meza, and Cesar German Castellanos-Dominguez. 2024. "A Regularized Physics-Informed Neural Network to Support Data-Driven Nonlinear Constrained Optimization" Computers 13, no. 7: 176. https://doi.org/10.3390/computers13070176
APA StylePerez-Rosero, D. A., Álvarez-Meza, A. M., & Castellanos-Dominguez, C. G. (2024). A Regularized Physics-Informed Neural Network to Support Data-Driven Nonlinear Constrained Optimization. Computers, 13(7), 176. https://doi.org/10.3390/computers13070176






