Abstract
Advancements in genomic technologies have paved the way for significant breakthroughs in cancer diagnostics, with DNA microarray technology standing at the forefront of identifying genetic expressions associated with various cancer types. Despite its potential, the vast dimensionality of microarray data presents a formidable challenge, necessitating efficient dimension reduction and gene selection methods to accurately identify cancerous tumors. In response to this challenge, this study introduces an innovative strategy for microarray data dimension reduction and crucial gene set selection, aiming to enhance the accuracy of cancerous tumor identification. Leveraging DNA microarray technology, our method focuses on pinpointing significant genes implicated in tumor development, aiding the development of sophisticated computerized diagnostic tools. Our technique synergizes gene selection with classifier training within a logistic regression framework, utilizing a generalized Fused LASSO (GFLASSO-LR) regularizer. This regularization incorporates two penalties: one for selecting pertinent genes and another for emphasizing adjacent genes of importance to the target class, thus achieving an optimal trade-off between gene relevance and redundancy. The optimization challenge posed by our approach is tackled using a sub-gradient algorithm, designed to meet specific convergence prerequisites. We establish that our algorithm’s objective function is convex, Lipschitz continuous, and possesses a global minimum, ensuring reliability in the gene selection process. A numerical evaluation of the method’s parameters further substantiates its effectiveness. Experimental outcomes affirm the GFLASSO-LR methodology’s high efficiency in processing high-dimensional microarray data for cancer classification. It effectively identifies compact gene subsets, significantly enhancing classification performance and demonstrating its potential as a powerful tool in cancer research and diagnostics.
1. Introduction
Currently, advancements in technology have made massive datasets, like DNA microarray data, fundamental to statistical analysis [1,2]. High-dimensional data pose challenges in classification tasks and gene subset identification [3]. DNA microarrays are vital in medicine and biology for various research purposes, including gene co-regulation, clinical diagnosis, and differential gene expression [4,5]. Microarray technology, crucial in cancer research, identifies genes critical to tumor growth and aids in developing diagnostic systems [6]. However, microarray data analysis is complex due to computational and biological challenges. The high cost of microarray experiments limits sample size, creating datasets with many genes but few samples [7,8], leading to computational instability and the curse of dimensionality [9,10]. Consequently, gene selection becomes a crucial yet difficult task.
Scientists aim to identify markers for lab testing to create effective disease treatments. Efficient gene selection improves understanding of gene–disease relationships and classifier quality, addressing the curse of dimensionality [11,12,13]. Gene selection, a significant challenge due to the gene-sample number disparity, requires advanced optimization methods [14,15]. Despite numerous gene selection methods aiming to enhance classification accuracy, further research is needed, particularly for diseases like cancer [16,17]. High classification accuracy is essential for personalized medicine, enabling better physician decision-making and potentially saving lives. Gene [18,19] selection algorithms include filter, wrapper, and embedded methods [20].
Filter methods evaluate genes independently, assigning scores to select high-scoring genes. Though easy to implement, they overlook gene interactions. Examples include the Fischer score, t-test, signal-to-noise ratio, information gain, and ReliefF [21,22,23,24,25]. Wrapper methods use classifiers to select gene subsets, testing candidate subsets for performance. Despite achieving high performance, they are computationally intensive and risk overfitting [20]. Embedded methods integrate selection into the learning algorithm, offering efficiency and performance without extensive classifier execution [26]. These methods consider gene dependencies but are algorithm-specific and computationally complex [27,28,29].
Filter methods evaluate genes independently, assigning scores to select high-scoring genes. Though easy to implement and computationally efficient, they have significant limitations: primarily, they overlook gene interactions, which can lead to suboptimal gene selection in complex biological processes where gene interactions play a crucial role. Examples include the Fischer score, t-test, signal-to-noise ratio, information gain, and ReliefF. Their simplicity and neglect of gene–gene interactions can lead to a lack of robustness in capturing the multifaceted nature of genetic influences on diseases [21,22,23,24,25]. Wrapper methods, on the other hand, use classifiers to select gene subsets, evaluating the performance of candidate subsets. While these methods can achieve high performance by considering gene interactions and utilizing the predictive power of classifiers, they come with their own set of limitations. They are computationally intensive, making them impractical for very large datasets, and they carry a significant risk of overfitting, especially when the number of genes vastly exceeds the number of samples. This can lead to models that perform well on training data but poorly on unseen data [20]. Embedded methods offer a middle ground by integrating gene selection directly into the learning algorithm, thus offering efficiency and potentially high performance without necessitating the execution of separate classifiers for feature selection. These methods can account for gene dependencies through their integration with the learning model, offering a more nuanced approach to gene selection. However, their algorithm-specific nature means that each method is tailored to a particular model or set of assumptions about the data, which can limit their applicability. Moreover, they can still be computationally complex, posing challenges for their use in large-scale genomic studies [27,28,29]. These limitations highlight the ongoing need for innovative solutions that balance accuracy, computational efficiency, and the ability to handle high-dimensional genomic data.
Regularized methods, particularly penalized logistic regression (PLR) with LASSO, are gaining traction for cancer classification [30,31,32,33,34,35,36,37,38]. While LASSO is effective for feature selection and model simplification, it has limitations such as potential bias in coefficient estimation, difficulty in handling highly correlated predictors, and a tendency to select only one variable from a group of highly correlated variables. These limitations prompted the development of the Elastic-Net (EN) penalty by Zou and Hastie [39], which combines the and penalties to better handle correlated predictors, and the adaptive LASSO (ALASSO) by Zou et al. [40], which introduces weights for penalization within the norm to improve variable selection accuracy.
To overcome the deficiencies in achieving the oracle property, Zou introduced ALASSO [40], which theoretically possesses the oracle property under certain conditions. However, the performance of ALASSO can be sensitive to the choice of weights, which may require additional tuning. Structured penalties, like Fused LASSO [41,42], further enhance LASSO by considering gene relationships, aiding in feature reduction and meaningful gene selection [43]. Despite its advantages, Fused LASSO can be computationally intensive for large datasets and may not perform well if the true underlying model does not adhere to its assumption of spatial or sequential coherence. The Fused LASSO and its theoretical foundations [44,45] have led to the Generalized Fused LASSO (GFLASSO) within linear regression [46,47], which penalizes coefficient differences based on a gene graph to encourage sparse and connected solution vectors [47]. GFLASSO further extends the applicability to more complex data structures but faces challenges in scalability and the need for a well-defined gene graph, which may not always be available or accurately represent biological relationships.
The norm penalties’ absolute values complicate minimization due to non- differentiability at zero, challenging analytical solution derivation. Initial solutions for linear regression included FLSA [48] and other algorithms [49,50,51]. For logistic regression, fewer algorithms exist, with Hofling et al. [46] applying quadratic approximation iteratively to the log-likelihood function. Table 1 presents a comparison of Contributions in DNA Microarray Data Analysis.

Table 1.
Comparison of Contributions in DNA Microarray Data Analysis.
In the wake of comprehensive literature analysis, it becomes evident that the frontier of gene selection for cancer research is ripe for innovation. Current methodologies, while robust, exhibit limitations in computational efficiency, model overfitting, and the nuanced understanding of gene interdependencies. This literature underscores the essential balance between gene selection’s computational demands and the need for precise, interpretable models capable of navigating the vast, complex landscape of genomic data. Notably, regularized regression methods like LASSO and its derivatives represent a significant stride towards addressing these challenges. However, their effectiveness is contingent upon the integration of gene relational structures and overcoming inherent mathematical complexities.
This study introduces an innovative algorithm, termed GFLASSO, which leverages sub-gradient methods and unfolds in two distinct phases: initially, a preprocessing step where a preliminary subset of genes is selected via a univariate filter method that utilizes Pearson’s correlation coefficient; followed by the application of an improved Generalized Fused Lasso technique, which also employs Pearson’s correlation coefficient to assess inter-gene relationships. The primary objective of this research is to showcase the effectiveness of our gene selection methodology in enhancing the classification of high-dimensional data, particularly within the context of cancer research. Overall, the main contributions of this study are summarized as follows:
- Introduced an improved approach for dimension reduction and important gene selection in cancer research using DNA microarray technology.
- Integrated gene selection with classifier training into a single process, enhancing the efficiency of identifying cancerous tumors.
- Formulated gene selection as a logistic regression problem with a generalized Fused LASSO (GFLASSO) regularizer, incorporating dual penalties to balance gene relevance and redundancy.
- Utilized a sub-gradient algorithm for optimization, demonstrating the algorithm’s objective function is convex, Lipschitzian, and possesses a global minimum, meeting necessary convergence conditions.
- Showed that the GFLASSO-LR method significantly improves cancer classification from high-dimensional microarray data, yielding compact and highly performant gene subsets.
The remainder of this paper is structured as follows: Section 2 provides a detailed presentation of the proposed method, beginning with preliminary concepts before delving into the sub-gradient method and its application for estimating . Subsequently, Section 3 evaluates the performance of our proposed approach using four well-known gene expression classification datasets, detailing both the parameter settings and the numerical results obtained. Finally, Section 4 concludes the paper and outlines directions for future work.
2. Methods
2.1. Preliminaries
In Microarray data, each value of is the measure of the expression level of the gene in the sample, this array contains real values, and there are no missing values. Where is the number of genes and is the number of samples.
DNA microarray analysis for cancer classification is formulated as a supervised classification problem. The limited number of samples that can be collected due to the high cost of preparing DNA microarrays presents a challenge for statistical learning techniques. Linear models, specifically logistic regression, are commonly used for discriminant analysis in supervised learning. In binary logistic regression, it is usual to consider the values of the variable to be explained as belonging to the set ; this is a binary classification.
Let denote the probability that the class of is 1, for any sample , , of the dataset matrix.
It can then be deduced that . The logistic regression model is written [52] as follows:
where denotes the vector of regression coefficients including a constant . This vector will be estimated from the training data. Without loss of generality, it was assumed that the genes are centered:
and
For clarity and simplicity, let us adopt the following notation. Let denote
- , or simply for any vector of , it was noted that
- is the usual scalar product.
Moving on, for ,
The probability of observing the response for a sample is written in a more compact way:
Let f be the “sigmoid” function used in the logistic regression defined by for any real z; the latter has a value in . It can be noticed then that .
The classification rule for a new example x via logistic regression is therefore defined by
The methods for estimating the coefficients include the statistical method called “maximum likelihood estimation”, which allows us to determine the values of the parameter of the model, which renders the following maximum value
This is equivalent to finding in , which maximizes the log-likelihood function.
Maximizing is the same as minimizing . Let us then note for all of . After some elementary calculations, we arrive at
In cancer classification, logistic regression is used to model the relationship between a set of independent variables (genes) and a binary dependent variable (tumor or normal class) by minimizing the function in Equation (1).
However, logistic regression may be limited in classifying high-dimensional data as the minimization problem may not have a unique solution, as shown by Albert et al. [53]. They found that when the dataset is completely or nearly completely separated, the estimators of (1) become infinite and non-unique, while in the presence of overlap in the data, the minimum of (1) exists and is finite.
In microarray data, the high number of genes can lead to overfitting and multicollinearity in the estimators () since only a few genes are actually associated with the response variable. To enhance classification accuracy, it is important to develop gene selection methods that eliminate irrelevant genes. One such method is penalized logistic regression (PLR), which adds a positive penalty to the likelihood function g, causing some coefficients to approach zero, a technique known as regularization. The penalized log-likelihood can be expressed as shown in Equation (2):
where represents the penalty term and is the regularization parameter that determines the extent of the penalty. For , this can lead to the solution of (1) if it exists. On the other hand, for high values of , the regularization term has a greater impact on the coefficient estimates. The selection of the tuning parameter is critical in fitting the model, and if it is chosen via cross-validation, the classifier can achieve satisfactory classification accuracy. These penalized methods are commonly used in gene selection and classification of high-dimensional data, as reported in [54].
In the following, we denote as the vector of size that represents a solution to the minimization problem (2), i.e.,
Several penalty terms have been explained and applied in the literature, namely, Ridge () [55], LASSO () [56], Elastic net [39], Adaptive LASSO [40], Fused LASSO and Generalized Fused LASSO [47], Relaxed LASSO [57], Group LASSO [58], Random LASSO [59], and many others. These penalties, along with logistic regression, can be used successfully to obtain high classification rates. We are specifically interested in the Generalized Fused LASSO penalty. This focus sets the stage for introducing the sub-gradient method.
2.2. Sub-Gradient Method
The sub-gradient method is a technique for minimizing non-differentiable convex functions, similar to the ordinary gradient method for differentiable functions. However, it has some key differences, such as its ability to handle non-differentiable functions directly and the lack of guarantee for decreasing the function value.
These methods were introduced in the 1960s by N.Z. Shor [60] for the unconstrained minimization of convex functions in the field of network transport. The first convergence results are attributed to Polyak [61] and Nemirovski [62], and they have been further developed by various researchers since then.
Consider a function , where is a convex set, and . We define a subgradient of f at as an element satisfying the following inequality:
The set of all subgradients is termed the subdifferential of f at , denoted .
For a convex function defined on a convex set , several properties of its subdifferential have been well-established [63]:
- Let , then is a non-empty, convex, bounded set.
- Assuming differentiability of f at , we have and
- Suppose is a convex set in , and let be convex functions with for . If , then the subdifferential sum rule is expressed as follows:
Let us now present some important examples of sub-differential calculation:
Example 1.
The norm function ():
Let
The sub-differential of f is the Cartesian product of the following intervals:
Example 2.
Let n be an integer greater than or equal to and with .
Let be the function defined on by
The subdifferential of is the Cartesian product of the following intervals:
With:
for all
2.2.1. Subgradient Algorithm
The classical subgradient method is designed to solve convex optimization problems without type constraints:
where represents a convex function. Let , where , be a sequence of positive numbers. The subgradient algorithm generated by is defined as follows: given an initial point , the iterative procedure is as follows:
We presuppose that problem (4) possesses an optimal solution and that f is convex and Lipschitz on .
Several methodologies have been proposed in the literature, as documented in [61,63,64,65,66,67], for selecting the sequence of steps to ensure convergence of the subgradient method. Note that
There are three main results that have been found:
- Suppose for all . Then there exists a positive constant such that
- Suppose thatThen, we have convergence as , and
- Suppose the generated sequence in (5) satisfies
2.2.2. Generalized Fused LASSO
Proposed by Tibshirani and Al [42], the Fused LASSO is an extension of LASSO aiming to improve its properties when the features are ordered. It adds another penalty to to encourage zero differences between successive coefficients. The idea of the Fused LASSO has been generalized in the context of linear regression models (and generalized linear models) [46,47]. This is accomplished by constructing a graph with vertices (representing genes in DNA microarray data), each corresponding to a coefficient, and a set of edges E. In the generalized Fused LASSO, differences for are penalized, with associated weights representing the degree of association between genes. The objective function is
The penalties in the Fused LASSO regularizer (8) are typically determined from the initial data. Here, represents the penalty applied to the difference between genes and . As increases, the penalty on also increases, making and more likely to be equal. The first penalty ensures many are zero, promoting sparsity. Therefore, tends to have sparse and equal coefficients for connected genes in the graph. The choice of and is determined using appropriate cross-validation methods [68].
Due to the penalty (8), some coefficients of are reduced to zero, indicating unused genes in the model. The parameters and control the degree of penalization, affecting the number of non-zero estimated coefficients. As increases, the number of null components in increases. The set of selected genes is defined as
where is the penalized logistic regression coefficient (8) associated with the gene for the penalty parameters and .
We formulate the problem of gene selection as a logistic regression problem (maximum log-likelihood) with a generalized Fused LASSO regularizer, a penalty that is rarely used in this type of problem. The selection is performed by minimizing (8).
To construct the graph and assign weights to each edge , we consider as the set of vertices (genes) associated with our DNA microarray data. The interaction between genes is measured using the Pearson correlation coefficient. An edge is formed between vertices k and l if and only if the absolute correlation between genes and is greater than or equal to a threshold . The weight of edge is defined as the absolute value of the correlation between and : . This way, the graph and the weights are established. The correlation coefficient between and is defined as
where is the covariance between and , is the standard deviation of , and is the standard deviation of .
The use of Fused LASSO is motivated by several factors [69]. One of the main advantages is its ability to handle high-dimensional data where the number of genes exceeds the number of samples. Traditional LASSO may struggle in such cases, while Elastic Net, though potentially outperforming LASSO, is relatively less efficient than Fused LASSO, especially when there are relationships among genes. Additionally, Fused LASSO explicitly regularizes the differences between neighboring coefficients using an norm regularizer, exploiting relationships between genes. This results in sparse coefficients, with non-zero components equal for some connected genes in the graph, balancing individual gene relevance and redundancy.
2.2.3. Structure of the Proposed Approach
The proposed approach consists of a two-step sequential process (as depicted in Figure 1). Firstly, a preprocessing phase eliminates irrelevant genes, selecting the top genes ranked by relevance determined by their correlation with the target class. Then, an embedded method is applied to the selected genes, involving the construction of a logistic regression classifier. The model is trained to find by solving the minimization problem outlined in Equation (8) using the subgradient algorithm.
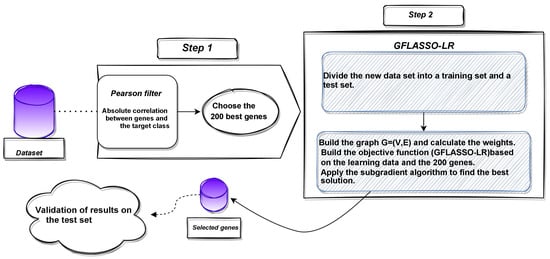
Figure 1.
Flowchart of the proposed approach () for gene selection in microarray data.
With respect to the estimation of in (8), since the function in question is not differentiable due to the presence of the absolute value, we use the subgradient algorithm to solve the minimization problem (8). This algorithm has not been previously used to solve the logistic regression problem with the Generalized Fused LASSO penalty. In the following, we demonstrate the convergence of this algorithm for (8).
2.3. Sub-Gradient for Estimating
It is known that the sub-gradient algorithm can converge to the optimal solution of a convex minimization problem when an appropriate step sequence is chosen, as long as the function in question meets the following conditions:
- It is convex.
- It admits a global minimum.
- It is Lipschitz.
To apply this algorithm to our problem (8), we must first ensure that the function meets these three conditions.
2.3.1. Characteristics and Convexity Analysis of the GFLASSO Penalty Function
It is important to note that
- 1.
- The convexity of :First, there isLet us show that g is convex on :
- The function is convex; it is a linear function on .
- The function is convex for all i in , so is convex for all i in . (It is the composition of an increasing function convex on and a convex function on ).
The function g is therefore convex on , being the sum of convex functions. On the other hand, the function is convex as the sum of convex functions.Next, we show that the function is convex.Indeed, let with . The function is convex. This is because , defined in Example (2), is composed of an affine function and another convex one, with . Then the function is convex as it is a sum of convex functions.Finally, we can deduce that the function is convex as it is a sum of convex functions. - 2.
- The existence of a global minimum of :We recall that a real-valued function is coercive if .We haveandwith for all i in .Additionally, we have. SoHence,Let us examine the expression for . Given that the function g is positive on and in (10) is strictly positive, it follows thatBased on the latest inequality, we can deduce that is a coercive function. Additionally, is continuous, so it attains a a global minimum at least once (see appendix in reference [70]).
- 3.
- The function is ℓ-Lipschitz on :We only have one condition left to establish to show that the sub-gradient algorithm converges to a global minimum of ; it is to prove that is ℓ-Lipschitzian on , i.e., find a positive ℓ such thatNote in passing that the Lipschitz constant ℓ depends on the choice of the norm on . Since all norms are equivalent on , whether a function is Lipschitz or not does not depend on the chosen norm.Let us start by showing that the function g is Lipschitz. We first haveThe function g is of class on . Find the partial derivatives of g:Let . We haveTherefore,Let . Then we haveAs we are working on the finite dimensional normed vector space , there then exists some positive such thatWe can notice that the real does not depend on ; more precisely it only depends on the training set. So we getSo g is a -Lipschitz function on by the mean value inequality.In the following, we will prove that the function is Lipschitz.Let . We haveSimilarly, since the weights ,Thereby,andBy norm equivalence, we can deduce that there are some positive and such thatFinally, it suffices to take to deduce that is ℓ-lipschitzian on .
2.3.2. Sub-Gradient Algorithm
After confirming the convergence of our sub-gradient algorithm for estimating , let us now detail the method for the objective function . The sub-differential sum rule states that . In this equation, is a function defined in the Example (2), and g is differentiable on ; so . The subdifferentials of the norm , and are provided in the Examples 1 and 2, respectively, which leads to the final expression
Thus, for a well-chosen sequence , the search algorithm for for problem (8) is as follows:
The use of the generalized Fused LASSO penalty in our classification model enables an embedded gene selection process. Genes associated with null coefficients in have no impact on the classification of new examples, as the classification rule in logistic regression is determined by the value of . If this value is less than , the example is classified as 0; otherwise, it is classified as 1. This approach fosters a more efficient and effective classification model by eliminating irrelevant genes.
3. Experiments and Results
This section presents the performance of our proposed approach on four well-known gene expression classification datasets (see Table 2). The parameter settings and numerical results will be described in the following subsections. The implementation of our proposed approach was conducted using MATLAB R2018a, and the datasets were divided into training and test sets to assess the performance of gene subset selection.

Table 2.
Description of datasets (DNA microarray) used in GFLASSO-LR.
3.1. Datasets
To evaluate our approach, we selected DNA microarray datasets related to cancer recognition, which are publicly available. These datasets have been utilized in multiple supervised classification studies (as shown in Table 2). They exhibit a variety of characteristics: some have a low number of samples, while others have a higher number. Additionally, all datasets have binary classes. Since our proposed method is designed for large-scale microarrays, all datasets consist of a high number of genes, ranging from 2000 to 12,600.
3.2. Settings
In our approach, we begin with a pre-processing step, which involves selecting the top 200 highest-ranked genes using the absolute correlation coefficient. Subsequently, we randomly split our dataset into a training set and a test set. Using the training set, we then construct our objective function (8). To minimize this function, we employ the sub-gradient algorithm (Algorithm 1). It is important to note that the performance of this algorithm is highly dependent on the choice of step size . A well-chosen can significantly impact both the convergence rate and the quality of the estimate obtained.
| Algorithm 1: Subgradient algorithm to minimize . |
|
3.2.1. Choice of
The choice of an appropriate step for the sub-gradient algorithm is an essential step in our study. To begin, we set , , and . Then, the “Prostate_Tumor” dataset is utilized to conduct a parametric study.
We start by selecting the 200 best-ranked genes and split the resulting dataset into two disjoint sets: 80% for training and 20% for testing. Our objective function is constructed based on the training set. The goal of this subsection is to choose a step size that accelerates the convergence of our algorithm to the global minimum. At this stage, we are not concerned with classifier testing, as our focus is solely on observing the behavior of the sub-gradient algorithm in finding the minimum of .
We initially compared the classic step to the step proposed by Alber et al. in [74], , where is a randomly chosen vector of (as outlined in Algorithm 1). We set a maximum number of iterations at 10,000. It is evident that these steps ensure the convergence of our algorithm from the sub-gradient to the global minimum.
From the results depicted in Figure 2, it is evident that using accelerates the convergence of the sub-gradient algorithm. This acceleration is attributed to the inclusion of the term in .
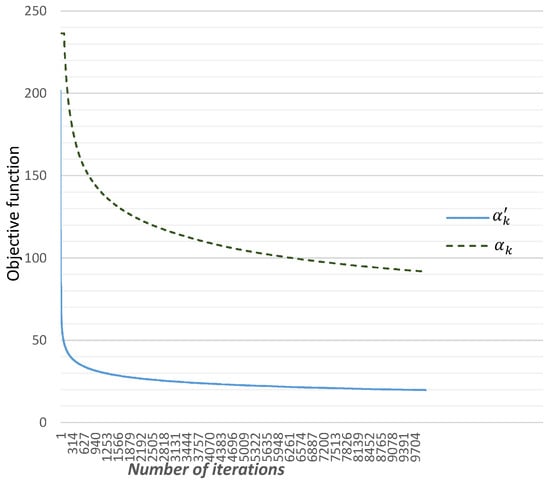
Figure 2.
Comparison between the steps and to minimize the function .
To determine the optimal step size, we drew inspiration from the work of Alber et al. in [74] and utilized steps of the form , where represents a randomly chosen vector of and denotes a sequence of positive terms satisfying
The final steps ensure the convergence of the subgradient algorithm. In the following, we compare different forms of the step , specifically those of the form with . Figure 3 illustrates how the objective function changes with the number of iterations for different values of . To enhance the interpretability of the data, we have plotted it on a logarithmic scale. Additionally, Table 3 presents the optimal values of the objective function obtained using the subgradient algorithm with different steps for various values of .
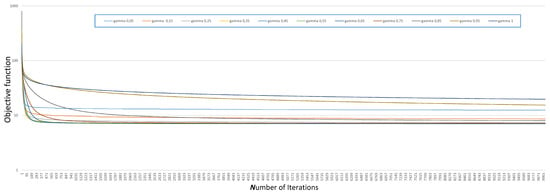
Figure 3.
Comparison between steps with different for the minimization of .

Table 3.
Comparison between steps with different for the minimization of .
3.2.2. Choice of and
After determining the optimal step size , we proceed to select the best values for the parameters and . We compare different combinations of these parameters by analyzing the gene set selected by minimizing , aiming to find values of and that achieve the highest classification rate on the test set while minimizing the number of genes used in the classification.
The experiments were conducted using the “Prostate_tumor” dataset, and the accuracy rates were determined using a 5-fold cross-validation method. Initially setting , and by varying , the results are shown in Table 4 for different values of (with ).

Table 4.
Comparison between the for the “Prostate_Tumor” dataset (aggregated values across the 5-fold Cross-validation with ).
Typically, we can observe that when , the results are better. Specifically, this value of results in high accuracy on test data (), while only utilizing 25 genes. However, as we increase , the number of selected genes decreases, which is a result of the penalty. After determining that is optimal, we proceed to determine the best value for . Table 5 shows the results obtained for different values of , with fixed at . Specifically, it is evident that when , the method employed corresponds to the classic LASSO approach. However, setting yields improved performance, achieving a high accuracy of 97.1% on the test data while utilizing only 22 genes. Consequently, based on these findings, the optimal values of and were selected for the final model.

Table 5.
Comparison between the for the “Prostate_Tumor” dataset (5 fold Cross-validation with ).
3.3. Results and Comparisons
Firstly, to limit the search space and accelerate the convergence speed of our proposed approach, we selected the initial subset of genes based on the Pearson correlation filter. Subsequently, the GFLASSO-LR algorithm was applied to determine the optimal gene subset. The quality of this subset was assessed based on the accuracy of the test set and the number of genes selected. Due to the non-deterministic nature of our proposed method, each dataset was randomly divided into a training set comprising 70% of the original dataset and a test set comprising 30%. This process was repeated in 50 independent runs for each dataset to ensure reliable results.
Table 6 summarizes the outcomes of our study across four microarray datasets: Colon, DLBCL, Prostate_Tumor, and Prostate. These results stem from experiments employing a range of gene selection techniques to assess their impact on classification accuracy, thereby validating and demonstrating the effectiveness of our proposed method. Specifically, the table compares performance metrics for two classifiers, KNN and SVM, both without selection and with the application of the Pearson filter. Additionally, it includes outcomes using logistic regression enhanced by LASSO and GFLASSO penalties, offering a comprehensive view of the method’s efficacy in gene selection for cancer classification.

Table 6.
The results obtained over 50 executions, without and with selection via the LASSO and GFLASSO penalties.
Our embedded methods (LASSO-LR and GFLASSO-LR) were implemented based on the following parameters:
- , which corresponds to a LASSO-LR type penalty.
- , which corresponds to a generalized Fused LASSO (GFLASSO-LR) type penalty.
The first column of the table displays the datasets used. The second column shows the performance measures, including accuracy (in percent) and the number of selected genes. The third and fourth columns show the results obtained using the 1NN and SVM classifiers, respectively, without gene selection. The fifth and sixth columns present the results obtained using the SVM and 1NN classifiers after having selected 200 genes via the Pearson correlation filter. The seventh and eighth columns present the results of experiments using our LASSO-LR and GFLASSO-LR approaches, respectively.
Figure 4, Figure 5 and Figure 6 show the average classification accuracy obtained from 50 experiments for different methods. According to these figures, the GFLASSO-LR approach shows good performance on the majority of datasets. More precisely, the highest average accuracy rates are obtained for the Colon, Prostate Tumor, and Prostate datasets.
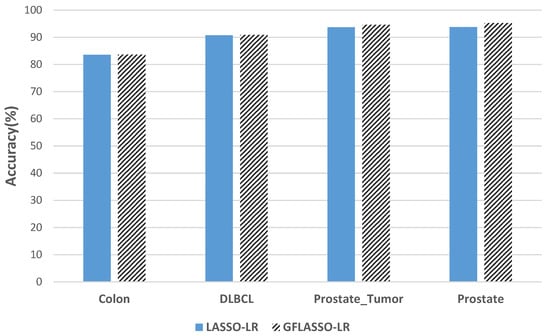
Figure 4.
Comparison of classification accuracy (LASSO-LR and GFLASSO-LR).
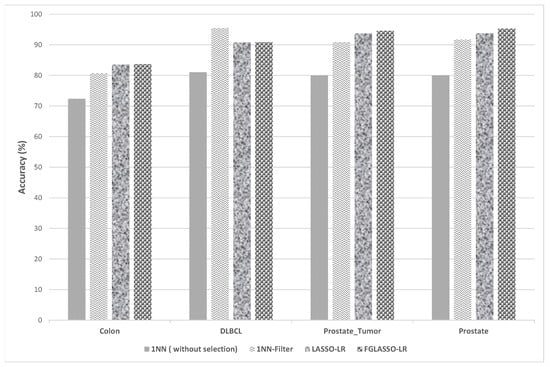
Figure 5.
Comparison of classification accuracy between 1NN, LASSO-LR and GFLASSO-LR.
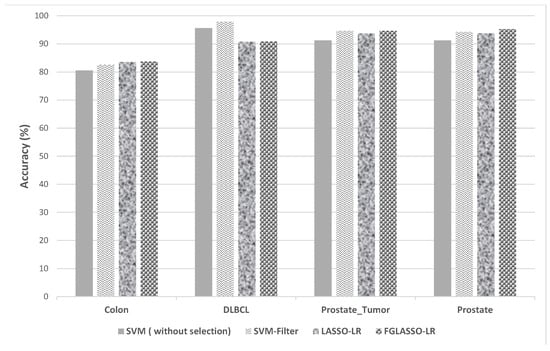
Figure 6.
Comparison of classification accuracy between SVM, LASSO-LR, and GFLASSO-LR.
From Table 6 and Figure 4, it is noteworthy that the GFLASSO-LR method outperforms the traditional LASSO-LR method in terms of accuracy for all datasets. This improvement is particularly significant for the datasets Prostate_Tumor and Prostate, which consist of a small number of genes ranging from 19 to 21. Additionally, both GFLASSO-LR and LASSO-LR methods achieve high classification accuracy (greater than or equal to 83.57%) using a small number of genes compared to the original number.
The effectiveness of our selection methods was compared to classifiers (1NN and SVM) both with and without selection, employing the Pearson filter. Figure 5 and Table 6 demonstrate that our GFLASSO-LR and LASSO-LR approaches outperform the 1NN classifier in both scenarios. Specifically, our methods succeed in enhancing accuracy for the majority of datasets. For instance, in the Colon dataset, an accuracy greater than or equal to 83.56% was achieved using less than 20 genes, indicating a significant improvement in classification accuracy (ranging from 3 to 11% difference) with fewer genes. The most notable improvement was observed for the Prostate dataset, where an accuracy of 94.6% was attained (with a 4–14% difference) using less than 21 genes.
Similarly, Figure 6 and Table 6 demonstrate the effectiveness of our gene selection approaches against the SVM classifier. Indeed, our methods show significant improvements in accuracy for the colon and prostate datasets, while using just fewer than 22 genes.
Afterward, we conducted a Kruskal–Wallis test to analyze the significance of the differences in accuracy obtained by our proposed GFLASSO-LR classifier compared to SVM and 1NN classifiers (without selection). The test revealed a statistically significant difference in performance among the classifiers (H-statistic , p-value ), emphasizing the impact of classifier choice on classification accuracy.
The boxplot (Figure 7) illustrates the performance distribution of GFLASSO-LR compared to the other classifiers across various datasets. GFLASSO-LR consistently achieves higher classification accuracies, particularly noticeable in the Colon and Prostate_Tumor datasets. This highlights the effectiveness of incorporating GFLASSO regularization techniques in logistic regression, enhancing classification performance in specific contexts. These findings emphasize the importance of selecting the appropriate classifier to achieve optimal classification outcomes for individual datasets.
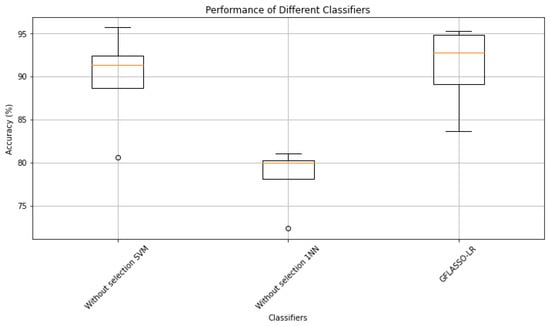
Figure 7.
Results of the Kruskal–Wallis Test: GFLASSO-LR vs. SVM and 1NN (Without Selection).
Overall, the results presented in the table show that the GFLASSO-LR algorithm can improve classification accuracy and decrease the number of selected genes. The proposed methods have important applications in the field of genomics and can advance the understanding of gene function and disease diagnosis. Based on the experiments we conducted, we can conclude that our gene selection approaches are well founded. Our methods achieved high classification accuracy in the datasets used in the study.
Comparison with Other Approaches
In this subsection, we compare our GFLASSO-LR method with algorithms referenced in the literature: [31,32,40,56,75,76]. All of these papers propose integrated methods based on different types of penalties and apply them to the gene selection problem. To make the comparison meaningful, experiments are performed under the same conditions for each algorithm. Our approach is run 50 times on each dataset, with the dataset randomly divided into two parts (70% for training and 30% for testing) in each run. The average accuracy on the test set and the average number of genes used in classification are chosen. It is noted that the authors of [31] performed 100 runs.
Table 7 summarizes the classification accuracy and the number of selected genes (from the original papers) for each approach. A dash (-) indicates that the result is not reported in the corresponding work. The results obtained by our approach are competitive with previous works.

Table 7.
Comparison between our method (GFLASSO-LR) and state-of-the-art methods.
For the Colon dataset, we achieve an accuracy rate of 83.67% using only 19 genes. Our method ranks second, outperforming the other five approaches, with the best performance achieved by the BLASSO approach (93%). For the DLBLC dataset, we obtain the third-best performance (90.87%) after the “New ALASSO” and “CBPLR” approaches, with a difference of less than 1%. For the “Prostate” dataset, we achieved the best performance (accuracy of 95.27%) followed by the “CBPLR” method with an accuracy of 93.6%. The number of genes selected by GFLASSO-LR is relatively similar to that of other methods, except for the Prostate dataset, which uses slightly more genes.
The results of this comparative analysis with previous embedded gene selection methods in cancer classification indicate that our improved generalized fused LASSO penalization approach is effective in the gene selection problem.
3.4. Time and Memory Complexity
3.4.1. Pre-Processing Step (Selecting the Top 200 Highest-Ranked Genes)
- Time Complexity: Computing correlation coefficients for each gene across all samples and selecting the top 200 genes: (as provided in the information).
- Memory Complexity: Storing microarray data and correlation coefficients: .
3.4.2. Splitting-GFLASSO-LR Algorithm
- Time Complexity: for randomly splitting the dataset into training and test sets.
- Memory Complexity: for storing the training and test sets.
3.4.3. Building the Objective Function Based on the Training Data and the 200 Genes
Regarding the time complexity, in the worst case, where each gene is correlated with every other gene, the number of edges in the graph would be . Additionally, computing the absolute correlation values between each pair of genes is estimated using .
3.4.4. Sub-Gradient Algorithm
Time Complexity: The dominant term in the time complexity is represented as follows.
Typically, the components and computational complexity of an optimization process can be summarized as follows:
- Constructing the graph and calculating weights: negligible compared to the overall complexity.
- Combining the subdifferentials: Once the subdifferentials of each component function are computed, they are combined according to the given expression. This involves a combination of nearly subdifferentials, resulting in a time complexity of .
- Iterating over the sub-gradient algorithm: iterations.
- Each iteration involves updating the coefficients using a sub-gradient: operations.
Memory Complexity: Storing the graph structure and weights: in the worst case. Storing intermediate results and coefficients: (since only one set of coefficients needs to be stored).
Overall, the analysis outlines a computationally intensive process with significant emphasis on handling gene interaction data efficiently. While time complexity primarily concerns the combinatorial interactions among genes and the iterative optimization process, memory complexity focuses on efficiently storing gene data, correlations, and algorithmic intermediates. The optimization aims to identify a subset of genes critical for further analysis, with considerations for computational and storage efficiencies.
3.5. Discussion
The discussion on the performance of the GFLASSO-LR approach compared to traditional and recent methods in gene selection for cancer classification underscores its practical utility and effectiveness. Our method’s superior or competitive performance across different datasets, particularly in achieving high classification accuracy with a relatively small number of genes, highlights its potential for advancing personalized medicine and genomic research. The ability to identify the most relevant genes from massive datasets with precision is crucial for understanding complex diseases like cancer. Our GFLASSO-LR approach not only simplifies the gene selection process but also ensures that the selected genes are highly indicative of the condition being studied, thus facilitating more accurate diagnoses and the development of targeted therapies.
Moreover, the consistency of our method’s performance across various datasets demonstrates its robustness and adaptability to different types of cancer, which is a significant advantage in the rapidly evolving field of genomics. The use of logistic regression with the GFLASSO penalty enhances the model’s ability to deal with the high dimensionality and multicollinearity inherent in microarray data, thereby overcoming some of the common challenges faced in genomic data analysis. However, it is worth noting that while our approach shows promise, further research is necessary to explore its full potential and limitations. Future studies could focus on refining the algorithm to improve efficiency and accuracy, as well as testing it on a wider range of datasets. Additionally, integrating our method with other data types, such as clinical and phenotypic information, could provide a more comprehensive understanding of the gene–disease relationships and further enhance its application in personalized medicine.
4. Conclusions
High-dimensional classification problems in microarray dataset analysis are a crucial area of research in cancer classification. In this paper, we propose and apply an improved method, GFLASSO-LR, for simultaneous gene coefficient estimation and selection to improve classification performance. We also demonstrate the convergence of the sub-gradient algorithm to solve the associated non-differential convex optimization problem.
The proposed method was evaluated based on the number of selected genes and classification accuracy on four sets of high-dimensional cancer classification data. The results consistently showed that GFLASSO-LR can significantly reduce the number of relevant genes and has superior accuracy compared to the classical LASSO method. Overall, the results demonstrate that GFLASSO is a promising method for accurately analyzing high-dimensional microarray data in cancer classification. The method can be applied to other types of high-dimensional classification data related to the medical domain. Future research could extend the present work to cover high-dimensional multiclass cancer data and focus on very high-dimensional microarray data for cancer classification.
Author Contributions
Conceptualization, A.B.-J.; Methodology, A.B.-J.; Software, A.B.-J.; Validation, A.B.-J. and S.M.D.; Formal analysis, S.E.B., A.M., Y.H., W.M. and H.A.-A.; Investigation, S.M.D., S.E.B., A.M., Y.H. and S.A.; Resources, S.M.D. and Y.H.; Writing—original draft, A.B.-J.; Writing—review & editing, S.M.D., S.E.B., A.M., Y.H., S.A., W.M. and H.A.-A.; Visualization, S.E.B., A.M. and S.A.; Supervision, S.M.D., S.E.B., A.M. and S.A.; Project administration, Y.H., W.M. and H.A.-A.; Funding acquisition, Y.H., W.M. and H.A.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Higher Education, Scientific Research and Innovation, the Digital Development Agency (DDA), and the National Center for Scientific and Technical Research (CNRST) under Project ALKHAWARIZMI/2020/19.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to data sensitivity and privacy concerns.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, M.; Ke, L.; Wang, L.; Deng, S.; Yu, X. A novel hybrid gene selection for tumor identification by combining multifilter integration and a recursive flower pollination search algorithm. Knowl.-Based Syst. 2023, 262, 110250. [Google Scholar] [CrossRef]
- Feng, S.; Jiang, X.; Huang, Z.; Li, F.; Wang, R.; Yuan, X.; Sun, Z.; Tan, H.; Zhong, L.; Li, S.; et al. DNA methylation remodeled amino acids biosynthesis regulates flower senescence in carnation (Dianthus caryophyllus). New Phytol. 2024, 241, 1605–1620. [Google Scholar] [CrossRef] [PubMed]
- Mehrabi, N.; Haeri Boroujeni, S.P.; Pashaei, E. An efficient high-dimensional gene selection approach based on the Binary Horse Herd Optimization Algorithm for biologicaldata classification. Iran J. Comput. Sci. 2024, 1–31. [Google Scholar] [CrossRef]
- Syu, G.D.; Dunn, J.; Zhu, H. Developments and applications of functional protein microarrays. Mol. Cell. Proteom. 2020, 19, 916–927. [Google Scholar] [CrossRef] [PubMed]
- Caraffi, S.G.; van der Laan, L.; Rooney, K.; Trajkova, S.; Zuntini, R.; Relator, R.; Haghshenas, S.; Levy, M.A.; Baldo, C.; Mandrile, G.; et al. Identification of the DNA methylation signature of Mowat-Wilson syndrome. Eur. J. Hum. Genet. 2024, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.; Jayaswal, N.; Kumar, S.; Sharma, P.K.; Behl, T.; Khalid, A.; Mohan, S.; Najmi, A.; Zoghebi, K.; Alhazmi, H.A. Unveiling the potential of proteomic and genetic signatures for precision therapeutics in lung cancer management. Cell. Signal. 2024, 113, 110932. [Google Scholar] [CrossRef]
- Ghavidel, A.; Pazos, P. Machine learning (ML) techniques to predict breast cancer in imbalanced datasets: A systematic review. J. Cancer Surviv. 2023, 1–25. [Google Scholar] [CrossRef]
- Bir-Jmel, A.; Douiri, S.M.; Elbernoussi, S. Gene selection via a new hybrid ant colony optimization algorithm for cancer classification in high-dimensional data. Comput. Math. Methods Med. 2019, 2019, 7828590. [Google Scholar] [CrossRef] [PubMed]
- Bir-Jmel, A.; Douiri, S.M.; Elbernoussi, S. Gene selection via BPSO and Backward generation for cancer classification. RAIRO-Oper. Res. 2019, 53, 269–288. [Google Scholar] [CrossRef]
- Sethi, B.K.; Singh, D.; Rout, S.K.; Panda, S.K. Long Short-Term Memory-Deep Belief Network based Gene Expression Data Analysis for Prostate Cancer Detection and Classification. IEEE Access 2023, 12, 1508–1524. [Google Scholar] [CrossRef]
- Maafiri, A.; Bir-Jmel, A.; Elharrouss, O.; Khelifi, F.; Chougdali, K. LWKPCA: A New Robust Method for Face Recognition Under Adverse Conditions. IEEE Access 2022, 10, 64819–64831. [Google Scholar] [CrossRef]
- Bir-Jmel, A.; Douiri, S.M.; Elbernoussi, S. Minimum redundancy maximum relevance and VNS based gene selection for cancer classification in high-dimensional data. Int. J. Comput. Sci. Eng. 2024, 27, 78–89. [Google Scholar]
- Maafiri, A.; Chougdali, K. Robust face recognition based on a new Kernel-PCA using RRQR factorization. Intell. Data Anal. 2021, 25, 1233–1245. [Google Scholar] [CrossRef]
- Amaldi, E.; Kann, V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theor. Comput. Sci. 1998, 209, 237–260. [Google Scholar] [CrossRef]
- Blum, A.L.; Rivest, R.L. Training a 3-node neural network is NP-complete. Neural Netw. 1992, 5, 117–127. [Google Scholar] [CrossRef]
- Yaqoob, A.; Verma, N.K.; Aziz, R.M. Optimizing gene selection and cancer classification with hybrid sine cosine and cuckoo search algorithm. J. Med. Syst. 2024, 48, 10. [Google Scholar] [CrossRef] [PubMed]
- Bechar, A.; Elmir, Y.; Medjoudj, R.; Himeur, Y.; Amira, A. Harnessing transformers: A leap forward in lung cancer image detection. In Proceedings of the 2023 6th International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 8–9 November 2023; pp. 218–223. [Google Scholar]
- Hamza, A.; Lekouaghet, B.; Himeur, Y. Hybrid whale-mud-ring optimization for precise color skin cancer image segmentation. In Proceedings of the 2023 6th International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 8–9 November 2023; pp. 87–92. [Google Scholar]
- Habchi, Y.; Himeur, Y.; Kheddar, H.; Boukabou, A.; Atalla, S.; Chouchane, A.; Ouamane, A.; Mansoor, W. Ai in thyroid cancer diagnosis: Techniques, trends, and future directions. Systems 2023, 11, 519. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Gu, Q.; Li, Z.; Han, J. Generalized fisher score for feature selection. arXiv 2012, arXiv:1202.3725. [Google Scholar]
- Jafari, P.; Azuaje, F. An assessment of recently published gene expression data analyses: Reporting experimental design and statistical factors. BMC Med. Inform. Decis. Mak. 2006, 6, 27. [Google Scholar] [CrossRef]
- Mishra, D.; Sahu, B. Feature selection for cancer classification: A signal-to-noise ratio approach. Int. J. Sci. Eng. Res. 2011, 2, 1–7. [Google Scholar]
- Wang, Z. Neuro-Fuzzy Modeling for Microarray Cancer Gene Expression Data; First year transfer report; University of Oxford: Oxford, UK, 2005. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Kishore, A.; Venkataramana, L.; Prasad, D.V.V.; Mohan, A.; Jha, B. Enhancing the prediction of IDC breast cancer staging from gene expression profiles using hybrid feature selection methods and deep learning architecture. Med. Biol. Eng. Comput. 2023, 61, 2895–2919. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Zhang, Z.; Sun, Z. Variable selection for partially linear varying coefficient quantile regression model. Int. J. Biomath. 2013, 6, 1350015. [Google Scholar] [CrossRef]
- Li, C.J.; Zhao, H.M.; Dong, X.G. Bayesian empirical likelihood and variable selection for censored linear model with applications to acute myelogenous leukemia data. Int. J. Biomath. 2019, 12, 1950050. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.P. Biomarker discovery from high-throughput data by connected network-constrained support vector machine. Expert Syst. Appl. 2023, 226, 120179. [Google Scholar] [CrossRef]
- Alharthi, A.M.; Lee, M.H.; Algamal, Z.Y. Gene selection and classification of microarray gene expression data based on a new adaptive L1-norm elastic net penalty. Inform. Med. Unlocked 2021, 24, 100622. [Google Scholar] [CrossRef]
- Alharthi, A.M.; Lee, M.H.; Algamal, Z.Y. Weighted L1-norm logistic regression for gene selection of microarray gene expression classification. Int. J. Adv. Sci. Eng. Inf. Technol. 2020, 4, 2088–5334. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Lee, M.H. Penalized logistic regression with the adaptive LASSO for gene selection in high-dimensional cancer classification. Expert Syst. Appl. 2015, 42, 9326–9332. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Lee, M.H. A two-stage sparse logistic regression for optimal gene selection in high-dimensional microarray data classification. Adv. Data Anal. Classif. 2019, 13, 753–771. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.P. A connected network-regularized logistic regression model for feature selection. Appl. Intell. 2022, 52, 11672–11702. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Liang, Y.; Zhang, H.; Chai, H.; Zhang, B.; Peng, C. Robust Sparse Logistic Regression with the Lq(0 < q < 1) Regularization for Feature Selection Using Gene Expression Data. IEEE Access 2018, 6, 68586–68595. [Google Scholar]
- Ijaz, M.; Asghar, Z.; Gul, A. Ensemble of penalized logistic models for classification of high-dimensional data. Commun.-Stat.-Simul. Comput. 2019, 50, 2072–2088. [Google Scholar] [CrossRef]
- Kastrin, A.; Peterlin, B. Rasch-based high-dimensionality data reduction and class prediction with applications to microarray gene expression data. Expert Syst. Appl. 2010, 37, 5178–5185. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Fan, M.; Ge, Q.; Qiao, B.; Zuo, X.; Jiang, B. Regression with Adaptive Lasso and Correlation based Penalty. Appl. Math. Model. 2021, 105, 179–196. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Bach, F.; Jenatton, R.; Mairal, J.; Obozinski, G. Structured sparsity through convex optimization. Stat. Sci. 2012, 27, 450–468. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Jang, W.; Lim, J.; Lazar, N.A.; Loh, J.M.; Yu, D. Some properties of generalized fused lasso and its applications to high dimensional data. J. Korean Stat. Soc. 2015, 44, 352–365. [Google Scholar] [CrossRef]
- Rinaldo, A. Properties and refinements of the fused lasso. Ann. Stat. 2009, 37, 2922–2952. [Google Scholar] [CrossRef]
- Qian, J.; Jia, J. On stepwise pattern recovery of the fused lasso. Comput. Stat. Data Anal. 2016, 94, 221–237. [Google Scholar] [CrossRef]
- Höfling, H.; Binder, H.; Schumacher, M. A coordinate-wise optimization algorithm for the Fused Lasso. arXiv 2010, arXiv:1011.6409. [Google Scholar]
- Viallon, V.; Lambert-Lacroix, S.; Hoefling, H.; Picard, F. On the robustness of the generalized fused lasso to prior specifications. Stat. Comput. 2016, 26, 285–301. [Google Scholar] [CrossRef]
- Hoefling, H. A path algorithm for the fused lasso signal approximator. J. Comput. Graph. Stat. 2010, 19, 984–1006. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, L.; Ye, J. An efficient algorithm for a class of fused lasso problems. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 323–332. [Google Scholar]
- Tibshirani, R.J.; Taylor, J. The solution path of the generalized lasso. Ann. Stat. 2011, 39, 1335–1371. [Google Scholar] [CrossRef]
- Johnson, N.A. A dynamic programming algorithm for the fused lasso and l 0-segmentation. J. Comput. Graph. Stat. 2013, 22, 246–260. [Google Scholar] [CrossRef]
- Fisher, R.A.; Yates, F. Statistical Tables for Biological, Agricultural and Medical Research; Oliver and Boyd: Edinburgh, UK, 1938. [Google Scholar]
- Albert, A.; Anderson, J.A. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 1984, 71, 1–10. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, C.; Luan, X.Z.; Leung, K.S.; Chan, T.M.; Xu, Z.B.; Zhang, H. Sparse logistic regression with a L1/2 penalty for gene selection in cancer classification. BMC Bioinform. 2013, 14, 198. [Google Scholar] [CrossRef] [PubMed]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Meinshausen, N. Relaxed lasso. Comput. Stat. Data Anal. 2007, 52, 374–393. [Google Scholar] [CrossRef]
- Meier, L.; Van De Geer, S.; Bühlmann, P. The group lasso for logistic regression. J. R. Stat. Soc. Ser. B Stat. Methodol. 2008, 70, 53–71. [Google Scholar] [CrossRef]
- Wang, S.; Nan, B.; Rosset, S.; Zhu, J. Random lasso. Ann. Appl. Stat. 2011, 5, 468. [Google Scholar] [CrossRef]
- Shor, N.Z. Application of the gradient-descent method to solution of the network transport problem. Cybern. Syst. Anal. 1967, 3, 43–45. [Google Scholar] [CrossRef]
- Polyak, B.T. Minimization of unsmooth functionals. USSR Comput. Math. Math. Phys. 1969, 9, 14–29. [Google Scholar] [CrossRef]
- Nemirovski, A.S.; Yudin, D.B. Cesari convergence of the gradient method of approximating saddle points of convex-concave functions. Dokl. Akad. Nauk. SSSR 1978, 239, 1056–1059. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Anstreicher, K.M.; Wolsey, L.A. Two “well-known” properties of subgradient optimization. Math. Program. 2009, 120, 213–220. [Google Scholar] [CrossRef]
- Polyak, B.T. A general method for solving extremal problems. Dokl. Akad. Nauk. SSSR 1967, . 174, 33–36. [Google Scholar]
- Shor, N.Z. Minimization Methods for Non-Differentiable Functions; Springer Science & Business Media: Berlin, Germany, 2012; Volume 3. [Google Scholar]
- Mordukhovich, B.S.; Nam, N.M. An Easy Path to Convex Analysis and Applications; Synthesis Lectures on Mathematics and Statistics; Springer: Cham, Switzerland, 2013; Volume 6. [Google Scholar]
- Huang, J.; Ma, S.; Zhang, C.H. The Iterated Lasso for High-Dimensional Logistic Regression; Technical report; The University of Iowa, Department of Statistics and Actuarial Sciences: Iowa City, IA, USA, 2008. [Google Scholar]
- Cui, L.; Bai, L.; Wang, Y.; Philip, S.Y.; Hancock, E.R. Fused lasso for feature selection using structural information. Pattern Recognit. 2021, 119, 108058. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Alon, U.; Barkai, N.; Notterman, D.A.; Gish, K.; Ybarra, S.; Mack, D.; Levine, A.J. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl. Acad. Sci. USA 1999, 96, 6745–6750. [Google Scholar] [CrossRef] [PubMed]
- Statnikov, A.; Aliferis, C.F.; Tsamardinos, I.; Hardin, D.; Levy, S. A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics 2005, 21, 631–643. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.; Febbo, P.G.; Ross, K.; Jackson, D.G.; Manola, J.; Ladd, C.; Tamayo, P.; Renshaw, A.A.; D’Amico, A.V.; Richie, J.P.; et al. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell 2002, 1, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Alber, Y.I.; Iusem, A.N.; Solodov, M.V. On the projected subgradient method for nonsmooth convex optimization in a Hilbert space. Math. Program. 1998, 81, 23–35. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Alhamzawi, R.; Ali, H.T.M. Gene selection for microarray gene expression classification using Bayesian Lasso quantile regression. Comput. Biol. Med. 2018, 97, 145–152. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).