1. Introduction
In symmetric cryptography, Boolean functions used in a cryptosystem are essential building blocks, and two of their most significant cryptographic properties are nonlinearity and an absolute indicator. Nonlinearity should be high to resist the best affine approximation attacks [
1] (in the case of stream ciphers) and linear cryptanalysis [
2] (in the case of block ciphers). On the other hand, it is important to achieve a low absolute indicator that, while providing resistance against differential and fault attacks (e.g., [
3,
4]) on stream ciphers, ensures good diffusion properties. For an even number of variables, optimal Boolean functions in terms of these two properties exist, and such functions are called bent [
5,
6]; however, since bent functions are not balanced, they cannot be directly used in a cryptosystem. Therefore, it is important to construct balanced Boolean functions with high nonlinearities and low absolute indicators.
Let us denote the maximum nonlinearity of a balanced
n-variable Boolean function by
. It has been conjectured [
7] for an even
n that
can be at most
, which is still unsettled. In [
7], this nonlinearity was achieved by making the all-zero block (of a length
) of a normal bent function balanced, which indeed provides the minimum number (
) of bit changes necessary to make a bent function balanced. However, it is well-known that highly nonlinear Boolean functions exist with better absolute indicator values than those of the construction in [
7]. In this direction, it was conjectured [
8] for an even
n that the maximum absolute indicator of a balanced Boolean function cannot be less than
. This conjecture was first disproved in [
9] for
by utilizing a heuristic search method beginning with a randomly generated bent function as its starting function. Shortly after that, by performing a steepest-descent-like search method within the class of 10-variable rotation-symmetric Boolean functions, it was also disproved [
10] for
. Apart from these two search results, theoretical constructions of balanced
n-variable Boolean functions with an absolute indicator of less than
were obtained recently in [
11,
12] for
(
) and for
(
), respectively. By suitably modifying the underlying Boolean functions of the constructions in [
11,
12], specific examples for
, 22, and 26 are demonstrated in [
11] and, subsequently, using the steepest-descent-like search method, these results are further improved in [
12], which provides additional examples for
, 14, 16, 20, and 24. Informally speaking, the Boolean functions obtained in [
11,
12] are constructed by modifying two blocks (with a length of
bits) of Dillon’s bent function [
5].
Evident from the above discussion, balanced Boolean functions with an even number of variables n achieving an absolute indicator of less than are mostly generated by modifying the bent functions. Here, we perform a genetic algorithm that also exploits a bent function to generate such balanced Boolean functions; however, there are some subtle differences, as follows:
Our search is realized among the balanced Boolean functions that are at a distance with a length of
from a bent function, and, hence, compared to, e.g., [
9], we do not need to seek to achieve the balancedness property during the search.
Though the Boolean functions generated from the construction in [
7] have the same distance, our search strategy does not restrict the corresponding bit changes to a specific block of a bent function.
We do not impose the conditions of a theoretical construction (e.g., [
11,
12]); rather, our search is more generic, and its search space is all the balanced Boolean functions that are closest to a bent function in terms of the Hamming distance.
Here, we point out that for the balanced
n-variable Boolean functions that we consider, a modified hill-climbing method was applied previously in [
13] for
and 12. In addition, for these numbers of variables, the bent functions were used in [
14] to form the initial population of a hybrid genetic algorithm, which was exploited to construct balanced Boolean functions without restricting their distance to the bent functions. Our approach basically applies a global optimization algorithm to the search space used in [
13] for even
, which yields better cryptographic properties than those obtained in the related literature. More specifically, the absolute indicators that we find improve the best-known values for
, and the Boolean functions with these absolute indicators achieve nonlinearity of greater than
for
. Further, the best-known nonlinearities are obtained for
.
Over the years, researchers have explored different metaheuristic techniques (such as local search, simulated annealing, particle swarm optimization, genetic algorithm, genetic programming, etc.) to design Boolean functions in various dimensions that satisfy multiple cryptographic properties. In the related literature, most of the works consider Boolean functions with numbers of the variables of up to at most 16, and the most commonly sought cryptographic properties to be optimized are balancedness, nonlinearity, and absolute indicator. We refer the reader to [
15] and the references therein for a recent survey of metaheuristic algorithms for the design of cryptographic Boolean functions. In the following section, we give a brief background on the cryptographic properties of Boolean functions. For a comprehensive survey and discussion of Boolean functions, we like to refer the reader to [
16,
17]. Next, in
Section 3, we describe the traditional genetic algorithm and present our search strategy, keeping the distance to a bent function unchanged during the search. The details of our search effort are given in
Section 4, and then we draw our conclusions in
Section 5.
2. Preliminaries
Let
be an
n-variable Boolean function, which is usually defined by its truth table
of a length
. The Hamming weight
of a Boolean function
f is the number of ones in its truth table, and the Hamming distance
between two Boolean functions
and
, both with the same number of input variables, is the number of places for which
and
differ in their truth tables, i.e.,
. If
for an
n-variable Boolean function
then
f is said to be balanced. A Boolean function
f with input variables
can be considered as a sum of the products (with all distinct orders) of the variables, i.e., it can be written as a multivariate polynomial over
:
where the coefficients
. This representation is unique and called the algebraic normal form (ANF). The largest number of variables in the product terms with nonzero coefficients is called the algebraic degree of
f and is denoted by
. The Boolean functions in the form of
, i.e., those with an algebraic degree of at most one, are referred to as affine functions, where
,
is the inner product of
and
. We denote the set of all
n-variable affine functions by
. An affine function is called a linear function if its constant term is equal to zero, and a Boolean function is called nonlinear if it is not affine.
The Walsh–Hadamard coefficients of an
n-variable Boolean function
f are the values of the integer-valued function over
given by
and the multi-set
, where
runs through
in lexicographic order, is called the Walsh–Hadamard spectrum of
f. The nonlinearity
of
f is defined as the minimum Hamming distance from all
n-variable affine functions, i.e.,
. As the distance between
f and the affine function
g can be computed by using the corresponding Walsh–Hadamard coefficient
,
can be expressed in terms of the maximum value in the absolute Walsh–Hadamard spectrum as follows:
The autocorrelation properties of a Boolean function are cryptographically important [
8,
18]. Let
f be an
n-variable Boolean function and
. The autocorrelation value of
f with respect to
d is given by
. The maximum absolute autocorrelation value, excluding
, is known as the absolute indicator of
f and denoted as
which should be small to provide good diffusion properties.
3. Genetic Algorithm
The genetic algorithm (GA) [
19], which is based on Darwin’s survival of the fittest principle, is the most widely applied evolutionary algorithm in optimization and search problems. The GA is based on the evolutionary process known as natural selection in which any parent, i.e., a pair of individuals, selected from a population produces an offspring. Mutations can occur in this process; however, after mutation, only the fittest individuals survive for the next generation. The general structure of the genetic algorithm used in our study is shown in
Figure 1. The initial population in
Figure 1 is composed of randomly generated balanced Boolean functions at the closest distance to a fixed bent function. The selection operation (using the elitism approach and the
k-tournament mechanism) is applied to the initial population to create the parent population from which the offspring are generated using our crossover strategy given by Algorithm 1. In the elitism approach, the fittest individuals in a population, i.e., the balanced Boolean functions with the best fitness values, survive. In contrast, in the
k-tournament method, the fittest one among randomly selected
k individuals survives. For a Boolean function
f, we use the cost function given in [
10,
20] as our fitness function here:
which can be considered as a measure proportional to the sum of the squared spectrum deviations from that of a bent function.
Though any bent function can be used, we randomly select a Maiorana–McFarland (MM)-type bent function [
21] from which the balanced Boolean functions are generated to form the initial population whose size is set to 1000 in our search. In our experiments, any bent function that we generate has a Hamming weight of
, i.e., the number of zeros is
more than the number of ones in its truth table. Next, we compute the fitness value of each individual within the initial population and then apply the elitism approach by selecting 100 of those with the best fitness values. Subsequently, out of the selected individuals, 40 are chosen as the parent population using the
k-tournament method, where we take
.
After generating the parent population, the algorithm enters the generation loop, which begins with a crossover operation. There are various crossover methods, such as one-point, two-point, uniform, and partial fit, which are used to obtain the offspring from the parent population. Here, we utilize the uniform crossover as given by Algorithm 1 in which the offspring produced from the mating of any two individuals (belonging to the parent population) that are at a distance of
from an
n-variable bent function keeps the same distance to that bent function. In Algorithm 1, the functions
f,
g,
, and
represent the bent function, the offspring, the first individual, and the second individual, respectively. The algorithm starts by checking each pair of the bits (belonging to the same position) of
and
and assigns their value to the offspring if both are equal. Then, as given by the next two steps, any position at which the bent function
f is zero and the first individual
(the second individual
) is one is assigned to
(resp.,
). The crossover operation is completed by assigning 0 to the randomly selected half of the positions in
, and 1 to the other half, where
and
are the sets formed by removing the positions belonging to both
and
from
and
, respectively. In the GA that we perform, the offspring is generated by using Algorithm 1 from each possible pair of individuals within the parent population. In other words, we take the crossover probability as one. It is to be noted that the offspring
g is balanced and has the distance
to the bent function
f.
| Algorithm 1 Uniform crossover operation |
| Input: |
| Output: g |
- 1:
for all such that - 2:
- 3:
- 4:
- 5:
- 6:
for all - 7:
for a randomly selected half of the positions
|
The mutation is applied to the offspring obtained from the crossover in order to ensure diversity. It is realized by flipping a randomly chosen pair of 0 and 1 in the truth table of an offspring such that the bent function is 0 at the corresponding positions of these two bits, which implies that the distance (to the bent function) remains the same after the mutation operation. Since the search space grows super-exponentially as the value n of the variables increases, high mutation probabilities may hinder exploration near the parents. Therefore, in our search, the probability of any offspring being mutated is taken as , which decreases as n increases. The offspring obtained after the mutation operation are added to the parent population (selected previously from the initial population). Then, a new parent population is formed by applying the selection operation mentioned earlier to the current population.
As the last stage of the loop, to provide additional diversity to the parent population, we apply a resetting step that is a slightly modified version of the one suggested in [
22]. An optional resetting step is applied in [
22], which keeps the fittest individual and randomly generates the remainder of the parent population if there is no improvement in the best fitness value for a number of generations. Here, we apply the resetting step by considering the fitness values of all individuals in the parent population of each generation. More specifically, if those values are the same for a generation, then one of them is kept, and the other 39 individuals are generated by forming a new population of size 1000 randomly and then applying the selection operation to them. Moreover, in this step, the GA outputs the fittest individual within the parent population of the current generation. The loop continues until the stopping criterion is met, which is the maximum number of generations, and, throughout our experiments, it varies between 100 and 20,000.
3.1. Tuning Phase
The performance of the GA depends upon fine-tuning parameters, such as the size of the initial population, the size of the parent population, and the number of individuals selected from the initial population. We conduct a parameter-tuning phase for 8-, 10-, and 12-variable Boolean functions to determine the values (aforementioned in
Section 3) of these parameters by performing a large number of experiments. More precisely, for each number of variables, we experiment with initial population sizes of 500, 1000, 1500, and 2000; parent population sizes of 20, 40, 60, and 80; and selection sizes of 50, 100, 150, and 200. After omitting the combinations for which the parent population size is greater than the selection size, there are 56 combinations left, and the parameter-tuning phase has a stopping criteria of 20,000 iterations for each combination. The set of the best-obtained parameters is used for all Boolean functions considered in this paper.
Since our aim is to optimize the nonlinearity of balanced Boolean functions, the combinations have been evaluated in terms of their corresponding nonlinearity results. Clearly, when a combination is evaluated in terms of the average value obtained, a bad solution can lead to the neglect of good solutions. Therefore, instead of average values, we consider the best values found to compare the combinations. For eight-variable Boolean functions, we observe that every combination of parameters reaches the best-known nonlinearity value of 116. For 10- and 12-variable cases, 11 and 4 combinations obtain the best-known nonlinearities of 492 and 2010, respectively. These combinations are given in
Table 1, where a combination is represented by a triplet (initial population size, selection size, parent population size). As can be seen, the best nonlinearity value is achieved for all initial populations with sizes 500, 1000, 1500, and 2000 in the case of 10 variables and for initial populations with sizes 1000 and 2000 in the case of 12 variables. Since the population sizes of 1000 and 2000 provide the best nonlinearity value for both cases, we opted for the size of 1000. Looking at the parent population sizes, it is seen that the best nonlinearity value of 492 is obtained for 10-variable Boolean functions with parent population sizes 20 and 40, while for 12-variable Boolean functions, the best nonlinearity value of 2010 is obtained with a parent population size of 40. Hence, we chose the parent population size of 40, which yields the best nonlinearity value for both the 10- and 12-variable cases. Finally, since the best nonlinearity value is achieved with a selection size of 100 for both 10- and 12-variable scenarios, we chose the selection size to be 100.
3.2. Performance Evaluation
The choice of the fitness function, along with the tuning of the parameters, plays a crucial role in the performance of the GA and the quality of solutions. In literature, Clark’s cost/fitness function [
23] is one of the most widely used ones for evolving Boolean functions; however, it has parameters that need to be tuned experimentally. As our fitness function (
given by Equation (
5)) does not require any experimental parameter, here, we evaluate the performance of our algorithm using two different fitness functions (given below) that do not involve experimental parameters.
While the fitness function
is simply the nonlinearity of
f, the other fitness function
is Gowers second-order norm of
f which, by comparing it with Clark’s fitness function, has been shown in [
14] to be efficient for reaching the optimal solutions. In
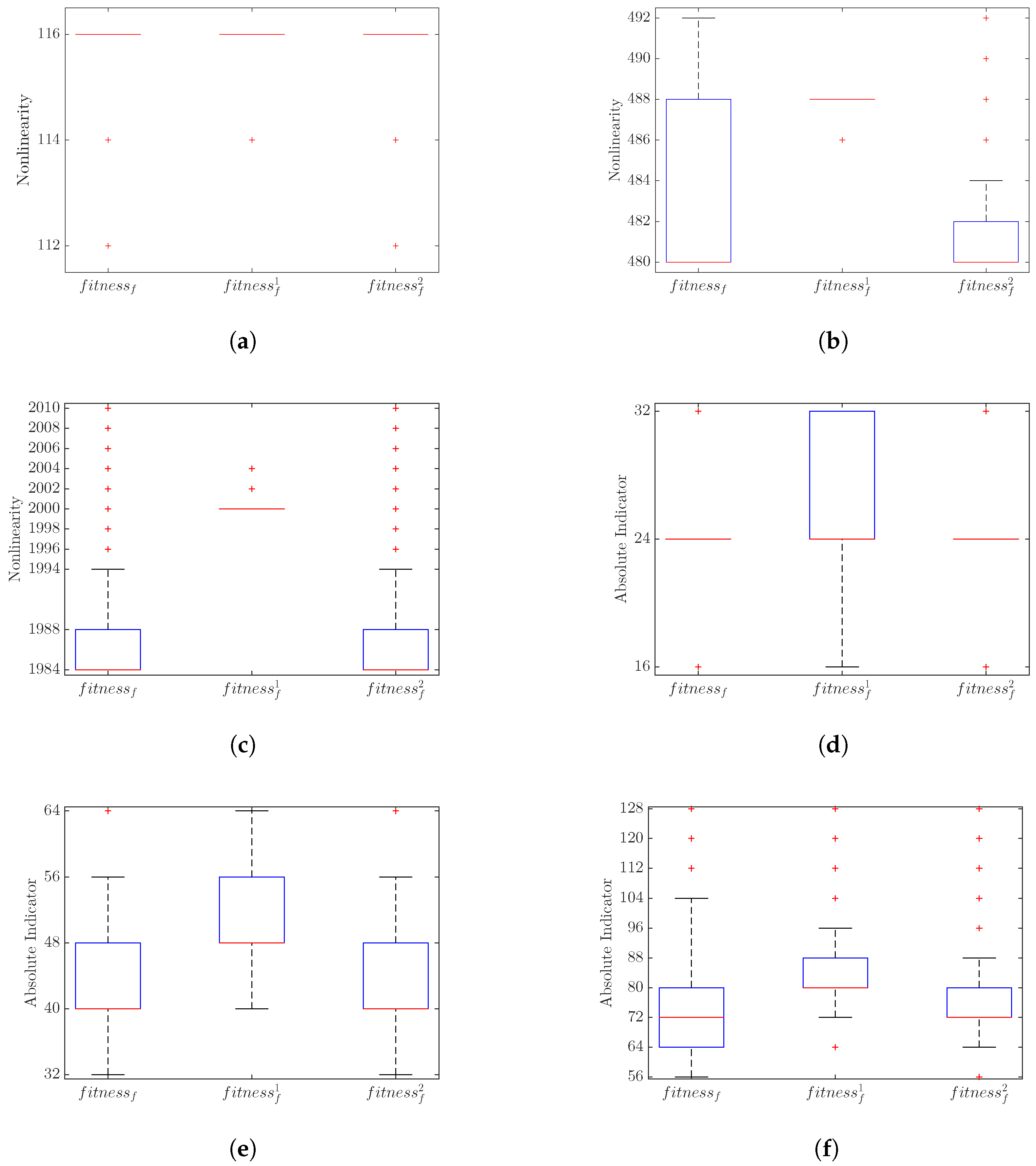
Figure 2, for the 8-, 10-, and 12-variable cases, the comparison results of the mentioned three fitness functions are presented in boxplot form. The boxplots shown in
Figure 2a–c (
Figure 2d–f) represent the nonlinearity (resp. the absolute indicator) distribution of 400,000 balanced Boolean functions generated by running the GA 20 times with 20,000 iterations each.
From
Figure 2a, it is seen that, when
or
is used, the boxplot distributions are the same, and the GA obtains nonlinearity values of 112, 114, and 116. Additionally, we observe that the GA with
does not produce the lowest nonlinearity (112) among them.
Figure 2b shows that the GA with
or
reaches the nonlinearity value of 492 (with the former one producing this nonlinearity more frequently), and the best-achieved nonlinearity by the GA with
is 488. In the case of 12 variables, as can be seen from
Figure 2c, the boxplot distributions indicating that the highest achieved nonlinearity value is 2010 are the same for
and
; however, the best-achieved nonlinearity value is 2004 for
.
Considering the boxplot distributions in
Figure 2d–f, we see that both
and
provide the same boxplots with lowest absolute indicator values of 16 and 32 for the cases of 8- and 10-variable Boolean functions, respectively. In addition, we observe that
and
outperforms
for the 10- and 12-variable cases by producing better absolute indicator values of 32 and 56, respectively. However, for the 8-variable case, the GA with
produces an absolute indicator value of 16 more frequently compared to the GA with
or
, and, similarly, for the 12-variable case, the GA with
produces an absolute indicator value of 56 more frequently compared to the GA with
.
From the boxplot distributions in
Figure 2, one can infer that though the GA with
provides more frequent generations of the nonlinearity value of 492 for the 10-variable case and the absolute indicator value of 56 for the 12-variable case, it exhibits a similar performance to the GA with
when we consider only the best-achieved results. Further, both of these generate better nonlinearity and absolute indicator values than the GA with
for the 10- and 12-variable cases.
The averages and standard deviations of the distributions of nonlinearity and absolute indicator values, which are represented with boxplots in
Figure 2, are given in
Table 2. As can be seen, for the cases of 10 and 12 variables, the average nonlinearity (absolute indicator) value obtained for
is greater (resp. less) than that obtained for
. Additionally, compared to
,
gives larger standard deviations for the nonlinearity and absolute indicator distributions. Therefore, for these cases, the statistical parameters provided by
seem to be better than those provided by
. In the eight-variable case, for both nonlinearity and absolute indicator values, though the standard deviations corresponding to
are larger than those corresponding to
,
gives worse average values than
. When we consider the average nonlinearity (absolute indicator) values found for
, we observe that they are better (resp. worse) than the other averages of the nonlinearity (resp. absolute indicator) distributions. It should be noticed that since
gives very small standard deviations (with the exception of the distribution of the absolute indicator values in the eight-variable case), the nonlinearity and absolute indicator values reached by
or
can be seen as less likely to be achieved with
.
4. Search Effort
The GA explained in the section above is performed by setting the experimental parameter values as summarized in
Table 3. The computer system that we utilize has the following specifications: Intel
® Core™ i5-9400F CPU (2.9 GHz, 9 MB cache, 6 cores), 16 GB RAM, and Windows 10 Pro 64-bit operating system. The GA is implemented in C programming language, and the typical consumed times for 100 generations are given in
Table 4 for all the values of
n of the variables we consider. We used 20 computers (each with the given specification) that work with all of the cores for about six months to obtain our results. All truth tables of our best-achived results can be found in [
24]. Among them, we have provided the truth tables of the Boolean functions with numbers of the variables 8, 10, and 12 in
Appendix A.
Clearly, the number
of the balanced
n-variable Boolean functions generated by flipping
bits of a single bent function is
, which is computed as given in
Table 4. Let
be the number of
n-variable bent functions. We know from [
25] that
(
), and it is unknown for
. Then, the search space is of the size
, which gives
in the case of
.
To better understand the efficiency of our search strategy, let us consider in particular the case of eight-variable Boolean functions. Using an exhaustive search, we enumerate all balanced Boolean functions with the best possible nonlinearity obtained from a randomly selected MM-type bent function f whose truth table is given as follows using hexadecimal notation:
3C3C5A5A33CC669900000FF066665AA5 0F0F3CC3696933336996555555AA00FF
As a result, we find that the number of those balanced functions is 6,346,334,872, and their classification is given in
Table 5, where the cryptographic properties are denoted by the triplet (nonlinearity; absolute indicator; algebraic degree). As can be seen from
Table 5, the best possible profile is
, and there are 34,336 balanced Boolean functions with that profile. Noting that
, one may obtain such a function in approximately
trials in a random search with a probability of
. We then perform the GA by using the bent function
f (to form the initial population) and setting the maximum number of generations to 20,000. In 50 runs, we observe that 4 of the
(
) generation outputs have the best profile, which shows the superiority of our method over a random search.
We now construct, as an example, a balanced eight-variable Boolean function with nonlinearity 116, absolute indicator 16, and algebraic degree 7. Let
, for all
, be a linear function determined by
, and let
be an MM-type bent function that can be seen as a concatenation of the distinct linear functions determined by
. Consider the bent function
f formed by the linear functions
corresponding to the
vectors,
, given in
Table 6. Flipping the eight bits
,
,
,
,
,
,
, and
of the bent function
f yields the balanced eight-variable Boolean function with the profile (116; 16; 7).
5. Conclusions
In
Table 7, denoting the cryptographic properties by the triplet (nonlinearity; absolute indicator; algebraic degree), we summarize and compare our best-achieved results with the present best results in [
9,
10,
11,
12] for even
. As can be seen, by applying the GA to the balanced
n-variable Boolean functions produced by flipping the minimum number (
) of bits of a bent function, we can achieve better absolute indicators (less than
), which were unknown before, for all
. In addition, we find that the corresponding nonlinearity values exceed
for
. The results also demonstrate examples of balanced Boolean functions with the best-known nonlinearity that are at the closest distance to a bent function for
. To the best of our knowledge, there is no nontrivial lower bound on the absolute indicator values, and we only know that the absolute indicator of a balanced Boolean function can be as low as eight. Hence, though the results given in
Table 7 improve the absolute indicator values in [
12], it is quite possible that one can achieve further improvements with sufficient computational power, especially for a large number of variables. On the other hand, as a long-standing open problem, it is still unknown whether there exists a balanced Boolean function with an even number
n of variables that achieves nonlinearity of greater than
for
, and, hence, it seems elusive to achieve this nonlinearity. For instance, it is unknown whether there exists a balanced eight-variable Boolean function with nonlinearity of 118.
Here, we mainly consider two of the most important cryptographic properties of balanced Boolean functions, which are nonlinearity and the absolute indicator. It should be noted that in order for a Boolean function to be used in a cryptosystem, one should also consider the other cryptographic properties, such as resiliency, algebraic immunity, and fast algebraic immunity. We think that it is possible to exploit our search strategy to optimize these properties as well by increasing the distance to the bent functions and designing the fitness function accordingly. However, since there is a trade-off among those cryptographic properties and improving one property may lead to the deterioration of another property, it seems quite probable to deterioriate our best-found cryptographic properties in
Table 7 while optimizing the other cryptographic properties. For instance, when compared to [
26], where two classes of one-resilient Boolean functions with the best-known absolute indicator values are constructed, one can see that the absolute indicator values presented in
Table 7 are better.