Abstract
Optimizing traffic signal control (TSC) at intersections continues to pose a challenging problem, particularly for large-scale traffic networks. It has been shown in past research that it is feasible to optimize the operations of individual TSC systems or a small collection of such systems. However, it has been computationally difficult to scale these solution approaches to large networks partly due to the curse of dimensionality that is encountered as the number of intersections increases. Fortunately, recent studies have recognized the potential of exploiting advancements in deep and reinforcement learning to address this problem, and some preliminary successes have been achieved in this regard. However, facilitating such intelligent solution approaches may require large amounts of infrastructure investments such as roadside units (RSUs) and drones, to ensure that connectivity is available across all intersections in the large network. This represents an investment that may be burdensome for the road agency. As such, this study builds on recent work to present a scalable TSC model that may reduce the number of enabling infrastructure that is required. This is achieved using graph attention networks (GATs) to serve as the neural network for deep reinforcement learning. GAT helps to maintain the graph topology of the traffic network while disregarding any irrelevant information. A case study is carried out to demonstrate the effectiveness of the proposed model, and the results show much promise. The overall research outcome suggests that by decomposing large networks using fog nodes, the proposed fog-based graphic RL (FG-RL) model can be easily applied to scale into larger traffic networks.
1. Introduction
With growing global populations, urbanization, and automobile ownership, urban transportation networks continue to experience increasing traffic congestion, with severe consequences that include travel delay, driver frustration, increased emissions, and reduced safety. The control of traffic at urban intersections which can help reduce congestion can be classified broadly as: passive and active. The former entails no explicit control over traffic operations at a given intersection; thus, movement through the intersection relies on driver awareness and compliance to the rules of the road (e.g., traffic signs and unsignalized roundabouts). On the other hand, active intersection control directly restricts some traffic movements to enable others at any given time block. The most prominent of these is the traffic signal. While traffic signals provide a relatively safe method of intersection control, efficiency has been elusive, particularly in intersections with high traffic volumes. According to the Federal Highway Administration (FHWA), poor signal timing can account for up to 10% of total traffic congestion [1,2]. The optimization and control of traffic signals represent a key strategy for the management of traffic congestion and improving traffic conditions in urban areas.
Given the significance of traffic signal control (TSC) in urban mobility and consequently on social and commercial activity, TSC research has received much attention. Broadly, TSC mechanisms can be placed into two categories: fixed-time traffic control and real-time traffic control. The former typically uses a pretimed program that controls the cycle and split times. Webster (1958) was one of the earliest researchers to present a fixed-time control model which had sought to minimize the average delay of vehicles [3]. For traffic flow conditions that are stable with little or no randomness, fixed-time traffic control is well suited. However, fixed-time models are unsuitable for highly stochastic and unstable traffic flow conditions. For these conditions, real-time traffic control that is responsive to traffic conditions is more suited. In real time traffic control, real-time traffic data are used, thereby allowing the signals to adjust accordingly, duly accounting for variations in traffic flow. A widely used real-time traffic controller is the actuated signal, which regulates its cycle and timings based on real-time traffic data received from detectors and sensors. Several applications of actuated signals have been developed and deployed successfully; yet still, actuated signals are not always effective in efficient control of traffic across multiple intersections simultaneously in large road networks This adversity arises when the signal is unable to cooperate with the signals at other intersections. Over the decades, several studies have shown that TSC methods such as actuated and pretimed controls are adequate for a single intersection or small networks [4,5]; however, but they do not lead to optimal solutions when they are applied to large networks.
With the imminent emergence of robust vehicular connectivity and automation technologies, researchers are investigating the efficacy of traffic signal control that leverages such technologies.
Scaling small-intersection TSC solutions to large networks has been a persistent challenge that has been investigated using various optimization algorithms. In recent years, there has been pronounced interest in other solution methods, including those that can take advantage of the plethora of data offered by new and advanced traffic sensors [6,7]. Deep learning and reinforcement learning concepts were introduced several decades ago [8,9]; however, continuing increases in computational capabilities have made their application more feasible, and therefore, fostered a new generation of deep and reinforcement learning algorithms for purposes of continuous and discrete control [10,11]. Parallel with the emergence of smart infrastructure technologies that facilitate real-time data collection and sharing such as roadside units (RSUs) and drones, there have been advancements in machine learning techniques. With these developments, it has become increasingly feasible to solve traffic signal control and other problems associated with intelligent transportation systems.
For these reasons, deep reinforcement learning (DRL) based approaches to TSC solution for large networks has become an increasingly studied topic. Wiering’s study was one of the earliest to propose the use of reinforcement learning algorithms for traffic signal control to minimize city-wide congestion [12]. Prashanth and Bhatnagar proposed reinforcement learning with function approximation for traffic signal control, using Q-learning for adaptive signal control [13]. Chu et al. (2020) proposed a multiagent deep reinforcement learning algorithm that could be applied to large-scale networks; they applied an actor critic network to recurrent neural network with long-short term memory (LSTM) [14]. Wang et al. proposed the cooperative double Q-learning (Co-DQL) model that leverages mean field approximation of all other agents in the network to significantly reduce model complexity and the curse of dimensionality [7]. Guo et al. (2019) presented six traffic control methods that utilize connected and automated vehicle (CAV) capabilities [6].
While the aforementioned studies utilize the state-of-the-art DRL approaches for TSC problems, an oft overlooked topic is the resource constraints that may restrict transportation agencies and other government entities from deploying data-facilitating infrastructure such as RSUs and drones. Additionally, with regard to studies that leveraged CAV capabilities, the realization is that there exists uncertainty on when CAVs will be deployed on public roads.
This study presents an alternative to scalable TSC models that can reduce the number of deployed data-facilitating infrastructure. The proposed model utilizes a graph attention network (GAT) to preserve the topology of the traffic network while focusing on relevant inputs to make traffic control decisions. Doing this allows the model to address large networks as well as variable-sized inputs. The proposed model is applicable where RSUs are deployed in an urban grid-like network, each serving as fog-nodes that collect data via detectors and share with other fog-nodes in its range, utilizing the information to control the phase and duration of the traffic lights in its control. The Q-network utilizes double estimators to approximate instead of maximizing over the estimated action values in the corresponding state to approximate the value of the next state (as is the case in standard Q-learning). Therefore, performance overestimation is avoided. Overall, the model extracts node embeddings from fog node features while also constructing an adjacency matrix that maps the topology of the connected fog nodes, which, in turn, are passed through the attention layer to be used for the Q-network. Unlike the models in the literature, the proposed model considers the preservation of network topology in the TSC problem using GATs. Additionally, recognizing that until CAVs are deployed on public roads, CAV-related solutions proposed in the literature cannot be applied in the practice, this paper proposes an intelligent, scalable traffic control model that can be integrated into large, urban networks without using CAVs directly.
2. Background
2.1. Reinforcement Learning
In general, reinforcement learning (RL) utilizes feedback of decisions, observations, and rewards. Deep reinforcement learning (DRL) combines RL with deep learning, which allows for end-to-end training of multilayer models that can solve complex problems. This is particularly useful for sequential decision making such as in robotics, video games, and traffic operations [10,14,15,16,17,18].
Due to the data-driven nature of traffic operations, and fueled by advancements in sensor and communication protocols, RL and DRL have been increasingly utilized to address problems in the transportation engineering domain. These applications include vehicle routing, signal control, vehicle control, and traffic operations. Du et al. (2021) presented the GAQ-EBkSP method, a DRL-based framework that dynamically routes urban traffic [19]. In the domain of individual signal timing problems, Li et al. (2016) proposed a DRL-based method for traffic signal timing, utilizing deep neural networks as the backbone for reinforcement learning [20]. For direct vehicle control, Koh et al. (2020) presented DRL-based real-time navigation using deep Q-learning based simulation, which has significant potential benefits particularly in urban transit studies [21].
One of the most popular single-agent RL method is Q-learning. Q-learning is a model-free reinforcement learning approach that can be considered as asynchronous dynamic programming, where agents learn optimal policies in Markovian domains through solving sequential decision making [22]. This is achieved by estimating the optimal value, , for each action during state . Because most problems have large state and action spaces to learn all action values separately, a parametrized value function can be learned instead. Thus, the standard Q-learning update for the parameter from taking action in state with observed reward and the subsequently resulting state, is:
where is the learning rate, and the target is defined as:
where the constant is a discount factor that adjusts the relative weight between immediate and later rewards.
Q-learning in multiagent reinforcement learning (MARL) differs primarily in that MARL is based on Markov game instead of a Markov decision process (MDP) [23]. Similarly to MDPs, Markov games can be represented as a tuple , where M is the number of agents, is the set of system states, is the action set of agent , is the reward function for agent , and is the transition function for moving from one state to another state given action . Partially observable Markov games additionally require , the set of observations of the hidden states, and , the observation probability distribution.
In MARL, each agent learns to choose its actions according to their respective strategies. At each time step, the system state transfer occurs by taking the joint action under the joint strategy , and each agent receives their immediate reward from the joint action. For each agent under joint policy and initial state , the expected discounted reward is:
Additionally, the agent-specific average reward can be found as:
2.2. Graph Neural Networks
Graph neural networks (GNNs) are able to preserve acyclic and nonacyclic graph topology, which can enhance road network representation particularly in the context of scalable network traffic signal control [24,25,26,27,28,29,30]. Due to the graphical nature of transportation networks, for both vehicles as well as roadways, GNNs can serve as robust neural network architectures for deep reinforcement learning [26,27]. Deep reinforcement learning requires a robust neural network architecture that enables forward and backpropagation for purposes of model training [28]. Graph convolutional networks (GCNs) can serve as powerful neural networks that can address graph data for deep reinforcement learning [26,27]. The nodes of a GCN layer aggregates its own observed states and those of its neighbors into embeddings. Given different relational graphs, the message propagation is as follows [30]:
where denotes the hidden state of node in the layer of the neural network, is layer dimensions, is the set of incoming messages, and is the transformation for the message from the nodes.
In essence, these node embeddings can address problems caused by variable length inputs to perform various sequential learning tasks given graph data, and error terms can be used to backpropagate to perform the requisite gradient descent for parameter tuning purposes.
3. Methodology
DRL Model Architecture
The fog-based graphic RL (FG-RL) model for TSC presented in this paper uses a scalable and decentralized methodology. Due to the inherent complexity associated with large networks, centralized models may not converge. Therefore, this study utilizes a decentralized approach. The graphical structure of the network topology is preserved with traffic signals and intersections, along with their relative adjacencies. The fog arrangement determines the topology of the connected entities and the number of the connected intersections within its range. As such, the adjacency matrix containing the relative adjacencies and connectivity of intersections vary corresponding to the distribution of RSUs (and in turn, the fog nodes) in the network and the number of road intersections overseen by each RSU. In DRL architecture, each RSU is represented as a fog node, which serves as an agent that makes decisions to select traffic signal phases for each of the intersections it oversees, with an overall goal of congestion reduction.
The network topology and information attention are modeled using GAT. The fog node can oversee multiple intersections, some of which may have few or no queued vehicles. Therefore, it must learn to divert attention away from relatively uncongested intersections and focus more on congested intersections. However, a given intersection’s congestion levels can vary drastically between episodes or even across different time-steps in one episode. As a result, applying an attention model can facilitate the learning process under conditions when such variations exist.
Each fog node produces node embeddings that encode node features . The state is a tuple of node feature matrix and an adjacency matrix , where is the total number of nodes, and is the number of features in each node. The feature matrix considers the states consistent with those in the literature [7,14], namely, (i) the cumulative delay of the first vehicle on each incoming lane at an intersection, and (ii) the total number of approaching vehicles on each incoming lane.
The network architecture is shown in Figure 1. At each time-step , the node feature matrix is fed as the input into a fully connected encoder denoted that generates node embeddings in dimensional embedding space
The node embeddings then are passed through the graph convolution with attention mechanism.
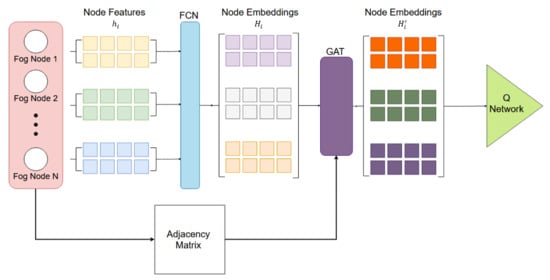
Figure 1.
GAT Model Architecture.
The adjacency matrix is weighted using the following attention mechanism:
where are coefficients computed by the attention mechanism defined in the literature [31]:
The output of the GAT layer is then used as inputs to the Q network to obtain the Q values. Further, experience relay and soft target update are utilized to enhance learning [11,31], and the model is trained on randomly sampled batches from a replay buffer. Thus, the architecture can be summarized as follows:
- FCN Encoder : Dense (32) + Dense (32)
- GAT Layer : GATConv (32)
- Q Network: Dense (32) + Dense (32) + Dense (64) + Dense (32)
- Output Layer: Dense (5)
4. Case Study
The case study utilized the Simulation of Urban MObility (SUMO) for traffic simulation [32], an open-source simulator that enables detailed tracking of vehicle and traffic light parameters. Sumo is a highly portable, microscopic, and continuous traffic simulation package designed to handle large networks. For an initial proof of concept, a small 6-node network is considered (Figure 2). The traffic signal parameters are defined as the pre-timed phases, with the RL agents selecting the appropriate phase for each intersection. Further, the lane-change parameters for the vehicles follow the LC2013 model, provided in SUMO. The vehicles are defined for car-following behavior but are permitted to change lanes if needed.
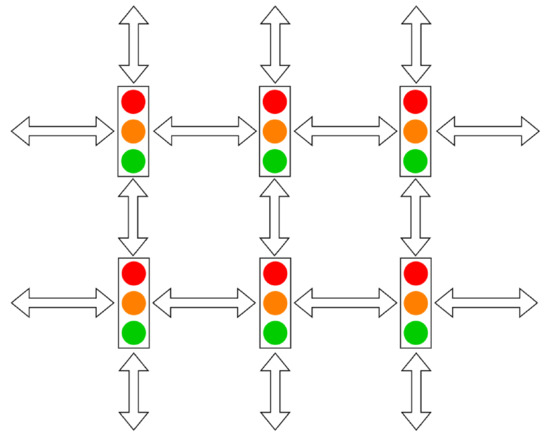
Figure 2.
Small Network of Signalized Intersections.
4.1. Network Descriptions
A small grid network was used for numerical experimentation, as shown in Figure 2. Two network settings are considered for numerical experimentation. The first setting utilizes a “smart cities” approach, where each intersection is connected via a central controller in a cloud environment. This setting is a fully observable Markov decision process or MDP. It must be noted that this is an ideal setting that has no constraints, meaning that all entities are assumed to be connected. While this can be achieved easily in simulation, it will need many connectivity facilitating infrastructure units to ensure that the entire network is connected. This could be problematic particularly at large networks.
The second setting utilizes the proposed fog-node approach, where intersections are grouped together by a small number of connectivity-facilitating infrastructure such as RSUs or drones. To assess the effects of multiple facilitating infrastructure with varying numbers and arrangements of connected intersections, this numerical example was conducted with two and three fog nodes, detailed in Figure 3. As previously stated, the two benefits of segmenting the whole network into smaller fog nodes are the improved scalability and the possibility of reducing the infrastructure (number of RSUs and/or drones) required to facilitate the intelligent TSC models.
Each westbound and eastbound road segment entering signalized intersections is a two-lane arterial comprised of a through lane and a left-turn lane. Each northbound and southbound road segment consists of a single through lane. Vehicles enter each outer road segments (10 total) at a flow rate of 2200 vehicles/hour. The vehicle origins and flows are randomly distributed.
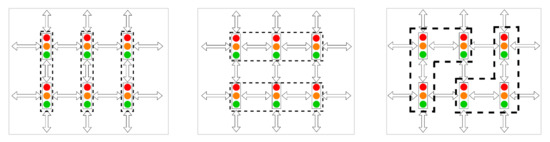
Figure 3.
Fog node deployment arrangements with connected intersections (0–3, 1–4, 2–5) (left); (0–1–2, 3–4–5) (middle); and (0–1–3, 2–4–5) (right).
4.2. Markov Decision Process Settings
Action Space
Each fog node controls the traffic signals in its range. As shown in Figure 3, the fog nodes control specific intersections under their “jurisdiction”. The fog node arrangements are as follows, with the top left intersection denoted as 0, and subsequent intersections are numbered from left to right and top to bottom.
Arrangement 1: intersections 0–3, 1–4, and 2–5 share information and control.
Arrangement 2: intersections 0–1–2 and 3–4–5 share information and control.
Arrangement 3: intersections 0–1–3 and 2–4–5 share information and control.
Fully-Observable: all intersections share information and control.
In the (0–3, 1–4, 2–5) arrangement, there are a total of three fog nodes, sharing data across only connected intersections. In the remaining two arrangements, there are only two fog nodes. Each signal can have one of five pre-determined phases, as is consistent with most literature and the practice [7,14]: east–west straight, east–west left-turn, three straight and left-turn phases for east, west, and north–south.
State Space
The local state observed within each fog node is defined as follows:
As stated previously, denotes the cumulative delay of the first vehicle for a given lane in an intersection, and denotes the total number of approaching vehicles on each incoming lane.
Rewards
The reward function consists of two main penalties:
The total reward is the negative weighted sum of the two penalties:
where are used to scale the two penalties. This numerical example used and .
5. Results
Figure 4 presents a comparison of the training results using 2 fog nodes versus a fully observable system.
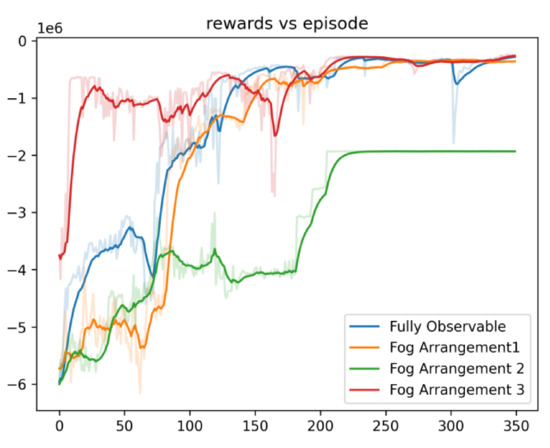
Figure 4.
Comparison of Training Results with Fog Node Arrangement vs. Fully Observable System.
For each setting, the model was trained using a soft target update set at and a learning rate of . Each model was trained for a total of 100,000 time steps, with 20,000 time steps for warm-up. Given these training parameters, the training results for the fully observable “smart cities” setting and the fog-node setting are shown in Figure 4. It can be seen that despite the lack of information sharing between fog nodes, the training performance is similar to the fully observable model with the exception of Arrangement 2 (0–1–2, 3–4–5).
However, despite strong training performance, the use of fog nodes results in higher average intersection delay, as shown in Figure 5. Over a 1000 time-step policy replay with randomized seed, the fully observable model exhibits the best performance, with 50.37 s of average intersection delay. On the other hand, the worst performance is obtained from an actuator-based, static traffic light system with an average intersection delay of 243.72 s. Among the fog node models, the models with only two fog nodes performed worse than the model with three fog nodes. The (0–1–2, 3–4–5) model outperformed the (0–1–3, 2–4–5) model by about 30 s (118.25 s vs. 148.26 s), and the (0–3, 1–4, 2–5) model performed the closest to the ideal fully observable scenario with an average intersection delay of 74.23 s.
The primary shortcoming of a fully observable model for traffic signal control problems is that fully observable TSC models are difficult to scale well due to the curse of dimensionality (dramatic increase in complexity as the number of connected nodes increases). These results indicate that the use of separately controlled fog nodes allows for comparable training performance while being more scalable, albeit at the cost of some performance. Based on the discrepancies in average intersection delays across fog node arrangements, there is an opportunity to achieve pareto-optimality, particularly in large networks.
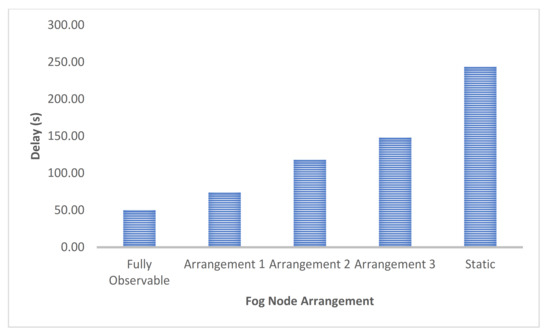
Figure 5.
Intersection Average Delay.
6. Conclusions
In order to create a more easily scalable and intelligent traffic signal control (TSC) model that can be applied to large networks, this paper proposed the use of graph attention networks (GATs) and fog-node architecture. The added benefit of segmenting large networks into smaller fog-nodes includes the possibility of reducing the number of smart infrastructure units required to facilitate the intelligent TSC models. Multiagent reinforcement learning based models for TSC typically can be affected by the curse of dimensionality. The proposed model addresses scalability in two ways: (i) graph attention that only utilizes relevant node features and neighbor node features to reduce the input complexity, and (ii) fog-nodes that break up the large network into manageable sizes. Preliminary findings show that the proposed model shows promising results that can be scaled into larger networks.
However, their performance in reducing average intersection delay may be relatively inferior compared to a fully observable model. As such, ongoing work on various fog node deployment arrangements and their performance, are expected to provide additional insights on the tradeoff between scalability and performance using the proposed GAT and fog-node architecture. Another promising research direction is to create a simplified or averaged performance within each fog node to reduce the data size and complexity, thereby allowing fog nodes to exchange data between each other to make decisions based on the performance of other fogs.
Author Contributions
Conceptualization, P.H., S.C. and R.D.; Formal analysis, P.H.; Funding acquisition, S.C. and S.L.; Methodology, S.C. and R.D.; Project administration, S.L.; Supervision, S.C. and S.L.; Validation, R.D.; Visualization, P.H.; Writing—original draft, P.H., S.C. and S.L.; Writing—review & editing, P.H., S.C. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Department of Transportation, Award #69A3551747105, and the APC has been waived by the publisher.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This work was supported by Purdue University’s Center for Connected and Automated Transportation (CCAT), a part of the larger CCAT consortium, a USDOT Region 5 University Transportation Center funded by the U.S. Department of Transportation, Award #69A3551747105. The contents of this paper reflect the views of the authors, who are responsible for the facts and the accuracy of the data presented herein, and do not necessarily reflect the official views or policies of the sponsoring organization.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FHWA. Traffic Congestion and Reliability: Trends and Advanced Strategies for Congestion Mitigation. 2020. Available online: https://ops.fhwa.dot.gov/congestion_report/executive_summary.htm (accessed on 3 July 2021).
- Zhao, D.; Dai, Y.; Zhang, Z. Computational intelligence in urban traffic signal control: A survey. IEEE Trans. Syst. Man Cybern. Part C 2011, 42, 485–494. [Google Scholar] [CrossRef]
- Webster, F.V. Traffic Signal Settings; Road Research Technical Paper no. 39; H.M.S.O: London, UK, 1958. [Google Scholar]
- Koonce, P.; Rodegerdts, L. Traffic Signal Timing Manual; No. FHWA-HOP-08-024; Federal Highway Administration: Washigton, DC, USA, 2008. [Google Scholar]
- Ceylan, H.; Bell, M.G.H. Traffic signal timing optimisation based on genetic algorithm approach, including drivers’ routing. Transp. Res. Part B Methodol. 2004, 38, 329–342. [Google Scholar] [CrossRef]
- Guo, Q.; Li, L.; Ban, X.J. Urban traffic signal control with connected and automated vehicles: A survey. Transp. Res. Part C Emerg. Technol. 2019, 101, 313–334. [Google Scholar] [CrossRef]
- Wang, X.; Ke, L.; Qiao, Z.; Chai, X. Large-Scale Traffic Signal Control Using a Novel Multiagent Reinforcement Learning. IEEE Trans. Cybern. 2021, 51, 174–187. [Google Scholar] [CrossRef] [PubMed]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- Lin, L.-J. Reinforcement Learning for Robots Using Neural Networks; Carnegie Mellon University: Pittsburgh PA, USA, 1992. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Wiering, M.A. Multi-agent reinforcement learning for traffic light control. In Machine Learning: Proceedings of the Seventeenth International Conference (ICML’2000); Morgan Kaufmann Publishers Inc: Stanford, CA, USA, 2000; pp. 1151–1158. [Google Scholar]
- Prashanth, L.A.; Bhatnagar, S. Reinforcement learning with function approximation for traffic signal control. IEEE Trans. Intell. Transp. Syst. 2010, 12, 412–421. [Google Scholar]
- Chu, T.; Wang, J.; Codeca, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1086–1095. [Google Scholar] [CrossRef] [Green Version]
- Vinitsky, E.; Parvate, K.; Kreidieh, A.; Wu, C.; Bayen, A. Lagrangian Control through Deep-RL: Applications to Bottleneck Decongestion. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, 2018, Maui, HI, USA, 4–7 November 2018; Volume 2018, pp. 759–765. [Google Scholar]
- Ha, P.Y.J.; Chen, S.; Dong, J.; Du, R.; Li, Y.; Labi, S. Leveraging the capabilities of connected and autonomous vehicles and multi-agent reinforcement learning to mitigate highway bottleneck congestion. arXiv 2020, arXiv:2010.05436. [Google Scholar]
- Liu, D.; Yang, C. A deep reinforcement learning approach to proactive content pushing and recommendation for mobile users. IEEE Access 2019, 7, 83120–83136. [Google Scholar] [CrossRef]
- Dong, J.; Chen, S.; Li, Y.; Du, R.; Steinfeld, A.; Labi, S. Space-weighted information fusion using deep reinforcement learning: The context of tactical control of lane-changing autonomous vehicles and connectivity range assessment. Transp. Res. Part C Emerg. Technol. 2021, 128, 103192. [Google Scholar] [CrossRef]
- Du, R.; Chen, S.; Dong, J.; Ha PY, J.; Labi, S. GAQ-EBkSP: A DRL-based Urban Traffic Dynamic Rerouting Framework using Fog-Cloud Architecture. In Proceedings of the 2021 IEEE International Smart Cities Conference (ISC2), Manchester, UK, 7–10 September 2021; pp. 1–7. [Google Scholar]
- Li, L.; Lv, Y.; Wang, F.Y. Traffic signal timing via deep reinforcement learning. IEEE/CAA J. Autom. Sin. 2016, 3, 247–254. [Google Scholar]
- Songsang, K.; Zhou, B.; Fang, H.; Yang, P.; Yang, Z.; Yang, Q.; Guan, L.; Ji, Z. Real-time deep reinforcement learning based vehicle navigation. Appl. Soft Comput. 2020, 96, 106694. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Xu, T.; Niu, X.; Tan, C.; Chen, E.; Xiong, H. STMARL: A Spatio-Temporal Multi-Agent Reinforcement Learning Approach for Cooperative Traffic Light Control. IEEE Trans. Mob. Comput. 2020. Available online: https://ieeexplore.ieee.org/document/9240060 (accessed on 3 July 2021).
- Wei, H.; Xu, N.; Zhang, H.; Zheng, G.; Zang, X.; Chen, C.; Zhang, W.; Zhu, Y.; Xu, K.; Li, Z. Colight: Learning network-level cooperation for traffic signal control. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1913–1922. [Google Scholar]
- Devailly, F.X.; Larocque, D.; Charlin, L. IG-RL: Inductive Graph Reinforcement Learning for Massive-Scale Traffic Signal Control. IEEE Trans Intell. Transp. Syst. 2021. Available online: https://ieeexplore.ieee.org/document/9405489 (accessed on 3 July 2021).
- Sikai, C.; Dong, J.; Ha, P.; Li, Y.; Labi, S. Graph neural network and reinforcement learning for multi-agent cooperative control of connected autonomous vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 838–857. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press Cambridge: Boston, MA, USA, 2016; Volume 1. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the European Semantic Web Conference, Crete, Greece, 3–7 June 2018; pp. 593–607. [Google Scholar]
- Velicković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent Development and Applications of SUMO—Simulation of Urban MObility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).