Matheuristic Algorithm for Job-Shop Scheduling Problem Using a Disjunctive Mathematical Model

Abstract

This paper focuses on the investigation of a new efficient method for solving machine scheduling and sequencing problems. The complexity of production systems significantly affects companies, especially small- and medium-sized enterprises (SMEs), which need to reduce costs and, at the same time, become more competitive and increase their productivity by optimizing their production processes to make manufacturing processes more efficient. From a mathematical point of view, most real-world machine scheduling and sequencing problems are classified as NP-hard problems. Different algorithms have been developed to solve scheduling and sequencing problems in the last few decades. Thus, heuristic and metaheuristic techniques are widely used, as are commercial solvers. In this paper, we propose a matheuristic algorithm to optimize the job-shop problem which combines a genetic algorithm with a disjunctive mathematical model, and the Coin-OR Branch & Cut open-source solver is employed. The matheuristic algorithm allows efficient solutions to be found, and cuts computational times by using an open-source solver combined with a genetic algorithm. This provides companies with an easy-to-use tool and does not incur costs associated with expensive commercial software licenses.

1. Introduction

Nowadays, rapidly growing economic markets, competitive pressures and increasingly challenging business environments are forcing increasingly more companies, especially small- and medium-sized enterprises (SMEs), to innovate their industrial manufacturing systems. SMEs have had to respond and adapt to a constantly changing organizational environment to deliver high-quality customized products. Consequently, SMEs supply chains are not static as they must respond to continuous change by adapting their control techniques, and coordinating and managing change in the way they operate and configure their businesses. Companies also have to manage their evolution toward participation in collaborative networks [1].

The market in which these companies currently operate is intensely volatile, which makes effective supply chain (SC) management critical to improve organizational performance as manufacturing systems become increasingly dynamic [2] due to new challenges in manufacturing industries, such as Industry 4.0 and the Internet of Things (IoT).

Researchers are showing much interest in improving the performance of enterprises and SC to generally cope with these dynamic environments by devising mechanisms and techniques that provide SMEs with affordable tools in cost, easy-to-use and computational efficiency terms. The search for solutions for company scheduling problems, such as job-shop scheduling problems (JSP), remains a relevant research topic [3]. This is because most of these real-world scheduling problems are too complex to be optimally solved and are often NP-hard. This means that exact techniques and some algorithms cannot solve them in effective computational times when the problem is too large. At the same time, solving them with commercial solvers is neither economically viable nor computationally efficient.

Mathematical formulations like mixed integer linear programming (MILP) models for JSP, have been around since the 1960s [4]. The leading formulations for this problem type are disjunctive formulation, rank-based formulation and time-indexed formulation [5].

Ku and Beck [5] compared these mathematical formulations with different solvers (CPLEX, GUROBI and SCIP, the first two are commercial and the last one is not), which showed that the disjunctive model outperformed the rank-based and time-indexed models.

In this context, a new matheuristic algorithm combining a genetic algorithm and the disjunctive model (MILP) is proposed in this study. Matheuristic algorithms are constructed by “the interoperation of metaheuristics and mathematical programming techniques” [6]. According to Ball [7] and Talbi [8], combinations or hybridizations of matheuristics can be classified into three approaches: (1) decomposition approaches, where the problem is decomposed into subproblems to be optimally solved; (2) improvement heuristics or metaheuristics, where the mathematical programming model is used to enhance an initial solution obtained by some heuristic or metaheuristic method; and (3) approaches employing the mathematical programming model to provide approximate solutions in which a relaxation of the problem toward optimality is solved.

The method presented in our study consists of a combination of a genetic algorithm and linear programming (LP) model (GA-LP) that is included in approach 2 of this classification. The main objective of this work is to test the non-commercial COIN-OR Branch and Cut (CBC) solver [9] for solving the JSP, combined with a genetic algorithm, in large or real instances. The experimental results confirm the feasibility and effectiveness of the proposed matheuristic compared to the solutions provided by the solver.

Accordingly, the document is structured as follows. Section 2 reviews work related to the application of matheuristic algorithms to the JSP. Section 3 presents the proposed JSP mathematical model in detail. Section 4 describes the matheuristic approach. Section 5 presents the computational experiments and discusses the results. Finally, Section 6 covers the conclusions of the performed work and future research lines.

2. Literature Review: Matheuristic Resolution Approaches

A wide variety of papers describes different models and algorithms to solve scheduling problems [10]. Many of these techniques correspond to mathematical models, heuristic and metaheuristic algorithms [11]. The application of these techniques depends on the application area, i.e., SC planning under uncertainty [12], closed loop SC [13], SC sustainable management [14] or green SC management [15]. These studies reviewed the models and algorithms employed to solve optimization problems in their specific field.

In this paper, we focus on the scheduling problem to be addressed at the operational decision-making level, and we pay particular attention to the JSP which is considered to be NP-hard. To address this problem, heuristic (H) and metaheuristic (MH) approaches have received much attention in the literature. Indeed, many literature surveys have been carried out over time. Thus, deterministic and stochastic optimization models have been developed to solve the JSP [3,16,17]. Moreover, other approaches including decomposition heuristics, dispatching heuristics, disjunctive representations of the problem, discrete simulation or rolling horizon approaches can be found in the literature [18].

To offer readers an overview on the studied topic, we reviewed how the literature has applied matheuristic approaches to solve the JSP. In our research, we applied the keywords “matheuristic” AND “job-shop scheduling problem”. Seventeen papers coincide with our research in the Scopus database. Some tackle flow shop scheduling problems, and others refer to reviews. After analyzing the abstracts and the whole contents of the papers, nine papers remained of the initial seventeen (see

Table 1. Literature review of matheuristic to solve the job-shop problem.

Reference	Job-Shop Problem Type	Matheuristic	Integrated Approaches		Programming Languages/Modeling Language/Solver	Experiment Size (Job × Machine)
			H+MILP	MH+MILP
Al-Hinai and Elmekkawy [18]	Flexible JSP	HGA		MILP + GA	C++ / - / - /	20 × 15
Li et al. [19]	Flexible JSP	TSPCB		MILP + TSPCB	C++ / - / - /	20 × 15
Li and Gao [20]	Flexible JSP	HGA TS		GA + TS	C++ / GAMS / CPLEX	15 × 10
Thiruvady et al. [21]	Resource-constrained JSP	MS CMSA ACO	Constructive heuristic	MILP + ACO MS CMSA	C++ / OpenMP / Gurobi	6 × 20
Rohaninejad et al. [22]	JSP Parallel Machines	GA_BH GA_ATC GA_MLS		MIP+GA	CPLEX	6 × 4
Dang et al. [23]	JSP Parallel machine	GA		ILP + GA	/ - /IBM ILOG / CPLEX	120 × 6
Cota et al. [26]	JSP with unrelated parallel machines	-	Multi-objective smart pool search matheuristic + MILP	-	/- / IBM ILOG / CPLEX	15 × 5
Ahmadian and Salehipour [24]	Just-in-time JSP	_	GT algorithm SBH VNS Relaxation neighborhoods	_	C++ /- / CPLEX	20 × 10
Son et al. [25]	Bounded-splitting jobs scheduling problem on a single machine in available time windows	GA TS	AH HSLPTR HMAXFR MAAS	TS + MAAS GA + MAAS	/- /-/ CPLEX	200 × 1

). Our review research is not without limitations as the search results may not fully cover all the matheuristic proposed in the literature for being named differently from the keywords used in our research “matheuristic”, e.g., hybrid algorithms.

As a general overview, the JSP was tackled from different perspectives, namely flexible JSP, dynamic JSP, resource constrained JSP, parallel machine JSP or just-in-time JSP. This review revealed that the most widely used metaheuristics are led by genetic algorithms and tabu search algorithms. The matheuristics presented to address the JSP integrates an MILP with a metaheuristic algorithm in most cases. Others consider an MILP combined with a constructive heuristic to increase the intelligence of the MILP and to reduce computational resolution times in large sized experiments.

Table 1 highlights some relevant characteristics of the matheuristic proposed in the analyzed works in terms of: (i) the type of addressed JSP; (ii) the proposed matheuristic; (iii) the integrated approaches used to define the matheuristic, including a heuristic algorithm combined with an MILP or a metaheuristics combined with an MILP; (iv) the employed programming language and modeling language, as well as the solver used to compute the exact method; and (v) the experiment size (job x machine). These features are based on the solution approaches defined in the framework proposed by [10].

In order to provide a profounder analysis, Al-Hinai and Elmekkawy [18] propose an approach to obtain a predictive schedule that minimizes machine breakdowns and responds to a flexible JSP. To this extent, a 2-stage hybrid genetic algorithm (HGA) is proposed: (i) the first stage optimizes the primary objective by minimizing the makespan and considering deterministic data without machine breakdowns; (ii) the second stage optimizes a bi-objective function (by considering robustness and stability) and integrates machine assignments and operations sequencing with the expected machine breakdowns. Continuing with the scope of a flexible JSP, a hybrid tabu search algorithm with a fast public critical block neighborhood structure (TSPCB) is proposed by Li et al. [19].

These authors present a mixture of four machine assignment rules and four operation scheduling rules to improve the quality of the initial solutions and provide the hybrid algorithm with good exploration capability. Then, they put forward an efficient neighborhood structure to perform local searches in the machine allocation module, which integrates three adaptive approaches. Finally, they present a speedup local search method with three types of insertion and swap neighborhood structures based on the public critical block theory. In line with this, Li and Gao [20] report an effective HGA that hybridizes the genetic algorithm (GA) and tabu search (TS) to address the flexible JSP with a view to minimize the makespan. The GA has a powerful global searching ability, and the TS has a valuable local searching ability.

Thiruvady et al. [21] deal with the Resource Constrained Job Scheduling (RCJS) problem by proposing two MIP-based matheuristic approaches that rely on the solution merging concept to learn from a population of solutions and to use an MIP to generate a “merged” solution in the subspace, which is spanned by a pool of heuristic solutions. The first approach is the Merge Search (MS) and the second is Construct, Merge, Solve and Adapt (CMSA).

Rohaninejad et al. [22] address the JSP of parallel machines with incompatible job families and proposes an efficient matheuristic algorithm based on the hybridization of a GA and a local search (LS) method based on mixed integer programming (MIP). The GA is used to optimize the subproblems related to determining the sequence of parts and the allocation of parts to machines. The allocation of parts to batches is performed by an effective heuristic named batching heuristic (GA_BH) by combining a GA with a batching heuristic (BH). Moreover, the authors propose a combination of a GA and a dispatching rule called Apparent Tardiness Cost (GA_ATC). Dang et al. [23] also deal with the JSP of parallel machines with tool replacements to schedule a set of jobs with tool requirements on identical parallel machines in a work center. To do so, the authors propose a mathematical model for the problem and a matheuristic that combines a GA and an integer linear programming (ILP) formulation to solve large datasets. The matheuristic integrates ILP into the GA framework as a local search step to enhance GA performance.

Ahmadian and Salehipour [24] deal with the just-in-time job-shop scheduling problem (JIT–JSP) with distinct due dates for operations with earliness and tardiness penalties. For this purpose, the authors propose a matheuristic algorithm that decomposes the problem into smaller subproblems to obtain optimal or near-optimal sequences to perform the operations for the subproblems, which provides a feasible schedule for the complete problem. The algorithm forms the subproblems by applying two neighborhoods. The employed algorithms are the Giffler Thompson (GT) algorithm, the Shifting Bottleneck Heuristic (SBH) algorithm, the variable neighborhood search (VNS), and the relaxation neighborhood.

Son et al. [25] address the problem of scheduling jobs with limited splitting on a single machine in the available time windows. These authors present an MILP formulation for this problem and propose different heuristics related to the assignment strategy, such as: assignment heuristic (AH); heuristic based on the shortest/longest processing time rules (HSLPTR); heuristic based on max flow resolution (HMAXFR); and heuristic based on a matching and assignment approach (MAAS). They also apply a combination between the proposed heuristics and metaheuristics, such as tabu search and the GA.

These authors also introduce another approach called exact for subset-jobs matheuristic, which combines mathematical programming, and a priority heuristic rule called the single-attribute priority rule.

Cota et al. [26] propose a solution to address the JSP with unrelated parallel machines with sequence-dependent setup times, and independent non-preemptible jobs, minimizing the makespan and the total consumption of electricity. The authors define a multi-objective smart pool search matheuristic for finding solutions near the Pareto front, in which different MILP problems are generated with different weights for aggregating both objective functions involved in the proposed formulation.

From the review, we can state that very few papers apply combined or hybrid algorithms, such as matheuristic algorithms. In other production fields, matheuristics have obtained good solutions. The research of Cabrera-Guerrero et al. [27] demonstrates that the combination of techniques, or hybridization, can be advantageous for solving complex problems, which is also demonstrated in [28]. Verbiest et al. [28] used a combination of an iterated local search algorithm (metaheuristics) with an MILP model to optimize production lines, design installed lines and allocate products. Their study compares the matheuristic approach with an exact method (MILP) to verify that the matheuristic offers efficient solutions and in a shorter calculation time. According to the results of the studied works, we conclude that matheuristic techniques are suitable for solving problems in realistic instances and allow good results to be obtained in acceptable computing times. Nevertheless, experiments are carried out on commercial solvers, which can be a drawback for those enterprises that cannot afford these tools. Moreover, the maximum data size used for experiments are 120 jobs on six machines, and 20 jobs on 10 machines, which cannot be completely representative of enterprises’ realistic data.

Although matheuristics is becoming increasingly well-known for its effectiveness and computational efficiency when dealing with large and NP-hard problems, there is still a long way to go in this field. The contribution of this research aims to provide a solution to the NP-hard JSP with the proposed matheuristic approach by combining a GA and an LP model using a non-commercial solver (CBC) and an open-source operating system (Linux) for a large set of instances.

3. Job-Shop Scheduling Problem: Disjunctive Mathematical Formulation

The JSP is an optimization problem in which a set of jobs to manufacture products is assigned to machines at particular times, while attempting to minimize the makespan [17]. Job-shop scheduling is still a problem that has been analyzed since 1954 [29], and is currently tackled given its impact on production costs and efficiency. Nowadays, the JSP remains in essence, but researchers focus on proposing resolution methods that enable enterprises to obtain optimal or near-optimal solutions in shorter computational times to boost the principles of agility, responsiveness and flexibility, all of which are framed within achieving resilience.

The literature proposes different mathematical formulations to model the JSP. Pan [30] presents a comparative analysis of these formulations, namely time-indexed formulation, rank-based formulation and disjunctive formulation. He concluded that the disjunctive model is more efficient because it has the fewest binary variables. More recent studies, such as that presented by Ku and Beck [5], confirm the functionality and effectiveness of the disjunctive model. Although other mathematical formulations exist, they are often combinations or variations of the formulations that we reviewed.

With this background, disjunctive formulation was chosen to model the JSP. To solve the JSP disjunctive problem, we propose combining disjunctive formulation (MILP model) and the GA to generate a matheuristic solution method, whose main aim is to find efficient solutions for large-sized problems and achieve shorter computational times.

The work is then validated by comparing the obtained solutions among the acquired results to solve the JSP disjunctive MILP with a coin-OR Branch & Cut open-source solver.

In this section, we formally define the JSP disjunctive MILP (see

Table 2. The mathematical notations used in the JSP formulation.

Sets
J	set of jobs, J $\in$ { 1,…, n}.
M	set of machines M $\in${1,…, m}
Parameters
pij	represents the processing time of job j on machine i.
${\sigma }_h^j$	denotes the h-th operation of job j
${\sigma }_m^j$	means the final operation of job j
$V$	sum of the processing times of all the operations $V={{\displaystyle \sum }}_{j\in J}{{\displaystyle \sum }}_{i\in M}pij$
Variables
xij	start time of job j on machine i.
zijk	1 if job j is before job k on machine i; 0 otherwise

). The disjunctive model is presented in Ku and Beck [5]. The JSP is given by a J finite set of n jobs or parts, and a finite set M of m machines or work centers. For each job j$\in$ J, the list $({\sigma }_1^j,\dots ,{\sigma }_h^j,\dots ,{\sigma }_m^j)$ of machines with the processing order of job j is provided. Only one job can be processed by each machine at a time. Once started, it must finish processing on that machine without any interruptions.

$$\min Cmax$$

(1)

$$\mathrm{s}.\mathrm{t}. x_{ij}\ge 0,\forall j\in J, i\in M$$

(2)

$$x_{{\sigma }_h^j,j}\ge x_{{\sigma }_{h-1}^j,j}+p_{{\sigma }_{h-1}^j,j},\forall j\in J, h=2,\dots , m$$

(3)

$$x_{ij}\ge x_{ik}+p_{ik}-V · z_{ijk},\forall j,k\in J,j<k, i\in M$$

(4)

$$x_{ik}\ge x_{ij}+p_{ij}-V · (1-z_{ijk}),\forall j,k\in J,j<k, i\in M$$

(5)

$$Cmax \ge x_{{\sigma }_m^j,j}+p_{{\sigma }_m^j,j},\forall j\in J$$

(6)

$$z_{ijk} \in \left\{0, 1\right\} \forall j,k\in J,i \in M$$

(7)

$$x_{ij} \in \mathbb{Z} \forall j,k\in J$$

(8)

The purpose is to obtain a scheduling of jobs on machines to minimize the makespan (Cmax). Constraint (2) guarantees that each job’s start time equals or exceeds 0. Constraint (3) assures that each operation of a job is carried out in the required order. Disjunctive Constraints (4) and (5) establish that there cannot be two jobs scheduled on one machine at the same time. It is necessary to assign V a large enough value to guarantee the correctness of (4) and (5). The completion time of any operation must not exceed the sum of the processing times of all the operations. Constraint (6) guarantees that the makespan is the longest completion time of the last operation of all the jobs as a minimum [5].

4. Materials and Methods

4.1. Proposed Matheuristic Approach

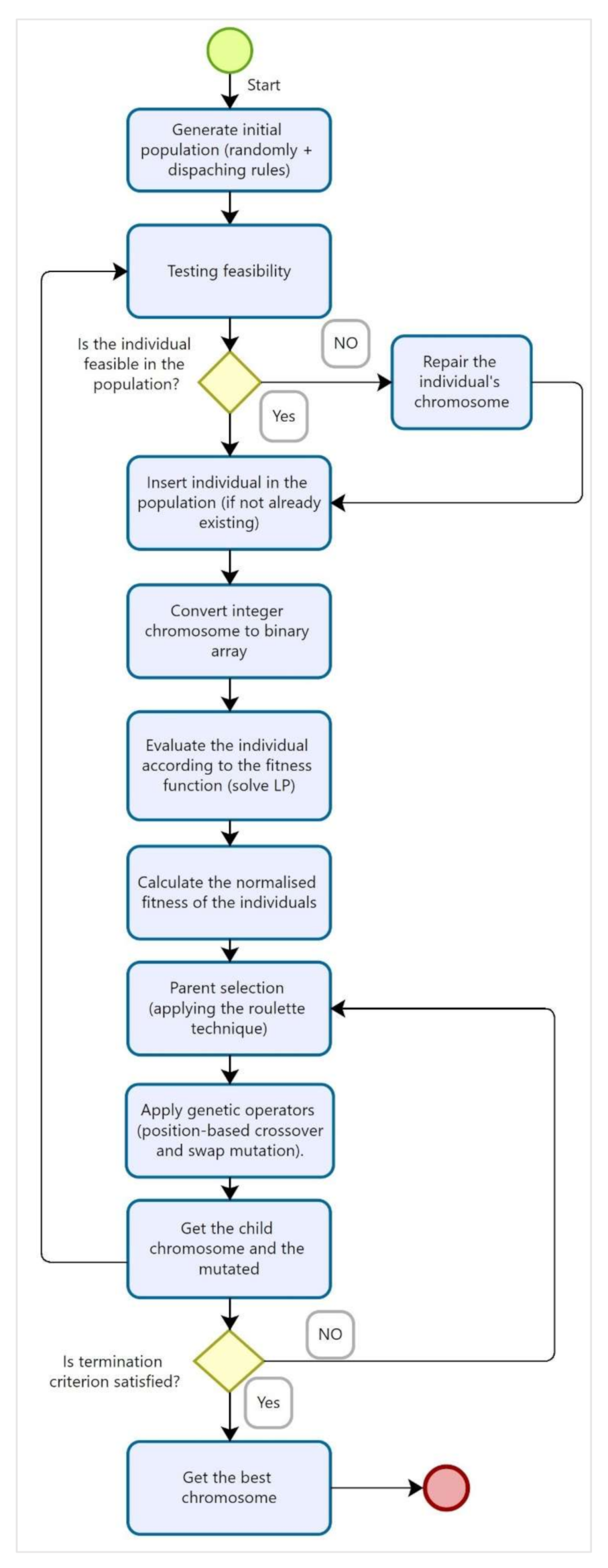
The aim of this section is to provide a matheuristic approach to solve the JSP quickly and efficiently, particularly for large-sized problems. To do so, we design a matheuristic approach by applying the metaheuristic procedure (GA) in an LP model (GA-LP). The flowchart of the matheuristic approach is shown in Figure 1. All the elements of the proposed matheuristic are separately detailed in the following subsections. The general procedure of the proposed approach is as follows:

Step 1: set the input parameters of the matheuristic (GA-LP);

Step 2: generate the initial population: generate individuals using dispatching heuristic rules and generate individuals randomly;

Step 3: evaluate whether the individuals forming the initial population are feasible;

Step 4: eliminate nonviable individuals and insert the feasible ones into the population;

Step 5: convert the integer chromosome generated by the GA into a binary chromosome;

Step 6: evaluate binary individuals using the LP model;

Step 7: normalize individuals’ fitness;

Step 8: select two individuals from the population (parents) and use genetic operators (crossover and mutation);

Step 9 evaluate the chromosomes of the offspring and check if chromosomes are feasible. Then, go to step 3.

Step 10: Are the termination criteria met?

If the termination criteria are met, the solution is obtained; otherwise, go to step 8.

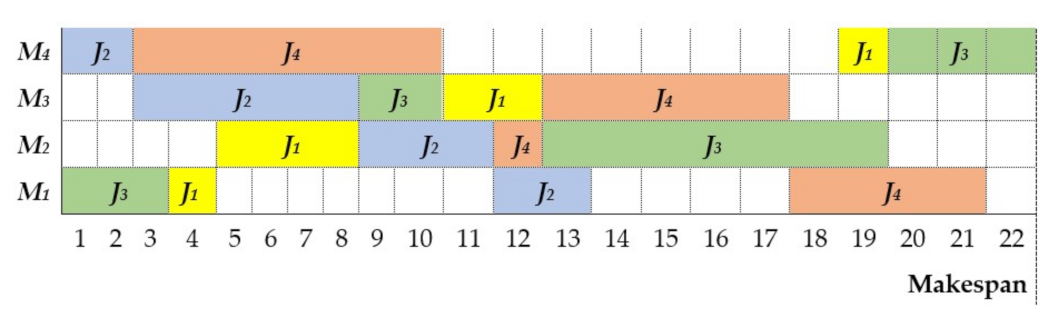
To properly define the proposed matheuristic, we pose a simple JSP example shown in

Table 3. The job-shop scheduling problem data.

Job	Processing Order of Jobs	Processing Times
1	σ11, σ22, σ33, σ44	p11 = 1; p21 = 4; p31 = 2; p41 = 1
2	σ14, σ23, σ32, σ41	p12 = 2; p22 = 3; p32 = 6; p42 = 2
3	σ11, σ23, σ32, σ44	p13 = 3; p23 = 7; p33 = 2; p43 = 3
4	σ14, σ22, σ33, σ41	p14 = 4; p24 = 1; p34 = 5; p44 = 8

. The data presented in Table 3 indicate that there are n = 4 jobs (J₁, J₂, J₃, J₄). The processing order of the jobs on the machines $\left({\sigma }_{mo}\right)$ are seen in the second column; for example, J₁ has σ₁₁, in which the first index represents the machine and the second denotes the processing order; i.e., job 1 has to be processed first on machine 1, followed by machines m₂, m₃, and m₄, respectively. The processing time of job j on machine i (p_ij) is shown in the third column of this table.

4.2. Initial Population

Genetic algorithms consist of a set of individuals. Each individual has a chromosome structure composed of genes where the value of each gene represents the jobs performed by each machine. The whole chromosome represents the solution to the problem (see Figure 2).

The GA starts by randomly generating a set of individuals, which is called the initial population. The chromosome of the randomly created individuals can cause the fitness function value to be deficient and can also generate infeasible solutions. Therefore, in the proposed methodology, we use heuristic priority rules to obtain better fitness values by, thus, employing genetic operators so that better solutions can be obtained. In our approach, 80% of the initial population is randomly generated and the rest is generated with the following heuristic priority rules:

▪

First In First Out—FIFO: the first job to arrive is the first to be served;

▪

Last In First Out—LIFO: the last job to arrive is the first to be served;

▪

Shortest Operation Time—SOT: the job that has the shortest processing time is selected. It achieves high flow rate and utilization rates;

▪

Longest Operation Time—LOT: the job with the longest processing time is selected. The longest operations are considered to be the most important and should be processed first;

▪

Shortest Remaining Operation Time—SROT: the priority job is the job with the lowest sum of the processing times for all the remaining operations to be performed;

▪

Longest Remaining Operation Time—LRPT: the priority job is the job with the largest sum of the processing times for all the remaining operations to be performed;

▪

Less Remaining Operations—LRO: the priority job is that with the fewest remaining operations to be performed;

▪

Most Remaining Operations—MRO: the priority job is that with the most remaining operations to be performed;

▪

Work In Next Queue—WINQ: the highest priority is given to the job that would be moved to the machine with the least work to do;

▪

Due Date—DD: the job with the closest delivery date is selected;

▪

Static Slack -SS: the job with the shortest time remaining until the delivery date is selected;

▪

Dynamic Slack—DS: time remaining until the delivery date minus the sum of all the remaining operation times. That with the shortest DS is selected;

▪

SS/Remaining Operation Time—SS/TPR: Static Slack divided by the sum of the remaining operation times of the remaining operations. The smallest one is selected;

▪

DS/Remaining Operation Time—DS/TPR: Dynamic Slack divided by the sum of the remaining operation times of the remaining operations. The smallest one is selected;

▪

SS/Remaining Operations—SS/RO: Static Slack divided by the number of remaining operations. The smallest one is selected;

▪

DS/Remaining Operations—DS/RO: Dynamic Slack divided by the number of remaining operations. The smallest one is selected.

4.3. Feasibility Tester

Randomly generated individuals in the initial population or individuals generated by the crossover and mutation operators may generate infeasible solutions. To avoid the LP having to evaluate infeasible solutions, which makes the matheuristic processing time longer, we present an approach to check the feasibility of individuals. To exemplify the feasibility checker,

Table 4. Sequence of jobs on machines.

Machines	Feasible Sequence				Infeasible Sequence				Corrected Sequence
1	J3	J1	J2	J4	J3	J1	J2	J4	J3	J1	J2	J4
2	J1	J2	J4	J3	J1	J2	J4	J3	J1	J2	J4	J3
3	J2	J3	J1	J4	J2	J1	J3	J4	J3	J2	J1	J4
4	J2	J4	J1	J3	J1	J2	J4	J3	J2	J1	J4	J3

shows the one feasible sequence and one infeasible sequence that should be corrected.

Infeasibility occurs when jobs do not satisfy the processing order on machines. Table 3 shows the processing order of the jobs on machines where, for example, J₁ has the processing order: σ₁₁, σ₂₂, σ₃₃, σ₄₄, i.e., J₁ should be processed first on M₁ and then on machines M₂, M₃, M₄ respectively. Figure 3 illustrates the feasible solution for all the jobs to fulfill the processing constraints.

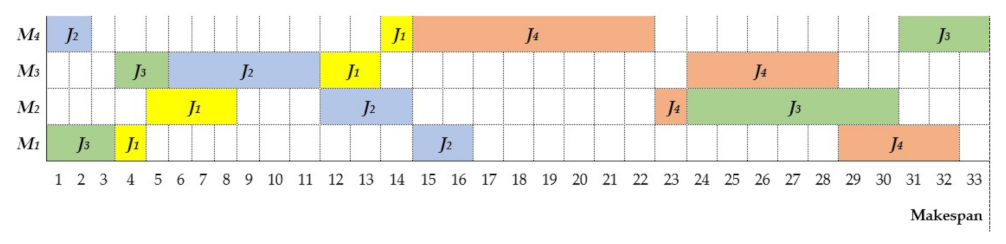
To exemplify the feasibility tester, we present an unviable solution (see Table 4). In Figure 4, we represent the solution, but, as observed, the sequence of J₁ does not comply with the processing order. In the same way, J₂ cannot be located as the processing order of J₂ is σ₁₄, σ₂₃, σ₃₂, σ₄₁. This means that it must first be processed on M₄ and then on M₃, M₂, M₁. However, J₁ on machine 4 leads to the processing order not being fulfilled because predecessor J₁ on machine 3 is processed after the job of its successor J₁ on machine 4. This is what causes the infeasibility in the chromosome of the individuals. Therefore, the chromosome must be repaired.

After verifying infeasibility, the feasibility tester changes the location of J₁ and J₂ on machine 4 and, in the same way, the positions of J₁, J₂, J₃ on machine 3 (see Table 4). After using the feasibility checker in Figure 5, the representation of the solution that meets all the precedence constraints is shown.

4.4. Fitness Function

The individuals in the population are evaluated with the fitness function, which measures the quality of solutions. The evaluation of individuals is performed using the disjunctive relaxed MILP model, i.e., an LP model. Thus, binary variable z_ijk represents whether job j is prior to job k on machine i, and is calculated by the GA. Hence, this variable is fixed to the LP. The binary variable is calculated sequentially with the GA, i.e., while the GA generates individuals, the LP evaluates that the chromosome meets the constraints of the disjunctive model described in Section 3.

As individuals have an integer chromosome and variable z_ijk is binary in nature, we convert the chromosome. For this purpose, we use the position of each gene as shown in Figure 6. Machine 1 has sequences J₃, J₁, J₂, J₄. We start by looking for the location of the first predecessor job, that is job 1, and this gene is in position 2. Then, we look for the successor job, which is job 2 that meets the condition of the position of the predecessor job being inferior to the successor job. Thus, we assign 1. This same condition is met by predecessor job J₁ and successor job J₄, but this condition is not met by J₃, which is in position 1.

Table 5. Precedence of jobs with binary array z_ij.

i	j	k	z
1	1	2	1
1	1	4	1
1	2	4	1
1	3	1	1
1	3	2	1
1	3	4	1
2	1	2	1
2	1	3	1
2	1	4	1
2	2	3	1
2	2	4	1
2	4	3	1
3	1	4	1
3	2	1	1
3	2	4	1
3	3	1	1
3	3	2	1
3	3	4	1
4	1	3	1
4	1	4	1
4	2	1	1
4	2	3	1
4	2	4	1
4	4	3	1

shows the result obtained with this process.

4.5. Selection

Before applying the selection operator, the normalized fitness of the individuals in the population is calculated with the difference between the highest fitness value and the fitness value of each individual.

The selection operator is in charge of deciding which individuals in the population will have the opportunity to reproduce. As a selection operator, we employ a roulette wheel approach [31]. This approach consists of the best individuals, according to their fitness, having the best opportunity to be selected with a uniform selection probability within the range [0…1].

4.6. Crossover Operator

The crossover operator used by the GA is the Partially Mapped Crossover Operator. Given the fact that the chromosome of the individuals has an ordered set of permutations, this operator allows for the creation of non-repeated permutation, which it does by choosing two crossover points at random that delimit the area to be inherited. The offspring takes any value of this area from one parent and the rest from the other, which can produce duplicates. To remove duplicates, this method uses a map, on which it checks the relation between the copied sections, and verifies if there is a duplicate gene or a missing gene in the chromosome.

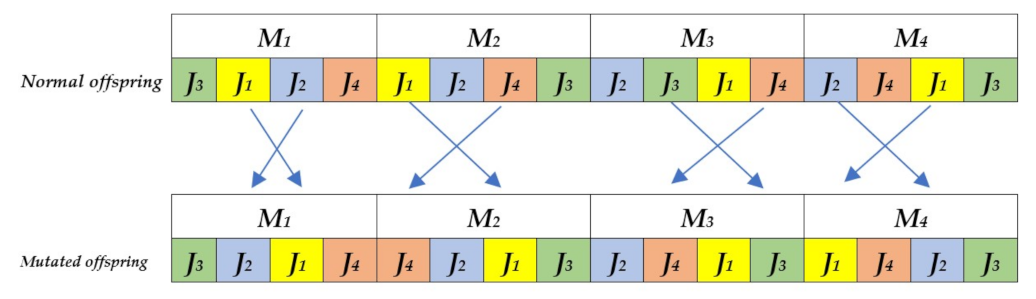
4.7. Mutation Operator

In this paper, we use swap mutation. This procedure is as shown in Figure 7, where we randomly select two positions from each machine, and then swap the genes at the selected positions to generate a mutated offspring. Our GA employs a mutation probability (pm = 1). As the mutated offspring can give a worse fitness value than the normal offspring [32], we insert the normal and the mutated one into the population if they do not exist after passing the feasibility tester.

5. Computational Experiments

The purpose of this study is to evaluate the performance of the non-commercial CBC solver with both the mathematical model and the matheuristic one on large or similar instances to those used by SMEs. To evaluate the performance of the proposed matheuristic, we test the performance of the disjunctive MILP model by using a CBC solver. For this purpose, we generate experiments that consist of a set of different sized problems (20 × 15, 20 × 20, 30 × 20). To do so, we use the large-scale instances of Taillard [33], specifically the instances labeled Ta11-Ta13, Ta26-Ta28 and Ta41-Ta43. The dataset can be found in [34]. The JSP is NP-hard for n ≥ 3 and m ≥ 2 [5].

The software followed in this research is a non-commercial optimization solver from the Computational Infrastructure for Operation Research (COIN-OR) community called the COIN-OR Branch and Cut Solver [9]. This open-source solver is generally employed for MILP problems. The MILP model and the matheuristic were implemented in Python with the Pyomo package [35]. Experiments were run by an Intel Core i7 2.80 GHz processor (8 GB RAM) in the Ubuntu 20.04.1 LTS operating system.

The GA-LP was run 10 times with the same problem instances. The stopping criterion of the mathematical model and matheuristic is 3600 s. The parameters used in the GA-LP are shown in

Table 6. GA-LP parameters.

Population size	100
Crossover operator	Partially Mapped Crossover
Selection operator	Roulette wheel
Mutation operator	Swap
Mutation ratio	1

. The average solutions (Cmax) of the GA-LP and the time in which the methods reached the best solutions are shown in

Table 7. Comparison of how the proposed approaches perform.

Problem	n × m	Methods
		CBC			Matheuristic (GA-LP)
		Cmax	CPU (sec)	D1 (%)	Cmax	CPU (sec)	D (%)
Ta11	20 × 15	2219	3567.57	35.55%	1637	198.67	0%
Ta12	20 × 15	-		-	1627	196.09	0%
Ta13	20 × 15	1902	3565.46	15.06%	1653	64.16	0%
Ta26	20 × 20	2483	2673.88	29.32%	1920	152.79	0%
Ta27	20 × 20	-		-	1982	234.88	0%
Ta28	20 × 20	1978	2948.2	3.55%	1910.2	267.64	0%
Ta41	30 × 20	3282	3227.24	32.82%	2471	366.47	0%
Ta42	30 × 20	-			2415	361.36	0%
Ta43	30 × 20	-			2350	373.08	0%

¹ Deviation = [(Obtained Value—Best Value)/Best Value].

.

The results show that the CBC solver cannot obtain good results for the Ta12, Ta27, Ta42 and Ta43 instances because of its computational difficulty. It is noteworthy that the matheuristic algorithm obtained good solutions in relatively shorter computational times than the CBC solver.

Figure 8 offers the results obtained with instances Ta11 (20 × 15), Ta25 (20 × 20) and Ta41 (30 × 20). The computational results of CBC for instances Ta12, Ta27, Ta42 and Ta43, are relatively bad, and do not converge to good solutions. For these instances, we changed the stopping criterion to check if the CBC solver can obtain better results, with a computing time of 4 h. We confirm that the result is still the same. The deviation value of these instances is not shown in Figure 8 as it cannot be compared with the matheuristic.

From Figure 8, it is deduced that the matheuristic produces better results and allows good solutions in short computational times. Table 7 shows the results of deviations, where the GA-LP approach provides the best solution for each problem size. GA-LP provides better solutions than CBC, especially with rising computational difficulty. All these results indicate that, by using 20% of the individuals in the initial population with heuristic priority rules, we can improve the efficiency of the proposed method for large instances.

The Figure 9 shows the box plots of the two proposed methods for instances Ta11, Ta26 and Ta41. The distribution of the results can be observed in the box plot. The stability of the matheuristic algorithm results is more stable than the CBC. According to the results. we conclude that GA-LP provides better solutions for all the instances in quality and solution time terms.

6. Conclusions and Further Work

The new production paradigms offer plenty of opportunities and challenges as they support the transformation of technology and market conditions for companies. The adaptation of companies to Industry 4.0 means that companies must look for technological tools that help to optimize their manufacturing processes. The adaptation to this technology is determined by adapting different technological tools to the companies. In many cases, SMEs cannot cope with all the technological changes given their cost. Thus, the use of open-source software can act as a valuable tool for companies.

In order to contribute to the literature, this paper presents a matheuristic that combines a GA with a relaxed MILP, solved using a non-commercial solver. We apply different priority heuristic rules to provide faster and more efficient solutions for large problems. The proposed matheuristic achieves good results for large instances. In short computational times, the CBC solver does not offer good results for large instances, but the CBC solver-GA combination provides better solutions in shorter computational times. In the literature, no experiments appear with a non-commercial solver for this instance size. This means that matheuristic can be a useful tool for those SMEs that do not wish to pay for commercial solvers as matheuristic is a useful tool that is easily implemented.

The comparison of the mathematical model, and the matheuristic approach shows that the GA-LP with heuristic priority rules provides good results compared to the CBC results. CBC for the instances of 30 jobs and 20 machines provides the best results in almost 1 h, while the matheuristic approach achieves the best results for these instances in under 400 s. After analyzing the two approaches presented to solve the JSP, we see that the GA-LP is a robust method, is able to achieve good results on instances with different complexities and has a faster convergence rate compared to CBC.

Therefore, future research lines include: improving the GA as the applied genetic operators are standard ones and the operators designed for the concrete problem would perform better; attempting other hybridizations can be performed using: other metaheuristics, such as GRASP, Memetic Algorithm, Particle Swarm Optimization, Tabu Search, Variable Neighborhood Search, and others identified in [10]; testing instances with different job and machine sizes and varying processing times. Other non-commercial solvers can be tested, such as SCIP (Solving Constraint Integer Programs) with commercial solvers like Gurobi and CPLEX.