1. Introduction
It is not a secret that artificial neural networks are nowadays predominant in machine learning applications. As the core component of Deep Learning methods, neural networks have revolutionized the field of predictions [
1,
2]. The first breakthrough was made in computer vision in 2012 with AlexNet, and since then, neural networks became the focus of research where the field is pushed forward every month with new state-of-the-art methods [
3]. Although neural networks are powerful models, they still suffer from many drawbacks. As they are being used in many fields and areas, they face new problems previously unseen.
The bar of expectations for neural networks now is so high that they need to provide human-level performance not only on the data they are trained, but also on different target datasets. However, they cannot do so easily as they are biased towards the dataset they were trained. This problem, known as Domain Gaps, is similar to the problem of overfitting, but in this case, the model generalizes well on the testing data but cannot generalize on new unseen datasets. This challenge increases when dealing with cultural heritage data which is generally difficult to label and acquire, and thus the trained model cannot generalize well.
Transfer Learning is the field of artificial intelligence that focuses on improving a model’s performance on a challenging target domain by leveraging data from a well-known source domain. In particular, Domain Adaptation is a subfield of Transfer Learning that aims to minimize the domain gap between the source and target domains, reducing the required data to train a neural network. This idea has become a best practice where it is considered abnormal to retrain a neural network from scratch but instead use a pre-trained model on a large dataset and then only retrain the last layers. This strategy improves the models’ performance drastically. However, this is still not enough since the source dataset classes do not necessarily overlap with the target domain. In industrial products, the solution is to collect more data and retrain the target model. Nevertheless, augmenting the dataset size is not feasible for cultural heritage data when only a few original artworks are preserved.
Cultural heritage data are challenging to acquire, demanding to label, and vary in style through different historical periods. First, finding medieval artwork images containing a particular type of musical instrument is difficult; the older the instrument, the fewer artworks that contain it are found. Second, as ancient artworks are generally damaged or deteriorated, experts may have difficulties in classifying the instruments. Finally, when dealing with images containing musical instruments from different historical periods, there are significant differences in how they were painted or sculpted. Besides, the instruments may differ according to the artwork supporting materials, such as paintings, manuscripts, photographs, or sculptures. Those difficulties make the training process on such heterogeneous images a more demanding task.
Knowledge Graphs (KG) played a significant role in preserving cultural heritage and modeling human expert knowledge. In the last ten years, hundreds of semantic data models, vocabularies, and knowledge graphs have been developed for digital humanities, such as MusicKG [
4], Sampo [
5], NOnt [
6], or CLARIAH [
7]. Knowledge graphs provide rich semantic context about the images’ content that is useful to extract class-informative embeddings. This article’s contribution is to add semantic information gathered in knowledge graphs when training neural networks with sparse and heterogeneous image datasets, which is the case of cultural heritage data. In this approach, we use knowledge graphs as an anchor for our deep learning models to organize and direct the model’s focus and incorporate not only visual information in the training process but also global and more connected information. We evaluate our method on our collected image dataset of Medieval Musical Instruments, which was annotated and carefully verified by five musicologists specialized in medieval musical instruments. The images we use as source data and their knowledge graph are extracted from the Musiconis dataset (see
Figure 1), whereas our target images came from the Vihuelas dataset [
8].
The rest of the paper sections are organized as follows.
Section 2 is an overview of related works.
Section 3 describes our model in detail. The empirical evaluation of our method is shown in
Section 4. Finally,
Section 5 summarizes the paper.
2. Related Works
Our paper combines transfer learning (domain adaptation) and knowledge graphs to create a novel domain adaptation method that is most suited for cultural heritage datasets. The current state-of-the-art methods rely widely on adversarial and generative models, which provide high performances compared to traditional techniques but require many unsupervised and unstructured data. On the contrary, for cultural heritage data, the number of samples is scarce, but each sample’s labeling and annotations are exhaustive. In most state-of-the-art methods in domain adaptation, a discriminator plays a core role in handling the domain independence characteristic for the latent space and is sometimes used to evaluate the performed adaptation’s efficiency. Knowledge graphs are powerful tools for modeling cultural heritage data, and their embeddings can be used to provide more information about the samples. In this section, we detail some related approaches on these topics and the advancements in the field.
2.1. Knowledge Graph Embeddings
Knowledge graph embeddings methods aim at mapping a component of a KG, including nodes, entities, and relationships between them, into a continuous vector space using algorithms such as Node2Vec. Machine learning models, mainly neural networks, can use the resulting vectors, as this structure is simpler than a graph structure, while preserving the inherent information and structure of the graph [
9]. These techniques have gained popularity due to their wide utility for downstream applications such as KG completion and relation extraction, Recommender Systems, Question Answering, and Relation Extraction from texts.
Knowledge graph embeddings (KGEs) are considered to be a low-dimensional representations of the nodes and relations in a knowledge graph. Knowledge graph embeddings are mappings on different parts of the knowledge graph into a vector space that satisfy certain properties and maintain the information that exists in the graph. Each method defines a score function which measures the distance of two nodes relative to their relation in the mapped embedding space. The goal of these score functions can be summarized as keeping the nodes which are connected to each other in the graph close in the mapped dimension and those which are not connected far from each other. The most famous score functions are TransE, TransR, RESCAL, DistMult, ComplEx, and RotatE [
9].
2.2. Deep Learning Applications Applied to Cultural Heritage
In recent years, multiple deep learning applications applied to cultural heritage (CH) have been developed, especially for images of ancient paintings and historical artworks. Most of CH’s applications are in the domain of computer vision. One of the major drawbacks of CH applications’ implementation is the quality and quantity of annotated datasets available to train and test deep learning algorithms. In general, the data are scarce, and copyrights restrict their reuse and publication. Several historical manuscript image datasets have been proposed [
10,
11,
12] with the goal of training and evaluating deep learning methods. Digitalized manuscripts datasets are mainly used for document analysis and text recognition [
13,
14,
15]. As we are interested in ancient musical instruments recognition, we need manuscripts that are illuminated. Among the existing illuminated manuscripts datasets, we can mention the HBA corpus [
16], or the HORAE dataset [
17], but none of them contain musical instruments. Other datasets containing artistic artworks are PrintArt [
18], BAM [
19], and OmniArt [
20].
Neural networks, ranging from Convolutional Neural Networks (CNNs) to Mask R-CNN [
21], are useful in recognizing high-level artworks features from the low-level image features like colors, shapes, and texture. Therefore, they are widely used in CH’s applications manipulating images of artworks and paintings, such as object detection [
22,
23], image classification [
18,
24,
25], image description and captioning [
26,
27,
28], or answering visual questions [
29] in artworks and paintings.
Writer Identification is another field that has attracted attention in this area; it classifies a page of handwritten historical document scans to their original author or artist. There exist two main streams for solving this task: the easier one is building a row-level model followed by a majority classifier using CNNs [
30], whereas the other is a facial recognition inspired method which embeds the whole scan and computes distances between the training data and the new samples. Another promising application of deep learning to medieval and historical works is predicting the creating date of artworks, like the approach presented in [
31] that used Convolutional Neural Networks and outperformed the traditional rule-based systems used before.
However, the use of deep learning techniques is not always enough to interpret artworks. The vision of a human expert is essential to understand the content and meaning of artworks fully. Therefore, state-of-the-art methods include ontologies and knowledge graphs that model human knowledge to improve neural networks results. These approaches with graph embeddings [
32] and graph neural networks [
33] aim at creating meaningful vector representations including structural graph information (such as nodes and edges) as well as the content information (such as texts or images) of each node. The method presented in this article combining knowledge graph embeddings with visual embeddings is a clear example of such approaches.
2.3. Domain Adaptation for Image Classification
Domain adaptation (DA) aims at reducing the domain gap between the source and target domains. In mathematical terms, there are two domains: the source domain
and the target domain
. DA improves the results on a task on the source domain
by leveraging the target domain’s data and its task
. In our case, we are interested in classification tasks, and thus both source and target tasks are classification problems; however, their domains’ marginal distributions differ, i.e.,
[
34].
There are two main subfields of domain adaptation which are closed-set and open-set. In closed-set domain adaptation [
35,
36], the classes of both domains are the same; in other words,
precisely, whereas in open-set domain adaptation, the classes might not be the same, but they share some common labels; in mathematical terms,
. Our work handles the case of open-set domain adaptation. It provides a more challenging scenario and more applicable in real-world cases, especially in cultural heritage datasets that rarely share the same classes between datasets as different tools and instruments were used in different historical periods.
3. Cultural Heritage Datasets
We evaluated our KG embedding-based domain adaptation approach on music iconographical data. The analysis of ancient artworks containing musical instruments brings valuable information on the instruments’ nature, physical characteristics, or playing methods. In this section, we present the image datasets and the knowledge graph used to test our proposal.
3.1. Medieval and Renaissance Musical Iconography as Source and Target Domains
As we mentioned before, transfer learning aims to improve a model’s performance on a target domain by reusing a trained model on an already-known source domain. This article uses an image dataset of medieval musical instruments as the source domain and a renaissance musical instruments database as the target domain. Previously in [
37], we presented a new manually annotated image dataset of historical musical instruments and a non-intrusive Transfer Learning method for object detection. While in [
38], we proposed another method for unsupervised domain adaptation, which starts by applying style transformations to the input images and train a transformation discriminator module to predict these style changes. Based on these previous articles, we reused the lessons learned to detect chordophones in medieval artworks, to detect herein vihuelas (a Spanish renaissance chordophone) from a small collection of images. In this article, we combined knowledge graph embeddings with visual embeddings from the images and trained a neural network with the combined embeddings to take our methods a step forward.
Musiconis database (
http://musiconis.huma-num.fr/en/, accessed on 30 July 2021): Musiconis is a meta-database containing a vast collection of artworks images from the Middle Ages. Currently, it is the largest collection of musical iconography representing sound and music between the 5th century and the 15th century. The original images come from several international partner institutions or museums, such as the National French Library in Paris, the Courtauld Institute of Art in London, or the Metropolitan Museum of Art in New York. The Musiconis database contains 2154 iconographic representations whose scenes not only contain musical but also vocal, acrobatic or choreographic performances. Musicologists deeply analyzed these scenes, and each musical instrument was carefully described with organological details.
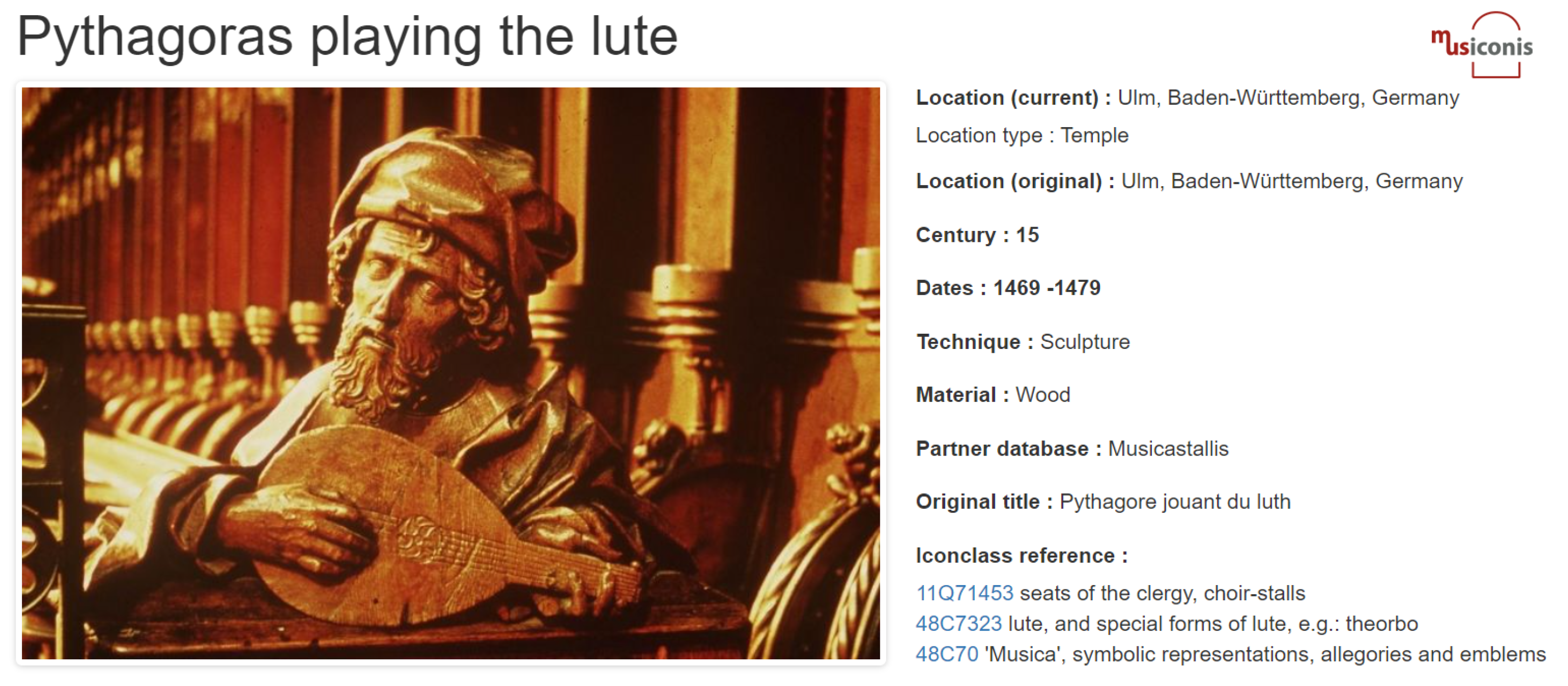
Figure 2 depicts a Musiconis’ example of a wood sculpture in a choir (area of a church that provides seating for the clergy and church choir) in which Pythagoras plays the lute (
http://musiconis.huma-num.fr/en/fiche/198/pythagore.html, accessed on 30 July 2021). From all the available images in Musiconis, we annotated a subset of 662 chordophones as the objective is to detect vihuelas, a small Renaissance chordophone. The image distribution is as follows: 112 are Citharas, 132 harps, 56 lutes, 75 lyres, and 327 vielles (217 vielles played with a bow).
Vihuela database (
https://vihuelagriffiths.com/, accessed on 30 July 2021): This database [
8] is a collection of artwork images depicting vihuelas from the Renaissance period. The vihuela was a popular string instrument in Spain and its colonies between the 15th and 16th centuries. This musical instrument has a shape similar to the modern guitar but is tuned like a lute. There is also a bowed version called “vihuela de arco”, which could be considered a modern violin precursor. Vihuelas also became popular in Italy and Portugal as they were easier to play and tune than other bowed string instruments. Even if there are several similarities between vihuelas and previous medieval chordophones, the principal difference is the vihuela’s body shape (like the number eight). Besides, the vihuela’s body is made from thin flat pieces of wood, which differs from previous string instruments whose bodies were carved from a single block of wood. From this database, we annotated 165 chordophones in total. As it is a dataset of vihuelas, most of the annotated instruments are from the lutes family. The image distribution is as follows: 130 lutes, 31 vielles (27 with a bow), five harps, and two lyres.
3.2. MusicKG: A Knowledge Graph of Medieval Musical Iconography
MusicKG is a multilingual knowledge graph (KG) of medieval musical iconography. This KG models as RDF triples the representations of sound and music in the Musiconis database. Following the W3C recommendations, MusicKG is linked to other popular Knowledge Graphs, such as Wikidata, Getty Vocabularies, Iconclass, MIMO, and Geonames. In MusicKG, not only the artwork characteristics (such as artist, material used, or inception) are modeled, but also all the different scenes inside that artwork (for example, a couple dancing and a musician playing behind). In turn, each scene is described exhaustively by depicting the performer’s characteristics (type, genre, clothing, and position), the musical instrument’s characteristics (type, family, and material), the sound created, and the analogies, if any. Even though MusicKG is an extensive graph of relationships between performances and iconographic entities, we decided to use only a subset of all the RDF triples to create embeddings. Using a smaller graph allows us to better visualize and interpret the results. Once our approach efficiency has been proven, we plan to use all the available RDF triples to exploit the full potential of the KG.
The Musiconis example presented before in
Figure 2 is depicted as a MusicKG artwork instance in
Figure 3. The main class is
Visual artwork (herein “artwork”) which is connected to the original sources through several predicates:
official website,
collection,
inventory number, and
described at URL. Furthermore, each artwork instance has a
title from Musiconis and a title from its original database in the
stated as property. Generally, several
images are associated with an artwork to capture all the details from different angles and different resolutions. Regarding dates, each artwork has
start time,
end time, and
time period that indicate the century, the date on which the artist began and finished creating the artwork, respectively. The relation
material used describes the material an artwork is made of, such as
Wood or
Ivory for sculptures; or
Textile for embroideries and tapestry weavings. The relation
fabrication method relates an artwork with its
Artistic technique, such as
Sculpture or
Painting.
4. Methodology
This section describes our approach for domain adaptation using knowledge graph embeddings as anchors for our encoders. We start by presenting the terminology used, then detailing the components of our method, and finally describing the losses to train the different components.
Before providing the mathematical functions and different losses, we establish the terminology and annotations used throughout the paper. We denote the source domain as where represent the input images with variant sizes, is their respective classes, and N being the size of the source dataset. In this approach, it is important to note that the source domain is associated with a preexisting knowledge graph that connects the images of the dataset with concepts in the graph, creating clusters of data around each concept. Thus, the images are linked together with not just the class information but also along several axes.
The target domain data are referred as , where represents the target images, represents their respective classes, and M being the size of the target dataset. Domain Adaptation deals with the case where these two datasets share similar classes but usually come from a different distribution (meaning they have some large differences in terms of style, which lead neural networks to be unable to generalize). As our research focuses on open-set domain adaptation, the classes of both domains overlap but do not necessarily have to be the same.
Our model contains two main components typically found in every computer vision classifier: the and the with an additional latent space mapper (the ) which converts the visual embeddings into the same dimensions as the knowledge graph embeddings (after training, it is considered to be a final layer of the Encoder). They are both present during the training and the inference phase. We can define our model function f as the composition of the Encoder function e and the classifier function c such that where maps the input images into a vectorial-1D latent space which is considered as the embedding of the visual information of the image, used later to classify it into its corresponding class using which maps the embeddings space into the label space.
Our model’s strength comes from a mathematical heuristic used to guide the neural network weight optimization through embedding anchors generated from the associated knowledge graph, which is based on Linear Discriminant Analysis (LDA).
4.1. Architecture
In this subsection, we detail the components of our method from a topology perspective. As shown in
Figure 4, the principal components are the
,
, and
.
Encoder: Our feature extractor
is a pre-trained pure Convolutional Neural Network extractor with weights
. In most cases it should contain only elements such as convolutional layers and max-pooling with a Flattening layer in the end, but as different pre-trained model architectures exist, the components of our model might vary to include things such as residual blocks. The Encoder aims at transferring the shape of the input images from a 2D array with 3 channels to a 1D vector that fully connected neural networks can use, as shown in the following formula:
In our formulation, is the annotation for the 1D vector space extracted by the pre-trained Encoder, which represents (extracts) the visual embedding of the image. For differentiation between the visual embedding and the knowledge graph embedding, we use a lower case v to index the visual embeddings. The embedding space is a flat vector of the same size for all images. In this case, it is a set of v float numbers such that depending on the model. The Encoder’s output is sent to the space-mapper, which is later used for training the Classifier. The desired behavior for the visual embeddings is to be a class-informative, meaning it extracts information about the label of the object in the image, and domain-independent, meaning images of the same class should be clustered together regardless of their original domain. In the rest of the section, we annotate the Encoder’s output of source domain samples as and the target samples latent space is . In the results section we use an encoder extracted from the pre-trained weights of Resnet 18 trained on ImageNet.
Dimension Mapper: We used a pre-trained model in order to improve the results of our models; this leads to having different latent spaces dimensions. The Dimension Mapper outputs the Encoder embeddings (which is in
) into the dimension of the knowledge graph embeddings (which is in
) as defined in the following operation:
Such that our Dimension Mapper is a function that maps the values as follows .
Classifier: We are using an Encoder/Classifier scenario. While the Encoder is the only pre-trained part and might include different layer types, the Classifier is a simplified fully-connected neural network (Multi-Layer Perceptron)
. This type of Classifier is commonly employed for all image classification cases, such as multi-class classification and binary classification, depending on the chosen final loss function (which might be a binary cross-entropy or cross-entropy). In this work, as our dataset contains several classes, we chose cross-entropy as the loss function. As indicated above, the input of our Classifier is the mapped visual latent space, which was transformed from
to
where
in our case. In contrast, the output is a 1-D probability vector that provides the model’s prediction and its probability of belonging to each class
. The classifier function is defined as follows:
In our annotations, we use to reference vector of per-class probabilities, which is the output of the classifier such that meaning it is shared between both domains regardless. Before starting the domain adaptation process, we first train the Encoder, Dimension Mapper, and Classifier on the source domain until we reach convergence. Later, we use the Classifier’s output for the target domain as pseudolabels, which will help us to better train the model, but only if the Classifier is confident in his decision. We set the threshold such that .
4.2. Losses
This section describes in detail the loss functions that our model uses to train its components.
Classification Loss: As expected, the first loss our model is trained on is the classification loss, which in our case is the cross-entropy loss function
that reduces the differences between the probability distributions of the output and the labels, as they are between 0 and 1, according to the following formula:
We use as a hyperparameter to control the contribution to the loss between the two domains. This loss affects the training of the Encoder, Classifier, and Dimension Mapper.
Anchoring Loss: The core contribution of our method relies on the anchoring loss, which takes the knowledge graph embeddings as anchors and brings the mapped visual embeddings closer to them, creating richer visual embeddings. This loss aims to embed more information in the Encoder’s training without using the data itself as input to the Classifier as it might be missing on some datasets and, most importantly, unavailable on new images. This loss allows our model to combine the increased accuracy of fusion models (which use multiple sources of input data, commonly, images and text, or images and a vector form the tabular data) with the speed and generalizability of one source model used for image classification. This loss is based on a traditional machine learning model, namely, Linear Discriminant Analysis (LDA) and Fisher’s linear discriminant aiming to map input data into a space that linearly separates the samples.
Our goal is not to make the latent space linearly separable as this is impossible in the case of image embeddings and might lead to performance degradations. In fact, the objective is only to reduce the distance between the mean of the source latent space
which are linked to that specific concept allowing the latent space of the mapped visual embeddings to contain more rich information about the source images that the Encoder will be forced to focus on and extract. Our loss follows the following formula:
The goals of this loss are (i) to reduce the distance between the center of mapped visual embeddings of a concept and their corresponding anchor , which is represented in the loss as (, and (ii) to reduce the distance between the center of mapped visual embeddings of a concept and its corresponding mapped visual embeddings ), which represented in the loss as . This formulation of the target proved to be faster in training than directly reducing the distance between the embeddings and their anchors one by one, and yet it provides the same gradients in the end. Our anchoring loss’s second aim is to augment the distance between the centers of the mapped visual embeddings to create more space between them such that . This loss is only used on different concepts and not the same one.
One downside of using this loss is that it usually has higher values than the classification loss and can influence the direction of classification. Besides, this loss is usually very imbalanced and depends on the random samples taken by the data loader and their classes/concepts, so we added a balancing factor to reduce its effect when the classes/concepts are not balanced enough.
4.3. Optimization
We can imagine our model trained on the weighted sum of both losses. Considering the different ratios of loss weights (Classification Loss is usually 10–15 times smaller than the Anchoring Loss), the importance of the Classification Loss (which is vital for the classification), and the performances of our final model; we decided to add a balancing parameter
, which is usually around [0.01, 0.03]. This optimization is summarized in the following formula:
For better understanding of the steps of our model, in Algorithm 1 we provide an algorithmic description that depicts the step-by-step operations needed for our method. The first step of our method starts by leveraging a knowledge graph that describes our source dataset, such as the century or the material used to create an artwork. Later, we create an embedding of each artwork based on its connections with the other nodes in the graph using the node2vec algorithm. These artwork level embeddings help us generate concept level embeddings which will be used as the anchors for training our neural networks. The second step is to train the neural network on Classification Loss, and minimize the overall distance between the center of visual concept embeddings and the normalized center of the knowledge graph concept embeddings. This method enables the Encoder part of the network to extract class-informative and structured latent space, allowing the Classifier to generalize better to other domains.
| Algorithm 1: Knowledge Graph Embedding based Domain Adaptation. |
![Computers 10 00094 i001]() |
5. Results
This section evaluates our method’s ability to embed knowledge graph extracted information to improve the results of image classifiers on complex datasets that suffer from class imbalance and small sample sizes. We used two datasets: the Musiconis dataset with its images, labels, and knowledge graph (MusicKG) and the vihuelas dataset with its images and labels. First, we describe the model’s abilities to generalize and present the per-class accuracy metrics against several baselines that do not use knowledge graphs and show that our model improves their results, proving the efficiency of adding knowledge graph data to computer vision deep learning-based models. Second, we evaluate our model’s performance when we change the source dataset’s size for training to show its sensitivity and resilience. Throughout the results section, all the reported results are the average of 5 runs of the model on the best hyperparameters found using k-fold cross-validation with k = 10. The train–test split is a stratified split with 80% for training and 20% for testing.
5.1. Class Level Evaluation
This subsection presents our enhanced performances against several baselines and shows that knowledge graphs can add value to computer vision models without altering the classification pipeline of classical deep learning-based image classification. We compare our model against three baselines: (1) : a deep learning model sharing our architecture but trained only with the images and labels of the source dataset; (2) : a deep learning model sharing our architecture but trained only with the images and labels of the target dataset; and (3) : a deep learning model sharing our architecture but trained with both the source and the target datasets’ images and labels.
We report the f1-scores for every main class in our dataset (Viele, Lute, Bow) and the macro F1-score for the models in
Table 1, as it strikes a good balance between precision and recall and evaluates the models much better than accuracy as the sample distribution among the classes differ broadly. We chose to use f1-scores for evaluation instead of accuracy as our dataset suffers from class imbalance and hence accuracy metrics are not very informative about the model’s performances. The table clearly shows that our method improves over the three baselines used for comparison. We can also see that the
model outperforms both baselines as it uses the two datasets. Surprisingly the
model outperformed the
model on some classes even though it was not trained on the target data.
5.2. Target Size Evaluation
In the previous subsection, we proved that our method outperforms the baselines. This subsection shows how our method performs against the and baselines when the target data’s size varies. This comparison is important since our method’s principal goal is to use datasets with tiny sample size (the general case of cultural heritage datasets) and still manage to get good results.
As shown in
Table 2, our model’s performances are always higher than the baselines, even in extreme cases. More importantly, our model’s performances were not affected as much as the baselines when reducing the target dataset’s sample size. We can also see that the
baseline was the most affected even though it is the most used technique for small data cases. We can also see that the
model still gives better performances than
and
. However, the drop of performance was significant, especially when going from 100% to 75% where it dropped from 71.83% to a 68.7%, unlike our model that only dropped 1.57% proving our method’s flexibility and efficiency even in extreme cases.
6. Conclusions
We presented a new approach to improve state-of-the-art domain adaptation methods using knowledge graph embeddings. We combined knowledge graph embeddings with visual embeddings from the images and trained a neural network with the combined embeddings as anchors. This method is particularly appropriate when dealing with sparse and heterogeneous datasets, like those we generally face in the digital humanities and cultural heritage domain. We evaluated our approach on two cultural heritage datasets of images containing medieval and renaissance musical instruments. The experimental results showed a significant increase in the baselines and state-of-the-art performance compared with other domain adaptation methods. Besides, our model’s performances were not affected as much as the baselines when reducing the target dataset’s size.