Abstract
Although the development of watermarking techniques has enabled designers to tackle normal processing attacks (e.g., amplitude scaling, noise addition, re-compression), robustness against malicious attacks remains a challenge. The discordant size content replacement attack is an attack against watermarking schemes which performs content replacement that increases or reduces the number of samples in the signal. This attack modifies the content and length of the signal, as well as desynchronizes the position of the watermark and its removal. In this paper, a source-channel coding approach for protecting an audio signal against this attack was applied. Before applying the source-channel encoding, a decimation technique was performed to reduce by one-half the number of samples in the original signal. This technique allowed compressing at a bit rate of 64 kbps and obtaining a watermarked audio signal with an excellent quality scale. In the watermark restoration, an interpolation was applied after the source-channel decoding to recover the content and the length. The procedure of decimation–interpolation was taken because it is a linear and time-invariant operation and is useful in digital audio. A synchronization strategy was designed to detect the positions where the number of samples in the signal was increased or reduced. The restoration ability of the proposed scheme was tested with a mathematical model of the discordant size content replacement attack. The attack model confirmed that it is necessary to design a synchronizing strategy to correctly extract the watermark and to recover the tampered signal. Experimental results show that the scheme has better restoration ability than state-of-the-art schemes. The scheme was able to restore a tampered area of around 20% with very good quality, and up to % with acceptable quality. The robustness against the discordant size content replacement attack was achieved with a transparency threshold above .
1. Introduction
Information security is becoming more and more important. Information hiding for the authentication and recovery of missing multimedia information has been extensively exploited in the last decade. A still challenging problem that causes loss of information is due to the various attacks that can tamper with a signal. Digital watermarking is one of the prospective solutions to this problem. Digital watermarking consists of embedding some information, known as a watermark, imperceptibly and securely in the original medium, to show ownership, content recovery, authenticate the multimedia, establish a secret communications channel, etc. [1]. In the case of content recovery, such watermarking is called self-recovery watermarking. Self-recovery watermarking has two properties: content authentication and self-reconstruction. In self-recovery schemes, a watermark is generated from the content of the original signal and embedded to combat tampering. The amount of the watermark that survives the tampering helps the receiver not only to detect the tampering and localize it, but also to recover the lost content, depending on the tampering rate and the structure applied for the watermark generation. A watermarked signal generated for this purpose is called a self-embedding signal [2]. One of the more severe attacks against watermarking schemes, called the discordant size content replacement attack, has been tried so as to counteract this technique. In an audio signal, this attack performs modifications to the content, causing it to have a meaning that is different from the original. Although most of the audio watermarking techniques have mainly been inspired by watermarking approaches for digital images, due to the temporal nature of audio signals, different strategies must be developed to deal with this attack. In the present paper, these modifications are considered as discordant size content replacement attacks. A discordant content replacement attack consists of replacing a set of samples from an audio signal with another set of samples that increases or reduces the number of samples in the signal, i.e., the attack is not uniformly applied. Consequently, the integrity and authentication of digital media is impaired [3,4]. The desynchronizing of the signal length has been the major problem to address due to the fact that the attack could generate content replacement of equal, larger or smaller size. These replacement sizes temporally change the signa, and when the signal contains a watermark, the watermark loses its original position, and as a consequence, the watermark is removed in the area attacked. For instance, content replacement attack which increases or reduces the number of samples in the signal would require the design of a synchronization strategy to detect the positions where the increase or reduction in samples took place, and to be able to determine the position of the next watermarked window. Hence, desynchronization is generated by the difference between a set of replacement samples and a set of replaced samples; i.e., desynchronization is defined by the number of samples added to or removed from the attacked signal.
This attack could be used against some applications, such as tampered speech, where certain words of a recorded phone conversation could be modified to change the original meaning; the tampered speech could be submitted to forensic analysis to determine its authenticity [5]. Another scenario is censorship in music, when the content has been modified by editing the song [6]. In these scenarios, the substituted content can be taken from another audio signal or could be artificially generated.
Recently, watermarking self-recovery schemes have started to become robust against content replacement attacks with sample sets of equal size, i.e., the number of replacement samples is the same as the number of replaced samples. This case is the simplest because the signal maintains its length after an attack; however, the discordant size content replacement attack could be applied by using content replacement of equal, larger, or smaller size. When the attack uses content replacement of larger or smaller size, the attacked signal is desynchronized in length. In these cases, the content replacement attack uses sets of samples from an audio signal with another set of samples that increases or reduces the number of samples in the signal, i.e., the attack is not uniformly applied. Such desynchronization in the signal length has been a major problem to address. In an audio signal, it is more probable that the discordant size content replacement attack can be applied. The audio signal has non-stationary signal features, and the temporality could be changed. This feature has complicated the developments of new schemes, because the signal changes with regard to time. A scheme should be capable of recovering the length of a desynchronized signal; this implies having a synchronization strategy and achieving robustness against the discordant size content replacement attack. In the receiver, the synchronization strategy must know the original signal length before an attack; if the synchronization strategy is not performed, the recovery fails.
In the literature, there are self-recovery schemes that try to address particular attacks. For instance, speech signal self-recovery schemes have been proposed in [2,7]. Both proposed self-recovery schemes restore a speech signal manipulated by the replacement of zeros in samples of the same size, but their solutions use different approaches. In [2], it has been shown that the digital signal self-recovery problem can be modeled as a source-channel coding problem. However, ref. [7] is based on embedding information, and the original signal is estimated by solving a linear equation with the least squares QR-factorization (LSQR) method. QR-factorization is particularly important in the least squares estimation of a nonlinear model where analytical techniques cannot be used. However, these schemes do not address a discordant size content replacement attack. Functional self-recovery schemes for audio signals have also been proposed in [3,8,9,10,11]. The schemes of [3,9,10,11] employ a channel coder to protect the watermark; however, the schemes [9,11] only apply content replacement of size equal to zeros that can perform recovery for tampered areas of up to 15% and 20%, respectively. The self-recovery scheme of [10] is robust against attacks other than the discordant content replacement attack. The scheme in [8] restores an audio signal when it has been tampered with by a content replacement attack of equal size, but it fails when the attack is discordant. In addition, another limitation is that it only restores audio signals that were attacked by less than , however, restoration is perfectly achieved. The only scheme that restores an audio signal tampered with by the discordant size content replacement attack is that proposed in [3]. This attack replaces regions of the signal with other content but uses sets of samples of different sizes, i.e., content replacement of equal, larger or smaller size. Consequently, the tampered watermarked signal is desynchronized in size and the watermark is lost. The scheme achieves a recovery from tampering with of the signal, using a source-channel coding, however, the compression quality is applied at a very low bit rate, i.e., 32 kilobits per second (kbps).
The existing watermarking schemes have a problem with robustness against the discordant size content replacement attack. The desynchronizing in the signal length has been the major problem to address. These replacement sizes temporally change the signal, and when the signal contains a watermark, the watermark loses its original position, and as a consequence, the watermark is removed in the attacked area. Hence, a discordant content replacement attack that increases or reduces the number of samples in the signal would require the design of a synchronizing strategy to detect the positions where the increase or reduction in samples took place and be able to determine the position of the next watermark window. Furthermore, a limitation to the existing methods is their recovery capacity against the discordant size content replacement attack. The schemes of [9,11] only address the case when the content replacement is of equal size with zeros, in which case they can perform a recovery when the tampered area is up to 15% and 20%, respectively. The scheme of [8] only performs a recovery when the tampered area is %, and only with sets of replacement samples of equal size, whereas [3] achieves a recovery until 20% with sample sets of equal, larger, and smaller sizes. The schemes are limited in the severity percentage. The present proposal contributes with a recovery of sets of replacement samples of equal, larger, and smaller sizes over 20% and % of the tampered area. This has been achieved due to the decimation and interpolation techniques included; the recovery quality is better than that of [3]. To evaluate the robustness of the scheme, a mathematical model of the discordant size content replacement attack was designed. Before this proposal, this attack was empirically handled.
This paper focuses on the development of a digital signal watermarking self-recovery scheme in the field of audio signals based on the scheme proposed in [3]. The proposed scheme shows the better quality of the recovered audio after the attack than that in the work of [3] by incrementing audio compression bitrate through decimation and interpolation operations. The scheme was modeled as a source-channel coding problem to generate the watermark from the original signal content, but two sampling techniques were added: decimation (downsampling) and interpolation (upsampling). The procedure of decimation and interpolation is used because it is a linear and time-invariant operation [12]. This property is useful in applications to signals and systems, communications systems, digital audio, etc. The scheme searches for operations that are invertible; hence, the decimation–interpolation techniques can be used in the recovery process because the decimation is an approximate inverse to the interpolation. Decimation reduces the input sampling rate by an integer factor M and interpolation increases the sampling rate by an integer factor L [12,13,14]. Hence, decimation with helps increase the compression ratio. This way, the compressed output symbols obtain a better quality since the signal has only been compressed by one-half. On the other hand, interpolation with recovers the compressed signal. In the step of the watermark generation, the decimation was applied before the source coding, i.e., over an original signal content copy with the goal of decreasing the signal size using an integer factor to obtain half of the signal samples. In the step of the watermark restoration, an interpolation using is applied after the source decoding, to restore the watermark in size and content. The decimation and interpolation obtain a double compression rate, larger than that shown in [3], and the host audio signal is self-recovered with better audio quality. Unlike the scheme proposed in [3], a mathematical model representing the discordant size content replacement attack was used to tamper with the watermarked audio signal. The model enables attacks with content replacement of equal, larger or smaller size, depending on the input parameters, i.e., the cardinality of the set of replaced samples, the cardinality of the set of replacement samples, the discordance generated by the attack and the start and end positions of the attack. The validation and evaluation of the audio signal self-recovery scheme by using a mathematical model is proposed to achieve robustness against the discordant size content replacement attack.
The remainder of this paper is organized as follows. The watermarking self-recovery scheme for an audio signal is introduced in Section 2. This Section also includes the formalization of the mathematical model of the discordant size content replacement attack. Experimental results and performance analysis are presented in Section 3. Finally, a discussion and the conclusions are given in Section 4.
2. Description of the Watermarking Scheme for Audio Signals Self-Recovery
The self-recovery algorithm proposed was developed on the basis of a small version and presented earlier in [3]. The goal of both algorithms is to recover signals that have been tampered with by a discordant size content replacement attack. In [3], the problem was modeled as a source-channel coding. In the source coding phase, an audio codec to compress the original audio was applied at a rate of 32 kbit/sec. Then, a channel coder was used to protect the source coding. The channel coding and hash information computed for each frame were used to construct the watermark, which was inserted in the least significant bits (LSB). The LSB technique is widely used for high payload data hiding applications, as one bit can be embedded within a binary word each time [1]. Then, the inverse process is performed to restore the tampered watermarked signal. The watermark extraction is applied using the LSB, i.e., to obtain the hash information and the channel coding. The hash information helps determine the tampered frames, meanwhile the channel coding is processed with a channel decoder and a source decoder. This part of the reconstructed watermark is applied to recover the tampered blocks of the host audio signal. The approach proposed in this paper adds a decimation and an interpolation process: the former to decrease and the latter to reconstruct the content and length of the original signal copy [12,13,14]. In addition, the mathematical model of the discordant size content replacement attack was introduced and used to evaluate the restoration capability of the scheme.
2.1. Reed–Solomon
Reed–Solomon (RS) codes are employed to recover the information destroyed by tampering [15]. These codes are used in communications and particularly in data storage systems. RS codes are a special class of nonbinary Bose–Chaudhuri–Hocquenghem (BCH) codes and are defined on a finite field (Galois field (GF) [15]. If the errors occur as a cluster, specifically if we have a burst of errors, then this code can correct any burst. This is the reason why RS codes are particularly attractive in channels with bursts of errors. When a content replacement attack is applied, this has a behavior similar to a burst of errors, since the samples are replaced in a contiguous sample set. The error correction capability of a systematic () code, which has parity check bits, can correct errors of length . b is defined as a sequence of b-bits errors, n as the block length, and k as the number of information sequences [16,17].
2.2. Watermark Generation and Embedding Algorithm
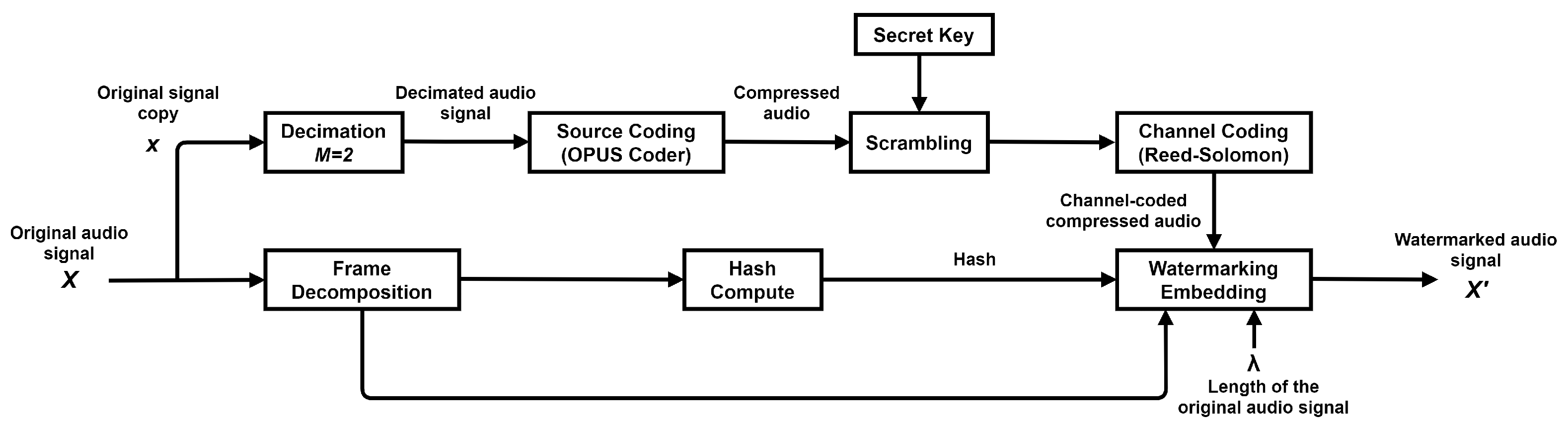
The scheme uses an original audio signal X of t seconds, a sampling frequency of 48 kHz, and 16 bits. First, the watermark is generated by using an original signal copy denoted by x. The copy x is decimated by an integer factor which yields one-half of the samples. The decimated values D are processed with the OPUS source coder [18] and the output symbols are concatenated to 16 bits; these symbols are scrambled with a secret key. The key length is the same as the concatenated symbol’s length. Therefore, if the concatenated symbols are formed by k samples, the length of the key is k. If the length of the key is k, then there are up to k! available keys. Furthermore, the larger the total number of samples is, the larger the number of available keys is. The secret key helps change the order of concatenated symbols before applying a channel coder. In the receiver, the secret key recovers the original order of the symbols. Hence, the secret key is known to both the embedding phase (transmitter end) and audio signal reconstruction phase (receiver end). The scrambled code is protected by applying the RS channel coder. Afterward, the original signal X is divided into frames and the hash information is computed on 14 MSB of each sample by frame. Finally, the watermark, formed by channel-coded symbols and hash information, is embedded in the two LSBs of the samples of each frame and the original signal length is embedded in the last frames. Thus, the watermarked signal is obtained. The overall flowchart is shown in Figure 1.
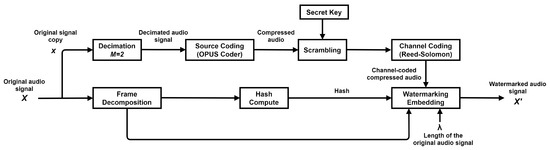
Figure 1.
Diagram of watermark generation and embedding.
The original audio signal is denoted by X, with a time of t seconds and a length . The original signal copy is represented by x and the decimation using the integer factor M is denoted by D. The output length of the source coding is fixed by and the source-coded symbols by k. The source-coded symbols k are the symbols concatenated to bits. The secret key is randomly taken, to provide security in the scrambled symbols, and the output symbols of the channel coding, applying RS, are denoted by n. The MSB bit number in each frame is represented by , the bit number of the hash symbols by , the bit number of the channel code by , the LSB bits available in each frame by , and the watermarked audio signal by . and denote the bit set of the symbols that are embedded in each frame. The watermark generation and embedding steps are performed as follows:
- The watermark generation is performed as the start point. The input parameter is the original audio signal X to be protected against the discordant size content replacement attack. Each feature of the audio signal corresponds with a time of t seconds, sampling frequency of 48 kHz, 16 bits and a length .
- Obtain x, the original signal copy, and decimate it by an integer factor of , i.e., , . With this process, the original signal X is only represented using one-half of its samples, with the goal of performing a compression over a small version and obtaining a better compression rate.
- The decimated values D are processed with the OPUS audio codec to compress it at the rate of 64 kbps. The compression ratio of the proposed scheme has a quality two times better than the rate used in the scheme [3]. The source coding output is of length to 8 bits per sample.
- The symbols obtained are concatenated to bits. Two symbols of 8 bits are used, forming a new source-code of size . It is important to perform this step because the RS channel codes work on symbols of length m.
- Scramble the code of k symbols with a secret key . The secret key must be shared between the transmitter and receiver to provide the required security of the embedding algorithm; its value is randomly chosen. The scrambling helps to avoid a tampering of a set of contiguous samples. The process of channel decoding would consider it as small tampering in different positions, which eases the restoration of the individual portions.
- To protect the scrambled code, Galois fields are used and after applying the RS coder, . The coder adds parity symbols of size , where k represents the original information symbols and represents the output channel coding. Thus, the first part of the watermark is obtained.
- The embedding process of the watermarking on the original audio is applied. First, the original audio signal X is decomposed into frames of 10 milliseconds; hence, the frame consists of 480 samples.
- Then, compute the hash information of the 14 most significant bits (MSB) of each sample by frame, i.e., the bits in each frame that are not modified. Use only 8 hash symbols or bits. The second part of the watermark is obtained.
- After that, distribute 56 symbols or bits of channel-code, and the 8 symbols or bits hash, replacing the two LSBs of the samples of each frame, i.e., bits that are available.
- Finally, insert the parameters and in the LSBs of the frames that are not watermarked. Each one is represented by 20 bits and 16 bits, respectively. They are distributed 24 times by frame. These values are embedded in the last frames on the assumption that the relevant information of the attacker is contained in the body of the audio signal. It is important to note that both parameters are useful in the extraction and restoration of the watermark. Therefore, the watermarked audio signal is then produced.
2.3. Mathematical Model That Describes the Attack
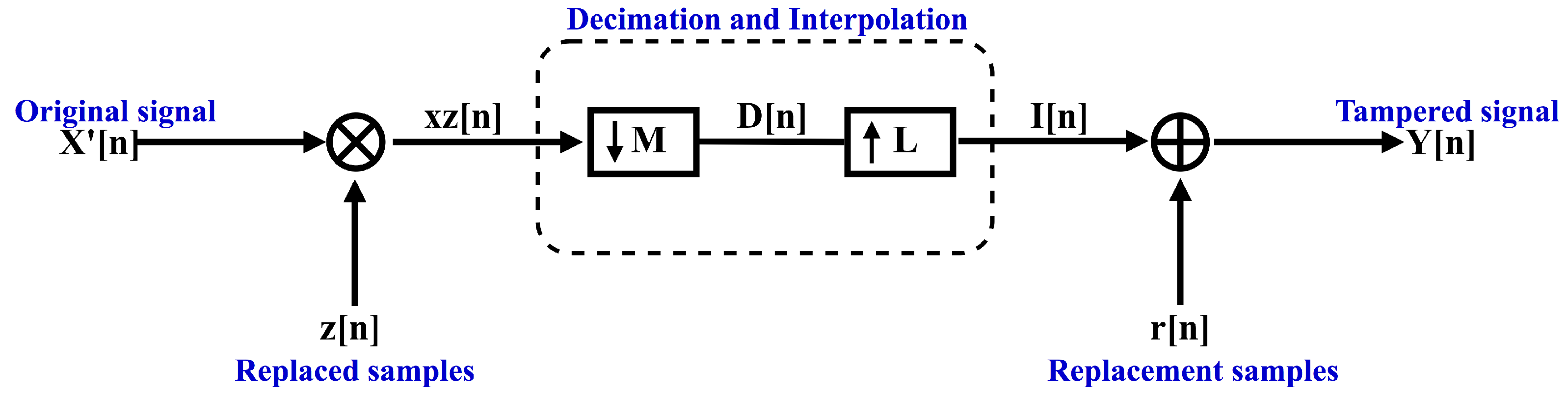
The decimation and interpolation techniques are used in modeling the attack [14]. In addition, content replacements of equal, larger and smaller sizes are considered as cases that could occur with tampering. The model receives an audio signal . A set of replaced samples Z over is put to zero before applying a set of replacement samples; so, is obtained. Afterward, a decimation with an integer factor M is applied in the set left with zero values in . The decimated block D is interpolated with an integer factor L. Finally, the interpolated block I is tampered with using a set of replacement samples r, and the tampered watermarked signal Y is obtained. The model is presented in Figure 2. The next steps describe the strategy of the algorithm.
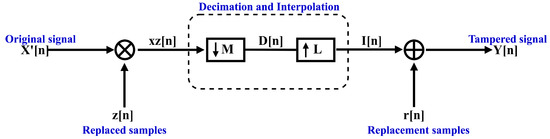
Figure 2.
Mathematical model of the discordant size content replacement attack.
- Define the input parameters as the size of the set of replaced samples i, the size of the set of replacement samples j, the discordance a (the difference between the number of samples of the original signal and the number of samples of the attacked signal), and the start and end positions of the attack, and , respectively.
- It is necessary to put to zero the set of replaced samples of size i before using the decimation technique. The process enables that the set of replaced samples have a preparation previous to applying the set of replacement samples. This set takes the place of the watermarked audio signal received, , of size and n indicating the n-th sample:The values in z, which has the same length as , contain sets of ‘0’s in the attacked area, and ‘1’s in the samples not tampered with:
- Prior to applying the decimation and interpolation technique to , it is necessary to compute a value, , that depends on the discordance of the attack, i.e., of equal, larger or smaller size. The quantity of samples added or removed by the attack is represented in the discordance. Without this value, one cannot obtain the integer factors used in the decimation and interpolation:When the cardinality of the set of replaced samples i is equal to the cardinality of the set of replacement samples j, i.e., , the value is equal to the first condition. The second condition takes place when the cardinality of the set of replacement samples j is larger than the set of replaced samples i. If the attack is performed with a smaller content replacement, i.e., if the cardinality of the set of replacement samples j is smaller than the set of replaced samples i, the third condition is executed.
- Independently of the value taken by , its value is converted to a fractional format, where the integer values L and M obtained represent the integer factors of the interpolation and decimation, respectively. The fractional format is as follows:
- The first sampling technique is applied, i.e., the decimation with an integer factor M. This technique is only performed on the original set of size i by replacing it with zero values using Equations (1) and (2). The set replaced is contained in and its process can be observed in the following equation:where is the downsampled sequence, obtained by taking a sample from the data sequence for every M samples (discarding samples for every M samples) [14]. The decimated block size is given by , and the size of the output signal is given by .
- The second sampling technique, namely the interpolation with an integer factor L, is applied. By using the decimated block of size , its process is described as follows:where D is the sequence to be upsampled by a factor of L, and is the upsampled sequence, obtained by adding zeros for each sample [14]. The end position of the interpolation is limited by . Hence, an interpolated block of size is obtained, and consequently an output signal of size is achieved.
- Once the decimation–interpolation process has finished, only the interpolated block is tampered with, using a set of replacement samples of size j. The set of replacement audio samples is added as follows:where the set of replacement audio samples takes the place of the replacement audio A:Therefore, the watermarked audio signal is tampered with by a discordant size content replacement attack. The result is the tampered watermarked audio signal Y.
The content replacement attack with duration change is a more general case. Some application scenarios, such as tampered speech [5] and cancellation of censorship in music [6], are examples where the attack could cause a desynchronization in the signal length, loss of the original position of the watermark, a change in the content of the host signal, and watermark loss in the tampered area. It is important to clarify that this paper is addressed to counteract the specific effects caused by the discordant size content replacement attack. The common channel operations are not discussed in this paper, supposing a noise-free communications channel for transmitting. However, these considerations will be included in a later study.
2.4. Extraction and Reconstruction of the Watermark
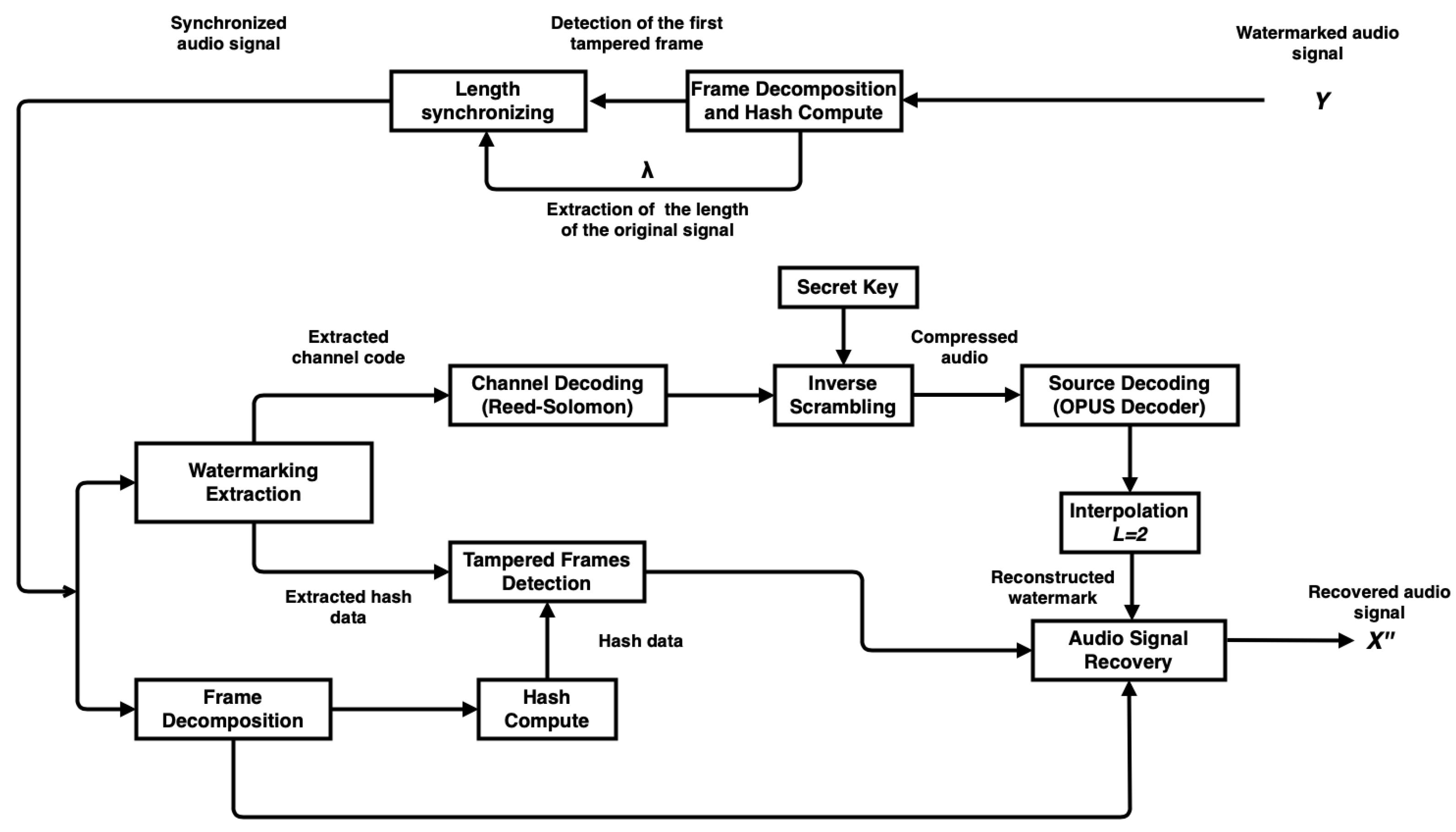
The inverse process of the tampered audio signal self-recovery is performed as follows. A tampered watermarked audio signal Y of size is received. First, a synchronizing strategy is developed with the length of the original signal extracted of Y and the length computed of Y. The tampered signal is synchronized by using only the first tampered frame, then the channel code and the hash information are extracted from the two LSBs of each frame. The synchronized signal is decomposed into frames, and for each frame, the computed hash information is compared to the extracted hash information of the same frame. The tampered frames are detected. The collected channel coding is input to the RS channel decoder, the inverse process of the scrambling is applied to the output symbols with a secret key, and they are converted from 16 to 8 bits. The OPUS source decoder is applied to the ordered symbols, and an interpolation with an integer factor is performed to reconstruct in size and content the watermark. The tampered frame content is replaced with the reconstructed watermark. Therefore, the recovered audio signal is produced. The overall flowchart is shown in Figure 3.
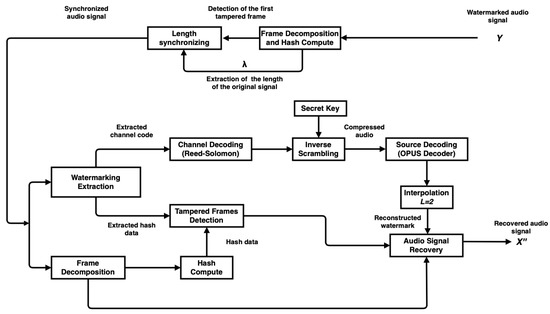
Figure 3.
Diagram of synchronization, extraction and reconstruction of the watermark.
The extraction and reconstruction of the watermark are performed as follows:
- A tampered watermarked audio signal Y of size is received. Extract and by taking the 30 last frames. Each frame contains 480 samples. The frames should be obtained starting from the last frame of the signal. Both parameters were repeated 24 times by frame, i.e., a total of 864 bits was distributed by each frame. It is possible to recover both parameters with only one frame that had not been tampered with.
- A synchronizing strategy is then developed. Once has been extracted, which is the length of the original audio signal, compute the length error using the size of the tampered signal received :
- Decompose the audio signal Y into frames of 480 samples or 10 milliseconds, in such a way as to extract the hash information from the LSBs of the samples of each frame, i.e., the eight symbols or bits embedded.
- Calculate the hash information for all MSBs of the samples of each frame, obtaining hash bits of the frame. Compare the extracted and calculated hash bits of each frame to determine the first tampered frame.
- Then, by only using the first tampered frame, it must be possible to synchronize Y. The process adds zeros or removes samples from this first tampered frame, depending on the value of the length error :
- If , add a set of zeros of size , where would be a positive value.
- Else if , remove a set of samples of size .
In the case where , the length of the tampered signal is the same as the original signal, and it is not necessary to synchronize the signal. - Once the tampered signal has been synchronized in length, , it is possible to compute the hash information and to extract the channel coding of each frame. Similarly as in the steps 3 and 4, all frames must be correctly determined. For each frame, the generated hash bits are compared to the embedded hash bits of the same frame. The frames are marked as healthy when the extracted and reproduced hash bits match, and otherwise tampered. Therefore, each tampered frame results in losing channel code symbols. The proposed method allows a channel code symbol length set to , and every frame hosts 56 channel code symbols or bits of channel code.
- Channel coding output bits are collected from the watermark bits of the audio signal. The collected channel coding output bits are input to the channel decoding module. Collect all of the bits of the channel code or 56 symbols of the 2 LSBs of the samples of each frame. The number of watermarked frames is where is the value extracted in step 1 which represents the total samples generated by the source coding.
- Pass the channel-coded symbols to the channel decoder, where and . This decoding process finds the k source-coded symbols. The channel decoder is used to compress the recovered audio.
- The inverse process of scrambling is applied to the k output symbols of the channel decoder in case of its successful decoding by using the secret key . This allows returning the symbols to their original positions.
- Convert the ordered output symbols of 16 bits to 8 bits, where the size of the new set of ordered symbols will be , i.e., the concatenation applied in the watermarking generation process is removed.
- Apply the OPUS source decoder to the new set of ordered symbols to find the compressed decimated signal D.
- After the source decoding, it is necessary to interpolate with an integer factor the output symbols of the source decoder using the spline method [19,20] to reconstruct in size and content the decimated signal:
- Replace the content of the tampered frames of with the recovered interpolated audio signal I, i.e., with the reconstructed watermark.
- This yields the recovered audio signal .
3. Experimental Results
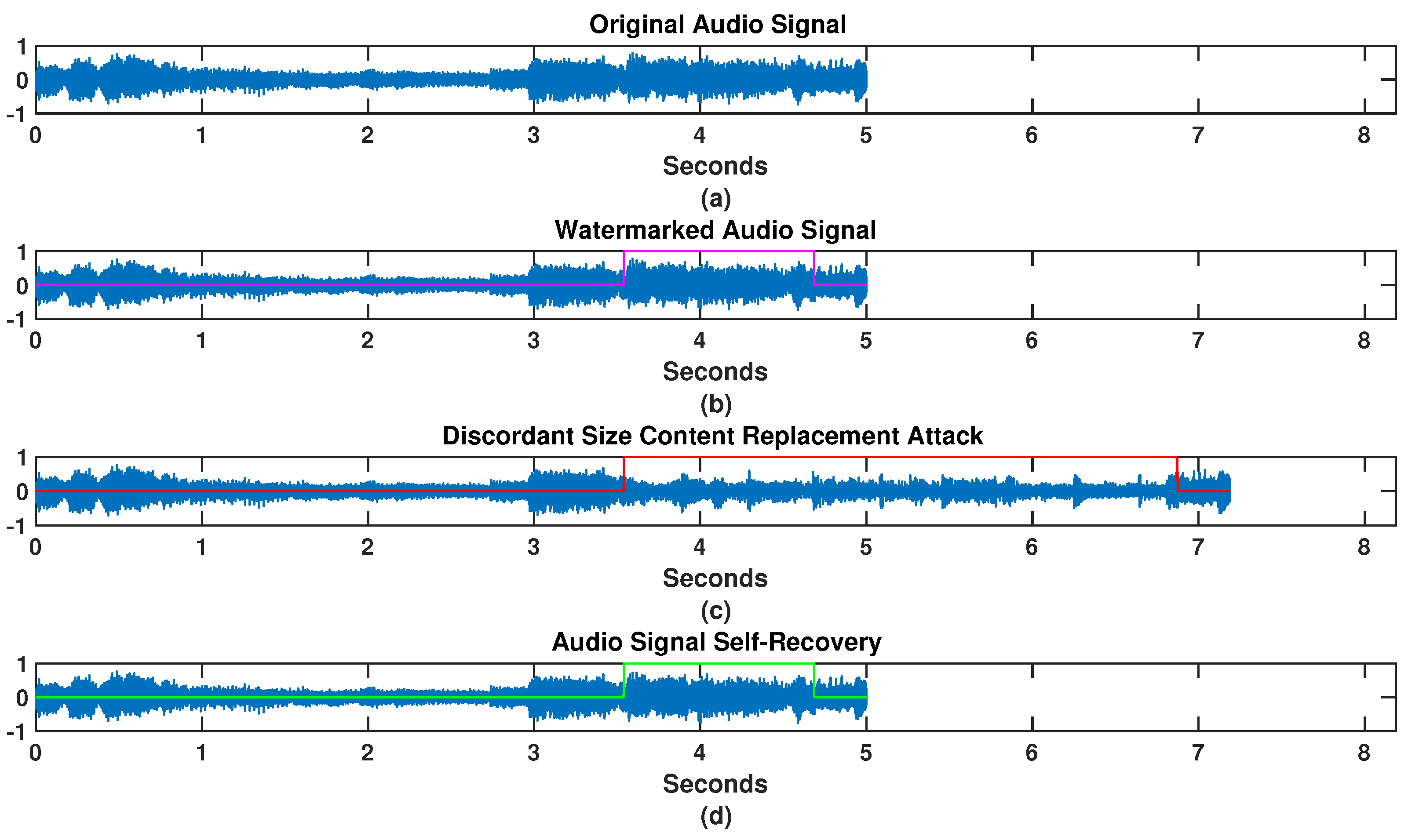
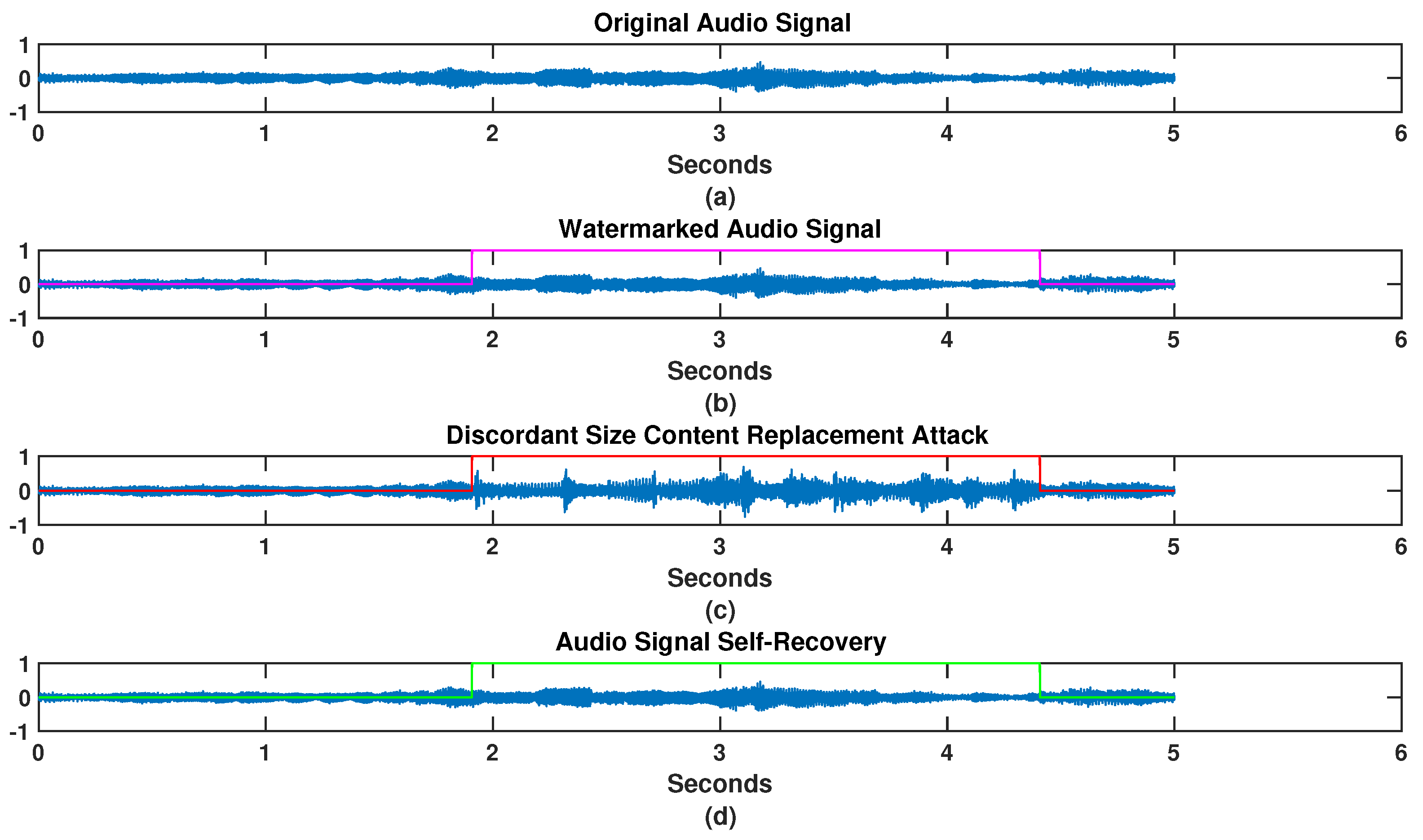
The evaluation of the proposed scheme was performed with 16 bits 48 kHz sampled music audio signals and a time of 5 s. A total of 150 audio signals were subject to the protection against possible tampering by the discordant size content replacement attack. The clips were randomly taken from a database that contains 982 CD-quality audio clips. All of the clips were musical, from different music styles ranging from classical to big band and including Latin pop and Caribbean rhythms; no music style classification was explicit (the dataset is fully available in [21]). The representation of the attack was proposed as a mathematical model with three cases of content replacements: equal, larger and smaller sizes. The content replacement sizes were randomly taken in each case. Each case uses six attack degrees, which is the number of the different replacements applied by the mathematical model to each input signal. The attacked area was randomly generated. This way, a total of tampered watermarked signals are obtained by case. Thus, the self-recovery algorithm works on a total of tampered signals, where 3 represents the size cases of discordant content replacement, i.e., equal, larger and smaller. The quality of the watermarked (WM) and recovered (Rec) audio signal compared to the original audio signal (Orig) is measured on the basis of the Perceptual Evaluation of Audio Quality (PEAQ) criterion. PEAQ is based on psychoacoustic principles; original and processed audio signals are transformed to a basilar membrane representation and differences are analyzed. The PEAQ performs a classification of an audio signal on a scale from 0 to corresponding to the objective difference grade (ODG) [22]. ODG equal to 0 indicates that distortion is imperceptible, thus, ODG equal to −4 means very annoying distortion [23]. The perceptual impact of the scheme was measured to determine whether the transparency threshold of ODG could be achieved. Furthermore, the reconstruction quality or distortion error of the scheme is evaluated using the Peak Signal-to-Noise Ratio (PSNR) metric [24]. PSNR is a widely used tool in digital signal processing as it quantifies signal quality after any performed process. To show the functionality of the proposed algorithm, an audio signal with a length of = 240,000 samples, s, was processed, as is shown in Figure 4a. The watermarked signal, Figure 4b, is obtained using the decimation technique and source-channel coding over an original signal copy, with a bit rate of 64 kbps. The channel coding obtained joined with the hash information is distributed in the LSBs of the samples by frames of the original audio signal. The watermarked signal is then tampered with using the mathematical model of a discordant size content replacement attack. A set of replacement samples of j = 160,000 and a set of replaced samples of i = 55,000 is input to the mathematical model. The discordance or samples added from the attack is a = 105,000, and the start and end positions of the attacked area were randomly generated. Then, as model output, a tampered watermarked audio signal with a length of = 345,000 samples, i.e., s, is obtained. The result of the tampering shows a temporal change with regard to the original audio signal, i.e., an increment of % of the signal total, as can be seen from Figure 4c. The tampered signal is delivered to the receiver. The hash information procedure at the receiver results in determining the tampered frames. The tampered signal is synchronized in length using the first tampered frame. So, the correct extraction of the channel symbols and detection of the tampered frames can be performed using the synchronized tampered audio signal. The channel symbols extracted are processed with the inverse module of the source-channel coding, and applying the interpolation to obtain the watermark reconstructed in length and content. Finally, the tampered frames of the synchronized tampered audio signal were recovered using the watermark. The result is shown in Figure 4d.
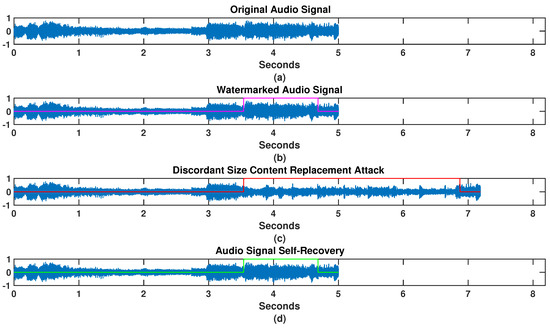
Figure 4.
Simulation results for the audio signal self-recovery scheme: (a) the original audio signal; (b) the watermarked audio signal, the color line indicates the region to be attacked; (c) the attacked watermarked audio signal, the color line indicates the attacked region; and (d) the restored audio signal, the color line indicates the recovered region.
In order to have a better comparison, the original, watermarked and recovered signals are shown in more detail in the subsequent results. In this study, the perceptual evaluation between the watermarked and original signals achieve, on average, an ODG = 0 and a PNSR = dB, i.e., an excellent audio quality and negligible distortion imposed by the watermark. The average quality of the audio signals recovered by the algorithm after a content replacement attack of equal size, is presented in Table 1. It can be observed that if the size of the attacked area i increases in equal size as the set of replacement samples j, where the attack degree represents the six different sizes of replacements of equal size, then the self-recovery process decreases (% recovery), the quality (ODG) of the recovered audio decreases, and the distortion error (PSNR) increases. However, in comparing the watermarked (WM) and original (Orig) audio signal with the recovered (Rec) one, one obtains an average above ODG = and a PSNR with a very small difference. This means that the recovered audio quality is classified between excellent and very good, i.e., the distortion is inaudible and the recovery error is negligible. Thus, the scheme has achieved a recovery of 90% of the total tampered signal in this case.

Table 1.
Average value of ODG and PSNR in the case of recovering against the content replacement of equal size.
The results of the recovered audio quality when the content replacement attack used a larger size are presented in Table 2. The similarity of the recovered (Rec) audio signals with regards to original (Orig) and watermarked (WM) audio signals were classified with an average value ODG over and a PSNR with a small variability. This result was achieved despite the fact that the set of replacement samples j was larger than the set of replaced samples i. Note that the recovery percentage decreases as the attack degree increases with six different larger replacements. Furthermore, there is a small decrease in ODG, and a small increase in recovery in terms of the PSNR. Hence, the algorithm was able to recover 92% of the tampered signals, and an excellent and very good audio quality were obtained. These ODG results have shown that the distortion transparency is imperceptible on the recovered signals, which is more than sufficient for the desired target of an ODG over .

Table 2.
Average value of ODG and PSNR in the case of recovering against content replacement of larger size.
In the third case, the quality of the recovery obtained by the algorithm is presented in Table 3. The tampering of watermarked audio signals with a content replacement of smaller size was performed, i.e., with a set of replacement samples j smaller than the set of replaced samples i. In this case, a portion of the set of replaced samples is removed by the process of the attack, so the possible accuracy of a restoration by the proposed scheme is limited. Despite the severity of the attacks, the scheme achieved a recovery of tampered audio signals, e.g., by using sets of replacement samples smaller than j = 12,000, the scheme has achieved a recovery percentage of less than 50%. Furthermore, in Table 3 it can be observed that the values of the ODG and PSNR decrease when increasing the severity of the attacks, when a set of replacement samples j of smaller size is used, which is to be expected, since lower ODG values indicate a more perceptible distortion in the recovered audio signals, while lower PSNR values indicate a greater difference between the host and restored audio signals. However, the audio quality achieves an audibility scale of excellent and very good for attack degrees larger than j = 15,000, and a good quality scale for attack degrees smaller than j = 12,000. Thus, the algorithm managed to recover 73% of the total tampered signal.

Table 3.
Average value of ODG and PSNR in the case of recovering against content replacement of smaller size.
In order to extend the performance evaluations, a large-scale tampering experiment was conducted with the goal of knowing whether the scheme was able to recover the content of audio signals subjected to a tampering of a continuous part of the watermarked audio, where a set of replaced samples i is higher than or equal to the total length of the audio signal. A total of 150 watermarked signals were tampered with six attack degrees in the three cases, resulting in tampered signals generated in each case. This way, a total of tampered signals was obtained by the mathematical model of the attack with 3 cases, i.e., equal, larger and smaller sizes. The quality of the recovered audio signals is presented in Table 4. The table only presents the resulting values with attack degrees where the algorithm achieved a recovery, i.e., the different sizes of tampering. With a tampering of one-half of the content, i.e., a set of replaced samples of i = 120,000, the algorithm recovered a percentage not larger than 30% of the total tampered signal in the three cases. Furthermore, with a small percentage, the scheme has managed to recover from tampering with up to i = 140,000 replaced samples, but this is not possible for higher sizes than this. The quality of the recovered audio decreases while the distortion error increases when the severity of the attacks are higher than one-half of the total length. The mean ODG values for the restored signals obtained a scale over , which means a restoration with acceptable quality; the quality of the watermarked (WM) and original (Orig) audio signals compared to the recovered one (Rec) is tested. Hence, the scheme is able to accomplish a restoration when from 50% to a maximum of % of the total length of the signal has been tampered with by the discordant size content replacement attack. This means that the scheme performed the recovery of a set of replaced samples i on a watermarked audio signal higher than one-half of its total length. The recovery limits are due to the attack size, the start and end positions of the attacked area, obtaining parameters that are useful in the synchronizing process, and the watermark extraction. If the extracted watermark information was tampered with above 50% of its total length, the scheme is not able to reconstruct the watermark and the host audio signal. Figure 5 shows the restoration of a watermarked audio signal tampered by one-half of its total length by a content replacement attack of equal size.

Table 4.
Average value of ODG and PSNR in signal recovery against content tampering higher or equal to one-half of its total length.
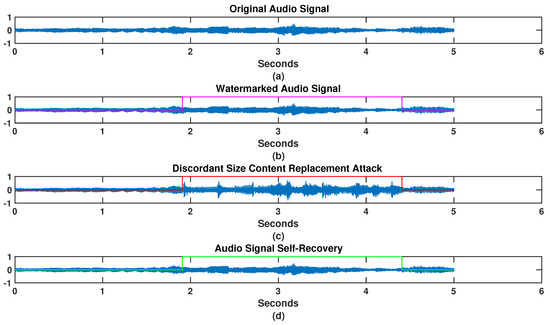
Figure 5.
Simulation results for an audio signal self-recovery with a tampering equal than to one-half of its total length: (a) the original audio signal; (b) the watermarked audio signal, the color line indicates the region to be attacked; (c) the attacked watermarked audio signal, the color line indicates the attacked region; and (d) the restored audio signal, the color line indicates the recovered region.
Comparative Results
In order to more clearly illustrate the advantages of the proposed scheme, a comparison between the proposed scheme and recent schemes [3,8,9,11] was performed. The results are shown in Table 5, where ✓ denotes that the corresponding scheme has the ability and ✗ denotes that the corresponding scheme does not have the ability to recover from discordant content replacements of equal, larger or smaller sizes. The % recovery denotes the tampered area percentage that the scheme is capable of recovering. These schemes have been chosen for comparison based on robustness against the discordant size content replacement attack and its recovery percentage. The discordant size content replacement attack performs modifications to the content by using another set of samples of different signals. The attack could generate content replacements of equal, larger or smaller sizes. These replacement sizes temporally change the signal. The schemes of [3,9,11] and the proposal of the present paper employ a channel coder to protect the watermark; however, the schemes of [9,11] only apply a content replacement of equal size with zeros and can perform a recovery until 15% and 20% of the tampered area, respectively. The scheme of [3] achieves a recovery with a tampered portion of around 20% of the signal total in each case and uses sets of samples from another audio signal to tamper the signal. The scheme of [8] only restores audio signals that were attacked by less than % over a content replacement of equal size. The three cases can be treated by the scheme of [3] and the present proposal; however, the proposed scheme achieves a recovery for the tampering of around 20% of the signal with good audio quality and up to % of its total length with an acceptable quality. The equal, larger or smaller sizes can be restored when sample sets are used from another audio signal. The present proposal can tolerate more tampering at the expense of sacrificing the quality of the recovered audio signal. The recovery percentage is limited by the fact that if the tampered portion is increased, the watermark loses the channel code information. These results were achieved because the decimation–interpolation techniques have helped to obtain a watermarked and recovered signal with better quality; the compression rate was increased and the watermark has obtained an excellent quality. It is important to add that the proposal has used a mathematical model of the discordant size content replacement attack to evaluate its performance; whilst the other schemes have not applied one.

Table 5.
Comparative results.
4. Discussion and Conclusions
In this paper, a self-recovery scheme for digital audio signals was proposed. The evaluation of the proposed scheme consisted in testing the restoration capability of the scheme after a discordant size content replacement attack was applied to watermarked audio signals. This attack desynchronizes the signal length, and in a watermarked signal, desynchronizes the position of the watermark and causes its removal. Furthermore, the attack performs modifications to the content, causing it to have a meaning that is different from the original. A mathematical model of the attack with content replacement of equal, larger and smaller size was developed and evaluated. To counteract the effects caused by the attack, a source-channel coding approach was applied to generate the watermarked audio signal. A decimation–interpolation technique is added to the process above. Thus, the decimation technique to be applied before the source-channel coding process was developed in this scheme. This technique has allowed a compression with a better quality at 64 kbps. A decimation, source coding, and channel coding were applied over an original signal copy. The channel coding output joined with hash information was distributed in the LSBs of the original audio signal. In the receiver, the signal delivered is synchronized in length. Then, the watermark was extracted and reconstructed by applying a channel decoding, source decoding and interpolation. Finally, the tampered frames, which are detected by comparing the computed and extracted hash information of the host audio signal, are recovered using the watermark. The experimental results show that it is possible to recover from tampering with content replacements that increase or reduce the number of samples in the audio signal, where the design requires a synchronization strategy. The perceptual impact of the encoding process has been determined, and it has been found that the distortion imposed by the watermark and distortion error are negligible, i.e., ODG = 0 and PSNR = dB. The evaluation of the restoration capability of the scheme, after an attack with six different percentages of severity applied to the watermarked signals, obtained a recovered audio quality between excellent and very good in the three cases. In other words, the scheme achieved an ODG average over , a very good audio quality, when a tampering around 20% of the signal total was performed. The recovered signals have had a small distortion error, PSNR, compared to the original and watermarked signals. In an extension of these experiments, a tampering higher or equal to one-half of the total length of the signal was evaluated: the scheme was able to achieve a restoration until the tampering reached % of the total length of the signal, with an average value of ODG above the threshold and acceptable quality. Hence, the audio signals restored by the scheme obtained an average transparency threshold above the set as our goal.
In conclusion, the obtained audio restoring capacity was better than that of the other state-of-the-art schemes, due to the decimation–interpolation techniques included. These helped increase the compression rate of the original signal, and as a result, a better audio quality in the recovery process was obtained. Furthermore, the technique allowed recovering from a tampering affecting an area higher or equal to one-half of the signal’s total length. The mathematical model of the discordant size content replacement attack allowed knowing that it is necessary to perform the signal synchronization using the original signal length. It is important to take into account the start and end positions of the attack because the attacked area and the survival of the watermark depend on these. The synchronizing of the tampered signal could be limited when the attack has replaced the last frames where the two parameters that are useful in this step were embedded. Then, the success or failure of the scheme depend on the size of the tampering and its position over the set of replaced samples. Hence, an audio signal self-recovery was only achieved if the original signal information was contained as a watermark and if the signal synchronizing was performed. Finally, it can be seen that by increasing the severity of the attacks, the recovered audio quality decreases, and the similitude error or distortion error increases. However, even for the most severe attack, the errors are relatively small. Furthermore, the watermarked audio signal can tolerate a higher tampering at the expense of sacrificing the quality of the recovered audio signal. Note that the recovered audio signal was not the original because a decimation technique and a lossy compression were applied. Hence, the recovered audio signal was only an approximation of the original audio signal. The restoration capability of the scheme is limited by the size of the attack. When the host audio signal loses more than 50% of the embedded watermark, the scheme is not able to reconstruct the watermark and recover the host audio signal. Thus, the proposed scheme is robust against a discordant size content replacement attack and the used techniques have allowed obtaining good experimental results.
The proposed scheme is suitable for speech restoration applications. Suppose that there is a recorded phone conversation, and this recording is subsequently modified to incriminate one of the interlocutors by modifying certain words of their speech. This tampered recording could be used against the person. A means to obtain the original words from the tampered speech could be part of the repair process and could prove the innocence of the accused. Another scenario for audio self-recovery is in the music industry. Some songs contain inappropriate language; for these songs to be included in radio airplay, the inappropriate content has to be censored by editing the songs. Offensive content is removed through re-sampling, bleeping, and replacing words with silence, sound effects or single tones. In a music distribution scenario, censored songs could be freely distributed, but premium users could pay a fee to remove the censorship. In the present paper, these modifications are addressed as content replacement attacks, thus the proposed algorithm has shown robustness to them. However, due to the well-known fragility of LSB embedding, the proposed scheme is weak against lossy compression. Future work considers the exploration of different embedding strategies to achieve lossy compression robustness.
Author Contributions
Conceptualization, J.J.G.-H.; data curation, J.J.G.-H.; formal analysis, J.J.G.-R.; funding acquisition, J.J.G.-H.; investigation, J.J.G.-R. and J.J.G.-H.; methodology, J.J.G.-R. and J.J.G.-H.; resources, J.J.G.-H.; supervision, J.J.G.-H.; validation, J.J.G.-R.; visualization, J.J.G.-R.; writing—original draft, J.J.G.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by PRODEP-SEP and CONACYT under grant PN-2017-01-5814, and Ph.D. scholarship No. 335972. There was no additional external funding received for this study.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset used in this work is fully available in [21].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cox, I.; Miller, M.; Bloom, J.; Fridrich, J.; Kalker, T. Digital Watermarking and Steganography, 2nd ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2008. [Google Scholar]
- Sarreshtedari, S.; Akhaee, M.A.; Abbasfar, A. A Watermarking Method for Digital Speech Self-recovery. IEEE/ACM Trans. Audio Speech Lang. Proc. 2015, 23, 1917–1925. [Google Scholar] [CrossRef]
- Gomez-Ricardez, J.J.; Garcia-Hernandez, J.J. An audio self-recovery scheme that is robust to discordant size content replacement attack. In Proceedings of the IEEE 61st International Midwest Symposium on Circuits and Systems, MWSCAS 2018, Windsor, ON, Canada, 5–8 August 2018; pp. 825–828. [Google Scholar] [CrossRef]
- Gomez-Ricardez, J.J.; Parra-Michel, R.; Garcia-Hernandez, J.J. Mathematical models for the discordant size content replacement attack. In Proceedings of the 2019 7th International Workshop on Biometrics and Forensics (IWBF), Cancun, Mexico, 2–3 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- National Forensic Science Technology Center (NFSTC). NFSTC: A Simplified Guide to Forensics Audio and Video Analysis; Technical Report; National Forensic Science Technology Center (NFSTC): Largo, FL, USA, 2010.
- Newton, H. Music Censorship: An Overview; George Washington University: Washington, DC, USA, 2012; Volume 1. [Google Scholar]
- Li, J.; Lu, W.; Zhang, C.; Wei, J.; Cao, X.; Dang, J. A Study on Detection and Recovery of Speech Signal Tampering. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 678–682. [Google Scholar] [CrossRef]
- Menendez-Ortiz, A.; Feregrino-Uribe, C.; García-Hernández, J.J.; Guzmán-Zavaleta, Z.J. Self-recovery scheme for audio restoration after a content replacement attack. Multimed. Tools Appl. 2017, 76, 14197–14224. [Google Scholar] [CrossRef]
- Hu, H.; Lee, T. Hybrid Blind Audio Watermarking for Proprietary Protection, Tamper Proofing, and Self-Recovery. IEEE Access 2019, 7, 180395–180408. [Google Scholar] [CrossRef]
- Fan, M.Q. A source coding scheme for authenticating audio signal with capability of self-recovery and anti-synchronization counterfeiting attack. Multimed. Tools Appl. 2019, 79, 1037–1055. [Google Scholar] [CrossRef]
- Hu, H.T.; Lu, Y.H. Frame-synchronous Blind Audio Watermarking for Tamper Proofing and Self-Recovery. Adv. Technol. Innov. 2020, 5, 18–32. [Google Scholar] [CrossRef]
- Jovanovic-Dolecek, G. Multirate Systems: Design and Applications: Design and Applications; Idea Group Pub.: Hershey, PA, USA, 2001. [Google Scholar]
- Oppenheim, A.; Willsky, A.; Nawab, S. Signals & Systems; Prentice-Hall Signal Processing Series; Prentice-Hall International: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Tan, L. Digital Signal Processing: Fundamentals and Applications; Digital Signal Processing SET; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Blahut, R.E. Algebraic Codes for Data Transmission; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Justesen, J.; Forchhammer, S. Two-Dimensional Information Theory and Coding: With Applications to Graphics Data and High-Density Storage Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Proakis, J.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2008. [Google Scholar]
- Xiph.Org Foundation. Opus Interactive Audio Codec. 2012. Available online: https://opus-codec.org (accessed on 10 December 2020).
- Faires, J.; Burden, R. Numerical Methods, 4th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Gupta, S. Numerical Methods for Engineers; New Age International (P) Limited: New Delhi, India, 1995. [Google Scholar]
- Garcia-Hernandez, J.J. Replication Data for: “On a Key-Based Secured Audio Data Hiding Scheme Robust to Volumetric Attack with Entropy-Based Embedding” Submitted to Entropy; Harvard Dataverse: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Thiede, T.; Treurniet, W.C.; Bitto, R.; Schmidmer, C.; Sporer, T.; Beerends, J.G.; Colomes, C. PEAQ—The ITU Standard for Objective Measurement of Perceived Audio Quality. J. Audio Eng. Soc 2000, 48, 3–29. [Google Scholar]
- Bosi, M.; Goldberg, R.E. Introduction to Digital Audio Coding and Standards; Engineering and Computer Science; Springer: New York, NY, USA, 2003. [Google Scholar]
- Furht, B.; Kirovski, D. Multimedia Watermarking Techniques and Applications (Internet and Communications Series); Auerbach Publications: Boston, MA, USA, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).