Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling
Abstract
1. Introduction
| Algorithm 1 The Pseudocode of the RR Algorithm in CPU Scheduling [15] |
| Step 1: Keep the ready queue as a FIFO queue of tasks Step 2: New tasks added to the tail of the queue will be selected, set a timer to interrupt after one time slot, and dispatch the tasks. Step 3: The task may have executed less than one time quantum. In this case:
the timer will go off and will cause an interruption to the OS. |
2. Literature Review
3. Problem Statement Gap Analysis
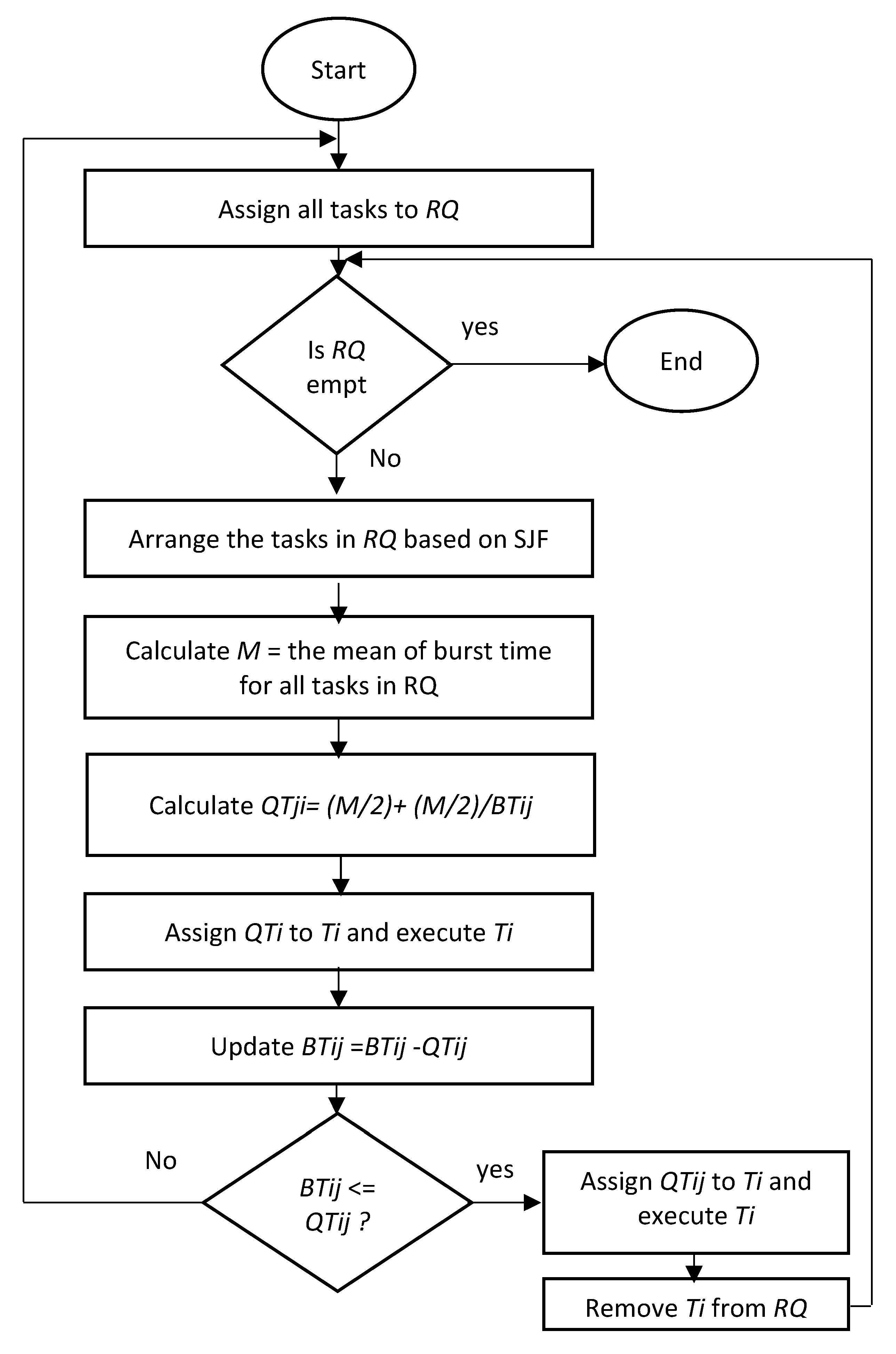
4. The Proposed Technique
- Sort all tasks in the ready queue in the STF manner.
- The m and values for all the tasks in the ready queue will be recalculated.
| Algorithm 2 Proposed DRRHA |
| Declarations Ti: Task i BTij: Burst time or the remaining burst time of task i in the round j RQ: Ready Queue Count_Iteration: an initialized value for iteration j and Quantum Time QTij M: The arithmetic mean of burst time of tasks. QTij: Quantum time assigned to task, Ti, in the round j |
| Input: Tasks, Ti Output: Rescheduling all tasks, Ti |
| BEGIN Submitted tasks in RQ based on arrival time. WHILE (RQ is not empty) BEGIN Arrange all arrived tasks in RQ based on SJF M = The mean of burst time of the tasks that arrived in RQ. For (each task Ti in RQ) BEGIN QTij = (M/2) + (M/2)/BTij Execute (Ti) BTij = BTij − QTij IF (BTij < QTij): Execute (Ti) again Else: Add Ti at the end of RQ IF (BTij (Ti) = 0) BEGIN Remove (Ti) from RQ M = The mean of burst time of the remaining tasks in the RQ. For (each task Ti in RQ): QTij = (M/2) + (M/2)/BTij End IF IF (a new task is arrived) BEGIN Sort all tasks in RQ based on SJF M = The mean of burst time of all tasks in the RQ. For (each task Ti in RQ): QTij = (M/2) + (M/2)/BTij End IF j++ END FOR END WHILE END |
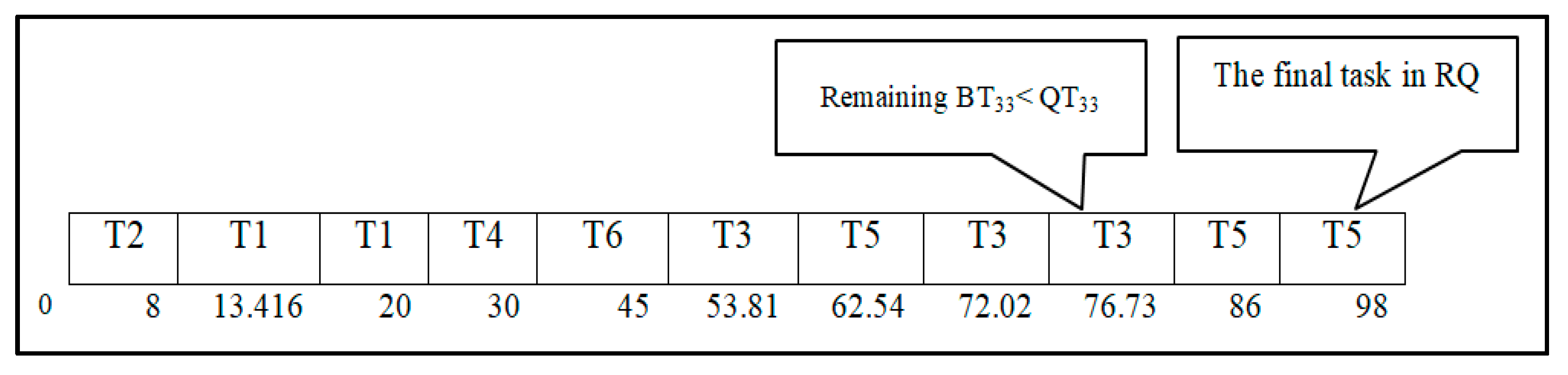
Case Study: The Impact of Integrating the Proposed Model (DRRHA) with the SJF Algorithm
- (1)
- Round 1
- (2)
- Round 2
- (3)
- Round 3
5. Simulation Settings
6. Evaluation and Discussion
- (1)
- Evaluating the proposed model by comparing it with SJF and FCFS algorithms to study the impact of integrating the proposed model with these algorithms;
- (2)
- Comparing the proposed model with the related algorithms from the literature review;
- (3)
- Evaluating the performance of the proposed model using two datasets: a real dataset and a randomly generated dataset.
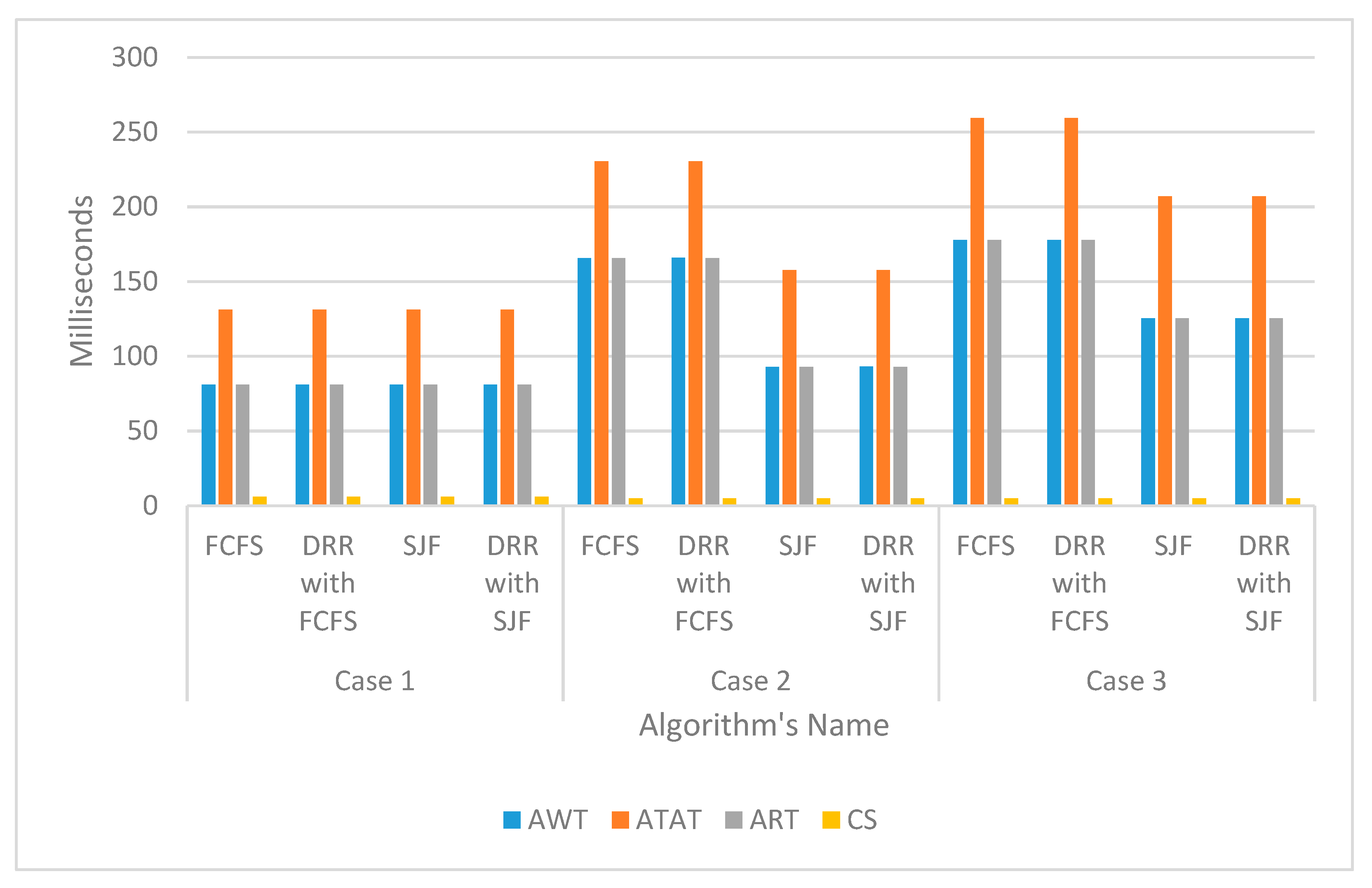
6.1. Evaluation of the Proposed Model (DRRHA) Considering SJF
6.2. Comparative Study on the Proposed Model (DRRHA) and the Related Algorithms
- A.
- The First Test
- B.
- The Second Test
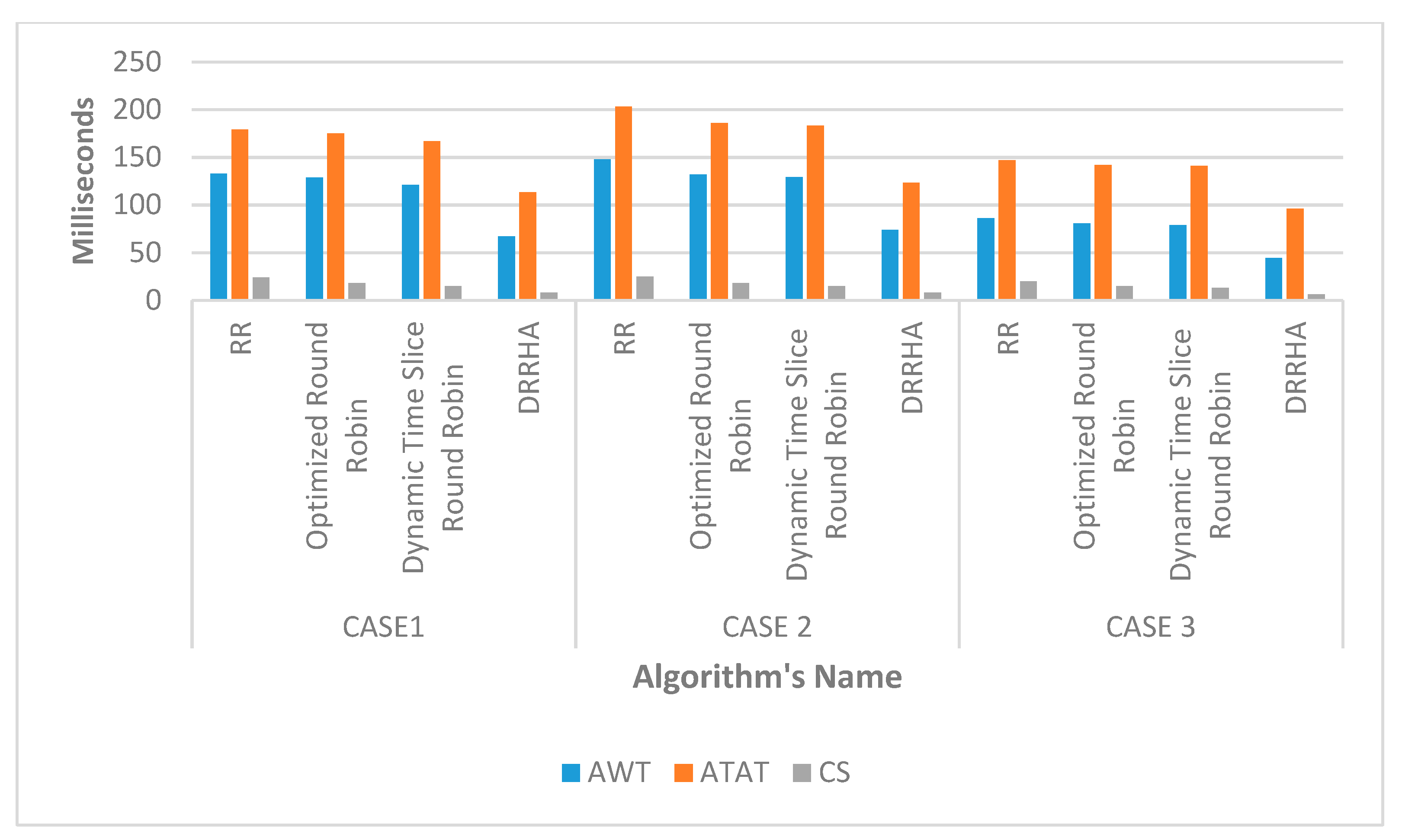
- C.
- The Third Test
- D.
- The Fourth Test
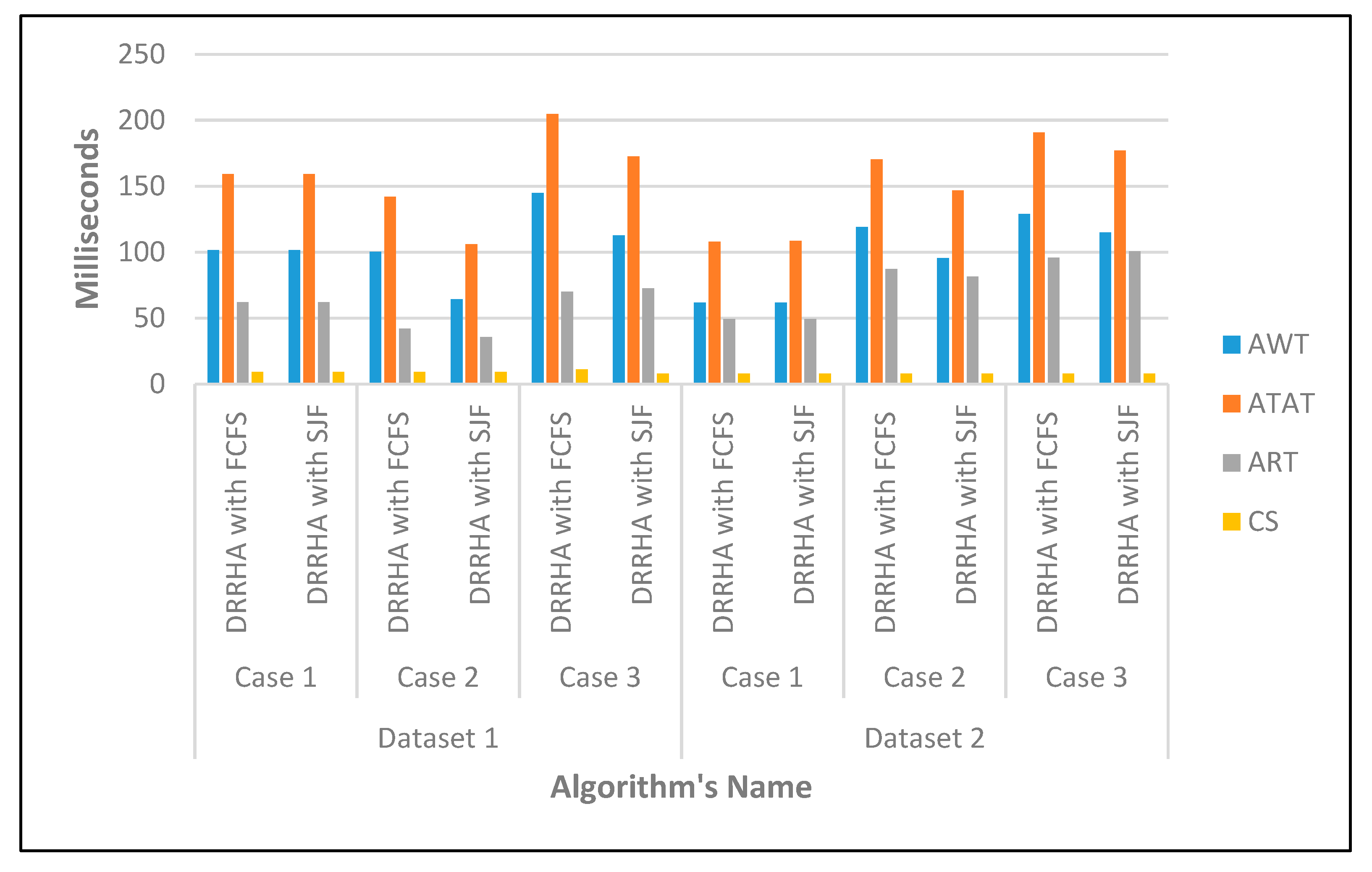
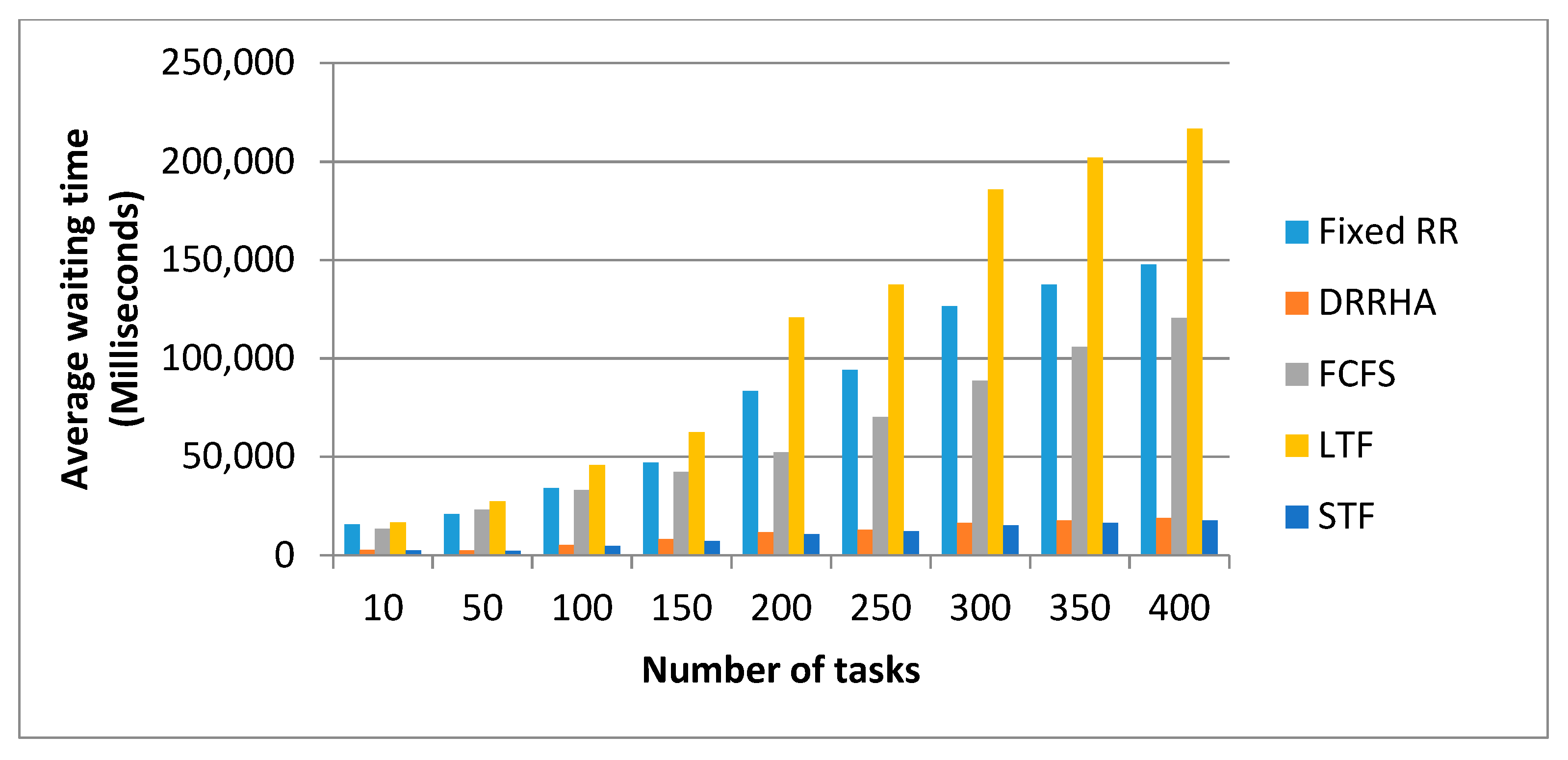
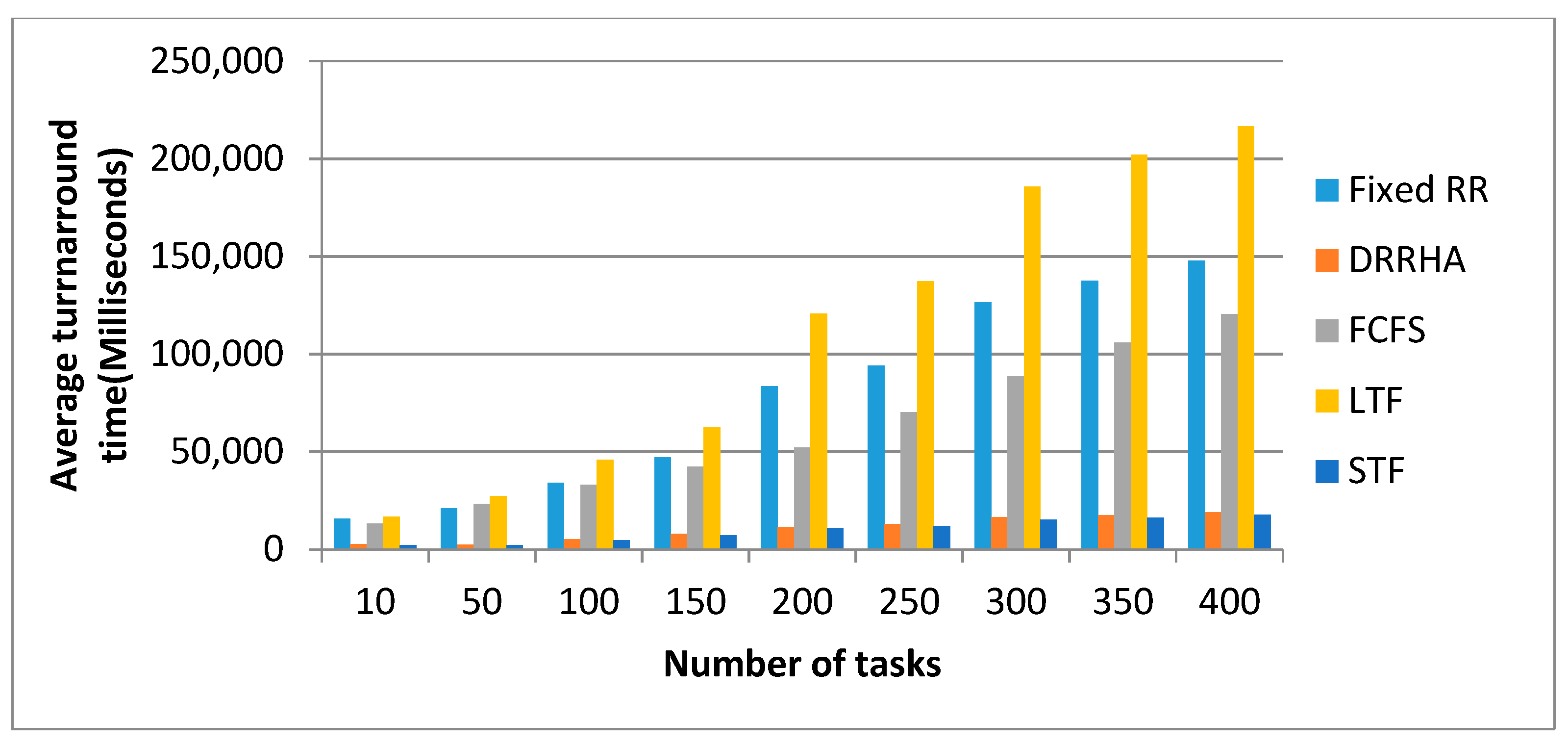
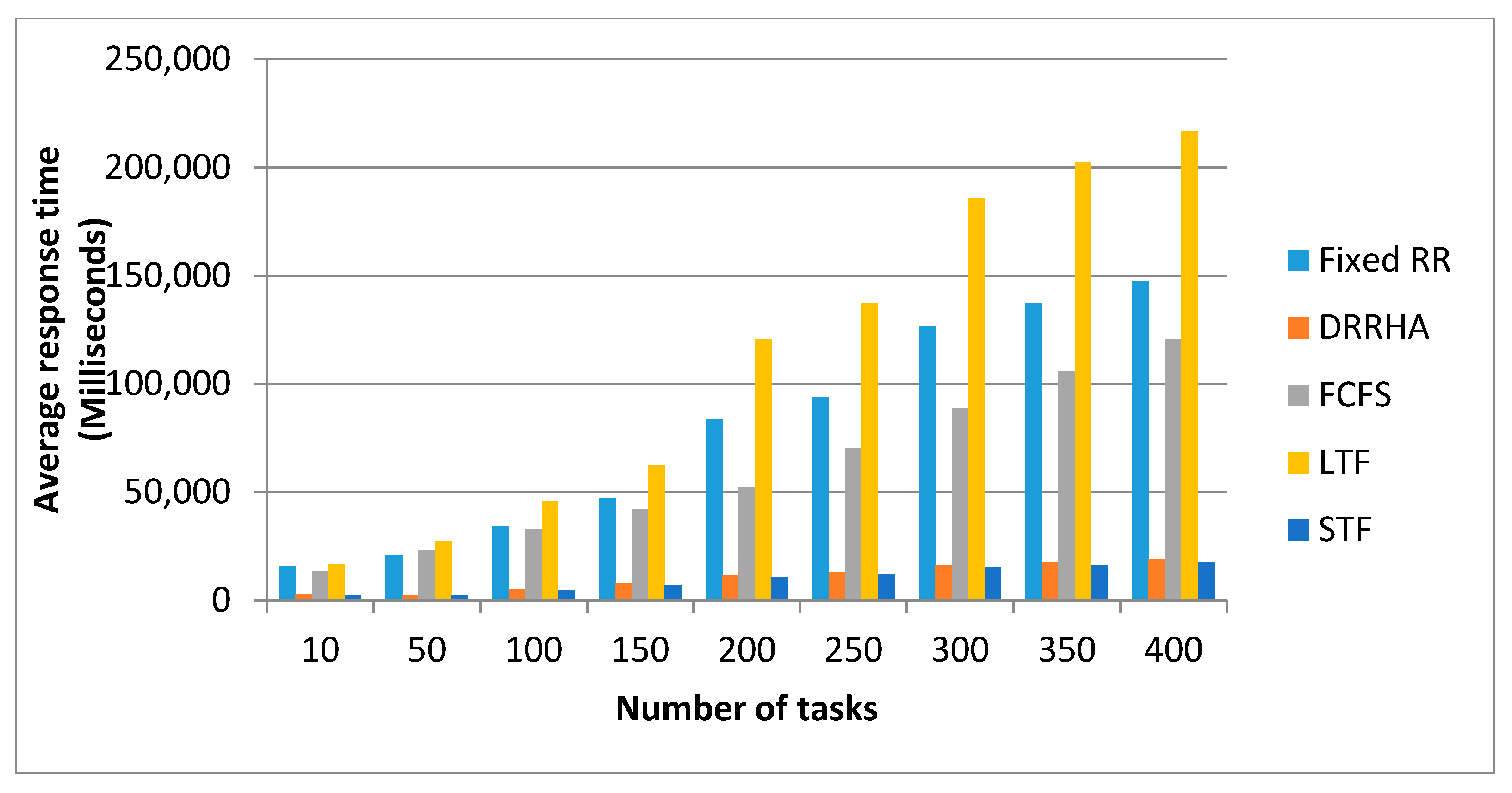
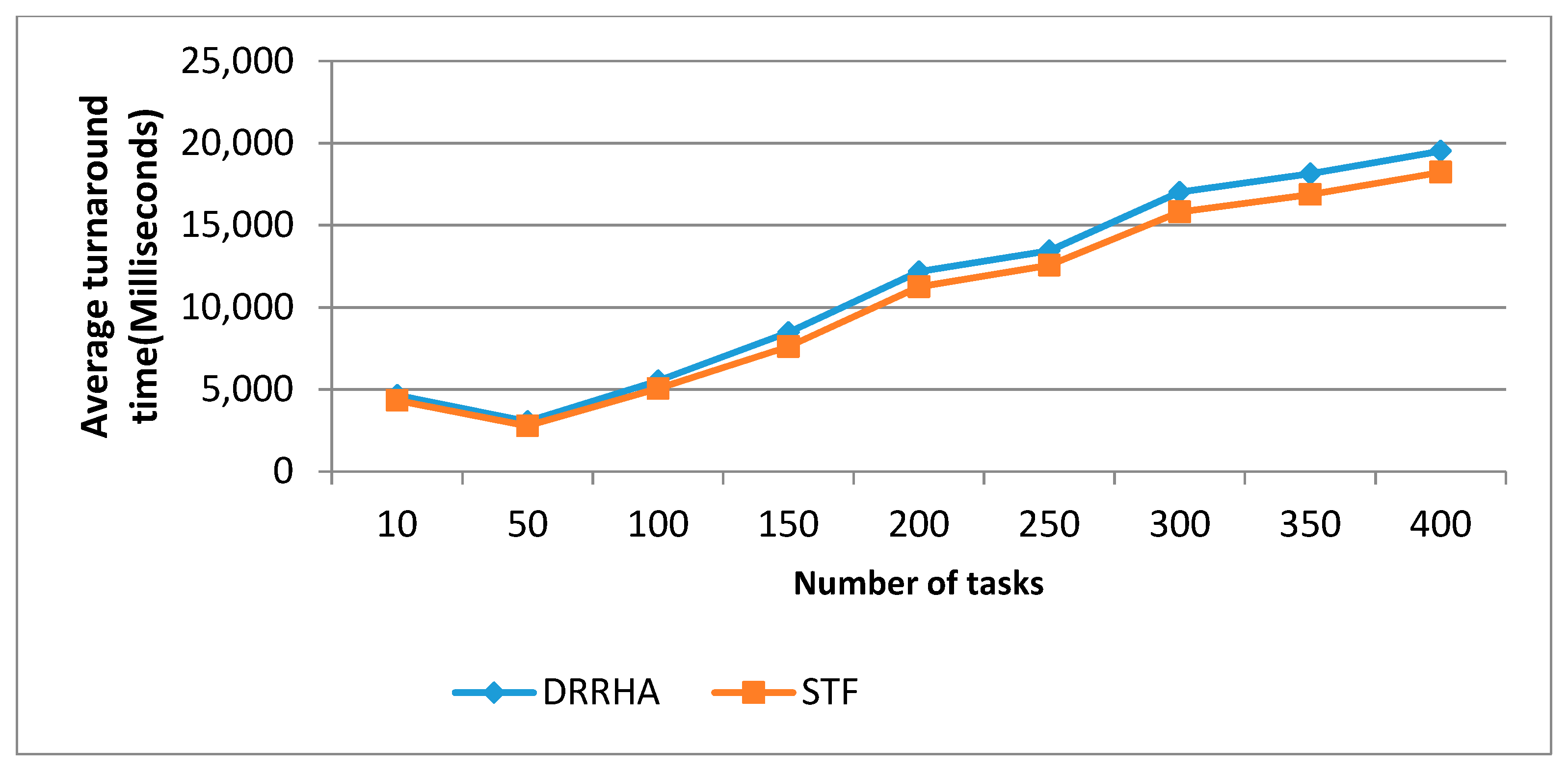
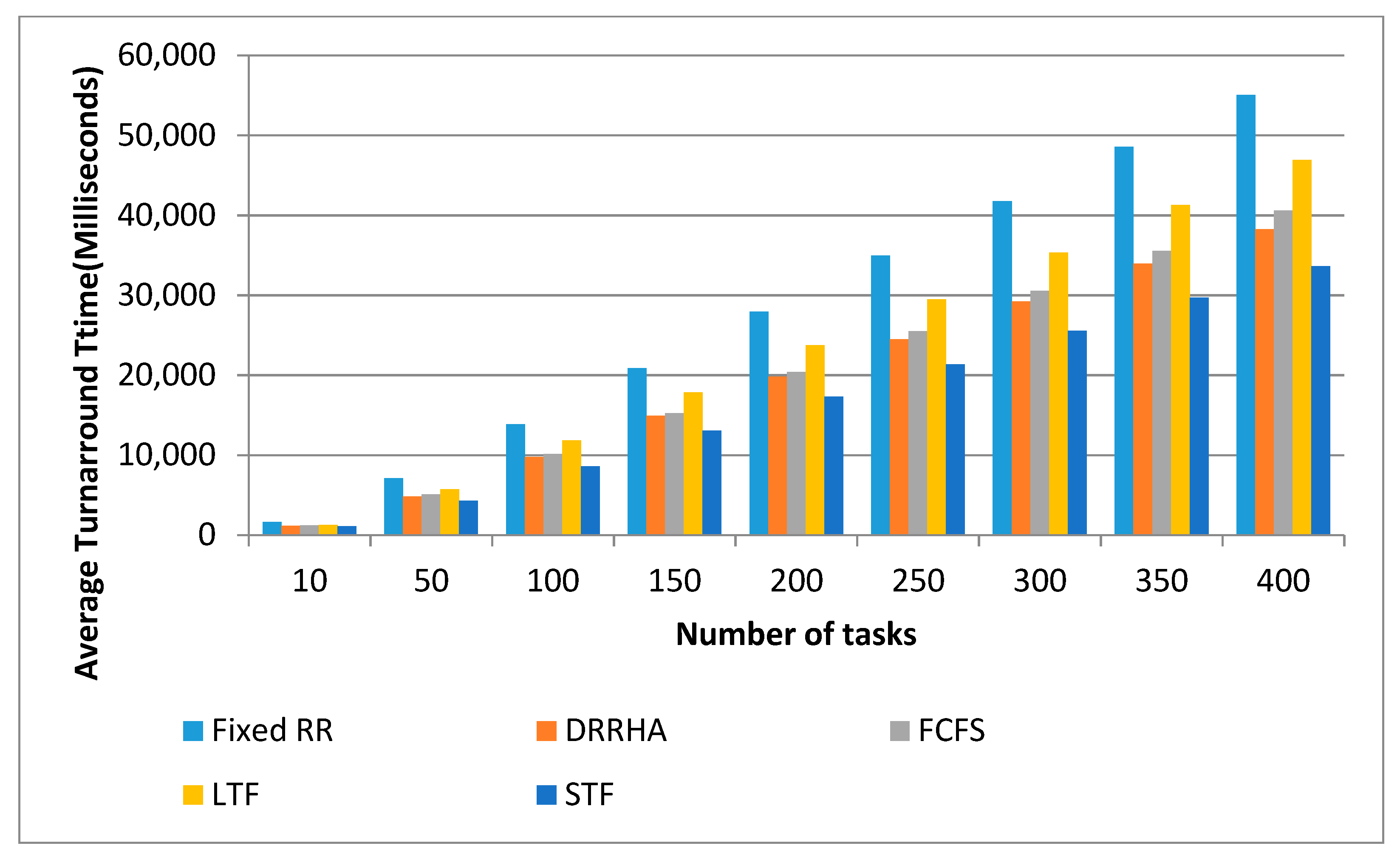
6.3. Evaluating the Performance of the Proposed Model (DRRHA) Using Datasets
- A.
- The First Experiment Using the NASA Dataset
- (1)
- The SJF algorithm and the DRRHA achieved the best performance, while the LJF algorithm was the worst;
- (2)
- There was a clear convergence in the performance of both the SJF algorithm and the DRRHA;
- (3)
- (4)
- The algorithms maintained the same performance despite the repeated experiments with an increasing number of tasks each time.
- (1)
- (2)
- Despite the superiority of these two algorithms and the convergence of their performance, it was found that the SJF algorithm outperformed the others in reducing the average waiting time by 12.61% and the turnaround time by 12.29%, while the DRRHA outperformed the others in reducing the average response time by 19.89%;
- (3)
- On the other hand, the longest job first (LJF) algorithm was the worst among the other algorithms.
- B.
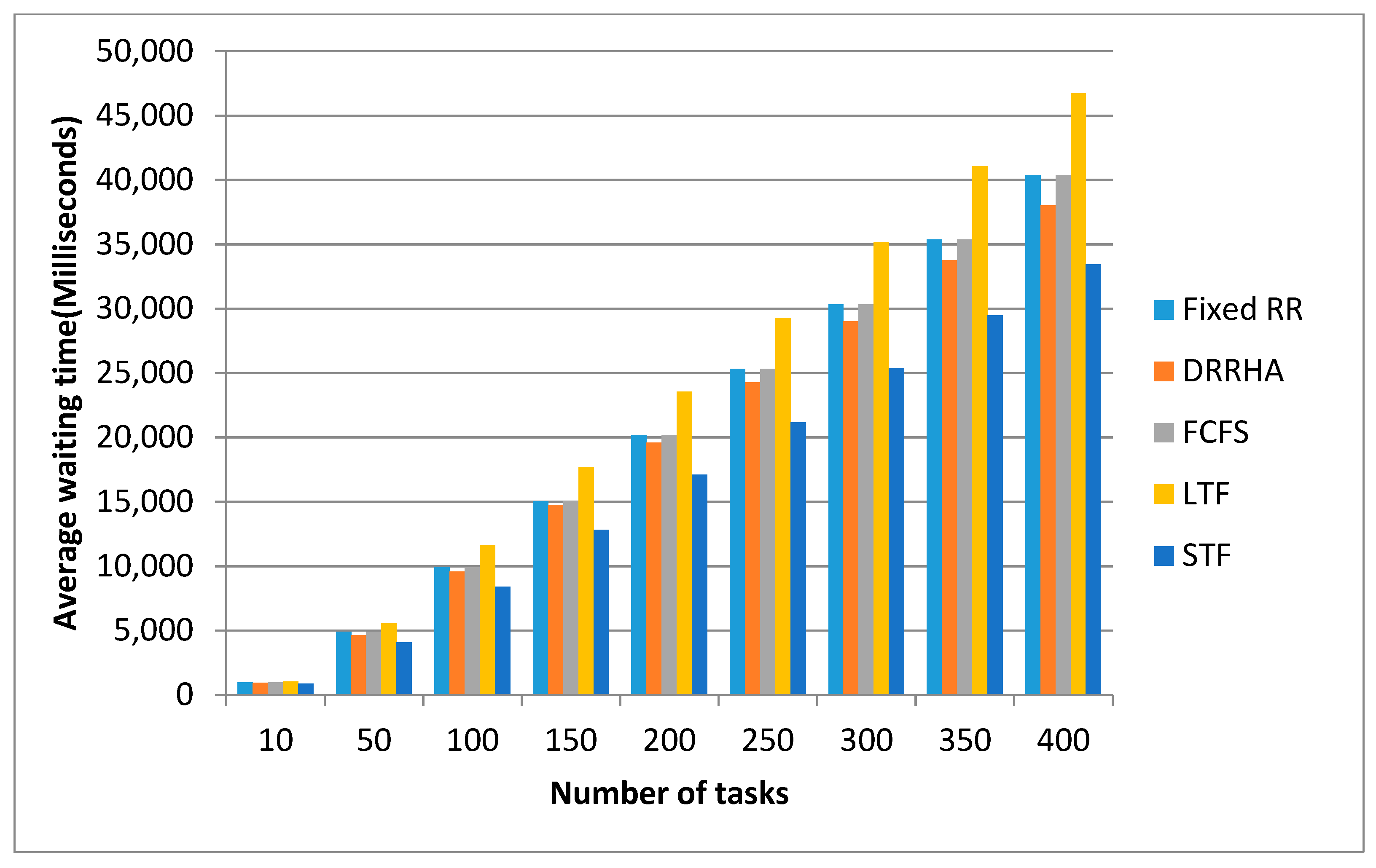
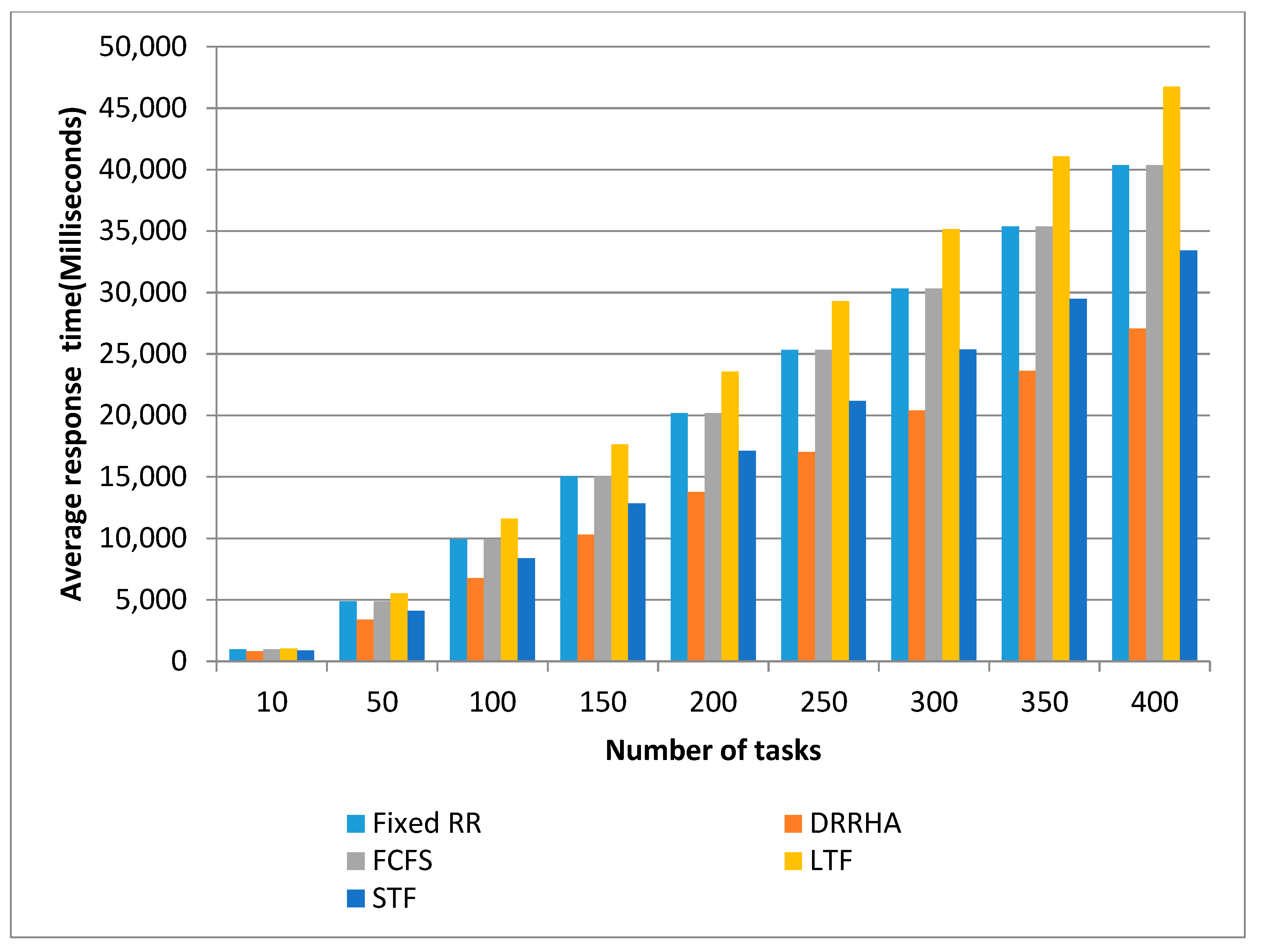
- The Second Experiment Using a Random Dataset
- (1)
- Calculating the optimal time quantum for each experiment using the mean of the burst times;
- (2)
- Repeating every experiment 50 times and then taking the average values of the waiting time, turnaround time, and response time.
- (1)
- The STF algorithm and the DRRHA had the best comparable performances;
- (2)
- The STF algorithm was slightly superior to the DRRHA in terms of the average waiting time by 21.09% and the turnaround time by 20.31%. However, the DRRHA outperformed the others in terms of decreasing the response time by 35.98%;
- (3)
- In contrast, the fixed RR algorithm had the worst performance in terms of reducing the average waiting time and turnaround time. The LJF algorithm was the worst in terms of reducing the average response time.
- (1)
- The STF algorithm and DRRHA outperformed the other algorithms in optimizing performance;
- (2)
- Both the STF algorithm and DRRHA had comparable performances, but the STF succeeded in reducing the average waiting time by 18.8% and reducing the average turnaround time by 18.34%. However, the DRRHA reduced the average response time by 29.65%;
- (3)
- The fixed RR algorithm had the worst performance, as it recorded high values in the average waiting time and turnaround time;
- (4)
- The LTF algorithm had the worst performance among other algorithms in terms of the average response time.
- For all the cases, the SJF algorithm and the proposed algorithm (DRRHA) achieved the best performance compared with the other algorithms;
- The SJF algorithm outperformed the DRRHA in terms of the average waiting time and turnaround time. This is because of the SJF algorithm mechanism, which executed the whole task in one round. In contrast, the DRRHA executed the task in several rounds, which may have led to putting the task in the ready queue several times;
- The DRRHA outperformed the SJF algorithm in terms of the average response time. This is because the DRRHA is preemptive, in which the current task might be paused to give a chance to another task in the ready queue. The SJF algorithm mechanism allows for responding to any new task after completing the entire previous task, which results in increasing the response time;
- When using the NASA dataset, the LJF algorithm had the worst performance among the other algorithms. This is because of the mechanism of the LJF algorithm, which imposes the implementation of the longest task in the queue first. In addition, the LJF algorithm does not allow for executing the next task until the current one is finished, which results in increasing the waiting time, turnaround time, and response time.
7. Conclusions
8. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Razaque, A.; Vennapusa, N.R.; Soni, N.; Janapati, G.S.; Vangala, K.R. Task scheduling in Cloud computing. In Proceedings of the 2016 IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 29 April 2016; Volume 8. [Google Scholar]
- Ohlman, B.; Eriksson, A.; Rembarz, R. What networking of information can do for cloud computing. In Proceedings of the Workshop on Enabling Technologies: Infrastructure for Collaborative Enterprises, WETICE, Groningen, The Netherlands, 29 June–1 July 2009; pp. 78–83. [Google Scholar]
- Taneja, B. An empirical study of most fit, max-min and priority task scheduling algorithms in cloud computing. In Proceedings of the International Conference on Computing, Communication & Automation, ICCCA 2015, Greater Noida, India, 15–16 May 2015; pp. 664–667. [Google Scholar]
- Lynn, T.; Xiong, H.; Dong, D.; Momani, B.; Gravvanis, G.A.; Filelis-Papadopoulos, C.; Elster, A.; Muhammad Zaki Murtaza Khan, M.; Tzovaras, D.; Giannoutakis, K.; et al. CLOUDLIGHTNING: A framework for a self-organising and self-managing heterogeneous cloud. In Proceedings of the CLOSER 2016, 6th International Conference on Cloud Computing and Services Science, Rome, Italy, 23–25 April 2016; Volume 1, pp. 333–338. [Google Scholar]
- Giannoutakis, K.M.; Filelis-Papadopoulos, C.K.; Gravvanis, G.A.; Tzovaras, D. Evaluation of self-organizing and self-managing heterogeneous high performance computing clouds through discrete-time simulation. Concurr. Comput. Pract. Exp. 2021, 33, e6326. [Google Scholar]
- Soltani, N.; Soleimani, B.; Barekatain, B. Heuristic Algorithms for Task Scheduling in Cloud Computing: A Survey. Int. J. Comput. Netw. Inf. Secur. 2017, 9, 16–22. [Google Scholar] [CrossRef][Green Version]
- Alhaidari, F.; Balharith, T.; Al-Yahyan, E. Comparative analysis for task scheduling algorithms on cloud computing. In Proceedings of the 2019 International Conference on Computer and Information Sciences, ICCIS 2019, Sakaka, Saudi Arabia, 3–4 April 2019; pp. 1–6. [Google Scholar]
- Li, X.; Zheng, M.C.; Ren, X.; Liu, X.; Zhang, P.; Lou, C. An improved task scheduling algorithm based on potential games in cloud computing. In Pervasive Computing and the Networked World; Zu, Q., Vargas-Vera, M., Hu, B., Eds.; ICPCA/SWS; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2013; Volume 8351. [Google Scholar]
- Tawfeek, M.; El-Sisi, A.; Keshk, A.; Torkey, F. Cloud task scheduling based on ant colony optimization. Int. Arab J. Inf. Technol. 2015, 12, 129–137. [Google Scholar]
- Masdari, M.; Salehi, F.; Jalali, M.; Bidaki, M. A Survey of PSO-Based Scheduling Algorithms in Cloud Computing. J. Netw. Syst. Manag. 2017, 25, 122–158. [Google Scholar] [CrossRef]
- Varma, P.S. A finest time quantum for improving shortest remaining burst round robin (srbrr) algorithm. J. Glob. Res. Comput. Sci. 2013, 4, 10–15. [Google Scholar]
- Singh, M.; Agrawal, R. Modified Round Robin algorithm (MRR). In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering, ICPCSI 2017, Chennai, India, 21–22 September 2017; pp. 2832–2839. [Google Scholar]
- Dorgham, O.H.M.; Nassar, M.O. Improved Round Robin Algorithm: Proposed Method to Apply {SJF} using Geometric Mean. Int. J. Adv. Stud. Comput. Sci. Eng. 2016, 5, 112–119. [Google Scholar]
- Balharith, T.; Alhaidari, F. Round Robin Scheduling Algorithm in CPU and Cloud Computing: A review. In Proceedings of the 2nd International Conference on Computer Applications and Information Security, ICCAIS 2019, Riyadh, Saudi Arabia, 1–3 May 2019; pp. 1–7. [Google Scholar]
- Tayal, S. Tasks scheduling optimization for the cloud computing systems. Int. J. Adv. Eng. Sci. Technol. 2011, 5, 111–115. [Google Scholar]
- Mishra, M.K.; Rashid, F. An Improved Round Robin CPU Scheduling Algorithm with Varying Time Quantum. Int. J. Comput. Sci. Eng. Appl. 2014, 4, 1–8. [Google Scholar]
- Jbara, Y.H. A new improved round robin-based scheduling algorithm-a comparative analysis. In Proceedings of the 2019 International Conference on Computer and Information Sciences, ICCIS 2019, Sakaka, Saudi Arabia, 3–4 April 2019; pp. 1–6. [Google Scholar]
- Srujana, R.; Roopa, Y.M.; Mohan, M.D.S.K. Sorted round robin algorithm. In Proceedings of the International Conference on Trends in Electronics and Informatics, ICOEI 2019, Tirunelveli, India, 23–25 April 2019; pp. 968–971. [Google Scholar]
- Sangwan, P.; Sharma, M.; Kumar, A. Improved round robin scheduling in cloud computing. Adv. Comput. Sci. Technol. 2017, 10, 639–644. [Google Scholar]
- Fiad, A.; Maaza, Z.M.; Bendoukha, H. Improved Version of Round Robin Scheduling Algorithm Based on Analytic Model. Int. J. Networked Distrib. Comput. 2020, 8, 195. [Google Scholar] [CrossRef]
- Faizan, K.; Marikal, A.; Anil, K. A Hybrid Round Robin Scheduling Mechanism for Process Management. Int. J. Comput. Appl. 2020, 177, 14–19. [Google Scholar] [CrossRef]
- Biswas, D. Samsuddoha Determining Proficient Time Quantum to Improve the Performance of Round Robin Scheduling Algorithm. Int. J. Mod. Educ. Comput. Sci. 2019, 11, 33–40. [Google Scholar] [CrossRef]
- Elmougy, S.; Sarhan, S.; Joundy, M. A novel hybrid of Shortest job first and round Robin with dynamic variable quantum time task scheduling technique. J. Cloud Comput. 2017, 6, 12. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, S.B.; Tang, D.Y. Task Scheduling Algorithm in Cloud Computing Based on Invasive Tumor Growth Optimization. Jisuanji Xuebao/Chin. J. Comput. 2018, 41, 1360–1375. [Google Scholar]
- Pradhan, P.; Behera, P.K.; Ray, B. Modified Round Robin Algorithm for Resource Allocation in Cloud Computing. Procedia Comput. Sci. 2016, 85, 878–890. [Google Scholar] [CrossRef]
- Dave, B.; Yadev, S.; Mathuria, M.; Sharma, Y.M. Optimize task scheduling act by modified round robin scheme with vigorous time quantum. In Proceedings of the International Conference on Intelligent Sustainable Systems, ICISS 2017, Palladam, India, 7–8 December 2017; pp. 905–910. [Google Scholar]
- Mishra, M.K. An improved round robin cpu scheduling algorithm. J. Glob. Res. Comput. Sci. 2012, 3, 64–69. [Google Scholar]
- Fayyaz, H.A.H.S.; Din, S.M.U.; Iqra. Efficient Dual Nature Round Robin CPU Scheduling Algorithm: A Comparative Analysis. Int. J. Multidiscip. Sci. Eng. 2017, 8, 21–26. [Google Scholar]
- Filho, M.C.S.; Oliveira, R.L.; Monteiro, C.C.; Inácio, P.R.M.; Freire, M.M. CloudSim Plus: A cloud computing simulation framework pursuing software engineering principles for improved modularity, extensibility and correctness. In Proceedings of the IM 2017—2017 IFIP/IEEE International Symposium on Integrated Network and Service Management, Lisbon, Portugal, 8–12 May 2017; pp. 400–406. [Google Scholar]
- Calheiros, R.N.; Ranjan, R.; Beloglazov, A.; De Rose, C.A.F.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Exp. 2010, 41, 23–50. [Google Scholar] [CrossRef]
- Saeidi, S.; Baktash, H.A. Determining the Optimum Time Quantum Value in Round Robin Process Scheduling Method. Int. J. Inf. Technol. Comput. Sci. 2012, 4, 67–73. [Google Scholar] [CrossRef][Green Version]
- Nayak, D.; Malla, S.K.; Debadarshini, D. Improved Round Robin Scheduling using Dynamic Time Quantum. Int. J. Comput. Appl. 2012, 38, 34–38. [Google Scholar] [CrossRef]
- Muraleedharan, A.; Antony, N.; Nandakumar, R. Dynamic Time Slice Round Robin Scheduling Algorithm with Unknown Burst Time. Indian J. Sci. Technol. 2016, 9, 16. [Google Scholar] [CrossRef][Green Version]
- Hemamalini, M.; Srinath, M.V. Memory Constrained Load Shared Minimum Execution Time Grid Task Scheduling Algorithm in a Heterogeneous Environment. Indian J. Sci. Technol. 2015, 8. [Google Scholar] [CrossRef]
- Negi, S. An Improved Round Robin Approach using Dynamic Time Quantum for Improving Average Waiting Time. Int. J. Comput. Appl. 2013, 69, 12–16. [Google Scholar] [CrossRef]
- Lang, L.H.P.; Litzenberger, R.H. Dividend announcements. Cash flow signalling vs. free cash flow hypothesis? J. Financ. Econ. 1989, 24, 181–191. [Google Scholar] [CrossRef]
- Feitelson, D.G.; Tsafrir, D.; Krakov, D. Experience with using the Parallel Workloads Archive. J. Parallel Distrib. Comput. 2014, 74, 2967–2982. [Google Scholar] [CrossRef]
- Nasa-Workload. 2019. Available online: http://www.cs.huji.ac.il/labs/parallel/workload (accessed on 14 August 2019).
- Aida, K. Effect of job size characteristics on job scheduling performance. In Job Scheduling Strategies for Parallel Processing; Feitelson, D.G., Rudolph, L., Eds.; Lecture Notes in Computer Science; JSSPP 2000; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1911. [Google Scholar]
- Alboaneen, D.A.; Tianfield, H.; Zhang, Y. Glowworm swarm optimisation based task scheduling for cloud computing. In Proceedings of the Second International Conference on Internet of things, Data and Cloud Computing, Cambridge, UK, 22–23 March 2017; pp. 1–7. [Google Scholar]
- Chiang, S.H.; Vernon, M.K. Dynamic vs. Static quantum-based parallel processor allocation. In Workshop on Job Scheduling Strategies for Parallel Processing; JSSPP 1996; Lecture Notes in Computer Science; Feitelson, D.G., Rudolph, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1162. [Google Scholar] [CrossRef]











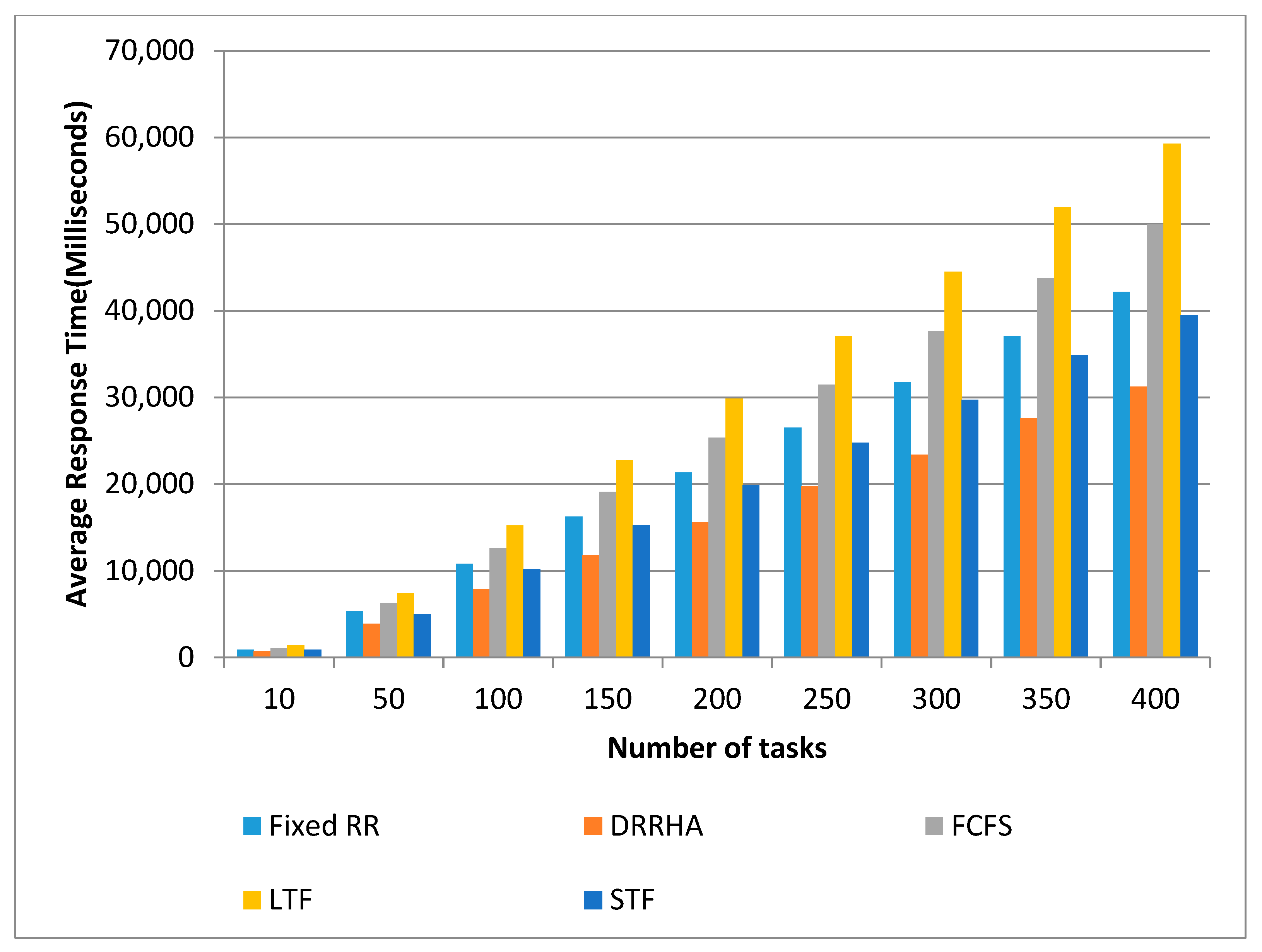


| Datasets with Zero Arrival Time | ||||||
|---|---|---|---|---|---|---|
| Task | Case 1 Increasing Order | Case 2 Decreasing Order | Case 3 Random Order | |||
| Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | |
| T1 | 0 | 20 | 0 | 105 | 0 | 105 |
| T2 | 0 | 25 | 0 | 85 | 0 | 60 |
| T3 | 0 | 35 | 0 | 55 | 0 | 120 |
| T4 | 0 | 50 | 0 | 43 | 0 | 48 |
| T5 | 0 | 80 | 0 | 35 | 0 | 75 |
| T6 | 0 | 90 | - | - | - | - |
| Task | Arrival Time | Burst Time |
|---|---|---|
| T1 | 0 | 12 |
| T2 | 0 | 8 |
| T3 | 1 | 23 |
| T4 | 2 | 10 |
| T5 | 3 | 30 |
| T6 | 4 | 15 |
| Round 1 | M = 10 | M/2 = 5 |
|---|---|---|
| Tasks | QTij = (M/2) + (M/2)/BTij | Remaining BTij |
| T2 | 5.625 | 2.375 |
| T1 | 5.416 | 6.584 |
| Task | Burst Time |
|---|---|
| T1 | 6.584 |
| T4 | 10 |
| T6 | 15 |
| T3 | 23 |
| T5 | 30 |
| Round 2 | M = 16.91 | M/2 = 8.45 |
|---|---|---|
| Tasks | QTij = (M/2) + (M/2)/BTij | Remaining BTij |
| T1 | 9.73 | 0 |
| T4 | 9.29 | 0.71 |
| T6 | 9.01 | 5.99 |
| T3 | 8.81 | 14.19 |
| T5 | 8.73 | 21.27 |
| Task | Burst Time |
|---|---|
| T3 | 14.19 |
| T5 | 21.27 |
| Round 3 | M = 17.73 | M/2 = 8.86 |
|---|---|---|
| Tasks | QTij = (M/2) + (M/2)/BTij | Remaining BTij |
| T3 | 9.48 | 4.71 |
| T5 | 9.27 | 12 |
| Task | Arrival Time | Burst Time | WT | TAT | RT |
|---|---|---|---|---|---|
| T1 | 0 | 12 | 8 | 20 | 0 |
| T2 | 0 | 8 | 0 | 8 | 5.416 |
| T3 | 1 | 23 | 52.73 | 75.73 | 13.416 |
| T4 | 2 | 10 | 18 | 28 | 22.22 |
| T5 | 3 | 30 | 65 | 95 | 32.22 |
| T6 | 4 | 15 | 26 | 41 | 40.95 |
| Average | 28.28833 | 44.62167 | 19.037 | ||
| Data Center Characteristics | |
| Parameters | Values |
| Data Center OS | Linux |
| Data Center VMM | Xen |
| Data Center Architecture | X86 |
| VM Parameters | |
| Image Size | 10,000 |
| VM_MIPS | 1000 |
| Bandwidth | 50,000 |
| VM Number of CPUs | 10 |
| Ram | 512 |
| Cloudlet Parameters | |
| Cloudlet File Size | 300 |
| Cloudlet Output Size | 300 |
| Cloudlet Utilization (CPU, BW, Ram) | Full |
| Data Sets with Zero Arrival Time | Data Sets with Non-Zero Arrival Time | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Task | Case 1 Increasing Order | Case 2 Decreasing Order | Case 3 Random Order | Case 1 Increasing Order | Case 2 DecreasingOrder | Case 3 Random Order | ||||||
| Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | |
| T1 | 0 | 30 | 0 | 77 | 0 | 80 | 0 | 14 | 0 | 80 | 0 | 65 |
| T2 | 0 | 34 | 0 | 54 | 0 | 45 | 2 | 34 | 2 | 74 | 1 | 72 |
| T3 | 0 | 62 | 0 | 45 | 0 | 62 | 6 | 45 | 3 | 70 | 4 | 50 |
| T4 | 0 | 74 | 0 | 19 | 0 | 34 | 8 | 62 | 4 | 18 | 6 | 43 |
| T5 | 0 | 88 | 0 | 14 | 0 | 78 | 14 | 77 | 5 | 14 | 7 | 80 |
| CASE 1 | CASE 2 | ||||
|---|---|---|---|---|---|
| Task | Arrival Time | Burst Time | Task | Arrival Time | Burst Time |
| T1 | 0 | 15 | 0 | 7 | 0 |
| T2 | 0 | 32 | 4 | 25 | 4 |
| T3 | 0 | 10 | 10 | 5 | 10 |
| T4 | 0 | 26 | 15 | 36 | 15 |
| T5 | 0 | 20 | 17 | 18 | 17 |
| First Test | ||
|---|---|---|
| The Metrics | Case 1 | Case 2 |
| Improvement (%) | Improvement (%) | |
| Avg. WT | 35% | 12% |
| Avg. TAT | 23% | 6% |
| Task | Case 1 | Case 2 | Case 3 | |||
|---|---|---|---|---|---|---|
| Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | |
| T1 | 0 | 14 | 0 | 33 | 0 | 15 |
| T2 | 0 | 34 | 2 | 22 | 4 | 77 |
| T3 | 0 | 45 | 5 | 48 | 15 | 30 |
| T4 | 0 | 62 | 7 | 70 | 20 | 85 |
| T5 | 0 | 77 | 9 | 74 | - | - |
| Second Test | ||||
|---|---|---|---|---|
| The Metrics | Case 1 | Case 2 | Case 3 | Overall |
| Improvement (%) | Improvement (%) | Improvement (%) | Improvement (%) | |
| Avg. WT | 58% | 54% | 56% | 56% |
| Avg. TAT | 38% | 39% | 38% | 38% |
| CS | 61% | 61% | 74% | 65% |
| Task | Case 1 | Case 2 | Case 3 | |||
|---|---|---|---|---|---|---|
| Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | |
| T1 | 0 | 12 | 0 | 42 | 0 | 11 |
| T2 | 0 | 11 | 0 | 32 | 0 | 10 |
| T3 | 0 | 22 | 0 | 82 | 0 | 22 |
| T4 | 0 | 31 | 0 | 45 | 0 | 31 |
| T5 | 0 | 21 | 0 | 22 | 0 | 25 |
| T6 | - | - | - | - | 0 | 13 |
| Third Test | ||||
|---|---|---|---|---|
| The Metrics | Case 1 | Case 2 | Case 3 | Overall |
| Improvement (%) | Improvement (%) | Improvement (%) | Improvement (%) | |
| Avg. WT | 6% | 53% | 28% | 29% |
| Avg. TAT | 4% | 35% | 20% | 20% |
| CS | −12% | 50% | 10% | 16% |
| Zero Arrival Time | Non-Zero Arrival Time | |||||||
|---|---|---|---|---|---|---|---|---|
| Task | Case 1 | Case 2 | Case 3 | Case 4 | ||||
| Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | Arrival Time | Burst Time | |
| T1 | 0 | 20 | 0 | 10 | 0 | 18 | 0 | 10 |
| T2 | 0 | 40 | 0 | 14 | 4 | 70 | 6 | 14 |
| T3 | 0 | 60 | 0 | 70 | 8 | 74 | 13 | 70 |
| T4 | 0 | 80 | 0 | 120 | 16 | 80 | 21 | 120 |
| Fourth Test | |||||
|---|---|---|---|---|---|
| The Metrics | Case 1 | Case 2 | Case 3 | Case 4 | Overall |
| Improvement (%) | Improvement (%) | Improvement (%) | Improvement (%) | Improvement (%) | |
| Avg. WT | 10% | 9% | 34% | 63% | 29% |
| Avg. TAT | 6% | 4% | 19% | 24% | 13% |
| Metrics | The Improvement Rate Achieved by the Proposed Model Compared with the Following Algorithms | |||
|---|---|---|---|---|
| IRRVQ | DTSRR | Improved RR [35] | SRDQ | |
| Avg. WT | 12% | 56% | 29% | 29% |
| Avg. TAT | 6% | 38% | 20% | 13% |
| No.CS | 12% | 65% | 16% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhaidari, F.; Balharith, T.Z. Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling. Computers 2021, 10, 63. https://doi.org/10.3390/computers10050063
Alhaidari F, Balharith TZ. Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling. Computers. 2021; 10(5):63. https://doi.org/10.3390/computers10050063
Chicago/Turabian StyleAlhaidari, Fahd, and Taghreed Zayed Balharith. 2021. "Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling" Computers 10, no. 5: 63. https://doi.org/10.3390/computers10050063
APA StyleAlhaidari, F., & Balharith, T. Z. (2021). Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling. Computers, 10(5), 63. https://doi.org/10.3390/computers10050063






