Towards Inferring Influential Facebook Users

Abstract

Because of the complexity of the actors and the relationships between them, social networks are always represented by graphs. This structure makes it possible to analyze the effectiveness of the network for the social actors who are there. This work presents a social network analysis approach that focused on processing Facebook pages and users who react to posts to infer influential people. In our study, we are particularly interested in studying the relationships between the posts of the page, and the reactions of fans (users) towards these posts. The topics covered include data crawling, graph modeling, and exploratory analysis using statistical tools and machine learning algorithms. We seek to detect influential people in the sense that the influence of a Facebook user lies in their ability to transmit and disseminate information. Once determined, these users have an impact on business for a specific brand. The proposed exploratory analysis has shown that the network structure and its properties have important implications for the outcome of interest.

1. Introduction

Social networks have experienced rapid exponential growth in recent years. They reach large companies and promote easier communication between its members. The operation of these networks has gone beyond its ordinary use and has developed tools for their analysis to take advantage of the mass of data provided [1,2,3,4].

Social network analysis is also focused on visualization techniques for exploring the structure of the network. It has gained a significant following in many fields of application. It has been used to examine how problems have been solved, how organizations interact with one another, and to understand the role of an individual in an organization [5,6,7]. These benefits are becoming increasingly difficult to extract because of the mathematical and statistical tools used in the analyses, which are not indisputable in the eyes of computer scientists.

Although the methods of analyzing complex data and, in particular, social networks, have completely revolutionized the world of IT (information technology), they remain difficult to exploit [8]. Indeed, social networks not only utilize base information, but go beyond this manipulation to extract the greatest amount of useful information on the interactions of the individuals ir regards and on the data of an individual in question [8,9,10].

It is, therefore, clear that these analyzes relate to the theory of social networks that conceive of social relations in terms of nodes and links. Nodes are usually the social actors in the network. They can be people, institutions, or even other entities, such as messages. The links represent the relationships between these nodes. In its simplest form, a social network is modeled to form a structure that can be analyzed with all of the significant links between the nodes. This form is generally modeled in a graph. It characterizes networked structures in terms of nodes (individual actors, people, or things within the network) and the ties, edges, or links (relationships or interactions) that connect them. This structure makes it possible to analyze the effectiveness of the network for the social actors within it. The problem has become a matter of analyzing the graphs that store these social networks [11].

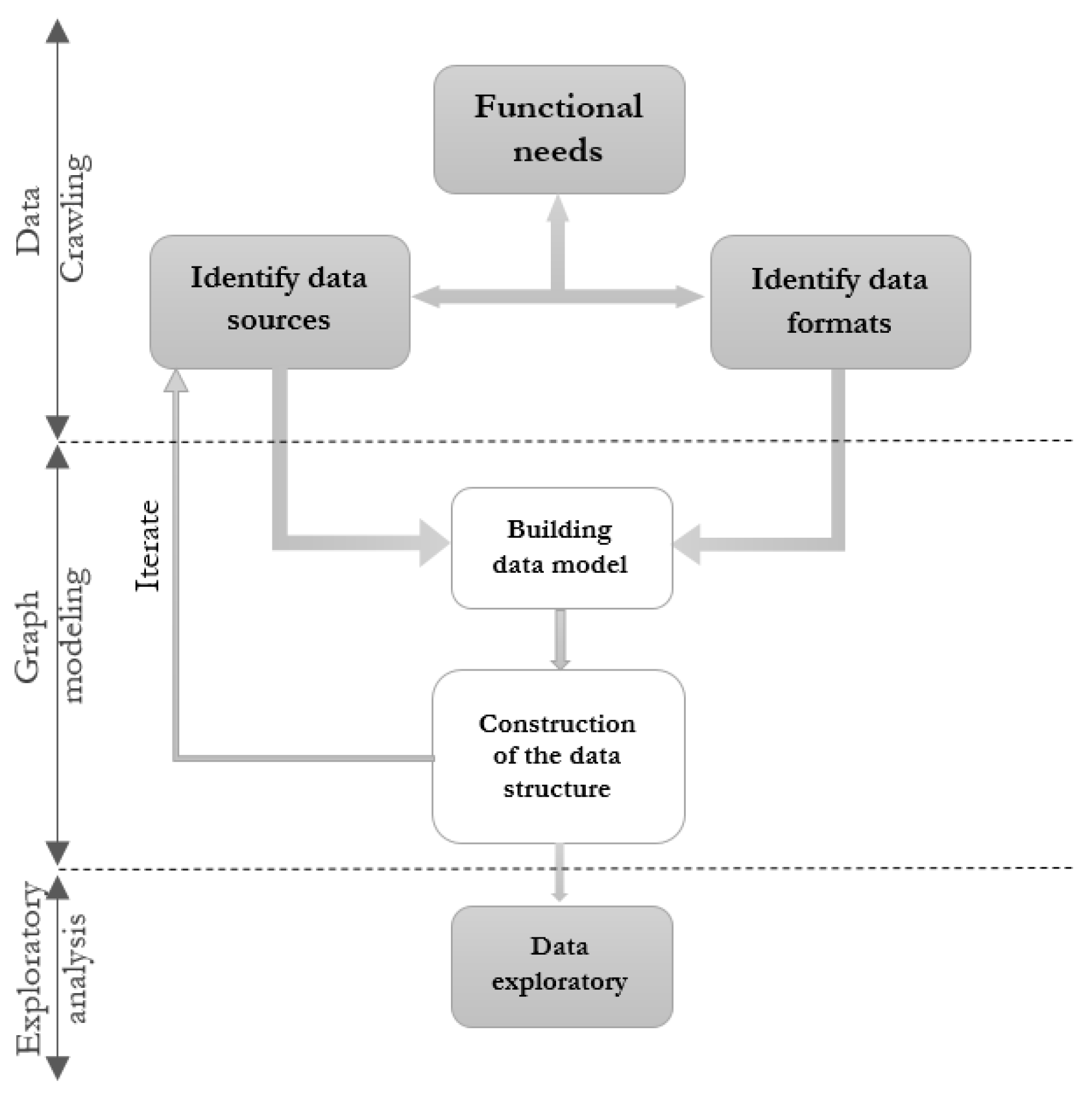
To accomplish our goal, an appropriate approach must be designed following the steps illustrated in the framework diagram illustrated by the Figure 1.

As shown in Figure 1, the methodological approach adopted essentially consists of the following three steps:

1.

Data crawling (or Data collection).

2.

Graph modeling.

3.

Exploratory analysis of graphs.

For data crawling, we first need to identify the relevant data sources, i.e., the Facebook source pages; then we extract the data from the page. We are mainly interested in extracting data from posts, comments (and their responses), and reactions from page fans towards the post concerned. The implemented crawler adopts the Depth First Search approach.

For graph modeling, we modeled two graphs: the USER-POST graph in which we are interested in studying the relationships between the fans of a given Facebook page and the different posts of the latter. In the USER–USER graph, we are interested in studying the relationships between the different people who reacted to the posts of a Facebook page to try to determine the most influential people among all the fans of the page.

For the exploratory analysis of graphs, we focused on both structure and community analysis and ranking of the social actors in the graph using statistical tools, and Machine Learning Algorithms (MLAs) [1,12,13,14].

Following the above steps, it was then necessary to interpret the difficulty level and the complexity of the existing analysis methods in order to propose a new approach, allowing one to display reports containing the data on the interactions and the individuals of a social network. We inspired our exploratory analysis from the big scholarly data framework proposed in [15]. It is called DICO (Discovery Information using COmmunity detection). It identifies overlapped communities of authors from bibliographic datasets by modeling author interactions through a novel graph-based data model jointly combining document metadata—authorship, citations—with semantic information. The used sources are DBLP and AMiner, the latter including abstracts and citations. This framework constitutes a lead for our approach.

Section 2 reviews data mining methods applied to graphs. Section 3, Section 4 and Section 5 are a bit more theoretical, as they present our methodological approach (data crawling, graph modeling, and exploratory analysis of graphs) to social network analysis. In Section 6, a performance analysis is brought forward to set the advantages of the implementation. Finally, we conclude in Section 7 our work and bring out some insights and potential future works.

2. Data Mining Methods Applied to Graphs: Literature Review

Data mining is based on the processing of data and the identification of characteristics and trends of information [16]. Graph clustering consists of cutting out and identifying, within a graph, the sets of strongly connected nodes to group them within a community [17,18]. It should make it possible to group the highly connected nodes and to separate those with little connection between them [19,20].

The different classification algorithms used in graph analysis are as follows:

• Fast Greedy: This algorithm is part of the descending hierarchical algorithm family. It tries to optimize a quality function called modularity in a greedy way. The method is fast and this algorithm is usually tried as a first approximation since it has no parameters to adjust. However, it is known to suffer from a resolution limitation, i.e., communities below a given size threshold (depending on the number of nodes and edges) will always be merged with neighboring communities [21].
• Walktrap: This algorithm is based on random walks. The general idea is that if you run a random walk on the graph, walks are more likely to stay within the same community because there are only a few arcs or edges that lead outside of a given community. Walktrap algorithm is a little slower than Fast greedy, but also a little more precise [22].
• Leading eigenvector: The Leading eigenvector algorithm is a hierarchical top-down algorithm that optimizes the modularity function. This algorithm is likely to give a higher modularity score than the Fast greedy algorithm, but it is a little slower than the latter [23].
• Label propagation: The Label propagation algorithm is a simple algorithm in which each node of the graph is associated with a different label. This algorithm is very fast but it gives different results depending on the initial configuration of the labels [24].
• Multilevel: Known also as the Louvain algorithm. It is a classification algorithm based on the measurement of the local modularity of a grouping of nodes [5].

Graph classification, or the problem of identifying the class labels of graphs in a dataset, is an important problem in social network analysis. The different classification methods used in social networks analysis are [25,26]:

• Degree centrality: For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ links, the Degree centrality $C_D\left(v\right)$ of a node v is defined as follows:

  $${\mathrm{C}}_{\mathrm{D}}\left(v\right)=\frac{deg\left(v\right)}{\left|V\right|-1}$$

  (1)

  with $deg\left(v\right)$ as the degree of the node v.
• Betweenness centrality: For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ links, the Betweenness centrality $C_B\left(v\right)$ of a node v is defined as follows:

  $${\mathrm{C}}_{\mathrm{B}}\left(v\right)=\sum _{u\ne v\ne w}\frac{{\sigma }_{uw}\left(v\right)}{{\sigma }_{uw}}$$

  (2)

  with:

  –

  ${\sigma }_{uw}$ representing the number of shortest paths going from the node t to the node u.

  –

  ${\sigma }_{uw}\left(v\right)$ representing the number of these paths passing through the node v.

• Closeness centrality: For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ links, the Closeness centrality $C_C\left(v\right)$ of a node v is defined as follows:

  $${\mathrm{C}}_{\mathrm{C}}\left(v\right)=\frac{1}{{\sum }_{w}d(v,w)}$$

  (3)

  with $d(v,w)$ as the length of the shortest path from the node v to the node w.
• Eigenvector centrality: Known also as eigencentrality, it is a measure of the node’s influence in a network. It is calculated by assigning scores to all nodes in the network based on the hypothesis: Connections to nodes with a high score contribute more to the score of the node in question than connections to nodes with low scores.
  For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ links, let consider the adjacency matrix $A=\left(a_{v,w}\right)$, such that $a_{v,w}=1$ if the nodes v and w are linked and $a_{v,w}=0$ otherwise.
  The relative score of the centrality of the vertex v can be defined as:

  $$x_v=\frac{1}{\lambda }\sum _{w\in M\left(v\right)}{x}_w=\frac{1}{\lambda }\sum _{w\in G}{a}_{v,w}{x}_w$$

  (4)

  with:

  –

  $M\left(v\right)$ as the set of neighbors of the node v.

  –

  $\lambda$ as a constant.

  With a small rearrangement, this can be rewritten in vectorial notation, similar to the eigenvector equation:

  $$\mathbf{Ax}=\lambda \mathbf{x}$$

  (5)
• PageRank: This algorithm is used by the Google search engine to rank sites in their search engine results. PageRank is a means used to measure the importance of the pages of the site and can be considered as a variant of the Eigenvector centrality.
  For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ links, let us consider the adjacency matrix $A=\left(a_{v,w}\right)$, such that $a_{v,w}=1$, if the nodes v and w are linked and $a_{v,w}=0$ otherwise.
  The PageRank of a v node satisfies the following equation:

  $$x_v=\alpha \sum _w{a}_{wv}\frac{x_w}{L\left(w\right)}+\frac{1-\alpha }{\left|V\right|}$$

  (6)

  with:

  –

  $\alpha$ as an attenuation factor between $(0,1)$.

  –

  $L\left(w\right)={\sum }_u{a}_{wu}$ as the number of neighbors of the node w.

3. Data Crawling

For the first step, which consists of collecting data from Facebook pages, two methods make it possible to extract data from the Web; namely, Web crawling and Web scrapping.

The data displayed by most sites cannot be viewed using a Web browser, for example, data from directories with yellow pages, data from real estate sites, social networks, stocks manufacturers, online sales sites, contact databases, etc. In addition, most sites do not offer the functionality to save a copy of the data they display.

The only option, then, is to copy/paste the data displayed by the site in your browser to a local file on your computer manually—a very tedious job that can take several hours or sometimes days to complete. Web scraping is the technique of automating this process so that, instead of manually copying data from websites, the Web scrapper will perform the same task in a fraction of the time [27].

It interacts with websites in the same way as a web browser. However, instead of displaying the data served by the website on the screen, the Web scrapper saves the data from the Web page to a file or local database. The legality of Web scrapping varies across the world from one country to another. In general, Web scrapping can be against the terms of the use of certain websites.

There are several sophisticated approaches and algorithms in the field of artificial intelligence concerning the crossing of graphs which are increasingly used in the implementation of Web crawlers. We can cite the followings algorithms:

• Breadth First Search [28].
• Depth First Search [28].
• Best First Search [29].
• Fish Search [29].
• A* Search [30].
• Adaptive A* Search [30].

Given the problem of the legality of Web scrapping in terms of violation of privacy, which also contradicts the conditions of use of Facebook, we opted for the Web crawling method.

We have also chosen to implement our crawler for the Facebook social network since the Web crawlers provided by the available open-source libraries do not meet our needs. For our study, we first need to identify the relevant data sources i.e., the Facebook source pages, then we extract the data from the page. We are mainly interested in extracting data from posts, comments (and their responses), and reactions from fans of the page towards the post concerned.

The implemented crawler adopts the Depth First Search approach [28]. It follows the steps presented in the Algorithm 1.

Algorithm 1 Facebook page crawler

Require: A Facebook page identifier. Ensure: Data dictionary D.   1: Initialize a dictionary D.   2: Extract the information from the Facebook page and save it in D.   3: Identify the posts on the page and save their identifiers in a list M.   4: Initialize a list N.   5: for all Post identifier in M do   6:      Extract the information from the post and save their identifiers in a dictionary E.   7:      Extract information relating to fan reactions from this post and save it in a list O.   8:      Identify the comments of the post and save their identifiers in a list P.   9:      Initialize a list Q. 10:      for all Comment identifier in P do 11:          Extract the information from the comment and save it in a dictionary F. 12:          Identify the responses to this comment and save their identifiers in a list R. 13:          Initialize a list S. 14:          for all Response identifier in R do 15:             Extract the information from the response and save it in a dictionary G. 16:             Add the dictionary G in the list S. 17:          end for 18:          Add the list S in the dictionary F. 19:          Add the dictionary F in the list Q. 20:      end for 21:      Add the list Q in the dictionary E. 22:      Add the dictionary E in the list N. 23: end for 24: Add the list N in the dictionary D 25: returnD.

The algorithm consists of browsing the WWW in order to establish its cartography using a program called Internet Bot, Web crawler, or even crawler [31].

Initially, this list does not contain any address and, generally, we initialize it with a small number of addresses, called initial candidates. For each of these addresses, the Internet Bot removes it from the list of addresses and downloads the associated web page, and identifies the links it contains. For each of these links, if the address is unknown, it is added to the list. The algorithm then chooses a new set of addresses to visit from among those it has just discovered and repeats the process. The stop criterion and can be any condition set by the user.

4. Graph Modeling

In this step, we will focus on graph modeling from data extracted from Facebook pages.

A graph is a standard object of mathematical modeling from graph theory [25]. Formally, a graph is an ordered pair $G=(V,E)$ comprising a set V of vertices also called nodes and a set E of edges called also arcs, which are two-element subsets of V. Indeed, an edge is associated with two vertices, and the association takes the form of the pair (ordered or unordered) comprising these two vertices [25].

A graph, in its most general definition, refers to a particular family of graphs called monopartite graphs (one-mode graph). These graphs are used to represent information on the links between a set of homogeneous nodes. However, in a social network, many actors can have many types of relationships. In this case, the use of monopartite graphs is not appropriate, given the heterogeneous nature of all the nodes, which brings us back to modeling using graphs from another family, which are called K-partite graphs.

By definition, a graph is said to be K-partite if the set of vertices that compose it is, or can be partitioned into K subsets, or parts, such that no edge has its ends in the same part. Similarly, we can imagine that we color the vertices with K colors so that no edge connects vertices of the same color. K-partite graphs can be oriented, non-oriented, simple, weighted graphs or any combination of these four types [25].

In our study, we seek to analyze the data from the Facebook pages, and we are particularly interested in studying the relationships between the posts of the page, and the reactions of fans (users) towards these posts. We will explain the methods proposed for the creation of different graphs.

4.1. USER–POST Graph

A bipartite graph is a graph from the family of K-partite graphs with $K=2$ [32]. To create a bipartite graph from the data of a given Facebook page, the Algorithm 2 is implemented.

Algorithm 2 USER–POST graph modeling

Require: Dictionary of data from a Facebook page D. Ensure: Bipartite graph.       Create an empty graph G.   2: for all Post ID in D do         if There is no node in the graph with the post ID then   4:          Create a new node in G and assign it a tag 0.         end if   6:   Initialize a set E.         Populate E with the identifiers of the Facebook users who have either reacted to this post or commented on the post.   8:    for all User ID in E do             if There is no node in G with the user ID then 10:             Create a new node in G and assign it a tag 1.             end if 12:        Create a link in G between the node representing the post and the node representing the user.           end for 14: end for       return G.

According to Algorithm 2, we are interested in studying the relationships between the fans of a given Facebook page and the different posts of the latter. In this case, we have two different entities: Facebook users and posts, which brings us back to using the K-partite graphs and, in particular, the bipartite graphs for modeling.

USER–USER Graph

Now we are interested in studying the relationships between the different people who reacted to the posts of a Facebook page to try to determine the most influential people among all the fans of the page. In this case, we have a single entity, which is the Facebook user, which brings us back to using single-party graphs for modeling.

To create the USER–USER graph, we will not need to use the data from the Facebook page. Instead, we will use the previously created graph: the USER–POST graph, and project the bipartite graph onto one of the two subsets of nodes: the USER nodes.

The projection of bipartite graphs is often used for the compression of information on bipartite graphs. Since the resulting graph (monopartite) of the projection is always less informative than the original bipartite graph, an appropriate method for the weighting of the links is often necessary and aims at minimizing the loss of information.

To create the USER–USER monopartite graph from the USER–POST bipartite graph, we follow the following steps presented in Algorithm 3.

Algorithm 3 USER–USER graph modeling

Require: USER-POST bipartite graph. Ensure: USER-USER monopartite graph.      Initialize a dictionary of lists D.      for all Node n with a tag 0 in G do 3:      Initialize a list L.          for all Edge a in G do              if n exists in a then 6:             Add the other node in L.              end if          end for 9:      Associate the list L (value) with the node n (key) in D.      end for      Initialize a list M. 12: for all Key c in D do           Add in M all tuples resulting from all possible combinations of existing nodes in the value list of c in D.      end for 15: Create an empty graph H.      for all Tuple $(x,y)$ in M do          if $(x,y)$ exists in H or $(y,x)$ exists in H then 18:          Increment the weight of the edge $(x,y)$ respectively $(y,x)$ by 1.          else              if x does not exist in H then 21:             Create the node x in H.              end if              if y does not exist in H then 24:             Create the node y in H.              end if               Create the edge b which connects x to y in H. 27:         Assign the weight 1 to b.          end if      end for 30: returnH.

5. Exploratory Analysis of Graphs

Once the graphs have been created, we move on to their exploratory analysis. This analysis includes:

1.

Structure analysis.

2.

Community analysis.

3.

Ranking (classification) of the social actors in the graph.

5.1. Structure Analysis

In this step, we are interested in exposing the structure of the graph, i.e., the information concerning the nodes and the arcs or edges in order to select the suitable algorithms which apply to the graph.

The measures and information that interest us are presented in

Table 1. Data from graph structure analysis.

Name	Description
Nodes	Number of nodes making up the graph
Edges	Number of arcs or edges constituting the graph
ZeroDegNodes	Number of nodes having a zero degree
ZeroInDegNodes	Number of nodes having a zero incoming degree
ZeroOutDegNodes	Number of nodes having a zero outgoing degree
NonZeroInOutDegNodes	Number of nodes having a non-zero incoming degree and a non-zero outgoing degree
DirEdges	Number of oriented arcs or edges
UndirEdges	Number of non-oriented arcs or edges
SelfEdges	Number of loops
ClosedTriangles	Number of closed triangles
OpenTriangles	Number of open triangles
Diameter	Diameter of the graph
Density	Density of the graph

.

5.2. Community Analysis

After analyzing the graph structure, we are interested in the graph community analysis.

• Detection of communities in the USER–POST graph
  In this part, we are interested in the detection of communities in the USER–POST bipartite graph. According to the literature, there are two methods for detecting communities in bipartite graphs [7].
  The first method stipulates that any bipartite graph can be treated as a monopartite graph by ignoring the partitioning of the nodes into two disjoint subsets. This approach is used when the interest is in discovering bipartite communities within the graph [7].
  The second method stipulates that, in a bipartite network, usually, one of the two subsets of nodes, called the primary set P, has more interest in a particular use than the other, called sub-set S. In this case, P can be considered as the set of nodes of a mono-party graph resulting from the projection of the bipartite graph. This approach is used when the real interest lies in the community structure of the graph generated by the set of primary nodes P [7].
  Our interest in detecting communities within bipartite graphs which consists in discovering bipartite graphs formed by users and posts pushes us to adopt the first approach. However, the algorithms that can be applied effectively on bipartite graphs are algorithms based on the principle of label propagation (in English Label propagation) or on the calculation of modularity [7].
  As for the family of algorithms based on the propagation of labels, we can have several community structures starting from the same initial condition. The effectiveness of these algorithms lies in knowing a priori the membership of some nodes in communities or classes [32]. For this reason, we decided to opt for an algorithm based on the calculation of modularity, which is reliable; in this same context, the algorithm which gives the best result is the Multilevel algorithm, also called Louvain’s algorithm [5].
• Detection of communities in the USER–USER graph
  In this step, we are interested in the detection of communities in the USER–USER monopartite graph. To do this, we must select the most suitable algorithm from the graph classification algorithms, which show good results according to our needs and taking into account the structure of the graph to analyze.
  In

  Table 2. Comparison of classification algorithms applied to graphs.

  Name	Oriented Graph Management	Valued Graph Management	Complexity
  Fast greedy	No	No	$\left|V\right|\left|E\right|log\left|E\right|$
  Walktrap	No	Yes	${\left|E\right|\left|V\right|}^2$
  Leading eigenvector	No	No	${\left|V\right|}^2+\left|E\right|$
  Label propagation	No	Yes	$\left|V\right|+\left|E\right|$
  Multilevel	No	Yes	${\left|V\right|}^{2}log\left|V\right|$

  , we present a comparison of the different algorithms presented in Section 4 in terms of performance and type of input graph for a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ arcs or edges.
  We can see from Table 2 that all the selected algorithms do not take into account the orientation of the edges in the graphs, that does not pose any problems since our USER–USER graph is undirected.
  The USER–USER graph is valued, and among the algorithms present in Section 6, only the Walktrap, Label propagation, and Multilevel algorithms support the weighting of edges.
  We will compare Walktrap, Label propagation, and Multilevel algorithms by unrolling them on real data and comparing the results with the real classification (ground truth). To do this, we selected a known dataset in the field of machine learning and social network analysis that relates to a karate club which was studied by Wayne W. Zachary [6] for a period of three years from 1970 to 1972. The network contains 34 members of a karate club, having 78 matched links between members who interacted outside the club. During the study, a conflict arose between the administrator John A and the instructor Mr. Hi, which led to the club being split in two. Half of the members formed a new club around Mr. Hi, the members of the other party found a new instructor or abandoned karate [6].
  This dataset has the following characteristics:

  –

  Number of vertex: 34.

  –

  Number of edges: 78.

  –

  Number of communities: 2.

  –

  Description: social network of friendships.

  Table 3. Comparison of classification algorithms applied to the social network of Zachary’s karate club.

  Algorithm	Detected Communities	Well Classified Nodes	Classification Rate
  Walktrap	5	18	52.94%
  Label propagation	4	23	67.64%
  Label propagation with initializaion	3	32	94.12%
  Multilevel	3	27	79.41%

  presents the results of applying Walktrap, Label propagation, and Multilevel algorithms on this dataset.
  According to Table 3, when applying the Walktrap algorithm on Zachary’s karate club dataset, we notice the presence of 5 communities compared to 2 in the real community structure if we consider that the communities were created at the center of nodes 1 and 34, respectively. In this case, the community around node 1 was well classified (nine nodes) and the community around node 34 was equally well classified (nine nodes) and, therefore, the rate of good classification compared to the real community structure is 52.94%.
  When applying the Label propagation algorithm, we notice the presence of 4 communities. The large communities were created at the center of nodes 1 and 34 and only one node of the community around node 1 was misclassified (11 nodes were well classified) and only one node of the community around node 34 was misclassified (12 nodes were well classified) and, therefore, the rate of good classification compared to the true community structure is of 67.64%.
  However, by initializing only nodes 1 and 34, the number of communities is equal to that of the true community structure. In this case, the whole community around node 1 was well classified and only two nodes of community around node 34 were misclassified and, therefore, the rate of good classification compared to the true community structure is 94.12%.
  When applying a Multilevel algorithm (Louvain algorithm), the communities were created at the center of nodes 1 and 34. In this case, the whole community around node 1 is well classified (10 nodes) and only two nodes were misclassified (17 nodes were well classified) and, therefore, the rate of good classification compared to the true community structure is 79.41%.
  From the results presented in Table 3, we can conclude that:

  –

  The Walktrap algorithm does not give a good rate of good classification (52.94%) which is almost equal to the rate of good classification of a random classification. But if it is well initialized, i.e., to regulate the number of random walks, this algorithm can detect the communities in depth.

  –

  The Label propagation algorithm gives a better result than Walktrap. However, this algorithm is still unreliable since it can cause various community structures with the same initial condition. However, it has the potential to be the best classification algorithm [24] if we have a priori knowledge of the membership of some nodes so, unmarked nodes will be more likely to adapt to those which are already labeled.

  –

  The Multilevel algorithm, also called the Louvain algorithm, is an algorithm that meets our performance compromise from the point of view of time complexity and the rate of good classification (79.41%).

5.3. Classification

We are now interested in determining the most influential nodes (users and positions) in the graph. For that, we had recourse to the analysis of centrality which aims to determine the nodes which play an important role in the graph [33].

Formally, centrality is a function with real values which applies to the nodes of a graph and to various applications such as the following:

• What influence does a person have in a social network?
• How is a street well used in a road network?
• How important is a web page?
• How important is a room in a building?

Table 4. Definition of the center of the graph for each centrality calculation method [34].

Method Name	Definition of the Graph Center
Degree centrality	The node connected to the largest number of nodes in the graph.
Betweenness centrality	The node which has the most influence in the transfer of information in the graph.
Closeness centrality	The node which is relatively close to all the other nodes of the graph.
Eigenvector centrality	The node which is connected to important neighbors (in terms of eigenvalue).
PageRank	The node with the most incoming connections.

presents the definition of the center of the graph for each method.

• Post classification
  We are interested in detecting the most popular posts in the network. To do this, we will only use the USER–POST graph. We are looking to rank the page’s posts in order of popularity. On a Facebook page, a post is popular if it is intensively commented on, shared or liked.
  In this context, in the USER–POST graph, a node representing a post is important if it has a large number of incoming connections, which exactly coincides with the definition of the center node, calculated using PageRank.
  For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ arcs or edges, let $L\left(n\right)$ be the set of nodes which point to the node n and let $C\left(n\right)$ be the degree leaving the node n.
  The post classification steps for the nodes of the G graph are represented by Algorithm 4.

Algorithm 4 Post classification

Require: Graph G, Depreciation factor q, Number of iterations i Ensure: Data dictionary (Key: node identifier, Value: Score)     Create an empty dictionary D.     for all Node n in V do          $D\left[n\right]=\frac{1}{\left|V\right|}$ 4: end for     while $i>0$ do         for all Node n in V do              $pr=q$ 8:         for all m in $L\left(n\right)$ do                 $pr+=\frac{D\left[m\right]}{C\left(m\right)}$             end for              $D\left[n\right]=pr$ 12:     end for          $i-=1$     end while     returnD.

• User ranking
  Next, we are interested in detecting the most influential users in the network. To do this, we will use the USER–POST graph and the USER–USER graph. In the USER–POST graph, we seek to detect influential people in the sense that the influence of a Facebook user on a page is related to the intensity of their activities, i.e., the user node is all the more important than the number of connections to the node nodes is important.
  In this case, the definition of the center node of the graph coincides with that of the degree centrality.
  For a graph $G=(V,E)$ containing $\left|V\right|$ nodes and $\left|E\right|$ arcs or edges, let $Deg\left(n\right)$ be the degree of node n.
  The steps for user ranking are represented by Algorithm 5.
  In the USER–USER graph, we seek to detect influential people in the sense that the influence of a Facebook user lies in their ability to transmit and disseminate information. In this context, the definition of the center node of the graph coincides with that of the betweenness centrality, where the most influential node is the one most likely to disconnect the graph if it is removed.
  For a graph $G=(V,E)$ containing $\left|V\right|$ knots and $\left|E\right|$ arcs or edges, let $Deg\left(n\right)$ be the degree of the node n.

Algorithm 5 User ranking

Require: Graph G Ensure: Data dictionary (Key: node identifier, Value: Score)     Create an empty dictionary D.     $s=\frac{1}{\left|V\right|-1}$     for all Node n in V do          $D\left[n\right]=s\ast Deg\left(n\right)$ 5: end for     returnD.

The steps for calculating the betweenness centrality for the nodes of the G graph are represented by Algorithm 6.

Algorithm 6 Calculation of betweeness centrality

Require: Graph G Ensure: Data dictionary (Key: node identifier, Value: Score)     for all Node n in V do          $D\left[n\right]=0$     end for     for all Node n in V do         for all Node $m\ne n$ in V do 6:          $P\left(m\right)=$ an empty list              $\sigma \left[m\right]=0$              $d\left[m\right]=-1$         end for          $\sigma \left[n\right]=1$          $d\left[n\right]=0$ 12:     Initialize a stack S           Add n to a waiting list Q           while Q is not empty do               Remove o from Q               Stack o in S               for all Node p of o do                 if $d\left[p\right]<0$ then                      Add p in Q                      $d\left[p\right]=d\left[o\right]+1$                 end if                 if $d\left[p\right]=d\left[o\right]+1$ then                      $\sigma \left[p\right]+=\sigma \left[o\right]$ 24:                 Add o in $P\left[p\right]$                 end if              end for          end while          for all Node n in V do               $\delta \left[n\right]=0$ 30:     end for           while S is not empty do              Depilate q from S              for all $r\in P\left[q\right]$ do                  $\delta \left[r\right]+=\frac{\sigma \left[r\right]}{\sigma \left[q\right]}.(1+\delta \left[q\right]$              end for 36:         if $q\ne n$ then                  $D\left[q\right]+=\delta \left[q\right]$              end if          end while      end for      returnD.

6. Computational Results

We are going to work on the data on an automobile brand’s Facebook pages collected in the period from 22 January to 29 January 2020. We have chosen to do our study over a short period (one week) for a good visualization of the graphs.

6.1. Data Crawling

Data crawling is done using the crawler whose algorithm has been presented in Algorithm 1.

Once the crawler is launched with the input parameters, the result is a file in JSON format containing the data of this page.

Table 5. Data extracted from the Facebook pages.

Name	Description
ID	Page ID
Name	Page name
Category	Page category
Link	Page URL
Is_Verified	Page status (verified with Facebook or not)
Likes	Number of Likes on the page
Talking_About_Count	How many people are talking about the page?

presents all the data extracted from the page and their meaning.

Table 6. Data extracted from a post on the Facebook page.

Name	Description
ID	Publication ID
From_ID	Identifier of the person who published the post
From_Name	Name of the person who published the post
Name	Publication name
Published_Date	Publication date
Type	Type of post
Message	Textual content of the post
Last_Reaction	Date of last post response
Shares_Count	Number of post shares
Comments_Count	Number of comments on the post
Reactions_Count	Number of post reactions

presents all the data extracted from a post on the page and their meaning.

Table 7. Data extracted from a comment or a response to a comment to a post on the Facebook page.

Name	Description
ID	Comment ID
From_ID	Identifier of the person who commented on the post
From_Name	Name of the commenter
Created_Time	Comment creation date
Message	Text content of the comment

presents all the data extracted from a comment or a response to a comment (a response to a comment is considered a comment) to a post on the page and their meaning.

Table 8. Data extracted from a reaction to a post on the Facebook page.

Name	Description
Profile_Id	Identifier of the account which reacted to the post
Type	Like, Love, Haha, Sad, Thankful, Wow, Angry

presents all the data extracted from a reaction to a post on the page and their meaning.

After extracting all the data relating to the page, posts, comments, and reactions, we calculate some statistics which we present in

Table 9. Statistics on a page.

Name	Description
Talking_About_Percent	Percentage of fans talking about the page
Total_Posts	Total number of posts retrieved
Max_Shares	The maximum number of shares encountered in a post
Avg_Shares	The average number of shares
Max_Comments	The maximum number of comments encountered in a post
Avg_Comments	Average number of comments
Max_Reactions	The maximum number of reactions encountered in a post
Avg_Reactions	The average number of reactions

.

6.2. Graph Modeling

We will present the result of the graph modeling step. We will start by exposing the result of USER–POST graph building and we will end with that of USER–USER.

• USER–POST graph
  The USER–POST graph is built from the data collected in the data crawling step using the Algorithm 2 and is saved in a GML (Geographical Markup Language) file. The graph is made up of 2727 nodes, including 6 nodes representing the posts and 2721 nodes representing the users who reacted to these posts, and 2824 edges.
  We used Gephi software for the visualization of the bipartite graph, shown in the Figure 2.
  The nodes in green color represent the posts on the automobile brand’s Facebook page and are more voluminous than the other nodes because the higher the degree of importance, the larger the size of the node. The pink nodes represent the Facebook users who reacted to these two posts.
  We can see that there are several agglomerations of user nodes, agglomerations formed at the outline of each green node, which represents the users who reacted to only this post and agglomerations located in the middle of the graph, which represents the users who reacted to several posts.
• USER–USER graph
  The USER–USER graph is built from the projection of the USER–POST graph on all the nodes which represent Facebook users according to the Algorithm 3.
  This graph consists of 2721 nodes representing the users and 811459 edges connecting them all. Figure 3 shows the USER–USER graph on the automobile brand’s Facebook page.
  According to Figure 3, the volume of the nodes is proportional to the degree that the largest nodes are the nodes with a large number of connections with other nodes, such as those located in the center of the graph.

6.3. Exploratory Analysis of Graphs

We used SNAP.py (Standford Network Analysis Platform), an interface written in Python, to facilitate the calculation of metrics related to the structure of graphs. It is a library of analysis and graph mining. It is written in C++ and easily scales up to manage graphs with hundreds of millions of nodes and billions of links. We also used the iGraph library for the calculation of centrality. We used Gephi for the visualization of graphs and communities. In this section, we will present the result of the exploratory graph analysis phase. This phase is composed of several stages which we will describe and for which we will present their results.

• Structure analysis:
  Table 10. Statistics relating to the structure of the USER–POST graph of the automobile brand Facebook page.

  Nodes	2721
  Edges	2824
  ZeroDegNodes	0
  ZeroInDegNodes	0
  ZeroOutDegNodes	0
  NonZeroIn-OutDegNodes	2727
  DirEdges	5648
  UndirEdges	2824
  Self-Edges	0
  ClosedTriangles	0
  OpenTriangles	812,486
  Diameter	4
  OpenTriangles	0.000760

  shows the output of the structure analysis module for the USER–POST graph on the automobile brand’s Facebook page.
  We can see that the USER–POST graph does not contain any closed triangles because the nodes which belong to the same set of nodes (USER and POST) are not connected, and this also results in a very low value of the density of graph.
  Table 11. Statistics relating to the structure of the USER–USER graph of the automobile brand’s Facebook page.

  Nodes	2721
  Edges	811,459
  ZeroDegNodes	0
  ZeroInDegNodes	0
  ZeroOutDegNodes	0
  NonZeroIn-OutDegNodes	2721
  DirEdges	1,622,918
  UndirEdges	811,459
  Self-Edges	0
  ClosedTriangles	163,292,896
  OpenTriangles	39,937,448
  Diameter	2
  OpenTriangles	0.219280

  illustrates the output of the structure analysis module for the USER–USER graph on the automobile brand’s Facebook page.
  Since closed triangles are triplets of nodes, constituting a complete graph at all the nodes, they are connected two by two. Among three user nodes USER1, USER2, and USER3 (representing users), if the connections USER1–USER2 and USER2–USER3 exist, there is a tendency for the new connection USER1–USER3 to be formed.
  The obtained number (163,292,896) (from Table 11) can be used to understand and predict the growth of networks, although it is only one of many mechanisms by which new connections are formed in complex networks. The prediction brings out users who share similar interests and experiences.
• Community detection:
  In this section, we are interested in the community structure of graphs. In the Section 4, it turned out that the Louvain algorithm is the most suitable community detection algorithm for our needs. We favored the use of Gephi for launching the algorithm on graphs since it is already implemented in the software.
  Figure 4 illustrates the output of the community analysis module for the USER–POST graph on the automobile brand’s Facebook page.
  We can see that the USER–POST graph contains six communities, one around each post. So there are six modular classes. Each node is classified according to the value of its local moduley.
  Figure 5 illustrates the output of the structure analysis module for the USER–USER graph on the automobile brand’s Facebook page.
  The USER–USER graph contains five communities and the user nodes have been classified according to their membership of the five modular classes.
• Post classification:
  We are interested in the classification of user nodes and posts in graphs. For this, we used iGraph for the calculation of centrality in the two graphs: USER–POST and USER–USER.
  In Section 4, we decided to use Algorithm 4 for ranking posts in order of popularity.
  Table 12. Ranking of posts by popularity according to PageRank score.

  USER ID	Rank	Score	Reactions
  288989481144140_1155599551149791	1	0.111769	956
  288989481144140_1156266114416468	2	0.106014	721
  288989481144140_1155498814493198	3	0.095657	697
  288989481144140_1156311837745229	4	0.088773	584
  288989481144140_1156296657746747	5	0.050012	394
  288989481144140_1157081717668241	6	0.007225	55

  presents the ranking of the six posts on the automobile brand’s Facebook page in order of popularity according to the PageRank score.
  We can see that the score of each node and its number of reactions are correlated. We can then say that PageRank is the appropriate measure for detecting the most popular posts in a USER–POST graph.
• User ranking:
  In Section 3, we decided to use the Algorithm 5 for ranking users in the USER–POST graph and the Algorithm 6 for ranking users in the USER–USER graph.
  To keep the anonymity of Facebook users, we have modified the identifiers of Facebook accounts by applying the hash function above.
  Table 13. Ranking of users in order of influence according to the degree centrality.

  USER ID	Rank	Score	Degree Centrality
  df7c5c336345dd40bcbc5f96f3a41d76	1	0.0022	6
  09f257edaf54277ca98a6cf7f0ee9f7d	2	0.0022	6
  fffcf05d2eea7818bc64bc408b3a32e8	3	0.0022	6
  44b857d2156a2c42fe3c414dd091d66f	4	0.0022	6
  e201cb2388dbc48c73172312e7e9d01f	5	0.0018	5
  3193669e781e9d8ccdae29642f9e5cc2	6	0.0015	4
  dbfa55b7d923931033e4942843cb6fa1	7	0.0015	4
  d2d0e33e15e9e8d9bf2ab5ef98c14f03	8	0.0015	4
  7cb687e8e43fff4b775310e0e044d78b	9	0.0015	4
  1d9c1405e3b239a4be58a6f43a5e1eff	10	0.0011	3

  presents the ranking of 10 users of the automobile brand’s Facebook page by order of influence according to the degree centrality.
  We can conclude from the Table 13 that degree centrality is a good metric for calculating the influence of users in the USER–POST graph since the score of the degree centrality of a user is correlated with the intensity of his activities.
  Table 14. Ranking of users in order of influence according to the Betweeness centrality.

  Identifier	Rank	Score	Betweeness Centrality
  df7c5c336345dd40bcbc5f96f3a41d76	1	0.0619	2720
  09f257edaf54277ca98a6cf7f0ee9f7d	2	0.0619	2720
  fffcf05d2eea7818bc64bc408b3a32e8	3	0.0619	2720
  44b857d2156a2c42fe3c414dd091d66f	4	0.0619	2720
  e201cb2388dbc48c73172312e7e9d01f	5	0.0577	2683
  7cb687e8e43fff4b775310e0e044d78b	6	0.0444	2402
  d2d0e33e15e9e8d9bf2ab5ef98c14f03	7	0.0377	2132
  2720661a4a3f9dd0fd24495b3eed8ab4	8	0.0267	1844
  de9cc87164441eccbd333d72ae546b30	9	0.0267	1844
  3193669e781e9d8ccdae29642f9e5cc2	10	0.0259	1919

  presents the ranking of 10 users of the automobile brand’s Facebook page by order of influence according to the score between betweenness centrality.
  By comparing the results obtained in Table 14 with those present in Table 13, we can conclude that the first five most influential users in the USER–POST graph are also influential in the USER–USER graph, but we found that the score of betweenness centrality of a node is not always correlated with its degree, which represents the number of connections with users in the USER–USER graph.
  The betweenness centrality remains a good measure of the influence of a user in the USER–USER graph since the nodes with a high score are connected to a large number of nodes that satisfy our need to detect users who are more likely to disconnect the USER–USER graph if they are removed.

7. Conclusions

The volume of data on the Internet is always growing. This exponentially growing dataset represented 1.2 zettabytes in 2010, then 2.9 zettabytes in 2012, and reached about 40 zettabytes in 2020, according to American specialists. Facebook currently generates 10 terabytes of data each day. Processing and managing these large amounts of data remains a very complicated challenge. The most common idea among researchers is to be able to use these masses of data to extract useful information. This work aimed to create a solution for analyzing massive data from social networks, thereby enabling marketing sector data to be generated from Facebook pages.

The proposed work studies the behavior of the individual at the micro-level, the pattern of relationships (network structure) at the macro level, and the interactions between the two. The analysis of the interaction structures that are involved in social network analysis is an important element in the analysis of the micro-macro link, how individual behavior and social phenomena are connected.

Some of the choices and assumptions that we made in this study could be theoretically questionable and that is part of the limit of our study. For example, the choice of centrality calculation methods, or the community detection algorithms that we used.

This work requires several improvements and new concepts to be exploited—namely, (i) crossing the data from Facebook pages with data from companies to closely monitor marketing partners; (ii) automatic content analysis for posts; (iii) adding a sentiment analysis module to identify comments from users; (iv) dealing with multimedia features; (v) extending the solution offered on other social networks, such as Twitter, Instagram, and Snapchat.

We can also extend our analysis to know how the Facebook network impacts the student experience at Imam Abdulrahman Bin Faisal University and, in particular, how it influences students’ social integration into university life.