Abstract
Deep neural networks have achieved almost human-level results in various tasks and have become popular in the broad artificial intelligence domains. Uncertainty estimation is an on-demand task caused by the black-box point estimation behavior of deep learning. The deep ensemble provides increased accuracy and estimated uncertainty; however, linearly increasing the size makes the deep ensemble unfeasible for memory-intensive tasks. To address this problem, we used model pruning and quantization with a deep ensemble and analyzed the effect in the context of uncertainty metrics. We empirically showed that the ensemble members’ disagreement increases with pruning, making models sparser by zeroing irrelevant parameters. Increased disagreement im-plies increased uncertainty, which helps in making more robust predictions. Accordingly, an energy-efficient compressed deep ensemble is appropriate for memory-intensive and uncertainty-aware tasks.
1. Introduction
In the last decade, deep neural networks have achieved state-of-the-art performance in various machine learning tasks. As a result, deep models are widely used in today’s computer vision, autonomous driving, and reinforcement learning subsidiaries. Further, larger networks tend to have better accuracy; however, the deeper the model, the more confident the prediction [1]. Deep neural networks make an overconfident, black-box point estimation because the neural network parameters comprise scalar matrices. Even in unseen data that come from another distribution, a neural network incorrectly predicts with high confidence. It is an unwilling property in risk-sensitive tasks, such as autonomous driving [2,3,4,5,6,7] and object detection [8,9,10,11,12,13] in a road scene. The deep learning model should be well-calibrated and know what is known and what is unknown to be precise about the prediction confidence.
In real life, a model for risk-sensitive tasks should not only care about accuracy but also how certain the prediction is. Epistemic uncertainty [14], which comes from model deficiency in the training data, is reduced by increasing the training data. However, increasing the training data is expensive, and, thus, we suggest that estimating the uncertainty is more convenient. In addition, aleatoric uncertainty, which comes from the intrinsic characteristics of the data, is irreducible. Predictive uncertainty is the summation of the aleatoric and epistemic uncertainties. Bayesian neural network methods [15,16,17,18] effectively measure uncertainty by considering distributions placed over the weights instead of fixed scalar weights. Distributions over the weights are robust to overfitting, but with challenging inferences and additional computational costs.
In deep learning, we require a scalable and straightforward uncertainty estimation method that increases stochasticity in a deep learning model. Monte Carlo (MC) dropout [19] is a sampling-based uncertainty estimation method which uses conventional dropout [20] with a Bernoulli mask in inference time. They proved that a dropout applies a neural network with random depth, and activation functions are approximately equivalent to the probabilistic deep Gaussian processes.
Ensemble [21] is a well-known method for improving the accuracy of machine learning tasks. The majority of the state-of-the-art performances in machine learning tasks have used ensembles to improve accuracy. Another sample-based uncertainty measuring method is the deep ensemble [22], which consists of randomly initialized, independently trained, and shared-architecture neural networks. The results showed excellent uncertainty estimation while increasing the accuracy. The deep ensemble is well generalized and well-calibrated in both similar training data distribution (in-distribution data) and outlying distribution (out-of-distribution data) [23]. Randomly initialized networks are close to each other in initialization, but they move further away in the function space during training. It is assumed that such function space diversity is the main reason for the excellent performance of the deep ensemble [24].
The deep ensemble improves accuracy through ensembling and effectively measures the uncertainty by maintaining diversity in the function space, thus increasing the disagreement in a distributional shift of inference data. However, cost remains the main challenge for the deep ensemble as the training, test time and ensemble size linearly increase in parallel with the increase in ensemble members. The deep ensemble is not applicable in memory-intensive tasks because of its increased size.
In deep learning, model compression techniques [25] dramatically reduce the model size compared with relatively insignificant to no accuracy degradation. Model pruning increases the model sparsity by zeroing the irrelevant parameters. Low-rank factorization decomposes the matrix tensor by estimating the informative parameters. Knowledge distillation learns a distilled model and trains a more compact network to reproduce a more extensive or ensemble network. Model quantization converts the parameter floating-point into 8 bits or less.
This study aims to decrease the deep ensemble size using model compression techniques and analyze the effect of model compression techniques on uncertainty estimation. We propose a simple strategy for decreasing the deep ensemble size, which is the main drawback of the deep ensemble. The proposed method decreases the size by using model pruning and quantization. We empirically showed that the ensemble members’ disagreement increases with model sparsity increases. Increased disagreement implies increased uncertainty, which helps in making more robust predictions.
This paper is organized as follows: first, this paper reviews related works. Then, it describes the methods, which include the problem setup and high-level summary, deep ensemble training and compression methodologies, and the evaluation metrics. The next section covers the presentation of the results. Finally, the discussion, concluding remarks, and recommendations for future work are presented in the last section.
2. Related Work
There are few notable works related to decreasing cost over the deep ensemble. To the best of our knowledge, the majority of the studies aim to increase uncertainty quantification while decreasing the cost by leveraging knowledge distillation. Nevertheless, no studies associated with the effect of model pruning on uncertainty estimation have been conducted thus far.
A multi-headed distilled network could mimic the deep ensemble behavior and im-prove the uncertainty measure [26]. The knowledge distillation technique decreases the deep ensemble cost, and the multi-head can maintain diversity in the deep ensemble. However, trainable parameter numbers decrease by approximately 20.0% relative to the M = 50 ensemble, which is an insufficient measurement to trade for ensemble performance in some tasks. Moreover, several studies suggest that five networks are sufficient for training the deep ensemble; thus, such a large ensemble need not be trained.
Malinin et al. [27] distilled an ensemble into the prior network [28], which models a conditional distribution over categorical distributions by parameterizing a Dirichlet distribution to disentangle the total uncertainty into data uncertainty and knowledge uncertainty. They used auxiliary data from another distribution during the training process to capture the knowledge uncertainty. Furthermore, the training process is cumbersome because hyperparameter selection is nontrivial.
Hu et al. [29] conducted uncertainty prediction as a prediction interval (PI) problem, which uses the upper and lower bounds to quantify the degree of uncertainty. The PI can-not be calculated by standard stochastic gradient descent, and a modified loss function is introduced. As an optimal subset ensemble from a pool of candidates (ensemble pruning) is selected, the inference time decreases, but there is no information on the size. The optimal number of models is redundant, and this could be problematic in memory-intensive tasks.
We assume that using the deep ensemble with knowledge distillation might lose the multimodality, which is the main advantage of its successful results. Correspondingly, because the baseline approach is a relatively simple and scalable method without any change in the model architecture, the compression method should also be as simple and scalable as the deep ensemble. We already know that model pruning [30,31,32,33,34] has a trade-off between accuracy and size. However, this is the first study conducted on the size, accuracy, and uncertainty measurement tradeoff in model pruning and deep ensembles.
This study analyzes the tradeoffs between the size, accuracy, and uncertainty estimation using a simple strategy comprising pruning and quantization with a deep ensemble (called a compressed deep ensemble). Nevertheless, neither improving the accuracy nor increasing the compression ratio is beyond the scope of this study. Pruning sacrifices the long tail part of the training dataset. It is a tricky part of the dataset to be predicted by both humans and models because of noise-contaminated, multiple, or wrongly labeled objects [34]. If pruning identifies such distinguishable instances, it is a favorable feature from an uncertainty perspective. Sparse initialization helps achieve greater diversity among initialization time units [35]. Thus, we believe that model pruning increases a non-zero parameter weight, and such an increased weight could positively affect the function space diversity. If the pruned and quantized deep ensemble’s accuracy and uncertainty losses are tolerable, we can use the compressed deep ensemble in memory-intensive and uncertainty-aware tasks. In addition, depending on the variety of sparsity ratios, pruning and quantization effects could differ in such tradeoffs. Furthermore, we can select a safe sparsity ratio limit using different sparsity levels.
3. Proposed Method
3.1. Problem Setup and High-Level Summary
We assume that the training dataset is comprised of N data points {x, y}, where x ∈ Rd represents d-dimensional features. For regression problems, the label y∈ R is a real-valued number. For classification problems, the label y ∈ {1, …, K} is assumed to be one of the K classes. We used a neural network to assign the prediction probability pθ (y| x) over the labels, where θ denotes the neural network’s parameters. In this study, we created an ensemble that comprises M number of independent neural networks.
3.2. Deep Ensemble
The deep ensemble consists of three simple recipes to measure the uncertainty. Selecting a proper score rule as a training criterion is the first recipe. The second recipe is training independent networks. They introduced adversarial training to smooth the predictive distributions, but it was not as effective as the abovementioned two recipes. A proper scoring rule is one where S (pθ, q) ≤ S (q, q) only if a predictive distribution is equal to the true distribution, where pθ denotes a predictive distribution, and q denotes the true distribution. Thus, networks can be trained by minimizing the loss L (θ) = -S (pθ, q). Popular loss functions meet the condition for the proper scoring rule; negative log-likelihood (NLL) for both regression and classification, root mean square error (RMSE) for regression, and Brier score for classification are all examples of proper scoring rules. Independent and randomly initialized shared architecture deep neural networks are key concepts in deep ensembles. Therefore, independently initialized ensemble members can simultaneously train. Since a base learner trained on a bootstrap sample sees only 63% unique data points, instead of using the bootstrap, the entire dataset is favorable [36], even though the deep ensemble was theoretically motivated by the bootstrap. Ovadia et al. [23] demonstrated that a deep ensemble consistently provides more reliable predictions in both shifted versions of the in-distribution data and out-of-distribution data in image classification tasks. Furthermore, the deep ensemble is applied on real-world tasks [37,38,39,40], including street-scene semantic segmentation, steering angle prediction, and natural language processing, and keeps better results. In the deep ensemble, all members are treated as a uniformly weighted mixture model, and the final prediction is the average of the predictions with Equation (1).
3.3. Model Pruning and Quantization
Model pruning decreases the model size by increasing the sparsity of the parameters as removing irrelevant parameters. In conventional pruning, the trained model is iteratively pruned until it attains the desired sparsity, and after pruning, the model with pruned parameters is retrained. The neural network model has a function f (x; W), then pruned model has a function f (x; W ⨀ M), where M ∈ {0, 1} is a pruning mask to remove the parameter. Practically, the pruned parameters of W are set to zero or entirely removed. Using zero weights, element-wise multiplication is redundant. As a result, the computational footprint also decreases. Blalock et al. [32] empirically showed that a large, sparse model performs better than a small dense model. Model quantization is a model compression technique that converts the parameter representation from floating-point 32 bits to 8 bits or fewer. Quantization is complementary to pruning techniques and is harmless for accuracy. Thus, we pruned and quantized the deep ensemble to decrease the linearly increasing size.
3.4. Strategy for Training from the Beginning
We propose a simple strategy suitable for training from the beginning. We randomly initialize the M shared architecture neural networks and independently train each model using the whole training set until achievable accuracy is attained. Thereafter, we prune neural networks until each model reached the required sparsity by using magnitude-based weight pruning, and a few epochs retrain the pruned networks. Finally, we quantize each model’s weights from and 32-bit floating point representation to an 8-bit representation. We assumed that we could obtain a lightweight ensemble by applying pruning and quantization, which is robust to unknown instances during the inference time.
3.5. Evaluation Metrics
We evaluated the standard deep ensemble as a baseline model and estimated accuracy, NLL, Brier score (2), zipped model size as a memory footprint, and compression ratio (3) in the in-distribution data. Brier score is computed as the squared error of the one-hot encoded true value and the predicted probability.
Compression ratio = (uncompressed size)/(compressed size)
There is no ground truth in the out-of-distribution data; thus, we cannot measure the accuracy in these data. Furthermore, there was no standard uncertainty metric. Hence, we evaluated entropy, ensemble disagreement (4), and the confidence curve proposed in [23] as uncertainty metrics. Additionally, we used ensemble ambiguity (5), which also measures the disagreement among the ensemble members, to measure the uncertainty. As proposed in [41], if the ensemble is strongly biased, the ensemble ambiguity will be small because the networks implement very similar functions and agree on even out-of-distribution data. As proposed in [22], ensemble disagreement counts the Kullback–Leibler divergence between the member network prediction and the mean prediction. Ensemble ambiguity is originally the variance of the weighted predictions of the ensemble around the weighted mean prediction. However, we treat the deep ensemble as uniformly weighted; the ensemble ambiguity in our study does not count the ensemble members’ weight. Such measures should be increased in the inference data that comes from another distribution from the training data distribution.
where
4. Experimental Setup
We first randomly initialized shared architecture member networks of deep ensemble and trained each network using the whole training set. After 20 epochs, each network achieved accuracy around 98.92 (±0.005). We trained the deep ensemble using the MNIST [42] handwritten digits dataset and used the Python 3, Tensorflow 2.3 [43] in the Ubuntu 18.04 operating system for implementation. The deep ensemble consists of five neural networks with two convolution layers and a fully connected layer. The hyperparameters and model summary are listed in Table 1. Subsequently, we applied a magnitude-based iterative pruning and 8-bit quantization for each member of deep ensembles using various sparsity levels: 25%, 50%, 75%, and 95% using the TensorFlow Model Optimization Toolkit. We used 10,000 test samples from the MNIST dataset as in-distribution data to evaluate the accuracy and loss, and another 18,724 test samples from the NotMNIST [44] alphabet dataset as out-of-distribution data to evaluate the uncertainty.

Table 1.
Model summary and hyperparameters.
5. Experimental Results
The results of the evaluation of the MNIST dataset are presented in Table 2. Accuracy was in-creased by 0.04%, and the entire ensemble size decreased by 4 times by pruning with 25% sparsity and quantization. However, pruning with 50–75% sparsity and quantization slightly reduces the accuracy by 0.01% and 0.05%, while decreasing the ensemble size by 5 times and 8 times. Pruning with 95% sparsity implies that only 5% of the trainable parameters are non-zero, and pruning with 95% sparsity degrades accuracy by ~1%. Overall, pruning with 25% sparsity and quantization showed a good result, but if we should reduce the size further, pruning with 50–75% sparsity is still applicable in the in-distribution data from the accuracy perspective.

Table 2.
Evaluation results of the MNIST dataset.
The confidence curves of the in-distribution and out-of-distribution data are displayed in Figure 1. The blue dots represent the results of the standard deep ensemble, and the solid lines represent the results of the pruned and quantized ensemble depending on the sparsity level. Confidence in the MNIST (Figure 1a) is higher than that of NotMNIST (Figure 1b), and if the confidence threshold τ = 90%, the ensemble classifies more than 90% of the MNIST samples, but only 16–32% of the NotMNIST samples. An increase in sparsity was associated with a decrease in confidence in both test datasets.
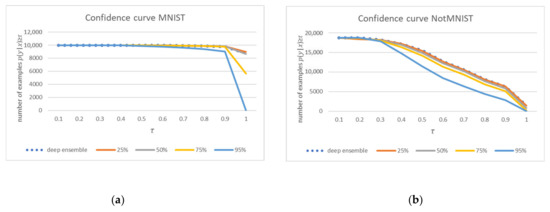
Figure 1.
Confidence curve of (a) the in-distribution data, and (b) out-of-distribution data.
The evaluation results of the out-of-distribution data are presented in Figure 2. All uncertainty metrics, including entropy, disagreement, and ensemble ambiguity, increased as sparsity increased; thus, pruning and quantization made the deep ensemble more robust in unseen data, especially in test data that comes from another distribution. The predictive distribution moves to a uniform distribution as uncertainty increases, meaning that the model randomly guesses. Figure 3 shows high disagreement samples from the MNIST dataset, and we can observe that majority of the highly disagreed samples are even indistinguishable by humans. Figure 4 shows the histograms of ensemble ambiguity, which significantly increases in out-of-distribution data rather than in-distribution data.
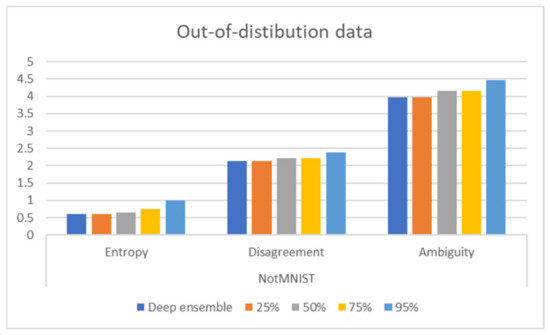
Figure 2.
Uncertainty measurements of NotMNIST, which shows the robustness of ensemble in out-of-distribution data.
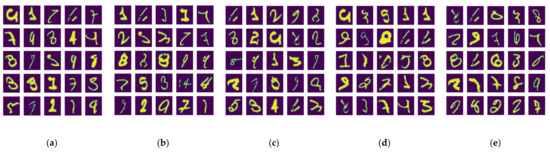
Figure 3.
High disagreement samples of MNIST: (a) standard deep ensemble, (b) 25% sparse ensemble, (c) 50% sparse ensemble, (d) 75% sparse ensemble, and (e) 95% sparse ensemble.
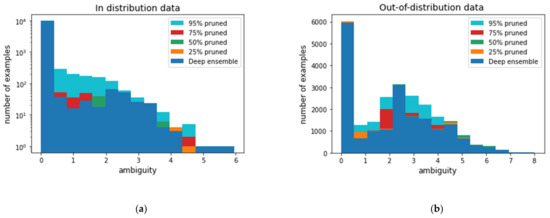
Figure 4.
Ensemble ambiguity of (a) the in-distribution data, and (b) out-of-distribution data.
Furthermore, the ensemble ambiguity increases as sparsity increases by pruning in both test datasets. Figure 5 shows histograms of entropy, and it shows a similar trend to that shown in Figure 4.
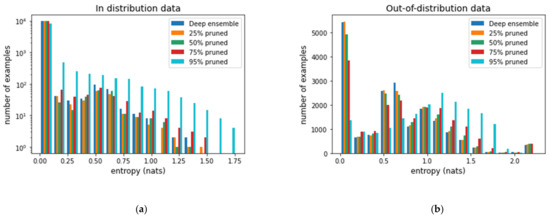
Figure 5.
Entropy of (a) the in-distribution data, (b) and out-of-distribution data.
Baseline evaluation metrics did not change significantly with respect to the deep ensemble for pruning and quantization. The size of the deep ensemble decreased by a magnitude, and 50% of the parameters in the pruned and quantized deep ensemble were almost the same size as a single model. However, the ensemble’s generalization error is lower than that of a single neural network, and it generalizes well in unseen data. In the in-distribution data, most disagreed instances were noisy, wrongly labeled, or multi-object instances that even humans could not distinguish immediately.
Moreover, for out-of-distribution data, increased disagreement helps distinguish data from a different distribution. Overall, pruning helps make more robust predictions in the inference time. Additionally, other uncertainty metrics, including entropy and ambiguity, increased. This makes pruned and quantized deep ensembles more robust compared to the standard deep ensemble baseline.
6. Discussion
We empirically showed that applying pruning and quantization into the deep ensemble decreased the ensemble size and increased the uncertainty metrics while showing a slight accuracy loss depending on the sparsity level. Pruning with 25–75% sparsity and quantization successfully addresses the problem associated with the linear increase in the size of the deep ensemble and shows solid performance. However, pruning with 95% sparsity noticeably degrades the accuracy.
There is a tradeoff between insignificant accuracy degradation, uncertainty, and memory footprint metric improvements. The pruned and quantized deep ensemble makes a less confident prediction and generalizes well by increasing the uncertainty metrics. Thus, pruning and quantization require a deep ensemble applicable to memory-intensive tasks in Internet-of-Things or mobile devices, while increased uncertainty metrics make the deep ensemble more robust in distribution shift.
However, there is one drawback to such a simple pruning and quantization strategy: the training time increases as pruning, re-training, and quantization occur. Typically, re-training epochs are relatively fewer than training epochs from initialization. However, pruning after initialization should be studied further by applying the proposed strategy to real-world tasks because pruning after initialization could save retraining time. Given the successful performance of deep learning in various domains, many pre-trained models have become available, making transfer learning an interesting research topic. Moreover, creating a diverse deep ensemble by applying pruning with a pre-trained single model could be another possible research direction.
The sparse matrix decreases the multiplication numbers, thus saving energy by ignoring the multiplication in zero weights. Furthermore, decreasing the size and saving energy is the main problem in mobile devices because of the slowly increasing battery capacity to compare the processor or memory capacity. Therefore, the compressed deep ensemble is deployable to memory-intensive and uncertainty-aware tasks, and decreased multiplication helps in energy conservation.
Author Contributions
Conceptualization, U.D. and J.H.L.; methodology, U.D.; software, U.D.; validation, B.C., J.W.S. and J.H.L.; formal analysis, B.C.; investigation, J.W.S.; resources, U.D.; data curation, U.D.; writing—original draft preparation, U.D.; writing—review and editing, U.D., J.H.L.; visualization, U.D.; supervision, J.H.L.; project administration, J.H.L.; funding acquisition, J.H.L., B.C., J.W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Foundation (NRF) of Korea, grant number 2017R1D1A1B03028929, 2019R1F1A1062094, and NRF-2020R1F1A1069361. The NRF was funded by the Korean Ministry of Education & the Ministry of Science and ICT.
Acknowledgments
This research was supported by Basic Science Research Program through the NRF of Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning; Precup, D., Teh, Y.W., Eds.; Proceedings of Machine Learning Research; PMLR: Sydney, Australia, 2017; Volume 70, pp. 1321–1330. [Google Scholar]
- Schneider, J. Exploiting Model Uncertainty Estimates for Safe Dynamic Control Learning. In Advances in Neural Information Processing Systems; Mozer, M.C., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; Volume 9. [Google Scholar]
- Osband, I.; Aslanides, J.; Cassirer, A. Randomized Prior Functions for Deep Reinforcement Learning. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Osband, I.; Blundell, C.; Pritzel, A.; Roy, B.V. Deep Exploration via Bootstrapped DQN. In Proceedings of the 30th International Conference on Neural Information Processing Systems; NIPS’16; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 4033–4041. [Google Scholar]
- Lütjens, B.; Everett, M.; How, J.P. Safe Reinforcement Learning with Model Uncertainty Estimates. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8662–8668. [Google Scholar] [CrossRef]
- Hoel, C.-J.; Wolff, K.; Laine, L. Tactical Decision-Making in Autonomous Driving by Reinforcement Learning with Uncertainty Estimation. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1563–1569. [Google Scholar] [CrossRef]
- Clements, W.R.; Delft, B.V.; Robaglia, B.-M.; Slaoui, R.B.; Toth, S. Estimating Risk and Uncertainty in Deep Reinforcement Learning. arXiv 2019, arXiv:1905.09638. Available online: https://arxiv.org/abs/1905.09638 (accessed on 15 January 2021).
- Le, M.T.; Diehl, F.; Brunner, T.; Knol, A. Uncertainty Estimation for Deep Neural Object Detectors in Safety-Critical Applications. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 3873–3878. [Google Scholar]
- He, Y.; Zhu, C.; Wang, J.; Savvides, M.; Zhang, X. Bounding Box Regression with Uncertainty for Accurate Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2888–2897. [Google Scholar]
- Loquercio, A.; Segu, M.; Scaramuzza, D. A General Framework for Uncertainty Estimation in Deep Learning. IEEE Robot. Autom. Lett. 2020, 5, 3153–3160. [Google Scholar] [CrossRef]
- Meyer, G.P.; Thakurdesai, N. Learning an Uncertainty-Aware Object Detector for Autonomous Driving. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 10521–10527. [Google Scholar]
- Arnez, F.; Espinoza, H.; Radermacher, A.; Terrier, F. A Comparison of Uncertainty Estimation Approaches in Deep Learning Components for Autonomous Vehicle Applications. In Proceedings of the Workshop on Artificial Intelligence Safety 2020 co-located with the 29th International Joint Conference on Artificial Intelligence and the 17th Pacific Rim International Conference on Artificial Intelligence (IJCAI-PRICAI 2020), Yokohama, Japan, 11–12 January 2021; Espinoza, H., McDermid, J., Huang, X., Castillo-Effen, M., Chen, X.C., Hernández-Orallo, J., Éigeartaigh, S.Ó., Mallah, R., Eds.; CEUR Workshop Proceedings. CEUR-WS.org: Aachen, North Rhine-Westphalia, Germany, 2020; Volume 2640. [Google Scholar]
- Harakeh, A.; Smart, M.; Waslander, S.L. BayesOD: A Bayesian Approach for Uncertainty Estimation in Deep Object Detectors. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 87–93. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Ditlevsen, O. Aleatory or Epistemic? Does It Matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Neal, R. Bayesian Learning via Stochastic Dynamics. In Advances in Neural Information Processing Systems; Hanson, S., Cowan, J., Giles, C., Eds.; Morgan-Kaufmann: Burlington, MA, USA, 1993; Volume 5. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1613–1622. [Google Scholar]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? In Proceedings of the 31st International Conference on Neural Information Processing Systems; NIPS’17; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5580–5590. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning; Balcan, M.F., Weinberger, K.Q., Eds.; Proceedings of Machine Learning Research; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles. In Proceedings of the 31st International Conference on Neural Information Processing Systems; NIPS’17; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6405–6416. [Google Scholar]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.V.; Lakshminarayanan, B.; Snoek, J. Can You Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift. arXiv 2019, arXiv:1906.02530. Available online: https://arxiv.org/abs/1906.02530 (accessed on 15 January 2021).
- Fort, S.; Hu, H.; Lakshminarayanan, B. Deep Ensembles: A Loss Landscape Perspective. arXiv 2019, arXiv:1912.02757. Available online: https://arxiv.org/abs/1912.02757 (accessed on 15 January 2021).
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. A Survey of Model Compression and Acceleration for Deep Neural Networks. arXiv 2017, arXiv:1710.09282. Available online: https://arxiv.org/abs/1710.09282 (accessed on 15 January 2021).
- Tran, L.; Veeling, B.S.; Roth, K.; Świątkowski, J.; Dillon, J.V.; Snoek, J.; Mandt, S.; Salimans, T.; Nowozin, S.; Jenatton, R. Hydra: Preserving Ensemble Diversity for Model Distillation. arXiv 2020, arXiv:2001.04694. Available online: https://arxiv.org/abs/2001.04694 (accessed on 15 January 2021).
- Malinin, A.; Mlodozeniec, B.; Gales, M. Ensemble Distribution Distillation. arXiv 2019, arXiv:1905.00076. Available online: https://arxiv.org/abs/1905.00076 (accessed on 15 January 2021).
- Malinin, A.; Gales, M. Predictive Uncertainty Estimation via Prior Networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Hu, R.; Huang, Q.; Chang, S.; Wang, H.; He, J. The MBPEP: A Deep Ensemble Pruning Algorithm Providing High Quality Uncertainty Prediction. Appl. Intell. 2019. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:1510.00149. Available online: https://arxiv.org/abs/1510.00149 (accessed on 15 January 2021).
- Zhu, M.; Gupta, S. To Prune, or Not to Prune: Exploring the Efficacy of Pruning for Model Compression. arXiv 2017, arXiv:1710.01878. Available online: https://arxiv.org/abs/1710.01878 (accessed on 15 January 2021).
- Blalock, D.; Ortiz, J.J.G.; Frankle, J.; Guttag, J. What Is the State of Neural Network Pruning? arXiv 2020, arXiv:2003.03033. Available online: https://arxiv.org/abs/2003.03033 (accessed on 15 January 2021).
- Gao, S. A Discover of Class and Image Level Variance between Different Pruning Methods on Convolutional Neural Networks. In 2020 IEEE International Conference on Smart Internet of Things (SmartIoT); IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 176–182. [Google Scholar]
- Hooker, S.; Courville, A.; Clark, G.; Dauphin, Y.; Frome, A. What Do Compressed Deep Neural Networks Forget? arXiv 2019, arXiv:1911.05248. Available online: https://arxiv.org/abs/1911.05248 (accessed on 15 January 2021).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; p. 296. [Google Scholar]
- Nixon, J.; Lakshminarayanan, B.; Tran, D. Why Are Bootstrapped Deep Ensembles Not Better? In Proceedings of the 2020 Conference on Neural Information Processing Systems, Online Conference, Canada, 6–12 December 2020. [Google Scholar]
- Gustafsson, F.K.; Danelljan, M.; Schön, T.B. Evaluating Scalable Bayesian Deep Learning Methods for Robust Computer Vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Snowmass, CO, USA, 16–18 June 2020; pp. 318–319. [Google Scholar]
- Hubschneider, C.; Hutmacher, R.; Zöllner, J.M. Calibrating Uncertainty Models for Steering Angle Estimation. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1511–1518. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. arXiv 2020, arXiv:2011.06225. Available online: https://arxiv.org/abs/2011.06225 (accessed on 15 January 2021).
- Josiah, D.; Jason, Z.; Jeremy, O.; Samual, M.; Maciej, T. Quantifying Uncertainty in Deep Learning Systems. 2020. Available online: https://docs.aws.amazon.com/prescriptive-guidance/latest/ml-quantifying-uncertainty/welcome.html (accessed on 15 January 2021).
- Krogh, A.; Vedelsby, J. Neural Network Ensembles, Cross Validation and Active Learning. In Proceedings of the 7th International Conference on Neural Information Processing Systems; NIPS’94; MIT Press: Cambridge, MA, USA, 1994; pp. 231–238. [Google Scholar]
- LeCun, Y.; Cortes, C. MNIST Handwritten Digit Data–base. Available online: http://yann.lecun.com/exdb/mnist (accessed on 15 January 2021).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2016, arXiv:1603.04467. Available online: https://arxiv.org/abs/1603.04467 (accessed on 15 January 2021).
- Kaggle notMNIST Dataset. Available online: https://www.kaggle.com/lubaroli/notmnist (accessed on 15 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).