Improving the Estimation of Prediction Increment Measures in Logistic and Survival Analysis
Simple Summary
Abstract
1. Introduction
1.1. ΔAUC for Evaluating Discrimination Improvement
1.2. NRI, NRI > 0, and IDI: Definitions and Controversaries
1.3. Challenges in Estimation of Discrimination Improvement Measures
2. Methods
2.1. General Framework: Logistic Regression
2.2. General Framework: Time-to-Event Regression
2.3. Measures of Discrimination Improvement
2.3.1. AUC and Overall C
2.3.2. NRI, NRI > 0, and NRI(t)
2.3.3. IDI and IDI(t)
2.4. Confidence Interval Estimation
3. Simulation Study Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gail, M.H.; Brinton, L.A.; Byar, D.P.; Corle, D.K.; Green, S.B.; Schairer, C.; Mulvihill, J.J. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J. Natl. Cancer Inst. 1989, 81, 1879–1886. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Griffith, J.L.; Schmidt, C.H.; Terrin, N. Measures for evaluating model performance. In Proceedings of the Biometrics Section; American Statistical Association: Alexandria, VA, USA, 1997; pp. 253–258. [Google Scholar]
- Steyerberg, E.W. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating; Springer Science+Business Media: New York, NY, USA, 2010. [Google Scholar]
- Spiegelman, D.; Colditz, G.A.; Hunter, D.; Hertzmark, E. Validation of the Gail et al. model for predicting individual breast cancer risk. J. Natl. Cancer Inst. 1994, 86, 600–607. [Google Scholar] [CrossRef]
- Rockhill, B.; Spiegelman, D.; Byrne, C.; Hunter, D.J.; Colditz, G.A. Validation of the Gail et al. model of breast cancer risk prediction and implications for chemoprevention. J. Natl. Cancer Inst. 2001, 93, 358–366. [Google Scholar] [CrossRef]
- Nickson, C.; Procopio, P.; Velentzis, L.S.; Carr, S.; Devereux, L.; Mann, G.B.; James, P.; Lee, G.; Wellard, C.; Campbell, I. Prospective validation of the NCI Breast Cancer Risk Assessment Tool (Gail Model) on 40,000 Australian women. Breast Cancer Res. BCR 2018, 20, 155. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Singh, V.; Mehta, G. Assessment of common risk factors and validation of the Gail model for breast cancer: A hospital-based study from Western India. Tzu Chi Med. J. 2020, 32, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Harrell, F.E., Jr. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer: New York, NY, USA, 2001. [Google Scholar]
- Pepe, M.S.; Kerr, K.F.; Longton, G.; Wang, Z. Testing for improvement in prediction model performance. Stat. Med. 2013, 32, 1467–1482. [Google Scholar] [CrossRef] [PubMed]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’Agostino, R.B. Overall C as a measure of discrimination in survival analysis: Model specific population value and confidence interval estimation. Stat. Med. 2004, 23, 2109–2123. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’Agostino, R.B., Sr.; D’Agostino, R.B., Jr.; Vasan, R.S. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Stat. Med. 2008, 27, 157–212. [Google Scholar] [CrossRef]
- Greenland, P.; O’Malley, P.G. When is a new prediction marker useful? A consideration of lipoprotein-associated phospholipase A2 and C-reactive protein for stroke risk. Arch. Intern. Med. 2005, 165, 2454–2456. [Google Scholar] [CrossRef]
- Cook, N.R. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007, 115, 928–935. [Google Scholar] [CrossRef] [PubMed]
- Pencina, M.J.; D’Agostino, R.B., Sr.; Steyerberg, E.W. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat. Med. 2011, 30, 11–21. [Google Scholar] [CrossRef]
- Chambless, L.E.; Cummiskey, C.P.; Cui, G. Several methods to assess improvement in risk prediction models: Extension to survival analysis. Stat. Med. 2011, 30, 22–38. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.S. Problems with risk reclassification methods for evaluating prediction models. Am. J. Epidemiol. 2011, 173, 1327–1335. [Google Scholar] [CrossRef]
- Kerr, K.F.; Wang, Z.; Janes, H.; McClelland, R.L.; Psaty, B.M.; Pepe, M.S. Net reclassification indices for evaluating risk prediction instruments: A critical review. Epidemiology 2014, 25, 114–121. [Google Scholar] [CrossRef]
- Hilden, J.; Gerds, T.A. A note on the evaluation of novel biomarkers: Do not rely on integrated discrimination improvement and net reclassification index. Stat. Med. 2014, 33, 3405–3414. [Google Scholar] [CrossRef]
- Gerds, T.A.; Hilden, J. Calibration of models is not sufficient to justify NRI. Stat. Med. 2014, 33, 3419–3420. [Google Scholar] [CrossRef] [PubMed]
- Leening, M.J.; Steyerberg, E.W.; Van Calster, B.; D’Agostino, R.B., Sr.; Pencina, M.J. Net reclassification improvement and integrated discrimination improvement require calibrated models: Relevance from a marker and model perspective. Stat. Med. 2014, 33, 3415–3418. [Google Scholar] [CrossRef]
- McKeague, I.W.; Qian, M. An adaptive resampling test for detecting the presence of significant predictors. J. Am. Stat. Assoc. 2015, 110, 1422–1433. [Google Scholar] [CrossRef]
- Demler, O.V.; Pencina, M.J.; D’Agostino, R.B., Sr. Misuse of DeLong test to compare AUCs for nested models. Stat. Med. 2012, 31, 2577–2587. [Google Scholar] [CrossRef]
- Kerr, K.F.; McClelland, R.L.; Brown, E.R.; Lumley, T. Evaluating the incremental value of new biomarkers with integrated discrimination improvement. Am. J. Epidemiol. 2011, 174, 364–374. [Google Scholar] [CrossRef] [PubMed]
- Harrell, F.E., Jr.; Lee, K.L.; Mark, D.B. Multivariable prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 1996, 15, 361–387. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; Wiley: Hoboken, NJ, USA, 1980; pp. 70–118. [Google Scholar]
- Nam, B.H.; D’Agostino, R.B. Goodness-of-Fit Tests and Model Validity; Birkhauser: Boston, MA, USA, 2002; Chapter 20. [Google Scholar]
- Pencina, M.J.; Steyerberg, E.W.; D’Agostino, R.B., Sr. Net reclassification index at event rate: Properties and relationships. Stat. Med. 2017, 36, 4455–4467. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Efron, B. Nonparametric standard errors and confidence intervals (with discussions). Can. J. Stat. 1981, 9, 139–172. [Google Scholar] [CrossRef]
- Hall, P. Theoretical comparison of bootstrap confidence intervals. Ann. Stat. 1988, 16, 927–953. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury: Pacific Grove, CA, USA, 2002. [Google Scholar]


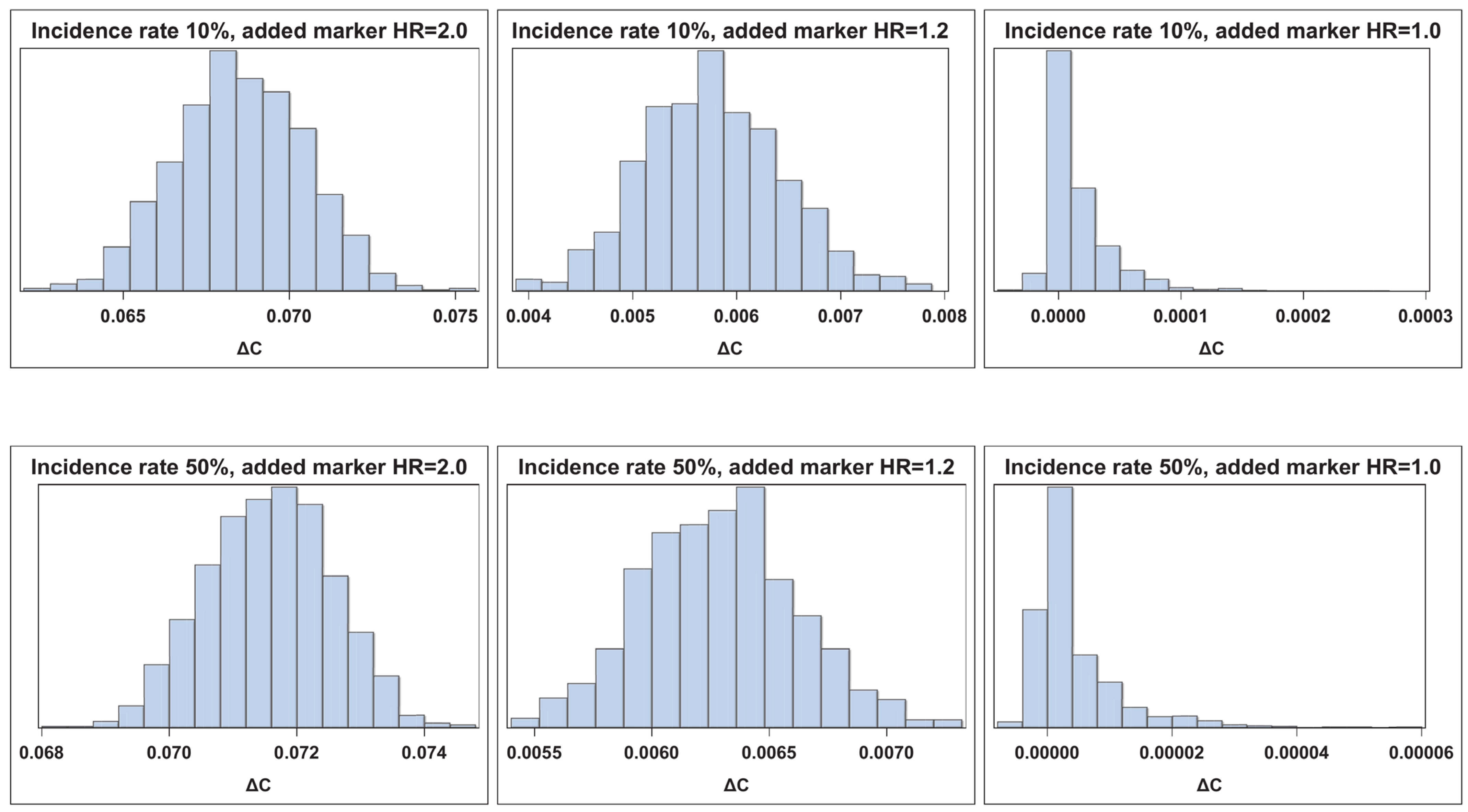
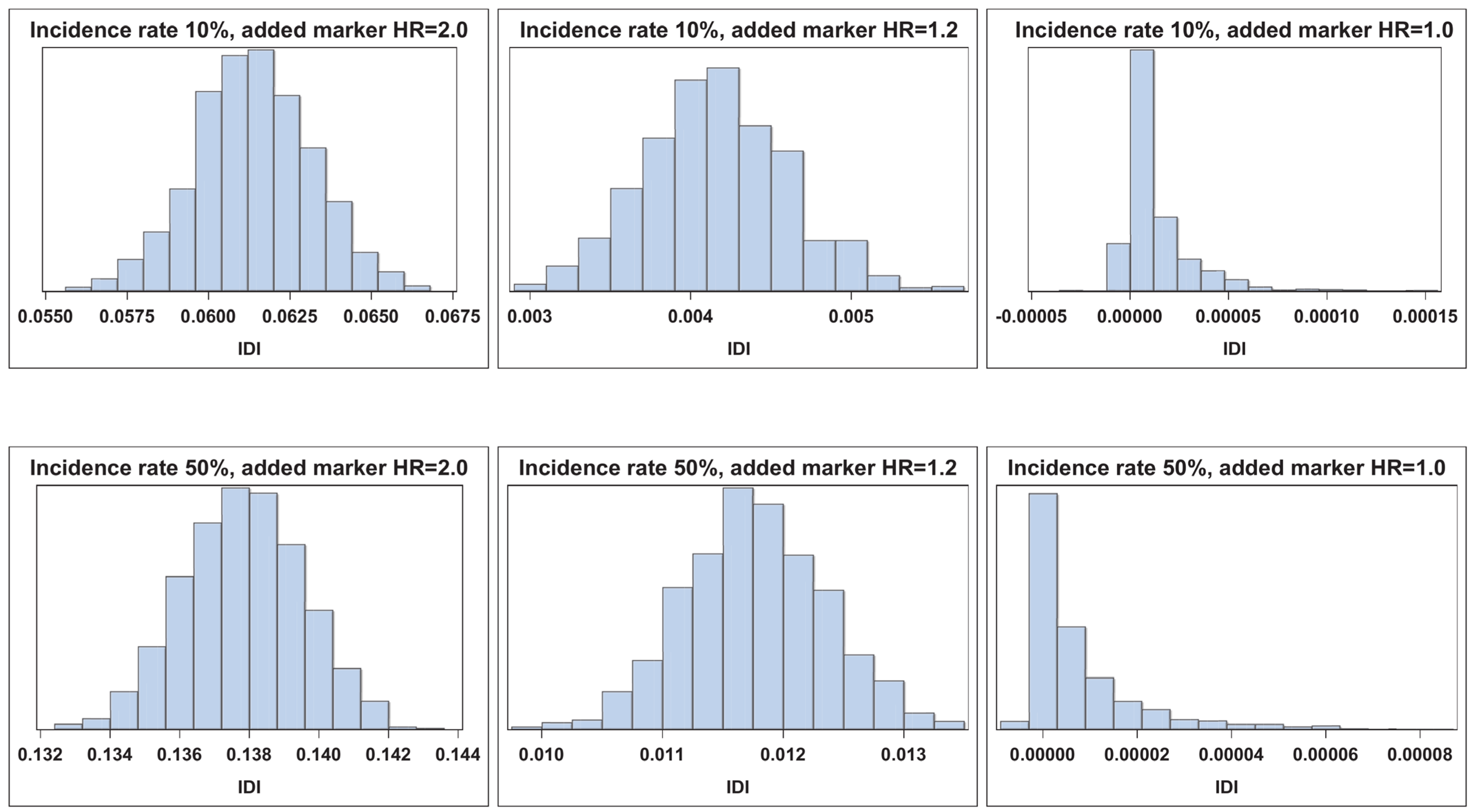
| n = 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strong New Marker (μY=1 = 0.8) | Moderate New Marker (μY=1 = 0.5) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 93.7 | 84.4 | 93.4 | 94.4 | 76.1 | 94.3 | 81.2 | 95.1 | 94.5 | 75.2 |
| Bias Corrected | 94.6 | 94.5 | 91.0 | 94.6 | 95.5 | 94.8 | 92.8 | 92.4 | 94.7 | 94.2 |
| Percentile | 94.7 | 97.0 | 97.5 | 95.5 | 95.4 | 94.7 | 97.4 | 99.1 | 96.2 | 94.0 |
| Bootstrap-t | 95.1 | 94.4 | 89.3 | 93.7 | 95.5 | 95.3 | 90.7 | 89.8 | 94.1 | 96.1 |
| Weak New Marker (μY=1 = 0.2) | Null New Marker (μY=1 = 0.0) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 90.6 | 86.4 | 93.5 | 95.4 | 71.0 | 100.0 | 94.6 | 94.1 | 95.8 | 94.0 |
| Bias Corrected | 93.3 | 88.0 | 87.6 | 93.8 | 92.7 | 98.4 | 90.5 | 89.7 | 96.0 | 95.5 |
| Percentile | 95.5 | 99.5 | 99.4 | 97.7 | 94.8 | 98.9 | 100.0 | 100.0 | 98.4 | 95.9 |
| Bootstrap-t | 87.4 | 84.8 | 83.6 | 88.7 | 87.9 | 98.6 | 88.1 | 86.0 | 90.0 | 98.4 |
| n = 300 | ||||||||||
| Strong New Marker (μY=1 = 0.8) | Moderate New Marker (μY=1 = 0.5) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 92.6 | 80.9 | 93.3 | 94.2 | 76.4 | 88.7 | 78.6 | 92.2 | 93.5 | 71.8 |
| Bias Corrected | 94.3 | 91.2 | 91.8 | 95.3 | 95.4 | 92.3 | 87.1 | 87.0 | 92.3 | 92.9 |
| Percentile | 94.4 | 97.6 | 99.2 | 97.2 | 94.9 | 95.9 | 99.1 | 99.7 | 98.4 | 94.8 |
| Bootstrap-t | 96.0 | 88.8 | 87.5 | 93.6 | 97.3 | 86.4 | 82.8 | 83.0 | 87.3 | 90.5 |
| Weak New Marker (μY=1 = 0.2) | Null New Marker (μY=1 = 0.0) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 88.4 | 79.1 | 91.8 | 96.4 | 75.3 | 99.5 | 89.9 | 93.2 | 93.9 | 96.8 |
| Bias Corrected | 91.0 | 83.1 | 85.5 | 89.7 | 85.6 | 98.4 | 88.0 | 87.4 | 94.6 | 94.5 |
| Percentile | 97.1 | 99.9 | 100.0 | 97.7 | 97.3 | 98.8 | 100.0 | 100.0 | 98.4 | 95.2 |
| Bootstrap-t | 86.1 | 85.0 | 82.8 | 82.2 | 73.3 | 96.9 | 89.7 | 86.7 | 89.0 | 97.8 |
| 3catNRI categories: [0.00, 0.05), [0.05, 0.20), and [0.20+). | ||||||||||
| 2catNRI categories: [0.00, 0.10) and [0.10+). | ||||||||||
| n = 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strong New Marker (μY=1 = 0.8) | Moderate New Marker (μY=1 = 0.5) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 95.5 | 89.7 | 93.8 | 95.7 | 70.4 | 94.5 | 90.4 | 93.9 | 93.6 | 69.9 |
| Bias Corrected | 95.5 | 94.2 | 94.2 | 96.3 | 96.0 | 94.2 | 93.6 | 93.0 | 94.4 | 94.4 |
| Percentile | 95.5 | 96.3 | 96.9 | 96.4 | 96.1 | 93.9 | 97.1 | 96.8 | 95.7 | 94.3 |
| Bootstrap-t | 95.5 | 93.4 | 93.4 | 94.5 | 96.6 | 94.6 | 91.7 | 91.2 | 94.5 | 95.2 |
| Weak New Marker (μY=1 = 0.2) | Null New Marker (μY=1 = 0.0) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 95.2 | 92.0 | 95.3 | 94.5 | 70.1 | 99.9 | 95.5 | 92.9 | 93.8 | 91.8 |
| Bias Corrected | 96.0 | 91.8 | 91.4 | 94.1 | 96.1 | 97.6 | 90.5 | 91.2 | 95.8 | 79.4 |
| Percentile | 95.4 | 99.6 | 99.3 | 96.1 | 95.8 | 97.8 | 100.0 | 100.0 | 98.0 | 78.4 |
| Bootstrap-t | 95.4 | 88.8 | 88.4 | 94.0 | 96.2 | 97.8 | 88.3 | 89.1 | 90.6 | 96.9 |
| n = 300 | ||||||||||
| Strong New Marker (μY=1 = 0.8) | Moderate New Marker (μY=1 = 0.5) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 94.4 | 89.8 | 96.1 | 93.8 | 71.7 | 93.1 | 89.8 | 95.0 | 94.3 | 71.4 |
| Bias Corrected | 94.9 | 93.5 | 94.0 | 94.0 | 94.3 | 94.9 | 90.6 | 91.5 | 94.9 | 94.5 |
| Percentile | 95.0 | 98.4 | 98.7 | 95.9 | 93.8 | 95.2 | 98.2 | 99.1 | 96.5 | 94.8 |
| Bootstrap-t | 95.9 | 91.0 | 90.7 | 93.7 | 96.1 | 95.6 | 88.6 | 88.0 | 94.4 | 96.4 |
| Weak New Marker (μY=1 = 0.2) | Null New Marker (μY=1 = 0.0) | |||||||||
| ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆AUC | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Asymptotic | 86.6 | 90.0 | 93.3 | 96.3 | 68.4 | 99.9 | 94.8 | 92.2 | 94.1 | 93.6 |
| Bias Corrected | 89.9 | 86.8 | 89.8 | 90.8 | 87.0 | 98.2 | 90.2 | 92.1 | 94.3 | 76.9 |
| Percentile | 98.8 | 100.0 | 100.0 | 99.1 | 98.1 | 98.4 | 100.0 | 100.0 | 97.3 | 72.1 |
| Bootstrap-t | 78.7 | 82.1 | 85.0 | 84.4 | 77.3 | 98.6 | 86.9 | 89.0 | 89.0 | 97.9 |
| 3catNRI categories: [0.00, 0.40), [0.40, 0.60), and [0.60+). | ||||||||||
| 2catNRI categories: [0.00, 0.50) and [0.50+). | ||||||||||
| n = 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strong New Marker (Adjusted HR = 2.0) | Moderate New Marker (Adjusted HR = 1.5) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 95.1 | 94.3 | 93.1 | 93.9 | 95.7 | 95.6 | 92.1 | 90.5 | 95.1 | 94.8 |
| Percentile | 95.2 | 96.9 | 98.4 | 95.5 | 95.8 | 95.3 | 97.5 | 98.4 | 96.5 | 94.8 |
| Bootstrap-t | 95.5 | 93.2 | 92.4 | 93.5 | 96.2 | 96.2 | 90.8 | 90.2 | 94.1 | 96.2 |
| Hybrid | 93.6 | 91.8 | 92.5 | 93.3 | 92.8 | 89.9 | 89.6 | 90.5 | 93.7 | 89.1 |
| Weak New Marker (Adjusted HR = 1.2) | Null New Marker (Adjusted HR = 1.0) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 93.2 | 86.0 | 89.2 | 92.5 | 93.2 | 98.3 | 89.1 | 90.1 | 95.0 | 91.2 |
| Percentile | 96.9 | 99.6 | 99.9 | 97.6 | 95.2 | 98.8 | 100.0 | 100.0 | 98.2 | 92.0 |
| Bootstrap-t | 91.7 | 85.2 | 86.9 | 91.7 | 95.0 | 97.9 | 84.9 | 85.1 | 91.9 | 98.7 |
| Hybrid | 75.7 | 86.8 | 90.0 | 91.1 | 76.6 | 100.0 | 94.2 | 90.9 | 90.7 | 100.0 |
| n = 300 | ||||||||||
| Strong New Marker (Adjusted HR = 2.0) | Moderate New Marker (Adjusted HR = 1.5) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 94.3 | 90.4 | 91.0 | 92.6 | 94.3 | 87.9 | 85.4 | 90.0 | 91.7 | 91.6 |
| Percentile | 94.2 | 97.8 | 99.2 | 97.1 | 94.5 | 95.6 | 99.7 | 99.8 | 98.9 | 96.7 |
| Bootstrap-t | 95.3 | 90.9 | 89.1 | 93.1 | 95.2 | 87.3 | 80.5 | 85.5 | 90.0 | 92.1 |
| Hybrid | 83.6 | 84.7 | 88.2 | 90.4 | 81.3 | 77.8 | 81.5 | 88.9 | 88.3 | 73.1 |
| Weak New Marker (Adjusted HR = 1.2) | Null New Marker (Adjusted HR = 1.0) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 92.6 | 82.5 | 89.1 | 89.2 | 84.5 | 98.5 | 85.7 | 84.3 | 93.4 | 84.8 |
| Percentile | 98.3 | 100.0 | 100.0 | 98.1 | 97.5 | 99.0 | 99.8 | 100.0 | 97.7 | 83.2 |
| Bootstrap-t | 82.1 | 73.3 | 79.0 | 87.3 | 82.2 | 96.9 | 78.1 | 77.9 | 90.8 | 95.2 |
| Hybrid | 92.4 | 91.0 | 87.9 | 86.5 | 66.3 | 99.7 | 93.3 | 84.1 | 89.6 | 99.7 |
| 3catNRI categories: [0.00, 0.05), [0.05, 0.20), and [0.20+). | ||||||||||
| 2catNRI categories: [0.00, 0.10) and [0.10+). | ||||||||||
| n = 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strong New Marker (Adjusted HR = 2.0) | Moderate New Marker (Adjusted HR = 1.5) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 95.6 | 94.1 | 95.2 | 94.5 | 94.5 | 95.0 | 93.4 | 92.9 | 94.5 | 95.7 |
| Percentile | 95.9 | 96.0 | 97.0 | 94.9 | 94.6 | 94.6 | 96.9 | 97.3 | 96.5 | 95.3 |
| Bootstrap-t | 95.7 | 93.4 | 95.3 | 94.2 | 94.7 | 94.9 | 93.0 | 92.6 | 94.8 | 95.4 |
| Hybrid | 95.9 | 93.8 | 95.0 | 94.3 | 94.2 | 94.0 | 93.2 | 92.7 | 94.9 | 95.0 |
| Weak New Marker (Adjusted HR = 1.2) | Null New Marker (Adjusted HR = 1.0) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 94.8 | 91.8 | 92.7 | 93.1 | 94.3 | 99.3 | 92.8 | 86.1 | 96.2 | 97.1 |
| Percentile | 94.8 | 98.2 | 99.1 | 94.9 | 94.4 | 99.4 | 100.0 | 100.0 | 98.5 | 97.9 |
| Bootstrap-t | 95.7 | 91.7 | 90.5 | 93.4 | 95.3 | 97.9 | 85.8 | 79.4 | 91.9 | 98.6 |
| Hybrid | 90.9 | 90.5 | 92.1 | 93.2 | 90.1 | 100.0 | 95.4 | 87.0 | 91.9 | 100.0 |
| n = 300 | ||||||||||
| Strong New Marker (Adjusted HR = 2.0) | Moderate New Marker (Adjusted HR = 1.5) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 95.2 | 92.7 | 92.8 | 94.9 | 95.0 | 95.4 | 92.5 | 93.4 | 93.9 | 94.8 |
| Percentile | 94.8 | 97.6 | 99.1 | 96.0 | 95.4 | 95.3 | 98.8 | 99.4 | 95.7 | 94.9 |
| Bootstrap-t | 95.1 | 92.9 | 91.6 | 94.5 | 95.2 | 95.8 | 92.5 | 91.9 | 93.9 | 96.3 |
| Hybrid | 93.3 | 92.0 | 91.8 | 94.1 | 92.6 | 88.3 | 91.3 | 92.3 | 93.6 | 88.5 |
| Weak New Marker (Adjusted HR = 1.2) | Null New Marker (Adjusted HR = 1.0) | |||||||||
| ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | ∆C | 3catNRI | 2catNRI | NRI > 0 | IDI | |
| Bias Corrected | 90.4 | 87.0 | 91.4 | 92.8 | 90.4 | 99.4 | 88.7 | 76.2 | 95.0 | 96.9 |
| Percentile | 98.0 | 99.8 | 99.9 | 98.9 | 96.8 | 99.5 | 100.0 | 100.0 | 98.6 | 97.6 |
| Bootstrap-t | 86.8 | 85.3 | 86.2 | 91.7 | 90.3 | 97.9 | 77.0 | 67.7 | 91.5 | 98.2 |
| Hybrid | 80.2 | 89.6 | 89.3 | 91.4 | 73.1 | 99.9 | 93.6 | 74.2 | 91.2 | 100.0 |
| 3catNRI categories: [0.00, 0.40), [0.40, 0.60), and [0.60+). | ||||||||||
| 2catNRI categories: [0.00, 0.50) and [0.50+). | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enserro, D.M.; Miller, A. Improving the Estimation of Prediction Increment Measures in Logistic and Survival Analysis. Cancers 2025, 17, 1259. https://doi.org/10.3390/cancers17081259
Enserro DM, Miller A. Improving the Estimation of Prediction Increment Measures in Logistic and Survival Analysis. Cancers. 2025; 17(8):1259. https://doi.org/10.3390/cancers17081259
Chicago/Turabian StyleEnserro, Danielle M., and Austin Miller. 2025. "Improving the Estimation of Prediction Increment Measures in Logistic and Survival Analysis" Cancers 17, no. 8: 1259. https://doi.org/10.3390/cancers17081259
APA StyleEnserro, D. M., & Miller, A. (2025). Improving the Estimation of Prediction Increment Measures in Logistic and Survival Analysis. Cancers, 17(8), 1259. https://doi.org/10.3390/cancers17081259







