Deep Learning: A Heuristic Three-Stage Mechanism for Grid Searches to Optimize the Future Risk Prediction of Breast Cancer Metastasis Using EHR-Based Clinical Data
Simple Summary
Abstract
1. Introduction
2. Methods
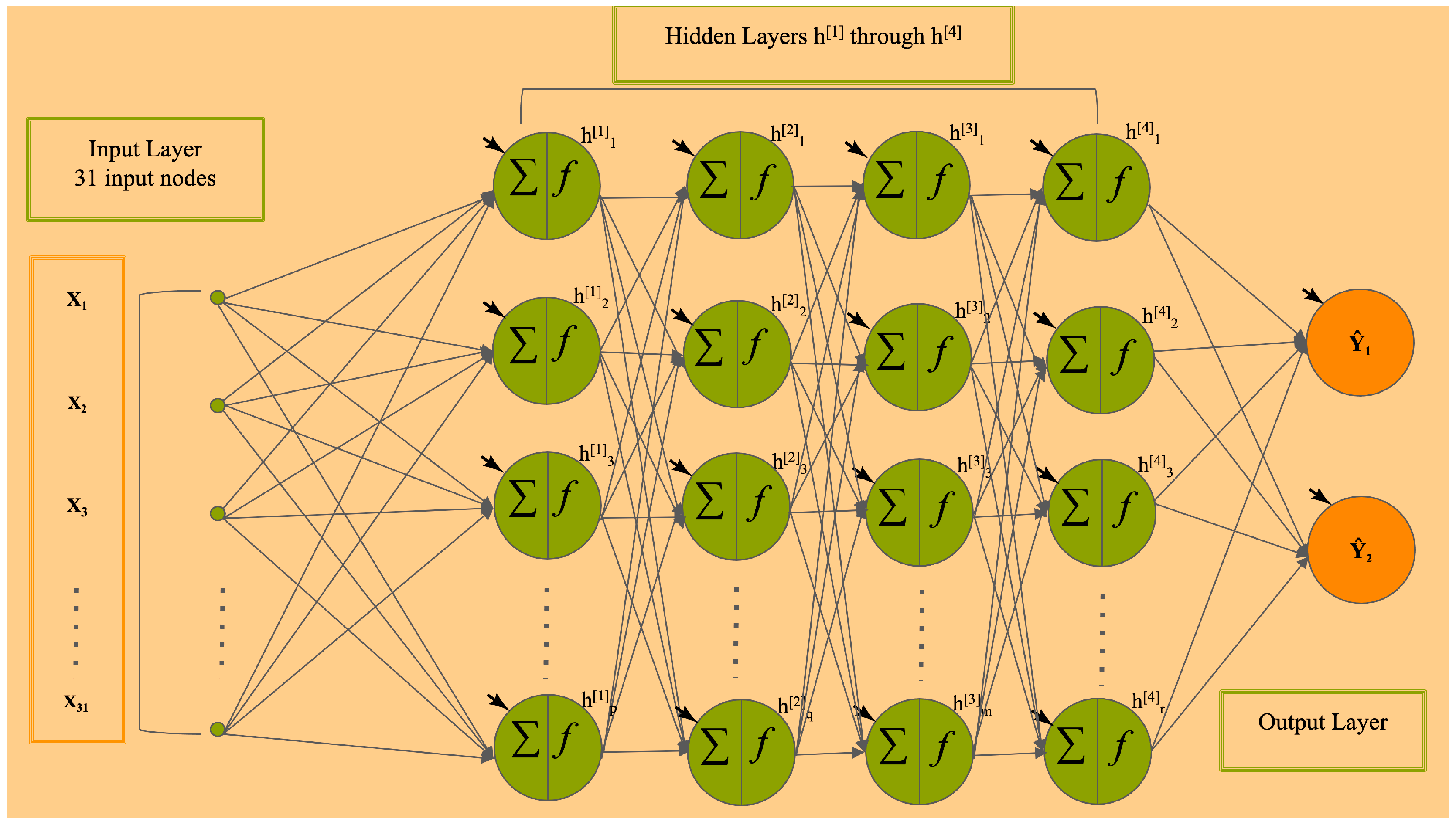
2.1. The DFNN Models
2.2. Datasets
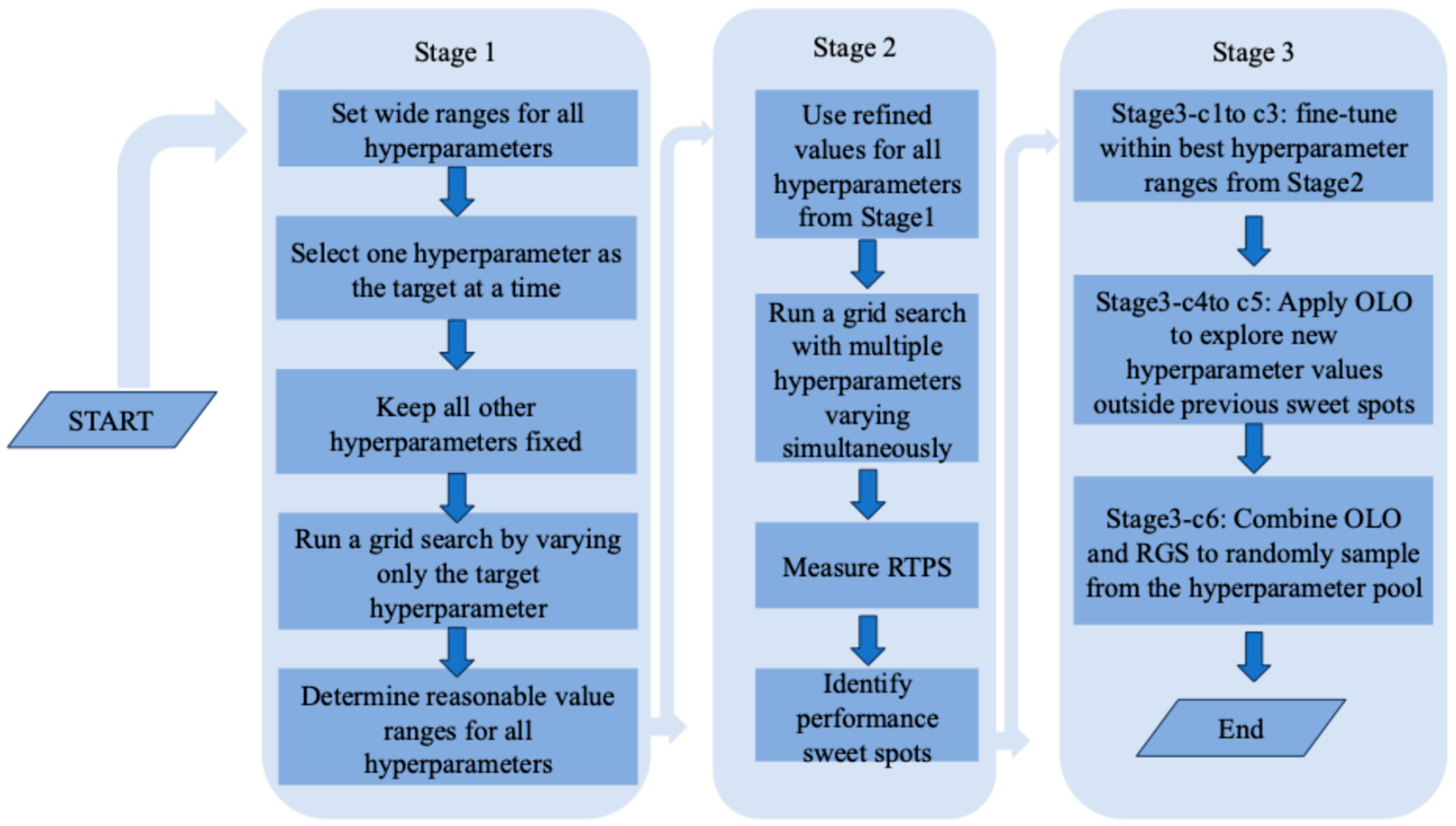
2.3. The Three-Stage Grid Search Mechanism and the Experiments
2.4. Prediction Performance Metrics and the 5-Fold Cross Validation Process
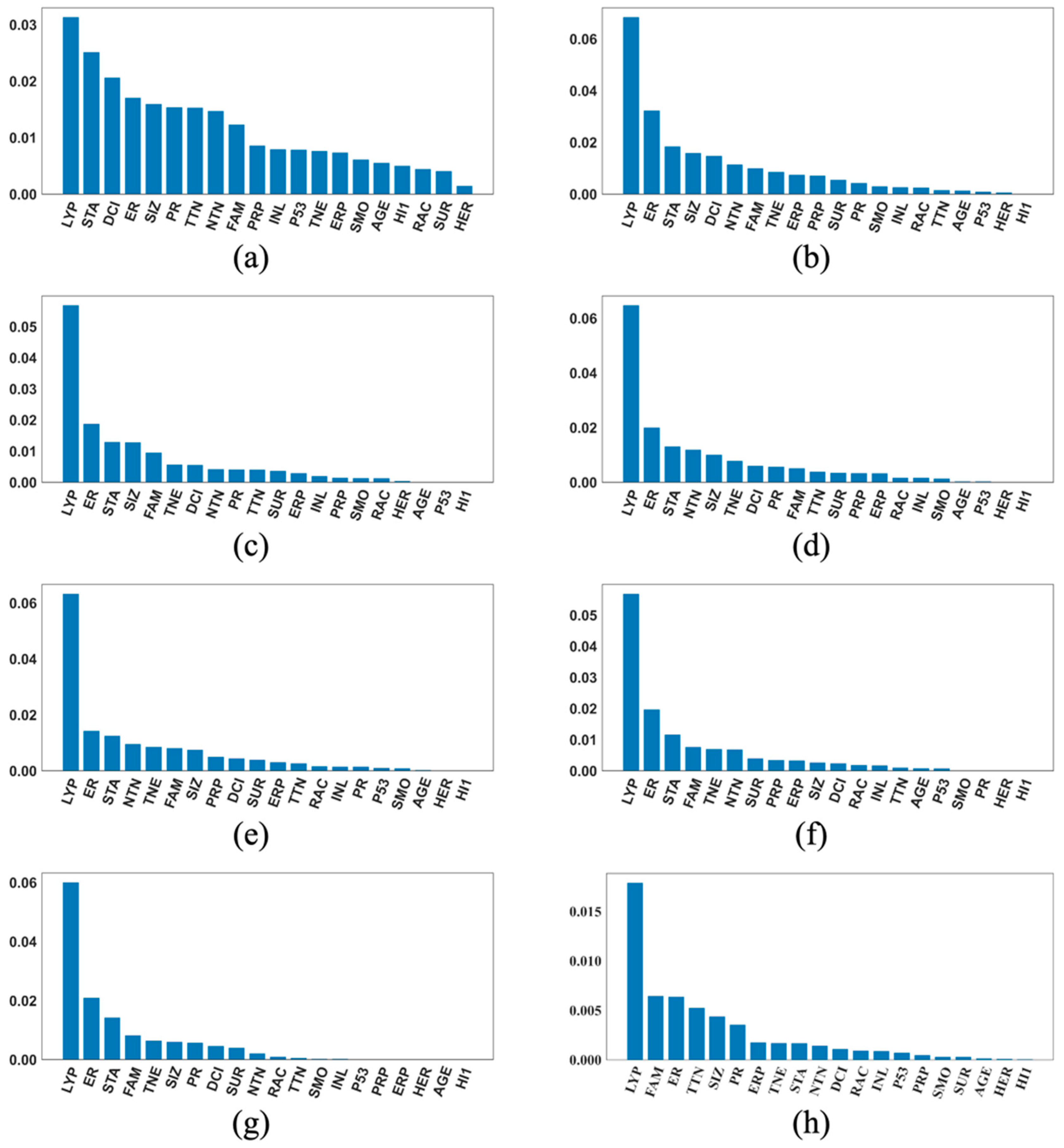
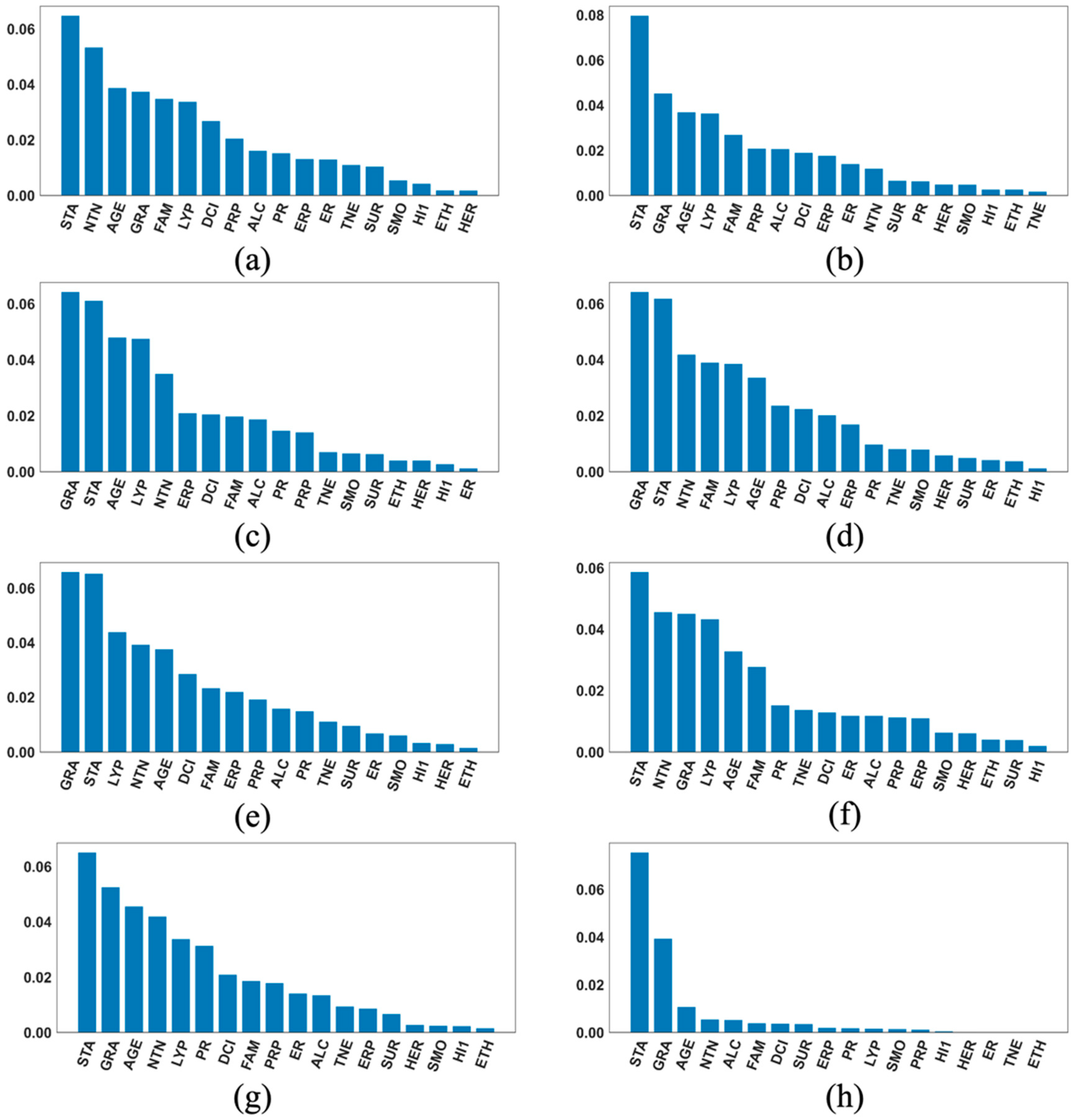
2.5. The SHAP Values and Plots
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gupta, G.P.; Massagué, J. Cancer Metastasis: Building a Framework. Cell 2006, 127, 679–695. [Google Scholar]
- Jiang, X.; Wells, A.; Brufsky, A.; Neapolitan, R. A Clinical Decision Support System Learned from Data to Personalize Treatment Recommendations towards Preventing Breast Cancer Metastasis. PLoS ONE 2019, 14, e0213292. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [PubMed]
- Jiang, X.; Xu, C. Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data. J. Clin. Med. 2022, 11, 5772. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Schwing, A.G.; Yuille, A.L.; Urtasun, R. Learning Deep Structured Models. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6–11 July 2015; Volume 3. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT: Cambridge, MA, USA, 2016. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning Bible. Healthc. Inform. Res. 2016, 22, 351–354. [Google Scholar]
- Cai, B.; Jiang, X. Computational Methods for Ubiquitination Site Prediction Using Physicochemical Properties of Protein Sequences. BMC Bioinform. 2016, 17, 116. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Cai, B.; Xue, D.; Lu, X.; Cooper, G.F.; Neapolitan, R.E. A Comparative Analysis of Methods for Predicting Clinical Outcomes Using High-Dimensional Genomic Datasets. J. Am. Med. Inform. Assoc. 2014, 21, e312–e319. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; RegGoodfellow, I.; Bengio, Y.; Courville, A. Regularization for Deep Learning. In Deep Learning; MIT Press: Cambridge, MA, USA, 2016; pp. 216–261. [Google Scholar]
- Brownlee, J. How to Choose Loss Functions When Training Deep Learning Neural Networks; Machine Learning Mastery: Santa Monica, CA, USA, 2019. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Ghojogh, B.; Crowley, M. The Theory Behind Overfitting, Cross Validation, Regularization, Bagging, and Boosting: Tutorial. arXiv 2019, arXiv:1905.12787. [Google Scholar]
- Jiang, X.; Neapolitan, R.E. Evaluation of a Two-Stage Framework for Prediction Using Big Genomic Data. Brief. Bioinform. 2015, 16, 912–921. [Google Scholar] [CrossRef]
- Cai, B.; Jiang, X. A Novel Artificial Neural Network Method for Biomedical Prediction Based on Matrix Pseudo-Inversion. J. Biomed. Inform. 2014, 48, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; Volume 9. [Google Scholar]
- Kim, L.S. Understanding the Difficulty of Training Deep Feedforward Neural Networks Xavier. In Proceedings of the International Joint Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; Volume 2. [Google Scholar]
- Xu, C.; Coen-Pirani, P.; Jiang, X. Empirical Study of Overfitting in Deep Learning for Predicting Breast Cancer Metastasis. Cancers 2023, 15, 1969. [Google Scholar] [CrossRef] [PubMed]
- Ngoc, T.T.; van Dai, L.; Phuc, D.T. Grid Search of Multilayer Perceptron Based on the Walk-Forward Validation Methodology. Int. J. Electr. Comput. Eng. 2021, 11, 1742–1751. [Google Scholar] [CrossRef]
- Siji George, C.G.; Sumathi, B. Grid Search Tuning of Hyperparameters in Random Forest Classifier for Customer Feedback Sentiment Prediction. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 173–178. [Google Scholar] [CrossRef]
- Michel, A.; Ro, V.; McGuinness, J.E.; Mutasa, S.; Terry, M.B.; Tehranifar, P.; May, B.; Ha, R.; Crew, K.D. Breast cancer risk prediction combining a convolutional neural network-based mammographic evaluation with clinical factors. Breast Cancer Res. Treat. 2023, 200, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Hamedi, S.Z.; Emami, H.; Khayamzadeh, M.; Rabiei, R.; Aria, M.; Akrami, M.; Zangouri, V. Application of machine learning in breast cancer survival prediction using a multimethod approach. Sci. Rep. 2024, 14, 30147. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Akselrod-Ballin, A.; Chorev, M.; Shoshan, Y.; Spiro, A.; Hazan, A.; Melamed, R.; Barkan, E.; Herzel, E.; Naor, S.; Karavani, E.; et al. Predicting Breast Cancer by Applying Deep Learning to Linked Health Records and Mammograms. Radiology 2019, 292, 331–342. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Farley, B.G.; Clark, W.A. Simulation of Self-Organizing Systems by Digital Computer. IRE Prof. Group Inf. Theory 1954, 4, 76–84. [Google Scholar] [CrossRef]
- Neapolitan, R.E.; Jiang, X. Neural Networks and Deep Learning. In Artificial Intelligence; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 389–411. [Google Scholar]
- Ran, L.; Zhang, Y.; Zhang, Q.; Yang, T. Convolutional Neural Network-Based Robot Navigation Using Uncalibrated Spherical Images. Sensors 2017, 17, 1341. [Google Scholar] [CrossRef]
- Deng, L.; Tur, G.; He, X.; Hakkani-Tur, D. Use of Kernel Deep Convex Networks and End-to-End Learning for Spoken Language Understanding. In Proceedings of the 2012 IEEE Workshop on Spoken Language Technology, SLT 2012—Proceedings, Miami, FL, USA, 2–5 December 2012. [Google Scholar]
- Fernández, S.; Graves, A.; Schmidhuber, J. An Application of Recurrent Neural Networks to Discriminative Keyword Spotting. In Artificial Neural Networks—ICANN 2007; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2007; Volume 4669 LNCS. [Google Scholar]
- Naik, N.; Madani, A.; Esteva, A.; Keskar, N.S.; Press, M.F.; Ruderman, D.; Agus, D.B.; Socher, R. Deep Learning-Enabled Breast Cancer Hormonal Receptor Status Determination from Base-Level H&E Stains. Nat. Commun. 2020, 11, 5727. [Google Scholar] [CrossRef] [PubMed]
- Min, S.; Lee, B.; Yoon, S. Deep Learning in Bioinformatics. Brief. Bioinform. 2017, 18, 851–869. [Google Scholar]
- Lundervold, A.S.; Lundervold, A. An Overview of Deep Learning in Medical Imaging Focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.W.; Huang, C.S.; Shih, C.C.; Chang, R.F. Axillary Lymph Node Metastasis Status Prediction of Early-Stage Breast Cancer Using Convolutional Neural Networks. Comput. Biol. Med. 2021, 130, 104206. [Google Scholar] [CrossRef]
- Papandrianos, N.; Papageorgiou, E.; Anagnostis, A.; Feleki, A. A Deep-Learning Approach for Diagnosis of Metastatic Breast Cancer in Bones from Whole-Body Scans. Appl. Sci. 2020, 10, 997. [Google Scholar] [CrossRef]
- Zhou, L.Q.; Wu, X.L.; Huang, S.Y.; Wu, G.G.; Ye, H.R.; Wei, Q.; Bao, L.Y.; Deng, Y.B.; Li, X.R.; Cui, X.W.; et al. Lymph Node Metastasis Prediction from Primary Breast Cancer US Images Using Deep Learning. Radiology 2020, 294, 19–28. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A Survey on Deep Learning in Medical Image Analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar]
- Mohanty, S.P.; Hughes, D.P.; Salathé, M. Using Deep Learning for Image-Based Plant Disease Detection. Front. Plant Sci. 2016, 7, 1419. [Google Scholar] [CrossRef]
- Shen, H. Towards a Mathematical Understanding of the Difficulty in Learning with Feedforward Neural Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Jiang, X.; Wells, A.; Brufsky, A.; Shetty, D.; Shajihan, K.; Neapolitan, R.E. Leveraging Bayesian Networks and Information Theory to Learn Risk Factors for Breast Cancer Metastasis. BMC Bioinform. 2020, 21, 298. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Shapley, L.S. Notes on the N-Person Game II: The Value of an n-Person Game; Rand Corporation Research Memoranda; RM-670; Rand Corporation: Santa Monica, CA, USA, 1951. [Google Scholar]
- Shapley, L.S. The Value of an N-Person Game. Contributions to the Theory of Games (AM-28), Volume II. In Classics in Game Theory; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the NAACL-HLT 2016—2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Proceedings of the Demonstrations Session, San Diego, CA, USA, 12–17 June 2016. [Google Scholar]
- Wishart, G.C.; Bajdik, C.D.; Dicks, E.; Provenzano, E.; Schmidt, M.K.; Sherman, M.; Greenberg, D.C.; Green, A.R.; Gelmon, K.A.; Kosma, V.M.; et al. PREDICT Plus: Development and validation of a prognostic model for early breast cancer that includes HER2. Br. J. Cancer 2012, 107, 800–807. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Baade, P.D.; Fowler, H.; Kou, K.; Dunn, J.; Chambers, S.K.; Pyke, C.; Aitken, J.F. A prognostic survival model for women diagnosed with invasive breast cancer in Queensland, Australia. Breast Cancer Res. Treat. 2022, 195, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Soerjomataram, I.; Louwman, M.W.; Ribot, J.G.; Roukema, J.A.; Coebergh, J.W. An overview of prognostic factors for long-term survivors of breast cancer. Breast Cancer Res. Treat. 2008, 107, 309–330. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Pan, H.; Gray, R.; Braybrooke, J.; Davies, C.; Taylor, C.; McGale, P.; Peto, R.; Pritchard, K.I.; Bergh, J.; Dowsett, M.; et al. 20-year risks of breast-cancer recurrence after stopping endocrine therapy at 5 years. N. Engl. J. Med. 2017, 377, 1836–1846. [Google Scholar] [CrossRef] [PubMed]
- Sang, Y.; Yang, B.; Mo, M.; Liu, S.; Zhou, X.; Chen, J.; Hao, S.; Huang, X.; Liu, G.; Shao, Z.; et al. Treatment and survival outcomes in older women with primary breast cancer: A retrospective propensity score-matched analysis. Breast 2022, 66, 24–30. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
| Hyperparameter Name Acronym * | NHL | NHN | AF | FI | O | LR | M | ID | DR | E | BS | L1 | L2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Values | 4 | 22 | 4 | 5 | 5 | 10 | 4 | 11 | 3 | 12 | 11 | 10 | 10 |
| Total # of Cases | # Positive Cases | # Negative Cases | # of Predictors | |
|---|---|---|---|---|
| LSM-RF-5year | 4189 | 437 | 3752 | 20 |
| LSM-RF-10year | 1827 | 572 | 1255 | 18 |
| LSM-RF-15year | 751 | 608 | 143 | 17 |
| Hyperparameter | Description | Values |
|---|---|---|
| Number of hidden layers | The depth of a DNN | 1, 2, 3, 4 |
| Number of hidden nodes in a hidden layer | Number of neurons in a hidden layer | 1–1005 |
| Activation function | It determines the value to be passed to the next node based on the value of the current node | Relu, Sigmoid, Softmax, Tanh |
| Kernel initializer | Assigning initial values to the internal model parameters | Constant, Glorot_normal, Glorot_uniform, He_normal, He_uniform |
| Optimizer | Optimizes internal model parameters towards minimizing the loss | SGD, Adam, Adagrad, Nadam, Adamax |
| Learning rate | Used by both SGD and Adagrad | 0.001~0.3 |
| Momentum | Smooths out the curve of gradients by moving average. Used by SGD. | 0~0.9 |
| Iteration-based decay | Iteration-based decay; updating learning rate by a decreasing factor in each epoch | 0~0.1 |
| Dropout rate | Manage overfitting and training time by randomly selecting nodes to ignore | 0~0.5 |
| Epochs | Number of times model is trained by each of the training set samples exactly one | 5~2000 |
| Batch_size | Unit number of samples fed to the optimizer before updating weights | 1 to the # of datapoints in a dataset |
| L1 | Sparsity regularization; | 0~0.03 |
| L2 | Weight decay regularization: it penalizes large weights to adjust the weight updating step | 0~0.2 |
| Group | Results | Stage1 | Stage2 | Stage3-c1 | Stage3-c2 | Stage3-c3 | Stage3-c4 | Stage3-c5 | Stage3-c6 |
|---|---|---|---|---|---|---|---|---|---|
| Top1 | best | 0.75301 | 0.74812 | 0.75024 | 0.75066 | 0.75418 | 0.75386 | 0.75250 | 0.75825 |
| Top5 | Avg | 0.75225 | 0.74725 | 0.74894 | 0.74980 | 0.75344 | 0.75260 | 0.75219 | 0.75532 |
| Top 10 | Avg | 0.75144 | 0.74682 | 0.74658 | 0.74923 | 0.75274 | 0.75179 | 0.75194 | 0.75435 |
| Top 50 | Avg | 0.74852 | 0.7456 | 0.74658 | 0.74767 | 0.75114 | 0.75031 | 0.75091 | 0.75206 |
| Top 100 | Avg | 0.74692 | 0.7449 | 0.74584 | 0.74704 | 0.75044 | 0.74956 | 0.75038 | 0.75122 |
| All | Avg | 0.66456 | 0.6839 | 0.72096 | 0.73505 | 0.73657 | 0.72052 | 0.71997 | 0.63960 |
| Group | Results | Stage1 | Stage2 | Stage3-c1 | Stage3-c2 | Stage3-c3 | Stage3-c4 | Stage3-c5 | Stage3-c6 |
|---|---|---|---|---|---|---|---|---|---|
| Top1 | best | 0.77789 | 0.78280 | 0.78802 | 0.79023 | 0.79152 | 0.78885 | 0.78059 | 0.78564 |
| Top5 | Avg | 0.77593 | 0.78141 | 0.78696 | 0.78897 | 0.79030 | 0.78762 | 0.77936 | 0.78272 |
| Top10 | Avg | 0.77511 | 0.78090 | 0.78626 | 0.78820 | 0.78980 | 0.78703 | 0.77889 | 0.78189 |
| Top50 | Avg | 0.77348 | 0.77942 | 0.78475 | 0.78644 | 0.78865 | 0.78553 | 0.77731 | 0.77992 |
| Top100 | Avg | 0.77257 | 0.77866 | 0.78402 | 0.78551 | 0.78797 | 0.78483 | 0.77652 | 0.77900 |
| All | Avg | 0.71344 | 0.73360 | 0.76124 | 0.75901 | 0.76702 | 0.76194 | 0.74336 | 0.68075 |
| Group | Results | Stage1 | Stage2 | Stage3-c1 | Stage3-c2 | Stage3-c3 | Stage3-c4 | Stage3-c5 | Stage3-c6 |
|---|---|---|---|---|---|---|---|---|---|
| Top1 | best | 0.86502 | 0.86548 | 0.88023 | 0.87463 | 0.87359 | 0.87551 | 0.87255 | 0.86657 |
| Top5 | Avg | 0.86232 | 0.86403 | 0.87632 | 0.87397 | 0.87337 | 0.87476 | 0.87095 | 0.86578 |
| Top 10 | Avg | 0.86105 | 0.86294 | 0.87426 | 0.87353 | 0.87280 | 0.87427 | 0.87028 | 0.86510 |
| Top 50 | Avg | 0.85806 | 0.86069 | 0.87073 | 0.87149 | 0.87082 | 0.87281 | 0.86872 | 0.86271 |
| Top 100 | Avg | 0.85678 | 0.85966 | 0.86950 | 0.87055 | 0.86954 | 0.87199 | 0.86789 | 0.86170 |
| All | Avg | 0.76512 | 0.78853 | 0.83167 | 0.84535 | 0.83399 | 0.83782 | 0.83731 | 0.75042 |
| Stage1 | Stage2 | Stage3-c1 | Stage3-c2 | Stage3-c3 | Stage3-c4 | Stage3-c5 | Stage3-c6 | ||
|---|---|---|---|---|---|---|---|---|---|
| 5 Y | Best-mean | 0.75301 | 0.74812 | 0.75024 | 0.75066 | 0.75418 | 0.75386 | 0.75250 | 0.75825 |
| Mid-point | 0.62650 | 0.62406 | 0.62512 | 0.62533 | 0.62709 | 0.62693 | 0.62625 | 0.62913 | |
| CHS | 39,112 | 510,494 | 203,991 | 101,250 | 202,500 | 404,726 | 408,625 | 43,035 | |
| TNS | 52,042 | 582,471 | 202,500 | 101,250 | 202,500 | 405,000 | 409,050 | 70,568 | |
| CHS/TNS | 0.75155 | 0.87643 | 0.99946 | 1.0 | 1.0 | 0.99932 | 0.99896 | 0.60984 | |
| Avg-mean | 0.71116 | 0.70278 | 0.72102 | 0.73505 | 0.73657 | 0.72059 | 0.72010 | 0.70415 | |
| 10 Y | Best_mean | 0.77789 | 0.78280 | 0.78802 | 0.79023 | 0.79152 | 0.78885 | 0.78059 | 0.78564 |
| Mid_point | 0.63895 | 0.64140 | 0.64401 | 0.64512 | 0.64576 | 0.64442 | 0.64029 | 0.64282 | |
| CHS | 48,517 | 635,770 | 202,500 | 60,750 | 202,495 | 405,000 | 404,994 | 83,896 | |
| TNS | 52,416 | 638,244 | 202,500 | 60,750 | 202,500 | 405,000 | 405,000 | 105,500 | |
| CHS/TNS | 0.92561 | 0.99612 | 1.0 | 1.0 | 0.99998 | 1.0 | 0.99999 | 0.79522 | |
| Avg_mean | 0.72116 | 0.73400 | 0.76124 | 0.75901 | 0.76702 | 0.76194 | 0.74337 | 0.72642 | |
| 15 Y | Best_mean | 0.86502 | 0.86548 | 0.88023 | 0.87463 | 0.87359 | 0.87551 | 0.87255 | 0.86657 |
| Mid_point | 0.68251 | 0.68274 | 0.69011 | 0.68731 | 0.68679 | 0.68776 | 0.68628 | 0.68328 | |
| CHS | 41,065 | 952,677 | 337,492 | 162,000 | 270,000 | 2,058,750 | 405,000 | 73,007 | |
| TNS | 52,090 | 1,048,575 | 337,500 | 162,000 | 270,000 | 2,058,750 | 405,000 | 93,000 | |
| CHS/TNS | 0.78835 | 0.90854 | 0.99998 | 1.0 | 1.0 | 1.0 | 1.0 | 0.78502 | |
| Avg_mean | 0.800615 | 0.80289 | 0.83167 | 0.84535 | 0.83399 | 0.83782 | 0.83731 | 0.81619 |
| Stage | 5-Year | 10-Year | 15-Year | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RTPS | TNS | TRT | RTPS | TNS | TRT | RTPS | TNS | TRT | |
| Stage1 | 42.42 | 52,042 | 613.23 | 26.57 | 52,416 | 386.87 | 20.06 | 52,090 | 290.25 |
| Stage2 | 5.65 | 582,471 | 914.72 | 3.36 | 638,244 | 594.86 | 2.49 | 1,048,575 | 725.06 |
| Stage3-c1 | 10.65 | 202,500 | 599.01 | 3.55 | 202,500 | 199.42 | 2.43 | 337,500 | 227.39 |
| Stage3-c2 | 11.97 | 101,250 | 336.54 | 5.49 | 60,750 | 92.66 | 1.63 | 162,000 | 73.17 |
| Stage3-c3 | 11.11 | 202,500 | 624.88 | 6.50 | 202,500 | 365.77 | 1.25 | 270,000 | 93.60 |
| Stage3-c4 | 25.46 | 405,000 | 2863.73 | 7.66 | 405,000 | 861.75 | 1.89 | 2,058,750 | 1080.01 |
| Stage3-c5 | 66.80 | 409,050 | 7590.07 | 29.44 | 405,000 | 3311.76 | 12.22 | 398,252 | 1352.36 |
| Stage3-c6 | 116.40 | 70,568 | 2281.77 | 51.05 | 105,500 | 1495.91 | 27.36 | 93,000 | 706.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Zhou, Y.; Xu, C.; Brufsky, A.; Wells, A. Deep Learning: A Heuristic Three-Stage Mechanism for Grid Searches to Optimize the Future Risk Prediction of Breast Cancer Metastasis Using EHR-Based Clinical Data. Cancers 2025, 17, 1092. https://doi.org/10.3390/cancers17071092
Jiang X, Zhou Y, Xu C, Brufsky A, Wells A. Deep Learning: A Heuristic Three-Stage Mechanism for Grid Searches to Optimize the Future Risk Prediction of Breast Cancer Metastasis Using EHR-Based Clinical Data. Cancers. 2025; 17(7):1092. https://doi.org/10.3390/cancers17071092
Chicago/Turabian StyleJiang, Xia, Yijun Zhou, Chuhan Xu, Adam Brufsky, and Alan Wells. 2025. "Deep Learning: A Heuristic Three-Stage Mechanism for Grid Searches to Optimize the Future Risk Prediction of Breast Cancer Metastasis Using EHR-Based Clinical Data" Cancers 17, no. 7: 1092. https://doi.org/10.3390/cancers17071092
APA StyleJiang, X., Zhou, Y., Xu, C., Brufsky, A., & Wells, A. (2025). Deep Learning: A Heuristic Three-Stage Mechanism for Grid Searches to Optimize the Future Risk Prediction of Breast Cancer Metastasis Using EHR-Based Clinical Data. Cancers, 17(7), 1092. https://doi.org/10.3390/cancers17071092







